Research Article
The Motion of a Neutrally Buoyant Ellipsoid Inside Square Tube Flows
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 233-249
-
- Article
- Export citation
New Conservative Finite Volume Element Schemes for the Modified Regularized Long Wave Equation
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 250-271
-
- Article
- Export citation
A-Posteriori Error Estimates for Uniform p-Version Finite Element Methods in Square
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 272-281
-
- Article
- Export citation
A New Family of Difference Schemes for Space Fractional Advection Diffusion Equation
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 282-306
-
- Article
- Export citation
Hill-Climbing Algorithm with a Stick for Unconstrained Optimization Problems
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 307-323
-
- Article
- Export citation
Robust Semi-Discrete and Fully Discrete Hybrid Stress Finite Element Methods for Elastodynamic Problems
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 324-348
-
- Article
- Export citation
Numerical Prediction of Natural Convection Flow in the Presence of Weak Magnetic Prandtl Number and Strong Magnetic Field with Algebraic Decay in Mainstream Velocity
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 349-361
-
- Article
- Export citation
Analysis of Solving Galerkin Finite Element Methods with Symmetric Pressure Stabilization for the Unsteady Navier-Stokes Equations Using Conforming Equal Order Interpolation
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 362-377
-
- Article
- Export citation
Thermoelastic Interaction in an Infinite Long Hollow Cylinder with Fractional Heat Conduction Equation
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 378-392
-
- Article
- Export citation
A High-Accuracy Mechanical Quadrature Method for Solving the Axisymmetric Poisson's Equation
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 393-406
-
- Article
- Export citation
An Immersed Finite Element Method for the Elasticity Problems with Displacement Jump
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 407-428
-
- Article
- Export citation
On the Generation of Instability Tollmien-Schlichting Waves by Free-Stream Turbulence
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 429-438
-
- Article
- Export citation
Analytical Model: Characteristics of Nanosecond Pulsed Plasma Synthetic Jet Actuator in Multiple-Pulsed Mode
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 439-462
-
- Article
- Export citation
Effects of Viscous Dissipation and Radiation on MHD Natural Convection in Oblique Porous Cavity with Constant Heat Flux
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 463-484
-
- Article
- Export citation
LES of Normally Impinging Elliptic Air-Jet Heat Transfer at Re=4400
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 485-500
-
- Article
- Export citation
A High-Efficient Algorithm for Parabolic Problems with Time-Dependent Coefficients
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 501-514
-
- Article
- Export citation

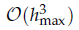 and low computing complexities. Moreover, the multivariate asymptotic error expansion of MQM accompanied with
and low computing complexities. Moreover, the multivariate asymptotic error expansion of MQM accompanied with 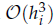 for all mesh widths
for all mesh widths 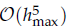 by the splitting extrapolation algorithm (SEA). Meanwhile, a posteriori asymptotic error estimate is derived, which can be used to construct self-adaptive algorithms. The numerical examples support our theoretical analysis.
by the splitting extrapolation algorithm (SEA). Meanwhile, a posteriori asymptotic error estimate is derived, which can be used to construct self-adaptive algorithms. The numerical examples support our theoretical analysis.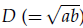 . The elliptic aspect ratio (
. The elliptic aspect ratio (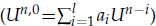 as good initial value of
as good initial value of