Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-24T18:35:09.457Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear Stability and B-convergence of Additive Runge-Kutta Methods for Nonlinear Stiff Problems

Published online by Cambridge University Press:  29 May 2015

Chao Yue ,
Aiguo Xiao  and
Hongliang Liu
Chao Yue
Affiliation:
School of Mathematics and Computational Science & Hunan Key Laboratory for Computation and Simulation in Science and Engineering, Xiangtan University, Hunan 411105, China School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China
Aiguo Xiao*
Affiliation:
School of Mathematics and Computational Science & Hunan Key Laboratory for Computation and Simulation in Science and Engineering, Xiangtan University, Hunan 411105, China
Hongliang Liu
Affiliation:
School of Mathematics and Computational Science & Hunan Key Laboratory for Computation and Simulation in Science and Engineering, Xiangtan University, Hunan 411105, China
*
*Corresponding author. Email: xag@xtu.edu.cn (A. G. Xiao)
Get access

Abstract

In this paper, we are devoted to nonlinear stability and B-convergence of additive Runge-Kutta (ARK) methods for nonlinear stiff problems with multiple stiffness. The concept of 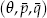-algebraic stability of ARK methods for a class of stiff problems Kστ is introduced, and it is proven that this stability implies some contractive properties of the ARK methods. Some results on optimal B-convergence of ARK methods for Kσ,0 are given. These new results extend the existing ones of RK methods and ARK methods in the references. Numerical examples test the correctness of our theoretical analysis.

Keywords

65L0865L20Stiff problemadditive Runge-Kutta methodimplicit-explicit methodB-convergencealgebraic stability
Type
Research Article
Information
Advances in Applied Mathematics and Mechanics , Volume 7 , Issue 4 , August 2015 , pp. 472 - 495
Copyright
Copyright © Global-Science Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Araújo, A., A note on B-stability of splitting methods, Computing Visual. Sci., 6 (2004), pp. 53–57.CrossRefGoogle Scholar
[2]Araújo, A., Murua, A. and Sanz-Serna, J. M., Symplectic methods based on decompositions, SIAM J. Numer. Anal., 34(5) (1997), pp. 1926–1947.Google Scholar
[3]Ascher, U. M., Ruuth, S. J. and Spiteri, R. J., Implicit-explicit Runge-Kutta methods for time-dependent partal differential equations, Appl. Numer. Math., 25 (1997), pp. 151–167.Google Scholar
[4]Boscarino, S. and Russo, G., Flux-explicit IMEX Runge-Kutta schemes for hyperbolic to parabolic relaxation problems, SIAM J. Numer. Anal., 51(1) (2013), pp. 163–190.CrossRefGoogle Scholar
[5]Bujanda, B. and Jorge, J. C., Stability results for fractional step discretization of time dependent coefficient evolutionary problems, Appl. Numer. Math., 38 (2001), pp. 69–85.Google Scholar
[6]Bujanda, B. and Jorge, J. C., Additive Runge-Kutta methods for the resolution of linear parabolic problems, J. Comput. Appl. Math., 140 (2002), pp. 99–117.Google Scholar
[7]Bujanda, B. and Jorge, J. C., Efficient linear implicit methods for nonlinear multidimensional parabolic problems, J. Comput. Appl. Math., 164–165 (2004), pp. 159–174.Google Scholar
[8]Burrage, K., Hundsdorfer, J. C. and Verwer, J. G., A study of B-convergence of Runge-Kutta methods, Computing, 36 (1986), pp. 17–34.CrossRefGoogle Scholar
[9]Burrage, K. and Hundsdorfer, W. H., The order of B-convergence of algebraically stable Runge-Kutta methods, Bit, 27 (1987), pp. 62–71.Google Scholar
[10]Burrage, K. and Butcher, J. C., Stability criteria for implicit Runge-Kutta methods, SIAM J. Numer. Anal., 16(1) (1979), pp. 46–57.CrossRefGoogle Scholar
[11]Dekker, K. and Verwer, J. G., Stability of Runge-Kutta Methods for Stiff Nonlinear Differential Equations, North-Holland, Amsterdam, 1984.Google Scholar
[12]Donat, R., Higueras, I. and Martinez-Gavara, A., Some theoretical results about stability for IMEX schemes applied to hyperbolic equations with stiff reaction terms, Kreiss, G.et al. (eds.), Numerical Mathematics and Advanced Applications, 2009, DOI 10.1007/978–3-642–11795-4 29, Springer-Verlag, 2010.Google Scholar
[13]Frank, R., Schneid, J. and Ueberhuber, C. W., The concept of B-convergence, SIAM J. Numer. Anal., 18(5) (1981), pp. 753–780.Google Scholar
[14]Frank, R., Schneid, J. and Ueberhuber, C. W., Stability properties of implicit Runge-Kutta methods, SIAM J. Numer. Anal., 22(3) (1985), pp. 497–514.CrossRefGoogle Scholar
[15]Frank, R., Schneid, J. and Ueberhuber, C. W., Order results of implicit Runge-Kutta methods applied stiff systems, SIAM J. Numer. Anal., 22(3) (1985), pp. 515–534.Google Scholar
[16]Garćia-Celayeta, B., Higueras, I. and Roldán, T., Contractivity/ monotonicity for additive Runge-Kutta methods: Inner product norms, Appl. Numer. Math., 56 (2006), pp. 862–878.Google Scholar
[17]Hairer, E. and Wanner, G., Solving Ordinary Differential Equations, Stiff and Differential-Algebraic Problems, Springer-Verlag, 1996.Google Scholar
[18]Higueras, I., Strong stability of additive Runge-Kutta methods, SIAM J. Numer. Anal., 44(4) (2006), pp. 1735–1758.Google Scholar
[19]Higueras, I., Mantas, J. M. and Roldán, T., Design and implementation of predictors for additive semi-implicit Runge-Kutta methods, SIAM J. Sci. Comput., 31(3) (2009), pp. 2131–2150.Google Scholar
[20]Hundsdorfer, W. and Verwer, J., Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations, Springer Series in Computational Mathematics, Springer, Berlin, 2003.CrossRefGoogle Scholar
[21]Kennedy, C. A. and Carpenter, M. H., Additive Runge-Kutta schemes for convection-diffusion-reaction equations, Appl. Numer. Math., 44(1–2) (2003), pp. 139–181.CrossRefGoogle Scholar
[22]Koto, T., IMEX Runge-Kutta schemes for reaction-diffusion equations, J. Comput. Appl. Math., 215 (2008), pp. 182–195.Google Scholar
[23]Kupka, F., Happenhofer, N., Higueras, I. and Koch, O., Total-variation-diminishing implicit-explicit Runge-Kutta methods for the simulation of double-diffusive convection in astrophysics, J. Comput. Phys., 231 (2012), pp. 3561–358.Google Scholar
[24]Liu, H. Y. and Zou, J., Some new additive Runge-Kutta methods and their applications, J. Comput. Appi. Math., 190(1–2) (2006), pp. 74–98.Google Scholar
[25]Li, S. F., Theory of Computational Methods for Stiff Differential Equations, Hunan Science and Technology Press, 1997 (in Chinese).Google Scholar
[26]Maeyama, S., Ishizawa, A., Watanabe, T. H., Nakajima, N., Tsuji-Iio, S. and T-Sutsui, H., A hybrid method of semi-Lagrangian and additive semi-implicit Runge-Kutta schemes for gyrokinetic Vlasov simulations, Computer Phys. Commun., 183 (2012), pp. 1986–1992.Google Scholar
[27]Pareschi, L. and Russo, G., Implicit-explicit Runge-Kutta schemes and applications to hyperbolic systems with relaxation, J. Sci. Comput., 25 (2005), pp. 129–155.Google Scholar
[28]Schlegel, M., Knolha, O., Arnold, M. and Wolke, R., Numerical solution of’multiscale problems in atmospheric modeling, Appl. Numer. Math., 62 (2012), pp. 1531–1543.Google Scholar
[29]Xiao, A. G., The order of B-convergence of Runge-Kutta methods, Natural Sci. J. Xiangtan University, 14(2) (1992), pp. 16–19.Google Scholar
[30]Xiao, A. G., -algebraic stability of Runge-Kutta methods, Mathematica Numerica Sinica, 15(4) (1993), pp. 440–448.Google Scholar
[31]Zhong, X. L., Additive semi-implicit Runge-Kutta methods for computing high speed noneauilib-rium reactive flows, J. Comput. Phys., 128 (1996), pp. 19–31.Google Scholar