Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Song, Mingzhan
Qian, Xu
Zhang, Hong
and
Song, Songhe
2017.
Hamiltonian Boundary Value Method for the Nonlinear Schrödinger Equation and the Korteweg-de Vries Equation.
Advances in Applied Mathematics and Mechanics,
Vol. 9,
Issue. 4,
p.
868.
Yan, Jinliang
Lai, Ming-Chih
Li, Zhilin
and
Zhang, Zhiyue
2017.
New Conservative Finite Volume Element Schemes for the Modified Regularized Long Wave Equation.
Advances in Applied Mathematics and Mechanics,
Vol. 9,
Issue. 2,
p.
250.
Li, Changzhao
and
Zhang, Juan
2019.
Lie Symmetry Analysis and Exact Solutions of Generalized Fractional Zakharov-Kuznetsov Equations.
Symmetry,
Vol. 11,
Issue. 5,
p.
601.
Li, Changzhao
and
Fang, Hui
2021.
Stochastic Bifurcations of Group-Invariant Solutions for a Generalized Stochastic Zakharov–Kuznetsov Equation.
International Journal of Bifurcation and Chaos,
Vol. 31,
Issue. 03,
p.
2150040.
Sun, Jian
Li, Xungui
Yang, Qiyong
Tian, Yi
Wang, Shaobo
and
Yang, Meiqing
2023.
Hydrodynamic numerical simulations based on residual cooperative neural network.
Advances in Water Resources,
Vol. 180,
Issue. ,
p.
104523.
Yang, Siqi
Sun, Jianqiang
and
Chen, Jie
2024.
High order energy-preserving method for the space fractional Klein–Gordon-Zakharov equations.
Journal of Computational Science,
Vol. 81,
Issue. ,
p.
102391.
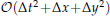 is proposed. The multi-symplectic conservation property of the new scheme is proved. The backward error analysis of the new multi-symplectic scheme is also implemented. The solitary wave evolution behaviors of the Zakharov-Kunetsov equation is investigated by the new multi-symplectic scheme. The accuracy of the scheme is analyzed.
is proposed. The multi-symplectic conservation property of the new scheme is proved. The backward error analysis of the new multi-symplectic scheme is also implemented. The solitary wave evolution behaviors of the Zakharov-Kunetsov equation is investigated by the new multi-symplectic scheme. The accuracy of the scheme is analyzed.

