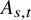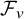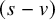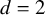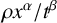308 results in 60Hxx
An extension of the stochastic sewing lemma and applications to fractional stochastic calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 April 2024, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Super-replication of life-contingent options under the Black–Scholes framework
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-15
-
- Article
- Export citation
Skew Ornstein–Uhlenbeck processes with sticky reflection and their applications to bond pricing
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-24
-
- Article
- Export citation
Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-42
-
- Article
- Export citation
Continuous dependence of stationary distributions on parameters for stochastic predator–prey models
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 22 February 2024, pp. 1-19
-
- Article
- Export citation
An exponential nonuniform Berry–Esseen bound of the maximum likelihood estimator in a Jacobi process
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 14 February 2024, pp. 1-18
-
- Article
- Export citation
Game-theoretic policy computing and simulation for blockchained buffering system via diffusion approximation
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 12 January 2024, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MODELLING WATER QUALITY WITH STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 09 January 2024, pp. 273-284
-
- Article
- Export citation
Speed of extinction for continuous-state branching processes in a weakly subcritical Lévy environment
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1-23
-
- Article
- Export citation
Stochastic differential equation approximations of generative adversarial network training and its long-run behavior
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1-25
-
- Article
- Export citation
SUPPORT THEOREM FOR PINNED DIFFUSION PROCESSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 241-264
- Print publication:
- March 2024
-
- Article
- Export citation
Heavy-traffic limits for parallel single-server queues with randomly split Hawkes arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 07 August 2023, pp. 1-25
-
- Article
- Export citation
Duality theory for exponential utility-based hedging in the Almgren–Chriss model
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1-19
-
- Article
- Export citation
PDE for the joint law of the pair of a continuous diffusion and its running maximum
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1171-1210
- Print publication:
- December 2023
-
- Article
- Export citation
Weakly interacting oscillators on dense random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 June 2023, pp. 255-278
- Print publication:
- March 2024
-
- Article
- Export citation
PRICING AND HEDGING OF VIX DERIVATIVES IN MODIFIED STOCHASTIC MODELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 June 2023, pp. 351-352
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
CONDITIONS FOR RECURRENCE AND TRANSIENCE FOR TIME-INHOMOGENEOUS BIRTH-AND-DEATH PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 393-402
- Print publication:
- April 2024
-
- Article
- Export citation
ESSAYS ON STRONG AND WEAK APPROXIMATIONS OF STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 175-176
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
Explosion of continuous-state branching processes with competition in a Lévy environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 68-81
- Print publication:
- March 2024
-
- Article
- Export citation