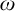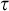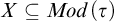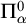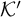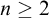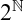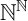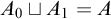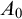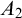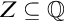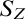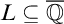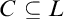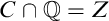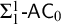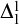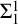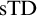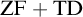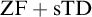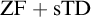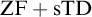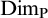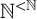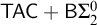131 results in 03DXX
Finite skew braces of square-free order and supersolubility
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A LOPEZ-ESCOBAR THEOREM FOR CONTINUOUS DOMAINS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
REGAININGLY APPROXIMABLE NUMBERS AND SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A WALK WITH GOODSTEIN
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-19
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
INTROENUMERABILITY, AUTOREDUCIBILITY, AND RANDOMNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 December 2023, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEGREE SPECTRA OF HOMEOMORPHISM TYPE OF COMPACT POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 December 2023, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Computability Theory on Polish Metric Spaces
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 February 2024, p. 664
- Print publication:
- December 2023
-
- Article
-
- You have access
- Export citation
Ordered Groups, Computability and Cantor-Bendixson Rank
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 February 2024, p. 664
- Print publication:
- December 2023
-
- Article
-
- You have access
- Export citation
NOTES ON SACKS’ SPLITTING THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 26 October 2023, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TOPOLOGICAL APPROACH TO UNDEFINABILITY IN ALGEBRAIC EXTENSIONS OF
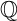 $\mathbb {Q}$
$\mathbb {Q}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 September 2023, pp. 626-655
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTABLE TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 18 September 2023, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FRACTAL DIMENSIONS OF k-AUTOMATIC SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 July 2023, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
COMPUTABLE VS DESCRIPTIVE COMBINATORICS OF LOCAL PROBLEMS ON TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE STRENGTH OF AN AXIOM OF FINITE CHOICE FOR BRANCHES IN TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1367-1386
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective Concept Classes of PAC and PACi Incomparable Degrees, Joins and Embedding of Degrees
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 July 2023, pp. 298-299
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
The first-order theory of binary overlap-free words is decidable
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INVESTIGATING THE COMPUTABLE FRIEDMAN–STANLEY JUMP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 17 May 2023, pp. 918-944
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME CONSEQUENCES OF
 ${\mathrm {TD}}$ AND
${\mathrm {TD}}$ AND 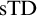 ${\mathrm {sTD}}$
${\mathrm {sTD}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1573-1589
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
COMPUTABLY COMPACT METRIC SPACES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 170-263
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE REVERSE MATHEMATICS OF
 ${\mathsf {CAC\ FOR\ TREES}}$
${\mathsf {CAC\ FOR\ TREES}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation