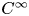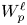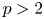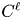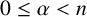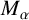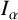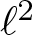254 results in 42Bxx
The local geometry of idempotent Schur multipliers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some remarks on Riesz transforms on exterior Lipschitz domains
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic Muckenhoupt weights characterized by parabolic fractional maximal and integral operators with time lag
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1-54
-
- Article
- Export citation
Boundedness on Triebel–Lizorkin spaces for the Calderón commutator with rough kernel
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1-13
-
- Article
- Export citation
Hardy spaces and Riesz transforms on a Lie group of exponential growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-32
-
- Article
- Export citation
An endpoint estimate for product singular integral operators on stratified Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Volterra operators between Hardy spaces of vector-valued Dirichlet series
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 286-300
- Print publication:
- March 2025
-
- Article
- Export citation
Functions with small BMO norm
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-15
-
- Article
- Export citation
Parametric Fourier and Mellin transforms of power-constructible functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 November 2024, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDEDNESS OF DIFFERENTIAL TRANSFORMS FOR FRACTIONAL HEAT SEMIGROUPS GENERATED BY SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 210-244
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
Compact bilinear operators and paraproducts revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 44-59
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Model structures, n-Gorenstein flat modules and PGF dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1241-1264
-
- Article
-
- You have access
- HTML
- Export citation
CORRECTION TO ‘CHOQUET INTEGRALS, HAUSDORFF CONTENT AND FRACTIONAL OPERATORS’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-3
-
- Article
-
- You have access
- HTML
- Export citation
The multilinear spherical maximal function in one dimension
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 25 September 2024, pp. 1045-1059
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SCHRÖDINGER PROPAGATOR ON WIENER AMALGAM SPACES IN THE FULL RANGE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 27 August 2024, pp. 953-969
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
On a localization-in-frequency approach for a class of elliptic problems with singular boundary data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
On some convexity questions of Handelman
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 936-939
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Unconditional convergence of eigenfunction expansions for abstract and elliptic operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
CHOQUET INTEGRALS, HAUSDORFF CONTENT AND FRACTIONAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. 355-366
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
-
- You have access
- HTML
- Export citation

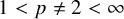
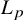
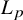
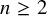
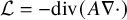
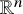

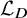
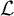

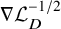
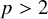
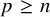
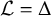

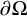
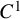
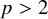
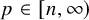
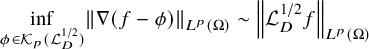
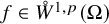
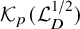
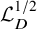
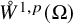
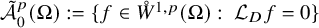
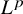
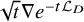
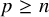
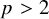









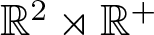
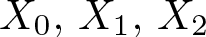

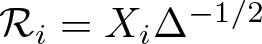
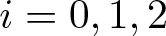
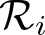
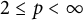
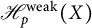
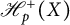
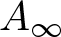



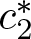




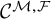
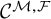
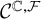
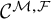
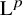
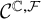
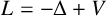
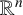
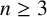
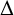
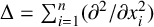

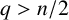
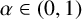
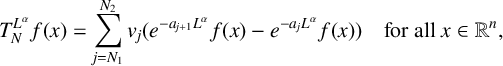
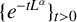
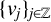
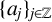
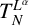
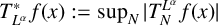
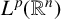
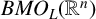
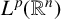
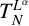
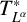
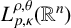
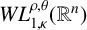





 . The homotopy category of this model structure is triangulated equivalent to the stable category
. The homotopy category of this model structure is triangulated equivalent to the stable category 

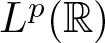
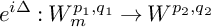
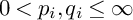 and
and