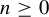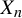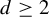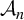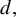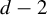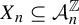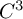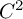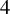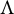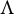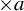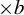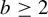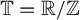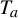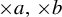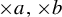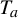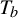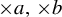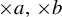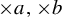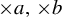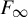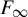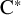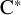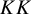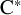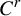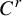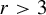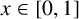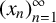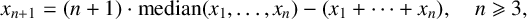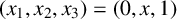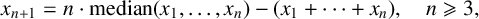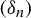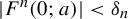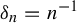113 results in 37Exx
On the Hausdorff dimension of invariant measures of piecewise smooth circle homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure transfer and S-adic developments for subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-35
-
- Article
- Export citation
Systems involving mean value formulas on trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-33
-
- Article
- Export citation
ON RESIDUES AND CONJUGACIES FOR GERMS OF 1-D PARABOLIC DIFFEOMORPHISMS IN FINITE REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1-35
-
- Article
- Export citation
Effective rigidity away from the boundary for centrally symmetric billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 28 September 2023, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Piecewise contracting maps on the interval: Hausdorff dimension, entropy, and attractors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 September 2023, pp. 1-10
-
- Article
- Export citation
Moser's theorem with frequency-preserving
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2023, pp. 1-31
-
- Article
- Export citation
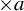 $\times a$ and
$\times a$ and 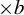 $\times b$ empirical measures, the irregular set and entropy
$\times b$ empirical measures, the irregular set and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1-20
-
- Article
- Export citation
On the dimension of stationary measures for random piecewise affine interval homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1-16
-
- Article
- Export citation
Statistical aspects of mean field coupled intermittent maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 945-957
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the abundance of k-fold semi-monotone minimal sets in bimodal circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 1269-1314
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finitely presented left orderable monsters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 06 July 2023, pp. 1367-1378
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hofer's geometry and topological entropy
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1250-1299
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chaotic tracial dynamics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 May 2023, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iterative roots of two-dimensional mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 241-258
-
- Article
- Export citation
Quantitative Heegaard Floer cohomology and the Calabi invariant
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 December 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotically holomorphic methods for infinitely renormalizable
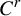 $C^r$ unimodal maps
$C^r$ unimodal maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 3636-3684
- Print publication:
- November 2023
-
- Article
- Export citation
THE AKIYAMA MEAN-MEDIAN MAP HAS UNBOUNDED TRANSIT TIME AND DISCONTINUOUS LIMIT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 298-307
- Print publication:
- October 2023
-
- Article
- Export citation
A characterization of Thurston’s Master Teapot
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 10 November 2022, pp. 3354-3382
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical recurrence in the real quadratic family
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 3255-3287
- Print publication:
- October 2023
-
- Article
- Export citation