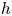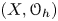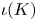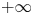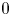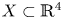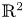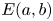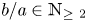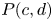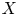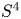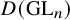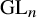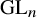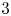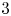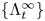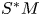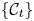145 results in 53Dxx
Stratification of the transverse momentum map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 518-585
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Bezrukavnikov–Kaledin quantization of symplectic varieties in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 411-450
- Print publication:
- February 2024
-
- Article
- Export citation
Locality of relative symplectic cohomology for complete embeddings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 10 October 2023, pp. 2551-2637
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted nonlinear flag manifolds as coadjoint orbits
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-Orientable Lagrangian Fillings of Legendrian Knots
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 123-153
- Print publication:
- January 2024
-
- Article
- Export citation
Selective symplectic homology with applications to contact non-squeezing
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 2458-2482
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hamiltonian knottedness and lifting paths from the shape invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 2416-2457
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Realization of GKM fibrations and new examples of Hamiltonian non-Kähler actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 24 August 2023, pp. 2149-2190
- Print publication:
- October 2023
-
- Article
- Export citation
On weighted-blowup formulae of genus zero orbifold Gromov–Witten invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1833-1871
- Print publication:
- September 2023
-
- Article
- Export citation
Multiple generalized cluster structures on
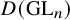 $D(\mathrm {GL}_n)$
$D(\mathrm {GL}_n)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 June 2023, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thurston’s fragmentation and c-principles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 25 April 2023, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Biharmonic almost complex structures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Rouquier dimension of wrapped Fukaya categories and a conjecture of Orlov
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 01 March 2023, pp. 437-487
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sheaf quantization of Legendrian isotopy
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 419-435
- Print publication:
- February 2023
-
- Article
- Export citation
Classification of generalized Einstein metrics on three-dimensional Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 2038-2095
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant Brill–Noether theory for elliptic operators and superrigidity of J-holomorphic maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hofer–Zehnder conjecture on weighted projective spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 87-108
- Print publication:
- January 2023
-
- Article
- Export citation
Quantitative Heegaard Floer cohomology and the Calabi invariant
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 December 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pseudo-holomorphic dynamics in the restricted three-body problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 663-693
- Print publication:
- May 2023
-
- Article
- Export citation
On Anosovity, divergence and bi-contact surgery
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 3288-3310
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation