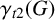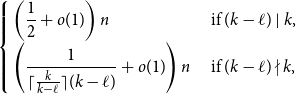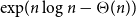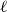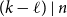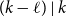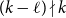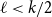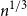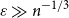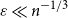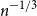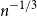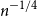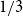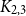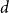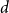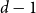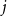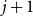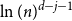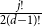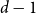911 results in 05Cxx
The List-Ramsey threshold for families of graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 20 September 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Domination inequalities and dominating graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
On the Ramsey numbers of daisies I
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
SPECTRAL CLUSTERING AND LONG TIMESERIES CLASSIFICATION
- Part of
-
- Journal:
- The ANZIAM Journal , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Ramsey numbers of daisies II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
List packing number of bounded degree graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
EXTREMAL GRAPHS FOR DEGREE SUMS AND DOMINATING CYCLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
GRAPHS WITH SEMITOTAL DOMINATION NUMBER HALF THEIR ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-8
-
- Article
-
- You have access
- HTML
- Export citation
Quenched worst-case scenario for root deletion in targeted cutting of random recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 September 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strong digraph groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting spanning subgraphs in dense hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
Random walks and the “Euclidean” association scheme in finite vector spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noise sensitivity of the minimum spanning tree of the complete graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 23 May 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric random intersection graphs with general connection probabilities
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Depths in random recursive metric spaces
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON HOMOMORPHISM GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rainbow Hamiltonicity in uniformly coloured perturbed digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximum chordal subgraphs of random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 03 May 2024, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
Turán problems in pseudorandom graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Behaviour of the minimum degree throughout the
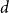 ${\textit{d}}$-process
${\textit{d}}$-process
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation