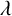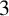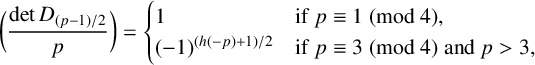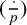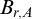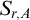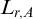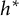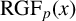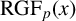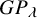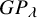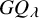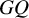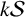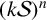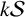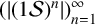279 results in 05-XX
Domination inequalities and dominating graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
INEQUALITIES AND UNIFORM ASYMPTOTIC FORMULAE FOR SPT-CRANK OF PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Maximizing weighted sums of binomial coefficients using generalized continued fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
ARITHMETIC PROPERTIES OF AN ANALOGUE OF t-CORE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
SOME COUNTING FORMULAE FOR
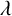 $\lambda $-QUIDDITIES OVER THE RINGS
$\lambda $-QUIDDITIES OVER THE RINGS  ${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Some congruences for 12-coloured generalized Frobenius partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
The distribution of the maximum protection number in simply generated trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSIONS AND LIMITS OF THE SPECKER–BLATTER THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lattice points in slices of prisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SOME CONGRUENCES INVOLVING CENTRAL BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Proof of some conjectural congruences involving Apéry and Apéry-like numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 508-527
-
- Article
-
- You have access
- HTML
- Export citation
GENERATING FUNCTIONS FOR THE QUOTIENTS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Combinatorial formulas for shifted dual stable Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 February 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONGRUENCES FOR RANKS OF PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 January 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
A Pipe Dream Perspective on Totally Symmetric Self-Complementary Plane Partitions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 January 2024, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the cross-product conjecture for the number of linear extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp large deviations and concentration inequalities for the number of descents in a random permutation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 810-833
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
COUNTING UNIONS OF SCHREIER SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 December 2023, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation