Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-25T08:03:23.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Degenerations of Leibniz and Anticommutative Algebras

Part of: General nonassociative rings Families, fibrations Algebraic groups

Published online by Cambridge University Press:  29 January 2019

Nurlan Ismailov ,
Ivan Kaygorodov  and
Yury Volkov
Nurlan Ismailov
Affiliation:
Universidade de São Paulo, IME, São Paulo, Brazil Institute of Mathematics and Mathematical Modeling, Almaty, Kazakhstan Email: nurlan.ismail@gmail.com
Ivan Kaygorodov
Affiliation:
Universidade Federal do ABCCMCC, Santo André, Brazil Email: kaygorodov.ivan@gmail.com
Yury Volkov
Affiliation:
Saint Petersburg State University, Saint Petersburg, Russia Email: wolf86_666@list.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

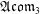We describe all degenerations of three-dimensional anticommutative algebras $\mathfrak{A}\mathfrak{c}\mathfrak{o}\mathfrak{m}_{3}$ and of three-dimensional Leibniz algebras 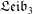$\mathfrak{L}\mathfrak{e}\mathfrak{i}\mathfrak{b}_{3}$ over 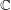$\mathbb{C}$. In particular, we describe all irreducible components and rigid algebras in the corresponding varieties.

Keywords

degenerationrigid algebraorbit closureanticommutative algebraLeibniz algebraLie algebra

MSC classification

Primary: 17A32: Leibniz algebras
Secondary: 14D06: Fibrations, degenerations 14L30: Group actions on varieties or schemes (quotients)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 3 , September 2019 , pp. 539 - 549
Copyright
© Canadian Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work was supported by FAPESP 17/15437-6, 17/21429-6; AP05131123 “Cohomological and structural problems of non-associative algebras”; RFBR 18-31-00001; the President’s Program “Support of Young Russian Scientists” (grant MK-2262.2019.1).

References

Alvarez, M. A., On rigid 2-step nilpotent Lie algebras . Algebra Colloq. 25(2018), 2, 349–360. https://doi.org/10.1142/S100538671800024X.Google Scholar
Alvarez, M. A., The variety of 7-dimensional 2-step nilpotent Lie algebras . Symmetry 10(2018), 1, 26. https://doi.org/10.3390/sym10010026.Google Scholar
Alvarez, M. A. and Hernández I., I., On degenerations of Lie superalgebras . Linear Multilinear Algebra, to appear. https://doi.org/10.1080/03081087.2018.1498060.Google Scholar
Alvarez, M. A., Hernández, I., and Kaygorodov, I., Degenerations of Jordan superalgebras . Bull. Malays. Math. Sci. Soc. 43(2020), https://doi.org/10.1007/s40840-018-0664-3.Google Scholar
Bekbaev, U., Complete classification of a class of m-dimensional algebras . J. Phys. Conf. Ser. 819(2017), 012012. https://doi.org/10.1088/1742-6596/819/1/012012.Google Scholar
Benes, T. and Burde, D., Degenerations of pre-Lie algebras . J. Math. Phys. 50(2009), 11, 112102. https://doi.org/10.1063/1.3246608.Google Scholar
Benes, T. and Burde, D., Classification of orbit closures in the variety of three dimensional Novikov algebras . J. Algebra Appl. 13(2014), 2, 1350081. https://doi.org/10.1142/S0219498813500813.Google Scholar
Burde, D., Degenerations of nilpotent Lie algebras . J. Lie Theory 9(1999), 1, 193–202.Google Scholar
Burde, D. and Steinhoff, C., Classification of orbit closures of 4-dimensional complex Lie algebras . J. Algebra 214(1999), 2, 729–739. https://doi.org/10.1006/jabr.1998.7714.Google Scholar
Calderón, A., Fernández Ouaridi, A., and Kaygorodov, I., The classification of n-dimensional anticommutative algebras with (n - 3)-dimensional annihilator . Comm. Algebra 47(2019), 1, 173–181. https://doi.org/10.1080/00927872.2018.1468909.Google Scholar
Casas, J., Insua, M., Ladra, M., and Ladra, S., An algorithm for the classification of 3-dimensional complex Leibniz algebras . Linear Algebra Appl. 436(2012), 9, 3747–3756. https://doi.org/10.1016/j.laa.2011.11.039.Google Scholar
Casas, J., Khudoyberdiyev, A., Ladra, M., and Omirov, B., On the degenerations of solvable Leibniz algebras . Linear Algebra Appl. 439(2013), 2, 472–487. https://doi.org/10.1016/j.laa.2013.03.029.Google Scholar
Fialowski, A. and Penkava, M., The moduli space of 4-dimensional nilpotent complex associative algebras . Linear Algebra Appl. 457(2014), 408–427. https://doi.org/10.1016/j.laa.2014.05.014.Google Scholar
Gainov, A. T., Binary Lie algebras of lower ranks. (Russian) . Algebra i Logika Sem. 2(1963), 4, 21–40.Google Scholar
Grunewald, F. and O’Halloran, J., Varieties of nilpotent Lie algebras of dimension less than six . J. Algebra 112(1988), 315–325. https://doi.org/10.1016/0021-8693(88)90093-2.Google Scholar
Grunewald, F. and O’Halloran, J., A characterization of orbit closure and applications . J. Algebra 116(1988), 163–175. https://doi.org/10.1016/0021-8693(88)90199-8.Google Scholar
Grunewald, F. and O’Halloran, J., Deformations of Lie algebras . J. Algebra 162(1993), 1, 210–224. https://doi.org/10.1006/jabr.1993.1250.Google Scholar
Horn, R. A. and Sergeichuk, V., Canonical matrices of bilinear and sesquilinear forms . Linear Algebra Appl. 428(2008), 1, 193–223. https://doi.org/10.1016/j.laa.2007.07.023.Google Scholar
Ismailov, N., Kaygorodov, I., and Volkov, Yu., The geometric classification of Leibniz algebras . Internat. J. Math. 29(2018), 5, 1850035. https://doi.org/10.1142/S0129167X18500350.Google Scholar
Kaygorodov, I., Popov, Yu., and Volkov, Yu., Degenerations of binary Lie and nilpotent Malcev algebras . Comm. Algebra 46(2018), 11, 4929–4940. https://doi.org/10.1080/00927872.2018.1459647.Google Scholar
Kaygorodov, I., Popov, Yu., Pozhidaev, A., and Volkov, Yu., Degenerations of Zinbiel and nilpotent Leibniz algebras . Linear Multilinear Algebra 66(2018), 4, 704–716. https://doi.org/10.1080/03081087.2017.1319457.Google Scholar
Kaygorodov, I. and Volkov, Yu., The variety of 2-dimensional algebras over an algebraically closed field . Canad. J. Math., to appear. https://doi.org/10.4153/S0008414X18000056.Google Scholar
Kaygorodov, I. and Volkov, Yu., Complete classification of algebras of level two . Moscow Math. J., to appear. arxiv:1710.08943.Google Scholar
Kobayashi, Yu., Shirayanagi, K., Takahasi, S., and Tsukada, M., Classification of three dimensional zeropotent algebras over an algebraically closed field . Comm. Algebra 45(2017), 12, 5037–5052. https://doi.org/10.1080/00927872.2017.1313426.Google Scholar
Khudoyberdiyev, A. and Omirov, B., The classification of algebras of level one . Linear Algebra Appl. 439(2013), 11, 3460–3463. https://doi.org/10.1016/j.laa.2013.09.020.Google Scholar
Khudoyberdiyev, A., Ladra, M., Masutova, K., and Omirov, B., Some irreducible components of the variety of complex (n + 1)-dimensional Leibniz algebras . J. Geom. Phys. 121(2017), 228–246. https://doi.org/10.1016/j.geomphys.2017.07.014.Google Scholar
Lauret, J., Degenerations of Lie algebras and geometry of Lie groups . Differ. Geom. Appl. 18(2003), 2, 177–194. https://doi.org/10.1016/S0926-2245(02)00146-8.Google Scholar
Loday, J.-L. and Pirashvili, T., Universal enveloping algebras of Leibniz algebras and (co)homology . Math. Ann. 296(1993), 1, 139–158. https://doi.org/10.1007/BF01445099.Google Scholar
Rakhimov, I. and Mohd Atan, K., On contractions and invariants of Leibniz algebras . Bull. Malays. Math. Sci. Soc. 35(2012), 557–565.Google Scholar
Seeley, C., Degenerations of 6-dimensional nilpotent Lie algebras over ℂ . Comm. Algebra 18(1990), 3493–3505. https://doi.org/10.1080/00927879008824088.Google Scholar