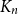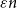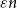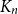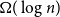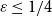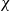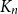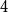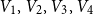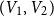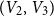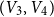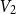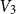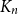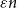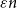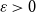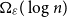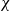1 results
Unavoidable patterns in locally balanced colourings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 01 June 2023, pp. 796-808
-
- Article
-
- You have access
- HTML
- Export citation
-
Which patterns must a two-colouring of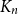
$K_n$ contain if each vertex has at least 
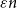$\varepsilon n$ red and 
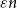$\varepsilon n$ blue neighbours? We show that when 
$\varepsilon \gt 1/4$,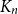 
$K_n$ must contain a complete subgraph on 
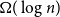$\Omega (\log n)$ vertices where one of the colours forms a balanced complete bipartite graph.When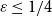
$\varepsilon \leq 1/4$, this statement is no longer true, as evidenced by the following colouring 
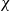$\chi$ of 
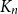$K_n$. Divide the vertex set into 
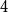$4$ parts nearly equal in size as 
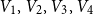$V_1,V_2,V_3, V_4$, and let the blue colour class consist of the edges between 
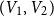$(V_1,V_2)$, 
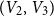$(V_2,V_3)$, 
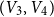$(V_3,V_4)$, and the edges contained inside 
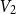$V_2$ and inside 
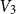$V_3$. Surprisingly, we find that this obstruction is unique in the following sense. Any two-colouring of 
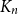$K_n$ in which each vertex has at least 
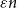$\varepsilon n$ red and 
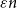$\varepsilon n$ blue neighbours (with 
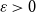$\varepsilon \gt 0$) contains a vertex set 
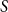$S$ of order 
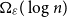$\Omega _{\varepsilon }(\log n)$ on which one colour class forms a balanced complete bipartite graph, or which has the same colouring as 
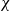$\chi$.
