1 results
Effective rigid analytic trivializations for Drinfeld modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 April 2022, pp. 713-742
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We develop tools for constructing rigid analytic trivializations for Drinfeld modules as infinite products of Frobenius twists of matrices, from which we recover the rigid analytic trivialization given by Pellarin in terms of Anderson generating functions. One advantage is that these infinite products can be obtained from only a finite amount of initial calculation, and consequently we obtain new formulas for periods and quasi-periods, similar to the product expansion of the Carlitz period. We further link to results of Gekeler and Maurischat on the
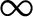$\infty $
-adic field generated by the period lattice.
