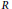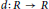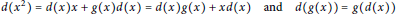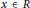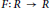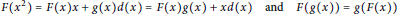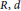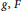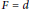1 results
Generalized Jordan Semiderivations in Prime Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 263-270
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
-
Let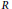
$R$ be a ring and let 
$g$ be an endomorphism of 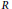$R$. The additive mapping 
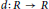$d:\,R\,\to \,R$ is called a Jordan semiderivation of 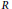$R$, associated with $g$, if
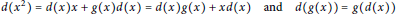$$d\left( {{x}^{2}} \right)=d\left( x \right)x+g\left( x \right)d\left( x \right)=d\left( x \right)g\left( x \right)+xd\left( x \right)\,\text{and}\,d\left( g\left( x \right) \right)=g\left( d\left( x \right) \right)$$for all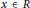
$x\,\in \,R$. The additive mapping 
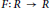$F:\,R\,\to \,R$ is called a generalized Jordan semiderivation of 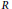$R$, related to the Jordan semiderivation 
$d$ and endomorphism $g$, if
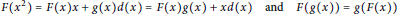$$F\left( {{x}^{2}} \right)=F\left( x \right)x+g\left( x \right)d\left( x \right)=F\left( x \right)g\left( x \right)+xd\left( x \right)\,\,and\,F\left( g\left( x \right) \right)=g\left( F\left( x \right) \right)$$for all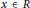
$x\,\in \,R$. In this paper we prove that if 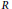$R$ is a prime ring of characteristic different from 2, $g$ an endomorphism of 
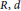$R,\,d$ a Jordan semiderivation associated with 
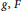$g,\,F$ a generalized Jordan semiderivation associated with $d$ and $g$, then 
$F$ is a generalized semiderivation of 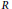$R$ and $d$ is a semiderivation of 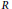$R$. Moreover, if 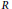$R$ is commutative, then 
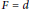$F\,=\,d$.
