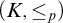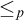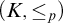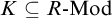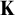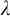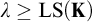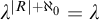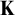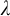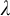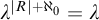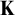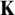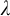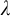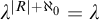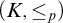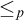Fisher [10] and Baur [6] showed independently in the seventies that if T is a complete first-order theory extending the theory of modules, then the class of models of T with pure embeddings is stable. In [25, 2.12], it is asked if the same is true for any abstract elementary class $(K, \leq _p)$ such that K is a class of modules and $\leq _p$ is the pure submodule relation. In this paper we give some instances where this is true:Theorem.

Assume R is an associative ring with unity. Let 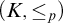$(K, \leq _p)$ be an AEC such that 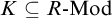$K \subseteq R\text {-Mod}$

and K is closed under finite direct sums, then:

• • If K is closed under pure-injective envelopes, then $\mathbf {K}$ is $\lambda $ -stable for every $\lambda \geq \operatorname {LS}(\mathbf {K})$ such that $\lambda ^{|R| + \aleph _0}= \lambda $ .

• • If K is closed under pure submodules and pure epimorphic images, then $\mathbf {K}$ is $\lambda $ -stable for every $\lambda $ such that $\lambda ^{|R| + \aleph _0}= \lambda $ .

• • Assume R is Von Neumann regular. If $\mathbf {K}$ is closed under submodules and has arbitrarily large models, then $\mathbf {K}$ is $\lambda $ -stable for every $\lambda $ such that $\lambda ^{|R| + \aleph _0}= \lambda $ .

As an application of these results we give new characterizations of noetherian rings, pure-semisimple rings, Dedekind domains, and fields via superstability. Moreover, we show how these results can be used to show a link between being good in the stability hierarchy and being good in the axiomatizability hierarchy.

Another application is the existence of universal models with respect to pure embeddings in several classes of modules. Among them, the class of flat modules and the class of 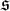$\mathfrak {s}$ -torsion modules.