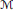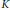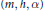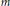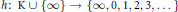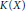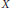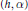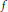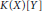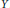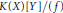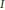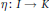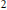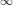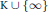Purely simple Kronecker modules 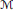 $M$, built from an algebraically closed field
$M$, built from an algebraically closed field 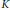 $K$, arise from a triplet
$K$, arise from a triplet 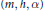 $\left( m,\,h,\,\alpha \right)$ where
$\left( m,\,h,\,\alpha \right)$ where 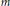 $m$ is a positive integer,
$m$ is a positive integer, 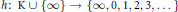 $h:\,K\,\cup \,\{\infty \}\,\to \,\{\infty ,\,0,\,1,\,2,\,3,\,.\,.\,.\,\}$ is a height function, and
$h:\,K\,\cup \,\{\infty \}\,\to \,\{\infty ,\,0,\,1,\,2,\,3,\,.\,.\,.\,\}$ is a height function, and  $\alpha$ is a
$\alpha$ is a 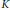 $K$-linear functional on the space
$K$-linear functional on the space 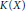 $K\left( X \right)$ of rational functions in one variable
$K\left( X \right)$ of rational functions in one variable 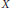 $X$. Every pair
$X$. Every pair 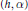 $\left( h,\,\alpha \right)$ comes with a polynomial
$\left( h,\,\alpha \right)$ comes with a polynomial 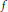 $f$ in
$f$ in 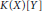 $K\left( X \right)\left[ Y\, \right]$ called the regulator. When the module
$K\left( X \right)\left[ Y\, \right]$ called the regulator. When the module 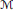 $M$ admits non-trivial endomorphisms,
$M$ admits non-trivial endomorphisms, 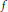 $f$ must be linear or quadratic in
$f$ must be linear or quadratic in 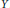 $Y$. In that case
$Y$. In that case 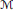 $M$ is purely simple if and only if
$M$ is purely simple if and only if 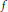 $f$ is an irreducible quadratic. Then the
$f$ is an irreducible quadratic. Then the 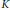 $K$-algebra End
$K$-algebra End 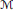 $M$ embeds in the quadratic function field
$M$ embeds in the quadratic function field 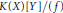 ${K\left( X \right)\left[ Y\, \right]}/{(f\,)}\;$. For some height functions
${K\left( X \right)\left[ Y\, \right]}/{(f\,)}\;$. For some height functions  $h$ of infinite support
$h$ of infinite support 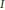 $I$, the search for a functional
$I$, the search for a functional  $\alpha$ for which
$\alpha$ for which 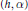 $\left( h,\,\alpha \right)$ has regulator
$\left( h,\,\alpha \right)$ has regulator  $0$ comes down to having functions
$0$ comes down to having functions 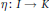 $\eta \,:\,I\,\to \,K$ such that no planar curve intersects the graph of
$\eta \,:\,I\,\to \,K$ such that no planar curve intersects the graph of  $\eta$ on a cofinite subset. If
$\eta$ on a cofinite subset. If 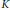 $K$ has characterictic not
$K$ has characterictic not 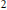 $2$, and the triplet
$2$, and the triplet 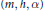 $\left( m,\,h,\,\alpha \right)$ gives a purely-simple Kronecker module
$\left( m,\,h,\,\alpha \right)$ gives a purely-simple Kronecker module 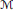 $M$ having non-trivial endomorphisms, then
$M$ having non-trivial endomorphisms, then  $h$ attains the value
$h$ attains the value 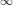 $\infty$ at least once on
$\infty$ at least once on 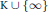 $\text{K}\,\cup \,\text{ }\!\!\{\!\!\text{ }\infty \text{ }\!\!\}\!\!\text{ }$ and
$\text{K}\,\cup \,\text{ }\!\!\{\!\!\text{ }\infty \text{ }\!\!\}\!\!\text{ }$ and  $h$ is finite-valued at least twice on
$h$ is finite-valued at least twice on 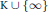 $\text{K}\,\cup \,\text{ }\!\!\{\!\!\text{ }\infty \text{ }\!\!\}\!\!\text{ }$. Conversely all these
$\text{K}\,\cup \,\text{ }\!\!\{\!\!\text{ }\infty \text{ }\!\!\}\!\!\text{ }$. Conversely all these  $h$ form part of such triplets. The proof of this result hinges on the fact that a rational function
$h$ form part of such triplets. The proof of this result hinges on the fact that a rational function  $r$ is a perfect square in
$r$ is a perfect square in 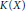 $K\left( X \right)$ if and only if
$K\left( X \right)$ if and only if  $r$ is a perfect square in the completions of
$r$ is a perfect square in the completions of 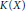 $K\left( X \right)$ with respect to all of its valuations.
$K\left( X \right)$ with respect to all of its valuations.