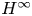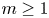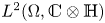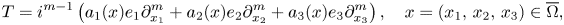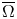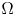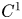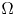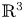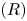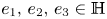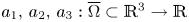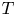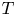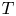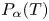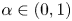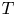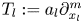Using the $H^{\infty }$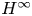 -functional calculus for quaternionic operators, we show how to generate the fractional powers of some densely defined differential quaternionic operators of order $m\geq 1$
-functional calculus for quaternionic operators, we show how to generate the fractional powers of some densely defined differential quaternionic operators of order $m\geq 1$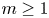 , acting on the right linear quaternionic Hilbert space $L^{2}(\Omega,\mathbb {C}\otimes \mathbb {H})$
, acting on the right linear quaternionic Hilbert space $L^{2}(\Omega,\mathbb {C}\otimes \mathbb {H})$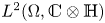 . The operators that we consider are of the type
. The operators that we consider are of the type
\begin{align*} T=i^{m-1}\left(a_1(x) e_1\partial_{x_1}^{m}+a_2(x) e_2\partial_{x_2}^{m}+a_3(x) e_3\partial_{x_3}^{m}\right), \quad x=(x_1,\, x_2,\, x_3)\in \overline{\Omega}, \end{align*}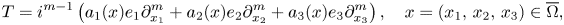
where $\overline {\Omega }$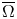 is the closure of either a bounded domain $\Omega$
is the closure of either a bounded domain $\Omega$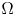 with $C^{1}$
with $C^{1}$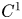 boundary, or an unbounded domain $\Omega$
boundary, or an unbounded domain $\Omega$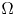 in $\mathbb {R}^{3}$
in $\mathbb {R}^{3}$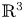 with a sufficiently regular boundary, which satisfy the so-called property $(R)$
with a sufficiently regular boundary, which satisfy the so-called property $(R)$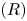 (see Definition 1.3), $e_1,\, e_2,\, e_3\in \mathbb {H}$
(see Definition 1.3), $e_1,\, e_2,\, e_3\in \mathbb {H}$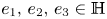 which are pairwise anticommuting imaginary units, $a_1,\,a_2,\, a_3: \overline {\Omega } \subset \mathbb {R}^{3}\to \mathbb {R}$
which are pairwise anticommuting imaginary units, $a_1,\,a_2,\, a_3: \overline {\Omega } \subset \mathbb {R}^{3}\to \mathbb {R}$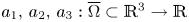 are the coefficients of $T$
are the coefficients of $T$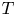 . In particular, it will be given sufficient conditions on the coefficients of $T$
. In particular, it will be given sufficient conditions on the coefficients of $T$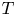 in order to generate the fractional powers of $T$
in order to generate the fractional powers of $T$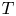 , denoted by $P_{\alpha }(T)$
, denoted by $P_{\alpha }(T)$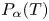 for $\alpha \in (0,1)$
for $\alpha \in (0,1)$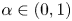 , when the components of $T$
, when the components of $T$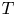 , i.e. the operators $T_l:=a_l\partial _{x_l}^{m}$
, i.e. the operators $T_l:=a_l\partial _{x_l}^{m}$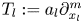 , do not commute among themselves. This kind of result is to be understood in the more general setting of the fractional diffusion problems. The method used to construct the fractional power of a quaternionic linear operator is a generalization of the method developed by Balakrishnan.
, do not commute among themselves. This kind of result is to be understood in the more general setting of the fractional diffusion problems. The method used to construct the fractional power of a quaternionic linear operator is a generalization of the method developed by Balakrishnan.