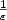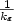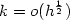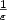We study the gradient flow for the total variation functional, which arises in image processing and geometric applications. We propose a variational inequality weak formulation for the gradient flow,and establish well-posedness of the problem by the energy method. The main idea of our approach is to exploit the relationship betweenthe regularized gradient flow (characterized by a small positive parameterε, see (1.7)) and the minimal surface flow [21]and the prescribed mean curvature flow [16].Since our approach is constructive and variational, finite element methods can be naturally applied to approximate weak solutions of the limiting gradient flow problem. We propose a fully discrete finite element method and establish convergence tothe regularized gradient flow problem as h,k → 0, and to the total variation gradient flow problem as h,k,ε → 0in general cases.Provided that the regularized gradient flow problem possessesstrong solutions, which is proved possible if the datum functionsare regular enough, we establish practical a priori error estimates for the fully discrete finite element solution, in particular, by focusing on the dependence of the error bounds on the regularization parameter ε. Optimal order error bounds are derived for the numerical solution under the meshrelation k = O(h2). In particular, it is shown thatall error bounds depend on $\frac{1}{\varepsilon}$ 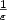 onlyin some lower polynomial order for small ε.
onlyin some lower polynomial order for small ε.