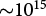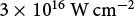891 results
10 - Sustainable Development Goal Indicators on Maternal Health and Socio-Economic Inequalities in India
-
-
- Book:
- India Population Report
- Published online:
- 15 August 2023
- Print publication:
- 31 May 2024, pp 347-388
-
- Chapter
- Export citation
4 - Mortality and Epidemiological Transition
-
-
- Book:
- India Population Report
- Published online:
- 15 August 2023
- Print publication:
- 31 May 2024, pp 110-170
-
- Chapter
- Export citation
Hot electron emission characteristics from thin metal foil targets irradiated by terawatt laser
-
- Journal:
- Laser and Particle Beams / Volume 42 / 2024
- Published online by Cambridge University Press:
- 17 April 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mechanism for axial pattern formation of concentrated suspension in a horizontal rotating cylinder
-
- Journal:
- Journal of Fluid Mechanics / Volume 985 / 25 April 2024
- Published online by Cambridge University Press:
- 16 April 2024, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Low-Molecular-Weight Heparin Salvage in Pedicled Flap Reconstruction in Head and Neck: A Prospective Cohort Study
-
- Journal:
- The Journal of Laryngology & Otology / Accepted manuscript
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-24
-
- Article
- Export citation
DNA methylation in necrotizing enterocolitis
-
- Journal:
- Expert Reviews in Molecular Medicine / Accepted manuscript
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- Export citation
FINITENESS OF CANONICAL QUOTIENTS OF DEHN QUANDLES OF SURFACES
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-18
-
- Article
- Export citation
Impact of universal chlorhexidine bathing with or without COVID-19 intensive training on staff and resident COVID-19 case rates in nursing homes
-
- Journal:
- Infection Control & Hospital Epidemiology , First View
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-4
-
- Article
- Export citation
Metrology for sub-Rayleigh-length target positioning in ~1022 W/cm2 laser-plasma experiments
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-58
-
- Article
-
- You have access
- Open access
- Export citation
Influence of Citric Acid and Glycine on the Adsorption of Mercury (II) by Kaolinite under Various pH Conditions
-
- Journal:
- Clays and Clay Minerals / Volume 44 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 28 February 2024, pp. 41-48
-
- Article
- Export citation
High touch surface bioburden associated with the use of disinfectants with and without continuously active disinfection in ambulatory care settings
-
- Journal:
- Infection Control & Hospital Epidemiology , First View
- Published online by Cambridge University Press:
- 20 February 2024, pp. 1-3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polarization insensitive passive loaded wideband metamaterial absorber
-
- Journal:
- International Journal of Microwave and Wireless Technologies , First View
- Published online by Cambridge University Press:
- 08 February 2024, pp. 1-9
-
- Article
- Export citation
Diagnostic stewardship to improve patient outcomes and healthcare-associated infection (HAI) metrics
- Part of
-
- Journal:
- Infection Control & Hospital Epidemiology / Volume 45 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 405-411
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantifying racial disparities in risk of invasive Staphylococcus aureus infection in Metropolitan Atlanta, Georgia, during the 2020–2021 coronavirus disease 2019 (COVID-19) pandemic
-
- Journal:
- Infection Control & Hospital Epidemiology / Volume 45 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 534-536
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Very long chain fatty acid–inhibiting herbicides: Current uses, site of action, herbicide-resistant weeds, and future
-
- Journal:
- Weed Technology / Volume 38 / 2024
- Published online by Cambridge University Press:
- 21 December 2023, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ten New Insights in Climate Science 2023/2024
-
- Journal:
- Global Sustainability / Accepted manuscript
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1-58
-
- Article
-
- You have access
- Open access
- Export citation
Genetic diversity and population structure analysis in early generations maize inbreds derived from local germplasm of Eastern Himalayan regions using microsatellite markers
-
- Journal:
- Plant Genetic Resources / Volume 21 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 29 November 2023, pp. 418-425
-
- Article
- Export citation
Collection, distribution, characterization and utilization of Indigofera oblongifolia Forssk.: an important underutilized multi-use leguminous shrub of Indian hot arid region
-
- Journal:
- Plant Genetic Resources / Volume 21 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 17 November 2023, pp. 369-376
-
- Article
- Export citation
7 - Music as the Language of the Bahujan Movement: Locating the Social History of the Dalit Shoshit Samaj Sangharsh Samiti
- from Part II - Popular Culture, Discourse, and Protest
-
-
- Book:
- Dalits in the New Millennium
- Published online:
- 12 July 2023
- Print publication:
- 16 November 2023, pp 115-132
-
- Chapter
- Export citation
Left ventricle hypertrophy and re-modeling in children with essential hypertension: does the race matter?
-
- Journal:
- Cardiology in the Young / Volume 34 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 906-913
-
- Article
- Export citation