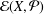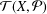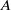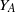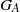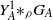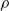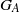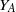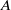11 results
Prefix monoids of groups and right units of special inverse monoids
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 30 October 2023, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted Brauer monoids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 731-750
- Print publication:
- August 2018
-
- Article
- Export citation
FINITE REGULAR BANDS ARE FINITELY RELATED – RETRACTION
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 30 March 2017, p. 352
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
THE IDEMPOTENT-GENERATED SUBSEMIGROUP OF THE KAUFFMAN MONOID
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 673-683
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Automorphism groups of countable algebraically closed graphs and endomorphisms of the random graph
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 160 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 21 January 2016, pp. 437-462
- Print publication:
- May 2016
-
- Article
- Export citation
IDEMPOTENT RANK IN THE ENDOMORPHISM MONOID OF A NONUNIFORM PARTITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 10 August 2015, pp. 73-91
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
ON FREE SPECTRA OF A CLASS OF FINITE INVERSE MONOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 March 2013, pp. 225-237
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
FINITE REGULAR BANDS ARE FINITELY RELATED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1-9
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
A universality result for endomorphism monoids of some ultrahomogeneous structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 635-656
-
- Article
-
- You have access
- Export citation
ON FREE SPECTRA OF LOCALLY TESTABLE SEMIGROUP VARIETIES
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 10 March 2011, pp. 623-629
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
ON RESIDUALLY FINITE VARIETIES OF INVOLUTION SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 December 2010, pp. 181-198
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation



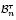 , comparing and contrasting it with the structure of the (untwisted) Brauer monoid
, comparing and contrasting it with the structure of the (untwisted) Brauer monoid 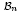 . We characterize Green's relations and pre-orders on
. We characterize Green's relations and pre-orders on