In this paper, we consider the following critical Kirchhoff type equation:
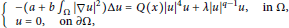 $$\left\{ _{u\,=\,0,\,\,\,\,\,\,\text{on}\,\partial \Omega \text{,}}^{-(a\,+\,b{{\int }_{\Omega }}|\nabla u{{|}^{2}})\Delta u\,=\,\text{Q(}x)|u{{|}^{4}}u\,+\,\lambda |u{{|}^{q-1}}u,\,\,\,\text{in}\,\Omega \text{,}} \right.$$
$$\left\{ _{u\,=\,0,\,\,\,\,\,\,\text{on}\,\partial \Omega \text{,}}^{-(a\,+\,b{{\int }_{\Omega }}|\nabla u{{|}^{2}})\Delta u\,=\,\text{Q(}x)|u{{|}^{4}}u\,+\,\lambda |u{{|}^{q-1}}u,\,\,\,\text{in}\,\Omega \text{,}} \right.$$
By using variational methods that are constrained to the Nehari manifold, we prove that the above equation has a ground state solution for the case when 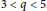 $3\,<\,q\,<\,5$. The relation between the number of maxima of
$3\,<\,q\,<\,5$. The relation between the number of maxima of 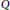 $\text{Q}$ and the number of positive solutions for the problem is also investigated.
$\text{Q}$ and the number of positive solutions for the problem is also investigated.