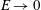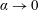8 results
Development of an EORTC Quality of Life Module for Renal Cell Cancer Patients: Phase I
-
- Journal:
- European Psychiatry / Volume 65 / Issue S1 / June 2022
- Published online by Cambridge University Press:
- 01 September 2022, p. S756
-
- Article
-
- You have access
- Open access
- Export citation
Mixing and entrainment are suppressed in inclined gravity currents
-
- Journal:
- Journal of Fluid Mechanics / Volume 873 / 25 August 2019
- Published online by Cambridge University Press:
- 28 June 2019, pp. 786-815
-
- Article
- Export citation
Nondestructive Materials Characterization in 3D by Laboratory Diffraction Contrast Tomography – Applications and Future Directions
-
- Journal:
- Microscopy and Microanalysis / Volume 22 / Issue S3 / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 1970-1971
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
Diffraction Contrast Tomography in the Laboratory – Applications and Future Directions
-
- Journal:
- Microscopy Today / Volume 24 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 17 June 2016, pp. 34-43
- Print publication:
- July 2016
-
- Article
-
- You have access
- HTML
- Export citation
3D Crystallographic Imaging Using Laboratory-Based Diffraction Contrast Tomography (DCT)
-
- Journal:
- Microscopy and Microanalysis / Volume 21 / Issue S3 / August 2015
- Published online by Cambridge University Press:
- 23 September 2015, pp. 603-604
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Experimental investigation of transitional flow in a toroidal pipe
-
- Journal:
- Journal of Fluid Mechanics / Volume 738 / 10 January 2014
- Published online by Cambridge University Press:
- 13 December 2013, pp. 463-491
-
- Article
- Export citation
Large volume, non-destructive 3D analysis of low-density materials and interfaces with phase contrast X-ray microscopy
-
- Journal:
- Microscopy and Microanalysis / Volume 18 / Issue S2 / July 2012
- Published online by Cambridge University Press:
- 23 November 2012, pp. 516-517
- Print publication:
- July 2012
-
- Article
- Export citation
Quantitative Reconstruction of Differential Phase Contrast Images Obtained With a Configured Detector Using a Scanning Transmission X-Ray Microscope
-
- Journal:
- Microscopy and Microanalysis / Volume 13 / Issue S02 / August 2007
- Published online by Cambridge University Press:
- 05 August 2007, pp. 1574-1575
- Print publication:
- August 2007
-
- Article
- Export citation