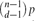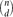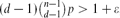14 results
Optimal group testing
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 811-848
-
- Article
- Export citation
The replica symmetric phase of random constraint satisfaction problems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 03 December 2019, pp. 346-422
-
- Article
- Export citation
The Number of Satisfying Assignments of Random Regular k-SAT Formulas
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 20 June 2018, pp. 496-530
-
- Article
- Export citation
Planting Colourings Silently
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 338-366
-
- Article
- Export citation
‘The Asymptotic Number of Connected d-Uniform Hypergraphs’ — CORRIGENDUM
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 373-375
-
- Article
-
- You have access
- Export citation
The Asymptotic Number of Connected d-Uniform Hypergraphs†
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 13 February 2014, pp. 367-385
-
- Article
- Export citation
Local Limit Theorems for the Giant Component of Random Hypergraphs†
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 13 February 2014, pp. 331-366
-
- Article
- Export citation
Graph Partitioning via Adaptive Spectral Techniques
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 13 November 2009, pp. 227-284
-
- Article
- Export citation
A Spectral Approach to Analysing Belief Propagation for 3-Colouring
-
- Journal:
- Combinatorics, Probability and Computing / Volume 18 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 24 March 2009, pp. 881-912
-
- Article
- Export citation
On the Laplacian Eigenvalues of Gn,p
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 923-946
-
- Article
- Export citation
Colouring Semirandom Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 4 / July 2007
- Published online by Cambridge University Press:
- 01 July 2007, pp. 515-552
-
- Article
- Export citation
Strong Refutation Heuristics for Random k-SAT
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 14 August 2006, pp. 5-28
-
- Article
- Export citation
Finding Large Independent Sets in Polynomial Expected Time
-
- Journal:
- Combinatorics, Probability and Computing / Volume 15 / Issue 5 / September 2006
- Published online by Cambridge University Press:
- 31 July 2006, pp. 731-751
-
- Article
- Export citation
The Lovász Number of Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 14 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 21 July 2005, pp. 439-465
-
- Article
- Export citation