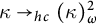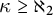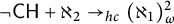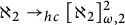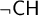1 Introduction
The paper studies weak versions of the Ramsey theorem on uncountable cardinals. Following [Reference Bergfalk, Hrušák and Shelah5], we say that a graph
![]() $G=(X,E)$
is highly connected if for every
$G=(X,E)$
is highly connected if for every
![]() $Y\subseteq X$
of cardinality strictly smaller than
$Y\subseteq X$
of cardinality strictly smaller than
![]() $|X|$
, the subgraph
$|X|$
, the subgraph
![]() $(X\setminus Y , E\cap [X\setminus Y]^2)$
is connected. Given cardinal numbers
$(X\setminus Y , E\cap [X\setminus Y]^2)$
is connected. Given cardinal numbers
![]() $\theta \leq \lambda \leq \kappa $
,
$\theta \leq \lambda \leq \kappa $
,
denotes the statement that for every
![]() $c:[\kappa ]^2\to \theta $
, there is an
$c:[\kappa ]^2\to \theta $
, there is an
![]() $\xi \in \theta $
and
$\xi \in \theta $
and
![]() $A\in [\kappa ]^\lambda $
such that
$A\in [\kappa ]^\lambda $
such that
![]() $(A, c^{-1}(\xi )\cap [A]^2)$
is highly connected, in which case we shall say that A is highly connected in color
$(A, c^{-1}(\xi )\cap [A]^2)$
is highly connected, in which case we shall say that A is highly connected in color
![]() $\xi $
.
$\xi $
.
The original motivation for studying this partition relation came from the study of higher derived limits in forcing extensions (see [Reference Bannister, Bergfalk, Moore and Todorcevic2, Reference Bergfalk, Hrušák and Lambie-Hanson4, Reference Bergfalk and Lambie-Hanson6, Reference Veličković and Vignati19] and [Reference Mitchell18]) and is related in spirit to both the partition hypotheses of [Reference Bannister, Bergfalk, Moore and Todorcevic2] and another weak Ramsey property concerning the so-called topological
![]() $K_\kappa $
(first studied by Erdős and Hajnal in [Reference Erdős and Hajnal8]) considered by Komjáth and Shelah in [Reference Komjáth and Shelah15].
$K_\kappa $
(first studied by Erdős and Hajnal in [Reference Erdős and Hajnal8]) considered by Komjáth and Shelah in [Reference Komjáth and Shelah15].
This paper continues the study initiated in [Reference Bergfalk, Hrušák and Shelah5] and further investigated in [Reference Bergfalk3, Reference Lambie-Hanson16] of those cardinals
![]() $\theta < \lambda \leq \kappa $
for which the
$\theta < \lambda \leq \kappa $
for which the
![]() $\to _{hc}$
arrow holds. Among the facts proved in [Reference Bergfalk, Hrušák and Shelah5] are:
$\to _{hc}$
arrow holds. Among the facts proved in [Reference Bergfalk, Hrušák and Shelah5] are:
-
• for every infinite cardinal
 $\kappa $
and natural number n,
$\kappa $
and natural number n,
 $\kappa \to _{hc}(\kappa )^2_n$
,
$\kappa \to _{hc}(\kappa )^2_n$
, -
• if
 $\kappa \leq 2^\theta $
, then
$\kappa \leq 2^\theta $
, then
 $\kappa \not \to _{hc}(\kappa )^2_\theta $
, and
$\kappa \not \to _{hc}(\kappa )^2_\theta $
, and -
• if
 $\lambda =\lambda ^\theta $
, then
$\lambda =\lambda ^\theta $
, then
 $\lambda ^+\to _{hc}(\lambda )^2_\theta $
;
$\lambda ^+\to _{hc}(\lambda )^2_\theta $
;
in particular,
![]() $2^\omega \not \to _{hc} (2^\omega )^2_\omega $
. On the other hand, it was shown there that assuming the existence of a weakly compact cardinal, consistently
$2^\omega \not \to _{hc} (2^\omega )^2_\omega $
. On the other hand, it was shown there that assuming the existence of a weakly compact cardinal, consistently
![]() $2^{\omega _1}\to _{hc}(2^{\omega _1})^2_\omega $
. However, in the model witnessing this relation,
$2^{\omega _1}\to _{hc}(2^{\omega _1})^2_\omega $
. However, in the model witnessing this relation,
![]() $2^{\omega _1}$
is weakly inaccessible, being a former large cardinal in a forcing extension by a poset satisfying a small chain condition.
$2^{\omega _1}$
is weakly inaccessible, being a former large cardinal in a forcing extension by a poset satisfying a small chain condition.
In light of the results mentioned above, the following natural questions were raised in [Reference Bergfalk3, Reference Bergfalk, Hrušák and Shelah5]:
-
(1) Is it consistent that
 $\kappa \to _{hc}(\kappa )^2_{\omega }$
holds for an accessible
$\kappa \to _{hc}(\kappa )^2_{\omega }$
holds for an accessible
 $\kappa $
? For example, when
$\kappa $
? For example, when
 $\kappa $
is
$\kappa $
is
 $\aleph _2$
or
$\aleph _2$
or
 $\aleph _{\omega +1}$
?
$\aleph _{\omega +1}$
? -
(2) Is
 $\aleph _2\to _{hc}(\aleph _1)^2_\omega $
equivalent to the Continuum Hypothesis?
$\aleph _2\to _{hc}(\aleph _1)^2_\omega $
equivalent to the Continuum Hypothesis?
Note that by a result of Lambie-Hanson [Reference Lambie-Hanson16], if
![]() $\kappa \to _{hc}(\kappa )^2_{\omega }$
holds, then
$\kappa \to _{hc}(\kappa )^2_{\omega }$
holds, then
![]() $\square (\kappa )$
necessarily fails. In particular, if
$\square (\kappa )$
necessarily fails. In particular, if
![]() $\aleph _2\to _{hc}(\aleph _2)^2_{\omega }$
were to hold, our arguments would require at least a weakly compact cardinal, and if
$\aleph _2\to _{hc}(\aleph _2)^2_{\omega }$
were to hold, our arguments would require at least a weakly compact cardinal, and if
![]() $\aleph _{\omega +1}\to _{hc}(\aleph _{\omega +1})^2_{\omega }$
were to hold, then our arguments would require significantly stronger large cardinals.
$\aleph _{\omega +1}\to _{hc}(\aleph _{\omega +1})^2_{\omega }$
were to hold, then our arguments would require significantly stronger large cardinals.
Here, we answer the first question in the positive and the second question in the negative by analyzing remnants of large cardinal properties on smaller cardinals after suitable forcing, often the Levy or Mitchell collapse, in the form of the existence of ideals having strong combinatorial properties.
We finish this section with a few more definitions and notations. Let
![]() $\kappa $
be a regular uncountable cardinal.
$\kappa $
be a regular uncountable cardinal.
Definition 1.2 Fix
![]() $k\in \omega $
. We let
$k\in \omega $
. We let
to abbreviate the assertion that for any
![]() $c: [\kappa ]^2\to \omega $
, there exist
$c: [\kappa ]^2\to \omega $
, there exist
![]() $H\in [\kappa ]^{\kappa }$
and
$H\in [\kappa ]^{\kappa }$
and
![]() $K \in [\omega ]^k$
such that
$K \in [\omega ]^k$
such that
![]() $(H, c^{-1}(K))\cap [H]^2)$
is highly connected.
$(H, c^{-1}(K))\cap [H]^2)$
is highly connected.
The following is a more refined variation of the highly connected partition relations, conditioned on the lengths of the paths.
Definition 1.3 Fix
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\kappa \to _{hc, <n}(\kappa )^2_\omega $
abbreviate
$\kappa \to _{hc, <n}(\kappa )^2_\omega $
abbreviate
![]() $\kappa \to _{hc}(\kappa )^2_\omega $
via paths of length
$\kappa \to _{hc}(\kappa )^2_\omega $
via paths of length
![]() $<n$
. More precisely, it asserts: for any
$<n$
. More precisely, it asserts: for any
![]() $c: [\kappa ]^2\to \omega $
, there exists
$c: [\kappa ]^2\to \omega $
, there exists
![]() $A\in [\kappa ]^\kappa $
and
$A\in [\kappa ]^\kappa $
and
![]() $i\in \omega $
such that for any
$i\in \omega $
such that for any
![]() $C\in [A]^{<\kappa }$
and
$C\in [A]^{<\kappa }$
and
![]() $\alpha ,\beta \in A \backslash C$
, there exist
$\alpha ,\beta \in A \backslash C$
, there exist
![]() $l<n$
and a path
$l<n$
and a path
![]() $\langle \gamma _k: k<l+1\rangle \subseteq A\backslash C$
with
$\langle \gamma _k: k<l+1\rangle \subseteq A\backslash C$
with
![]() $\gamma _0=\alpha $
and
$\gamma _0=\alpha $
and
![]() $ \gamma _{l}=\beta $
such that for all
$ \gamma _{l}=\beta $
such that for all
![]() $j<l$
,
$j<l$
,
![]() $c(\gamma _{j}, \gamma _{j+1})=i$
.
$c(\gamma _{j}, \gamma _{j+1})=i$
.
The organization of the paper is:
-
(1) in Section 2, we establish the consistency of
 $\aleph _2\to _{hc} (\aleph _1)^2_{\omega } $
and
$\aleph _2\to _{hc} (\aleph _1)^2_{\omega } $
and
 $\neg \mathsf {CH}$
,
$\neg \mathsf {CH}$
, -
(2) in Section 3, we isolate and investigate 2-precipitous ideals (see Definition 3.1) whose existence implies
 $\kappa \to _{hc}[\kappa ]^2_{\omega ,2}$
,
$\kappa \to _{hc}[\kappa ]^2_{\omega ,2}$
, -
(3) in Section 4, we demonstrate two methods of constructing 2-precipitous ideals and show that
 $\aleph _2\to _{hc}[\aleph _2]^2_{\omega ,2} + 2^{\aleph _0} \geq \aleph _2$
is consistent,
$\aleph _2\to _{hc}[\aleph _2]^2_{\omega ,2} + 2^{\aleph _0} \geq \aleph _2$
is consistent, -
(4) in Section 5, we deduce the consistency of
 $\aleph _2\to _{hc}(\aleph _2)^2_{\omega }$
from an ideal hypothesis,
$\aleph _2\to _{hc}(\aleph _2)^2_{\omega }$
from an ideal hypothesis, -
(5) in Section 6, we sketch how to use large cardinals to establish the consistency of the ideal hypothesis used in Section 5,
-
(6) in Section 7, we show we cannot improve the result in Section 6 by making the lengths of the paths required to connect vertices shorter,
-
(7) finally in Section 8, we finish with some open questions.
2 The consistency of
 $\aleph _2\to _{hc} (\aleph _1)^2_{\omega } + \neg \mathsf {CH}$
$\aleph _2\to _{hc} (\aleph _1)^2_{\omega } + \neg \mathsf {CH}$
We call an ideal I on
![]() $\omega _1 \aleph _1$
-proper with respect to
$\omega _1 \aleph _1$
-proper with respect to
![]() $S\subseteq P_{\aleph _2}(H(\theta ))$
where
$S\subseteq P_{\aleph _2}(H(\theta ))$
where
![]() $\theta $
is a large enough regular cardinal if for any
$\theta $
is a large enough regular cardinal if for any
![]() $M\in S$
and
$M\in S$
and
![]() $X\in M\cap I^+$
, there exists an extension
$X\in M\cap I^+$
, there exists an extension
![]() $Y\subseteq _I X$
such that Y is
$Y\subseteq _I X$
such that Y is
![]() $(M,I^+)$
-generic, meaning that for any dense
$(M,I^+)$
-generic, meaning that for any dense
![]() $D\subseteq I^+$
with
$D\subseteq I^+$
with
![]() $D\in M$
and any
$D\in M$
and any
![]() $Y'\subseteq _I Y$
, there exists
$Y'\subseteq _I Y$
, there exists
![]() $Z\in D\cap M$
such that
$Z\in D\cap M$
such that
![]() $Y'\cap Z\in I^+$
.
$Y'\cap Z\in I^+$
.
Lemma 2.1 If I is
![]() $\aleph _1$
-proper with respect to
$\aleph _1$
-proper with respect to
![]() $\{M\}$
with
$\{M\}$
with
![]() $M\prec H(\theta )$
of size
$M\prec H(\theta )$
of size
![]() $\aleph _1$
containing I, then whenever
$\aleph _1$
containing I, then whenever
![]() $Y\in I^+$
is an
$Y\in I^+$
is an
![]() $(M, I^+)$
-generic condition, the following holds:
$(M, I^+)$
-generic condition, the following holds:
for any
![]() $E\subseteq I^+$
in M, if there is some
$E\subseteq I^+$
in M, if there is some
![]() $Y'\in E$
such that
$Y'\in E$
such that
![]() $Y\subseteq _I Y'$
, then there exists
$Y\subseteq _I Y'$
, then there exists
![]() $Z\in E\cap M$
such that
$Z\in E\cap M$
such that
![]() $Y\cap Z\in I^+$
.
$Y\cap Z\in I^+$
.
Proof Define a dense subseteq
![]() $D_E\subseteq I^+$
in M as follows:
$D_E\subseteq I^+$
in M as follows:
![]() $A\in D_E$
iff either there exists
$A\in D_E$
iff either there exists
![]() $B\in E$
,
$B\in E$
,
![]() $A\subseteq _I B$
or for all
$A\subseteq _I B$
or for all
![]() $B\in E$
,
$B\in E$
,
![]() $A\cap B =_I \emptyset $
. By the hypothesis, there exists
$A\cap B =_I \emptyset $
. By the hypothesis, there exists
![]() $Z'\in D_E\cap M$
such that
$Z'\in D_E\cap M$
such that
![]() $Y\cap Z'\in I^+$
. Note that there exists
$Y\cap Z'\in I^+$
. Note that there exists
![]() $Z\in E$
such that
$Z\in E$
such that
![]() $Z'\subseteq _I Z$
since
$Z'\subseteq _I Z$
since
![]() $Z'\cap Y \neq _I \emptyset $
and
$Z'\cap Y \neq _I \emptyset $
and
![]() $Y\subseteq _I Y'\in E$
. The elementarity of M then guarantees the existence of such
$Y\subseteq _I Y'\in E$
. The elementarity of M then guarantees the existence of such
![]() $Z\in M$
.
$Z\in M$
.
If I is
![]() $\aleph _2$
-saturated, then I is
$\aleph _2$
-saturated, then I is
![]() $\aleph _1$
-proper with respect to a closed unbounded subset of
$\aleph _1$
-proper with respect to a closed unbounded subset of
![]() $P_{\aleph _2}(H(\theta ))$
for sufficiently large
$P_{\aleph _2}(H(\theta ))$
for sufficiently large
![]() $\theta $
. There are many models where
$\theta $
. There are many models where
![]() $\omega _1$
carries a
$\omega _1$
carries a
![]() $\sigma $
-complete
$\sigma $
-complete
![]() $\aleph _2$
-saturated ideal and
$\aleph _2$
-saturated ideal and
![]() $\mathsf {CH}$
fails. For example, they are both consequences of Martin’s Maximum [Reference Foreman, Magidor and Shelah10].
$\mathsf {CH}$
fails. For example, they are both consequences of Martin’s Maximum [Reference Foreman, Magidor and Shelah10].
Proposition 2.2 If there exists a
![]() $\sigma $
-complete
$\sigma $
-complete
![]() $\aleph _1$
-proper ideal on
$\aleph _1$
-proper ideal on
![]() $\omega _1$
with respect to a stationary subset of
$\omega _1$
with respect to a stationary subset of
![]() $\{X\in P_{\aleph _2}(H(\theta )): \sup X\cap \omega _2\in \mathrm {cof}(\omega _1) \}$
for some large enough
$\{X\in P_{\aleph _2}(H(\theta )): \sup X\cap \omega _2\in \mathrm {cof}(\omega _1) \}$
for some large enough
![]() $\theta $
, then
$\theta $
, then
![]() $\aleph _2\to _{hc} (\aleph _1)^2_{\omega }$
.Footnote
1
$\aleph _2\to _{hc} (\aleph _1)^2_{\omega }$
.Footnote
1
Proof Given
![]() $c: [\omega _2]^2\to \omega $
, we will find
$c: [\omega _2]^2\to \omega $
, we will find
![]() $A\in [\omega _1]^{\aleph _1}$
and
$A\in [\omega _1]^{\aleph _1}$
and
![]() $B\in [\omega _2 \setminus \omega _1]^{\aleph _1}$
satisfying the following properties: there exists
$B\in [\omega _2 \setminus \omega _1]^{\aleph _1}$
satisfying the following properties: there exists
![]() $k\in \omega $
such that:
$k\in \omega $
such that:
-
(1) for any
 $\alpha _0,\alpha _1\in A$
, there are uncountably many
$\alpha _0,\alpha _1\in A$
, there are uncountably many
 $\beta \in B$
such that
$\beta \in B$
such that
 $c(\alpha _0,\beta )=k=c(\alpha _1, \beta )$
, and
$c(\alpha _0,\beta )=k=c(\alpha _1, \beta )$
, and -
(2) for any
 $\beta _0\in B$
, there are uncountably many
$\beta _0\in B$
, there are uncountably many
 $\alpha \in A$
satisfies that
$\alpha \in A$
satisfies that
 $c(\alpha ,\beta _0)=k$
.
$c(\alpha ,\beta _0)=k$
.
Claim 2.3
![]() $A\cup B$
is highly connected in the color k.
$A\cup B$
is highly connected in the color k.
Proof of the claim
Let C be the countable set of vertices being removed. If
![]() $\alpha _0, \alpha _1\in A\backslash C$
, then it follows immediately by the first requirement that there is some
$\alpha _0, \alpha _1\in A\backslash C$
, then it follows immediately by the first requirement that there is some
![]() $\beta \in B\backslash C$
such that
$\beta \in B\backslash C$
such that
![]() $c(\alpha _0,\beta )=c(\alpha _1,\beta )=k$
.
$c(\alpha _0,\beta )=c(\alpha _1,\beta )=k$
.
Let us check the case when
![]() $\alpha \in A\backslash C$
and
$\alpha \in A\backslash C$
and
![]() $\beta \in B\backslash C$
. We can find some large enough
$\beta \in B\backslash C$
. We can find some large enough
![]() $\alpha '\in A\backslash C$
such that
$\alpha '\in A\backslash C$
such that
![]() $c(\alpha ',\beta )=k$
. After that, we find some
$c(\alpha ',\beta )=k$
. After that, we find some
![]() $\beta '\in B \backslash C$
such that
$\beta '\in B \backslash C$
such that
![]() $c(\alpha ',\beta ')=k=c(\alpha ,\beta ')$
. Then
$c(\alpha ',\beta ')=k=c(\alpha ,\beta ')$
. Then
![]() $\alpha $
is connected to
$\alpha $
is connected to
![]() $\beta $
via the k-path:
$\beta $
via the k-path:
![]() $\alpha , \beta ', \alpha ',\beta $
.
$\alpha , \beta ', \alpha ',\beta $
.
If
![]() $\beta _0,\beta _1\in B\backslash C$
, then we can easily reduce to the previous case by finding some large enough
$\beta _0,\beta _1\in B\backslash C$
, then we can easily reduce to the previous case by finding some large enough
![]() $\alpha _0\in A\backslash C$
such that
$\alpha _0\in A\backslash C$
such that
![]() $c(\alpha _0, \beta _0)=k$
. Apply the previous analysis to
$c(\alpha _0, \beta _0)=k$
. Apply the previous analysis to
![]() $\alpha _0\in A\backslash C, \beta _1\in B\backslash C$
.
$\alpha _0\in A\backslash C, \beta _1\in B\backslash C$
.
We proceed to find
![]() $A, B, k$
as above. For each
$A, B, k$
as above. For each
![]() $\alpha \in \omega _2\backslash \omega _1$
and
$\alpha \in \omega _2\backslash \omega _1$
and
![]() $i\in \omega $
, let
$i\in \omega $
, let
Let
![]() $M\prec H(\theta )$
of size
$M\prec H(\theta )$
of size
![]() $\aleph _1$
contain
$\aleph _1$
contain
![]() $I, c$
with
$I, c$
with
![]() $\sup M\cap \omega _2\in \mathrm {cof}(\omega _1)$
, and let
$\sup M\cap \omega _2\in \mathrm {cof}(\omega _1)$
, and let
![]() $Y\in I^+$
be
$Y\in I^+$
be
![]() $(M,I^+)$
-generic. Let
$(M,I^+)$
-generic. Let
![]() $\rho \in \omega _2 \backslash \sup M\cap \omega _2$
. By the
$\rho \in \omega _2 \backslash \sup M\cap \omega _2$
. By the
![]() $\sigma $
-completeness of I, find some
$\sigma $
-completeness of I, find some
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $A=Y\cap X_{\rho , k}\in I^+$
, which is still
$A=Y\cap X_{\rho , k}\in I^+$
, which is still
![]() $(M,I^+)$
-generic, since it extends Y which is
$(M,I^+)$
-generic, since it extends Y which is
![]() $(M, I^+)$
-generic. Finally, let us define B recursively. Let
$(M, I^+)$
-generic. Finally, let us define B recursively. Let
![]() $\langle a^i=(a^i_0, a^i_1): i<\omega _1\rangle $
enumerate
$\langle a^i=(a^i_0, a^i_1): i<\omega _1\rangle $
enumerate
![]() $[A]^2$
with unbounded repetitions. Suppose we have defined
$[A]^2$
with unbounded repetitions. Suppose we have defined
![]() $\langle \beta _j: j<\alpha \rangle $
for some
$\langle \beta _j: j<\alpha \rangle $
for some
![]() $\alpha <\omega _1$
satisfying that for all
$\alpha <\omega _1$
satisfying that for all
![]() $j<\alpha $
,
$j<\alpha $
,
-
(1)
 $a^j\subseteq X_{\beta _j, k}$
and
$a^j\subseteq X_{\beta _j, k}$
and -
(2)
 $X_{\beta _j,k}\cap A\in I^+$
.
$X_{\beta _j,k}\cap A\in I^+$
.
It is clear if we may extend the construction through all
![]() $\alpha <\omega _1$
, then
$\alpha <\omega _1$
, then
![]() $A, B=\{\beta _j: j<\omega _1\}$
and k are as desired.
$A, B=\{\beta _j: j<\omega _1\}$
and k are as desired.
Suppose we are at the
![]() $\alpha $
th step of the construction, and let us find
$\alpha $
th step of the construction, and let us find
![]() $\beta _\alpha $
maintaining the same requirements. Let
$\beta _\alpha $
maintaining the same requirements. Let
![]() $\bar {\beta }=\min (M \backslash \sup _{j<\alpha }\beta _j)<\sup M\cap \omega _2$
. Consider
$\bar {\beta }=\min (M \backslash \sup _{j<\alpha }\beta _j)<\sup M\cap \omega _2$
. Consider
![]() $E=\{X_{\beta ,k}\in I^+: a^\alpha _0, a^\alpha _1\in X_{\beta ,k}, \beta>\bar {\beta }\}$
. In particular,
$E=\{X_{\beta ,k}\in I^+: a^\alpha _0, a^\alpha _1\in X_{\beta ,k}, \beta>\bar {\beta }\}$
. In particular,
![]() $E\in M$
and
$E\in M$
and
![]() $A\subseteq _I X_{\rho ,k}\in E$
. By Lemma 2.1, there exists a
$A\subseteq _I X_{\rho ,k}\in E$
. By Lemma 2.1, there exists a
![]() $\beta>\bar {\beta }$
such that
$\beta>\bar {\beta }$
such that
![]() $X_{\beta ,k}\in M\cap E$
such that
$X_{\beta ,k}\in M\cap E$
such that
![]() $A\cap X_{\beta ,k}\in I^+$
; letting
$A\cap X_{\beta ,k}\in I^+$
; letting
![]() $\beta _\alpha =\beta $
completes the
$\beta _\alpha =\beta $
completes the
![]() $\alpha $
th step.
$\alpha $
th step.
3 2-precipitous ideals on
 $\kappa $
and
$\kappa $
and
 $\kappa \to _{hc} [\kappa ]^2_{\omega ,2}$
$\kappa \to _{hc} [\kappa ]^2_{\omega ,2}$
Lambie-Hanson [Reference Lambie-Hanson16] showed that adding weakly compact many Cohen reals forces that
![]() $2^\omega \to _{hc} [2^\omega ]^2_{\omega ,2}$
, in contrast with the ZFC fact that
$2^\omega \to _{hc} [2^\omega ]^2_{\omega ,2}$
, in contrast with the ZFC fact that
![]() $2^\omega \not \to _{hc} (2^\omega )^2_{\omega }$
. He also demonstrated that such partition relations already have nontrivial consistency strength, by showing that
$2^\omega \not \to _{hc} (2^\omega )^2_{\omega }$
. He also demonstrated that such partition relations already have nontrivial consistency strength, by showing that
![]() $\square (\kappa )$
implies
$\square (\kappa )$
implies
![]() $\kappa \not \to _{hc}[\kappa ]^2_{\omega , <\omega }$
.
$\kappa \not \to _{hc}[\kappa ]^2_{\omega , <\omega }$
.
In this section, we investigate the ideal hypothesis on
![]() $\kappa $
that implies
$\kappa $
that implies
![]() $\kappa \to _{hc} [\kappa ]^2_{\omega ,2}$
. In particular, such analysis enables us to have more consistent scenarios, such as a model where
$\kappa \to _{hc} [\kappa ]^2_{\omega ,2}$
. In particular, such analysis enables us to have more consistent scenarios, such as a model where
![]() $2^{\aleph _0}\geq \aleph _2$
and
$2^{\aleph _0}\geq \aleph _2$
and
![]() $\aleph _2\to _{hc} [\aleph _2]^2_{\omega ,2}$
both hold.
$\aleph _2\to _{hc} [\aleph _2]^2_{\omega ,2}$
both hold.
Definition 3.1 We say an ideal I on
![]() $\kappa $
is 2-precipitous if Player Empty does not have a winning strategy in the following game
$\kappa $
is 2-precipitous if Player Empty does not have a winning strategy in the following game
![]() $G_{I}$
with perfect information: Player Empty and Nonempty take turns playing a
$G_{I}$
with perfect information: Player Empty and Nonempty take turns playing a
![]() $\subseteq $
-decreasing sequence of pairs of I-positive sets
$\subseteq $
-decreasing sequence of pairs of I-positive sets
![]() $\langle (A_n, B_n): n\in \omega \rangle $
with Player Empty starting the game. Player Nonempty wins iff there exist
$\langle (A_n, B_n): n\in \omega \rangle $
with Player Empty starting the game. Player Nonempty wins iff there exist
![]() $\alpha <\beta $
with
$\alpha <\beta $
with
![]() $\alpha \in \bigcap _{n\in \omega } A_n$
and
$\alpha \in \bigcap _{n\in \omega } A_n$
and
![]() $\beta \in \bigcap _{n\in \omega } B_n$
.
$\beta \in \bigcap _{n\in \omega } B_n$
.
Lemma 3.2 Fix a dense subset
![]() $D\subseteq P(\kappa )/I$
. Player Empty has a winning strategy in
$D\subseteq P(\kappa )/I$
. Player Empty has a winning strategy in
![]() $G_I$
iff Player Empty has a winning strategy
$G_I$
iff Player Empty has a winning strategy
![]() $\sigma $
in
$\sigma $
in
![]() $G_I$
such that
$G_I$
such that
![]() $range(\sigma )\subseteq \{A \backslash M: A\in D, M\in I\}$
.
$range(\sigma )\subseteq \{A \backslash M: A\in D, M\in I\}$
.
Proof Let us show the nontrivial direction
![]() $(\rightarrow )$
. Fix a winning strategy
$(\rightarrow )$
. Fix a winning strategy
![]() $\sigma $
of Player Empty. The input of
$\sigma $
of Player Empty. The input of
![]() $\sigma $
will be
$\sigma $
will be
![]() $(I^+\times I^+)^{<\omega }$
, corresponding to the sequence of positive sets Player Nonempty has played so far. Let
$(I^+\times I^+)^{<\omega }$
, corresponding to the sequence of positive sets Player Nonempty has played so far. Let
![]() $\pi : I^+ \to I^+$
be a map such that
$\pi : I^+ \to I^+$
be a map such that
![]() $\pi (B)=A \backslash M$
where
$\pi (B)=A \backslash M$
where
![]() $(A,M)\in D\times I$
is least (with respect to some fixed well-ordering) such that
$(A,M)\in D\times I$
is least (with respect to some fixed well-ordering) such that
![]() $A\backslash M\subseteq B$
. Such
$A\backslash M\subseteq B$
. Such
![]() $\pi $
exists since D is dense in
$\pi $
exists since D is dense in
![]() $P(\kappa )/I$
. Consider
$P(\kappa )/I$
. Consider
![]() $\sigma '=\pi \circ \sigma $
. Clearly, the range of
$\sigma '=\pi \circ \sigma $
. Clearly, the range of
![]() $\sigma '$
is a subset of
$\sigma '$
is a subset of
![]() $\{A\backslash M: A\in D, M\in I\}$
. To see that it is a winning strategy for Player Empty, suppose
$\{A\backslash M: A\in D, M\in I\}$
. To see that it is a winning strategy for Player Empty, suppose
![]() $\langle (A_n, B_n): n\in \omega \rangle $
is a play such that Player Empty plays according to
$\langle (A_n, B_n): n\in \omega \rangle $
is a play such that Player Empty plays according to
![]() $\sigma '$
. Notice that
$\sigma '$
. Notice that
![]() $\langle (A^{\prime }_n, B^{\prime }_n): n\in \omega \rangle $
, where
$\langle (A^{\prime }_n, B^{\prime }_n): n\in \omega \rangle $
, where
![]() $(A^{\prime }_n, B^{\prime }_n)=(A_n, B_n)$
when n is odd and
$(A^{\prime }_n, B^{\prime }_n)=(A_n, B_n)$
when n is odd and
![]() $(A^{\prime }_n,B^{\prime }_n)=\sigma (\langle (A_{2k-1}, B_{2k-1}): 2k-1<n\rangle )$
is a legal play where Player Empty is playing according to
$(A^{\prime }_n,B^{\prime }_n)=\sigma (\langle (A_{2k-1}, B_{2k-1}): 2k-1<n\rangle )$
is a legal play where Player Empty is playing according to
![]() $\sigma $
. As a result, there do not exist
$\sigma $
. As a result, there do not exist
![]() $\alpha <\beta $
such that
$\alpha <\beta $
such that
![]() $\alpha \in \bigcap _{n\in \omega } A_n' \subseteq \bigcap _{n\in \omega } A_n$
and
$\alpha \in \bigcap _{n\in \omega } A_n' \subseteq \bigcap _{n\in \omega } A_n$
and
![]() $\beta \in \bigcap _{n\in \omega } B_n'\subseteq \bigcap _{n\in \omega } B_n$
. Therefore,
$\beta \in \bigcap _{n\in \omega } B_n'\subseteq \bigcap _{n\in \omega } B_n$
. Therefore,
![]() $\sigma '$
is a winning strategy for Player Empty.
$\sigma '$
is a winning strategy for Player Empty.
Theorem 3.3 If
![]() $\kappa $
carries a uniform normal
$\kappa $
carries a uniform normal
![]() $2$
-precipitous ideal, then
$2$
-precipitous ideal, then
![]() $\kappa \to _{hc}[\kappa ]^2_{\omega , 2}$
.
$\kappa \to _{hc}[\kappa ]^2_{\omega , 2}$
.
Proof Fix a uniform normal
![]() $2$
-precipitous ideal I on
$2$
-precipitous ideal I on
![]() $\kappa $
and a coloring
$\kappa $
and a coloring
![]() $c: [\kappa ]^2\to \omega $
. Given
$c: [\kappa ]^2\to \omega $
. Given
![]() $A,B$
two sets of ordinals, we let
$A,B$
two sets of ordinals, we let
![]() $A\otimes B=\{(\alpha ,\beta )\in A\times B: \alpha <\beta \}$
. We say a pair of I-positive sets
$A\otimes B=\{(\alpha ,\beta )\in A\times B: \alpha <\beta \}$
. We say a pair of I-positive sets
![]() $(B_0,B_1)$
is
$(B_0,B_1)$
is
![]() $(i,j)$
-frequent if for any I-positive sets
$(i,j)$
-frequent if for any I-positive sets
![]() $B_0'\subseteq B_0$
,
$B_0'\subseteq B_0$
,
![]() $B_1'\subset B_1$
, there are:
$B_1'\subset B_1$
, there are:
-
•
 $\alpha <\beta $
with
$\alpha <\beta $
with
 $\alpha \in B_0', \beta \in B_1'$
such that
$\alpha \in B_0', \beta \in B_1'$
such that
 $c(\alpha ,\beta )=i$
and
$c(\alpha ,\beta )=i$
and -
•
 $\beta '<\alpha '$
with
$\beta '<\alpha '$
with
 $\beta '\in B_1'$
,
$\beta '\in B_1'$
,
 $\alpha '\in B_0'$
such that
$\alpha '\in B_0'$
such that
 $c(\beta ',\alpha ')=j$
.
$c(\beta ',\alpha ')=j$
.
Claim 3.4 There exists a pair of I-positive sets
![]() $(B_0, B_1)$
and
$(B_0, B_1)$
and
![]() $i,j\in \omega $
such that
$i,j\in \omega $
such that
![]() $(B_0, B_1)$
is
$(B_0, B_1)$
is
![]() $(i,j)$
-frequent.
$(i,j)$
-frequent.
Proof of the claim
Starting with a positive pair
![]() $(A_0, A_1)$
, we find some
$(A_0, A_1)$
, we find some
![]() $i\in \omega $
and positive
$i\in \omega $
and positive
![]() $(C_0,C_1)\subseteq (A_0, A_1)$
such that
$(C_0,C_1)\subseteq (A_0, A_1)$
such that
![]() $(C_0, C_1)$
satisfies the first requirement of the
$(C_0, C_1)$
satisfies the first requirement of the
![]() $(i,j)$
-frequency, namely, for all positive sets
$(i,j)$
-frequency, namely, for all positive sets
![]() $C_0'\subseteq C_0, C_1'\subseteq C_1$
, there are
$C_0'\subseteq C_0, C_1'\subseteq C_1$
, there are
![]() $(\alpha ,\beta )\in C_0'\otimes C_1'$
such that
$(\alpha ,\beta )\in C_0'\otimes C_1'$
such that
![]() $c(\alpha ,\beta )=i$
. Suppose for the sake of contradiction that such
$c(\alpha ,\beta )=i$
. Suppose for the sake of contradiction that such
![]() $(C_0,C_1)$
and i do not exist. We define a strategy
$(C_0,C_1)$
and i do not exist. We define a strategy
![]() $\sigma $
for Player Empty: they start by playing
$\sigma $
for Player Empty: they start by playing
![]() $(A^0, B^0)=_{def}(A_0,A_1)$
. At stage
$(A^0, B^0)=_{def}(A_0,A_1)$
. At stage
![]() $2i$
, denoting the game played so far is
$2i$
, denoting the game played so far is
![]() $\langle (A^k, B^k): k<2i\rangle $
, by the hypothesis, there are positive
$\langle (A^k, B^k): k<2i\rangle $
, by the hypothesis, there are positive
![]() $(A',B')\subseteq (A^{2i-1}, B^{2i-1})$
such that no
$(A',B')\subseteq (A^{2i-1}, B^{2i-1})$
such that no
![]() $(\alpha ,\beta ) \in A'\otimes B'$
satisfies
$(\alpha ,\beta ) \in A'\otimes B'$
satisfies
![]() $c(\alpha ,\beta )=i$
. Player Empty then plays
$c(\alpha ,\beta )=i$
. Player Empty then plays
![]() $(A^{2i}, B^{2i})=(A',B')$
. Since by the hypothesis of I, Player Empty does not have a winning strategy, there is a play
$(A^{2i}, B^{2i})=(A',B')$
. Since by the hypothesis of I, Player Empty does not have a winning strategy, there is a play
![]() $\langle (A^n,B^n): n\in \omega \rangle $
where Player Empty plays according to the strategy
$\langle (A^n,B^n): n\in \omega \rangle $
where Player Empty plays according to the strategy
![]() $\sigma $
, but in the end, there are
$\sigma $
, but in the end, there are
![]() $(\alpha ,\beta ) \in \bigcap _{n\in \omega } A^n \otimes \bigcap _{n\in \omega } B^n$
. However, if
$(\alpha ,\beta ) \in \bigcap _{n\in \omega } A^n \otimes \bigcap _{n\in \omega } B^n$
. However, if
![]() $c(\alpha ,\beta )=k$
, then at stage
$c(\alpha ,\beta )=k$
, then at stage
![]() $2k$
, the strategy of Empty makes sure
$2k$
, the strategy of Empty makes sure
![]() $c" A^{2k}\otimes B^{2k}$
omits
$c" A^{2k}\otimes B^{2k}$
omits
![]() $\{k\}$
, which is a contradiction.
$\{k\}$
, which is a contradiction.
Finally, we repeat the previous argument with input
![]() $(C_1, C_0)$
in place of
$(C_1, C_0)$
in place of
![]() $(A_0, A_1)$
to find positive
$(A_0, A_1)$
to find positive
![]() $(B_1, B_0)\subseteq (C_1, C_0)$
and
$(B_1, B_0)\subseteq (C_1, C_0)$
and
![]() $j\in \omega $
satisfying the second condition of the
$j\in \omega $
satisfying the second condition of the
![]() $(i,j)$
-frequency, as desired.
$(i,j)$
-frequency, as desired.
Fix an
![]() $(i,j)$
-frequent pair
$(i,j)$
-frequent pair
![]() $(B_0,B_1)$
. We strengthen this property of
$(B_0,B_1)$
. We strengthen this property of
![]() $(B_0, B_1)$
by using the normality of I. Recall that for any positive
$(B_0, B_1)$
by using the normality of I. Recall that for any positive
![]() $S\in I^+$
,
$S\in I^+$
,
![]() $I^*\restriction S$
denotes the dual filter of I restricted to S.
$I^*\restriction S$
denotes the dual filter of I restricted to S.
Claim 3.5 For any I-positive
![]() $B_0'\subseteq B_0, B_1'\subseteq B_1$
,
$B_0'\subseteq B_0, B_1'\subseteq B_1$
,
-
•
 $\{\alpha \in B_0: \{\beta \in B_1': c(\alpha ,\beta )=i\}\in I^+\}\in I^*\restriction B_0$
,
$\{\alpha \in B_0: \{\beta \in B_1': c(\alpha ,\beta )=i\}\in I^+\}\in I^*\restriction B_0$
, -
•
 $\{\beta '\in B_1: \{\alpha '\in B_0': c(\beta ',\alpha ')=j\}\in I^+\}\in I^*\restriction B_1$
.
$\{\beta '\in B_1: \{\alpha '\in B_0': c(\beta ',\alpha ')=j\}\in I^+\}\in I^*\restriction B_1$
.
Proof of the claim
Let us just show the first part; the proof of the second part is identical. Suppose for the sake of contradiction that
![]() $B^0=_{def}\{\alpha \in B_0: B^1_{\alpha }=_{def}\{\beta \in B_1': c(\alpha ,\beta )=i\}\in I\}\in I^+$
. Since I is normal,
$B^0=_{def}\{\alpha \in B_0: B^1_{\alpha }=_{def}\{\beta \in B_1': c(\alpha ,\beta )=i\}\in I\}\in I^+$
. Since I is normal,
![]() $B^1=\bigtriangledown _{\alpha \in B^0} B^1_\alpha \in I$
. Applying the assumption that
$B^1=\bigtriangledown _{\alpha \in B^0} B^1_\alpha \in I$
. Applying the assumption that
![]() $(B_0, B_1)$
is
$(B_0, B_1)$
is
![]() $(i,j)$
-frequent to
$(i,j)$
-frequent to
![]() $B^0$
and
$B^0$
and
![]() $B_1'\backslash B^1$
, we get
$B_1'\backslash B^1$
, we get
![]() $(\alpha ,\beta )\in B^0 \otimes (B_1' \backslash B^1)$
such that
$(\alpha ,\beta )\in B^0 \otimes (B_1' \backslash B^1)$
such that
![]() $c(\alpha ,\beta )=i$
. However, by the definition of
$c(\alpha ,\beta )=i$
. However, by the definition of
![]() $B^1$
,
$B^1$
,
![]() $\beta \in B^1$
, which is a contradiction.
$\beta \in B^1$
, which is a contradiction.
Applying Claim 3.5, we find
![]() $B_0^*\in I^*\restriction B_0, B_1^*\in I^*\restriction B_1$
such that:
$B_0^*\in I^*\restriction B_0, B_1^*\in I^*\restriction B_1$
such that:
-
(1) for any
 $\alpha \in B^*_0$
,
$\alpha \in B^*_0$
,
 $\{\beta \in B^*_1: c(\alpha ,\beta )=i\}\in I^+$
and
$\{\beta \in B^*_1: c(\alpha ,\beta )=i\}\in I^+$
and -
(2) for any
 $\beta '\in B^*_1$
,
$\beta '\in B^*_1$
,
 $\{\alpha '\in B^*_0: c(\beta ',\alpha ')=j\}\in I^+$
.
$\{\alpha '\in B^*_0: c(\beta ',\alpha ')=j\}\in I^+$
.
Let us check that
![]() $(B_0^* \cup B^*_1, c^{-1}(\{i,j\}))$
is a highly connected subgraph of size
$(B_0^* \cup B^*_1, c^{-1}(\{i,j\}))$
is a highly connected subgraph of size
![]() $\aleph _2$
. Given
$\aleph _2$
. Given
![]() $C\in [B_0^* \cup B^*_1]^{\leq \aleph _1}$
,
$C\in [B_0^* \cup B^*_1]^{\leq \aleph _1}$
,
![]() $\alpha ,\beta \in B_0^* \cup B^*_1 \backslash C$
, we need to find an
$\alpha ,\beta \in B_0^* \cup B^*_1 \backslash C$
, we need to find an
![]() $(i,j)$
-valued path connecting them in
$(i,j)$
-valued path connecting them in
![]() $B_0^* \cup B^*_1 \backslash C$
. Consider the following cases.
$B_0^* \cup B^*_1 \backslash C$
. Consider the following cases.
-
•
 $\alpha \in B^*_0, \beta \in B^*_1$
: let
$\alpha \in B^*_0, \beta \in B^*_1$
: let
 $A_\alpha =\{\gamma \in B^*_1: c(\alpha ,\gamma )=i\}\in I^+$
and let
$A_\alpha =\{\gamma \in B^*_1: c(\alpha ,\gamma )=i\}\in I^+$
and let
 $B_\beta =\{\eta \in B^*_0: c(\beta , \eta )=j\}\in I^+$
. Since
$B_\beta =\{\eta \in B^*_0: c(\beta , \eta )=j\}\in I^+$
. Since
 $(B^*_0, B^*_1) $
is
$(B^*_0, B^*_1) $
is
 $(i,j)$
-frequent, we can find
$(i,j)$
-frequent, we can find
 $(\gamma ,\eta )\in (A_\alpha \backslash C)\otimes (B_\beta \backslash C)$
such that
$(\gamma ,\eta )\in (A_\alpha \backslash C)\otimes (B_\beta \backslash C)$
such that
 $c(\gamma ,\eta )=j$
. Then the path
$c(\gamma ,\eta )=j$
. Then the path
 $\alpha , \gamma , \eta , \beta $
is as desired.
$\alpha , \gamma , \eta , \beta $
is as desired. -
•
 $\alpha , \beta \in B^*_0$
or
$\alpha , \beta \in B^*_0$
or
 $\alpha , \beta \in B^*_1$
: we can reduce to the previous case by moving either
$\alpha , \beta \in B^*_1$
: we can reduce to the previous case by moving either
 $\alpha $
or
$\alpha $
or
 $\beta $
to the other side using an edge of c-color either i or j.
$\beta $
to the other side using an edge of c-color either i or j.
4 The consistency of the existence of a 2-precipitous ideal
In this section, we discuss two forcing constructions of a 2-precipitous ideal on
![]() $\kappa $
. The first is cardinal preserving and the second involves collapsing cardinals. First, let us record some characterizations of 2-precipitous ideals analogous to those of precipitous ideals in [Reference Jech and Prikry14].
$\kappa $
. The first is cardinal preserving and the second involves collapsing cardinals. First, let us record some characterizations of 2-precipitous ideals analogous to those of precipitous ideals in [Reference Jech and Prikry14].
Definition 4.1
A tree T of maximal antichains of
![]() $P(\kappa )/I \times P(\kappa )/I$
is a sequence of maximal antichains
$P(\kappa )/I \times P(\kappa )/I$
is a sequence of maximal antichains
![]() $\langle \mathcal {A}_n: n\in \omega \rangle $
of
$\langle \mathcal {A}_n: n\in \omega \rangle $
of
![]() $P(\kappa )/I \times P(\kappa )/I$
such that
$P(\kappa )/I \times P(\kappa )/I$
such that
![]() $\mathcal {A}_{n+1}$
refines
$\mathcal {A}_{n+1}$
refines
![]() $\mathcal {A}_n$
for each
$\mathcal {A}_n$
for each
![]() $n\in \omega $
. A branch through T is a decreasing sequence of conditions
$n\in \omega $
. A branch through T is a decreasing sequence of conditions
![]() $\langle b_n: n\in \omega \rangle $
such that
$\langle b_n: n\in \omega \rangle $
such that
![]() $b_n\in \mathcal {A}_n$
.
$b_n\in \mathcal {A}_n$
.
The proof by Jech and Prikry [Reference Jech and Prikry14] (see also [Reference Foreman9, Proposition 2.7]) essentially gives the following.
Theorem 4.2 [Reference Jech and Prikry14]
I is 2-precipitous if for any pair of positive sets
![]() $(C_0, C_1)$
and a tree T of maximal antichains
$(C_0, C_1)$
and a tree T of maximal antichains
![]() $\langle \mathcal {A}_n : n\in \omega \rangle $
below
$\langle \mathcal {A}_n : n\in \omega \rangle $
below
![]() $(C_0,C_1)$
, there exists a sequence
$(C_0,C_1)$
, there exists a sequence
![]() $\langle (A_n,B_n): n\in \omega \rangle $
such that:
$\langle (A_n,B_n): n\in \omega \rangle $
such that:
-
(1)
 $\langle (A_n, B_n): n\in \omega \rangle $
is a branch through the tree T and
$\langle (A_n, B_n): n\in \omega \rangle $
is a branch through the tree T and -
(2) there exist
 $\alpha <\beta $
such that
$\alpha <\beta $
such that
 $\alpha \in \bigcap _{n\in \omega } A_n$
and
$\alpha \in \bigcap _{n\in \omega } A_n$
and
 $\beta \in \bigcap _{n\in \omega } B_n$
.
$\beta \in \bigcap _{n\in \omega } B_n$
.
Remark 4.3 Suppose that we are given a dense subset
![]() $D\subseteq P(\kappa )/I$
. By Lemma 3.2, it is no loss of generality to assume that
$D\subseteq P(\kappa )/I$
. By Lemma 3.2, it is no loss of generality to assume that
![]() $ \{(C_0,C_1)\} \cup \bigcup _{n\in \omega }\mathcal {A}_n\subseteq \{A\backslash M: A\in D, M\in I\}\times \{A\backslash M: A\in D, M\in I\}$
.
$ \{(C_0,C_1)\} \cup \bigcup _{n\in \omega }\mathcal {A}_n\subseteq \{A\backslash M: A\in D, M\in I\}\times \{A\backslash M: A\in D, M\in I\}$
.
For the rest of this section, we will apply Remark 4.3 liberally. Also, it turns out that suppressing the quotiented ideal I does not affect the reasoning. Therefore, to avoid cumbersome notations, we will further assume that
![]() $\mathcal {A}_n\subseteq D\times D$
for all
$\mathcal {A}_n\subseteq D\times D$
for all
![]() $n\in \omega $
. Given a partial order
$n\in \omega $
. Given a partial order
![]() $\mathbb {P}$
, we denote the complete Boolean algebra generated by
$\mathbb {P}$
, we denote the complete Boolean algebra generated by
![]() $\mathbb {P}$
as
$\mathbb {P}$
as
![]() $\mathbb {B}(\mathbb {P})$
.
$\mathbb {B}(\mathbb {P})$
.
Proposition 4.4 If I is a
![]() $\kappa $
-complete normal ideal on
$\kappa $
-complete normal ideal on
![]() $\kappa $
and
$\kappa $
and
![]() $P(\kappa )/I\simeq \mathbb {B}(Add(\omega ,\lambda ))$
for some
$P(\kappa )/I\simeq \mathbb {B}(Add(\omega ,\lambda ))$
for some
![]() $\lambda $
, then I is 2-precipitous.
$\lambda $
, then I is 2-precipitous.
Proof Let
![]() $\pi : \mathbb {B}(Add(\omega ,\lambda ))\to P(\kappa )/I$
be an isomorphism. For each
$\pi : \mathbb {B}(Add(\omega ,\lambda ))\to P(\kappa )/I$
be an isomorphism. For each
![]() $r\in Add(\omega ,\lambda )$
, let
$r\in Add(\omega ,\lambda )$
, let
![]() $X_r = \pi (r)$
. Here, we identify
$X_r = \pi (r)$
. Here, we identify
![]() $Add(\omega ,\lambda )$
as a dense subset of
$Add(\omega ,\lambda )$
as a dense subset of
![]() $\mathbb {B}(Add(\omega ,\lambda ))$
,
$\mathbb {B}(Add(\omega ,\lambda ))$
,
![]() $D=\{X_r: r\in Add(\omega ,\lambda )\}$
.
$D=\{X_r: r\in Add(\omega ,\lambda )\}$
.
Suppose for the sake of contradiction that I is not 2-precipitous. By Theorem 4.2, there exist a
![]() $(C_0,C_1)$
and a tree T of maximal antichains below
$(C_0,C_1)$
and a tree T of maximal antichains below
![]() $(C_0,C_1)$
for which conditions (1) and (2) simultaneously hold. Note that since
$(C_0,C_1)$
for which conditions (1) and (2) simultaneously hold. Note that since
![]() $P(\kappa )/I\times P(\kappa )/I$
is c.c.c., each
$P(\kappa )/I\times P(\kappa )/I$
is c.c.c., each
![]() $\mathcal {A}_n \subseteq D\times D$
is countable. Find
$\mathcal {A}_n \subseteq D\times D$
is countable. Find
![]() $r_0,r_1\in Add(\omega ,\lambda )$
such that
$r_0,r_1\in Add(\omega ,\lambda )$
such that
![]() $C_i=X_{r_i}$
for
$C_i=X_{r_i}$
for
![]() $i<2$
.
$i<2$
.
Let
![]() $G\subseteq P(\kappa )/I$
be a generic filter containing
$G\subseteq P(\kappa )/I$
be a generic filter containing
![]() $C_0$
. Then, in
$C_0$
. Then, in
![]() $V[G]$
, there is a generic elementary embedding
$V[G]$
, there is a generic elementary embedding
![]() $j: V\to M$
which can be taken to be the ultrapower embedding with respect to the added generic V-ultrafilter extending the dual filter of I.
$j: V\to M$
which can be taken to be the ultrapower embedding with respect to the added generic V-ultrafilter extending the dual filter of I.
Consider
![]() $T^{\prime }_n=\{B^*: \exists (A^*,B^*)\in j(\mathcal {A}_n), \kappa \in A^*\}$
. Note that
$T^{\prime }_n=\{B^*: \exists (A^*,B^*)\in j(\mathcal {A}_n), \kappa \in A^*\}$
. Note that
![]() $\langle T^{\prime }_n: n\in \omega \rangle \in M$
since
$\langle T^{\prime }_n: n\in \omega \rangle \in M$
since
![]() $V[G]\models {}^{\omega }M\subseteq M$
by [Reference Foreman9, Proposition 2.14]. Note that
$V[G]\models {}^{\omega }M\subseteq M$
by [Reference Foreman9, Proposition 2.14]. Note that
![]() $T^{\prime }_n\subseteq j"V$
. This follows from the fact that each
$T^{\prime }_n\subseteq j"V$
. This follows from the fact that each
![]() $\mathcal {A}_n$
is countable, and hence
$\mathcal {A}_n$
is countable, and hence
![]() $j(\mathcal {A}_n)=j" \mathcal {A}_n$
.
$j(\mathcal {A}_n)=j" \mathcal {A}_n$
.
Claim 4.5 In M,
![]() $T^{\prime }_n$
is a maximal antichain below
$T^{\prime }_n$
is a maximal antichain below
![]() $j(C_1)$
for the poset
$j(C_1)$
for the poset
![]() $j(P(\kappa )/I)$
.
$j(P(\kappa )/I)$
.
Proof of the claim
Suppose not. By the product lemma,
![]() $\mathcal {B}=\{B: \exists (A,B)\in \mathcal {A}_n, A\in G\}$
is a maximal antichain for
$\mathcal {B}=\{B: \exists (A,B)\in \mathcal {A}_n, A\in G\}$
is a maximal antichain for
below
![]() $X_{r_1}$
in
$X_{r_1}$
in
![]() $V[G]$
. We can enumerate
$V[G]$
. We can enumerate
In particular,
![]() $\langle p_n: n\in \omega \rangle $
is a maximal antichain for
$\langle p_n: n\in \omega \rangle $
is a maximal antichain for
![]() $Add(\omega ,\lambda )$
below
$Add(\omega ,\lambda )$
below
![]() $r_1$
in
$r_1$
in
![]() $V[G]$
.
$V[G]$
.
If
![]() $\langle j(X_{p_n}): n\in \omega \rangle $
is not a maximal antichain in
$\langle j(X_{p_n}): n\in \omega \rangle $
is not a maximal antichain in
![]() $j(P(\kappa )/I)\simeq j(\mathbb {B}(Add(\omega ,\lambda )))$
, then there exists a condition
$j(P(\kappa )/I)\simeq j(\mathbb {B}(Add(\omega ,\lambda )))$
, then there exists a condition
![]() $r\in Add(\omega , j(\lambda ))$
such that
$r\in Add(\omega , j(\lambda ))$
such that
![]() $X_r^*=_{\mathrm {def}}j(\pi )(r)$
is incompatible with any condition in the set
$X_r^*=_{\mathrm {def}}j(\pi )(r)$
is incompatible with any condition in the set
![]() $\{j(X_{p_n}): n\in \omega \}$
. This means r is incompatible with any condition in
$\{j(X_{p_n}): n\in \omega \}$
. This means r is incompatible with any condition in
![]() $\{j(p_n): n\in \omega \}$
. Since
$\{j(p_n): n\in \omega \}$
. Since
![]() $j(p_n)=j"p_n$
, we may assume
$j(p_n)=j"p_n$
, we may assume
![]() $r\in Add(\omega ,j"\lambda )$
. Let
$r\in Add(\omega ,j"\lambda )$
. Let
![]() $r^*=j^{-1}(r)$
. Then
$r^*=j^{-1}(r)$
. Then
![]() $r^*\in Add(\omega ,\lambda )/r_1$
is incompatible with any condition in
$r^*\in Add(\omega ,\lambda )/r_1$
is incompatible with any condition in
![]() $\{p_n: n\in \omega \}$
. This contradicts with the fact that
$\{p_n: n\in \omega \}$
. This contradicts with the fact that
![]() $\langle p_n: n\in \omega \rangle $
is a maximal antichain subset of
$\langle p_n: n\in \omega \rangle $
is a maximal antichain subset of
![]() $Add(\omega ,\lambda )$
below
$Add(\omega ,\lambda )$
below
![]() $r_1$
in
$r_1$
in
![]() $V[G]$
.
$V[G]$
.
Let
![]() $H\subseteq j(P(\kappa )/I)$
be a generic filter over
$H\subseteq j(P(\kappa )/I)$
be a generic filter over
![]() $V[G]$
containing
$V[G]$
containing
![]() $j(D)$
. Since
$j(D)$
. Since
![]() $M\models j(P(\kappa )/I)$
is a
$M\models j(P(\kappa )/I)$
is a
![]() $j(\kappa )$
-complete and
$j(\kappa )$
-complete and
![]() $\aleph _1$
-saturated ideal, H gives rise to an ultrapower embedding
$\aleph _1$
-saturated ideal, H gives rise to an ultrapower embedding
![]() $k: M\to N$
with critical point
$k: M\to N$
with critical point
![]() $j(\kappa )$
. Consider
$j(\kappa )$
. Consider
![]() $b=\{(A_n,B_n): (\kappa ,j(\kappa ))\in k(j(A_n))\times k(j(B_n))\}$
. By Claim 4.8, H meets
$b=\{(A_n,B_n): (\kappa ,j(\kappa ))\in k(j(A_n))\times k(j(B_n))\}$
. By Claim 4.8, H meets
![]() $T^{\prime }_n$
for all
$T^{\prime }_n$
for all
![]() $n\in \omega $
. As a result,
$n\in \omega $
. As a result,
![]() $k\circ j(b)=k\circ j"b$
is a branch
$k\circ j(b)=k\circ j"b$
is a branch
![]() $\langle (A^*_n, B^*_n): n\in \omega \rangle $
through
$\langle (A^*_n, B^*_n): n\in \omega \rangle $
through
![]() $k(j(T))$
in
$k(j(T))$
in
![]() $V[G*H]$
with
$V[G*H]$
with
![]() $(\kappa ,j(\kappa ))\in \bigcap _{n\in \omega } A^*_n \otimes \bigcup _{n\in \omega } B^*_n$
. Since N is well-founded, there is such a branch in N. By the elementarity of
$(\kappa ,j(\kappa ))\in \bigcap _{n\in \omega } A^*_n \otimes \bigcup _{n\in \omega } B^*_n$
. Since N is well-founded, there is such a branch in N. By the elementarity of
![]() $k\circ j$
, T has a branch
$k\circ j$
, T has a branch
![]() $\langle (A_n, B_n): n\in \omega \rangle $
in V for which there are
$\langle (A_n, B_n): n\in \omega \rangle $
in V for which there are
![]() $\alpha <\beta $
with
$\alpha <\beta $
with
![]() $\alpha \in \bigcap _{n\in \omega } A_n$
and
$\alpha \in \bigcap _{n\in \omega } A_n$
and
![]() $\beta \in \bigcap _{n\in \omega } B_n$
.
$\beta \in \bigcap _{n\in \omega } B_n$
.
It is easy to see that if
![]() $P(\kappa )/I$
has a
$P(\kappa )/I$
has a
![]() $\sigma $
-closed dense subset, then I is 2-precipitous. However, in this case, it is necessary that
$\sigma $
-closed dense subset, then I is 2-precipitous. However, in this case, it is necessary that
![]() $2^{\aleph _0} < \kappa $
.
$2^{\aleph _0} < \kappa $
.
The second construction gives a scenario where
![]() $\kappa $
is a small uncountable cardinal (like
$\kappa $
is a small uncountable cardinal (like
![]() $\aleph _2$
) and
$\aleph _2$
) and
![]() $\mathrm {CH}$
fails. In particular, such an ideal can be constructed using the Mitchell collapse [Reference Mitchell18].Footnote
2
$\mathrm {CH}$
fails. In particular, such an ideal can be constructed using the Mitchell collapse [Reference Mitchell18].Footnote
2
Recall the Mitchell forcing from [Reference Mitchell18] (the representation of the forcing here is due to Abraham; see [Reference Abraham1] and [Reference Cummings7, Section 23])
![]() $\mathbb {M}(\omega ,\lambda )$
consists of conditions of the form
$\mathbb {M}(\omega ,\lambda )$
consists of conditions of the form
![]() $(p,r)$
where
$(p,r)$
where
![]() $p\in Add(\omega ,\lambda )$
and r is a function on
$p\in Add(\omega ,\lambda )$
and r is a function on
![]() $\lambda $
of countable support such that for any
$\lambda $
of countable support such that for any
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $\Vdash _{Add(\omega ,\alpha )} r(\alpha )$
is a condition in
$\Vdash _{Add(\omega ,\alpha )} r(\alpha )$
is a condition in
![]() $Add(\omega _1,1)$
. The order is that
$Add(\omega _1,1)$
. The order is that
![]() $(p_2, r_2)\leq (p_1, r_1)$
iff
$(p_2, r_2)\leq (p_1, r_1)$
iff
![]() $p_2\supset p_1$
,
$p_2\supset p_1$
,
![]() $supp(r_2)\supset supp(r_1)$
, and for any
$supp(r_2)\supset supp(r_1)$
, and for any
![]() $\alpha \in supp(r_1)$
,
$\alpha \in supp(r_1)$
,
![]() $p_2\restriction \alpha \Vdash _{Add(\omega ,\alpha )} r_2(\alpha )\leq _{Add(\omega _1,1)} r_1(\alpha )$
.
$p_2\restriction \alpha \Vdash _{Add(\omega ,\alpha )} r_2(\alpha )\leq _{Add(\omega _1,1)} r_1(\alpha )$
.
Define R to be the poset consisting of countably supported functions r with domain
![]() $\lambda $
such that for each
$\lambda $
such that for each
![]() $\alpha \in supp(r)$
,
$\alpha \in supp(r)$
,
![]() $r(\alpha )$
is an
$r(\alpha )$
is an
![]() $Add(\omega , \alpha )$
-name for a condition in
$Add(\omega , \alpha )$
-name for a condition in
![]() $Add(\omega _1, 1)$
. The order of R is the following:
$Add(\omega _1, 1)$
. The order of R is the following:
![]() $r_2\leq _R r_1$
iff
$r_2\leq _R r_1$
iff
![]() $supp(r_2)\supset supp(r_1)$
and for any
$supp(r_2)\supset supp(r_1)$
and for any
![]() $\alpha \in supp(r_1)$
,
$\alpha \in supp(r_1)$
,
![]() $\Vdash _{Add(\omega ,\alpha )} r_2(\alpha )\leq _{Add(\omega _1, 1)} r_1(\alpha )$
.
$\Vdash _{Add(\omega ,\alpha )} r_2(\alpha )\leq _{Add(\omega _1, 1)} r_1(\alpha )$
.
The following are standard facts about this forcing (see [Reference Cummings7]):
-
(1)
 $\mathbb {M}(\omega ,\lambda )$
projects onto
$\mathbb {M}(\omega ,\lambda )$
projects onto
 $Add(\omega ,\lambda )$
by projecting onto the first coordinate.
$Add(\omega ,\lambda )$
by projecting onto the first coordinate. -
(2)
 $Add(\omega ,\lambda )\times R$
projects onto
$Add(\omega ,\lambda )\times R$
projects onto
 $\mathbb {M}(\omega ,\lambda )$
by the identity map.
$\mathbb {M}(\omega ,\lambda )$
by the identity map.
Remark 4.6 Whenever
![]() $(p_2, r_2)\leq _{\mathbb {M}(\omega ,\lambda )}(p_1, r_1)$
, there exists
$(p_2, r_2)\leq _{\mathbb {M}(\omega ,\lambda )}(p_1, r_1)$
, there exists
![]() $r_2'\in R$
with
$r_2'\in R$
with
![]() $dom(r_2')=dom(r_2)$
such that
$dom(r_2')=dom(r_2)$
such that
![]() $r_2'\leq _{R} r_1$
and
$r_2'\leq _{R} r_1$
and
![]() $p_2\restriction \alpha \Vdash _{Add(\omega ,\alpha )} r_2(\alpha )=r_2'(\alpha )$
for any
$p_2\restriction \alpha \Vdash _{Add(\omega ,\alpha )} r_2(\alpha )=r_2'(\alpha )$
for any
![]() $\alpha \in dom(r_2)$
. In other words,
$\alpha \in dom(r_2)$
. In other words,
![]() $(p_2, r_2)$
and
$(p_2, r_2)$
and
![]() $(p_2, r_2')$
are equivalent conditions. We will use this fact freely in the following proofs.
$(p_2, r_2')$
are equivalent conditions. We will use this fact freely in the following proofs.
Note that the poset R has the property that any countable decreasing sequence has a greatest lower bound.
Proposition 4.7 If
![]() $P(\kappa )/I\simeq \mathbb {B}(\mathbb {M}(\omega ,\lambda ))$
for some
$P(\kappa )/I\simeq \mathbb {B}(\mathbb {M}(\omega ,\lambda ))$
for some
![]() $\lambda $
, then I is 2-precipitous.
$\lambda $
, then I is 2-precipitous.
Proof Let
![]() $\pi : \mathbb {M}(\omega ,\lambda )\to D$
be an isomorphism where
$\pi : \mathbb {M}(\omega ,\lambda )\to D$
be an isomorphism where
![]() $D\subseteq P(\kappa )/I$
is a dense subset. For any
$D\subseteq P(\kappa )/I$
is a dense subset. For any
![]() $(p,r)\in \mathbb {M}(\omega ,\lambda )$
, let
$(p,r)\in \mathbb {M}(\omega ,\lambda )$
, let
![]() $X_{p,r}$
denote
$X_{p,r}$
denote
![]() $\pi (p,r)$
. Assume for the sake of contradiction that I is not 2-precipitous. Fix a winning strategy
$\pi (p,r)$
. Assume for the sake of contradiction that I is not 2-precipitous. Fix a winning strategy
![]() $\sigma $
for Player Empty in the game
$\sigma $
for Player Empty in the game
![]() $G_I$
. We may assume
$G_I$
. We may assume
![]() $\sigma $
satisfies the conclusion of Lemma 3.2 applied to D. To avoid cumbersome notations, we will assume for simplicity that
$\sigma $
satisfies the conclusion of Lemma 3.2 applied to D. To avoid cumbersome notations, we will assume for simplicity that
![]() $\sigma $
outputs elements from
$\sigma $
outputs elements from
![]() $D\times D$
, as discussed after Remark 4.3. We will use
$D\times D$
, as discussed after Remark 4.3. We will use
![]() $\sigma $
to construct a tree of antichains
$\sigma $
to construct a tree of antichains
![]() $T=\langle \mathcal {A}_n: n\in \omega \rangle $
below
$T=\langle \mathcal {A}_n: n\in \omega \rangle $
below
![]() $\sigma (\emptyset )=(A,B)=(X_{p^{-1}_a, r^{-1}_a}, X_{p^{-1}_b, r^{-1}_b})=\mathcal {A}_{-1}$
satisfying the following additional properties:
$\sigma (\emptyset )=(A,B)=(X_{p^{-1}_a, r^{-1}_a}, X_{p^{-1}_b, r^{-1}_b})=\mathcal {A}_{-1}$
satisfying the following additional properties:
-
(1)
 $\mathcal {A}_{n+1}$
refines
$\mathcal {A}_{n+1}$
refines
 $\mathcal {A}_n$
.
$\mathcal {A}_n$
. -
(2)
 $\mathcal {A}_n=\langle (a^n_i, b^n_i):i<\gamma _n\rangle \subseteq D$
is countable (note that it is not maximal anymore).
$\mathcal {A}_n=\langle (a^n_i, b^n_i):i<\gamma _n\rangle \subseteq D$
is countable (note that it is not maximal anymore). -
(3) For each
 $n\in \omega ,i\in \gamma _n$
, there are unique
$n\in \omega ,i\in \gamma _n$
, there are unique
 $(p^n_{i,a}, r^n_{i,a}),(p^n_{i,b}, r^n_{i,b}) \in \mathbb {M}(\omega ,\lambda )$
such that
$(p^n_{i,a}, r^n_{i,a}),(p^n_{i,b}, r^n_{i,b}) \in \mathbb {M}(\omega ,\lambda )$
such that
 $X_{p^n_{i,a}, r^n_{i,a}}=a^n_i$
and
$X_{p^n_{i,a}, r^n_{i,a}}=a^n_i$
and
 $X_{p^n_{i,b}, r^n_{i,b}}=b^n_i$
.
$X_{p^n_{i,b}, r^n_{i,b}}=b^n_i$
. -
(4) For any n and
 $i<j\in \gamma _n$
,
$i<j\in \gamma _n$
,
 $(r^n_{j,a}, r^n_{j,b})\leq _{R\times R} (r^n_{i,a}, r^n_{i,b})$
.
$(r^n_{j,a}, r^n_{j,b})\leq _{R\times R} (r^n_{i,a}, r^n_{i,b})$
. -
(5) For any lower bound
 $(r_0, r_1)$
for
$(r_0, r_1)$
for
 $\langle (r^n_{i,a}, r^n_{i,b}): i\in \gamma _n\rangle $
, we have that
$\langle (r^n_{i,a}, r^n_{i,b}): i\in \gamma _n\rangle $
, we have that
 $\mathcal {A}_n \downarrow (r_0, r_1)=_{def} \{X_{p^n_{i,a}, r_0}, X_{p^n_{i,b}, r_1}: i\in \gamma _n\}$
is a maximal antichain in
$\mathcal {A}_n \downarrow (r_0, r_1)=_{def} \{X_{p^n_{i,a}, r_0}, X_{p^n_{i,b}, r_1}: i\in \gamma _n\}$
is a maximal antichain in
 $(A\cap X_{\emptyset , r_0}, B\cap X_{\emptyset ,r_1})$
.
$(A\cap X_{\emptyset , r_0}, B\cap X_{\emptyset ,r_1})$
. -
(6) For any n and
 $i,j$
,
$i,j$
,
 $(r^{n+1}_{j,a}, r^{n+1}_{j,b})\leq _{R\times R} (r^n_{i,a}, r^n_{i,b})$
.
$(r^{n+1}_{j,a}, r^{n+1}_{j,b})\leq _{R\times R} (r^n_{i,a}, r^n_{i,b})$
. -
(7) For any branch
 $\langle (A_n,B_n): n\in \omega \rangle $
through T, there do not exist
$\langle (A_n,B_n): n\in \omega \rangle $
through T, there do not exist
 $\alpha <\beta $
such that
$\alpha <\beta $
such that
 $\alpha \in \bigcap _{n\in \omega } A_n$
and
$\alpha \in \bigcap _{n\in \omega } A_n$
and
 $\beta \in \bigcap _{n\in \omega } B_n$
.
$\beta \in \bigcap _{n\in \omega } B_n$
.
Assuming that the construction of such T is possible, let us derive a contradiction. Let
![]() $(r_a, r_b)$
be the greatest lower bound in
$(r_a, r_b)$
be the greatest lower bound in
![]() $R\times R$
for
$R\times R$
for
![]() $\langle \langle (r^n_{i,a}, r^n_{i,b}): i\in \gamma _n\rangle : n\in \omega \rangle $
. By property (5), we know that for each n,
$\langle \langle (r^n_{i,a}, r^n_{i,b}): i\in \gamma _n\rangle : n\in \omega \rangle $
. By property (5), we know that for each n,
![]() $\mathcal {A}_n\downarrow (r_a, r_b)$
is a maximal antichain below
$\mathcal {A}_n\downarrow (r_a, r_b)$
is a maximal antichain below
![]() $(X_{\emptyset , r_a}\cap A, X_{\emptyset , r_b}\cap B)$
as a subset of
$(X_{\emptyset , r_a}\cap A, X_{\emptyset , r_b}\cap B)$
as a subset of
![]() $(P(\kappa )/I)^V$
in
$(P(\kappa )/I)^V$
in
![]() $V[G]$
.
$V[G]$
.
Force over V to get a generic
![]() $G\subseteq P(\kappa )/I$
over V containing
$G\subseteq P(\kappa )/I$
over V containing
![]() $X_{\emptyset ,r_a}\cap A$
. Using G, we find an elementary embedding
$X_{\emptyset ,r_a}\cap A$
. Using G, we find an elementary embedding
![]() $j: V\to M$
with critical point
$j: V\to M$
with critical point
![]() $\kappa $
. In
$\kappa $
. In
![]() $V[G]$
, consider the tree
$V[G]$
, consider the tree
![]() $T'$
consisting of
$T'$
consisting of
![]() $\mathcal {A}_n'=\{j(C): \kappa \in j(D), (D,C)\in \mathcal {A}_n \downarrow (r_a, r_b)\}$
. Notice that by property (5) and the product lemma,
$\mathcal {A}_n'=\{j(C): \kappa \in j(D), (D,C)\in \mathcal {A}_n \downarrow (r_a, r_b)\}$
. Notice that by property (5) and the product lemma,
![]() $\mathcal {A}^*_n=\{C: j(C)\in \mathcal {A}^{\prime }_n\}$
is a maximal antichain below
$\mathcal {A}^*_n=\{C: j(C)\in \mathcal {A}^{\prime }_n\}$
is a maximal antichain below
![]() $X_{\emptyset , r_b}\cap B$
.
$X_{\emptyset , r_b}\cap B$
.
Claim 4.8 For each
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\mathcal {A}_n' \subseteq j(P(\kappa )/I)$
is a maximal antichain below
$\mathcal {A}_n' \subseteq j(P(\kappa )/I)$
is a maximal antichain below
![]() $j(B)\cap X_{\emptyset ,j(r_b)}$
in
$j(B)\cap X_{\emptyset ,j(r_b)}$
in
![]() $V[G]$
(and in M, since
$V[G]$
(and in M, since
![]() $V[G]\models {}^\omega M\subseteq M$
).
$V[G]\models {}^\omega M\subseteq M$
).
Proof of the claim
Otherwise, we can find
![]() $(p, r^*)\in j(\mathbb {M}(\omega ,\lambda ))$
below
$(p, r^*)\in j(\mathbb {M}(\omega ,\lambda ))$
below
![]() $(\emptyset , j(r_b))$
such that
$(\emptyset , j(r_b))$
such that
![]() $X_{p,r^*}^*=_{\mathrm {def}}j(\pi )((p,r^*))\subseteq j(B)\cap X_{\emptyset , j(r_b)}$
and
$X_{p,r^*}^*=_{\mathrm {def}}j(\pi )((p,r^*))\subseteq j(B)\cap X_{\emptyset , j(r_b)}$
and
![]() $X_{p,r^*}^*$
is incompatible with any element in
$X_{p,r^*}^*$
is incompatible with any element in
![]() $\mathcal {A}^{\prime }_n$
. By changing to an equivalent condition if necessary, we may assume that
$\mathcal {A}^{\prime }_n$
. By changing to an equivalent condition if necessary, we may assume that
![]() $r^*\leq _{j(R)} j(r_b) $
. As a result,
$r^*\leq _{j(R)} j(r_b) $
. As a result,
![]() $p\perp _{j(Add(\omega ,\lambda ))}j(p^n_{k,b})$
for all
$p\perp _{j(Add(\omega ,\lambda ))}j(p^n_{k,b})$
for all
![]() $k\in \omega $
. Consider
$k\in \omega $
. Consider
![]() $p'=j^{-1}(p)\in Add(\omega ,\lambda )$
. Then
$p'=j^{-1}(p)\in Add(\omega ,\lambda )$
. Then
![]() $p'\perp _{Add(\omega ,\lambda )} p^n_{k,b}$
for all
$p'\perp _{Add(\omega ,\lambda )} p^n_{k,b}$
for all
![]() $k\in \omega $
. As a result,
$k\in \omega $
. As a result,
![]() $X_{p', r_{b}}$
is incompatible with each element in
$X_{p', r_{b}}$
is incompatible with each element in
![]() $\mathcal {A}^*_n$
, but
$\mathcal {A}^*_n$
, but
![]() $X_{p', r_b}\cap B\cap X_{\emptyset , r_b}\in I^+$
, which is a contradiction to the fact that
$X_{p', r_b}\cap B\cap X_{\emptyset , r_b}\in I^+$
, which is a contradiction to the fact that
![]() $\mathcal {A}^*_n$
is a maximal antichain below
$\mathcal {A}^*_n$
is a maximal antichain below
![]() $X_{\emptyset , r_b}\cap B$
.
$X_{\emptyset , r_b}\cap B$
.
Let
![]() $H\subseteq j(P(\kappa )/I)$
be a V-generic filter containing
$H\subseteq j(P(\kappa )/I)$
be a V-generic filter containing
![]() $j(B\cap X_{\emptyset , r_b})$
. Then, in
$j(B\cap X_{\emptyset , r_b})$
. Then, in
![]() $V[G*H]$
, we can form an elementary embedding
$V[G*H]$
, we can form an elementary embedding
![]() $k: M\to N$
with critical point
$k: M\to N$
with critical point
![]() $j(\kappa )$
. Consider
$j(\kappa )$
. Consider
![]() $b=\{(A_n,B_n): (\kappa ,j(\kappa ))\in j(A_n)\otimes k(j(B_n)), (A_n, B_n)\in \mathcal {A}_n, n\in \omega \}$
. By Claim 4.8,
$b=\{(A_n,B_n): (\kappa ,j(\kappa ))\in j(A_n)\otimes k(j(B_n)), (A_n, B_n)\in \mathcal {A}_n, n\in \omega \}$
. By Claim 4.8,
![]() $k\circ j"b\in V[G*H]$
is a branch through
$k\circ j"b\in V[G*H]$
is a branch through
![]() $k(j(T))$
violating property (7) as witnessed by
$k(j(T))$
violating property (7) as witnessed by
![]() $(\kappa , j(\kappa ))$
. Since N is a well-founded inner model of
$(\kappa , j(\kappa ))$
. Since N is a well-founded inner model of
![]() $V[G*H]$
, there is such a branch in N. By the elementarity of
$V[G*H]$
, there is such a branch in N. By the elementarity of
![]() $k\circ j$
, there is such a branch in V through T violating property (7), which is a contradiction.
$k\circ j$
, there is such a branch in V through T violating property (7), which is a contradiction.
Let us turn to the construction of T. We will construct T levelwise recursion. Let
![]() $\mathcal {A}_{-1}=\sigma (\emptyset )=(A,B)=(X_{p^{-1}_a, r^{-1}_a}, X_{p^{-1}_b, r^{-1}_b})$
. To avoid excessive repetitions, we will assume that all the conditions from
$\mathcal {A}_{-1}=\sigma (\emptyset )=(A,B)=(X_{p^{-1}_a, r^{-1}_a}, X_{p^{-1}_b, r^{-1}_b})$
. To avoid excessive repetitions, we will assume that all the conditions from
![]() $\mathbb {M}(\omega ,\lambda )\times \mathbb {M}(\omega ,\lambda )$
extend
$\mathbb {M}(\omega ,\lambda )\times \mathbb {M}(\omega ,\lambda )$
extend
![]() $((p^{-1}_a, r^{-1}_a),(p^{-1}_b, r^{-1}_b))$
.
$((p^{-1}_a, r^{-1}_a),(p^{-1}_b, r^{-1}_b))$
.
Let us first define
![]() $T(0)=\mathcal {A}_0$
. Recursively, suppose we have defined
$T(0)=\mathcal {A}_0$
. Recursively, suppose we have defined
![]() $\mathcal {A}_{0,<\eta }=\langle (X_{p^0_{i,a}, r^0_{i,a}}, X_{p^0_{i,b}, r^0_{i,b}}): i<\eta \rangle $
(partially) satisfying property (4). Let
$\mathcal {A}_{0,<\eta }=\langle (X_{p^0_{i,a}, r^0_{i,a}}, X_{p^0_{i,b}, r^0_{i,b}}): i<\eta \rangle $
(partially) satisfying property (4). Let
![]() $(t_0,t_1)$
be a lower bound for
$(t_0,t_1)$
be a lower bound for
![]() $\langle (r^0_{i,a}, r^0_{i,b}): i<\eta \rangle $
in
$\langle (r^0_{i,a}, r^0_{i,b}): i<\eta \rangle $
in
![]() $R\times R$
. If there exists
$R\times R$
. If there exists
![]() $(q_0, t^{\prime }_0)\leq (p_a^{-1}, t_0), (q_1, t^{\prime }_1)\leq (p_b^{-1}, t_1)$
such that
$(q_0, t^{\prime }_0)\leq (p_a^{-1}, t_0), (q_1, t^{\prime }_1)\leq (p_b^{-1}, t_1)$
such that
![]() $(X_{q_0, t^{\prime }_0}, X_{q_1, t^{\prime }_1})$
is incompatible with any element in
$(X_{q_0, t^{\prime }_0}, X_{q_1, t^{\prime }_1})$
is incompatible with any element in
![]() $\mathcal {A}_{0,<\eta }$
, let
$\mathcal {A}_{0,<\eta }$
, let
![]() $(Y^0_{\eta ,a}, Y^0_{\eta ,b})$
be one such
$(Y^0_{\eta ,a}, Y^0_{\eta ,b})$
be one such
![]() $(X_{q_0, t^{\prime }_0}, X_{q_1, t^{\prime }_1})$
. Then we define
$(X_{q_0, t^{\prime }_0}, X_{q_1, t^{\prime }_1})$
. Then we define
![]() $(X_{p^0_{\eta ,a}, r^0_{\eta ,a}}, X_{p^0_{\eta ,b}, r^0_{\eta ,b}})$
to be
$(X_{p^0_{\eta ,a}, r^0_{\eta ,a}}, X_{p^0_{\eta ,b}, r^0_{\eta ,b}})$
to be
![]() $\sigma (\langle \emptyset , (Y^0_{\eta ,a}, Y^0_{\eta ,b})\rangle )$
. Notice that this process must stop at some countable stage
$\sigma (\langle \emptyset , (Y^0_{\eta ,a}, Y^0_{\eta ,b})\rangle )$
. Notice that this process must stop at some countable stage
![]() $\gamma _0<\omega _1$
since
$\gamma _0<\omega _1$
since
![]() $\{(p^0_{i,a}, p^0_{i,b}): i<\gamma _0\}$
is an antichain in
$\{(p^0_{i,a}, p^0_{i,b}): i<\gamma _0\}$
is an antichain in
![]() $Add(\omega , \lambda )\times Add(\omega ,\lambda )$
below
$Add(\omega , \lambda )\times Add(\omega ,\lambda )$
below
![]() $(p_a^{-1}, p_b^{-1})$
, which satisfies the countable chain condition. Let us verify all the properties are satisfied. Properties (1)–(4) and (6) are satisfied by the construction. Property (7) is not relevant at this stage. Property (5) is satisfied since we only stop when the process described above cannot be continued, which is exactly saying property (5) is satisfied.
$(p_a^{-1}, p_b^{-1})$
, which satisfies the countable chain condition. Let us verify all the properties are satisfied. Properties (1)–(4) and (6) are satisfied by the construction. Property (7) is not relevant at this stage. Property (5) is satisfied since we only stop when the process described above cannot be continued, which is exactly saying property (5) is satisfied.
In general, the definition of
![]() $\mathcal {A}_{n+1}$
is very similar to the construction above. Basically, for each
$\mathcal {A}_{n+1}$
is very similar to the construction above. Basically, for each
![]() $(C_0, C_1)\in \mathcal {A}_n$
, we repeat the process above with
$(C_0, C_1)\in \mathcal {A}_n$
, we repeat the process above with
![]() $(C_0,C_1)$
playing the role of
$(C_0,C_1)$
playing the role of
![]() $\mathcal {A}_{-1}$
. One difference, in order to satisfy property (6), is that at the beginning of the construction, we let
$\mathcal {A}_{-1}$
. One difference, in order to satisfy property (6), is that at the beginning of the construction, we let
![]() $(h_0, h_1)$
be the lower bound in
$(h_0, h_1)$
be the lower bound in
![]() $R\times R$
for
$R\times R$
for
![]() $\langle (r^n_{i,a}, r^n_{i,b}): i<\gamma _n\rangle $
and work below
$\langle (r^n_{i,a}, r^n_{i,b}): i<\gamma _n\rangle $
and work below
![]() $((p_a^{-1}, h_0), (p_b^{-1}, h_1))$
in
$((p_a^{-1}, h_0), (p_b^{-1}, h_1))$
in
![]() $\mathbb {M}(\omega ,\lambda )\times \mathbb {M}(\omega ,\lambda )$
.
$\mathbb {M}(\omega ,\lambda )\times \mathbb {M}(\omega ,\lambda )$
.
Finally, to see that property (7) is satisfied, notice that any branch b through T corresponds to a play of the game
![]() $G_I$
where Player Empty is playing according to their winning strategy
$G_I$
where Player Empty is playing according to their winning strategy
![]() $\sigma $
. More precisely, b is the sequence of sets played by Player Empty according to
$\sigma $
. More precisely, b is the sequence of sets played by Player Empty according to
![]() $\sigma $
in a play of the game
$\sigma $
in a play of the game
![]() $G_I$
. As a result, the winning condition of Player Empty ensures (7) is satisfied.
$G_I$
. As a result, the winning condition of Player Empty ensures (7) is satisfied.
Corollary 4.9 It is consistent that
![]() $\aleph _2\to _{hc}[\aleph _2]^2_{\omega ,2}$
and
$\aleph _2\to _{hc}[\aleph _2]^2_{\omega ,2}$
and
![]() $2^{\aleph _0}\geq \aleph _2$
.
$2^{\aleph _0}\geq \aleph _2$
.
Proof Let
![]() $\kappa $
be a measurable cardinal. Then, in
$\kappa $
be a measurable cardinal. Then, in
![]() $V^{\mathbb {M}(\omega ,\kappa )}$
,
$V^{\mathbb {M}(\omega ,\kappa )}$
,
![]() $2^{\aleph _0}\geq \aleph _2$
and there is an ideal satisfying the hypothesis of Proposition 4.7 (see, for example, [Reference Cummings7, Theorem 23.2]). Apply Proposition 4.7 and Theorem 3.3.
$2^{\aleph _0}\geq \aleph _2$
and there is an ideal satisfying the hypothesis of Proposition 4.7 (see, for example, [Reference Cummings7, Theorem 23.2]). Apply Proposition 4.7 and Theorem 3.3.
5
 $\sigma $
-closed ideals and monochromatic highly connected subgraphs
$\sigma $
-closed ideals and monochromatic highly connected subgraphs
In this section, we prove the following theorem.
Theorem 5.1 Suppose that a regular cardinal
![]() $\kappa $
carries a countably complete uniform ideal I such that there exists a dense
$\kappa $
carries a countably complete uniform ideal I such that there exists a dense
![]() $\sigma $
-closed collection
$\sigma $
-closed collection
![]() $H\subseteq I^+$
. Then
$H\subseteq I^+$
. Then
![]() $\kappa \to _{hc}(\kappa )^2_\omega $
. Moreover,
$\kappa \to _{hc}(\kappa )^2_\omega $
. Moreover,
![]() $\kappa \to _{hc, <4}(\kappa )^2_\omega $
holds.
$\kappa \to _{hc, <4}(\kappa )^2_\omega $
holds.
Fix an ideal I as in the hypothesis of Theorem 5.1. It is worth comparing such ideals with those of the previous section:
-
• We do not insist that I is normal any more.
-
• We impose the stronger requirement that the ideal has a
 $\sigma $
-closed dense subset; note that any such ideal is 2-precipitous.
$\sigma $
-closed dense subset; note that any such ideal is 2-precipitous.
Fix a coloring
![]() $c: [\kappa ]^2\to \omega $
. Given
$c: [\kappa ]^2\to \omega $
. Given
![]() $B_0, B_1\in I^+$
and
$B_0, B_1\in I^+$
and
![]() $i\in \omega $
, we say that
$i\in \omega $
, we say that
![]() $(B_0,B_1)$
is i-frequent if for any positive
$(B_0,B_1)$
is i-frequent if for any positive
![]() $B_0'\subseteq B_0$
and positive
$B_0'\subseteq B_0$
and positive
![]() $B_1'\subseteq B_1$
, it is the case that
$B_1'\subseteq B_1$
, it is the case that
![]() $\{\alpha \in B_0': \{\beta \in B_1': c(\alpha ,\beta )=i\}\in I^+\}\in I^+$
.
$\{\alpha \in B_0': \{\beta \in B_1': c(\alpha ,\beta )=i\}\in I^+\}\in I^+$
.
Remark 5.2 Equivalently,
![]() $(B_0,B_1)$
is i-frequent if for any positive
$(B_0,B_1)$
is i-frequent if for any positive
![]() $B_1'\subseteq B_1$
, it is the case that
$B_1'\subseteq B_1$
, it is the case that
![]() $\{\alpha \in B_0: \{\beta \in B_1': c(\alpha ,\beta )=i\}\in I^+\}\in I^*\restriction B_0$
. See the argument in Claim 3.5.
$\{\alpha \in B_0: \{\beta \in B_1': c(\alpha ,\beta )=i\}\in I^+\}\in I^*\restriction B_0$
. See the argument in Claim 3.5.
Claim 5.3 There exist a positive
![]() $B\in I^+$
and
$B\in I^+$
and
![]() $i\in \omega $
such that for any positive
$i\in \omega $
such that for any positive
![]() $B'\subseteq B$
, there are positive
$B'\subseteq B$
, there are positive
![]() $B_0, B_1\subseteq B'$
such that
$B_0, B_1\subseteq B'$
such that
![]() $(B_0,B_1)$
is i-frequent.
$(B_0,B_1)$
is i-frequent.
In the following proof, to avoid repetitions, whenever we mention a positive set, we implicitly assume that the positive set is in the
![]() $\sigma $
-closed dense collection H.
$\sigma $
-closed dense collection H.
Proof Suppose otherwise for the sake of contradiction. For
![]() $A\in I^+$
and
$A\in I^+$
and
![]() $j\in \omega $
, let
$j\in \omega $
, let
![]() $(*)_{A,j}$
abbreviate the assertion: there are positive sets
$(*)_{A,j}$
abbreviate the assertion: there are positive sets
![]() $B_0, B_1\subseteq A$
such that
$B_0, B_1\subseteq A$
such that
![]() $(B_0, B_1)$
is j-frequent. By the hypothesis, we can recursively define
$(B_0, B_1)$
is j-frequent. By the hypothesis, we can recursively define
![]() $\langle B^{\prime }_k \in I^+: k\in \omega \rangle $
such that:
$\langle B^{\prime }_k \in I^+: k\in \omega \rangle $
such that:
-
•
 $B^{\prime }_0 = \kappa $
,
$B^{\prime }_0 = \kappa $
, -
• for any
 $k\in \omega $
,
$k\in \omega $
,
 $B^{\prime }_{k+1}\subseteq B^{\prime }_k$
and
$B^{\prime }_{k+1}\subseteq B^{\prime }_k$
and
 $\neg (*)_{B^{\prime }_{k+1},k}$
.
$\neg (*)_{B^{\prime }_{k+1},k}$
.
Let
![]() $B'=\bigcap _{k\in \omega } B^{\prime }_k$
. By the
$B'=\bigcap _{k\in \omega } B^{\prime }_k$
. By the
![]() $\sigma $
-closure of I, we have that
$\sigma $
-closure of I, we have that
![]() $B'\in I^+$
. Then it satisfies that for any
$B'\in I^+$
. Then it satisfies that for any
![]() $i\in \omega $
, such that there are no positive
$i\in \omega $
, such that there are no positive
![]() $B_0, B_1\subseteq B'$
such that
$B_0, B_1\subseteq B'$
such that
![]() $(B_0, B_1)$
is i-frequent.
$(B_0, B_1)$
is i-frequent.
Recursively construct an
![]() $\omega $
-sequence of pairs of I-positive sets
$\omega $
-sequence of pairs of I-positive sets
as follows: start with
![]() $(B',B')=(C_{-1}, D_{-1})$
; since it is not
$(B',B')=(C_{-1}, D_{-1})$
; since it is not
![]() $0$
-frequent, there are positive
$0$
-frequent, there are positive
![]() $(C_0, D_0)$
such that for all
$(C_0, D_0)$
such that for all
![]() $\alpha \in C_0$
,
$\alpha \in C_0$
,
![]() $\{\beta \in D_0: c(\alpha ,\beta )=0\}\in I$
. In general, as
$\{\beta \in D_0: c(\alpha ,\beta )=0\}\in I$
. In general, as
![]() $(C_i, D_i)$
is not (
$(C_i, D_i)$
is not (
![]() $i+1$
)-frequent, we can find
$i+1$
)-frequent, we can find
![]() $(C_{i+1}, D_{i+1})$
such that for all
$(C_{i+1}, D_{i+1})$
such that for all
![]() $\alpha \in C_i$
,
$\alpha \in C_i$
,
![]() $\{\beta \in D_i: c(\alpha ,\beta )=i+1\}\in I$
. Let
$\{\beta \in D_i: c(\alpha ,\beta )=i+1\}\in I$
. Let
![]() $C^*=\bigcap _{i\in \omega } C_i$
and
$C^*=\bigcap _{i\in \omega } C_i$
and
![]() $D^*=\bigcap _{i\in \omega } D_i$
. By the
$D^*=\bigcap _{i\in \omega } D_i$
. By the
![]() $\sigma $
-closure of I, both
$\sigma $
-closure of I, both
![]() $C^*$
and
$C^*$
and
![]() $D^*$
are in
$D^*$
are in
![]() $I^+$
. By the
$I^+$
. By the
![]() $\sigma $
-completeness of the ideal, we can find some i and
$\sigma $
-completeness of the ideal, we can find some i and
![]() $\alpha \in C^*$
such that
$\alpha \in C^*$
such that
![]() $\{\beta \in D^*: c(\alpha ,\beta )=i\}\in I^+$
. However, this contradicts with the assumption that
$\{\beta \in D^*: c(\alpha ,\beta )=i\}\in I^+$
. However, this contradicts with the assumption that
![]() $\alpha \in C_i$
.
$\alpha \in C_i$
.
To finish the proof of Theorem 5.1, by repeatedly applying Claim 5.3, we can find
![]() $\langle B_n\in I^+: n\in \omega \rangle $
and
$\langle B_n\in I^+: n\in \omega \rangle $
and
![]() $i\in \omega $
such that for any
$i\in \omega $
such that for any
![]() $n<k$
,
$n<k$
,
![]() $(B_n, B_k)$
is i-frequent.
$(B_n, B_k)$
is i-frequent.
Given
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $B_n^*\subseteq B_n$
be the collection of
$B_n^*\subseteq B_n$
be the collection of
![]() $\alpha \in B_n$
satisfying that for any
$\alpha \in B_n$
satisfying that for any
![]() $k>n$
,
$k>n$
,
![]() $\{\beta \in B_k: c(\alpha ,\beta )=i\}\in I^+$
. Notice that
$\{\beta \in B_k: c(\alpha ,\beta )=i\}\in I^+$
. Notice that
![]() $B^*_n=_I B_n$
by Remark 5.2 and the fact that I is
$B^*_n=_I B_n$
by Remark 5.2 and the fact that I is
![]() $\sigma $
-complete.
$\sigma $
-complete.
We claim that
![]() $B=\bigcup _{n\in \omega } B^*_n$
is highly connected in the color i. Given
$B=\bigcup _{n\in \omega } B^*_n$
is highly connected in the color i. Given
![]() $\alpha <\beta \in B$
and
$\alpha <\beta \in B$
and
![]() $C\in [B]^{<\kappa }$
, there must be some
$C\in [B]^{<\kappa }$
, there must be some
![]() $n_0, n_1 \in \omega $
such that
$n_0, n_1 \in \omega $
such that
![]() $\alpha \in B^*_{n_0}$
and
$\alpha \in B^*_{n_0}$
and
![]() $\beta \in B^*_{n_1}$
. Find
$\beta \in B^*_{n_1}$
. Find
![]() $k>\max \{n_0, n_1\}$
. By the hypothesis,
$k>\max \{n_0, n_1\}$
. By the hypothesis,
![]() $C_0=\{\gamma \in B_k^*: c(\alpha ,\gamma )=i\}\in I^+$
and
$C_0=\{\gamma \in B_k^*: c(\alpha ,\gamma )=i\}\in I^+$
and
![]() $C_1=\{\gamma \in B_{k+1}^*: c(\beta ,\gamma )=i\}\in I^+$
. As
$C_1=\{\gamma \in B_{k+1}^*: c(\beta ,\gamma )=i\}\in I^+$
. As
![]() $(B_k, B_{k+1})$
is i-frequent, we can find
$(B_k, B_{k+1})$
is i-frequent, we can find
![]() $\gamma _0\in C_0\setminus C$
and
$\gamma _0\in C_0\setminus C$
and
![]() $\gamma _1\in C_1 \setminus C$
such that
$\gamma _1\in C_1 \setminus C$
such that
![]() $c(\gamma _0, \gamma _1)=i$
. As a result,
$c(\gamma _0, \gamma _1)=i$
. As a result,
![]() $\alpha , \gamma _0, \gamma _1, \beta $
is the required path of color i.
$\alpha , \gamma _0, \gamma _1, \beta $
is the required path of color i.
6 Remarks on the consistency of the ideal hypothesis
For regular cardinal
![]() $\lambda \geq \kappa $
, if
$\lambda \geq \kappa $
, if
![]() $\kappa $
be
$\kappa $
be
![]() $\lambda $
-supercompact, we show that in
$\lambda $
-supercompact, we show that in
![]() $V^{Coll(\omega _1, <\kappa )}$
,
$V^{Coll(\omega _1, <\kappa )}$
,
![]() $\lambda $
carries a
$\lambda $
carries a
![]() $\kappa $
-complete uniform ideal which admits a dense and
$\kappa $
-complete uniform ideal which admits a dense and
![]() $\sigma $
-closed collection of positive sets. The construction is due to Galvin, Jech, and Magidor [Reference Galvin, Jech and Magidor11] and, independently to Laver [Reference Laver17]. We supply a proof for the sake of completeness.
$\sigma $
-closed collection of positive sets. The construction is due to Galvin, Jech, and Magidor [Reference Galvin, Jech and Magidor11] and, independently to Laver [Reference Laver17]. We supply a proof for the sake of completeness.
Let U be a fine normal ultrafilter on
![]() $P_{\kappa }\lambda $
. By a theorem of Solovay (see [Reference Hugh Woodin, Davis and Rodríguez13, Theorem 14] for a proof), there exists
$P_{\kappa }\lambda $
. By a theorem of Solovay (see [Reference Hugh Woodin, Davis and Rodríguez13, Theorem 14] for a proof), there exists
![]() $B\in U$
such that
$B\in U$
such that
![]() $a\in B\mapsto \sup a$
is injective. Let
$a\in B\mapsto \sup a$
is injective. Let
![]() $j: V\to M\simeq Ult(V, U)$
. Let
$j: V\to M\simeq Ult(V, U)$
. Let
![]() $\delta =\sup j"\lambda $
. Let
$\delta =\sup j"\lambda $
. Let
![]() $G\subseteq Coll(\omega _1, <\kappa )$
be generic over V. It is well known that if
$G\subseteq Coll(\omega _1, <\kappa )$
be generic over V. It is well known that if
![]() $H\subseteq Coll(\omega _1,[\kappa , j(\kappa )))$
is generic over
$H\subseteq Coll(\omega _1,[\kappa , j(\kappa )))$
is generic over
![]() $V[G]$
, then we can lift j to
$V[G]$
, then we can lift j to
![]() $j^+: V[G]\to M[G*H]$
in
$j^+: V[G]\to M[G*H]$
in
![]() $V[G*H]$
.
$V[G*H]$
.
In
![]() $V[G]$
, consider the ideal
$V[G]$
, consider the ideal
The fact that I is
![]() $\kappa $
-complete and uniform is immediate. Let us show that there exists a dense
$\kappa $
-complete and uniform is immediate. Let us show that there exists a dense
![]() $\sigma $
-closed collection of positive sets.
$\sigma $
-closed collection of positive sets.
For each
![]() $r\in Coll(\omega _1, <j(\kappa ))^M/G$
, there exists a function
$r\in Coll(\omega _1, <j(\kappa ))^M/G$
, there exists a function
![]() $f_r: B\to P$
such that
$f_r: B\to P$
such that
![]() $j(f_r)(j" \lambda )=r$
. Define
$j(f_r)(j" \lambda )=r$
. Define
![]() $X_r=\{\sup a: a\in B, f_r(a)\in G\}$
.
$X_r=\{\sup a: a\in B, f_r(a)\in G\}$
.
Claim 6.1
![]() $X_r\in I^+$
.
$X_r\in I^+$
.
Proof It suffices to check that
![]() $r\Vdash \delta \in j^+(X_r)$
. Let
$r\Vdash \delta \in j^+(X_r)$
. Let
![]() $H\subseteq Coll(\omega _1, <j(\kappa ))^M/G$
containing r be generic over
$H\subseteq Coll(\omega _1, <j(\kappa ))^M/G$
containing r be generic over
![]() $V[G]$
, then we can lift j to
$V[G]$
, then we can lift j to
![]() $j^+: V[G]\to M[H]$
. In particular,
$j^+: V[G]\to M[H]$
. In particular,
![]() $H=j^+(G)$
. Since
$H=j^+(G)$
. Since
![]() $j(f_r)(j"\lambda )=r\in j^+(G)$
, we have that
$j(f_r)(j"\lambda )=r\in j^+(G)$
, we have that
![]() $\delta \in j^+(X_r)$
.
$\delta \in j^+(X_r)$
.
Claim 6.2
![]() $X_r\subseteq _I X_{r'}$
iff
$X_r\subseteq _I X_{r'}$
iff
![]() $r\leq _{Coll(\omega _1, <j(\kappa ))^M/G} r'$
.
$r\leq _{Coll(\omega _1, <j(\kappa ))^M/G} r'$
.
Proof If
![]() $r\leq r'$
, then it is clear that
$r\leq r'$
, then it is clear that
![]() $X_r\subseteq _I X_{r'}$
. For the other direction, suppose for the sake of contradiction that
$X_r\subseteq _I X_{r'}$
. For the other direction, suppose for the sake of contradiction that
![]() $r\not \leq _{Coll(\omega _1, <j(\kappa ))^M/G} r'$
. In particular, there is some extension
$r\not \leq _{Coll(\omega _1, <j(\kappa ))^M/G} r'$
. In particular, there is some extension
![]() $r^*$
of r that is incompatible with
$r^*$
of r that is incompatible with
![]() $r'$
. Then
$r'$
. Then
![]() $r^*\Vdash \delta \in j^+(X_r)\setminus j^+(X_{r'})$
. Hence,
$r^*\Vdash \delta \in j^+(X_r)\setminus j^+(X_{r'})$
. Hence,
![]() $X_{r}\not \subseteq _I X_{r'}$
.
$X_{r}\not \subseteq _I X_{r'}$
.
As a result,
is
![]() $\sigma $
-closed, since
$\sigma $
-closed, since
![]() $ Coll(\omega _1, <j(\kappa ))^M/G$
is
$ Coll(\omega _1, <j(\kappa ))^M/G$
is
![]() $\sigma $
-closed in
$\sigma $
-closed in
![]() $V[G]$
.
$V[G]$
.
Claim 6.3 For any
![]() $X\in I^+$
, there exists some r such that
$X\in I^+$
, there exists some r such that
![]() $X_r\subseteq _I X$
.
$X_r\subseteq _I X$
.
Proof Let
![]() $r\in Coll(\omega _1, <j(\kappa ))^M/G$
force that
$r\in Coll(\omega _1, <j(\kappa ))^M/G$
force that
![]() $\delta \in j^+(X)$
. We show that
$\delta \in j^+(X)$
. We show that
![]() $X_r\subseteq _{I} X$
. Otherwise, there is some
$X_r\subseteq _{I} X$
. Otherwise, there is some
![]() $r'$
forcing that
$r'$
forcing that
![]() $\delta \in j^+(X_r)\setminus j^+(X)$
. In particular,
$\delta \in j^+(X_r)\setminus j^+(X)$
. In particular,
![]() $r'$
forces that
$r'$
forces that
![]() $j(f_r)(j"\lambda )=r\in j^+(G)$
. By the separability of the forcing,
$j(f_r)(j"\lambda )=r\in j^+(G)$
. By the separability of the forcing,
![]() $r'\leq _{Coll(\omega _1, <j(\kappa ))^M/G} r$
. This contradicts the fact that r forces
$r'\leq _{Coll(\omega _1, <j(\kappa ))^M/G} r$
. This contradicts the fact that r forces
![]() $\delta \in j^+(X)$
.
$\delta \in j^+(X)$
.
The following is now immediate from the preceding arguments, coupled with Theorem 5.1.
Theorem 6.4
-
(1) If
 $\kappa $
is measurable, then in
$\kappa $
is measurable, then in
 $V^{Coll(\omega _1, <\kappa )}$
,
$V^{Coll(\omega _1, <\kappa )}$
,
 $\aleph _2\to _{hc}(\aleph _2)^2_{\omega }$
.
$\aleph _2\to _{hc}(\aleph _2)^2_{\omega }$
. -
(2) If
 $\kappa $
is supercompact, then in
$\kappa $
is supercompact, then in
 $V^{Coll(\omega _1, <\kappa )}$
, for all regular cardinal
$V^{Coll(\omega _1, <\kappa )}$
, for all regular cardinal
 $\lambda \geq \aleph _2$
,
$\lambda \geq \aleph _2$
,
 $\lambda \to _{hc}(\lambda )^2_{\omega }$
.
$\lambda \to _{hc}(\lambda )^2_{\omega }$
.
Some large cardinal assumption is necessary to establish the consistency of
![]() $\kappa \to _{hc}(\kappa )^2_{\omega }$
, as shown in [Reference Lambie-Hanson16].
$\kappa \to _{hc}(\kappa )^2_{\omega }$
, as shown in [Reference Lambie-Hanson16].
7 The lengths of the paths
In Section 5, we have shown that if there exists a
![]() $\sigma $
-complete uniform ideal on
$\sigma $
-complete uniform ideal on
![]() $\omega _2$
admitting a
$\omega _2$
admitting a
![]() $\sigma $
-closed collection of dense positive sets, then
$\sigma $
-closed collection of dense positive sets, then
![]() $\omega _2\to _{hc, <4} (\omega _2)^2_\omega $
. One natural question is whether we can improve the conclusion to
$\omega _2\to _{hc, <4} (\omega _2)^2_\omega $
. One natural question is whether we can improve the conclusion to
![]() $\omega _2\to _{hc, <3} (\omega _2)^2_\omega $
. In this section, we show that the answer is no, at least not from the same hypothesis.
$\omega _2\to _{hc, <3} (\omega _2)^2_\omega $
. In this section, we show that the answer is no, at least not from the same hypothesis.
Remark 7.1 If there is a
![]() $\sigma $
-closed forcing P such that in
$\sigma $
-closed forcing P such that in
![]() $V^P$
, there is a transitive class M and an elementary embedding
$V^P$
, there is a transitive class M and an elementary embedding
![]() $j: V\to M$
with critical point
$j: V\to M$
with critical point
![]() $\kappa $
, then
$\kappa $
, then
![]() $\kappa \to _{hc}(\kappa )^2_\omega $
holds. Essentially the same proof from Section 5 works.
$\kappa \to _{hc}(\kappa )^2_\omega $
holds. Essentially the same proof from Section 5 works.
Theorem 7.2 It is consistent relative to the existence of a measurable cardinal that
![]() $\aleph _2\to _{hc, <4} (\aleph _2)^2_\omega $
but
$\aleph _2\to _{hc, <4} (\aleph _2)^2_\omega $
but
![]() $\aleph _2\not \to _{hc, <3} (\aleph _2)^2_\omega $
.
$\aleph _2\not \to _{hc, <3} (\aleph _2)^2_\omega $
.
Proof Let
![]() $\kappa $
be a measurable cardinal. We will make use of a forcing poset
$\kappa $
be a measurable cardinal. We will make use of a forcing poset
![]() $\mathbb {P}_{\kappa }$
due to Komjáth and Shelah [Reference Komjáth and Shelah15, Theorem 7]. The final forcing will be
$\mathbb {P}_{\kappa }$
due to Komjáth and Shelah [Reference Komjáth and Shelah15, Theorem 7]. The final forcing will be
![]() $Coll(\omega _1, <\kappa )* \mathbb {P}_{\kappa }$
. It follows from Komjáth and Shelah’s work that
$Coll(\omega _1, <\kappa )* \mathbb {P}_{\kappa }$
. It follows from Komjáth and Shelah’s work that
![]() $\aleph _2\not \to _{hc, <3} (\aleph _2)^2_\omega $
in the final model. More specifically, this was proved in Claim 4 inside the proof of Theorem 7 of [Reference Komjáth and Shelah15]. Note that
$\aleph _2\not \to _{hc, <3} (\aleph _2)^2_\omega $
in the final model. More specifically, this was proved in Claim 4 inside the proof of Theorem 7 of [Reference Komjáth and Shelah15]. Note that
![]() $(*)$
in [Reference Komjáth and Shelah15] is a consequence of
$(*)$
in [Reference Komjáth and Shelah15] is a consequence of
![]() $\aleph _2\to _{hc, <3} (\aleph _2)^2_\omega $
.
$\aleph _2\to _{hc, <3} (\aleph _2)^2_\omega $
.
Let
![]() $G\subseteq Coll(\omega _1, <\kappa )* \mathbb {P}_{\kappa }$
be a generic filter over V. By Remark 7.1 applied in
$G\subseteq Coll(\omega _1, <\kappa )* \mathbb {P}_{\kappa }$
be a generic filter over V. By Remark 7.1 applied in
![]() $V[G]$
(namely, replacing the occurrences of “V” there with “
$V[G]$
(namely, replacing the occurrences of “V” there with “
![]() $V[G]$
”), it is enough to check that in a further countably closed forcing extension over
$V[G]$
”), it is enough to check that in a further countably closed forcing extension over
![]() $V[G]$
, there exists an elementary embedding
$V[G]$
, there exists an elementary embedding
![]() $j: V[G]\to M$
with critical point
$j: V[G]\to M$
with critical point
![]() $\omega _2^{V[G]}=\kappa $
.
$\omega _2^{V[G]}=\kappa $
.
To that end, let us recall the definition of
![]() $\mathbb {P}_\kappa $
: conditions consist of
$\mathbb {P}_\kappa $
: conditions consist of
![]() $(S, f, \mathcal {H}, h)$
such that:
$(S, f, \mathcal {H}, h)$
such that:
-
•
 $S\in [\kappa ]^{\leq \aleph _0}$
,
$S\in [\kappa ]^{\leq \aleph _0}$
, -
•
 $f: [S]^2\to [\omega ]^\omega $
,
$f: [S]^2\to [\omega ]^\omega $
, -
•
 $\mathcal {H}\subseteq [S]^\omega $
,
$\mathcal {H}\subseteq [S]^\omega $
,
 $|\mathcal {H}|\leq \aleph _0$
, for each
$|\mathcal {H}|\leq \aleph _0$
, for each
 $H\in \mathcal {H}$
,
$H\in \mathcal {H}$
,
 $otp(H)=\omega $
and for any
$otp(H)=\omega $
and for any
 $H, H'\in \mathcal {H}$
,
$H, H'\in \mathcal {H}$
,
 $H\cap H'$
is finite,
$H\cap H'$
is finite, -
• if
 $\alpha \in S$
,
$\alpha \in S$
,
 $H\in \mathcal {H}$
with
$H\in \mathcal {H}$
with
 $\min H < \alpha $
, then
$\min H < \alpha $
, then
 $|\{\beta \in H: h(H)\in f(\alpha ,\beta )\}|\leq 1$
.
$|\{\beta \in H: h(H)\in f(\alpha ,\beta )\}|\leq 1$
.
The order is:
![]() $(S', f', \mathcal {H}', h')\leq (S, f, \mathcal {H}, h)$
iff
$(S', f', \mathcal {H}', h')\leq (S, f, \mathcal {H}, h)$
iff
![]() $S'\supset S$
,
$S'\supset S$
,
![]() $\mathcal {H}'\supset \mathcal {H}$
,
$\mathcal {H}'\supset \mathcal {H}$
,
![]() $f'\restriction [S]^2 = f$
,
$f'\restriction [S]^2 = f$
,
![]() $h'\restriction \mathcal {H} = h$
and for any
$h'\restriction \mathcal {H} = h$
and for any
![]() $H\in \mathcal {H}'-\mathcal {H}$
,
$H\in \mathcal {H}'-\mathcal {H}$
,
![]() $H\not \subseteq S$
. Note that
$H\not \subseteq S$
. Note that
![]() $\mathbb {P}_\kappa $
is a countably closed forcing of size
$\mathbb {P}_\kappa $
is a countably closed forcing of size
![]() $\kappa $
.
$\kappa $
.
Let
![]() $j: V\to M$
witness that
$j: V\to M$
witness that
![]() $\kappa $
is measurable. Let
$\kappa $
is measurable. Let
![]() $G*H\subseteq Coll(\omega _1,<\kappa )*\mathbb {P}_\kappa $
. Let
$G*H\subseteq Coll(\omega _1,<\kappa )*\mathbb {P}_\kappa $
. Let
![]() $G^*\subseteq Coll(\omega _1, <j(\kappa ))/G*H$
be generic over
$G^*\subseteq Coll(\omega _1, <j(\kappa ))/G*H$
be generic over
![]() $V[G*H]$
. This is possible since
$V[G*H]$
. This is possible since
![]() $Coll(\omega _1,<\kappa )*\mathbb {P}_\kappa $
regularly embeds into
$Coll(\omega _1,<\kappa )*\mathbb {P}_\kappa $
regularly embeds into
![]() $Coll(\omega _1, <j(\kappa ))$
with a countably closed quotient (see [Reference Cummings7, Theorem 14.3]). As a result, we can lift
$Coll(\omega _1, <j(\kappa ))$
with a countably closed quotient (see [Reference Cummings7, Theorem 14.3]). As a result, we can lift
![]() $j: V[G]\to M[G^*]$
. In order to lift further to
$j: V[G]\to M[G^*]$
. In order to lift further to
![]() $V[G*H]$
, we need to force
$V[G*H]$
, we need to force
![]() $j(\mathbb {P}_\kappa )/H$
over
$j(\mathbb {P}_\kappa )/H$
over
![]() $V[G^*]$
. It suffices to show that in
$V[G^*]$
. It suffices to show that in
![]() $V[G^*]$
,
$V[G^*]$
,
![]() $j(\mathbb {P}_\kappa )/H$
is countably closed.
$j(\mathbb {P}_\kappa )/H$
is countably closed.
Suppose
![]() $\langle p_n=_{def} (S_n, f_n, \mathcal {H}_n, h_n): n\in \omega \rangle \subseteq j(\mathbb {P}_\kappa )/H$
is a decreasing sequence. We want to show that
$\langle p_n=_{def} (S_n, f_n, \mathcal {H}_n, h_n): n\in \omega \rangle \subseteq j(\mathbb {P}_\kappa )/H$
is a decreasing sequence. We want to show that
![]() $q=\bigcup _{n\in \omega } p_n$
is the lower bound desired. For this, we only need to verify that
$q=\bigcup _{n\in \omega } p_n$
is the lower bound desired. For this, we only need to verify that
![]() $q\in j(\mathbb {P}_\kappa )/H$
. More explicitly, we need to verify that q is compatible with
$q\in j(\mathbb {P}_\kappa )/H$
. More explicitly, we need to verify that q is compatible with
![]() $h\in H$
for any
$h\in H$
for any
![]() $h\in H$
. For each
$h\in H$
. For each
![]() $p=(S_p,f_p,\mathcal {H}_p, h_p)\in j(\mathbb {P}_\kappa )$
, let
$p=(S_p,f_p,\mathcal {H}_p, h_p)\in j(\mathbb {P}_\kappa )$
, let
![]() $p\restriction \kappa $
denote the condition:
$p\restriction \kappa $
denote the condition:
![]() $(S_p\cap \kappa , f_p\restriction [S_p\cap \kappa ]^2, \mathcal {H}_p\cap P(\kappa ), h_p\restriction (\mathcal {H}_p\cap P(\kappa )))$
. It is not hard to check that
$(S_p\cap \kappa , f_p\restriction [S_p\cap \kappa ]^2, \mathcal {H}_p\cap P(\kappa ), h_p\restriction (\mathcal {H}_p\cap P(\kappa )))$
. It is not hard to check that
![]() $p\restriction \kappa \in \mathbb {P}_\kappa $
and
$p\restriction \kappa \in \mathbb {P}_\kappa $
and
![]() $p\leq _{j(\mathbb {P}_\kappa )} p\restriction \kappa $
.
$p\leq _{j(\mathbb {P}_\kappa )} p\restriction \kappa $
.
Claim 7.3
![]() $p\in j(\mathbb {P}_\kappa )/H$
iff
$p\in j(\mathbb {P}_\kappa )/H$
iff
![]() $p\restriction \kappa \in H$
.
$p\restriction \kappa \in H$
.
Proof of the claim
If
![]() $p\restriction \kappa \in H$
, to see
$p\restriction \kappa \in H$
, to see
![]() $p\in j(\mathbb {P}_\kappa )/H$
, it suffices to see that for any
$p\in j(\mathbb {P}_\kappa )/H$
, it suffices to see that for any
![]() $r\leq _{\mathbb {P}_\kappa } p\restriction \kappa $
and
$r\leq _{\mathbb {P}_\kappa } p\restriction \kappa $
and
![]() $r\in H$
, r is compatible with p. To check that
$r\in H$
, r is compatible with p. To check that
![]() $r\cup p$
can be extended to a condition, it suffices to check that for any
$r\cup p$
can be extended to a condition, it suffices to check that for any
![]() $B\in \mathcal {H}_r\setminus \mathcal {H}_p$
,
$B\in \mathcal {H}_r\setminus \mathcal {H}_p$
,
![]() $B\not \subseteq S_p$
and for any
$B\not \subseteq S_p$
and for any
![]() $B\in \mathcal {H}_p\setminus \mathcal {H}_r$
,
$B\in \mathcal {H}_p\setminus \mathcal {H}_r$
,
![]() $B\not \subseteq S_r$
. To see the former, note that if
$B\not \subseteq S_r$
. To see the former, note that if
![]() $B\in \mathcal {H}_r\setminus \mathcal {H}_p$
, then
$B\in \mathcal {H}_r\setminus \mathcal {H}_p$
, then
![]() $B\in \mathcal {H}_r \setminus \mathcal {H}_{p\restriction \kappa }$
, since
$B\in \mathcal {H}_r \setminus \mathcal {H}_{p\restriction \kappa }$
, since
![]() $r\leq p\restriction \kappa $
,
$r\leq p\restriction \kappa $
,
![]() $B\not \subseteq S_p\cap \kappa $
. Since
$B\not \subseteq S_p\cap \kappa $
. Since
![]() $B\subseteq \kappa $
, we have
$B\subseteq \kappa $
, we have
![]() $B\not \subseteq S_p$
. To see the latter, note that
$B\not \subseteq S_p$
. To see the latter, note that
![]() $B\in \mathcal {H}_p\setminus \mathcal {H}_r$
implies that
$B\in \mathcal {H}_p\setminus \mathcal {H}_r$
implies that
![]() $B\in \mathcal {H}_p \setminus \mathcal {H}_{p\restriction \kappa }$
. In particular,
$B\in \mathcal {H}_p \setminus \mathcal {H}_{p\restriction \kappa }$
. In particular,
![]() $B\cap [\kappa ,j(\kappa ))\neq \emptyset $
. Hence,
$B\cap [\kappa ,j(\kappa ))\neq \emptyset $
. Hence,
![]() $B\not \subseteq S_r$
since
$B\not \subseteq S_r$
since
![]() $S_r\subseteq \kappa $
.
$S_r\subseteq \kappa $
.
If
![]() $p\in j(\mathbb {P}_\kappa )/H$
, then for any
$p\in j(\mathbb {P}_\kappa )/H$
, then for any
![]() $h\in H$
, h and p are compatible. In particular, since
$h\in H$
, h and p are compatible. In particular, since
![]() $p\leq p\restriction \kappa $
, we know that any
$p\leq p\restriction \kappa $
, we know that any
![]() $h\in H$
is compatible with
$h\in H$
is compatible with
![]() $p\restriction \kappa $
. This implies that
$p\restriction \kappa $
. This implies that
![]() $p\restriction \kappa \in H$
.
$p\restriction \kappa \in H$
.
To finish the proof, since for each
![]() $n\in \omega $
, by Claim 7.3 and the fact that
$n\in \omega $
, by Claim 7.3 and the fact that
![]() $p_n\in j(\mathbb {P}_\kappa )/H$
, we have that
$p_n\in j(\mathbb {P}_\kappa )/H$
, we have that
![]() $p_n\restriction \kappa \in H$
. As a result, we must have
$p_n\restriction \kappa \in H$
. As a result, we must have
![]() $q\restriction \kappa \in H$
. By Claim 7.3, we have
$q\restriction \kappa \in H$
. By Claim 7.3, we have
![]() $q\in j(\mathbb {P}_\kappa )/H$
.
$q\in j(\mathbb {P}_\kappa )/H$
.
8 Open questions
Question 8.1 Starting from the existence of a weakly compact cardinal, can one force that
![]() $\aleph _2\to _{hc}(\aleph _2)^2_{\omega }$
?
$\aleph _2\to _{hc}(\aleph _2)^2_{\omega }$
?
It is possible to use a weaker assumption than the existence of a measurable cardinal to run the proof of Theorem 5.1. In particular, we can use a strongly Ramsey cardinal instead. Recall that
![]() $\kappa $
is strongly Ramsey if for any
$\kappa $
is strongly Ramsey if for any
![]() $A\subset \kappa $
, there is a
$A\subset \kappa $
, there is a
![]() $\kappa $
-model M containing A (namely, M is a transitive model of
$\kappa $
-model M containing A (namely, M is a transitive model of
![]() $\mathrm {ZFC}^-$
containing
$\mathrm {ZFC}^-$
containing
![]() $\kappa $
and is closed under
$\kappa $
and is closed under
![]() $<\kappa $
-sequences), such that there exists a
$<\kappa $
-sequences), such that there exists a
![]() $\kappa $
-complete M-ultrafilter that is weakly amenable to M, meaning that for any
$\kappa $
-complete M-ultrafilter that is weakly amenable to M, meaning that for any
![]() $\mathcal {F}\in M$
and
$\mathcal {F}\in M$
and
![]() $|\mathcal {F}|\leq \kappa $
,
$|\mathcal {F}|\leq \kappa $
,
![]() $\mathcal {F}\cap U \in M$
. See [Reference Gitman12] for more information on Ramsey-like cardinals. However, being a strongly Ramsey cardinal is a much stronger condition than being a weakly compact cardinal.
$\mathcal {F}\cap U \in M$
. See [Reference Gitman12] for more information on Ramsey-like cardinals. However, being a strongly Ramsey cardinal is a much stronger condition than being a weakly compact cardinal.
Question 8.2 Is
![]() $\aleph _2\to _{hc,<3} (\aleph _2)^2_{\omega }$
consistent?
$\aleph _2\to _{hc,<3} (\aleph _2)^2_{\omega }$
consistent?
Question 8.3 Can one separate
![]() $\aleph _2\to _{hc,<m} (\aleph _2)^2_{\omega }$
from
$\aleph _2\to _{hc,<m} (\aleph _2)^2_{\omega }$
from
![]() $\aleph _2\to _{hc,<n} (\aleph _2)^2_{\omega }$
where
$\aleph _2\to _{hc,<n} (\aleph _2)^2_{\omega }$
where
![]() $4\leq m<n\leq \omega $
?
$4\leq m<n\leq \omega $
?
Question 8.4 Is
![]() $\aleph _2\not \to _{hc}(\aleph _1)^2_{\omega }$
consistent?
$\aleph _2\not \to _{hc}(\aleph _1)^2_{\omega }$
consistent?
Our next problem is more open-ended, which concerns the natural generalizations of
![]() $2$
-precipitous ideals. Recall that we have shown that the existence of a uniform normal
$2$
-precipitous ideals. Recall that we have shown that the existence of a uniform normal
![]() $2$
-precipitous ideal on
$2$
-precipitous ideal on
![]() $\kappa $
implies that
$\kappa $
implies that
![]() $\kappa \geq \omega _2$
.
$\kappa \geq \omega _2$
.
Problem 8.5 For
![]() $n\geq 2$
and an ideal I on
$n\geq 2$
and an ideal I on
![]() $\kappa \geq \aleph _2$
, find a natural definition of n-precipitousness that generalizes Definition 3.1 in the case that
$\kappa \geq \aleph _2$
, find a natural definition of n-precipitousness that generalizes Definition 3.1 in the case that
![]() $n=2$
, such that if
$n=2$
, such that if
![]() $\kappa $
carries a uniform normal n-precipitous ideal, then
$\kappa $
carries a uniform normal n-precipitous ideal, then
![]() $\kappa \geq \aleph _n$
.
$\kappa \geq \aleph _n$
.
The referee suggested the following interesting problem, which is worth further investigation. Fix cardinals
![]() $\kappa ,\lambda ,\theta $
and an ideal
$\kappa ,\lambda ,\theta $
and an ideal
![]() $\mathcal {J}$
on
$\mathcal {J}$
on
![]() $\lambda $
containing
$\lambda $
containing
![]() $[\lambda ]^{<\lambda }$
. For any set X of order type
$[\lambda ]^{<\lambda }$
. For any set X of order type
![]() $\lambda $
, let
$\lambda $
, let
![]() $\mathcal {J}_X$
be the ideal on X moved from
$\mathcal {J}_X$
be the ideal on X moved from
![]() $\mathcal {J}$
using the order isomorphism between X and
$\mathcal {J}$
using the order isomorphism between X and
![]() $\lambda $
.
$\lambda $
.
Problem 8.6 Investigate the following partition relations:
![]() $\kappa \to _{\mathcal {J}-hc}(\lambda )^2_\theta $
which asserts that for any
$\kappa \to _{\mathcal {J}-hc}(\lambda )^2_\theta $
which asserts that for any
![]() $c: [\kappa ]^2\to \theta $
, there are
$c: [\kappa ]^2\to \theta $
, there are
![]() $X\subset \kappa $
of order type
$X\subset \kappa $
of order type
![]() $\lambda $
and
$\lambda $
and
![]() $i\in \theta $
such that for any
$i\in \theta $
such that for any
![]() $J\in \mathcal {J}_X$
,
$J\in \mathcal {J}_X$
,
![]() $(X\setminus J, c^{-1}(i)\cap [X\setminus J]^2)$
is connected.
$(X\setminus J, c^{-1}(i)\cap [X\setminus J]^2)$
is connected.
Acknowledgments
We thank Stevo Todorcevic and Spencer Unger for helpful discussions and comments. We are grateful to the anonymous referee, whose helpful suggestions, corrections, and comments greatly improve the exposition of this paper.