Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-25T03:41:01.554Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative uniformly positive entropy of induced amenable group actions

Part of: Topological dynamics

Published online by Cambridge University Press:  17 March 2023

KAIRAN LIU  and
RUNJU WEI
KAIRAN LIU
Affiliation:
College of Mathematics and Statistics, Chongqing University, Chongqing 401331, P. R. China (e-mail: lkr111@cqu.edu.cn)
RUNJU WEI*
Affiliation:
Department of Mathematics, University of Science and Technology of China, Hefei, Anhui 230026, P. R. China
*
(e-mail: wrj3219@mail.ustc.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a countably infinite discrete amenable group. It should be noted that a G-system 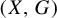$(X,G)$ naturally induces a G-system 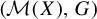$(\mathcal {M}(X),G)$, where 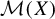$\mathcal {M}(X)$ denotes the space of Borel probability measures on the compact metric space X endowed with the weak*-topology. A factor map 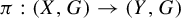$\pi : (X,G)\to (Y,G)$ between two G-systems induces a factor map 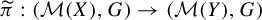$\widetilde {\pi }:(\mathcal {M}(X),G)\to (\mathcal {M}(Y),G)$. It turns out that 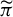$\widetilde {\pi }$ is open if and only if $\pi $ is open. When Y is fully supported, it is shown that 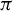$\pi $ has relative uniformly positive entropy if and only if 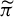$\widetilde {\pi }$ has relative uniformly positive entropy.

Keywords

relative uniformly positive entropyinduced systemrelative independence

MSC classification

Primary: 37B40: Topological entropy
Secondary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 2 , February 2024 , pp. 569 - 593
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E., Auslander, J. and Nagar, A.. Dynamics of induced systems. Ergod. Th. & Dynam. Sys. 37(7) (2017), 2034–2059.CrossRefGoogle Scholar
Banks, J.. Chaos for induced hyperspace maps. Chaos Solitons Fractals 25(3) (2005), 681–685.CrossRefGoogle Scholar
Bauer, W. and Sigmund, K.. Topological dynamics of transformations induced on the space of probability measures. Monatsh. Math. 79 (1975), 81–92.10.1007/BF01585664CrossRefGoogle Scholar
Bernardes, N. C. Jr., Darji, U. B. and Vermersch, R. M.. Uniformly positive entropy of induced transformations. Ergod. Th. & Dynam. Sys. 42(1) (2022), 9–18.CrossRefGoogle Scholar
Billingsley, P.. Convergence of Probability Measures, 2nd edn. John Wiley & Sons, Inc., New York, 1999.10.1002/9780470316962CrossRefGoogle Scholar
Blanchard, F.. Fully positive topological entropy and topological mixing. Symbolic Dynamics and Its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135). Ed. P. Walters. American Mathematical Society, Providence, RI, 1992, pp. 95–105.CrossRefGoogle Scholar
Blanchard, F.. A disjointness theorem involving topological entropy. Bull. Soc. Math. France 121(4) (1993), 465–478.10.24033/bsmf.2216CrossRefGoogle Scholar
Blanchard, F., Glasner, E. and Host, B.. A variation on the variational principle and applications to entropy pairs. Ergod. Th. & Dynam. Sys. 17(1) (1997), 29–43.10.1017/S0143385797069794CrossRefGoogle Scholar
Blanchard, F., Host, B., Maass, A., Martinez, S. and Rudolph, D. J.. Entropy pairs for a measure. Ergod. Th. & Dynam. Sys. 15(4) (1995), 621–632.10.1017/S0143385700008579CrossRefGoogle Scholar
Boyle, M., Fiebig, D. and Fiebig, U.. Residual entropy, conditional entropy and subshift covers. Forum Math. 14(5) (2002), 713–757.CrossRefGoogle Scholar
Downarowicz, T. and Serafin, J.. Fiber entropy and conditional variational principles in compact non-metrizable spaces. Fund. Math. 172(3) (2002), 217–247.10.4064/fm172-3-2CrossRefGoogle Scholar
Dudley, R. M.. Real Analysis and Probability (Cambridge Studies in Advanced Mathematics, 74). Cambridge University Press, Cambridge, 2002.10.1017/CBO9780511755347CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. Strictly ergodic, uniform positive entropy models. Bull. Soc. Math. France 122(3) (1994), 399–412.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. Topological entropy of extensions. Ergodic Theory and Its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Note Series, 205). Eds. K. E. Petersen and I. A. Salam. Cambridge University Press, Cambridge, 1995, pp. 299–307.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. Quasi-factors of zero entropy systems. J. Amer. Math. Soc. 8(3) (1995), 665–686.Google Scholar
Glasner, E. and Ye, X.. Local entropy theory. Ergod. Th. & Dynam. Sys. 29(2) (2009), 321–356.CrossRefGoogle Scholar
Huang, W. and Ye, X.. A local variational relation and applications. Israel J. Math. 151(2006), 237–279.10.1007/BF02777364CrossRefGoogle Scholar
Huang, W., Ye, X. and Zhang, G.. A local variational principle for conditional entropy. Ergod. Th. & Dynam. Sys. 26(1) (2006), 219–245.CrossRefGoogle Scholar
Huang, W., Ye, X. and Zhang, G.. Relative entropy tuples, relative U.P.E. and C.P.E. extensions. Israel J. Math. 158 (2007), 249–283.CrossRefGoogle Scholar
Huang, W., Ye, X. and Zhang, G.. Local entropy theory for a countable discrete amenable action. J. Funct. Anal. 261 (2011), 1028–1082.CrossRefGoogle Scholar
Karpovsky, M. G. and Milman, V. D.. Coordinate density of sets of vectors. Discrete Math. 24(2) (1978), 177–184.CrossRefGoogle Scholar
Kechris, A. S.. Classical Descriptive Set Theory. Spinger-Verlag, New York, 1995.10.1007/978-1-4612-4190-4CrossRefGoogle Scholar
Kerr, D. and Li, H.. Dynamical entropy in Banach spaces. Invent. Math. 162(3) (2005), 649–686.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Independence in topological and C*-dynamics. Math. Ann. 338(4) (2007), 869–926.10.1007/s00208-007-0097-zCrossRefGoogle Scholar
Kerr, D. and Li, H.. Ergodic Theory: Independence and Dichotomies (Springer Monographs in Mathematics, 304). Springer, Cham, 2016.10.1007/978-3-319-49847-8CrossRefGoogle Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. (2) 16(3) (1977), 568–576.CrossRefGoogle Scholar
Lemańczyk, M. and Siemaszko, A.. A note on the existence of a largest topological factor with zero entropy. Proc. Amer. Math. Soc. 129(2) (2001), 475–482.CrossRefGoogle Scholar
Lindenstrauss, E.. Pointwise theorem for amenable groups. Invent. Math. 146(2) (2001), 259–295.CrossRefGoogle Scholar
Ornstein, D. S. and Weiss, B.. Entropy theory and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.CrossRefGoogle Scholar
Park, K. K. and Siemaszko, A.. Relative topological pinsker factors and entropy pairs. Monatsh. Math. 134 (2001), 67–79.CrossRefGoogle Scholar
Rudolph, D. J. and Weiss, B.. Entropy and mixing for amenable groups actions. Ann. of Math. (2) 151(3) (2000), 1119–1150.10.2307/121130CrossRefGoogle Scholar
Sauer, N.. On the density of families of sets. J. Combin. Theory Ser. A 13 (1972), 145–147.10.1016/0097-3165(72)90019-2CrossRefGoogle Scholar
Sharma, P. and Nagar, A.. Inducing sensitivity on hyperspaces. Topology Appl. 157(13) (2010), 2052–2058.CrossRefGoogle Scholar
Shelah, S.. A combinatorial problem; stability and order for models and theories in infinitary languages. Pacific J. Math., 41 (1972), 247–261.10.2140/pjm.1972.41.247CrossRefGoogle Scholar
Ward, T. and Zhang, Q.. The Abramov–Rokhlin entropy addition formula for amenable group actions. Monatsh. Math. 114(3–4) (1992), 317–329.10.1007/BF01299386CrossRefGoogle Scholar
Weiss, B.. Actions of amenable groups. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310). Eds. S. Bezuglyi and S. Kolyada. Cambridge University Press, Cambridge, 2003, pp. 226–262.CrossRefGoogle Scholar
Zhou, X. and Qiao, Y.. Zero sequence entropy and entropy dimension. Discrete Contin. Dyn. Syst. 37(1) (2017), 435–448.Google Scholar
Zimmer, R. J.. Hyperfinite factors and amenable ergodic actions. Invent. Math. 41(1) (1977), 23–31.CrossRefGoogle Scholar