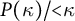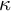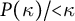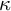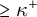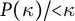1 Introduction
This paper concerns trees of maximal antichains in
![]() $P(\kappa )/{<}\kappa $
for
$P(\kappa )/{<}\kappa $
for
![]() $\kappa $
a regular cardinal of uncountable cofinality. In one’s imagination, trees can grow downward or upward; typically for us here, they grow downward when the tree relation has something to do with the subset relation. Every level of these trees is a maximal antichain and is a refinement of the levels above it. A node of the tree may be viewed as both an element of
$\kappa $
a regular cardinal of uncountable cofinality. In one’s imagination, trees can grow downward or upward; typically for us here, they grow downward when the tree relation has something to do with the subset relation. Every level of these trees is a maximal antichain and is a refinement of the levels above it. A node of the tree may be viewed as both an element of
![]() $[\kappa ]^{\kappa }$
and as its equivalence class modulo the ideal
$[\kappa ]^{\kappa }$
and as its equivalence class modulo the ideal
![]() $P_{\kappa }\kappa $
.
$P_{\kappa }\kappa $
.
If a tree of maximal antichains T has the property that there is no maximal antichain refining all levels simultaneously, call this tree a distributivity tree. Equivalently, the intersection of the downward closure of the antichains on each level of T is not open dense. It may be that this intersection is nonempty, but by choosing a witness
![]() $x \in [\kappa ]^{\kappa }$
to non-density,
$x \in [\kappa ]^{\kappa }$
to non-density,
![]() $T \restriction x$
is a tree of maximal antichains in
$T \restriction x$
is a tree of maximal antichains in
![]() $P(x)/{<}\kappa $
so that the intersection of the downward closure of the antichains on each level of
$P(x)/{<}\kappa $
so that the intersection of the downward closure of the antichains on each level of
![]() $T \restriction x$
is empty. Call such a distributivity tree full; so if there is a distributivity tree of some height, there is a full distributivity tree of the same height. Accordingly, the adjective full is assumed and omitted. Trees of maximal antichains are necessarily pruned, in that every node has extensions to every level. A set
$T \restriction x$
is empty. Call such a distributivity tree full; so if there is a distributivity tree of some height, there is a full distributivity tree of the same height. Accordingly, the adjective full is assumed and omitted. Trees of maximal antichains are necessarily pruned, in that every node has extensions to every level. A set
![]() $x \in [\kappa ]^{\kappa }$
is often identified with its enumerating function
$x \in [\kappa ]^{\kappa }$
is often identified with its enumerating function
![]() $f_{x} : \kappa \rightarrow \kappa ,$
where
$f_{x} : \kappa \rightarrow \kappa ,$
where
![]() $f_x(\alpha )$
is the
$f_x(\alpha )$
is the
![]() $\alpha {\textrm {th}}$
element of x, denoted
$\alpha {\textrm {th}}$
element of x, denoted
![]() $x(\alpha )$
.
$x(\alpha )$
.
For us, a path is a descending sequence through the tree of any length
![]() $\alpha \leq \textrm {ht}(T)$
, while a branch is a path through the entire tree of length
$\alpha \leq \textrm {ht}(T)$
, while a branch is a path through the entire tree of length
![]() $\textrm {ht}(T)$
. The set of all branches through a tree T is denoted
$\textrm {ht}(T)$
. The set of all branches through a tree T is denoted
![]() $[T]$
. If T is a distributivity tree, then the nodes in any branch
$[T]$
. If T is a distributivity tree, then the nodes in any branch
![]() $b \in [T]$
must form a tower in
$b \in [T]$
must form a tower in
![]() $P(\kappa )/{<}\kappa $
, i.e., a
$P(\kappa )/{<}\kappa $
, i.e., a
![]() $\subseteq ^{*}$
-descending sequence with no
$\subseteq ^{*}$
-descending sequence with no
![]() $x \in [\kappa ]^{\kappa }$
almost contained in each element of the sequence. Conversely, if T is a tree of maximal antichains where the nodes in every branch
$x \in [\kappa ]^{\kappa }$
almost contained in each element of the sequence. Conversely, if T is a tree of maximal antichains where the nodes in every branch
![]() $b \in [T]$
form a tower, T is a full distributivity tree. In particular, a tree of maximal antichains with no branches is a full distributivity tree. A special sort of full distributivity tree T is a base tree which is one where for every
$b \in [T]$
form a tower, T is a full distributivity tree. In particular, a tree of maximal antichains with no branches is a full distributivity tree. A special sort of full distributivity tree T is a base tree which is one where for every
![]() $x \in [\kappa ]^{\kappa }$
, there exists
$x \in [\kappa ]^{\kappa }$
, there exists
![]() $t \in T$
with
$t \in T$
with
![]() $t \subseteq ^{*} x$
.
$t \subseteq ^{*} x$
.
For
![]() $\kappa $
with
$\kappa $
with
![]() $\textrm {cf}(\kappa )>\omega $
, there is a distributivity tree T of maximal antichains with
$\textrm {cf}(\kappa )>\omega $
, there is a distributivity tree T of maximal antichains with
![]() $\textrm {ht}(T)=\omega $
. Similarly, for
$\textrm {ht}(T)=\omega $
. Similarly, for
![]() $\kappa $
with
$\kappa $
with
![]() $\textrm {cf}(\kappa )=\omega $
, there exists a distributivity tree of height
$\textrm {cf}(\kappa )=\omega $
, there exists a distributivity tree of height
![]() $\omega _1$
. For these
$\omega _1$
. For these
![]() $\kappa $
, there can be no distributivity tree of height
$\kappa $
, there can be no distributivity tree of height
![]() $\omega $
because all such trees have branches and there are no towers of length
$\omega $
because all such trees have branches and there are no towers of length
![]() $\textrm {cf}(\kappa )$
. This tree then also has no maximal paths of countable length.
$\textrm {cf}(\kappa )$
. This tree then also has no maximal paths of countable length.
These distributivity trees of heights
![]() $\omega $
and
$\omega $
and
![]() $\omega _1$
(for
$\omega _1$
(for
![]() $\textrm {cf}(\kappa )>\omega $
and
$\textrm {cf}(\kappa )>\omega $
and
![]() $\textrm {cf}(\kappa )=\omega $
, respectively) were originally constructed combinatorially by Balcar and Vopěnka (see [Reference Balcar and Vopěnka1]) and can also be built more abstractly with forcing technology (see [Reference Galgon6]).
$\textrm {cf}(\kappa )=\omega $
, respectively) were originally constructed combinatorially by Balcar and Vopěnka (see [Reference Balcar and Vopěnka1]) and can also be built more abstractly with forcing technology (see [Reference Galgon6]).
![]() $\kappa $
-Aronszajn trees can be used to build distributivity trees of height
$\kappa $
-Aronszajn trees can be used to build distributivity trees of height
![]() $\kappa $
(Proposition 2.2).
$\kappa $
(Proposition 2.2).
It was asked by V. Fischer, M. Koelbing, and W. Wohofsky whether (1) there can exist a distributivity tree for
![]() $P(\kappa )/{<}\kappa $
of regular height strictly above
$P(\kappa )/{<}\kappa $
of regular height strictly above
![]() $\kappa $
and (2) whether regular cardinals strictly between
$\kappa $
and (2) whether regular cardinals strictly between
![]() $\omega $
and
$\omega $
and
![]() $\kappa $
can be the heights of distributivity trees (see the discussion at the end of Section 8 and Question 9.5 from [Reference Fischer, Koelbing and Wohofsky3]). In what follows we show that affirmative answers to both questions hold in certain models. The study of the spectrum of heights of distributivity and base trees in various models for
$\kappa $
can be the heights of distributivity trees (see the discussion at the end of Section 8 and Question 9.5 from [Reference Fischer, Koelbing and Wohofsky3]). In what follows we show that affirmative answers to both questions hold in certain models. The study of the spectrum of heights of distributivity and base trees in various models for
![]() $\kappa = \omega $
(and the structure of maximal paths through those trees) has recently seen a resurgence of interest (e.g., [Reference Brendle2], [Reference Fischer, Koelbing and Wohofsky4], [Reference Fischer, Koelbing and Wohofsky5]), motivating what follows for the
$\kappa = \omega $
(and the structure of maximal paths through those trees) has recently seen a resurgence of interest (e.g., [Reference Brendle2], [Reference Fischer, Koelbing and Wohofsky4], [Reference Fischer, Koelbing and Wohofsky5]), motivating what follows for the
![]() $\kappa> \omega $
case.
$\kappa> \omega $
case.
2 Partition-type short distributivity trees
Let
![]() $\kappa>\omega $
be regular. For a tree of maximal antichains T with
$\kappa>\omega $
be regular. For a tree of maximal antichains T with
![]() $\textrm {ht}(T)\leq \kappa $
, by iteratively removing from every node all ordinals not contained in every node above it, we may assume that the tree relation for T is the subset relation and not the subset modulo
$\textrm {ht}(T)\leq \kappa $
, by iteratively removing from every node all ordinals not contained in every node above it, we may assume that the tree relation for T is the subset relation and not the subset modulo
![]() $P_{\kappa }\kappa $
relation (
$P_{\kappa }\kappa $
relation (
![]() $\subseteq $
and not
$\subseteq $
and not
![]() $\subseteq ^{*}$
). A special case of a tree of maximal antichains T is one where every level of T is of cardinality less than
$\subseteq ^{*}$
). A special case of a tree of maximal antichains T is one where every level of T is of cardinality less than
![]() $\kappa $
. If additionally
$\kappa $
. If additionally
![]() $\textrm {ht}(T) < \kappa $
, by working within a set of ordinals common to each of the unions over nodes on every level and by taking symmetric differences between elements on every level and removing from every node all ordinals not contained in every node above it, we may assume that each level of T is a partition of
$\textrm {ht}(T) < \kappa $
, by working within a set of ordinals common to each of the unions over nodes on every level and by taking symmetric differences between elements on every level and removing from every node all ordinals not contained in every node above it, we may assume that each level of T is a partition of
![]() $\kappa $
and the tree relation is
$\kappa $
and the tree relation is
![]() $\subseteq $
. Call such a tree a partition-type tree.
$\subseteq $
. Call such a tree a partition-type tree.
Definition 2.1 For a tree T with
![]() $\textrm {ht}(T)=\kappa $
, if
$\textrm {ht}(T)=\kappa $
, if
![]() $|[T]| \geq \lambda \geq \kappa ^+$
but
$|[T]| \geq \lambda \geq \kappa ^+$
but
![]() $|\textrm {Lev}_{\xi }(T)| < \mu $
for every
$|\textrm {Lev}_{\xi }(T)| < \mu $
for every
![]() $\xi < \kappa $
for some
$\xi < \kappa $
for some
![]() $\mu \leq \lambda $
, call T a
$\mu \leq \lambda $
, call T a
![]() $(\mu ,\kappa ,\lambda )$
-Kurepa tree.
$(\mu ,\kappa ,\lambda )$
-Kurepa tree.
Some parameters are often omitted. For example, if
![]() $\mu = \kappa ^+$
and
$\mu = \kappa ^+$
and
![]() $\lambda = \kappa ^+$
, then a
$\lambda = \kappa ^+$
, then a
![]() $(\mu , \kappa , \lambda )$
-Kurepa tree is a tree of cardinality
$(\mu , \kappa , \lambda )$
-Kurepa tree is a tree of cardinality
![]() $\kappa $
with at least
$\kappa $
with at least
![]() $\kappa ^+$
many branches. This is called a weak
$\kappa ^+$
many branches. This is called a weak
![]() $\kappa $
-Kurepa tree. A
$\kappa $
-Kurepa tree. A
![]() $(\omega _1,\omega _1,\omega _2)$
-Kurepa tree is the traditional Kurepa tree.
$(\omega _1,\omega _1,\omega _2)$
-Kurepa tree is the traditional Kurepa tree.
Proposition 2.1 Suppose
![]() $\kappa $
is regular. A partition-type distributivity tree for
$\kappa $
is regular. A partition-type distributivity tree for
![]() $\kappa $
of height
$\kappa $
of height
![]() $\mu <\kappa $
is necessarily a
$\mu <\kappa $
is necessarily a
![]() $(\kappa ,\mu ,\kappa )$
-Kurepa tree, while the existence of a
$(\kappa ,\mu ,\kappa )$
-Kurepa tree, while the existence of a
![]() $(\kappa ,\mu ,\kappa )$
-Kurepa tree implies the existence of a partition-type distributivity tree for
$(\kappa ,\mu ,\kappa )$
-Kurepa tree implies the existence of a partition-type distributivity tree for
![]() $\kappa $
of height
$\kappa $
of height
![]() $\mu $
.
$\mu $
.
Proof First, the intersection along every branch of a partition-type distributivity tree of height
![]() $\mu $
for
$\mu $
for
![]() $\kappa $
must be of cardinality less than
$\kappa $
must be of cardinality less than
![]() $\kappa $
and so because for every
$\kappa $
and so because for every
![]() $\xi \in \kappa $
, there is a unique node t on every level of the tree such that
$\xi \in \kappa $
, there is a unique node t on every level of the tree such that
![]() $\xi \in t$
, there must be at least
$\xi \in t$
, there must be at least
![]() $\kappa $
-many branches through the tree.
$\kappa $
-many branches through the tree.
On the other hand, take
![]() $\kappa $
-many branches in a
$\kappa $
-many branches in a
![]() $(\kappa ,\mu ,\kappa )$
-Kurepa tree T sufficient to generate the tree and identify them with ordinals in
$(\kappa ,\mu ,\kappa )$
-Kurepa tree T sufficient to generate the tree and identify them with ordinals in
![]() $\kappa $
. By regularity, we can remove every node which doesn’t have
$\kappa $
. By regularity, we can remove every node which doesn’t have
![]() $\kappa $
-many of these branches through it and so assume that every node in T has
$\kappa $
-many of these branches through it and so assume that every node in T has
![]() $\kappa $
-many of these branches through it. Form the partition-type distributivity tree
$\kappa $
-many of these branches through it. Form the partition-type distributivity tree
![]() $T'$
for
$T'$
for
![]() $\kappa $
where each partition element is the collection of branches (ordinals) inside the downward cones of a node on every level of T. Levels are of size less than
$\kappa $
where each partition element is the collection of branches (ordinals) inside the downward cones of a node on every level of T. Levels are of size less than
![]() $\kappa $
so the resulting tree is a partition-type tree of maximal antichains for
$\kappa $
so the resulting tree is a partition-type tree of maximal antichains for
![]() $\kappa $
of height
$\kappa $
of height
![]() $\mu $
. Furthermore, every branch forms a tower because there is at most a single ordinal contained in the intersection along the branch.
$\mu $
. Furthermore, every branch forms a tower because there is at most a single ordinal contained in the intersection along the branch.
Proposition 2.1 shows, for example, that if the
![]() $\textrm {CH}$
holds, then as the full binary tree on
$\textrm {CH}$
holds, then as the full binary tree on
![]() $\omega _1$
is a weak Kurepa tree, there exists a partition-type distributivity tree of height
$\omega _1$
is a weak Kurepa tree, there exists a partition-type distributivity tree of height
![]() $\omega _1$
for
$\omega _1$
for
![]() $\kappa = \omega _2$
. More generally, for some
$\kappa = \omega _2$
. More generally, for some
![]() $\kappa $
if
$\kappa $
if
![]() $\mu <\kappa $
is minimal with
$\mu <\kappa $
is minimal with
![]() $2^{\mu } \geq \kappa $
, then a partition-type distributivity tree of height
$2^{\mu } \geq \kappa $
, then a partition-type distributivity tree of height
![]() $\mu $
for
$\mu $
for
![]() $\kappa $
may be built via a suitable injection from
$\kappa $
may be built via a suitable injection from
![]() $\kappa $
to branches through the full binary tree of height
$\kappa $
to branches through the full binary tree of height
![]() $\mu $
.
$\mu $
.
Proposition 2.2 A distributivity tree for
![]() $\kappa $
of height
$\kappa $
of height
![]() $\kappa $
where every level is of size less than
$\kappa $
where every level is of size less than
![]() $\kappa $
is necessarily a
$\kappa $
is necessarily a
![]() $\kappa $
-Aronszajn tree and, moreover, if there exists a
$\kappa $
-Aronszajn tree and, moreover, if there exists a
![]() $\kappa $
-Aronszajn tree, then there is a distributivity tree for
$\kappa $
-Aronszajn tree, then there is a distributivity tree for
![]() $\kappa $
of height
$\kappa $
of height
![]() $\kappa $
where every level is of size less than
$\kappa $
where every level is of size less than
![]() $\kappa $
.
$\kappa $
.
Proof There are no towers of length
![]() $\kappa $
, so such a distributivity tree cannot have branches. On the other hand, we can identify nodes in an Aronszajn tree with ordinals in
$\kappa $
, so such a distributivity tree cannot have branches. On the other hand, we can identify nodes in an Aronszajn tree with ordinals in
![]() $\kappa $
and note that the downward nodal cones for levels of the tree are (modulo
$\kappa $
and note that the downward nodal cones for levels of the tree are (modulo
![]() $P_{\kappa }\kappa $
) partitions of
$P_{\kappa }\kappa $
) partitions of
![]() $\kappa $
into
$\kappa $
into
![]() $<\kappa $
-many pieces. The resulting tree of maximal antichains has no branches and so is a distributivity tree.
$<\kappa $
-many pieces. The resulting tree of maximal antichains has no branches and so is a distributivity tree.
A tree T of limit height is pruned if every node
![]() $s \in T$
has at least one compatible node in T on every level of T, i.e., if
$s \in T$
has at least one compatible node in T on every level of T, i.e., if
![]() $\textrm {ht}(T \restriction s) = \textrm {ht}(T)$
. Say that a tree T is cofinally splitting if it is pruned and every node
$\textrm {ht}(T \restriction s) = \textrm {ht}(T)$
. Say that a tree T is cofinally splitting if it is pruned and every node
![]() $s \in T$
is splittable in T, meaning that s extends to two mutually incompatible nodes
$s \in T$
is splittable in T, meaning that s extends to two mutually incompatible nodes
![]() $t_1, t_2$
(i.e., neither
$t_1, t_2$
(i.e., neither
![]() $t_1 <_T t_2$
nor
$t_1 <_T t_2$
nor
![]() $t_2 <_T t_1$
). If a pruned tree is not cofinally splitting, non-splittable nodes occur in T. In some cases, T eventually comprises only such nodes: say that T is eventually nonsplitting if for some
$t_2 <_T t_1$
). If a pruned tree is not cofinally splitting, non-splittable nodes occur in T. In some cases, T eventually comprises only such nodes: say that T is eventually nonsplitting if for some
![]() $\alpha < \textrm {ht}(T)$
, every
$\alpha < \textrm {ht}(T)$
, every
![]() $s \in \textrm {Lev}_{\beta }(T)$
for
$s \in \textrm {Lev}_{\beta }(T)$
for
![]() $\beta \in (\alpha , \textrm {ht}(T))$
is not splittable.
$\beta \in (\alpha , \textrm {ht}(T))$
is not splittable.
Observation 2.3 Cofinally splitting trees that are too narrow relative to their heights cannot exist: If
![]() $\kappa $
is regular and there exists
$\kappa $
is regular and there exists
![]() $\mu < \kappa $
and a pruned tree T of height
$\mu < \kappa $
and a pruned tree T of height
![]() $\kappa $
with
$\kappa $
with
![]() $|\textrm {Lev}_{\alpha }(T)|<\mu $
for every
$|\textrm {Lev}_{\alpha }(T)|<\mu $
for every
![]() $\alpha < \kappa $
, then T is not cofinally splitting. In fact, T is eventually nonsplitting.
$\alpha < \kappa $
, then T is not cofinally splitting. In fact, T is eventually nonsplitting.
Proof It suffices to show that for a pruned tree T of height
![]() $\kappa $
with
$\kappa $
with
![]() $|\textrm {Lev}_{\alpha }(T)|<\mu $
for every
$|\textrm {Lev}_{\alpha }(T)|<\mu $
for every
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $[T] \neq \emptyset $
. Because then if T were not eventually nonsplitting, we could witness
$[T] \neq \emptyset $
. Because then if T were not eventually nonsplitting, we could witness
![]() $\mu $
-many distinct branches through the tree all splitting below some level
$\mu $
-many distinct branches through the tree all splitting below some level
![]() $\xi < \kappa $
by choosing splittable nodes on sufficiently higher and higher levels and looking at branches through the restrictions of the tree to the incompatible nodes witnessing splittability. But then
$\xi < \kappa $
by choosing splittable nodes on sufficiently higher and higher levels and looking at branches through the restrictions of the tree to the incompatible nodes witnessing splittability. But then
![]() $|\textrm {Lev}_{\xi }(T)| \geq \mu $
, a contradiction. Choose
$|\textrm {Lev}_{\xi }(T)| \geq \mu $
, a contradiction. Choose
![]() $\mu $
minimal so that
$\mu $
minimal so that
![]() $|\textrm {Lev}_{\alpha }(T)|<\mu $
for every
$|\textrm {Lev}_{\alpha }(T)|<\mu $
for every
![]() $\alpha < \kappa $
. For every
$\alpha < \kappa $
. For every
![]() $\alpha $
of cofinality
$\alpha $
of cofinality
![]() $\mu $
in
$\mu $
in
![]() $\kappa $
(write
$\kappa $
(write
![]() $\alpha \in \textrm {cof}(\mu ) \cap \kappa $
), choose some
$\alpha \in \textrm {cof}(\mu ) \cap \kappa $
), choose some
![]() $s_{\alpha } \in \textrm {Lev}_{\alpha }(T)$
. Without loss of generality, we may assume that T has no splitting at limit levels, so all splitting between
$s_{\alpha } \in \textrm {Lev}_{\alpha }(T)$
. Without loss of generality, we may assume that T has no splitting at limit levels, so all splitting between
![]() $s_{\alpha }$
and the other nodes on level
$s_{\alpha }$
and the other nodes on level
![]() $\alpha $
is witnessed below some level
$\alpha $
is witnessed below some level
![]() $\beta < \alpha $
. Let
$\beta < \alpha $
. Let
![]() $f(\alpha )=\beta $
and choose a stationary
$f(\alpha )=\beta $
and choose a stationary
![]() $S \subseteq \textrm {cof}(\mu ) \cap \kappa $
, where f is the constant function
$S \subseteq \textrm {cof}(\mu ) \cap \kappa $
, where f is the constant function
![]() $f " S = \{\xi \}$
. But then on a
$f " S = \{\xi \}$
. But then on a
![]() $\kappa $
-sized subset
$\kappa $
-sized subset
![]() $A \subseteq S$
, every
$A \subseteq S$
, every
![]() $s_{\alpha } \restriction \xi $
is the same
$s_{\alpha } \restriction \xi $
is the same
![]() $\overline {s}_{\xi }$
for some particular
$\overline {s}_{\xi }$
for some particular
![]() $\overline {s}_{\xi } \in \textrm {Lev}_{\xi }(T)$
. But then for
$\overline {s}_{\xi } \in \textrm {Lev}_{\xi }(T)$
. But then for
![]() $\alpha <\beta $
in A, we have
$\alpha <\beta $
in A, we have
![]() $s_{\beta }\restriction \alpha = s_{\alpha }$
. So
$s_{\beta }\restriction \alpha = s_{\alpha }$
. So
![]() $b_A=\{s \in T : \textrm { for some } \alpha \in A, s = s_{\alpha } \restriction \textrm {lh}(s)\} \in [T]$
.
$b_A=\{s \in T : \textrm { for some } \alpha \in A, s = s_{\alpha } \restriction \textrm {lh}(s)\} \in [T]$
.
Observation 2.3 shows that a tree of maximal antichains for
![]() $\kappa $
with levels of size less than
$\kappa $
with levels of size less than
![]() $\kappa $
of height
$\kappa $
of height
![]() $\geq \kappa ^+$
is eventually nonsplitting. So for example, there is no distributivity tree of height
$\geq \kappa ^+$
is eventually nonsplitting. So for example, there is no distributivity tree of height
![]() $\omega _2$
for
$\omega _2$
for
![]() $\omega _1$
with countable levels (any such tree of maximal antichains eventually stabilizes, so in particular, a non-tower branch through the tree exists).
$\omega _1$
with countable levels (any such tree of maximal antichains eventually stabilizes, so in particular, a non-tower branch through the tree exists).
Observation 2.3 and Propositions 2.1 and 2.2 cover all scenarios for the spectrum of distributivity tree heights for
![]() $\kappa $
where the levels are partitions of
$\kappa $
where the levels are partitions of
![]() $\kappa $
modulo
$\kappa $
modulo
![]() $P_{\kappa }\kappa $
. By collapsing certain large cardinals in specific ways, however, we can build models where, for example, no weak Kurepa trees exist for
$P_{\kappa }\kappa $
. By collapsing certain large cardinals in specific ways, however, we can build models where, for example, no weak Kurepa trees exist for
![]() $\omega _1$
. The analysis above does not resolve whether a distributivity tree for
$\omega _1$
. The analysis above does not resolve whether a distributivity tree for
![]() $\omega _2$
of height
$\omega _2$
of height
![]() $\omega _1$
exists in such models; it just implies that any such tree must have levels of size greater than
$\omega _1$
exists in such models; it just implies that any such tree must have levels of size greater than
![]() $\omega _2$
.
$\omega _2$
.
3 Short base trees with wide levels
Let
![]() $\textrm {MAD}(\kappa )$
denote the set of cardinalities of maximal almost disjoint families in
$\textrm {MAD}(\kappa )$
denote the set of cardinalities of maximal almost disjoint families in
![]() $P(\kappa )/{<}\kappa $
. Let
$P(\kappa )/{<}\kappa $
. Let
![]() $\mathfrak {a}_{\kappa } = \textrm {min}\{\textrm {MAD}(\kappa ) \cap (\kappa ,2^{\kappa }]\}$
. If MAD families are all of sufficiently large size or in the form of partitions of
$\mathfrak {a}_{\kappa } = \textrm {min}\{\textrm {MAD}(\kappa ) \cap (\kappa ,2^{\kappa }]\}$
. If MAD families are all of sufficiently large size or in the form of partitions of
![]() $\kappa $
, we can build base trees for
$\kappa $
, we can build base trees for
![]() $\kappa $
of heights in the cardinal interval
$\kappa $
of heights in the cardinal interval
![]() $[\omega ,\kappa )$
. A preliminary shorthand definition is useful.
$[\omega ,\kappa )$
. A preliminary shorthand definition is useful.
Definition 3.1 For
![]() $x,y \in [\kappa ]^{\kappa }$
, say that x is discontinuous (everywhere) relative to y if for every
$x,y \in [\kappa ]^{\kappa }$
, say that x is discontinuous (everywhere) relative to y if for every
![]() $\beta \in \textrm {lim}(\kappa )$
,
$\beta \in \textrm {lim}(\kappa )$
,
![]() $x(\beta )> \textrm {min}(y \,{\backslash}\, \textrm {sup}\{x(\xi ) : \xi \in \beta \})$
.
$x(\beta )> \textrm {min}(y \,{\backslash}\, \textrm {sup}\{x(\xi ) : \xi \in \beta \})$
.
We also say x is almost everywhere discontinuous relative to y (and just discontinuous relative to y if the context is clear) when for some
![]() $\gamma < \kappa $
for every limit
$\gamma < \kappa $
for every limit
![]() $\beta \in (\gamma ,\kappa )$
,
$\beta \in (\gamma ,\kappa )$
,
![]() $x(\beta )> \textrm {min}(y \,{\backslash}\, \textrm {sup}\{x(\xi ) : \xi \in \beta \})$
. Of particular interest is when
$x(\beta )> \textrm {min}(y \,{\backslash}\, \textrm {sup}\{x(\xi ) : \xi \in \beta \})$
. Of particular interest is when
![]() $x \subseteq y$
. If
$x \subseteq y$
. If
![]() $x \subseteq y$
, x being discontinuous everywhere relative to y is equivalent to saying that
$x \subseteq y$
, x being discontinuous everywhere relative to y is equivalent to saying that
![]() $x(\beta )> y(\beta )$
for every
$x(\beta )> y(\beta )$
for every
![]() $\beta < \kappa $
, i.e., for the inverse enumerating functions for x and
$\beta < \kappa $
, i.e., for the inverse enumerating functions for x and
![]() $y,$
we have
$y,$
we have
![]() $f^{-1}_x(\alpha ) < f^{-1}_y(\alpha )$
for every
$f^{-1}_x(\alpha ) < f^{-1}_y(\alpha )$
for every
![]() $\alpha \in x$
. For example, if
$\alpha \in x$
. For example, if
![]() $y \in [\kappa ]^{\kappa }$
, then the set of successor ordinals in its order topology is everywhere discontinuous relative to y. Similarly, if
$y \in [\kappa ]^{\kappa }$
, then the set of successor ordinals in its order topology is everywhere discontinuous relative to y. Similarly, if
![]() $x \subseteq ^{*} y,$
then x being almost everywhere discontinuous relative to y is equivalent to saying that for all
$x \subseteq ^{*} y,$
then x being almost everywhere discontinuous relative to y is equivalent to saying that for all
![]() $\beta $
above some ordinal
$\beta $
above some ordinal
![]() $\gamma < \kappa $
,
$\gamma < \kappa $
,
![]() $x(\beta )>y(\beta )$
and for every large enough
$x(\beta )>y(\beta )$
and for every large enough
![]() $\alpha \in x$
,
$\alpha \in x$
,
![]() $f^{-1}_x(\alpha ) < f^{-1}_y(\alpha )$
. If x is almost everywhere discontinuous relative to y and
$f^{-1}_x(\alpha ) < f^{-1}_y(\alpha )$
. If x is almost everywhere discontinuous relative to y and
![]() $y \subseteq ^{*} z$
, then x is almost everywhere discontinuous relative to z. With
$y \subseteq ^{*} z$
, then x is almost everywhere discontinuous relative to z. With
![]() $\textrm {cf}(\kappa )>\omega $
, there can be no (
$\textrm {cf}(\kappa )>\omega $
, there can be no (
![]() $\omega +1$
)-length
$\omega +1$
)-length
![]() $\subseteq ^{*}$
-descending sequence of elements of
$\subseteq ^{*}$
-descending sequence of elements of
![]() $[\kappa ]^{\kappa }$
each of which is almost everywhere discontinuous relative to its predecessors, i.e., such an infinite
$[\kappa ]^{\kappa }$
each of which is almost everywhere discontinuous relative to its predecessors, i.e., such an infinite
![]() $\subseteq ^{*}$
-descending sequence of elements in
$\subseteq ^{*}$
-descending sequence of elements in
![]() $[\kappa ]^{\kappa }$
forms a tower.
$[\kappa ]^{\kappa }$
forms a tower.
Theorem 3.1 Suppose
![]() $\kappa>\omega $
is regular with
$\kappa>\omega $
is regular with
![]() $\mathfrak {a}_{\kappa }=2^{\kappa }$
. For
$\mathfrak {a}_{\kappa }=2^{\kappa }$
. For
![]() $\omega \leq \mu < \kappa $
, there exists a base tree of height
$\omega \leq \mu < \kappa $
, there exists a base tree of height
![]() $\mu $
for
$\mu $
for
![]() $\kappa $
with levels of cardinality
$\kappa $
with levels of cardinality
![]() $2^{\kappa }$
.
$2^{\kappa }$
.
Proof The tree is built iteratively. We give the general idea, then go into more detail. There will be two types of nodes: “root” nodes and “tower” nodes. Every tower node is associated with a tower through the tree passing through that node. Immediately below every root node will be at most one tower node and also
![]() $2^{\kappa }$
-many root nodes together forming a maximal antichain with respect to that node. This collection of root nodes is referred to as a root node family. Note that if a root node family in
$2^{\kappa }$
-many root nodes together forming a maximal antichain with respect to that node. This collection of root nodes is referred to as a root node family. Note that if a root node family in
![]() $[z]^{\kappa }$
for some
$[z]^{\kappa }$
for some
![]() $z \in [\kappa ]^{\kappa }$
is maximal with respect to being both almost disjoint and everywhere discontinuous relative to z, then in fact the root node family is MAD in
$z \in [\kappa ]^{\kappa }$
is maximal with respect to being both almost disjoint and everywhere discontinuous relative to z, then in fact the root node family is MAD in
![]() $[z]^{\kappa }$
because any almost disjoint set y can be shrunk to an everywhere discontinuous (relative to y) almost disjoint set by, e.g., taking the collection of successor ordinals in its order topology. In the subsequent level, every set x hitting
$[z]^{\kappa }$
because any almost disjoint set y can be shrunk to an everywhere discontinuous (relative to y) almost disjoint set by, e.g., taking the collection of successor ordinals in its order topology. In the subsequent level, every set x hitting
![]() $2^{\kappa }$
-many elements of the root node family is diagonalized against, in the sense that a tower node (and associated tower) is added below which is a subset of x. Immediately below every tower node will be exactly one tower node and also a root node family. In fact, below every tower node is a continuous strictly descending
$2^{\kappa }$
-many elements of the root node family is diagonalized against, in the sense that a tower node (and associated tower) is added below which is a subset of x. Immediately below every tower node will be exactly one tower node and also a root node family. In fact, below every tower node is a continuous strictly descending
![]() $\mu $
-length tower with empty intersection through T. If
$\mu $
-length tower with empty intersection through T. If
![]() $r \subseteq s$
in T and r is a root node, then r will be everywhere discontinuous relative to s. Therefore at limit levels of T, only paths containing finitely many root nodes have nonempty intersection. These paths are exactly the intersections along some continuous
$r \subseteq s$
in T and r is a root node, then r will be everywhere discontinuous relative to s. Therefore at limit levels of T, only paths containing finitely many root nodes have nonempty intersection. These paths are exactly the intersections along some continuous
![]() $\mu $
-tower added previously; by continuity, the nodes extending these paths are the appropriate limit elements of those towers. Every branch in
$\mu $
-tower added previously; by continuity, the nodes extending these paths are the appropriate limit elements of those towers. Every branch in
![]() $[T]$
then forms a tower and it remains to be seen that every level of T is a maximal antichain.
$[T]$
then forms a tower and it remains to be seen that every level of T is a maximal antichain.
Describing the construction in more detail, for a tower node
![]() $s \in \textrm {Lev}_{\xi }(T),$
its associated tower is denoted
$s \in \textrm {Lev}_{\xi }(T),$
its associated tower is denoted
![]() $\langle t^s_{\alpha } : \alpha < \mu \rangle $
with
$\langle t^s_{\alpha } : \alpha < \mu \rangle $
with
![]() $t^s_{\alpha } \in \textrm {Lev}_{\alpha }(T),$
where
$t^s_{\alpha } \in \textrm {Lev}_{\alpha }(T),$
where
![]() $t^s_{\nu }$
is the predecessor of s on level
$t^s_{\nu }$
is the predecessor of s on level
![]() $\nu $
written
$\nu $
written
![]() $t^s_{\nu } = s \restriction \nu $
for every
$t^s_{\nu } = s \restriction \nu $
for every
![]() $\nu < \xi $
(and
$\nu < \xi $
(and
![]() $t^{s}_{\xi }=s$
). Here,
$t^{s}_{\xi }=s$
). Here,
![]() $\langle t^s_{\alpha } : \xi \leq \alpha < \mu \rangle $
is a strictly decreasing continuous
$\langle t^s_{\alpha } : \xi \leq \alpha < \mu \rangle $
is a strictly decreasing continuous
![]() $\mu $
-length tower consisting entirely of tower nodes with empty intersection through T starting with s. So while the tower
$\mu $
-length tower consisting entirely of tower nodes with empty intersection through T starting with s. So while the tower
![]() $\langle t^s_{\alpha } : \alpha < \mu \rangle $
may contain root nodes inside the initial portion below level
$\langle t^s_{\alpha } : \alpha < \mu \rangle $
may contain root nodes inside the initial portion below level
![]() $\xi $
, as above the end segment
$\xi $
, as above the end segment
![]() $\langle t^s_{\alpha } : \xi \leq \alpha < \mu \rangle $
only contains tower nodes. For
$\langle t^s_{\alpha } : \xi \leq \alpha < \mu \rangle $
only contains tower nodes. For
![]() $\xi $
limit,
$\xi $
limit,
![]() $\textrm {Lev}_{\xi }(T)$
then comprises the partial continuous intersections along
$\textrm {Lev}_{\xi }(T)$
then comprises the partial continuous intersections along
![]() $\mu $
-towers added in previous steps. By continuity, such a node is of the form
$\mu $
-towers added in previous steps. By continuity, such a node is of the form
![]() $t^s_{\xi }$
for some tower node s added previously. Its associated tower is the same,
$t^s_{\xi }$
for some tower node s added previously. Its associated tower is the same,
![]() $\langle t^{(t^s_{\xi })}_{\alpha } : \alpha < \mu \rangle = \langle t^s_{\alpha } : \alpha < \mu \rangle $
.
$\langle t^{(t^s_{\xi })}_{\alpha } : \alpha < \mu \rangle = \langle t^s_{\alpha } : \alpha < \mu \rangle $
.
Now we describe how the successor levels
![]() $\textrm {Lev}_{\xi +1}(T)$
are formed. Let
$\textrm {Lev}_{\xi +1}(T)$
are formed. Let
![]() $s \in \textrm {Lev}_{\xi }(T)$
. If s is a tower node (which will, for example, always be the case if
$s \in \textrm {Lev}_{\xi }(T)$
. If s is a tower node (which will, for example, always be the case if
![]() $\xi $
is a limit), then first add the tower element
$\xi $
is a limit), then first add the tower element
![]() $t^s_{\xi +1} \in \textrm {Lev}_{\xi +1}(T)$
from
$t^s_{\xi +1} \in \textrm {Lev}_{\xi +1}(T)$
from
![]() $\langle t^{s}_{\alpha } : \alpha < \mu \rangle $
. Furthermore, assign to
$\langle t^{s}_{\alpha } : \alpha < \mu \rangle $
. Furthermore, assign to
![]() $t^s_{\xi +1}$
the same tower as for s, i.e.,
$t^s_{\xi +1}$
the same tower as for s, i.e.,
![]() $\langle t^{(t^s_{\xi +1})}_{\alpha } : \alpha < \mu \rangle = \langle t^s_{\alpha } : \alpha < \mu \rangle $
. Additionally, let
$\langle t^{(t^s_{\xi +1})}_{\alpha } : \alpha < \mu \rangle = \langle t^s_{\alpha } : \alpha < \mu \rangle $
. Additionally, let
![]() $z = s \,{\backslash}\, t^s_{\xi +1}$
denote the nodal difference between the two successive tower elements and note that because the towers are strictly decreasing,
$z = s \,{\backslash}\, t^s_{\xi +1}$
denote the nodal difference between the two successive tower elements and note that because the towers are strictly decreasing,
![]() $|z|=\kappa $
. Split z into a
$|z|=\kappa $
. Split z into a
![]() $2^{\kappa }$
-sized maximal almost disjoint root node family in
$2^{\kappa }$
-sized maximal almost disjoint root node family in
![]() $[z]^{\kappa }$
all of whose elements are everywhere discontinuous relative to z. Associate this family with every resulting root node r and denote the family accordingly as
$[z]^{\kappa }$
all of whose elements are everywhere discontinuous relative to z. Associate this family with every resulting root node r and denote the family accordingly as
![]() $R_r$
.
$R_r$
.
Next, we consider the case where
![]() $s \in \textrm {Lev}_{\xi }(T)$
is a root node. It is associated with a
$s \in \textrm {Lev}_{\xi }(T)$
is a root node. It is associated with a
![]() $2^{\kappa }$
-sized root node family
$2^{\kappa }$
-sized root node family
![]() $R_s$
, which is MAD in the relevant
$R_s$
, which is MAD in the relevant
![]() $z \in [\kappa ]^{\kappa }$
and allows the key diagonalization step to take place. Let
$z \in [\kappa ]^{\kappa }$
and allows the key diagonalization step to take place. Let
![]() $X = \{x \in [z]^{\kappa } : |\{r \in R_s : |x \cap r|=\kappa \}|=2^{\kappa }\}$
be the set of
$X = \{x \in [z]^{\kappa } : |\{r \in R_s : |x \cap r|=\kappa \}|=2^{\kappa }\}$
be the set of
![]() $x \in [z]^{\kappa }$
hitting
$x \in [z]^{\kappa }$
hitting
![]() $2^{\kappa }$
-many elements of
$2^{\kappa }$
-many elements of
![]() $R_s$
. We want to add at least one tower inside every such x below some suitable r. Because
$R_s$
. We want to add at least one tower inside every such x below some suitable r. Because
![]() $|X| \leq 2^{\kappa }$
and every
$|X| \leq 2^{\kappa }$
and every
![]() $x \in X$
has
$x \in X$
has
![]() $2^{\kappa }$
-many options for which r to choose (i.e., which r with
$2^{\kappa }$
-many options for which r to choose (i.e., which r with
![]() $|r \cap x|=\kappa $
), this is easy to arrange by ordering X and
$|r \cap x|=\kappa $
), this is easy to arrange by ordering X and
![]() $R_s$
in type
$R_s$
in type
![]() $2^{\kappa }$
and letting the
$2^{\kappa }$
and letting the
![]() $\gamma {\textrm {th}}$
element of X,
$\gamma {\textrm {th}}$
element of X,
![]() $X(\gamma )$
, be assigned to the
$X(\gamma )$
, be assigned to the
![]() $\delta {\textrm {th}}$
element r of
$\delta {\textrm {th}}$
element r of
![]() $R_s$
with
$R_s$
with
![]() $\delta $
minimal such that
$\delta $
minimal such that
![]() $|X(\gamma ) \cap r| = \kappa $
and none of the
$|X(\gamma ) \cap r| = \kappa $
and none of the
![]() $X(\gamma ')$
for
$X(\gamma ')$
for
![]() $\gamma ' < \gamma $
has been assigned to r previously.
$\gamma ' < \gamma $
has been assigned to r previously.
With the help of this assignment, for every
![]() $x \in X$
, add a tower node
$x \in X$
, add a tower node
![]() $s' \subseteq (x \cap r)$
with
$s' \subseteq (x \cap r)$
with
![]() $s' \in \textrm {Lev}_{\xi +1}(T)$
and
$s' \in \textrm {Lev}_{\xi +1}(T)$
and
![]() $|r \,{\backslash}\, s'| = \kappa $
. This
$|r \,{\backslash}\, s'| = \kappa $
. This
![]() $s' = t^{s'}_{\xi +1}$
is associated with the resulting tower
$s' = t^{s'}_{\xi +1}$
is associated with the resulting tower
![]() $\langle t^{s'}_{\alpha } : \alpha < \mu \rangle $
, where
$\langle t^{s'}_{\alpha } : \alpha < \mu \rangle $
, where
![]() $\langle t^{s'}_{\alpha } : \xi +1 \leq \alpha < \mu \rangle $
is a strictly decreasing continuous sequence with empty intersection inside
$\langle t^{s'}_{\alpha } : \xi +1 \leq \alpha < \mu \rangle $
is a strictly decreasing continuous sequence with empty intersection inside
![]() $x \cap r$
. Next, let
$x \cap r$
. Next, let
![]() $z = r \,{\backslash}\, s'$
and split z into a
$z = r \,{\backslash}\, s'$
and split z into a
![]() $2^{\kappa }$
-sized root node family and associate every resulting root node with this family. Finally, to every root node r of
$2^{\kappa }$
-sized root node family and associate every resulting root node with this family. Finally, to every root node r of
![]() $R_s$
which did not have an element of x assigned to it, split r directly into a
$R_s$
which did not have an element of x assigned to it, split r directly into a
![]() $2^{\kappa }$
-sized root node family and associate all resulting root nodes with that family. This completes the construction of level
$2^{\kappa }$
-sized root node family and associate all resulting root nodes with that family. This completes the construction of level
![]() $\xi +1$
. To summarize, below tower nodes from level
$\xi +1$
. To summarize, below tower nodes from level
![]() $\xi $
, we added the next tower node in the sequence along with a root node family inside the resulting nodal difference, while below root nodes from level
$\xi $
, we added the next tower node in the sequence along with a root node family inside the resulting nodal difference, while below root nodes from level
![]() $\xi $
(depending on how their root node families facilitated diagonalization), we added a root node family and possibly a tower node and associated tower inside the relevant x.
$\xi $
(depending on how their root node families facilitated diagonalization), we added a root node family and possibly a tower node and associated tower inside the relevant x.
This concludes the construction of T as a tree of antichains of height
![]() $\mu $
where every branch through T forms a tower. Note that MAD families are added below every node from level
$\mu $
where every branch through T forms a tower. Note that MAD families are added below every node from level
![]() $\xi $
on level
$\xi $
on level
![]() $\xi +1$
, so to show T is a distributivity tree, we only need to see that for
$\xi +1$
, so to show T is a distributivity tree, we only need to see that for
![]() $\xi \in \textrm {lim}(\mu )$
,
$\xi \in \textrm {lim}(\mu )$
,
![]() $\textrm {Lev}_{\xi }(T)$
is a maximal antichain. Suppose for every
$\textrm {Lev}_{\xi }(T)$
is a maximal antichain. Suppose for every
![]() $\nu < \xi $
,
$\nu < \xi $
,
![]() $\textrm {Lev}_{\nu }(T)$
is maximal. Let
$\textrm {Lev}_{\nu }(T)$
is maximal. Let
![]() $x \in [\kappa ]^{\kappa }$
. If the cardinality of the set of nodes on each level hitting x is less than
$x \in [\kappa ]^{\kappa }$
. If the cardinality of the set of nodes on each level hitting x is less than
![]() $\kappa $
for every
$\kappa $
for every
![]() $\nu $
, then by taking symmetric differences between nodal elements on each level and by removing fewer than
$\nu $
, then by taking symmetric differences between nodal elements on each level and by removing fewer than
![]() $\kappa $
-many elements from x, we may view
$\kappa $
-many elements from x, we may view
![]() $T_{\xi } \restriction x$
as a partition-type tree of maximal antichains in
$T_{\xi } \restriction x$
as a partition-type tree of maximal antichains in
![]() $[x]^{\kappa }$
of height
$[x]^{\kappa }$
of height
![]() $\xi <\mu <\kappa $
. Every ordinal in x is associated with a branch through
$\xi <\mu <\kappa $
. Every ordinal in x is associated with a branch through
![]() $T_{\xi } \restriction x$
by looking at the unique node on each level containing it. However, nonempty branches through
$T_{\xi } \restriction x$
by looking at the unique node on each level containing it. However, nonempty branches through
![]() $T_{\xi } \restriction x$
only contain finitely many root nodes so are determined by some intermediate-level tower node. Therefore,
$T_{\xi } \restriction x$
only contain finitely many root nodes so are determined by some intermediate-level tower node. Therefore,
![]() $\kappa $
-many ordinals in x must determine the same branch leading to some
$\kappa $
-many ordinals in x must determine the same branch leading to some
![]() $t^{s}_{\xi }$
which by continuity must then intersect x in a set of size
$t^{s}_{\xi }$
which by continuity must then intersect x in a set of size
![]() $\kappa $
.
$\kappa $
.
If instead x hits at least
![]() $\kappa $
-many elements on some level of T below
$\kappa $
-many elements on some level of T below
![]() $\xi $
, then because
$\xi $
, then because
![]() $\mathfrak {a}_{\kappa }=2^{\kappa }$
, there is some minimal level
$\mathfrak {a}_{\kappa }=2^{\kappa }$
, there is some minimal level
![]() $\eta < \xi < \kappa $
, where x hits
$\eta < \xi < \kappa $
, where x hits
![]() $2^{\kappa }$
-many nodes in
$2^{\kappa }$
-many nodes in
![]() $\textrm {Lev}_{\eta }(T)$
. By the argument above,
$\textrm {Lev}_{\eta }(T)$
. By the argument above,
![]() $\eta $
is not a limit (there are not enough nonempty branches through
$\eta $
is not a limit (there are not enough nonempty branches through
![]() $T_{\eta } \restriction x$
). So, suppose fewer than
$T_{\eta } \restriction x$
). So, suppose fewer than
![]() $\kappa $
many nodes on level
$\kappa $
many nodes on level
![]() $\eta $
but
$\eta $
but
![]() $2^{\kappa }$
-many nodes on level
$2^{\kappa }$
-many nodes on level
![]() $\eta +1$
hit x. By construction, nodes on level
$\eta +1$
hit x. By construction, nodes on level
![]() $\eta $
are associated with exactly one root node family on level
$\eta $
are associated with exactly one root node family on level
![]() $\eta +1$
, so
$\eta +1$
, so
![]() $2^{\kappa }$
-many of these nodes from level
$2^{\kappa }$
-many of these nodes from level
![]() $\eta +1$
must fall among the same root node family R. But then by construction at level
$\eta +1$
must fall among the same root node family R. But then by construction at level
![]() $\eta +2$
, we will have added a tower node
$\eta +2$
, we will have added a tower node
![]() $s=t^s_{\eta +2} \subseteq x \cap r$
for some
$s=t^s_{\eta +2} \subseteq x \cap r$
for some
![]() $r \in R$
hitting x, which extends to a
$r \in R$
hitting x, which extends to a
![]() $\mu $
-length tower through T inside x. In particular, the limit node of this tower at level
$\mu $
-length tower through T inside x. In particular, the limit node of this tower at level
![]() $\xi $
,
$\xi $
,
![]() $t^{s}_{\xi }$
, is a subset of x. Thus, T is a distributivity tree.
$t^{s}_{\xi }$
, is a subset of x. Thus, T is a distributivity tree.
Furthermore, for any
![]() $x \in [\kappa ]^{\kappa }$
, the only time that there might not exist
$x \in [\kappa ]^{\kappa }$
, the only time that there might not exist
![]() $s \in T$
with
$s \in T$
with
![]() $s \subseteq x$
would be if fewer than
$s \subseteq x$
would be if fewer than
![]() $\kappa $
-many nodes hit x on every level of T. But by removing fewer than
$\kappa $
-many nodes hit x on every level of T. But by removing fewer than
![]() $\kappa $
-many elements from x and from overlapping nodes on each level of T, we may assume
$\kappa $
-many elements from x and from overlapping nodes on each level of T, we may assume
![]() $T \restriction x$
is a partition-type tree of maximal antichains in
$T \restriction x$
is a partition-type tree of maximal antichains in
![]() $[x]^{\kappa }$
. But then for any
$[x]^{\kappa }$
. But then for any
![]() $\alpha \in x$
,
$\alpha \in x$
,
![]() $\alpha $
is in a unique nodal element in every
$\alpha $
is in a unique nodal element in every
![]() $\textrm {Lev}_{\xi }(T)$
for
$\textrm {Lev}_{\xi }(T)$
for
![]() $\xi < \mu $
, i.e.,
$\xi < \mu $
, i.e.,
![]() $\alpha $
is contained in the intersection of a branch through T, which is impossible. So T is a base tree.
$\alpha $
is contained in the intersection of a branch through T, which is impossible. So T is a base tree.
A construction of a base tree of minimal height
![]() $\mu = \omega _1$
for
$\mu = \omega _1$
for
![]() $\textrm {cf}(\kappa ) = \omega $
under additional cardinal arithmetic assumptions is provided in [Reference Galgon6].
$\textrm {cf}(\kappa ) = \omega $
under additional cardinal arithmetic assumptions is provided in [Reference Galgon6].
4 A tall base tree with wide levels
Under the same restrictions on the spectrum of MAD family cardinalities as in Theorem 3.1, we can prove that distributivity trees of height at least
![]() $\kappa ^+$
exist. The following lemma is useful in the construction and is an instance of the phenomenon that trees too simple in structure do not admit complex subtrees.
$\kappa ^+$
exist. The following lemma is useful in the construction and is an instance of the phenomenon that trees too simple in structure do not admit complex subtrees.
Lemma 4.1 For
![]() $\mu < \kappa $
regular cardinals, the tree
$\mu < \kappa $
regular cardinals, the tree
![]() $T^{\kappa }_{<\mu } \subseteq {}^{<\kappa }\kappa $
consisting of sequences with fewer than
$T^{\kappa }_{<\mu } \subseteq {}^{<\kappa }\kappa $
consisting of sequences with fewer than
![]() $\mu $
-many nonzero values does not contain any
$\mu $
-many nonzero values does not contain any
![]() $\kappa $
-Aronszajn subtrees.
$\kappa $
-Aronszajn subtrees.
Proof A more general structure theorem is true for subtrees of
![]() $T^{\kappa }_{<\mu }$
(Theorem 1.5.8 in [Reference Galgon6]), however, the lemma can also be proven directly via an argument similar to the proof of Observation 2.3 (Proposition 1.5.20 in [Reference Galgon6]). We omit the details.
$T^{\kappa }_{<\mu }$
(Theorem 1.5.8 in [Reference Galgon6]), however, the lemma can also be proven directly via an argument similar to the proof of Observation 2.3 (Proposition 1.5.20 in [Reference Galgon6]). We omit the details.
Theorem 4.2 Suppose
![]() $\kappa>\omega $
is regular with
$\kappa>\omega $
is regular with
![]() $\mathfrak {a}_{\kappa }=2^{\kappa }$
. If there is a tower of length
$\mathfrak {a}_{\kappa }=2^{\kappa }$
. If there is a tower of length
![]() $\kappa ^+$
, then there exists a base tree of height
$\kappa ^+$
, then there exists a base tree of height
![]() $\kappa ^+$
for
$\kappa ^+$
for
![]() $\kappa $
with levels of cardinality
$\kappa $
with levels of cardinality
![]() $2^{\kappa }$
.
$2^{\kappa }$
.
Proof Essentially, we do the same thing as in Theorem 3.1, except we add
![]() $\kappa ^+$
-length
$\kappa ^+$
-length
![]() $\subseteq ^{*}$
-towers below elements in the root node families. We follow the notation of the proof of Theorem 3.1, but in the following when referring to tower nodes, we omit the localizing superscripts (s, etc.) as any necessary context will be clear. Only the subscripts indicating tree level are written for simplicity. At successors, we do ensure that for every
$\subseteq ^{*}$
-towers below elements in the root node families. We follow the notation of the proof of Theorem 3.1, but in the following when referring to tower nodes, we omit the localizing superscripts (s, etc.) as any necessary context will be clear. Only the subscripts indicating tree level are written for simplicity. At successors, we do ensure that for every
![]() $\xi \in \kappa ^+$
,
$\xi \in \kappa ^+$
,
![]() $t_{\xi +1} \subseteq t_{\xi }$
with
$t_{\xi +1} \subseteq t_{\xi }$
with
![]() $|t_{\xi } \,{\backslash}\, t_{\xi +1}| = \kappa $
. These tower sequences are no longer continuous at limits; indeed, we ensure purposeful discontinuity and non-normality at limits so that for every
$|t_{\xi } \,{\backslash}\, t_{\xi +1}| = \kappa $
. These tower sequences are no longer continuous at limits; indeed, we ensure purposeful discontinuity and non-normality at limits so that for every
![]() $\beta \in \textrm {lim}(\kappa ^+)$
, there exists
$\beta \in \textrm {lim}(\kappa ^+)$
, there exists
![]() $x \in [\kappa ]^{\kappa }$
with
$x \in [\kappa ]^{\kappa }$
with
![]() $|x \,{\backslash}\, t_{\beta }| = \kappa $
and
$|x \,{\backslash}\, t_{\beta }| = \kappa $
and
![]() $x \subseteq ^{*} t_{\xi }$
for every
$x \subseteq ^{*} t_{\xi }$
for every
![]() $\xi < \beta $
.
$\xi < \beta $
.
At limit levels
![]() $\xi \in \kappa ^+$
, unlike as in Theorem 3.1 where we took intersections along all paths eventually traveling along a tower added previously forming the single element
$\xi \in \kappa ^+$
, unlike as in Theorem 3.1 where we took intersections along all paths eventually traveling along a tower added previously forming the single element
![]() $t_{\xi }$
, in the present setting we add this previously defined tower element and also a root node family. Each of these tower nodes
$t_{\xi }$
, in the present setting we add this previously defined tower element and also a root node family. Each of these tower nodes
![]() $t_{\xi }$
is associated with a path
$t_{\xi }$
is associated with a path
![]() $p=\{p_{\nu } : \nu < \xi \}$
through the tree (along which every node is eventually a tower node). We can also associate with this path a family of
$p=\{p_{\nu } : \nu < \xi \}$
through the tree (along which every node is eventually a tower node). We can also associate with this path a family of
![]() $2^{\kappa }$
-many root nodes
$2^{\kappa }$
-many root nodes
![]() $\{r_{\delta } : \delta \in 2^{\kappa }\}$
which are all almost everywhere discontinuous relative to the nodes in p and for which
$\{r_{\delta } : \delta \in 2^{\kappa }\}$
which are all almost everywhere discontinuous relative to the nodes in p and for which
![]() $\{r_{\delta } : \delta \in 2^{\kappa }\} \cup \{t_{\xi }\}$
is a maximal almost disjoint collection in
$\{r_{\delta } : \delta \in 2^{\kappa }\} \cup \{t_{\xi }\}$
is a maximal almost disjoint collection in
![]() $A_p = \{x \in [\kappa ]^{\kappa } : x \subseteq ^{*} p_{\nu } \textrm { for every } \nu \in \xi \}$
. We call this a path-type root node family.
$A_p = \{x \in [\kappa ]^{\kappa } : x \subseteq ^{*} p_{\nu } \textrm { for every } \nu \in \xi \}$
. We call this a path-type root node family.
At successor levels
![]() $\xi +1$
, much as in Theorem 3.1, we:
$\xi +1$
, much as in Theorem 3.1, we:
-
• add the (successor-type) root node families in the tower nodal differences
 $t_{\xi } \,{\backslash}\, t_{\xi +1}$
,
$t_{\xi } \,{\backslash}\, t_{\xi +1}$
, -
• for every root node family
 $R = \{r_{\delta } : \delta \in 2^{\kappa }\}$
from level
$R = \{r_{\delta } : \delta \in 2^{\kappa }\}$
from level
 $\xi $
, look at the collection of
$\xi $
, look at the collection of
 $x \in [\kappa ]^{\kappa }$
hitting
$x \in [\kappa ]^{\kappa }$
hitting
 $2^{\kappa }$
-many members of R and for every such x ensure that a
$2^{\kappa }$
-many members of R and for every such x ensure that a
 $\kappa ^+$
-length tower is added below an appropriate
$\kappa ^+$
-length tower is added below an appropriate
 $r_{\delta }$
inside
$r_{\delta }$
inside
 $x \cap r_{\delta }$
, with
$x \cap r_{\delta }$
, with
 $t_{\xi +1}$
on level
$t_{\xi +1}$
on level
 $\xi +1$
,
$\xi +1$
, -
• add a root node family below every
 $r_{\delta }$
not assigned such an x, and finally
$r_{\delta }$
not assigned such an x, and finally -
• for every root node
 $r_{\delta }$
that was assigned such an x, add a root node family inside the nodal difference
$r_{\delta }$
that was assigned such an x, add a root node family inside the nodal difference
 $r_{\delta } \,{\backslash}\, t_{\xi +1}$
between that root node and its first associated tower element added on level
$r_{\delta } \,{\backslash}\, t_{\xi +1}$
between that root node and its first associated tower element added on level
 $\xi +1$
.
$\xi +1$
.
Note that if some x hits
![]() $2^{\kappa }$
-many nodes on level
$2^{\kappa }$
-many nodes on level
![]() $\xi +1$
and hits, e.g., fewer than
$\xi +1$
and hits, e.g., fewer than
![]() $\kappa $
-many nodes on level
$\kappa $
-many nodes on level
![]() $\xi $
, then necessarily x hits
$\xi $
, then necessarily x hits
![]() $2^{\kappa }$
-many nodes in a particular root node family; so that at the next step
$2^{\kappa }$
-many nodes in a particular root node family; so that at the next step
![]() $\xi +2$
, a tower is added inside x.
$\xi +2$
, a tower is added inside x.
We have constructed a tree of antichains of height
![]() $\kappa ^+$
; we need to see that these are maximal. The successor step is immediate as all nodes are split into MAD collections, so let
$\kappa ^+$
; we need to see that these are maximal. The successor step is immediate as all nodes are split into MAD collections, so let
![]() $\xi \in \textrm {lim}(\kappa ^+)$
and suppose that
$\xi \in \textrm {lim}(\kappa ^+)$
and suppose that
![]() $\textrm {Lev}_{\nu }(T)$
is a maximal antichain for every
$\textrm {Lev}_{\nu }(T)$
is a maximal antichain for every
![]() $\nu < \xi $
. Consider first the case where
$\nu < \xi $
. Consider first the case where
![]() $\textrm {cf}(\xi )=\mu <\kappa $
, and let
$\textrm {cf}(\xi )=\mu <\kappa $
, and let
![]() $x \in [\kappa ]^{\kappa }$
. By fixing a continuous
$x \in [\kappa ]^{\kappa }$
. By fixing a continuous
![]() $\textrm {cf}(\xi )$
-ladder to
$\textrm {cf}(\xi )$
-ladder to
![]() $\xi $
of levels, in a slight abuse of notation, let
$\xi $
of levels, in a slight abuse of notation, let
![]() $T_{\xi } \restriction x$
denote the tree of maximal antichains in
$T_{\xi } \restriction x$
denote the tree of maximal antichains in
![]() $[x]^{\kappa }$
of height
$[x]^{\kappa }$
of height
![]() $\mu $
in the natural way. If
$\mu $
in the natural way. If
![]() $|\textrm {Lev}_{\nu }(T_{\xi } \restriction x)|<\kappa $
for every
$|\textrm {Lev}_{\nu }(T_{\xi } \restriction x)|<\kappa $
for every
![]() $\nu < \mu $
, then by removing fewer than
$\nu < \mu $
, then by removing fewer than
![]() $\kappa $
-many elements from x and choosing suitable representatives for each tree node, we may assume that this is a partition-type
$\kappa $
-many elements from x and choosing suitable representatives for each tree node, we may assume that this is a partition-type
![]() $\subseteq $
-tree of height
$\subseteq $
-tree of height
![]() $\mu $
where every root node is everywhere discontinuous relative to all nodes above it. As in the proof to Theorem 3.1 then, every ordinal in x is associated with a branch through this partition system and, moreover, associated with the final node where that branch no longer follows only its specified sequence of tower nodes. So
$\mu $
where every root node is everywhere discontinuous relative to all nodes above it. As in the proof to Theorem 3.1 then, every ordinal in x is associated with a branch through this partition system and, moreover, associated with the final node where that branch no longer follows only its specified sequence of tower nodes. So
![]() $\kappa $
-many ordinals in x, call them
$\kappa $
-many ordinals in x, call them
![]() $x'$
, are contained in the intersection along the same branch
$x'$
, are contained in the intersection along the same branch
![]() $\{t_{f(\nu )} : \nu < \mu \}$
for the ladder
$\{t_{f(\nu )} : \nu < \mu \}$
for the ladder
![]() $f : \mu \rightarrow \xi $
through the tree. Note that
$f : \mu \rightarrow \xi $
through the tree. Note that
![]() $A= \{y \in [\kappa ]^{\kappa } : y \subseteq ^{*} t_{\nu } \textrm { for every } \nu < \xi \} = \{y \in [\kappa ]^{\kappa } : y \subseteq ^{*} t_{f(\nu )} \textrm { for every } \nu < \mu \} $
, so because at level
$A= \{y \in [\kappa ]^{\kappa } : y \subseteq ^{*} t_{\nu } \textrm { for every } \nu < \xi \} = \{y \in [\kappa ]^{\kappa } : y \subseteq ^{*} t_{f(\nu )} \textrm { for every } \nu < \mu \} $
, so because at level
![]() $\xi $
the appropriate
$\xi $
the appropriate
![]() $\{t_{\xi }\} \cup \{r_{\delta } : \delta \in 2^{\kappa }\}$
is maximal with respect to A, some element hits
$\{t_{\xi }\} \cup \{r_{\delta } : \delta \in 2^{\kappa }\}$
is maximal with respect to A, some element hits
![]() $x'$
and so hits x.
$x'$
and so hits x.
Next, suppose that for some minimal
![]() $\nu < \xi $
,
$\nu < \xi $
,
![]() $|\textrm {Lev}_{\nu }(T_{\xi } \restriction x)| = 2^{\kappa }$
. If
$|\textrm {Lev}_{\nu }(T_{\xi } \restriction x)| = 2^{\kappa }$
. If
![]() $\nu $
is of the form
$\nu $
is of the form
![]() $\eta +1$
, then necessarily x hits
$\eta +1$
, then necessarily x hits
![]() $2^{\kappa }$
-many nodes inside a particular successor-type root node family, so at step
$2^{\kappa }$
-many nodes inside a particular successor-type root node family, so at step
![]() $\nu +1$
, a tower will be added inside x. In particular then, some tower node on level
$\nu +1$
, a tower will be added inside x. In particular then, some tower node on level
![]() $\xi $
is inside x. If
$\xi $
is inside x. If
![]() $\nu $
is a limit and
$\nu $
is a limit and
![]() $|\textrm {Lev}_{\eta }(T_{\nu } \restriction x)| < \kappa $
for every
$|\textrm {Lev}_{\eta }(T_{\nu } \restriction x)| < \kappa $
for every
![]() ${\eta < \nu }$
, then because there are fewer than
${\eta < \nu }$
, then because there are fewer than
![]() $\textrm {cf}(2^{\kappa })$
-many branches through
$\textrm {cf}(2^{\kappa })$
-many branches through
![]() $T_{\nu } \restriction x$
passing through only finitely many root nodes (a necessary condition for x to hit a node on level
$T_{\nu } \restriction x$
passing through only finitely many root nodes (a necessary condition for x to hit a node on level
![]() $\nu $
below a
$\nu $
below a
![]() $\subseteq ^{*}$
-sequence), x must hit
$\subseteq ^{*}$
-sequence), x must hit
![]() $2^{\kappa }$
-many root nodes within some particular
$2^{\kappa }$
-many root nodes within some particular
![]() $A_{p}$
path-type root node family, so that a tower is added inside x at step
$A_{p}$
path-type root node family, so that a tower is added inside x at step
![]() $\nu +1$
.
$\nu +1$
.
Consider next the case where
![]() $\textrm {cf}(\xi )=\kappa $
. For simplicity and by using a ladder to
$\textrm {cf}(\xi )=\kappa $
. For simplicity and by using a ladder to
![]() $\xi $
, assume
$\xi $
, assume
![]() $\xi = \kappa $
. We need to see that
$\xi = \kappa $
. We need to see that
![]() $\textrm {Lev}_{\xi }(T)$
is a maximal antichain. If for some minimal
$\textrm {Lev}_{\xi }(T)$
is a maximal antichain. If for some minimal
![]() $\nu < \xi $
,
$\nu < \xi $
,
![]() $2^{\kappa }$
-many nodes in
$2^{\kappa }$
-many nodes in
![]() $\textrm {Lev}_{\nu }(T)$
hit x, then the analysis above shows that whether
$\textrm {Lev}_{\nu }(T)$
hit x, then the analysis above shows that whether
![]() $\nu $
is successor or limit, there is a particular root node family on level
$\nu $
is successor or limit, there is a particular root node family on level
![]() $\nu $
inside of which x hits
$\nu $
inside of which x hits
![]() $2^{\kappa }$
-many elements. But then at level
$2^{\kappa }$
-many elements. But then at level
![]() $\nu +1$
, we added a tower inside x below one of those elements.
$\nu +1$
, we added a tower inside x below one of those elements.
On the other hand, if fewer than
![]() $\kappa $
-many nodes in every
$\kappa $
-many nodes in every
![]() $\textrm {Lev}_{\nu }(T)$
hit x for every
$\textrm {Lev}_{\nu }(T)$
hit x for every
![]() $\nu < \xi $
, then because there can be no
$\nu < \xi $
, then because there can be no
![]() $(\omega +1)$
-length sequences of root nodes, it must be that
$(\omega +1)$
-length sequences of root nodes, it must be that
![]() $\textrm {T}_{\xi } \restriction x$
(a
$\textrm {T}_{\xi } \restriction x$
(a
![]() $\kappa $
-tree of maximal antichains in
$\kappa $
-tree of maximal antichains in
![]() $[x]^{\kappa }$
) is isomorphic to a subtree of
$[x]^{\kappa }$
) is isomorphic to a subtree of
![]() $T^{\kappa }_{<\omega }$
. Lemma 4.1 implies that
$T^{\kappa }_{<\omega }$
. Lemma 4.1 implies that
![]() $T_{\xi } \restriction x$
is not
$T_{\xi } \restriction x$
is not
![]() $\kappa $
-Aronszajn, so there is some
$\kappa $
-Aronszajn, so there is some
![]() $b \in [T_{\xi } \restriction x]$
. Because there are no towers of length
$b \in [T_{\xi } \restriction x]$
. Because there are no towers of length
![]() $\kappa $
, there exists
$\kappa $
, there exists
![]() $x' \in A_b$
with
$x' \in A_b$
with
![]() $x' \in [x]^{\kappa }$
, where
$x' \in [x]^{\kappa }$
, where
![]() $A_b = \{y \in [\kappa ]^{\kappa } : y \subseteq ^{*} b_{\nu } \textrm { for every } \nu < \xi \}$
. By maximality,
$A_b = \{y \in [\kappa ]^{\kappa } : y \subseteq ^{*} b_{\nu } \textrm { for every } \nu < \xi \}$
. By maximality,
![]() $x'$
hits at least one element in the associated
$x'$
hits at least one element in the associated
![]() $\{r_{\delta } : \delta \in 2^{\kappa }\} \cup \{t_{\xi }\}$
.
$\{r_{\delta } : \delta \in 2^{\kappa }\} \cup \{t_{\xi }\}$
.
Finally, having constructed T, let’s see that it is a base tree. Let
![]() $x \in [\kappa ]^{\kappa }$
. The analysis above shows that in the first level where
$x \in [\kappa ]^{\kappa }$
. The analysis above shows that in the first level where
![]() $T \restriction x$
has
$T \restriction x$
has
![]() $2^{\kappa }$
-many nodes, necessarily x hits
$2^{\kappa }$
-many nodes, necessarily x hits
![]() $2^{\kappa }$
-many nodes in some successor-type or path-type root node family, so that a tower is added inside x in the subsequent level. However, if
$2^{\kappa }$
-many nodes in some successor-type or path-type root node family, so that a tower is added inside x in the subsequent level. However, if
![]() $T \restriction x$
has fewer than
$T \restriction x$
has fewer than
![]() $\kappa $
-many nodes on each level, then Observation 2.3 shows that for all sufficiently large
$\kappa $
-many nodes on each level, then Observation 2.3 shows that for all sufficiently large
![]() $\alpha < \kappa ^+$
,
$\alpha < \kappa ^+$
,
![]() $\textrm {Lev}_{\alpha }(T \restriction x)$
only comprises some distinguished
$\textrm {Lev}_{\alpha }(T \restriction x)$
only comprises some distinguished
![]() $\mu $
-many tower nodes
$\mu $
-many tower nodes
![]() $\{t^{\xi }_{\alpha } : \xi < \mu \}$
for some
$\{t^{\xi }_{\alpha } : \xi < \mu \}$
for some
![]() $\mu < \kappa $
, which is impossible. In detail, if so then
$\mu < \kappa $
, which is impossible. In detail, if so then
![]() $x \subseteq ^{*} \bigcup _{\xi < \mu } t^{\xi }_{\alpha }$
for every sufficiently large
$x \subseteq ^{*} \bigcup _{\xi < \mu } t^{\xi }_{\alpha }$
for every sufficiently large
![]() $\alpha $
. So
$\alpha $
. So
![]() $\overline {x} \subseteq \bigcup _{\xi < \mu } t^{\xi }_{\alpha }$
for some
$\overline {x} \subseteq \bigcup _{\xi < \mu } t^{\xi }_{\alpha }$
for some
![]() $\overline {x} \in [x]^{\kappa }$
cofinally often. For every
$\overline {x} \in [x]^{\kappa }$
cofinally often. For every
![]() $\beta \in \overline {x}$
and such
$\beta \in \overline {x}$
and such
![]() $\alpha < \kappa ^+$
, we can find
$\alpha < \kappa ^+$
, we can find
![]() $\xi < \mu $
with
$\xi < \mu $
with
![]() $\beta \in t^{\xi }_{\alpha }$
. Then if
$\beta \in t^{\xi }_{\alpha }$
. Then if
![]() $\overline {\overline {x}}$
is a
$\overline {\overline {x}}$
is a
![]() $\kappa $
-sized set of these
$\kappa $
-sized set of these
![]() $\beta $
sharing the same
$\beta $
sharing the same
![]() $\xi $
, we have
$\xi $
, we have
![]() $\overline {\overline {x}} \subseteq ^{*} t^{\xi }_{\alpha }$
cofinally often. This is a contradiction as the
$\overline {\overline {x}} \subseteq ^{*} t^{\xi }_{\alpha }$
cofinally often. This is a contradiction as the
![]() $t^{\xi }_{\alpha }$
elements form a tower.
$t^{\xi }_{\alpha }$
elements form a tower.
In addition to understanding the heights of distributivity (base) trees for, e.g.,
![]() $P(\omega )/{<}\omega $
, there has also recently been a desire to understand their nature in terms of degree of path closure. For example, the main result of [Reference Fischer, Koelbing and Wohofsky4] is that any base tree for
$P(\omega )/{<}\omega $
, there has also recently been a desire to understand their nature in terms of degree of path closure. For example, the main result of [Reference Fischer, Koelbing and Wohofsky4] is that any base tree for
![]() $P(\omega )/{<}\omega $
of regular height
$P(\omega )/{<}\omega $
of regular height
![]() $\lambda $
larger than the distributivity number
$\lambda $
larger than the distributivity number
![]() $\mathfrak {h}$
has maximal paths which are not branches.
$\mathfrak {h}$
has maximal paths which are not branches.
Another way to see that result (and in fact something stronger) is to note that the degree of closure in one base tree T translates to a preponderance of paths of that length in any other base tree
![]() $T'$
. Specifically, if a base tree T has the property that there are no maximal paths of length
$T'$
. Specifically, if a base tree T has the property that there are no maximal paths of length
![]() $\leq \nu $
, then the set of paths of length
$\leq \nu $
, then the set of paths of length
![]() $\nu $
is dense in every base tree
$\nu $
is dense in every base tree
![]() $T'$
. Start with
$T'$
. Start with
![]() $s' \in T'$
, then find
$s' \in T'$
, then find
![]() $s_0 \subseteq ^{*} s'$
in T, then
$s_0 \subseteq ^{*} s'$
in T, then
![]() $s^{\prime }_0 \subseteq ^{*} s_0$
below
$s^{\prime }_0 \subseteq ^{*} s_0$
below
![]() $s'$
in
$s'$
in
![]() $T'$
, etc. forming
$T'$
, etc. forming
![]() $s' \supseteq ^{*} s_0 \supseteq ^{*} s^{\prime }_0 \supseteq ^{*} s_1 \ldots $
. At limit stages
$s' \supseteq ^{*} s_0 \supseteq ^{*} s^{\prime }_0 \supseteq ^{*} s_1 \ldots $
. At limit stages
![]() $\xi < \nu $
, we use the closure of T to find some
$\xi < \nu $
, we use the closure of T to find some
![]() $s_{\xi }$
almost contained in every element in the chain and refine that to
$s_{\xi }$
almost contained in every element in the chain and refine that to
![]() $s^{\prime }_{\xi }$
within
$s^{\prime }_{\xi }$
within
![]() $T'$
by the base property. This means, in particular, that any base tree of height
$T'$
by the base property. This means, in particular, that any base tree of height
![]() $\lambda $
with
$\lambda $
with
![]() $\textrm {cf}(\lambda )> \mathfrak {h}$
cannot have the property that all
$\textrm {cf}(\lambda )> \mathfrak {h}$
cannot have the property that all
![]() $\leq \mathfrak {h}$
-length paths can be extended (i.e., many are maximal and so are not branches).
$\leq \mathfrak {h}$
-length paths can be extended (i.e., many are maximal and so are not branches).
The same argument applies in the
![]() $P(\kappa )/{<}\kappa $
setting and it is therefore not surprising that the
$P(\kappa )/{<}\kappa $
setting and it is therefore not surprising that the
![]() $\kappa ^+$
-length base tree we built in Theorem 4.2 has a preponderance of maximal
$\kappa ^+$
-length base tree we built in Theorem 4.2 has a preponderance of maximal
![]() $\omega $
-length paths, given that if
$\omega $
-length paths, given that if
![]() $\mathfrak {a}_{\kappa }=2^{\kappa }$
(which holds under, e.g.,
$\mathfrak {a}_{\kappa }=2^{\kappa }$
(which holds under, e.g.,
![]() $2^{\kappa }=\kappa ^+$
) a base tree also exists of height
$2^{\kappa }=\kappa ^+$
) a base tree also exists of height
![]() $\omega $
.
$\omega $
.
5 A base tree of height
 $\kappa $
$\kappa $
We saw in Proposition 2.2 that
![]() $\kappa $
-Aronszajn trees can be used to build distributivity trees for
$\kappa $
-Aronszajn trees can be used to build distributivity trees for
![]() $\kappa $
of height
$\kappa $
of height
![]() $\kappa $
where the levels are partitions of
$\kappa $
where the levels are partitions of
![]() $\kappa $
modulo
$\kappa $
modulo
![]() $P_{\kappa }\kappa $
. For
$P_{\kappa }\kappa $
. For
![]() $\kappa $
with the tree property, however, these objects do not exist. Nonetheless, if
$\kappa $
with the tree property, however, these objects do not exist. Nonetheless, if
![]() $\mathfrak {a}_{\kappa }=2^{\kappa }$
as in Theorems 3.1 and 4.2, base trees of height
$\mathfrak {a}_{\kappa }=2^{\kappa }$
as in Theorems 3.1 and 4.2, base trees of height
![]() $\kappa $
can be built.
$\kappa $
can be built.
Theorem 5.1 Suppose
![]() $\kappa>\omega $
is regular with
$\kappa>\omega $
is regular with
![]() $\mathfrak {a}_{\kappa }=2^{\kappa }$
. There exists a base tree for
$\mathfrak {a}_{\kappa }=2^{\kappa }$
. There exists a base tree for
![]() $\kappa $
of height
$\kappa $
of height
![]() $\kappa $
with levels of cardinality
$\kappa $
with levels of cardinality
![]() $2^{\kappa }$
.
$2^{\kappa }$
.
Proof Fix a strictly increasing sequence of limit ordinals
![]() $\langle \delta _{\nu } : \nu < \kappa \rangle $
cofinal in
$\langle \delta _{\nu } : \nu < \kappa \rangle $
cofinal in
![]() $\kappa $
. Essentially, we do the same thing as in Theorem 3.1, except instead of just adding one tower for every relevant x in our diagonalization step, we add
$\kappa $
. Essentially, we do the same thing as in Theorem 3.1, except instead of just adding one tower for every relevant x in our diagonalization step, we add
![]() $\kappa $
-many
$\kappa $
-many
![]() $\subseteq $
-towers indexed by
$\subseteq $
-towers indexed by
![]() $\nu $
for every relevant
$\nu $
for every relevant
![]() $x \in [\kappa ]^{\kappa }$
(hitting
$x \in [\kappa ]^{\kappa }$
(hitting
![]() $2^{\kappa }$
-many elements in the root node family). So in this setting, every such x has
$2^{\kappa }$
-many elements in the root node family). So in this setting, every such x has
![]() $\kappa $
-many associated
$\kappa $
-many associated
![]() $r_{\nu }$
’s, and each
$r_{\nu }$
’s, and each
![]() $r_{\nu }$
has a
$r_{\nu }$
has a
![]() $\delta _{\nu }$
-length tower added below it inside
$\delta _{\nu }$
-length tower added below it inside
![]() $x \cap r_{\nu }$
. These towers are strictly descending with empty intersection, continuous at limits, and of length
$x \cap r_{\nu }$
. These towers are strictly descending with empty intersection, continuous at limits, and of length
![]() $\delta _{\nu }$
. All root nodes are everywhere discontinuous relative to their immediate predecessor and so the only nodes on limit levels
$\delta _{\nu }$
. All root nodes are everywhere discontinuous relative to their immediate predecessor and so the only nodes on limit levels
![]() $\xi $
can be nonempty tower elements
$\xi $
can be nonempty tower elements
![]() $t_{\xi }$
formed by the intermediate-length intersections along a continuous
$t_{\xi }$
formed by the intermediate-length intersections along a continuous
![]() $\delta _{\nu }$
-length tower added previously. Note that unlike as in Theorem 3.1, at limit stages in this construction many tower paths are maximal (empty intersection) as the
$\delta _{\nu }$
-length tower added previously. Note that unlike as in Theorem 3.1, at limit stages in this construction many tower paths are maximal (empty intersection) as the
![]() $\delta _{\nu }$
-length towers expire.
$\delta _{\nu }$
-length towers expire.
At successors, form level
![]() $\xi +1$
of the tree first by splitting every tower nodal difference
$\xi +1$
of the tree first by splitting every tower nodal difference
![]() $t_{\xi } \,{\backslash}\, t_{\xi +1}$
component into a
$t_{\xi } \,{\backslash}\, t_{\xi +1}$
component into a
![]() $2^{\kappa }$
-sized MAD (in
$2^{\kappa }$
-sized MAD (in
![]() $t_{\xi } \,{\backslash}\, t_{\xi +1}$
) family of root nodes everywhere discontinuous relative to
$t_{\xi } \,{\backslash}\, t_{\xi +1}$
) family of root nodes everywhere discontinuous relative to
![]() $t_{\xi }$
. Additionally, address each of the root node families from level
$t_{\xi }$
. Additionally, address each of the root node families from level
![]() $\xi $
(note that if
$\xi $
(note that if
![]() $\xi $
is a limit no such families exist) as follows. These families will be formed inside tower nodal differences or inside root nodes and are MAD with respect to the relevant
$\xi $
is a limit no such families exist) as follows. These families will be formed inside tower nodal differences or inside root nodes and are MAD with respect to the relevant
![]() $z \in [\kappa ]^{\kappa }$
. We add for every
$z \in [\kappa ]^{\kappa }$
. We add for every
![]() $x \in [z]^{\kappa }$
which hits
$x \in [z]^{\kappa }$
which hits
![]() $2^{\kappa }$
-many elements in the root node family
$2^{\kappa }$
-many elements in the root node family
![]() $\kappa $
-many towers
$\kappa $
-many towers
![]() $\{\langle t^{\nu }_{\alpha } : \alpha < \delta _{\nu } \rangle : \nu < \kappa \}$
, each below some r from the root node family hitting x, with all ordinals in all tower elements inside
$\{\langle t^{\nu }_{\alpha } : \alpha < \delta _{\nu } \rangle : \nu < \kappa \}$
, each below some r from the root node family hitting x, with all ordinals in all tower elements inside
![]() $r \cap x$
. Add other root node families inside any root nodes not associated with such an x and inside all resulting nodal differences between the r’s and the first tower elements. T is a tree of antichains of height
$r \cap x$
. Add other root node families inside any root nodes not associated with such an x and inside all resulting nodal differences between the r’s and the first tower elements. T is a tree of antichains of height
![]() $\kappa $
. We show each level is maximal by induction.
$\kappa $
. We show each level is maximal by induction.
The successor case is clear, so let
![]() $\xi $
be a limit in
$\xi $
be a limit in
![]() $\kappa $
and
$\kappa $
and
![]() $x \in [\kappa ]^{\kappa }$
. Suppose the cardinality of every level of
$x \in [\kappa ]^{\kappa }$
. Suppose the cardinality of every level of
![]() $T_{\xi } \restriction x$
is less than
$T_{\xi } \restriction x$
is less than
![]() $\kappa $
. This is argued as in Theorem 3.1. By removing fewer than
$\kappa $
. This is argued as in Theorem 3.1. By removing fewer than
![]() $\kappa $
many elements from x, we may assume this is a partition-type tree of maximal antichains of height
$\kappa $
many elements from x, we may assume this is a partition-type tree of maximal antichains of height
![]() $\xi <\kappa $
, so that to every ordinal in x, we may associate a branch through the tree for which that ordinal is contained in the intersection of nodes along the branch. Any branch with nonempty intersection through this tree eventually travels exclusively along some
$\xi <\kappa $
, so that to every ordinal in x, we may associate a branch through the tree for which that ordinal is contained in the intersection of nodes along the branch. Any branch with nonempty intersection through this tree eventually travels exclusively along some
![]() $\delta _{\nu }$
-length tower, and there are fewer than
$\delta _{\nu }$
-length tower, and there are fewer than
![]() $\kappa $
-many such towers in this scenario, but these towers are continuous so the relevant
$\kappa $
-many such towers in this scenario, but these towers are continuous so the relevant
![]() $t_{\xi }$
intersects
$t_{\xi }$
intersects
![]() $\kappa $
-many ordinals in x at level
$\kappa $
-many ordinals in x at level
![]() $\xi $
. This argument also shows that the minimal level (if one exists) where x hits
$\xi $
. This argument also shows that the minimal level (if one exists) where x hits
![]() $2^{\kappa }$
-many elements of the tree is not a limit. We may then assume that for some
$2^{\kappa }$
-many elements of the tree is not a limit. We may then assume that for some
![]() $\eta < \xi $
, x hits fewer than
$\eta < \xi $
, x hits fewer than
![]() $\kappa $
many nodes on level
$\kappa $
many nodes on level
![]() $\eta $
but
$\eta $
but
![]() $2^{\kappa }$
-many on level
$2^{\kappa }$
-many on level
![]() $\eta +1$
, so that necessarily x hits
$\eta +1$
, so that necessarily x hits
![]() $2^{\kappa }$
-many nodes within the same root node family. So, in particular, towers of length
$2^{\kappa }$
-many nodes within the same root node family. So, in particular, towers of length
![]() $\delta _{\nu }$
for every
$\delta _{\nu }$
for every
![]() $\delta _{\nu } \in (\xi ,\kappa )$
are added at level
$\delta _{\nu } \in (\xi ,\kappa )$
are added at level
![]() $\eta +2$
inside x, such that the relevant
$\eta +2$
inside x, such that the relevant
![]() $t_{\xi }$
are subsets of x on level
$t_{\xi }$
are subsets of x on level
![]() $\xi $
.
$\xi $
.
We showed T is a tree of maximal antichains of height
![]() $\kappa $
. Any maximal path in T either has countable cofinality and contains an
$\kappa $
. Any maximal path in T either has countable cofinality and contains an
![]() $\omega $
-subsequence of root nodes or eventually coincides with a
$\omega $
-subsequence of root nodes or eventually coincides with a
![]() $\delta _{\nu }$
-tower sequence. Therefore
$\delta _{\nu }$
-tower sequence. Therefore
![]() $[T] = \emptyset $
, so T is a distributivity tree. Furthermore, the proof to Theorem 4.2 shows T is a base tree:
$[T] = \emptyset $
, so T is a distributivity tree. Furthermore, the proof to Theorem 4.2 shows T is a base tree:
![]() $T \restriction x$
cannot only have levels of size less than
$T \restriction x$
cannot only have levels of size less than
![]() $\kappa $
because then
$\kappa $
because then
![]() $T \restriction x$
is isomorphic to a subtree of
$T \restriction x$
is isomorphic to a subtree of
![]() $T^{\kappa }_{<\omega }$
which has no
$T^{\kappa }_{<\omega }$
which has no
![]() $\kappa $
-Aronszajn subtrees (and we know
$\kappa $
-Aronszajn subtrees (and we know
![]() $T \restriction x$
is branchless). But then some minimal level
$T \restriction x$
is branchless). But then some minimal level
![]() $T \restriction x$
is of cardinality
$T \restriction x$
is of cardinality
![]() $2^{\kappa }$
and we subsequently add
$2^{\kappa }$
and we subsequently add
![]() $\kappa $
-many towers inside x.
$\kappa $
-many towers inside x.
6 Base trees with heights along the tower spectrum
By choosing
![]() $\subseteq ^{*}$
-towers of multiple lengths (as done with
$\subseteq ^{*}$
-towers of multiple lengths (as done with
![]() $\subseteq $
-towers in Theorem 5.1) below elements of root node families and using the arguments from Theorems 3.1, 5.1, and 4.2 to cover the limit levels
$\subseteq $
-towers in Theorem 5.1) below elements of root node families and using the arguments from Theorems 3.1, 5.1, and 4.2 to cover the limit levels
![]() $\xi $
for
$\xi $
for
![]() $\textrm {cf}(\xi )<\kappa $
,
$\textrm {cf}(\xi )<\kappa $
,
![]() $\textrm {cf}(\xi )=\kappa $
, and
$\textrm {cf}(\xi )=\kappa $
, and
![]() $\textrm {cf}(\xi )>\kappa $
, we can build tall base trees of many different lengths depending on the spectrum of cardinalities of towers in
$\textrm {cf}(\xi )>\kappa $
, we can build tall base trees of many different lengths depending on the spectrum of cardinalities of towers in
![]() $P(\kappa )/{<}\kappa $
.
$P(\kappa )/{<}\kappa $
.
Theorem 6.1 Suppose
![]() $\kappa>\omega $
is regular with
$\kappa>\omega $
is regular with
![]() $\mathfrak {a}_{\kappa }=2^{\kappa }$
. If
$\mathfrak {a}_{\kappa }=2^{\kappa }$
. If
![]() $\lambda>\kappa $
is either the (regular) length of a tower in
$\lambda>\kappa $
is either the (regular) length of a tower in
![]() $P(\kappa )/{<}\kappa $
or the limit of such cardinalities, then there exists a base tree of height
$P(\kappa )/{<}\kappa $
or the limit of such cardinalities, then there exists a base tree of height
![]() $\lambda $
for
$\lambda $
for
![]() $\kappa $
with levels of cardinality
$\kappa $
with levels of cardinality
![]() $2^{\kappa }$
.
$2^{\kappa }$
.
Proof Because this proof is so similar to that of Theorems 3.1, 4.2, and 5.1, we provide only a sketch while highlighting any novel situations. If
![]() $\lambda \geq \kappa ^+$
is the regular length of a tower, then the proof to Theorem 4.2 can be mimicked with
$\lambda \geq \kappa ^+$
is the regular length of a tower, then the proof to Theorem 4.2 can be mimicked with
![]() $\lambda $
in place of
$\lambda $
in place of
![]() $\kappa ^+$
. The argument for why intermediate limit levels
$\kappa ^+$
. The argument for why intermediate limit levels
![]() $\xi $
of the tree remain maximal depends on whether
$\xi $
of the tree remain maximal depends on whether
![]() $\textrm {cf}(\xi )<\kappa $
,
$\textrm {cf}(\xi )<\kappa $
,
![]() $\textrm {cf}(\xi )=\kappa $
, or
$\textrm {cf}(\xi )=\kappa $
, or
![]() $\textrm {cf}(\xi )>\kappa $
. The new case to consider is when
$\textrm {cf}(\xi )>\kappa $
. The new case to consider is when
![]() $\textrm {cf}(\xi )>\kappa $
which is handled in essentially the same manner as we showed that the tree of height
$\textrm {cf}(\xi )>\kappa $
which is handled in essentially the same manner as we showed that the tree of height
![]() $\kappa ^+$
in Theorem 4.2 has the base property. Specifically, let
$\kappa ^+$
in Theorem 4.2 has the base property. Specifically, let
![]() $x \in [\kappa ]^{\kappa }$
and first suppose that
$x \in [\kappa ]^{\kappa }$
and first suppose that
![]() $|\textrm {Lev}_{\nu }(T_{\xi } \restriction x)|<\kappa $
for every
$|\textrm {Lev}_{\nu }(T_{\xi } \restriction x)|<\kappa $
for every
![]() $\nu < \xi $
(by considering a
$\nu < \xi $
(by considering a
![]() $\textrm {cf}(\xi )$
-ladder to
$\textrm {cf}(\xi )$
-ladder to
![]() $\xi $
, we may assume
$\xi $
, we may assume
![]() $\xi $
is a regular cardinal
$\xi $
is a regular cardinal
![]() $\geq \kappa ^+$
). Observation 2.3 shows that
$\geq \kappa ^+$
). Observation 2.3 shows that
![]() $T_{\xi } \restriction x$
eventually stabilizes so that for some
$T_{\xi } \restriction x$
eventually stabilizes so that for some
![]() $\mu < \kappa $
, for all sufficiently large
$\mu < \kappa $
, for all sufficiently large
![]() $\nu < \xi $
,
$\nu < \xi $
,
![]() $\textrm {Lev}_{\nu }(T_{\xi } \restriction x)$
only comprises
$\textrm {Lev}_{\nu }(T_{\xi } \restriction x)$
only comprises
![]() $\mu $
-many tower nodes
$\mu $
-many tower nodes
![]() $\{t^{\eta }_{\nu } : \eta < \mu \}$
. So for some
$\{t^{\eta }_{\nu } : \eta < \mu \}$
. So for some
![]() $\eta < \mu $
, there exists
$\eta < \mu $
, there exists
![]() $x' \in [x]^{\kappa }$
with
$x' \in [x]^{\kappa }$
with
![]() $x' \subseteq ^{*} t^{\eta }_{\nu }$
cofinally often in
$x' \subseteq ^{*} t^{\eta }_{\nu }$
cofinally often in
![]() $\xi $
, i.e.,
$\xi $
, i.e.,
![]() $x' \in A_p = \{y \in [\kappa ]^{\kappa } : y \subseteq ^{*} t^{\eta }_{\nu } \textrm { for every } \nu < \xi \}$
. By maximality then,
$x' \in A_p = \{y \in [\kappa ]^{\kappa } : y \subseteq ^{*} t^{\eta }_{\nu } \textrm { for every } \nu < \xi \}$
. By maximality then,
![]() $x'$
and so x hits at least one element in the associated
$x'$
and so x hits at least one element in the associated
![]() $\{r_{\delta } : \delta \in 2^{\kappa }\} \cup \{t^{\eta }_{\xi }\}$
. On the other hand, if for some minimal level
$\{r_{\delta } : \delta \in 2^{\kappa }\} \cup \{t^{\eta }_{\xi }\}$
. On the other hand, if for some minimal level
![]() $\nu < \xi $
,
$\nu < \xi $
,
![]() $|\textrm {Lev}_{\nu }(T_{\xi } \restriction x)| = 2^{\kappa }$
, then whether
$|\textrm {Lev}_{\nu }(T_{\xi } \restriction x)| = 2^{\kappa }$
, then whether
![]() $\nu $
is a successor or limit x must in fact hit
$\nu $
is a successor or limit x must in fact hit
![]() $2^{\kappa }$
-many nodes within a particular successor-type or path-type root node family at level
$2^{\kappa }$
-many nodes within a particular successor-type or path-type root node family at level
![]() $\nu $
, so that a
$\nu $
, so that a
![]() $\lambda $
-tower inside x is added at level
$\lambda $
-tower inside x is added at level
![]() $\nu +1$
passing through level
$\nu +1$
passing through level
![]() $\xi $
. The novel situation over Theorem 4.2 is where
$\xi $
. The novel situation over Theorem 4.2 is where
![]() $\nu $
is a limit with
$\nu $
is a limit with
![]() $\textrm {cf}(\nu )>\kappa $
and as above because there are only
$\textrm {cf}(\nu )>\kappa $
and as above because there are only
![]() $\mu $
-many paths through
$\mu $
-many paths through
![]() $T_{\nu } \restriction x$
, x hits
$T_{\nu } \restriction x$
, x hits
![]() $2^{\kappa }$
-many nodes within a particular path-type root node family at level
$2^{\kappa }$
-many nodes within a particular path-type root node family at level
![]() $\nu $
. Similarly, if
$\nu $
. Similarly, if
![]() $\textrm {cf}(\nu )=\kappa $
, then there are at most
$\textrm {cf}(\nu )=\kappa $
, then there are at most
![]() $\kappa ^{<\omega }=\kappa < \textrm {cf}(2^{\kappa })$
-many path-type root node families and if
$\kappa ^{<\omega }=\kappa < \textrm {cf}(2^{\kappa })$
-many path-type root node families and if
![]() $\textrm {cf}(\nu )<\kappa $
, there are fewer than
$\textrm {cf}(\nu )<\kappa $
, there are fewer than
![]() $\kappa $
-many, so in all cases, x hits
$\kappa $
-many, so in all cases, x hits
![]() $2^{\kappa }$
-many nodes within a particular path-type root node family and a tower is added inside x at level
$2^{\kappa }$
-many nodes within a particular path-type root node family and a tower is added inside x at level
![]() $\nu +1$
passing through level
$\nu +1$
passing through level
![]() $\xi $
. The resulting tree T of regular height
$\xi $
. The resulting tree T of regular height
![]() $\lambda \geq \kappa ^+$
is shown to be a base tree as in Theorem 4.2: For any set
$\lambda \geq \kappa ^+$
is shown to be a base tree as in Theorem 4.2: For any set
![]() $x \in [\kappa ]^{\kappa }$
, the above shows that if any level of
$x \in [\kappa ]^{\kappa }$
, the above shows that if any level of
![]() $T \restriction x$
has size
$T \restriction x$
has size
![]() $2^{\kappa }$
, then a tower is added inside x, while if all levels have size less than
$2^{\kappa }$
, then a tower is added inside x, while if all levels have size less than
![]() $\kappa $
, then a
$\kappa $
, then a
![]() $\kappa $
-sized subset of x is almost contained in members of a tower sequence cofinally often, which is a contradiction.
$\kappa $
-sized subset of x is almost contained in members of a tower sequence cofinally often, which is a contradiction.
If
![]() $\lambda $
is the limit of lengths of towers of regular lengths
$\lambda $
is the limit of lengths of towers of regular lengths
![]() $\geq \kappa ^+$
in
$\geq \kappa ^+$
in
![]() $P(\kappa )/{<}\kappa $
, then the proof to Theorem 5.1 can be roughly mimicked with this sequence of cardinalities in place of the
$P(\kappa )/{<}\kappa $
, then the proof to Theorem 5.1 can be roughly mimicked with this sequence of cardinalities in place of the
![]() $\langle \delta _{\nu } \rangle $
sequence from Theorem 5.1, with the caveat that the towers added below every relevant
$\langle \delta _{\nu } \rangle $
sequence from Theorem 5.1, with the caveat that the towers added below every relevant
![]() $x \in [\kappa ]^{\kappa }$
are now
$x \in [\kappa ]^{\kappa }$
are now
![]() $\subseteq ^{*}$
-towers as in Theorem 4.2 and not
$\subseteq ^{*}$
-towers as in Theorem 4.2 and not
![]() $\subseteq $
-towers. Note that
$\subseteq $
-towers. Note that
![]() $\lambda \leq 2^{\kappa }$
in all cases. To show maximality of all intermediate levels
$\lambda \leq 2^{\kappa }$
in all cases. To show maximality of all intermediate levels
![]() $\xi < \lambda $
, as usual and as above branches through any induced tree
$\xi < \lambda $
, as usual and as above branches through any induced tree
![]() $T_{\xi } \restriction x$
with nonempty pseudointersection are formed and the process proceeds. The method for identifying such a branch depends on the cofinality of
$T_{\xi } \restriction x$
with nonempty pseudointersection are formed and the process proceeds. The method for identifying such a branch depends on the cofinality of
![]() $\xi $
. Similarly, it is argued depending on the cofinality of
$\xi $
. Similarly, it is argued depending on the cofinality of
![]() $\lambda $
that
$\lambda $
that
![]() $T \restriction x$
cannot have levels of size
$T \restriction x$
cannot have levels of size
![]() $<\kappa $
everywhere, and so the resulting distributivity tree must in fact be a base tree.
$<\kappa $
everywhere, and so the resulting distributivity tree must in fact be a base tree.