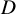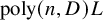1 Introduction
Can we solve polynomial systems in polynomial time? This question received different answers in different contexts. The NP-completeness of deciding the feasibility of a general polynomial system in both Turing and BSS models of computation is certainly an important difficulty, but it does not preclude efficient algorithms for computing all the zeros of a polynomial system or solving polynomial systems with as many equations as variables, for which the feasibility over algebraically closed fields is granted under genericity hypotheses. And indeed, there are several ways of computing all
![]() ${D}^n$
zeros of a generic polynomial system of n equations of degree
${D}^n$
zeros of a generic polynomial system of n equations of degree
![]() ${D}> 1$
in n variables with
${D}> 1$
in n variables with
![]() $\operatorname {poly}({D}^n)$
arithmetic operations (e.g., [Reference Giusti, Lecerf and Salvy21, Reference Lakshman30, Reference Renegar36]). Smale’s 17th problem [Reference Smale47] is a clear-cut formulation of the problem in a numerical setting. It asks for an algorithm, with polynomial average complexity, for computing one approximate zero of a given polynomial system, where the complexity is to be measured with respect to the dense input size N, that is, the number of possible monomials in the input system. Recall that an approximate zero of a polynomial system is a point from which Newton’s iteration converges doubly exponentially. Smale’s question was given recently a positive answer after seminal work by [Reference Shub and Smale40–Reference Shub and Smale44], fundamental contributions by [Reference Beltrán and Pardo7, Reference Beltrán and Pardo8, Reference Shub39], as well as our work [Reference Bürgisser and Cucker14, Reference Lairez28]. The basic algorithmic idea underlying all these is continuation along linear paths. To find a zero of a system
$\operatorname {poly}({D}^n)$
arithmetic operations (e.g., [Reference Giusti, Lecerf and Salvy21, Reference Lakshman30, Reference Renegar36]). Smale’s 17th problem [Reference Smale47] is a clear-cut formulation of the problem in a numerical setting. It asks for an algorithm, with polynomial average complexity, for computing one approximate zero of a given polynomial system, where the complexity is to be measured with respect to the dense input size N, that is, the number of possible monomials in the input system. Recall that an approximate zero of a polynomial system is a point from which Newton’s iteration converges doubly exponentially. Smale’s question was given recently a positive answer after seminal work by [Reference Shub and Smale40–Reference Shub and Smale44], fundamental contributions by [Reference Beltrán and Pardo7, Reference Beltrán and Pardo8, Reference Shub39], as well as our work [Reference Bürgisser and Cucker14, Reference Lairez28]. The basic algorithmic idea underlying all these is continuation along linear paths. To find a zero of a system
![]() $F=(f_1,\ldots ,f_n)$
of n polynomials in n variables of degree at most
$F=(f_1,\ldots ,f_n)$
of n polynomials in n variables of degree at most
![]() ${D}$
, we first construct another system G with a built-in zero
${D}$
, we first construct another system G with a built-in zero
![]() $\zeta _0 \in \mathbb {C}^n$
and consider the family
$\zeta _0 \in \mathbb {C}^n$
and consider the family
![]() $F_t \,{\stackrel {.}{=}}\, tF+(1-t)G$
of polynomial systems. If G is generic enough, the zero
$F_t \,{\stackrel {.}{=}}\, tF+(1-t)G$
of polynomial systems. If G is generic enough, the zero
![]() $\zeta _0$
of G extends as a continuous family
$\zeta _0$
of G extends as a continuous family
![]() $(\zeta _t)$
with
$(\zeta _t)$
with
![]() $F_t(\zeta _t)=0$
, so that
$F_t(\zeta _t)=0$
, so that
![]() $\zeta _1$
is a zero of F. It is possible to compute an approximation of
$\zeta _1$
is a zero of F. It is possible to compute an approximation of
![]() $\zeta _1$
by tracking
$\zeta _1$
by tracking
![]() $\zeta _t$
in finitely many steps. From the perspective of complexity analysis, the focal points are the choice of
$\zeta _t$
in finitely many steps. From the perspective of complexity analysis, the focal points are the choice of
![]() $(G,\zeta _0)$
and the estimation of the number of steps necessary for a correct approximation of
$(G,\zeta _0)$
and the estimation of the number of steps necessary for a correct approximation of
![]() $\zeta _1$
(the cost of each step being not an issue as it is
$\zeta _1$
(the cost of each step being not an issue as it is
![]() $O(N)$
). The problem of choosing an initial pair
$O(N)$
). The problem of choosing an initial pair
![]() $(G,\zeta _0)$
was for a long while a major obstacle in complexity analysis. It was solved by [Reference Beltrán and Pardo7], who introduced an algorithm to sample a random polynomial system G together with a zero
$(G,\zeta _0)$
was for a long while a major obstacle in complexity analysis. It was solved by [Reference Beltrán and Pardo7], who introduced an algorithm to sample a random polynomial system G together with a zero
![]() $\zeta _0$
of it and provided a
$\zeta _0$
of it and provided a
![]() $\operatorname {poly}(n,{D})N^2$
bound for the average number of steps in the numerical continuation starting from
$\operatorname {poly}(n,{D})N^2$
bound for the average number of steps in the numerical continuation starting from
![]() $(G,\zeta _0)$
. This idea was followed in subsequent works, with occasional cost improvements that decreased the exponent in N for the average number of steps. Note that for a system of n polynomial equations of degree
$(G,\zeta _0)$
. This idea was followed in subsequent works, with occasional cost improvements that decreased the exponent in N for the average number of steps. Note that for a system of n polynomial equations of degree
![]() ${D}$
in n variables,
${D}$
in n variables,
![]() $N =n \binom {{D}+n}{n}$
, and, therefore,
$N =n \binom {{D}+n}{n}$
, and, therefore,
![]() $N \geqslant 2^{\min ({D}, n)}$
. Regarding Smale’s question, an
$N \geqslant 2^{\min ({D}, n)}$
. Regarding Smale’s question, an
![]() $N^{O(1)}$
bound on this number is satisfactory, but the question was posed, how much can the exponent in this bound be reduced?
$N^{O(1)}$
bound on this number is satisfactory, but the question was posed, how much can the exponent in this bound be reduced?
1.1 Rigid continuation paths
The first part of this work [Reference Lairez29]Footnote
1
gave an answer. It introduced continuation along rigid paths: the systems
![]() $F_t$
have the form
$F_t$
have the form
![]() $F_t \,{\stackrel {.}{=}}\, \left (f_1 \circ u_{1}(t),\ldots ,f_n \circ u_{n}(t)\right )$
, where the
$F_t \,{\stackrel {.}{=}}\, \left (f_1 \circ u_{1}(t),\ldots ,f_n \circ u_{n}(t)\right )$
, where the
![]() $u_{i}(t)\in U(n+1)$
are unitary matrices that depend continuously on the parameter t, while
$u_{i}(t)\in U(n+1)$
are unitary matrices that depend continuously on the parameter t, while
![]() $f_1,\dotsc ,f_n$
are fixed homogeneous polynomials. Compared to the previous setting, the natural parameter space for the continuation is not any more the full space of all polynomial systems of a given degree pattern but rather the group
$f_1,\dotsc ,f_n$
are fixed homogeneous polynomials. Compared to the previous setting, the natural parameter space for the continuation is not any more the full space of all polynomial systems of a given degree pattern but rather the group
![]() $U(n+1)^n$
, denoted
$U(n+1)^n$
, denoted
![]() ${\mathcal {U}}$
. We developed analogues of Beltrán and Pardo’s [Reference Beltrán and Pardo8] results for rigid paths. Building on this, we could prove a
${\mathcal {U}}$
. We developed analogues of Beltrán and Pardo’s [Reference Beltrán and Pardo8] results for rigid paths. Building on this, we could prove a
![]() $\operatorname {poly}(n,{D})$
bound on the average number of continuation steps required to compute one zero of a Kostlan random polynomial system,Footnote
2
yielding a
$\operatorname {poly}(n,{D})$
bound on the average number of continuation steps required to compute one zero of a Kostlan random polynomial system,Footnote
2
yielding a
![]() $N^{1+o(1)}$
total complexity bound. This is the culmination of several results in this direction, which improved the average analysis number of continuation steps (see Table 1) for solving random dense polynomial systems.
$N^{1+o(1)}$
total complexity bound. This is the culmination of several results in this direction, which improved the average analysis number of continuation steps (see Table 1) for solving random dense polynomial systems.
Table 1 Comparison of previous complexity analysis of numerical continuation algorithms for solving systems of n polynomial equations of degree
![]() ${D}$
in n variables. The parameter
${D}$
in n variables. The parameter
![]() $N = n \binom {n+{D}}{n}$
is the dense input size. The parameter
$N = n \binom {n+{D}}{n}$
is the dense input size. The parameter
![]() $\sigma $
is the standard deviation for a noncentred distribution, in the context of smoothed analysis. Some results are not effective in that they do not lead to a complete algorithm to solve polynomial systems.
$\sigma $
is the standard deviation for a noncentred distribution, in the context of smoothed analysis. Some results are not effective in that they do not lead to a complete algorithm to solve polynomial systems.

1.2 Refinement of Smale’s question
What is at stake beyond Smale’s question is the understanding of numerical continuation as it happens in practice with a heuristic computation of the step lengths.Footnote
3
Experiments have shown that certified algorithms in the Shub-Smale line perform much smaller steps—and consequently many more steps—than heuristic methods for numerical continuation [Reference Beltrán and Leykin4, Reference Beltrán and Leykin5]. In spite of progress in designing better and better heuristics (e.g., [Reference Telen, VanBarel and Verschelde48, Reference Timme49]), the design of efficient algorithms for certified numerical continuation remains an important aspiration. With a view on closing the gap between rigorous step-length estimates and heuristics, a first observation—demonstrated experimentally by [Reference Hauenstein and Liddell23] and confirmed theoretically in Part I—highlights the role of higher-order derivatives. Shub and Smale’s first-order step-length computation seems powerless in obtaining
![]() $\operatorname {poly}(n, {D})$
bounds on the number of steps: we need to get closer to Smale’s
$\operatorname {poly}(n, {D})$
bounds on the number of steps: we need to get closer to Smale’s
![]() $\gamma $
to compute adequate step lengths. Smale’s
$\gamma $
to compute adequate step lengths. Smale’s
![]() $\gamma $
can be seen as a measure of condition for a system F. It captures some, but not all, of the properties of F captured by its classic condition number
$\gamma $
can be seen as a measure of condition for a system F. It captures some, but not all, of the properties of F captured by its classic condition number
![]() $\mu $
. In exchange, its expectation for random systems is smaller (see Section 2 for a more detailed discussion).
$\mu $
. In exchange, its expectation for random systems is smaller (see Section 2 for a more detailed discussion).
However, estimating the higher-order derivatives occurring in
![]() $\gamma $
is expensive. Thus, while using
$\gamma $
is expensive. Thus, while using
![]() $\gamma $
improves the average number of steps, it introduces a burden in the step-length computation. In Part I, we obtained a
$\gamma $
improves the average number of steps, it introduces a burden in the step-length computation. In Part I, we obtained a
![]() $\operatorname {poly}(n, {D}) N$
complexity bound for estimating the variant
$\operatorname {poly}(n, {D}) N$
complexity bound for estimating the variant
![]() $\hat {\gamma }_{\mathrm {Frob}}$
of
$\hat {\gamma }_{\mathrm {Frob}}$
of
![]() $\gamma $
(Proposition I.32) which, we showed, can be used to estimate step lengths. This cost is quasilinear with respect to the input size, we can hardly do better. But is N the right parameter to measure complexity? From a practical point of view, N is not so much relevant. Often N is much larger than the number of coefficients that actually define the input system, for example, when the system is sparse or structured. This observation is turned to practical account by treating the input system not as a linear combination of monomials but as a black-box evaluation function, that is, as a routine that computes the value of the components of the system at any given point. Most implementations of numerical continuation do this. In this perspective, N does not play any role, and there is a need for adapting to this setting the computation of
$\gamma $
(Proposition I.32) which, we showed, can be used to estimate step lengths. This cost is quasilinear with respect to the input size, we can hardly do better. But is N the right parameter to measure complexity? From a practical point of view, N is not so much relevant. Often N is much larger than the number of coefficients that actually define the input system, for example, when the system is sparse or structured. This observation is turned to practical account by treating the input system not as a linear combination of monomials but as a black-box evaluation function, that is, as a routine that computes the value of the components of the system at any given point. Most implementations of numerical continuation do this. In this perspective, N does not play any role, and there is a need for adapting to this setting the computation of
![]() $\gamma $
. Designing algorithms for black-box inputs and analysing their complexity for dense Gaussian random polynomial systems is interesting but misses an important point. The evaluation complexity of a random dense polynomial system is
$\gamma $
. Designing algorithms for black-box inputs and analysing their complexity for dense Gaussian random polynomial systems is interesting but misses an important point. The evaluation complexity of a random dense polynomial system is
![]() $\Theta (N)$
, whereas the benefit of considering a black-box input is precisely to investigate systems with much lower evaluation complexity, and such systems have measure zero in the space of all polynomial systems. It is conceivable, even from the restricted perspective of numerical polynomial system solving, that intrinsically, polynomial systems with low evaluation complexity behave in a different way than random dense polynomial systems. So Smale’s original question of solving polynomial systems in polynomial time leads to the following refined question:
$\Theta (N)$
, whereas the benefit of considering a black-box input is precisely to investigate systems with much lower evaluation complexity, and such systems have measure zero in the space of all polynomial systems. It is conceivable, even from the restricted perspective of numerical polynomial system solving, that intrinsically, polynomial systems with low evaluation complexity behave in a different way than random dense polynomial systems. So Smale’s original question of solving polynomial systems in polynomial time leads to the following refined question:
Can we compute an approximate zero of a structured polynomial system F given by black-box evaluation functions with
![]() $\operatorname {poly}(n, {D})$
many arithmetic operations and evaluations of F on average?
$\operatorname {poly}(n, {D})$
many arithmetic operations and evaluations of F on average?
We use algebraic branching programs (ABPs), a widely studied concept in algebraic complexity theory (see Section 1.8), as a model of computation for polynomials with low evaluation complexity. Further, we introduce a natural model of Gaussian random algebraic branching programs in order to capture the aspect of randomisation. The main result of this paper is an affirmative answer to the above refined question in this model.
1.3 Polynomial systems given by black-box evaluation
The model of computation is the BSS model, extended with rational exponentiation for convenience and a ‘6th type of node’, as introduced by [Reference Shub and Smale44], that computes an exact zero in the complex projective line
![]() ${\mathbb {P}}^1$
of a bivariate homogeneous polynomial given an approximate zero (this is used in the sampling step) (see Part I, Section 4.3.1 for a discussion). The term ‘black-box’ refers to a mode of computation with polynomials where we assume only the ability to evaluate them at a complex point. Concretely, the polynomials are represented by programs, or BSS machines. For a black-box polynomial
${\mathbb {P}}^1$
of a bivariate homogeneous polynomial given an approximate zero (this is used in the sampling step) (see Part I, Section 4.3.1 for a discussion). The term ‘black-box’ refers to a mode of computation with polynomials where we assume only the ability to evaluate them at a complex point. Concretely, the polynomials are represented by programs, or BSS machines. For a black-box polynomial
![]() ${f \in \mathbb {C}[z_1,\dotsc ,z_n]}$
, we denote by
${f \in \mathbb {C}[z_1,\dotsc ,z_n]}$
, we denote by
![]() $L(f)$
the number of operations performed by the program representing f to evaluate f at a point in
$L(f)$
the number of operations performed by the program representing f to evaluate f at a point in
![]() $\mathbb {C}^n$
. For a polynomial system
$\mathbb {C}^n$
. For a polynomial system
![]() $F = (f_1,\dotsc ,f_n)$
, we write
$F = (f_1,\dotsc ,f_n)$
, we write
![]() $L(F) \,{\stackrel {.}{=}}\, L(f_1)+\dotsb + L(f_n)$
. It is possible that evaluating F costs less than evaluating its components separately, as some computations may be shared, but we cannot save more than a factor n, so we ignore the issue. More generally, in this article, we will not enter the details of the
$L(F) \,{\stackrel {.}{=}}\, L(f_1)+\dotsb + L(f_n)$
. It is possible that evaluating F costs less than evaluating its components separately, as some computations may be shared, but we cannot save more than a factor n, so we ignore the issue. More generally, in this article, we will not enter the details of the
![]() $\operatorname {poly}(n,{D})$
factors. The ability to evaluate first-order derivatives will also be used. For a univariate polynomial f of degree at most
$\operatorname {poly}(n,{D})$
factors. The ability to evaluate first-order derivatives will also be used. For a univariate polynomial f of degree at most
![]() ${D}$
, the derivative at
${D}$
, the derivative at
![]() $0$
can be computed from evaluations using the formula
$0$
can be computed from evaluations using the formula
 $$ \begin{align} f'(0) = \frac1{{D}+1} \sum_{i=0}^{{D}} \omega^{-i} f(\omega^{i}), \end{align} $$
$$ \begin{align} f'(0) = \frac1{{D}+1} \sum_{i=0}^{{D}} \omega^{-i} f(\omega^{i}), \end{align} $$
where
![]() $\omega \in \mathbb {C}$
is a primitive
$\omega \in \mathbb {C}$
is a primitive
![]() $({D}+1)$
th root of unity. Similar formulas hold for multivariate polynomials. In practice, automatic differentiation (e.g., [Reference Baur and Strassen2]) may be used. In any case, we can evaluate the Jacobian matrix of a black-box polynomial system F with
$({D}+1)$
th root of unity. Similar formulas hold for multivariate polynomials. In practice, automatic differentiation (e.g., [Reference Baur and Strassen2]) may be used. In any case, we can evaluate the Jacobian matrix of a black-box polynomial system F with
![]() $\operatorname {poly}(n,{D}) L(F)$
operations. Since this is below the resolution that we chose, we do not make specific assumptions on the evaluation complexity of the Jacobian matrix. Moreover, the degree of a black-box polynomial can be computed with probability 1 in the BSS model by evaluation and interpolation along a lineFootnote
4
, so there is no need for the degree to be specified separately.
$\operatorname {poly}(n,{D}) L(F)$
operations. Since this is below the resolution that we chose, we do not make specific assumptions on the evaluation complexity of the Jacobian matrix. Moreover, the degree of a black-box polynomial can be computed with probability 1 in the BSS model by evaluation and interpolation along a lineFootnote
4
, so there is no need for the degree to be specified separately.
1.4 The
 $\Gamma (f)$
number
$\Gamma (f)$
number
Beyond the evaluation complexity
![]() $L(F)$
, the hardness of computing a zero of F in our setting depends on an averaged
$L(F)$
, the hardness of computing a zero of F in our setting depends on an averaged
![]() $\gamma $
number. For a polynomial
$\gamma $
number. For a polynomial
![]() $f \in \mathbb {C}[z_0,\dotsc ,z_n]$
, we define
$f \in \mathbb {C}[z_0,\dotsc ,z_n]$
, we define

where the triple norm
![]() of a k-multilinear map A is defined as
of a k-multilinear map A is defined as
![]() $\sup \frac {\|A(z_1,\dotsc ,z_k)\|}{\|z_1\|\dotsb \|z_k\|}$
. We note that this definition coincides with the one in [Reference Shub and Smale44] and [Reference Dedieu16, §4] since we deal here with a single polynomial, not a system (see Section 2.3 for the relations between different definitions of
$\sup \frac {\|A(z_1,\dotsc ,z_k)\|}{\|z_1\|\dotsb \|z_k\|}$
. We note that this definition coincides with the one in [Reference Shub and Smale44] and [Reference Dedieu16, §4] since we deal here with a single polynomial, not a system (see Section 2.3 for the relations between different definitions of
![]() $\gamma $
).
$\gamma $
).
If f is homogeneous and
![]() $[z] \in \mathbb {P}^n$
is a projective point, we define
$[z] \in \mathbb {P}^n$
is a projective point, we define
![]() $\gamma (f, [z]) \,{\stackrel {.}{=}}\, \gamma (f, z)$
, for some representative
$\gamma (f, [z]) \,{\stackrel {.}{=}}\, \gamma (f, z)$
, for some representative
![]() $z\in \mathbb {S}(\mathbb {C}^{n+1})$
. The definition does not depend on the representative. By Lemma I.11 (in Part I),
$z\in \mathbb {S}(\mathbb {C}^{n+1})$
. The definition does not depend on the representative. By Lemma I.11 (in Part I),
![]() $\gamma (f, z) \ge \frac 12 ({D}-1)$
if f is homogeneous of degree
$\gamma (f, z) \ge \frac 12 ({D}-1)$
if f is homogeneous of degree
![]() ${D}$
, and
${D}$
, and
![]() $\gamma (f, z) =0$
if
$\gamma (f, z) =0$
if
![]() ${D}=1$
. For computational purposes, we prefer the Frobenius
${D}=1$
. For computational purposes, we prefer the Frobenius
![]() $\gamma $
number introduced in Part I:
$\gamma $
number introduced in Part I:
 $$ \begin{align} \gamma_{\mathrm{Frob}}(f,z) \,{\stackrel{.}{=}}\, \sup_{k\geqslant 2} \left(\left\| \mathrm{d} _zf \right\|^{-1} \left\| \tfrac{1}{k!} \mathrm{d} _z^kf \right\|_{\mathrm{Frob}}\right)^{\frac{1}{k-1}}, \end{align} $$
$$ \begin{align} \gamma_{\mathrm{Frob}}(f,z) \,{\stackrel{.}{=}}\, \sup_{k\geqslant 2} \left(\left\| \mathrm{d} _zf \right\|^{-1} \left\| \tfrac{1}{k!} \mathrm{d} _z^kf \right\|_{\mathrm{Frob}}\right)^{\frac{1}{k-1}}, \end{align} $$
where
![]() $\|-\|_{\mathrm {Frob}}$
is the Frobenius norm of a multilinear map (see I, Section 4.2). The two variants are tightly related (Lemma I.29):
$\|-\|_{\mathrm {Frob}}$
is the Frobenius norm of a multilinear map (see I, Section 4.2). The two variants are tightly related (Lemma I.29):
We will not need to here define, or use, the
![]() $\gamma $
number of a polynomial system. For a homogeneous polynomial
$\gamma $
number of a polynomial system. For a homogeneous polynomial
![]() $f \in \mathbb {C}[z_0,\dotsc ,z_n]$
of degree
$f \in \mathbb {C}[z_0,\dotsc ,z_n]$
of degree
![]() ${D}\ge 2$
, we define the averaged
${D}\ge 2$
, we define the averaged
![]() $\gamma $
number as
$\gamma $
number as
where
![]() $\zeta $
is a uniformly distributed zero of f in
$\zeta $
is a uniformly distributed zero of f in
![]() $\mathbb {P}^n$
. Recall that
$\mathbb {P}^n$
. Recall that
![]() $\mathbb {P}^n$
has a unique (up to scaling) Riemannian metric that is invariant under the action of the unitary group
$\mathbb {P}^n$
has a unique (up to scaling) Riemannian metric that is invariant under the action of the unitary group
![]() $U(n+1)$
: it is the Fubini–Study metric. It induces, by restriction, a Riemannian metric on the zero set of f (minus the singular points, if any). This Riemannian metric induces, in turn, a measure on the zero set of f with finite total volume, which makes the uniform distribution well-defined (for more details, see [Reference Griffiths and Harris22, pp. 27ff]). As shown in Corollary I.9, this distribution can also be obtained by sampling a uniformly distributed line L in
$U(n+1)$
: it is the Fubini–Study metric. It induces, by restriction, a Riemannian metric on the zero set of f (minus the singular points, if any). This Riemannian metric induces, in turn, a measure on the zero set of f with finite total volume, which makes the uniform distribution well-defined (for more details, see [Reference Griffiths and Harris22, pp. 27ff]). As shown in Corollary I.9, this distribution can also be obtained by sampling a uniformly distributed line L in
![]() $\mathbb {P}^n$
and then sampling a uniformly distributed point in
$\mathbb {P}^n$
and then sampling a uniformly distributed point in
![]() $V(f) \cap L$
(which is a finite set with probability one).
$V(f) \cap L$
(which is a finite set with probability one).
For a homogeneous polynomial system
![]() $F = (f_1,\dotsc ,f_n)$
, we define
$F = (f_1,\dotsc ,f_n)$
, we define
 $$ \begin{align} \Gamma(F) \,{\stackrel{.}{=}}\, \left( \Gamma(f_1)^2 +\dotsb + \Gamma(f_n)^2 \right)^{\frac12} \leqslant \sum_{i=1}^n \Gamma(f_i). \end{align} $$
$$ \begin{align} \Gamma(F) \,{\stackrel{.}{=}}\, \left( \Gamma(f_1)^2 +\dotsb + \Gamma(f_n)^2 \right)^{\frac12} \leqslant \sum_{i=1}^n \Gamma(f_i). \end{align} $$
While
![]() $L(F)$
reflects an algebraic structure,
$L(F)$
reflects an algebraic structure,
![]() $\Gamma (F)$
reflects a numerical aspect. In the generic case, where all the
$\Gamma (F)$
reflects a numerical aspect. In the generic case, where all the
![]() $f_i$
have only regular zeros,
$f_i$
have only regular zeros,
![]() $\Gamma (F)$
is finite (see Remark 2.1).
$\Gamma (F)$
is finite (see Remark 2.1).
Let
![]() $d_1,\dotsc ,d_n$
be integers
$d_1,\dotsc ,d_n$
be integers
![]() $\geqslant 2$
, and let
$\geqslant 2$
, and let
![]() ${\mathcal {H}}$
be the space of homogeneous polynomial systems
${\mathcal {H}}$
be the space of homogeneous polynomial systems
![]() $(f_1,\dotsc ,f_n)$
with
$(f_1,\dotsc ,f_n)$
with
![]() $f_i \in \mathbb {C}[z_0,\dotsc ,z_n]$
homogeneous of degree
$f_i \in \mathbb {C}[z_0,\dotsc ,z_n]$
homogeneous of degree
![]() $d_i$
. Let
$d_i$
. Let
![]() ${D} \,{\stackrel {.}{=}}\, \max _i d_i$
. Let
${D} \,{\stackrel {.}{=}}\, \max _i d_i$
. Let
![]() ${\mathcal {U}}$
be the group
${\mathcal {U}}$
be the group
![]() $U(n+1)^n$
made of n copies of the group of unitary matrices of size
$U(n+1)^n$
made of n copies of the group of unitary matrices of size
![]() $n+1$
. For
$n+1$
. For
![]() ${\mathbf u} = (u_1,\dotsc ,u_n) \in {\mathcal {U}}$
and
${\mathbf u} = (u_1,\dotsc ,u_n) \in {\mathcal {U}}$
and
![]() $F = (f_1,\dotsc ,f_n) \in {\mathcal {H}}$
, we define the action
$F = (f_1,\dotsc ,f_n) \in {\mathcal {H}}$
, we define the action
It plays a major role in the setting of rigid continuation paths. Note that
![]() $\Gamma $
is unitarily invariant:
$\Gamma $
is unitarily invariant:
![]() $\Gamma ({\mathbf u}\cdot F)=\Gamma (F)$
for any
$\Gamma ({\mathbf u}\cdot F)=\Gamma (F)$
for any
![]() ${\mathbf u} \in {\mathcal {U}}$
. Concerning L, we have
${\mathbf u} \in {\mathcal {U}}$
. Concerning L, we have
![]() $L({\mathbf u} \cdot F) \leqslant L(F) + O(n^3)$
, using (1.7) as a formula to evaluate
$L({\mathbf u} \cdot F) \leqslant L(F) + O(n^3)$
, using (1.7) as a formula to evaluate
![]() ${\mathbf u} \cdot F$
(note that the matrices
${\mathbf u} \cdot F$
(note that the matrices
![]() $u_i$
are unitary, so the inverse is simply the Hermitian transpose).
$u_i$
are unitary, so the inverse is simply the Hermitian transpose).
1.5 Main results I
In our first main result, we design the randomised Algorithm BoostBlackBoxSolve in the setting of rigid continuation paths (see Section 4.3) for computing with high probability an approximate zero of a black-box polynomial system F. We say that
![]() $z\in {{\mathbb {P}}^n}$
is an approximate zero of a homogeneous polynomial system F, if there is a zero
$z\in {{\mathbb {P}}^n}$
is an approximate zero of a homogeneous polynomial system F, if there is a zero
![]() $\zeta \in {{\mathbb {P}}^n}$
of F, such that for any
$\zeta \in {{\mathbb {P}}^n}$
of F, such that for any
![]() $k\geqslant 0$
,
$k\geqslant 0$
,
where
![]() $d_{\mathbb {P}}$
is the geodesic distance in
$d_{\mathbb {P}}$
is the geodesic distance in
![]() ${{\mathbb {P}}^n}$
and
${{\mathbb {P}}^n}$
and
![]() ${\mathcal {N}}_F$
the projective Newton iteration [Reference Bürgisser and Cucker15, §16.6].
${\mathcal {N}}_F$
the projective Newton iteration [Reference Bürgisser and Cucker15, §16.6].
Theorem 1.1 (Termination and correctness)
Let
![]() $F = (f_1,\dotsc ,f_n)$
be a homogeneous polynomial system with only regular zeros. On input F, given as a black-box evaluation program, and
$F = (f_1,\dotsc ,f_n)$
be a homogeneous polynomial system with only regular zeros. On input F, given as a black-box evaluation program, and
![]() $\varepsilon> 0$
, Algorithm BoostBlackBoxSolve terminates almost surely and computes a point
$\varepsilon> 0$
, Algorithm BoostBlackBoxSolve terminates almost surely and computes a point
![]() $z^*\in \mathbb {P}^n$
, which is an approximate zero of F with probability at least
$z^*\in \mathbb {P}^n$
, which is an approximate zero of F with probability at least
![]() $1-\varepsilon $
.
$1-\varepsilon $
.
Algorithm BoostBlackBoxSolve is a randomised algorithm of Monte Carlo type: the output is only correct with given probability. Nonetheless, this probability is bounded below, independently of F. This is in strong contrast with, for example, the main result of [Reference Shub and Smale44], where the probability of success is relative to the randomness of the input: on some set of input of measure
![]() $1-\varepsilon $
, their algorithm always succeeds, while on the complement, it always fails. The algorithm presented here succeeds with probability at least
$1-\varepsilon $
, their algorithm always succeeds, while on the complement, it always fails. The algorithm presented here succeeds with probability at least
![]() $1-\varepsilon $
for any input with regular zeros (it may not terminate if this regularity hypothesis is not satisfied).
$1-\varepsilon $
for any input with regular zeros (it may not terminate if this regularity hypothesis is not satisfied).
Let
![]() ${\text {cost}_{\mathrm {BBBS}}}(F, \varepsilon )$
be the number of operations performed by Algorithm BoostBlackBoxSolve on input F and
${\text {cost}_{\mathrm {BBBS}}}(F, \varepsilon )$
be the number of operations performed by Algorithm BoostBlackBoxSolve on input F and
![]() $\varepsilon $
. This is a random variable because the algorithm is randomised. As in many previous works, we are unable to bound precisely
$\varepsilon $
. This is a random variable because the algorithm is randomised. As in many previous works, we are unable to bound precisely
![]() ${\text {cost}_{\mathrm {BBBS}}}(F, \varepsilon )$
, or its expectation over the internal randomisation for a fixed F. Instead, we introduce a randomisation of the input polynomial system F. So we consider a random input H and study instead the expectation of
${\text {cost}_{\mathrm {BBBS}}}(F, \varepsilon )$
, or its expectation over the internal randomisation for a fixed F. Instead, we introduce a randomisation of the input polynomial system F. So we consider a random input H and study instead the expectation of
![]() ${\text {cost}_{\mathrm {BBBS}}}(H, \varepsilon )$
over both H and the internal randomisation. The randomisation that we introduce is a random unitary change of variable on each equation of F. In other words, we consider
${\text {cost}_{\mathrm {BBBS}}}(H, \varepsilon )$
over both H and the internal randomisation. The randomisation that we introduce is a random unitary change of variable on each equation of F. In other words, we consider
![]() $H = {\mathbf u}\cdot F$
for a random uniformly distributed
$H = {\mathbf u}\cdot F$
for a random uniformly distributed
![]() ${\mathbf u} \in {\mathcal {U}}$
. Since
${\mathbf u} \in {\mathcal {U}}$
. Since
![]() ${\mathcal {U}}$
is a compact group, the uniform distribution is characterised as the unique probability measure on
${\mathcal {U}}$
is a compact group, the uniform distribution is characterised as the unique probability measure on
![]() ${\mathcal {U}}$
which is invariant under left multiplication: the Haar measure. We say that a system
${\mathcal {U}}$
which is invariant under left multiplication: the Haar measure. We say that a system
![]() $F=(f_1,\dotsc ,f_n)$
is square-free if
$F=(f_1,\dotsc ,f_n)$
is square-free if
![]() $f_1,\dotsc ,f_n$
are square-free nonzero polynomials. Importantly, this implies that with probability 1,
$f_1,\dotsc ,f_n$
are square-free nonzero polynomials. Importantly, this implies that with probability 1,
![]() ${\mathbf u}\cdot F$
has only regular zeros when
${\mathbf u}\cdot F$
has only regular zeros when
![]() ${\mathbf u} \in {\mathcal {U}}$
is uniformly distributed.
${\mathbf u} \in {\mathcal {U}}$
is uniformly distributed.
Theorem 1.2 (Complexity analysis)
Let
![]() $F=(f_1,\dotsc ,f_n)$
be a square-free homogeneous polynomial system with degrees at most
$F=(f_1,\dotsc ,f_n)$
be a square-free homogeneous polynomial system with degrees at most
![]() ${D}$
in
${D}$
in
![]() $n+1$
variables. Let
$n+1$
variables. Let
![]() ${\mathbf u} \in {\mathcal {U}}$
be uniformly distributed, and let
${\mathbf u} \in {\mathcal {U}}$
be uniformly distributed, and let
![]() $H = {\mathbf u} \cdot F$
. On input H, given as a black-box evaluation program, and
$H = {\mathbf u} \cdot F$
. On input H, given as a black-box evaluation program, and
![]() $\varepsilon>0$
, Algorithm BoostBlackBoxSolve terminates after
$\varepsilon>0$
, Algorithm BoostBlackBoxSolve terminates after
operations on average. ‘On average’ refers to expectation with respect to both the random draws made by the algorithm and the random variable
![]() ${\mathbf u}$
, but F is fixed.
${\mathbf u}$
, but F is fixed.
In addition to the foundations laid in Part I, the main underlying tool is a Monte Carlo method for estimating Smale’s
![]() $\gamma $
number: with
$\gamma $
number: with
![]() $\operatorname {poly}(n, {D}) \log \frac 1\varepsilon $
evaluations of f, we can estimate
$\operatorname {poly}(n, {D}) \log \frac 1\varepsilon $
evaluations of f, we can estimate
![]() $\gamma (f, z)$
within a factor
$\gamma (f, z)$
within a factor
![]() $\operatorname {poly}(n, {D})$
with probability at least
$\operatorname {poly}(n, {D})$
with probability at least
![]() $1-\varepsilon $
(see Theorem 3.3). This turns both the computation of the step length and the whole zero-finding process into Monte Carlo algorithms themselves and, as a consequence, BoostBlackBoxSolve departs from the simple structure of continuation algorithms described above. During execution, BoostBlackBoxSolve draws real numbers from the standard Gaussian distribution to compute the initial pair
$1-\varepsilon $
(see Theorem 3.3). This turns both the computation of the step length and the whole zero-finding process into Monte Carlo algorithms themselves and, as a consequence, BoostBlackBoxSolve departs from the simple structure of continuation algorithms described above. During execution, BoostBlackBoxSolve draws real numbers from the standard Gaussian distribution to compute the initial pair
![]() $(G,\zeta )$
and estimate various
$(G,\zeta )$
and estimate various
![]() $\gamma _{\mathrm {Frob}}$
. The average cost in Theorem 1.2 is considered with respect to both this inner randomisation of the algorithm and the randomness of the input
$\gamma _{\mathrm {Frob}}$
. The average cost in Theorem 1.2 is considered with respect to both this inner randomisation of the algorithm and the randomness of the input
![]() ${\mathbf u}$
(or F in Corollary 1.3 below).
${\mathbf u}$
(or F in Corollary 1.3 below).
BoostBlackBoxSolve actually performs the continuation procedure several times, possibly with different initial pairs, as well as a validation routine that drastically decreases the probability that the returned point is not an approximate zero of F. Its complexity analysis reflects this more complicated structure.
In contrast with many previous works, BoostBlackBoxSolve does not always succeed: its result can be wrong with a small given probability
![]() $\varepsilon $
, but the doubly logarithmic dependence of the complexity with respect to
$\varepsilon $
, but the doubly logarithmic dependence of the complexity with respect to
![]() $\varepsilon $
is satisfactory. We do not know if it is optimal, but it seems difficult, in the black-box model, to obtain an algorithm with similar complexity bounds, but that succeeds (i.e. returns a certified approximate zero) with probability one: to the best of our knowledge, all algorithms for certifying zeros need some global information—be it the Weyl norm of the system [Reference Hauenstein and Sottile24], evaluation in interval arithmetic [Reference Rump and Graillat38] or Smale’s
$\varepsilon $
is satisfactory. We do not know if it is optimal, but it seems difficult, in the black-box model, to obtain an algorithm with similar complexity bounds, but that succeeds (i.e. returns a certified approximate zero) with probability one: to the best of our knowledge, all algorithms for certifying zeros need some global information—be it the Weyl norm of the system [Reference Hauenstein and Sottile24], evaluation in interval arithmetic [Reference Rump and Graillat38] or Smale’s
![]() $\alpha $
number involving all higher derivatives—which we cannot estimate with probability 1 in the black-box model with only
$\alpha $
number involving all higher derivatives—which we cannot estimate with probability 1 in the black-box model with only
![]() $\operatorname {poly}(n,{D})$
evaluations. So unless we add an ad hoc hypothesis (such as a bound on the coefficients in the monomial basis), we do not know how to certify an approximate zero in the black-box model.
$\operatorname {poly}(n,{D})$
evaluations. So unless we add an ad hoc hypothesis (such as a bound on the coefficients in the monomial basis), we do not know how to certify an approximate zero in the black-box model.
Theorem 1.2 can be interpreted as an average analysis on an orbit of the action of
![]() ${\mathcal {U}}$
on
${\mathcal {U}}$
on
![]() ${\mathcal {H}}$
. More generally, we may assume a random input
${\mathcal {H}}$
. More generally, we may assume a random input
![]() $F \in {\mathcal {H}}$
where the distribution of F is unitarily invariant, meaning that for any
$F \in {\mathcal {H}}$
where the distribution of F is unitarily invariant, meaning that for any
![]() ${\mathbf u}\in {\mathcal {U}}$
,
${\mathbf u}\in {\mathcal {U}}$
,
![]() ${\mathbf u} \cdot F$
and F have the same distribution. This leads to the following statement.
${\mathbf u} \cdot F$
and F have the same distribution. This leads to the following statement.
Corollary 1.3. Let
![]() $F \in {\mathcal {H}}$
be a random polynomial system, which is almost surely square-free, with unitarily invariant distribution. Let L be an upper bound on
$F \in {\mathcal {H}}$
be a random polynomial system, which is almost surely square-free, with unitarily invariant distribution. Let L be an upper bound on
![]() $L(F)$
, and put
$L(F)$
, and put
![]() $\Gamma = {\mathbb {E}} [ \Gamma (F)^2]^{\frac 12}$
. On input F (given as a black-box evaluation program) and
$\Gamma = {\mathbb {E}} [ \Gamma (F)^2]^{\frac 12}$
. On input F (given as a black-box evaluation program) and
![]() $\varepsilon> 0$
, Algorithm BoostBlackBoxSolve terminates after
$\varepsilon> 0$
, Algorithm BoostBlackBoxSolve terminates after
operations on average.
The quantity
![]() $\Gamma (F)$
strongly influences the average complexity in Theorem 1.2 and Corollary 1.3, and while it is natural to expect the complexity to depend on numerical aspects of F, it is desirable to quantify this dependence by studying random distributions of F [Reference Smale46]. It was shown in Part I that if
$\Gamma (F)$
strongly influences the average complexity in Theorem 1.2 and Corollary 1.3, and while it is natural to expect the complexity to depend on numerical aspects of F, it is desirable to quantify this dependence by studying random distributions of F [Reference Smale46]. It was shown in Part I that if
![]() $F\in {\mathcal {H}}$
is a Kostlan random polynomial system, then
$F\in {\mathcal {H}}$
is a Kostlan random polynomial system, then
![]() ${\mathbb {E}}[ \Gamma (F)^2 ] = \operatorname {poly}(n, {D})$
(Lemma I.38). Together with the standard bound
${\mathbb {E}}[ \Gamma (F)^2 ] = \operatorname {poly}(n, {D})$
(Lemma I.38). Together with the standard bound
![]() $L(F)=O(N)$
(see [Reference Bürgisser, Clausen and Shokrollahi13, Exercise 21.9(1)]), we immediately obtain from Corollary 1.3 the following complexity analysis, similar to the main result of Part I (Theorem I.40) but assuming only a black-box representation of the input polynomial system.
$L(F)=O(N)$
(see [Reference Bürgisser, Clausen and Shokrollahi13, Exercise 21.9(1)]), we immediately obtain from Corollary 1.3 the following complexity analysis, similar to the main result of Part I (Theorem I.40) but assuming only a black-box representation of the input polynomial system.
Corollary 1.4. Let
![]() $F \in {\mathcal {H}}$
be a Kostlan random polynomial system. On input F and
$F \in {\mathcal {H}}$
be a Kostlan random polynomial system. On input F and
![]() $\varepsilon> 0$
, Algorithm BoostBlackBoxSolve terminates after
$\varepsilon> 0$
, Algorithm BoostBlackBoxSolve terminates after
![]() $\operatorname {poly}(n, {D}) \cdot N \cdot \log \log \varepsilon ^{-1}$
operations and evaluations of F on average.
$\operatorname {poly}(n, {D}) \cdot N \cdot \log \log \varepsilon ^{-1}$
operations and evaluations of F on average.
Our second main result (Theorem 1.5 below) states that exact same bound for polynomial systems given by independent Gaussian random algebraic branching programs. We next introduce this model.
1.6 Algebraic branching programs
Following [Reference Nisan32], an ABP of degree
![]() ${D}$
is a labeled directed acyclic graph with one source and one sink, with a partition of the vertices into levels, numbered from 0 to
${D}$
is a labeled directed acyclic graph with one source and one sink, with a partition of the vertices into levels, numbered from 0 to
![]() ${D}$
, such that each edge goes from level i to level
${D}$
, such that each edge goes from level i to level
![]() $i+1$
. The source is the only vertex at level 0, and the sink is the only vertex at level
$i+1$
. The source is the only vertex at level 0, and the sink is the only vertex at level
![]() ${D}$
. Each edge is labelled with a homogeneous linear form in the input variables
${D}$
. Each edge is labelled with a homogeneous linear form in the input variables
![]() $z_0,\dotsc ,z_n$
. The weight of a directed path is defined as the product of the labels of its edges. By definition, an ABP computes the polynomial obtained as the sum of the weights over all paths from the source to the sink. It is a homogeneous polynomial of degree
$z_0,\dotsc ,z_n$
. The weight of a directed path is defined as the product of the labels of its edges. By definition, an ABP computes the polynomial obtained as the sum of the weights over all paths from the source to the sink. It is a homogeneous polynomial of degree
![]() ${D}$
. The width r of the ABP is the maximum of the cardinalities of the level sets. The size s of the ABP, which is defined as the number of its vertices, satisfies
${D}$
. The width r of the ABP is the maximum of the cardinalities of the level sets. The size s of the ABP, which is defined as the number of its vertices, satisfies
![]() $r \le s \le ({D}-1)r +2$
. Any homogeneous polynomial f can be computed by an ABP, and the minimum size or width of an ABP computing f are important measures of the complexity of f (see Section 1.8).
$r \le s \le ({D}-1)r +2$
. Any homogeneous polynomial f can be computed by an ABP, and the minimum size or width of an ABP computing f are important measures of the complexity of f (see Section 1.8).
While ABPs provide an elegant graphical way of formalising computations with polynomials, we will use an equivalent matrix formulation. Suppose that the ith level set has
![]() $r_i$
vertices and let
$r_i$
vertices and let
![]() $A_i(z)$
denote the weighted adjacency matrix of format
$A_i(z)$
denote the weighted adjacency matrix of format
![]() $r_{i-1}\times r_i$
, whose entries are the labels of the edges between vertices of level
$r_{i-1}\times r_i$
, whose entries are the labels of the edges between vertices of level
![]() $i-1$
and level i. Thus, the entries of
$i-1$
and level i. Thus, the entries of
![]() $A_i(z)$
are linear forms in the variables
$A_i(z)$
are linear forms in the variables
![]() $z_0,\ldots ,z_n$
. The polynomial
$z_0,\ldots ,z_n$
. The polynomial
![]() $f(z)$
computed by the ABP can then be expressed as the trace of iterated matrix multiplication, namely,
$f(z)$
computed by the ABP can then be expressed as the trace of iterated matrix multiplication, namely,
Indeed, after expanding the matrix product, we see that the right-hand side is nothing but the sum of the weights of all paths in the directed graph from the source to the sink.
It is convenient to relax the assumption
![]() $r_0=r_{D}=1$
to
$r_0=r_{D}=1$
to
![]() $r_0=r_{D}$
. Compared to the description in terms of ABPs, this adds some flexibility because the trace is invariant under cyclic permutation of the matrices
$r_0=r_{D}$
. Compared to the description in terms of ABPs, this adds some flexibility because the trace is invariant under cyclic permutation of the matrices
![]() $A_i(z)$
.
$A_i(z)$
.
Using the associativity of matrix multiplication, we can evaluate
![]() $f(z)$
efficiently by iterated matrix multiplication with a total of
$f(z)$
efficiently by iterated matrix multiplication with a total of
![]() $O({D} r^2 (n+r))$
arithmetic operations. Indeed, each of the at most
$O({D} r^2 (n+r))$
arithmetic operations. Indeed, each of the at most
![]() ${D} r^2$
entries of the matrices is a linear form in the variables
${D} r^2$
entries of the matrices is a linear form in the variables
![]() $z_0,\dotsc ,z_n$
, and thus, these entries can be evaluated with a total of
$z_0,\dotsc ,z_n$
, and thus, these entries can be evaluated with a total of
![]() $O({D} r^2 n)$
operations. Then it remains to perform r matrix multiplications, which amount to additional
$O({D} r^2 n)$
operations. Then it remains to perform r matrix multiplications, which amount to additional
![]() $O({D} r^3)$
operations.
$O({D} r^3)$
operations.
1.7 Main results II
Given positive integers
![]() $r_1,\dotsc ,r_{{D}-1}$
, we can form a random ABP (that we call Gaussian random ABP) of degree
$r_1,\dotsc ,r_{{D}-1}$
, we can form a random ABP (that we call Gaussian random ABP) of degree
![]() ${D}$
by considering a directed acyclic graph with
${D}$
by considering a directed acyclic graph with
![]() $r_i$
vertices in the layer i (for
$r_i$
vertices in the layer i (for
![]() $1\leqslant i \leqslant {D}-1$
), one vertex in the layers 0 and
$1\leqslant i \leqslant {D}-1$
), one vertex in the layers 0 and
![]() ${D}$
and all possible edges from a layer to the next, labelled by linear forms in
${D}$
and all possible edges from a layer to the next, labelled by linear forms in
![]() $z_0\ldots ,z_n$
with independent and identically distributed complex Gaussian coefficients. This is equivalent to assuming that the adjacency matrices are linear forms
$z_0\ldots ,z_n$
with independent and identically distributed complex Gaussian coefficients. This is equivalent to assuming that the adjacency matrices are linear forms
![]() $A_{i}(z) = A_{i0} z_0 +\cdots + A_{in} z_n$
with independent complex standard Gaussian matrices
$A_{i}(z) = A_{i0} z_0 +\cdots + A_{in} z_n$
with independent complex standard Gaussian matrices
![]() $A_{ij} \in \mathbb {C}^{r_{i-1} \times r_i}$
.
$A_{ij} \in \mathbb {C}^{r_{i-1} \times r_i}$
.
We call a Gaussian random ABP irreducible if all layers (except the first and the last) have at least two vertices. The polynomial computed by an irreducible Gaussian random ABP is almost surely irreducible (Lemma 5.1), and conversely, the polynomial computed by a Gaussian random ABP that is not irreducible is not irreducible; which justifies the naming.
Recall the numerical parameter
![]() $\Gamma $
entering the complexity of numerical continuation in the rigid setting (see (1.5) and Theorem 1.2). The second main result in this article is an upper bound on the expectation of
$\Gamma $
entering the complexity of numerical continuation in the rigid setting (see (1.5) and Theorem 1.2). The second main result in this article is an upper bound on the expectation of
![]() $\Gamma (f)$
, when f is computed by a Gaussian random ABP. Remarkably, the bound does not depend on the sizes
$\Gamma (f)$
, when f is computed by a Gaussian random ABP. Remarkably, the bound does not depend on the sizes
![]() $r_i$
of the layers defining the Gaussian random ABP, in particular, it is independent of its width!
$r_i$
of the layers defining the Gaussian random ABP, in particular, it is independent of its width!
Theorem 1.5. If f is the random polynomial computed by an irreducible Gaussian random ABP of degree
![]() ${D}$
, then
${D}$
, then
The distribution of the polynomial computed by a Gaussian random ABP is unitarily invariant so, as a consequence of Corollary 1.3, we obtain polynomial complexity bounds for solving polynomial systems made of Gaussian random ABPs.
Corollary 1.6. If
![]() $f_1,\dotsc ,f_n$
are independent irreducible Gaussian random ABPs of degree at most
$f_1,\dotsc ,f_n$
are independent irreducible Gaussian random ABPs of degree at most
![]() ${D}$
and evaluation complexity at most L, then BoostBlackBoxSolve, on input
${D}$
and evaluation complexity at most L, then BoostBlackBoxSolve, on input
![]() $f_1,\dotsc ,f_n$
and
$f_1,\dotsc ,f_n$
and
![]() $\varepsilon> 0$
, terminates after
$\varepsilon> 0$
, terminates after
operations on average.
This result provides an answer to the refined Smale’s problem raised at the end of Section 1.2, where ‘structured’ is interpreted as ‘low evaluation complexity in the ABP model’.
The polynomial systems computed by ABPs of width r form a zero measure subset of
![]() ${\mathcal {H}}$
when n and
${\mathcal {H}}$
when n and
![]() ${D}$
are large enough. More precisely, they form a subvariety of
${D}$
are large enough. More precisely, they form a subvariety of
![]() ${\mathcal {H}}$
of dimension at most
${\mathcal {H}}$
of dimension at most
![]() $r^2 {D} n$
, while the dimension of
$r^2 {D} n$
, while the dimension of
![]() ${\mathcal {H}}$
grows superpolynomially with n and
${\mathcal {H}}$
grows superpolynomially with n and
![]() ${D}$
. Note also that a polynomial f computed by a Gaussian random ABP may be almost surely singular (in the sense that the projective hypersurface that it defines is singular) (see Lemma 5.2). This strongly contrasts with previously considered stochastic models of polynomial systems.
${D}$
. Note also that a polynomial f computed by a Gaussian random ABP may be almost surely singular (in the sense that the projective hypersurface that it defines is singular) (see Lemma 5.2). This strongly contrasts with previously considered stochastic models of polynomial systems.
Lastly, it would be interesting to describe the limiting distribution of the polynomial computed by a Gaussian random ABP as the size of the layers goes to infinity. Since this question is out of the scope of this article, we leave it open.
1.8 On the role of algebraic branching programs
To motivate our choice of the model of ABPs, we point out here their important role in algebraic complexity theory, notably in Valiant’s algebraic framework of NP-completeness ([Reference Valiant51, Reference Valiant52]; see also [Reference Bürgisser11]). This model features the complexity class
![]() $\mathrm {VBP}$
, which models efficiently computable polynomials as sequences of multivariate complex polynomials
$\mathrm {VBP}$
, which models efficiently computable polynomials as sequences of multivariate complex polynomials
![]() $f_n$
, where the degree of
$f_n$
, where the degree of
![]() $f_n$
is polynomially bounded in n and the homogenisation of
$f_n$
is polynomially bounded in n and the homogenisation of
![]() $f_n$
can be computed by an ABP of width polynomially bounded in n. It is known [Reference Malod and Portier31, Reference Toda50] that the sequence of determinants of generic
$f_n$
can be computed by an ABP of width polynomially bounded in n. It is known [Reference Malod and Portier31, Reference Toda50] that the sequence of determinants of generic
![]() $n\times n$
matrices is complete for the class
$n\times n$
matrices is complete for the class
![]() $\mathrm {VBP}$
: this means the determinants have efficient computations in this model, and, moreover, any
$\mathrm {VBP}$
: this means the determinants have efficient computations in this model, and, moreover, any
![]() $(f_n)\in \mathrm {VBP}$
can be tightly reduced to a sequence of determinants in the sense that
$(f_n)\in \mathrm {VBP}$
can be tightly reduced to a sequence of determinants in the sense that
![]() $f_n$
can be written as the determinant of a matrix, whose entries are affine linear forms, and such that the size of the matrix is polynomially bounded in n. The related complexity class
$f_n$
can be written as the determinant of a matrix, whose entries are affine linear forms, and such that the size of the matrix is polynomially bounded in n. The related complexity class
![]() $\mathrm {VP}$
consists of the sequences of multivariate complex polynomials
$\mathrm {VP}$
consists of the sequences of multivariate complex polynomials
![]() $f_n$
, such that the degree of
$f_n$
, such that the degree of
![]() $f_n$
grows at most polynomially in n and such that
$f_n$
grows at most polynomially in n and such that
![]() $f_n$
can be computed by an arithmetic circuit (equivalently, straight-line program) of size polynomially bounded in n. While it is clear that
$f_n$
can be computed by an arithmetic circuit (equivalently, straight-line program) of size polynomially bounded in n. While it is clear that
![]() $\mathrm {VBP}\subseteq \mathrm {VP}$
, it is a longstanding open question whether equality holds. However, after relaxing ‘polynomially bounded’ to ‘quasi-polynomially bounded’Footnote
5
, the classes collapse (e.g., see [Reference Malod and Portier31]). These results should make clear the relevance and universality of the model of ABPs. Moreover, [Reference Valiant51] defined another natural complexity class
$\mathrm {VBP}\subseteq \mathrm {VP}$
, it is a longstanding open question whether equality holds. However, after relaxing ‘polynomially bounded’ to ‘quasi-polynomially bounded’Footnote
5
, the classes collapse (e.g., see [Reference Malod and Portier31]). These results should make clear the relevance and universality of the model of ABPs. Moreover, [Reference Valiant51] defined another natural complexity class
![]() $\mathrm {VNP}$
, formalising efficiently definable polynomials for which the sequence of permanents of generic matrices is complete. Valiant’s conjecture
$\mathrm {VNP}$
, formalising efficiently definable polynomials for which the sequence of permanents of generic matrices is complete. Valiant’s conjecture
![]() $\mathrm {VBP}\ne \mathrm {VNP}$
is a version of the famous
$\mathrm {VBP}\ne \mathrm {VNP}$
is a version of the famous
![]() $\mathrm {P}\ne \mathrm {NP}$
conjecture.
$\mathrm {P}\ne \mathrm {NP}$
conjecture.
1.9 Organisation of paper
In Section 2, we first recall the basics of the complexity analysis of numerical continuation algorithms and summarise the results obtained in Part I. Section 3 is devoted to numerical continuation algorithms when the functions are given by a black-box. We introduce, here, a sampling algorithm to estimate
![]() $\gamma _{\mathrm {Frob}}$
with high probability in this setting. Section 4 is devoted to the complexity analysis of the new algorithm on input
$\gamma _{\mathrm {Frob}}$
with high probability in this setting. Section 4 is devoted to the complexity analysis of the new algorithm on input
![]() ${\mathbf u}\cdot F$
with random u. In particular, in Section 4.3, we consider the problem of certifying an approximate zero in the black-box model, and we prove Theorem 1.2. Finally, Section 5 presents the proof of Theorem 1.5, our second main result.
${\mathbf u}\cdot F$
with random u. In particular, in Section 4.3, we consider the problem of certifying an approximate zero in the black-box model, and we prove Theorem 1.2. Finally, Section 5 presents the proof of Theorem 1.5, our second main result.
2 Numerical continuation with few steps
2.1 The classical setting
Numerical continuation algorithms have been so far the main tool for the complexity analysis of numerical solving of polynomial systems. We present, here, the main line of the theory as developed by [Reference Beltrán3, Reference Beltrán and Pardo7, Reference Beltrán and Pardo8, Reference Shub and Smale40, Reference Shub and Smale41, Reference Shub and Smale43, Reference Shub and Smale44]. The general idea to solve a polynomial system
![]() $F \in \mathcal {H}$
consists of embedding F in a one-parameter continuous family
$F \in \mathcal {H}$
consists of embedding F in a one-parameter continuous family
![]() $(F_t)_{t\in [0,1]}$
of polynomial systems, such that
$(F_t)_{t\in [0,1]}$
of polynomial systems, such that
![]() $F_1 = F$
and a zero of
$F_1 = F$
and a zero of
![]() $F_0$
, say,
$F_0$
, say,
![]() $\zeta _0\in \mathbb {P}^n$
, is known. Then, starting from
$\zeta _0\in \mathbb {P}^n$
, is known. Then, starting from
![]() $t=0$
and
$t=0$
and
![]() $z=\zeta _0$
, t and z are updated to track a zero of
$z=\zeta _0$
, t and z are updated to track a zero of
![]() $F_t$
all along the path from
$F_t$
all along the path from
![]() $F_0$
to
$F_0$
to
![]() $F_1$
, as follows:
$F_1$
, as follows:
where
![]() $\Delta t$
needs to be defined. The idea is that z always stays close to
$\Delta t$
needs to be defined. The idea is that z always stays close to
![]() $\zeta _t$
, the zero of
$\zeta _t$
, the zero of
![]() $F_t$
obtained by continuing
$F_t$
obtained by continuing
![]() $\zeta _0$
. To ensure correctness, the increment
$\zeta _0$
. To ensure correctness, the increment
![]() $\Delta t$
should be chosen small enough. But the bigger
$\Delta t$
should be chosen small enough. But the bigger
![]() $\Delta t$
is, the fewer iterations will be necessary, meaning a better complexity. The size of
$\Delta t$
is, the fewer iterations will be necessary, meaning a better complexity. The size of
![]() $\Delta t$
is typically controlled with, on the one hand, effective bounds on the variations of the zeros of
$\Delta t$
is typically controlled with, on the one hand, effective bounds on the variations of the zeros of
![]() $F_t$
as t changes, and on the other hand, effective bounds on the convergence of Newton’s iteration. The general principle to determine
$F_t$
as t changes, and on the other hand, effective bounds on the convergence of Newton’s iteration. The general principle to determine
![]() $\Delta t$
is the following, in very rough terms because a precise argument generally involves lengthy computations. The increment
$\Delta t$
is the following, in very rough terms because a precise argument generally involves lengthy computations. The increment
![]() $\Delta t$
should be small enough so that
$\Delta t$
should be small enough so that
![]() $\zeta _{t}$
is in the basin of attraction around
$\zeta _{t}$
is in the basin of attraction around
![]() $\zeta _{t+\Delta t}$
of Newton’s iteration for
$\zeta _{t+\Delta t}$
of Newton’s iteration for
![]() $F_{t+\Delta t}$
. This leads to the rule-of-thumb
$F_{t+\Delta t}$
. This leads to the rule-of-thumb
![]() $\| \Delta \zeta _t \| \rho (F_{t+\Delta t}, \zeta _{t+\Delta t}) \lesssim 1$
, where
$\| \Delta \zeta _t \| \rho (F_{t+\Delta t}, \zeta _{t+\Delta t}) \lesssim 1$
, where
![]() $\Delta \zeta _t = \zeta _{t+\Delta t} - \zeta _{t}$
and
$\Delta \zeta _t = \zeta _{t+\Delta t} - \zeta _{t}$
and
![]() $\rho (F_t, \zeta _t)$
is the inverse of the radius of the basin of attraction of Newton’s iteration. A condition that we can rewrite as
$\rho (F_t, \zeta _t)$
is the inverse of the radius of the basin of attraction of Newton’s iteration. A condition that we can rewrite as
 $$ \begin{align} \frac{1}{\Delta t} \gtrsim \rho(F_t, \zeta_t) \left\| \frac{\Delta \zeta_t}{\Delta t} \right\|,\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \frac{1}{\Delta t} \gtrsim \rho(F_t, \zeta_t) \left\| \frac{\Delta \zeta_t}{\Delta t} \right\|,\\[-15pt]\nonumber \end{align} $$
assuming that
The factor
![]() $\frac {\Delta \zeta _t}{\Delta t}$
is almost the derivative
$\frac {\Delta \zeta _t}{\Delta t}$
is almost the derivative
![]() $\dot \zeta _t$
of
$\dot \zeta _t$
of
![]() $\zeta _t$
with respect to t. It is generally bounded using a condition number
$\zeta _t$
with respect to t. It is generally bounded using a condition number
![]() $\mu (F_t, \zeta _t)$
, that is the largest variation of the zero
$\mu (F_t, \zeta _t)$
, that is the largest variation of the zero
![]() $\zeta _t$
after a perturbation of
$\zeta _t$
after a perturbation of
![]() $F_t$
in
$F_t$
in
![]() $\mathcal {H}$
, so that
$\mathcal {H}$
, so that
 $$ \begin{align} \left\| \frac{\Delta \zeta_t}{\Delta t} \right\| \simeq \| \dot \zeta_t \| \leqslant \mu(F_t, \zeta_t) \|\dot F_t\|,\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \left\| \frac{\Delta \zeta_t}{\Delta t} \right\| \simeq \| \dot \zeta_t \| \leqslant \mu(F_t, \zeta_t) \|\dot F_t\|,\\[-15pt]\nonumber \end{align} $$
where
![]() $\dot F_t$
(respectively,
$\dot F_t$
(respectively,
![]() $\dot \zeta _t$
) is the derivative of F (respectively,
$\dot \zeta _t$
) is the derivative of F (respectively,
![]() $\zeta _t$
) with respect to t, and the right-hand side is effectively computable. The parameter
$\zeta _t$
) with respect to t, and the right-hand side is effectively computable. The parameter
![]() $\rho (F_t, \zeta _t)$
is much deeper. Smale’s
$\rho (F_t, \zeta _t)$
is much deeper. Smale’s
![]() $\alpha $
-theory has been a preferred tool to deal with it in many complexity analyses. The number
$\alpha $
-theory has been a preferred tool to deal with it in many complexity analyses. The number
![]() $\gamma $
takes a prominent role in the theory and controls the convergence of Newton’s iteration [Reference Smale45]:
$\gamma $
takes a prominent role in the theory and controls the convergence of Newton’s iteration [Reference Smale45]:
![]() $\rho (F_t, \zeta _t) \lesssim \gamma (F_t, \zeta _t)$
(for the definition of
$\rho (F_t, \zeta _t) \lesssim \gamma (F_t, \zeta _t)$
(for the definition of
![]() $\gamma (F,\zeta )$
, e.g. see Equation (8) in Part I.) So we obtain the condition
$\gamma (F,\zeta )$
, e.g. see Equation (8) in Part I.) So we obtain the condition
that ensures the correctness of the algorithm. A rigorous argument requires a nice behaviour of both factors
![]() $\gamma (F_t, \zeta _t)$
and
$\gamma (F_t, \zeta _t)$
and
![]() $\mu (F_t, \zeta _t)$
as t varies, this is a crucial point, especially in view of the assumption (2.2). The factor
$\mu (F_t, \zeta _t)$
as t varies, this is a crucial point, especially in view of the assumption (2.2). The factor
![]() $\|\dot F_t\|$
is generally harmless; the factor
$\|\dot F_t\|$
is generally harmless; the factor
![]() $\mu (F_t, \zeta _t)$
is important, but the variations with respect to t are generally easy to handle; however, the variations of
$\mu (F_t, \zeta _t)$
is important, but the variations with respect to t are generally easy to handle; however, the variations of
![]() $\gamma (F_t, \zeta _t)$
are more delicate. This led [Reference Shub and Smale40] to consider the upper bound (called ‘higher-derivative estimate’)
$\gamma (F_t, \zeta _t)$
are more delicate. This led [Reference Shub and Smale40] to consider the upper bound (called ‘higher-derivative estimate’)
with the same
![]() $\mu $
as above, and the subsequent correctness condition
$\mu $
as above, and the subsequent correctness condition
Choosing at each iteration
![]() $\Delta t$
to be the largest possible value allowed by (2.6), we obtain a numerical continuation algorithm, with adaptive step length, whose number K of iterations is bounded, as shown first by [Reference Shub39], by
$\Delta t$
to be the largest possible value allowed by (2.6), we obtain a numerical continuation algorithm, with adaptive step length, whose number K of iterations is bounded, as shown first by [Reference Shub39], by
 $$ \begin{align} K \lesssim \int_0^1 \mu(F_t, \zeta_t)^2 \|\dot F_t\| \mathrm{d} t. \end{align} $$
$$ \begin{align} K \lesssim \int_0^1 \mu(F_t, \zeta_t)^2 \|\dot F_t\| \mathrm{d} t. \end{align} $$
It remains to choose the starting system
![]() $F_0$
, with a built-in zero
$F_0$
, with a built-in zero
![]() $\zeta _0$
, and the path from
$\zeta _0$
, and the path from
![]() $F_0$
to
$F_0$
to
![]() $F_1$
. For complexity analyses, the most common choice of path is a straight-line segment in the whole space of polynomial systems
$F_1$
. For complexity analyses, the most common choice of path is a straight-line segment in the whole space of polynomial systems
![]() $\mathcal {H}$
. For the choice of the starting system
$\mathcal {H}$
. For the choice of the starting system
![]() $F_0$
, [Reference Beltrán and Pardo6, Reference Beltrán and Pardo7] have shown that a Kostlan random system is a relevant choice and that there is a simple algorithm to sample a random system with a known zero. If
$F_0$
, [Reference Beltrán and Pardo6, Reference Beltrán and Pardo7] have shown that a Kostlan random system is a relevant choice and that there is a simple algorithm to sample a random system with a known zero. If
![]() $F_1$
is also a random Gaussian system, then all the intermediate systems
$F_1$
is also a random Gaussian system, then all the intermediate systems
![]() $F_t$
are also random Gaussian, and using (2.7), we obtain a bound, following Beltrán and Pardo, on the expected number of iterations in the numerical continuation from
$F_t$
are also random Gaussian, and using (2.7), we obtain a bound, following Beltrán and Pardo, on the expected number of iterations in the numerical continuation from
![]() $F_0$
to
$F_0$
to
![]() $F_1$
:
$F_1$
:
where
![]() $\zeta $
is a random zero of F. The dimension of
$\zeta $
is a random zero of F. The dimension of
![]() $\mathcal {H}$
is the number of coefficients in F, it is the input size. For n equations of degree
$\mathcal {H}$
is the number of coefficients in F, it is the input size. For n equations of degree
![]() ${D}$
in n variables, we compute
${D}$
in n variables, we compute
 $$ \begin{align} \dim \mathcal{H} = n \binom{n+{D}}{n}. \end{align} $$
$$ \begin{align} \dim \mathcal{H} = n \binom{n+{D}}{n}. \end{align} $$
This is larger than any polynomial in n and
![]() ${D}$
(as n and
${D}$
(as n and
![]() ${D}$
go to
${D}$
go to
![]() $\infty $
), but is much smaller than
$\infty $
), but is much smaller than
![]() ${D}^n$
, the generic number of solutions of such a system. The cost of an iteration (computing the step size and performing one Newton iteration) is also bounded by the input size. So we have an algorithm whose average complexity is polynomial in the input size. This is a major complexity result because it breaks the
${D}^n$
, the generic number of solutions of such a system. The cost of an iteration (computing the step size and performing one Newton iteration) is also bounded by the input size. So we have an algorithm whose average complexity is polynomial in the input size. This is a major complexity result because it breaks the
![]() $\operatorname {poly}({D}^n)$
barrier set by algorithms that compute all solutions simultaneously. However, the bound (2.8) on the expected number of iterations is still much larger than what heuristic algorithms seem to achieve.
$\operatorname {poly}({D}^n)$
barrier set by algorithms that compute all solutions simultaneously. However, the bound (2.8) on the expected number of iterations is still much larger than what heuristic algorithms seem to achieve.
A first idea to design a faster algorithm would be to search for a better continuation path in order to lower the right-hand side in (2.7). Such paths do exist and can give a
![]() $\operatorname {poly}(n,{D})$
bound on
$\operatorname {poly}(n,{D})$
bound on
![]() $\mathbb {E}[K]$
[Reference Beltrán and Shub9]. Unfortunately, their computation requires, in the current state of the art, to solve the target system first. A second approach focuses on sharpening the correctness condition (2.6), that is, on making bigger continuation steps. The comparison of (2.6) with heuristics shows that there is room for improvement [Reference Beltrán and Leykin4, Reference Beltrán and Leykin5]. In devising this condition, two inequalities are too generous. Firstly, Inequality (2.3) bounds the variation of
$\mathbb {E}[K]$
[Reference Beltrán and Shub9]. Unfortunately, their computation requires, in the current state of the art, to solve the target system first. A second approach focuses on sharpening the correctness condition (2.6), that is, on making bigger continuation steps. The comparison of (2.6) with heuristics shows that there is room for improvement [Reference Beltrán and Leykin4, Reference Beltrán and Leykin5]. In devising this condition, two inequalities are too generous. Firstly, Inequality (2.3) bounds the variation of
![]() $\zeta _t$
by the worst-case variation. The average worst-case variation can only grow with the dimension of the parameter space,
$\zeta _t$
by the worst-case variation. The average worst-case variation can only grow with the dimension of the parameter space,
![]() $\dim \mathcal {H}$
, and it turns out to be much bigger than the average value of
$\dim \mathcal {H}$
, and it turns out to be much bigger than the average value of
![]() $\|\dot \zeta _t\|$
, which is
$\|\dot \zeta _t\|$
, which is
![]() $\operatorname {poly}(n,{D})$
. This was successfully exploited by [Reference Armentano, Beltrán, Bürgisser, Cucker and Shub1] to obtain the bound
$\operatorname {poly}(n,{D})$
. This was successfully exploited by [Reference Armentano, Beltrán, Bürgisser, Cucker and Shub1] to obtain the bound
![]() $\mathbb {E}[K] \lesssim \sqrt {\dim \mathcal {H}}$
for random Gaussian systems. They used straight-line continuation paths but a finer computation of the step size. The other inequality that turns out to be too coarse is (2.5): the higher derivatives need to be handled more accurately.
$\mathbb {E}[K] \lesssim \sqrt {\dim \mathcal {H}}$
for random Gaussian systems. They used straight-line continuation paths but a finer computation of the step size. The other inequality that turns out to be too coarse is (2.5): the higher derivatives need to be handled more accurately.
2.2 Rigid continuation paths
In Part I, we introduced rigid continuation paths to obtain, in the case of random Gaussian systems, the bound
![]() $\mathbb {E}[K] \leqslant \operatorname {poly}(n, {D})$
. To solve a polynomial system
$\mathbb {E}[K] \leqslant \operatorname {poly}(n, {D})$
. To solve a polynomial system
![]() $F = (f_1,\dotsc ,f_n) \in \mathcal {H}$
in
$F = (f_1,\dotsc ,f_n) \in \mathcal {H}$
in
![]() $n+1$
homogeneous variables, we consider continuation paths having the form
$n+1$
homogeneous variables, we consider continuation paths having the form
where
![]() $u_1(t),\dotsc ,u_n(t) \in U(n+1)$
are unitary matrices depending on the parameter t, with
$u_1(t),\dotsc ,u_n(t) \in U(n+1)$
are unitary matrices depending on the parameter t, with
![]() $u_i(T)=\operatorname {id}$
, for some
$u_i(T)=\operatorname {id}$
, for some
![]() $T> 0$
. We could choose
$T> 0$
. We could choose
![]() $T = 1$
, but instead, we impose
$T = 1$
, but instead, we impose
![]() $\| \dot u_1 \|^2 + \dotsb + \|\dot u_n\|^2 \leqslant 1$
(the path is called 1-Lipschitz continuous), following Part I. Note that we can choose
$\| \dot u_1 \|^2 + \dotsb + \|\dot u_n\|^2 \leqslant 1$
(the path is called 1-Lipschitz continuous), following Part I. Note that we can choose
![]() $T\leqslant 4n$
(see I, Section 4.3.2). The parameter space for the numerical continuation is not
$T\leqslant 4n$
(see I, Section 4.3.2). The parameter space for the numerical continuation is not
![]() $\mathcal {H}$
anymore but
$\mathcal {H}$
anymore but
![]() $U(n+1)^n$
, denoted
$U(n+1)^n$
, denoted
![]() ${\mathcal {U}}$
, a real manifold of dimension
${\mathcal {U}}$
, a real manifold of dimension
![]() $n^3$
. For
$n^3$
. For
![]() ${\mathbf u} = (u_1,\dotsc ,u_n) \in {\mathcal {U}}$
and
${\mathbf u} = (u_1,\dotsc ,u_n) \in {\mathcal {U}}$
and
![]() $F \in \mathcal {H}$
, we denote
$F \in \mathcal {H}$
, we denote
We developed in this setting an analogue of Beltrán and Pardo’s algorithm. Firstly, we sample uniformly
![]() ${\mathbf v} \in {\mathcal {U}}$
together with a zero of the polynomial system
${\mathbf v} \in {\mathcal {U}}$
together with a zero of the polynomial system
![]() ${\mathbf v} \cdot F$
. The same kind of construction as in the Gaussian case makes it possible to perform this operation without solving any polynomial system (only n univariate equations). Then, we construct a 1-Lipschitz-continuous path
${\mathbf v} \cdot F$
. The same kind of construction as in the Gaussian case makes it possible to perform this operation without solving any polynomial system (only n univariate equations). Then, we construct a 1-Lipschitz-continuous path
![]() $({\mathbf u}_t)_{t\in [0,T]}$
in
$({\mathbf u}_t)_{t\in [0,T]}$
in
![]() ${\mathcal {U}}$
between
${\mathcal {U}}$
between
![]() ${\mathbf v}$
and the unit
${\mathbf v}$
and the unit
![]() $\mathbf {1}_{\mathcal {U}}$
in
$\mathbf {1}_{\mathcal {U}}$
in
![]() ${\mathcal {U}}$
, and perform numerical continuation using
${\mathcal {U}}$
, and perform numerical continuation using
![]() $F_t\, {\stackrel {.}{=}}\, {\mathbf u}_t \cdot F$
. The general strategy sketched in Section 2.1 applies, but the rigid setting features important particularities. The most salient of them is the average conditioning, that is, the average worst-case variation of
$F_t\, {\stackrel {.}{=}}\, {\mathbf u}_t \cdot F$
. The general strategy sketched in Section 2.1 applies, but the rigid setting features important particularities. The most salient of them is the average conditioning, that is, the average worst-case variation of
![]() $\zeta _t$
with respect to infinitesimal variations of
$\zeta _t$
with respect to infinitesimal variations of
![]() ${\mathbf u}_t$
. It is now
${\mathbf u}_t$
. It is now
![]() $\operatorname {poly}(n)$
(see I, Section 3.2), mostly because the dimension of the parameter space is
$\operatorname {poly}(n)$
(see I, Section 3.2), mostly because the dimension of the parameter space is
![]() $\operatorname {poly}(n)$
. Besides, the way the continuation path is designed preserves the geometry of the equations. This is reflected in a better behaviour of
$\operatorname {poly}(n)$
. Besides, the way the continuation path is designed preserves the geometry of the equations. This is reflected in a better behaviour of
![]() $\gamma (F_t, \zeta _t)$
as t varies, which makes it possible to use an upper bound much finer than (2.5), that we called the split
$\gamma (F_t, \zeta _t)$
as t varies, which makes it possible to use an upper bound much finer than (2.5), that we called the split
![]() $\gamma $
number. In the case of a random Gaussian input, we obtained in the end a
$\gamma $
number. In the case of a random Gaussian input, we obtained in the end a
![]() $\operatorname {poly}(n,{D})$
bound on the average number of iterations for performing numerical continuation along rigid paths.
$\operatorname {poly}(n,{D})$
bound on the average number of iterations for performing numerical continuation along rigid paths.
2.3 The split
 $\gamma $
number
$\gamma $
number
Computing a good upper bound of the
![]() $\gamma $
number is the key to make bigger continuation steps. We recall, here, the upper bound introduced in Part I. The incidence condition number of
$\gamma $
number is the key to make bigger continuation steps. We recall, here, the upper bound introduced in Part I. The incidence condition number of
![]() $F = (f_1,\dotsc ,f_n)$
at z is
$F = (f_1,\dotsc ,f_n)$
at z is
where
![]() $\dagger $
denotes the Moore–Penrose pseudoinverse [Reference Bürgisser and Cucker15, p. 17] and
$\dagger $
denotes the Moore–Penrose pseudoinverse [Reference Bürgisser and Cucker15, p. 17] and
![]() $F_z$
the normalised system
$F_z$
the normalised system
 $$ \begin{align} F_z\, {\stackrel{.}{=}}\, \left( \frac{f_1}{\|\mathrm{d} _z f_1\|},\dotsc, \frac{f_n}{\|\mathrm{d} _z f_n\|} \right). \end{align} $$
$$ \begin{align} F_z\, {\stackrel{.}{=}}\, \left( \frac{f_1}{\|\mathrm{d} _z f_1\|},\dotsc, \frac{f_n}{\|\mathrm{d} _z f_n\|} \right). \end{align} $$
When z is a zero of F, this quantity depends only on the angles formed by the tangent spaces at z of the n hypersurfaces
![]() $\left \{f_i=0 \right \}$
(see I, Sections 2.1 and 3 for more details). It is closely related to the intersection condition number introduced by [Reference Bürgisser12]. In the context of rigid paths, it is also the natural condition number: the variation of a zero
$\left \{f_i=0 \right \}$
(see I, Sections 2.1 and 3 for more details). It is closely related to the intersection condition number introduced by [Reference Bürgisser12]. In the context of rigid paths, it is also the natural condition number: the variation of a zero
![]() $\zeta $
of a polynomial system
$\zeta $
of a polynomial system
![]() ${\mathbf u} \cdot F$
under a perturbation of
${\mathbf u} \cdot F$
under a perturbation of
![]() ${\mathbf u}$
is bounded by
${\mathbf u}$
is bounded by
![]() $\kappa ({\mathbf u} \cdot F,\zeta )$
(Lemma I.16). Moreover, F being fixed, if
$\kappa ({\mathbf u} \cdot F,\zeta )$
(Lemma I.16). Moreover, F being fixed, if
![]() ${\mathbf u} \in {\mathcal {U}}$
is uniformly distributed and if
${\mathbf u} \in {\mathcal {U}}$
is uniformly distributed and if
![]() $\zeta $
is a uniformly distributed zero of
$\zeta $
is a uniformly distributed zero of
![]() ${\mathbf u} \cdot F$
, then
${\mathbf u} \cdot F$
, then
![]() $\mathbb {E}[\kappa ({\mathbf u}\cdot F, \zeta )^2] \leqslant 6n^2$
(Proposition I.17).
$\mathbb {E}[\kappa ({\mathbf u}\cdot F, \zeta )^2] \leqslant 6n^2$
(Proposition I.17).
The split
![]() $\gamma $
number (see I, Section 2.5 for more details) is defined as
$\gamma $
number (see I, Section 2.5 for more details) is defined as
It tightly upper bounds
![]() $\gamma (F, z)$
in that (Theorem I.13)
$\gamma (F, z)$
in that (Theorem I.13)

Whereas
![]() $\gamma (F, z)$
does not behave nicely as a function of F, the split variant behaves well in the rigid setting: F being fixed, the function
$\gamma (F, z)$
does not behave nicely as a function of F, the split variant behaves well in the rigid setting: F being fixed, the function
![]() ${\mathcal {U}} \times \mathbb {P}^n \to \mathbb {R}$
,
${\mathcal {U}} \times \mathbb {P}^n \to \mathbb {R}$
,
![]() $({\mathbf u}, z) \mapsto \hat {\gamma }({\mathbf u} \cdot F, z)^{-1}$
is 13-Lipschitz continuous (Lemma I.21).Footnote
6
This makes it possible to perform numerical continuation. Note that we need not compute
$({\mathbf u}, z) \mapsto \hat {\gamma }({\mathbf u} \cdot F, z)^{-1}$
is 13-Lipschitz continuous (Lemma I.21).Footnote
6
This makes it possible to perform numerical continuation. Note that we need not compute
![]() $\gamma $
exactly, an estimate within a fixed ratio is enough. For computational purposes, we rather use the variant
$\gamma $
exactly, an estimate within a fixed ratio is enough. For computational purposes, we rather use the variant
![]() $\gamma _{\mathrm {Frob}}$
, defined in (1.3), in which the operator norm is replaced by a Hermitian norm. It induces a split
$\gamma _{\mathrm {Frob}}$
, defined in (1.3), in which the operator norm is replaced by a Hermitian norm. It induces a split
![]() $\gamma _{\mathrm {Frob}}$
number
$\gamma _{\mathrm {Frob}}$
number
as in (2.14). Algorithm 1 describes the computation of an approximate zero of a polynomial system
![]() ${\mathbf u} \cdot F$
, given a zero of some
${\mathbf u} \cdot F$
, given a zero of some
![]() ${\mathbf v}\cdot F$
(it is the same as Algorithm I.2, with
${\mathbf v}\cdot F$
(it is the same as Algorithm I.2, with
![]() $\hat {\gamma }_{\mathrm {Frob}}$
for g and
$\hat {\gamma }_{\mathrm {Frob}}$
for g and
![]() $C=15$
, which gives the constant 240 that appears in Algorithm 1). As an analogue of (2.7), Theorem I.23 bounds the number K of continuation steps performed by Algorithm 1 as an integral over the continuation path:
$C=15$
, which gives the constant 240 that appears in Algorithm 1). As an analogue of (2.7), Theorem I.23 bounds the number K of continuation steps performed by Algorithm 1 as an integral over the continuation path:
 $$ \begin{align} K \leqslant 325 \int_0^T \kappa({\mathbf w}_t\cdot F, \zeta_t) \hat \gamma_{\mathrm{Frob}}({\mathbf w}_t\cdot F, \zeta_t) \mathrm{d} t. \end{align} $$
$$ \begin{align} K \leqslant 325 \int_0^T \kappa({\mathbf w}_t\cdot F, \zeta_t) \hat \gamma_{\mathrm{Frob}}({\mathbf w}_t\cdot F, \zeta_t) \mathrm{d} t. \end{align} $$
Based on this bound, we obtained in Part I the following average analysis.
Let
![]() $F = (f_1,\dotsc ,f_n) \in {\mathcal {H}}$
be a square-free polynomial system. Then, for uniformly random
$F = (f_1,\dotsc ,f_n) \in {\mathcal {H}}$
be a square-free polynomial system. Then, for uniformly random
![]() ${\mathbf u},{\mathbf v} \in {\mathcal {U}}$
and a uniformly random zero
${\mathbf u},{\mathbf v} \in {\mathcal {U}}$
and a uniformly random zero
![]() $\zeta \in {{\mathbb {P}}^n}$
of
$\zeta \in {{\mathbb {P}}^n}$
of
![]() ${\mathbf v}\cdot F$
, Algorithm 1 terminates almost surely and outputs an approximate zero of
${\mathbf v}\cdot F$
, Algorithm 1 terminates almost surely and outputs an approximate zero of
![]() ${\mathbf u}\cdot F$
. Moreover, the number K of continuation steps it performs satisfies
${\mathbf u}\cdot F$
. Moreover, the number K of continuation steps it performs satisfies
![]() ${\mathbb {E}}[K] \leqslant 9000 n^3\,\Gamma (F)$
(Theorem I.27 with
${\mathbb {E}}[K] \leqslant 9000 n^3\,\Gamma (F)$
(Theorem I.27 with
![]() $\mathfrak g_i = {\gamma _{\mathrm {Frob}}}$
and
$\mathfrak g_i = {\gamma _{\mathrm {Frob}}}$
and
![]() $C'=5$
—by Lemma I.31—which multiplies the constant 1,800 in its statement). Here,
$C'=5$
—by Lemma I.31—which multiplies the constant 1,800 in its statement). Here,
![]() $\Gamma (F)$
denotes the crucial parameter introduced in (1.6).
$\Gamma (F)$
denotes the crucial parameter introduced in (1.6).
In case we cannot compute
![]() $\gamma _{\mathrm {Frob}}$
exactly, but instead an upper bound A, such that
$\gamma _{\mathrm {Frob}}$
exactly, but instead an upper bound A, such that
![]() $\gamma _{\mathrm {Frob}} \leqslant A \leqslant M \gamma _{\mathrm {Frob}}$
, for some fixed
$\gamma _{\mathrm {Frob}} \leqslant A \leqslant M \gamma _{\mathrm {Frob}}$
, for some fixed
![]() $M \geqslant 1$
, the algorithm works as well, but the bound on the average number of continuation steps is multiplied by M (see Remark I.28):
$M \geqslant 1$
, the algorithm works as well, but the bound on the average number of continuation steps is multiplied by M (see Remark I.28):
Remark 2.1. It is not completely clear for which systems F does
![]() $\Gamma (F)$
take finite or infinite value. Since
$\Gamma (F)$
take finite or infinite value. Since
![]() $\Gamma (F)^2=\Gamma (f_1)^2+\dotsb +\Gamma (f_n)^2$
, it suffices to look only at
$\Gamma (F)^2=\Gamma (f_1)^2+\dotsb +\Gamma (f_n)^2$
, it suffices to look only at
![]() $\Gamma (f)$
for some homogeneous polynomial
$\Gamma (f)$
for some homogeneous polynomial
![]() $f\in \mathbb {C}[z_0,\dotsc ,z_n]$
. Let
$f\in \mathbb {C}[z_0,\dotsc ,z_n]$
. Let
![]() $X= \left \{ \zeta \in \mathbb {P}^n \mathrel {}\middle |\mathrel {} f(\zeta ) = 0 \right \}$
and
$X= \left \{ \zeta \in \mathbb {P}^n \mathrel {}\middle |\mathrel {} f(\zeta ) = 0 \right \}$
and
![]() $\Sigma = \left \{ \zeta \in X\mathrel {}\middle |\mathrel {} \mathrm {d} _{\zeta } f = 0 \right \}$
be its singular locus. If
$\Sigma = \left \{ \zeta \in X\mathrel {}\middle |\mathrel {} \mathrm {d} _{\zeta } f = 0 \right \}$
be its singular locus. If
![]() $\Sigma = \varnothing $
, then
$\Sigma = \varnothing $
, then
![]() $x\mapsto \gamma (f, x)$
is continuous, hence, bounded on the compact set X, and it follows that
$x\mapsto \gamma (f, x)$
is continuous, hence, bounded on the compact set X, and it follows that
![]() $\Gamma (f) < \infty $
. In the case where
$\Gamma (f) < \infty $
. In the case where
![]() $\Sigma $
has codimension 1 or 0 in X, we can show that
$\Sigma $
has codimension 1 or 0 in X, we can show that
![]() $\Gamma (f) = \infty $
. But the general situation is not clear. In particular, it would be interesting to interpret
$\Gamma (f) = \infty $
. But the general situation is not clear. In particular, it would be interesting to interpret
![]() $1/\Gamma (f)$
as the distance to some set of polynomials.
$1/\Gamma (f)$
as the distance to some set of polynomials.
To obtain an interesting complexity result for a given class of unitarily invariant distributions of polynomial systems F, based on numerical continuation along rigid paths and Inequality (2.18), we need, firstly, to specify how to compute or approximate
![]() $\gamma _{\mathrm {Frob}}$
at a reasonable cost, and secondly, to estimate the expectation of
$\gamma _{\mathrm {Frob}}$
at a reasonable cost, and secondly, to estimate the expectation of
![]() $\Gamma (F)$
over F. For the application to dense Gaussian systems, considered in Part I,
$\Gamma (F)$
over F. For the application to dense Gaussian systems, considered in Part I,
![]() $\gamma _{\mathrm {Frob}}$
is computed directly, using the monomial representation of the system to compute all higher derivatives, and the estimation of
$\gamma _{\mathrm {Frob}}$
is computed directly, using the monomial representation of the system to compute all higher derivatives, and the estimation of
![]() $\Gamma (F)$
is mostly standard. Using the monomial representation is not efficient anymore in the black-box model. We will rely instead on a probabilistic estimation of
$\Gamma (F)$
is mostly standard. Using the monomial representation is not efficient anymore in the black-box model. We will rely instead on a probabilistic estimation of
![]() $\gamma _{\mathrm {Frob}}$
, within a factor
$\gamma _{\mathrm {Frob}}$
, within a factor
![]() $\operatorname {poly}(n, {D})$
. However, this estimation may fail with small probability, compromising the correctness of the result.
$\operatorname {poly}(n, {D})$
. However, this estimation may fail with small probability, compromising the correctness of the result.
3 Fast numerical continuation for black-box functions
3.1 Weyl norm
We recall, here, how to characterise the Weyl norm of a homogeneous polynomial as an expectation, which is a key observation behind Algorithm GammaProb to approximate
![]() $\gamma _{\mathrm {Frob}}(f, z)$
by random sampling.
$\gamma _{\mathrm {Frob}}(f, z)$
by random sampling.
Let
![]() $f \in \mathbb {C}[z_0,\dotsc ,z_n]$
be a homogeneous polynomial of degree
$f \in \mathbb {C}[z_0,\dotsc ,z_n]$
be a homogeneous polynomial of degree
![]() ${D}> 0$
. In the monomial basis, f decomposes as
${D}> 0$
. In the monomial basis, f decomposes as
![]() $\sum _\alpha c_\alpha z^\alpha $
, where
$\sum _\alpha c_\alpha z^\alpha $
, where
![]() $\alpha = (\alpha _0,\dotsc ,\alpha _n)$
is a multi-index. The Weyl norm of f is defined as
$\alpha = (\alpha _0,\dotsc ,\alpha _n)$
is a multi-index. The Weyl norm of f is defined as
 $$ \begin{align} \|f\|_W^2\, {\stackrel{.}{=}} \,\sum_\alpha \frac{\alpha_0! \dotsb \alpha_n!}{{D}!} {\left| {c_\alpha} \right|}^2. \end{align} $$
$$ \begin{align} \|f\|_W^2\, {\stackrel{.}{=}} \,\sum_\alpha \frac{\alpha_0! \dotsb \alpha_n!}{{D}!} {\left| {c_\alpha} \right|}^2. \end{align} $$
The following statement seems to be classical.
Lemma 3.1. Let f be a homogeneous polynomial of degree
![]() ${D}$
.
${D}$
.
-
(i) For a uniformly distributed w in the Euclidean unit ball of
 $\mathbb {C}^{n+1}$
, we have
$\mathbb {C}^{n+1}$
, we have  $$\begin{align*}\|f\|_W^2 = \binom{n+1+{D}}{{D}} \mathbb{E} \left[ {\left| {f(w)} \right|}^2 \right]. \end{align*}$$
$$\begin{align*}\|f\|_W^2 = \binom{n+1+{D}}{{D}} \mathbb{E} \left[ {\left| {f(w)} \right|}^2 \right]. \end{align*}$$
-
(ii) For a uniformly distributed z in the unit sphere of
 $\mathbb C^{n+1}$
, we have
$\mathbb C^{n+1}$
, we have  $$\begin{align*}\|f\|_W^2 = \binom{n+{D}}{{D}} \mathbb{E} \left[ {\left| {f(z)} \right|}^2 \right]. \end{align*}$$
$$\begin{align*}\|f\|_W^2 = \binom{n+{D}}{{D}} \mathbb{E} \left[ {\left| {f(z)} \right|}^2 \right]. \end{align*}$$
Proof. Let H be the space of homogeneous polynomials of degree
![]() ${D}$
in
${D}$
in
![]() $z_0,\dotsc ,z_n$
. Both left-hand and right-hand sides of the first stated equality define a norm on H coming from a Hermitian inner product. The monomial basis is orthogonal for both: this is obvious for Weyl’s norm. For the
$z_0,\dotsc ,z_n$
. Both left-hand and right-hand sides of the first stated equality define a norm on H coming from a Hermitian inner product. The monomial basis is orthogonal for both: this is obvious for Weyl’s norm. For the
![]() $L^2$
-norm, this is [Reference Rudin37, Proposition 1.4.8]. So it only remains to check that the claim holds true when f is a monomial. By [Reference Rudin37, Proposition 1.4.9(2)], if
$L^2$
-norm, this is [Reference Rudin37, Proposition 1.4.8]. So it only remains to check that the claim holds true when f is a monomial. By [Reference Rudin37, Proposition 1.4.9(2)], if
![]() $w^{\alpha } = w_0^{\alpha _0}\cdots w_n^{\alpha _n}$
is a monomial of degree
$w^{\alpha } = w_0^{\alpha _0}\cdots w_n^{\alpha _n}$
is a monomial of degree
![]() ${D}$
, we have
${D}$
, we have
which is the claim. The second equality follows similarly from [Reference Rudin37, Proposition 1.4.9(1)].
The following inequalities will also be useful.
Lemma 3.2. For any homogeneous polynomial
![]() $f \in \mathbb {C}[z_0,\dotsc ,z_n]$
of degree
$f \in \mathbb {C}[z_0,\dotsc ,z_n]$
of degree
![]() ${D}$
,
${D}$
,
 $$ \begin{align*} \binom{n+{D}}{{D}}^{-1} \|f\|^2_W \leqslant \max_{z\in {\mathbb{S}}(\mathbb{C}^{n+1})} {\left| {f(z)} \right|}^2 = \max_{w\in B(\mathbb{C}^{n+1})} {\left| {f(w)} \right|}^2 \leqslant \|f\|_W^2. \end{align*} $$
$$ \begin{align*} \binom{n+{D}}{{D}}^{-1} \|f\|^2_W \leqslant \max_{z\in {\mathbb{S}}(\mathbb{C}^{n+1})} {\left| {f(z)} \right|}^2 = \max_{w\in B(\mathbb{C}^{n+1})} {\left| {f(w)} \right|}^2 \leqslant \|f\|_W^2. \end{align*} $$
Proof. The first inequality follows directly from the second equality of Lemma 3.1. It is clear that the maximum is reached on the boundary. For the second inequality, we may assume (because of the unitary invariance of
![]() $\|-\|_W$
) that the maximum of
$\|-\|_W$
) that the maximum of
![]() $|f|$
on the unit ball is reached at
$|f|$
on the unit ball is reached at
![]() $(1,0,\dotsc ,0)$
. Besides, the coefficient
$(1,0,\dotsc ,0)$
. Besides, the coefficient
![]() $c_{{D},0,\dotsc ,0}$
of f is
$c_{{D},0,\dotsc ,0}$
of f is
![]() $f(1,0,\dotsc ,0)$
. Therefore,
$f(1,0,\dotsc ,0)$
. Therefore,
3.2 Probabilistic evaluation of the gamma number
The main reason for introducing the Frobenius norm in the
![]() $\gamma $
number, instead of the usual operator norm, is the equality (Lemma I.30)
$\gamma $
number, instead of the usual operator norm, is the equality (Lemma I.30)
where
![]() $\|f(z+\bullet )_k\|_W$
is the Weyl norm of the homogeneous component of degree k of the shifted polynomial
$\|f(z+\bullet )_k\|_W$
is the Weyl norm of the homogeneous component of degree k of the shifted polynomial
![]() $x\mapsto f(z+x)$
. It follows that
$x\mapsto f(z+x)$
. It follows that
 $$ \begin{align} \gamma_{\mathrm{Frob}}(f, z) = \sup_{k\geqslant 2} \left( \left\| \mathrm{d} _zf \right\|^{-1} \|f(z+\bullet)_k\|_W \right)^{\frac{1}{k-1}}.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \gamma_{\mathrm{Frob}}(f, z) = \sup_{k\geqslant 2} \left( \left\| \mathrm{d} _zf \right\|^{-1} \|f(z+\bullet)_k\|_W \right)^{\frac{1}{k-1}}.\\[-15pt]\nonumber \end{align} $$
This equality opens up interesting ways for estimating
![]() $\gamma _{\mathrm {Frob}}$
, and, therefore,
$\gamma _{\mathrm {Frob}}$
, and, therefore,
![]() $\gamma $
. We used it to compute
$\gamma $
. We used it to compute
![]() $\gamma _{\mathrm {Frob}}$
efficiently when f is a dense polynomial given in the monomial basis (see Section I.4.3.3). In that context, we would compute the shift
$\gamma _{\mathrm {Frob}}$
efficiently when f is a dense polynomial given in the monomial basis (see Section I.4.3.3). In that context, we would compute the shift
![]() $f(z+\bullet )$
in the same monomial basis in quasilinear time as
$f(z+\bullet )$
in the same monomial basis in quasilinear time as
![]() $\min (n,{D})\to \infty $
. From there, the quantities
$\min (n,{D})\to \infty $
. From there, the quantities
![]() $ \|f(z+\bullet )_k\|_W$
can be computed in linear time. In the black-box model, however, the monomial expansions (of either f or
$ \|f(z+\bullet )_k\|_W$
can be computed in linear time. In the black-box model, however, the monomial expansions (of either f or
![]() $f(z+\bullet )$
) cannot fit into a
$f(z+\bullet )$
) cannot fit into a
![]() $\operatorname {poly}(n, {D}) L(f)$
complexity bound, because the number of monomials of degree
$\operatorname {poly}(n, {D}) L(f)$
complexity bound, because the number of monomials of degree
![]() ${D}$
in
${D}$
in
![]() $n+1$
variables is not
$n+1$
variables is not
![]() $\operatorname {poly}(n,{D})$
. Nonetheless, we can obtain a good enough approximation of
$\operatorname {poly}(n,{D})$
. Nonetheless, we can obtain a good enough approximation of
![]() $\|f(z+\bullet )_k\|_W$
with a few evaluations but a nonzero probability of failure. This is the purpose of Algorithm 2, which we analyse in the next theorem.
$\|f(z+\bullet )_k\|_W$
with a few evaluations but a nonzero probability of failure. This is the purpose of Algorithm 2, which we analyse in the next theorem.
Theorem 3.3. Given
![]() $f \in \mathbb {C}[x_0,\dotsc ,x_n]$
as a black-box function, an upper bound
$f \in \mathbb {C}[x_0,\dotsc ,x_n]$
as a black-box function, an upper bound
![]() ${D}$
on its degree, a point
${D}$
on its degree, a point
![]() $z \in \mathbb {C}^{n+1}$
and some
$z \in \mathbb {C}^{n+1}$
and some
![]() $\varepsilon> 0$
, Algorithm 2 (GammaProb) computes some
$\varepsilon> 0$
, Algorithm 2 (GammaProb) computes some
![]() $\Gamma \geqslant 0$
, such that
$\Gamma \geqslant 0$
, such that
with probability at least
![]() $1-\varepsilon $
, using
$1-\varepsilon $
, using
![]() $O\left ( {D} \log \left (\frac {D}\varepsilon \right ) (L(f) + n + \log {D})\right )$
operations.
$O\left ( {D} \log \left (\frac {D}\varepsilon \right ) (L(f) + n + \log {D})\right )$
operations.
Moreover, for any
![]() $t \ge 1$
,
$t \ge 1$
,
 $$\begin{align*}\mathbb{P} \left[ \Gamma \leqslant \frac{\gamma_{\mathrm{Frob}}(f, z)}{t} \right] \leqslant \varepsilon ^{1+ \frac12 \log_2 t}.\\[-15pt] \end{align*}$$
$$\begin{align*}\mathbb{P} \left[ \Gamma \leqslant \frac{\gamma_{\mathrm{Frob}}(f, z)}{t} \right] \leqslant \varepsilon ^{1+ \frac12 \log_2 t}.\\[-15pt] \end{align*}$$

Note that we currently do not know how to estimate
![]() $\gamma _{\mathrm {Frob}}$
within an arbitrarily small factor. The key in Theorem 3.3 is to write each
$\gamma _{\mathrm {Frob}}$
within an arbitrarily small factor. The key in Theorem 3.3 is to write each
![]() $\|f(z+\bullet )_k\|_W^2$
as an expectation (this is classical, see Section 3.1) and to approximate it by sampling (there are some obstacles). We assume that
$\|f(z+\bullet )_k\|_W^2$
as an expectation (this is classical, see Section 3.1) and to approximate it by sampling (there are some obstacles). We assume that
![]() $z = 0$
by changing f to
$z = 0$
by changing f to
![]() $f(z + \bullet )$
, which is harmless because the evaluation complexity is changed to
$f(z + \bullet )$
, which is harmless because the evaluation complexity is changed to
![]() $L(f) + O(n)$
. Furthermore, the homogeneous components
$L(f) + O(n)$
. Furthermore, the homogeneous components
![]() $f_k$
of f are accessible as black-box functions; this is the content of the next lemma.
$f_k$
of f are accessible as black-box functions; this is the content of the next lemma.
Lemma 3.4. Given
![]() $w \in {\mathbb {C}}^{n+1}$
, one can compute
$w \in {\mathbb {C}}^{n+1}$
, one can compute
![]() $f_0(w),\dotsc ,f_{D}(w)$
, with
$f_0(w),\dotsc ,f_{D}(w)$
, with
![]() $O({D} (L(f) + n + \log {D}))$
arithmetic operations.
$O({D} (L(f) + n + \log {D}))$
arithmetic operations.
Proof. We first compute all
![]() $f(\xi ^i w)$
, for
$f(\xi ^i w)$
, for
![]() $0\leqslant i \leqslant {D}$
for some primitive root of unity
$0\leqslant i \leqslant {D}$
for some primitive root of unity
![]() $\xi $
of order
$\xi $
of order
![]() ${D}+1$
. This takes
${D}+1$
. This takes
![]() $({D}+1) L(f) + O({D} n)$
arithmetic operations. Since
$({D}+1) L(f) + O({D} n)$
arithmetic operations. Since
 $$ \begin{align} f(\xi^i w) = \sum_{k=0}^{D} \xi^{i k} f_k(w), \end{align} $$
$$ \begin{align} f(\xi^i w) = \sum_{k=0}^{D} \xi^{i k} f_k(w), \end{align} $$
we recover the numbers
![]() $f_k(w)$
with the inverse Fourier transform,
$f_k(w)$
with the inverse Fourier transform,
 $$ \begin{align} f_k(w) = \frac{1}{{D}+1}\sum_{i = 0}^{D} \xi^{-ik} f(\xi^i w). \end{align} $$
$$ \begin{align} f_k(w) = \frac{1}{{D}+1}\sum_{i = 0}^{D} \xi^{-ik} f(\xi^i w). \end{align} $$
We may assume that
![]() ${D}$
is a power of two (
${D}$
is a power of two (
![]() ${D}$
is only required to be an upper bound on the degree of f), and the fast Fourier transform algorithm has an
${D}$
is only required to be an upper bound on the degree of f), and the fast Fourier transform algorithm has an
![]() $O({D}\log {D})$
complexity bound to recover the
$O({D}\log {D})$
complexity bound to recover the
![]() $f_k(z)$
(with slightly more complicated formulas, we can also use
$f_k(z)$
(with slightly more complicated formulas, we can also use
![]() $\xi = 2$
to keep close to the pure BSS model).
$\xi = 2$
to keep close to the pure BSS model).
We now focus on the probabilistic estimation of
![]() $\|f_k\|_W$
via a few evaluations of
$\|f_k\|_W$
via a few evaluations of
![]() $f_k$
. Let
$f_k$
. Let
![]() $B\, {\stackrel {.}{=}}\, {B({\mathbb {C}}^{n+1})}$
denote the Euclidean unit ball in
$B\, {\stackrel {.}{=}}\, {B({\mathbb {C}}^{n+1})}$
denote the Euclidean unit ball in
![]() $\mathbb {C}^{n+1}$
, and let
$\mathbb {C}^{n+1}$
, and let
![]() $w \in B$
be a uniformly distributed random variable. By Lemma 3.1, we have
$w \in B$
be a uniformly distributed random variable. By Lemma 3.1, we have
 $$ \begin{align} \|f_k\|_W^2 = \binom{n+1+k}{k} {\mathbb{E}} \left[ {\left| {f_k(w)} \right|}^2 \right]. \end{align} $$
$$ \begin{align} \|f_k\|_W^2 = \binom{n+1+k}{k} {\mathbb{E}} \left[ {\left| {f_k(w)} \right|}^2 \right]. \end{align} $$
The expectation in the right-hand side can be estimated with finitely many samples of
![]() ${\left | {f_k(w)} \right |}^2$
. To obtain a rigorous confidence interval, we study some statistical properties of
${\left | {f_k(w)} \right |}^2$
. To obtain a rigorous confidence interval, we study some statistical properties of
![]() ${\left | {f_k(w)} \right |}^2$
. Let
${\left | {f_k(w)} \right |}^2$
. Let
![]() $w_1,\dotsc ,w_s$
be independent uniformly distributed variables in B, and let
$w_1,\dotsc ,w_s$
be independent uniformly distributed variables in B, and let
 $$ \begin{align} \hat{\textsf{m}}_k^2 \,{\stackrel{.}{=}}\, \frac1s \sum_{i=1}^s {\left| {f_k(w_i)} \right|}^2 \end{align} $$
$$ \begin{align} \hat{\textsf{m}}_k^2 \,{\stackrel{.}{=}}\, \frac1s \sum_{i=1}^s {\left| {f_k(w_i)} \right|}^2 \end{align} $$
denote their empirical mean. Let
![]() $\textsf {m}_k^2\, {\stackrel {.}{=}}\, {\mathbb {E}}[ \hat {\textsf {m}}^2_k ] = {\mathbb {E}}[ |f_k(w)|^2 ]$
be the mean that we want to estimate (note that both
$\textsf {m}_k^2\, {\stackrel {.}{=}}\, {\mathbb {E}}[ \hat {\textsf {m}}^2_k ] = {\mathbb {E}}[ |f_k(w)|^2 ]$
be the mean that we want to estimate (note that both
![]() $\textsf {m}_k$
and
$\textsf {m}_k$
and
![]() $ \hat {\textsf {m}}_k$
depend on
$ \hat {\textsf {m}}_k$
depend on
![]() $f_k$
; we suppressed this dependence in the notation).
$f_k$
; we suppressed this dependence in the notation).
The next proposition shows that
![]() $\hat {\textsf {m}}_k^2$
estimates
$\hat {\textsf {m}}_k^2$
estimates
![]() $\textsf {m}_k^2$
within a
$\textsf {m}_k^2$
within a
![]() $\operatorname {poly}(n,k)^{k}$
factor with very few samples. The upper bound is obtained by a standard concentration inequality (Hoeffding’s inequality). The lower bound is more difficult, and very specific to the current setting, because we need to bound
$\operatorname {poly}(n,k)^{k}$
factor with very few samples. The upper bound is obtained by a standard concentration inequality (Hoeffding’s inequality). The lower bound is more difficult, and very specific to the current setting, because we need to bound
![]() $\textsf {m}_k^2$
away from zero with only a small number of samples. Concentration inequalities do not apply because the standard deviation may be larger than the expectation, so a confidence interval whose radius is comparable to the standard deviation (which is what we can hope for with a small number of samples) may contain negative values.
$\textsf {m}_k^2$
away from zero with only a small number of samples. Concentration inequalities do not apply because the standard deviation may be larger than the expectation, so a confidence interval whose radius is comparable to the standard deviation (which is what we can hope for with a small number of samples) may contain negative values.
Proposition 3.5. For any
![]() $0\leqslant k \leqslant {D}$
, we have, with probability at least
$0\leqslant k \leqslant {D}$
, we have, with probability at least
![]() $1 - 2^{1-s}$
,
$1 - 2^{1-s}$
,
where s is the number of samples.
Before proceeding with the proof, we state two lemmas, the principle of which comes from [Reference Ji, Kollar and Shiffman26, Lemma 8].
Lemma 3.6. Let
![]() $g \in {\mathbb {C}}[z]$
be a univariate polynomial of degree k, and let
$g \in {\mathbb {C}}[z]$
be a univariate polynomial of degree k, and let
![]() $c \in {\mathbb {C}}$
be its leading coefficient. For any
$c \in {\mathbb {C}}$
be its leading coefficient. For any
![]() $\eta> 0$
,
$\eta> 0$
,
Proof. Let
![]() $u_1,\dotsc ,u_k \in \mathbb {C}$
be the roots of g, with multiplicities, so that
$u_1,\dotsc ,u_k \in \mathbb {C}$
be the roots of g, with multiplicities, so that
The distance of some
![]() $z\in \mathbb {C}$
to the set
$z\in \mathbb {C}$
to the set
![]() $S \,{\stackrel {.}{=}}\, \left \{ u_1,\dotsc ,u_k \right \}$
is the minimum of all
$S \,{\stackrel {.}{=}}\, \left \{ u_1,\dotsc ,u_k \right \}$
is the minimum of all
![]() ${\left | {z-u_i} \right |}$
. In particular
${\left | {z-u_i} \right |}$
. In particular
 $$ \begin{align} \operatorname{dist}(z, S)^k \leqslant \prod_{i=1}^k {\left| {z-u_i} \right|} = {\left| {c} \right|}^{-1} {\left| {g(z)} \right|}. \end{align} $$
$$ \begin{align} \operatorname{dist}(z, S)^k \leqslant \prod_{i=1}^k {\left| {z-u_i} \right|} = {\left| {c} \right|}^{-1} {\left| {g(z)} \right|}. \end{align} $$
Therefore,
 $$ \begin{align} \left\{ z\in \mathbb{C} \mathrel{}\middle|\mathrel{} {\left| {g(z)} \right|}^2 \leqslant \eta \right\} \subset \bigcup_{i=1}^k B \left( u_i, {\left| {c} \right|}^{-\frac1k} \eta^{\frac{1}{2k}} \right), \end{align} $$
$$ \begin{align} \left\{ z\in \mathbb{C} \mathrel{}\middle|\mathrel{} {\left| {g(z)} \right|}^2 \leqslant \eta \right\} \subset \bigcup_{i=1}^k B \left( u_i, {\left| {c} \right|}^{-\frac1k} \eta^{\frac{1}{2k}} \right), \end{align} $$
where
![]() $B(u_i, r) \subseteq \mathbb {C}$
is the disk of radius r around
$B(u_i, r) \subseteq \mathbb {C}$
is the disk of radius r around
![]() $u_i$
. The volume of
$u_i$
. The volume of
![]() $B(u_i, r)$
is
$B(u_i, r)$
is
![]() $\pi r^2$
, so the claim follows directly.
$\pi r^2$
, so the claim follows directly.
Lemma 3.7. If
![]() $w \in B$
is a uniformly distributed random variable, then for all
$w \in B$
is a uniformly distributed random variable, then for all
![]() $\eta> 0$
,
$\eta> 0$
,
 $$\begin{align*}{\mathbb{P}} \left[ {\left| {f_k(w)} \right|}^2 \leqslant \eta \max_{\mathbb{S}} |f_k|^2 \right] \leqslant (n+1)k\eta^{\frac{1}{k}}, \end{align*}$$
$$\begin{align*}{\mathbb{P}} \left[ {\left| {f_k(w)} \right|}^2 \leqslant \eta \max_{\mathbb{S}} |f_k|^2 \right] \leqslant (n+1)k\eta^{\frac{1}{k}}, \end{align*}$$
where
![]() $\max _{\mathbb {S}} |f_k|$
is the maximum value of
$\max _{\mathbb {S}} |f_k|$
is the maximum value of
![]() $|f_k|$
on the unit sphere in
$|f_k|$
on the unit sphere in
![]() $\mathbb {C}^{n+1}$
.
$\mathbb {C}^{n+1}$
.
Proof. Let c be the coefficient of
![]() $x_n^k$
in
$x_n^k$
in
![]() $f_k$
. It is the value of
$f_k$
. It is the value of
![]() $f_k$
at
$f_k$
at
![]() $(0,\dotsc ,0,1)$
. Up to a unitary change of coordinates,
$(0,\dotsc ,0,1)$
. Up to a unitary change of coordinates,
![]() $|f_k|$
reaches a maximum at
$|f_k|$
reaches a maximum at
![]() $(0,\dotsc ,0,1)$
so that
$(0,\dotsc ,0,1)$
so that
![]() $c = \max _{\mathbb {S}} |f_k|$
. Up to scaling, we may further assume that
$c = \max _{\mathbb {S}} |f_k|$
. Up to scaling, we may further assume that
![]() $c=1$
. For any
$c=1$
. For any
![]() $(p_0,\ldots ,p_{n-1}) \in {\mathbb {C}}^{n}$
,
$(p_0,\ldots ,p_{n-1}) \in {\mathbb {C}}^{n}$
,
by Lemma 3.6 applied to the polynomial
![]() $g(z) = f_k(p_0,\dotsc ,p_{n-1}, z)$
, which, by construction, is monic. It follows, from the inclusion
$g(z) = f_k(p_0,\dotsc ,p_{n-1}, z)$
, which, by construction, is monic. It follows, from the inclusion
![]() $B(\mathbb {C}^{n+1})\subseteq B(\mathbb {C}^n) \times \mathbb {C}$
, that
$B(\mathbb {C}^{n+1})\subseteq B(\mathbb {C}^n) \times \mathbb {C}$
, that
Using
![]() $\operatorname {vol} B(\mathbb {C}^{n}) = \frac {\pi ^n}{n!}$
and dividing both sides by
$\operatorname {vol} B(\mathbb {C}^{n}) = \frac {\pi ^n}{n!}$
and dividing both sides by
![]() $\operatorname {vol} B(\mathbb {C}^{n+1})$
concludes the proof.
$\operatorname {vol} B(\mathbb {C}^{n+1})$
concludes the proof.
Lemma 3.8. For any
![]() $\eta> 0$
, we have
$\eta> 0$
, we have
Proof. Put
![]() $M \,{\stackrel {.}{=}}\, \max _{\mathbb {S}} {\left | {f_k} \right |}$
. If
$M \,{\stackrel {.}{=}}\, \max _{\mathbb {S}} {\left | {f_k} \right |}$
. If
![]() $\hat {\textsf {m}}_k^2 \le \eta M^2$
, then at least
$\hat {\textsf {m}}_k^2 \le \eta M^2$
, then at least
![]() $\lceil s/2 \rceil $
samples among
$\lceil s/2 \rceil $
samples among
![]() ${\left | {f(w_1)} \right |}^2,\dotsc ,{\left | {f(w_s)} \right |}^2$
satisfy
${\left | {f(w_1)} \right |}^2,\dotsc ,{\left | {f(w_s)} \right |}^2$
satisfy
![]() ${\left | {f(w_i)} \right |}^2 \leqslant 2\eta M^2$
. By the union bound and Lemma 3.7, we obtain,
${\left | {f(w_i)} \right |}^2 \leqslant 2\eta M^2$
. By the union bound and Lemma 3.7, we obtain,
 $$ \begin{align} {\mathbb{P}} \left[ \hat{\textsf{m}}_k^2 \leqslant \eta M^2 \right] &\leqslant \binom{s}{\lceil s/2 \rceil} {\mathbb{P}} \left[ {\left| {f(w)} \right|}^2 \leqslant 2 \eta M^2 \right]^{\lceil s/2 \rceil} \end{align} $$
$$ \begin{align} {\mathbb{P}} \left[ \hat{\textsf{m}}_k^2 \leqslant \eta M^2 \right] &\leqslant \binom{s}{\lceil s/2 \rceil} {\mathbb{P}} \left[ {\left| {f(w)} \right|}^2 \leqslant 2 \eta M^2 \right]^{\lceil s/2 \rceil} \end{align} $$
To conclude, we note that
![]() $\textsf {m}_k \leqslant M$
.
$\textsf {m}_k \leqslant M$
.
Proof of Proposition 3.5
With
![]() $\eta \,{\stackrel {.}{=}}\, \left (32 nk \right )^{-k}$
, Lemma 3.8 gives
$\eta \,{\stackrel {.}{=}}\, \left (32 nk \right )^{-k}$
, Lemma 3.8 gives
It follows that
which is the stated left-hand inequality.
For the right-hand inequality, we apply Hoeffding’s inequality, (e.g., [Reference Boucheron, Lugosi and Massart10, Theorem 2.8]). The variable
![]() $s \hat {\textsf {m}}_k^2$
is a sum of s independent variables lying in the interval
$s \hat {\textsf {m}}_k^2$
is a sum of s independent variables lying in the interval
![]() $[0, M^2]$
, where we, again, abbreviate
$[0, M^2]$
, where we, again, abbreviate
![]() $M \,{\stackrel {.}{=}}\, \max _{\mathbb {S}} {\left | {f_k} \right |}$
. Accordingly, for any
$M \,{\stackrel {.}{=}}\, \max _{\mathbb {S}} {\left | {f_k} \right |}$
. Accordingly, for any
![]() $C \geqslant 1$
,
$C \geqslant 1$
,
 $$ \begin{align} {\mathbb{P}} \left[ \hat{\textsf{m}}_k^2 \geqslant C \textsf{m}_k^2 \right] = {\mathbb{P}} \left[ s \hat{\textsf{m}}_k^2 - s \textsf{m}^2_k \geqslant (C-1) s \textsf{m}^2_k \right] \leqslant \exp \left( - \frac{2 (C-1)^2 s^2 \textsf{m}_k^4}{sM^4} \right). \end{align} $$
$$ \begin{align} {\mathbb{P}} \left[ \hat{\textsf{m}}_k^2 \geqslant C \textsf{m}_k^2 \right] = {\mathbb{P}} \left[ s \hat{\textsf{m}}_k^2 - s \textsf{m}^2_k \geqslant (C-1) s \textsf{m}^2_k \right] \leqslant \exp \left( - \frac{2 (C-1)^2 s^2 \textsf{m}_k^4}{sM^4} \right). \end{align} $$
By Lemma 3.2 combined with (3.8), we have
 $$ \begin{align} M^2 \le \binom{n+1+k}{k} \textsf{m}^2_k. \end{align} $$
$$ \begin{align} M^2 \le \binom{n+1+k}{k} \textsf{m}^2_k. \end{align} $$
Applying this bound, we obtain
 $$ \begin{align} {\mathbb{P}} \left[ \hat{\textsf{m}}_k^2 \geqslant C \textsf{m}_k^2 \right] \leqslant \exp \left( - \frac{2 (C-1)^2 s}{\binom{n+1+k}{k}^2} \right). \end{align} $$
$$ \begin{align} {\mathbb{P}} \left[ \hat{\textsf{m}}_k^2 \geqslant C \textsf{m}_k^2 \right] \leqslant \exp \left( - \frac{2 (C-1)^2 s}{\binom{n+1+k}{k}^2} \right). \end{align} $$
We choose
![]() $C = (6n)^k$
and simplify further using the inequality
$C = (6n)^k$
and simplify further using the inequality
![]() $\binom {m+k}{k} \le \frac {(m+k)^k}{k!} \le (e(m+k)/k)^k$
and
$\binom {m+k}{k} \le \frac {(m+k)^k}{k!} \le (e(m+k)/k)^k$
and
![]() $e(n+1+k)/k \le e(n+3)/2$
(use
$e(n+1+k)/k \le e(n+3)/2$
(use
![]() $k\ge 2$
) to obtain
$k\ge 2$
) to obtain
 $$ \begin{align} \frac{C-1}{\binom{n+1+k}{k}} &\geqslant \frac{(6n)^k - 1 }{\left( \frac{e (n+3)}{2} \right)^{k}} \geqslant \left( \frac{12 n}{e (n+3)} \right)^{k} - \left( \frac{2}{e(n+3)} \right)^{k} \end{align} $$
$$ \begin{align} \frac{C-1}{\binom{n+1+k}{k}} &\geqslant \frac{(6n)^k - 1 }{\left( \frac{e (n+3)}{2} \right)^{k}} \geqslant \left( \frac{12 n}{e (n+3)} \right)^{k} - \left( \frac{2}{e(n+3)} \right)^{k} \end{align} $$
 $$ \begin{align} &\geqslant \left( \frac{3}{e} \right)^2 - \left( \frac{2}{4 e} \right)^2 \geqslant \sqrt{\frac12 \log{2}}. \end{align} $$
$$ \begin{align} &\geqslant \left( \frac{3}{e} \right)^2 - \left( \frac{2}{4 e} \right)^2 \geqslant \sqrt{\frac12 \log{2}}. \end{align} $$
We obtain, therefore
Combined with (3.21), the union bound implies
and the proposition follows.
Proof of Theorem 3.3
Recall that we assume that
![]() $z=0$
. Proposition 3.5 can be rephrased as follows: with probability at least
$z=0$
. Proposition 3.5 can be rephrased as follows: with probability at least
![]() $1-2^{1-s}$
, we have
$1-2^{1-s}$
, we have
Defining
 $$ \begin{align} c^2_k\, {\stackrel{.}{=}}\, \binom{n+1+k}{k} (32 n k)^k \hat{\textsf{m}}^2_k , \end{align} $$
$$ \begin{align} c^2_k\, {\stackrel{.}{=}}\, \binom{n+1+k}{k} (32 n k)^k \hat{\textsf{m}}^2_k , \end{align} $$
using that by (3.8)
 $$ \begin{align} \|f_k\|_W^2 = \binom{n+1+k}{k} \textsf{m}_k^2 , \end{align} $$
$$ \begin{align} \|f_k\|_W^2 = \binom{n+1+k}{k} \textsf{m}_k^2 , \end{align} $$
and applying the union bound, we, therefore, see that
holds for all
![]() $2\le k\le {D}$
, with probability at least
$2\le k\le {D}$
, with probability at least
![]() $1-{D} 2^{1-s}$
. If we chose
$1-{D} 2^{1-s}$
. If we chose
![]() $s = \left \lceil 1 + \log _2 \frac {D}\varepsilon \right \rceil $
, then
$s = \left \lceil 1 + \log _2 \frac {D}\varepsilon \right \rceil $
, then
![]() ${D} 2^{1-s} \leqslant \varepsilon $
. Recall from (3.4) and (3.5) that
${D} 2^{1-s} \leqslant \varepsilon $
. Recall from (3.4) and (3.5) that
Noting that
![]() $(192 n^2 k)^{\frac {k}{k-1}} \leqslant (192 n^2 {D})^2$
, for
$(192 n^2 k)^{\frac {k}{k-1}} \leqslant (192 n^2 {D})^2$
, for
![]() $2\leqslant k\leqslant {D}$
, we conclude that the random variable
$2\leqslant k\leqslant {D}$
, we conclude that the random variable
which is returned by Algorithm 2, indeed satisfies
with probability at least
![]() $1-\varepsilon $
, which proves the first assertion.
$1-\varepsilon $
, which proves the first assertion.
For the assertion on the number of operations, it suffices to note that by Lemma 3.4, the computation of the derivative
![]() $d_0f$
and of
$d_0f$
and of
![]() $\hat {\textsf {m}}_2,\dotsc ,\hat {\textsf {m}}_{D}$
can be done with
$\hat {\textsf {m}}_2,\dotsc ,\hat {\textsf {m}}_{D}$
can be done with
![]() $O(s{D} (L(f) + n + \log {D}))$
arithmetic operations.
$O(s{D} (L(f) + n + \log {D}))$
arithmetic operations.
It only remains to check, for any
![]() $t \geqslant 1$
, the tail bound
$t \geqslant 1$
, the tail bound
 $$ \begin{align} \mathbb{P} \left[ \Gamma \leqslant \frac{\gamma_{\mathrm{Frob}} (f, z)}{t} \right] \leqslant \varepsilon ^{1+\frac12 \log_2 t}. \end{align} $$
$$ \begin{align} \mathbb{P} \left[ \Gamma \leqslant \frac{\gamma_{\mathrm{Frob}} (f, z)}{t} \right] \leqslant \varepsilon ^{1+\frac12 \log_2 t}. \end{align} $$
Unfolding the definitions (3.33) and (3.34) and using, again, (3.31), we obtain
 $$ \begin{align} \mathbb{P} \left[ \Gamma \leqslant \frac{\gamma_{\mathrm{Frob}} (f, z)}{t} \right] &\leqslant \sum_{k=2}^{D} \mathbb{P} \left[ (32nk)^k \hat{\textsf{m}}_k^2 \leqslant t^{-2 (k-1)} \textsf{m}_k^2 \right] \end{align} $$
$$ \begin{align} \mathbb{P} \left[ \Gamma \leqslant \frac{\gamma_{\mathrm{Frob}} (f, z)}{t} \right] &\leqslant \sum_{k=2}^{D} \mathbb{P} \left[ (32nk)^k \hat{\textsf{m}}_k^2 \leqslant t^{-2 (k-1)} \textsf{m}_k^2 \right] \end{align} $$
 $$ \begin{align} &\leqslant \sum_{k=2}^{D} \left( 8 nk \cdot \left( (32nk)^k t^{2(k-1)} \right)^{-\frac1k} \right)^{\frac s2}, \qquad \text{by Lemma~3.8}, \end{align} $$
$$ \begin{align} &\leqslant \sum_{k=2}^{D} \left( 8 nk \cdot \left( (32nk)^k t^{2(k-1)} \right)^{-\frac1k} \right)^{\frac s2}, \qquad \text{by Lemma~3.8}, \end{align} $$
 $$ \begin{align} &= \sum_{k=2}^{D} \left( \frac14 t^{-2\frac{k-1}{k}} \right)^{\frac s2} \leqslant {D} 2^{-s} t^{-\frac s2}. \end{align} $$
$$ \begin{align} &= \sum_{k=2}^{D} \left( \frac14 t^{-2\frac{k-1}{k}} \right)^{\frac s2} \leqslant {D} 2^{-s} t^{-\frac s2}. \end{align} $$
Since
![]() $s = \left \lceil 1 + \log _2 \frac {D}\varepsilon \right \rceil $
, we have
$s = \left \lceil 1 + \log _2 \frac {D}\varepsilon \right \rceil $
, we have
![]() ${D} 2^{-s} \leqslant \varepsilon $
. Furthermore,
${D} 2^{-s} \leqslant \varepsilon $
. Furthermore,
![]() $s \geqslant -\log _2 \varepsilon $
, so
$s \geqslant -\log _2 \varepsilon $
, so
which proves (3.36).
3.3 A Monte-Carlo continuation algorithm
We deal, here, with the specifics of a numerical continuation with a step-length computation that may be wrong.
The randomised algorithm for the evaluation of the step length can be plugged into the rigid continuation algorithm (Algorithm 1). There is no guarantee, however, that the randomised computations of the
![]() $\gamma _{\mathrm {Frob}}$
fall within the confidence interval described in Theorem 3.3 and, consequently, there is no guarantee that the corresponding step-length estimation is accurate. If step lengths are underestimated, we don’t control any more the complexity: as the step lengths go to zero, the number of steps goes to infinity. Overestimating a single step length, instead, may undermine the correctness of the result, and the subsequent behaviour of the algorithm is unknown (it may even not to terminate). So we introduce a limit on the number of continuation steps. Algorithm 3 is a corresponding modification of Algorithm 1. When reaching the limit on the number of steps, this algorithm halts with a failure notification.
$\gamma _{\mathrm {Frob}}$
fall within the confidence interval described in Theorem 3.3 and, consequently, there is no guarantee that the corresponding step-length estimation is accurate. If step lengths are underestimated, we don’t control any more the complexity: as the step lengths go to zero, the number of steps goes to infinity. Overestimating a single step length, instead, may undermine the correctness of the result, and the subsequent behaviour of the algorithm is unknown (it may even not to terminate). So we introduce a limit on the number of continuation steps. Algorithm 3 is a corresponding modification of Algorithm 1. When reaching the limit on the number of steps, this algorithm halts with a failure notification.

Proposition 3.9. On input F,
![]() ${\mathbf u}$
,
${\mathbf u}$
,
![]() ${\mathbf v}$
,
${\mathbf v}$
,
![]() $\zeta $
,
$\zeta $
,
![]() $K_{\max }$
, and
$K_{\max }$
, and
![]() $\varepsilon $
, such that
$\varepsilon $
, such that
![]() $\zeta $
is a zero of
$\zeta $
is a zero of
![]() ${\mathbf v} \cdot F$
, the randomised Algorithm BoundedBlackBoxNC (Algorithm 3) either fails or returns some
${\mathbf v} \cdot F$
, the randomised Algorithm BoundedBlackBoxNC (Algorithm 3) either fails or returns some
![]() $z^* \in \mathbb {P}^n$
. In the latter case,
$z^* \in \mathbb {P}^n$
. In the latter case,
![]() $z^*$
is an approximate zero of
$z^*$
is an approximate zero of
![]() ${\mathbf u} \cdot F$
with probability at least
${\mathbf u} \cdot F$
with probability at least
![]() $1-\varepsilon $
. The total number of operations is
$1-\varepsilon $
. The total number of operations is
![]() $\operatorname {poly}(n,{D}) \cdot K_{\max } \log \left ( K_{\max } \varepsilon ^{-1} \right ) \cdot L(F)$
.
$\operatorname {poly}(n,{D}) \cdot K_{\max } \log \left ( K_{\max } \varepsilon ^{-1} \right ) \cdot L(F)$
.
Proof. Assume
![]() $z^*\in {\mathbb {P}}^n$
is returned which is not an approximate zero of F. This implies that one of the estimations of
$z^*\in {\mathbb {P}}^n$
is returned which is not an approximate zero of F. This implies that one of the estimations of
![]() $\gamma _{\mathrm {Frob}}(f,z)$
, computed by the GammaProb subroutines, yielded a result that is smaller than the actual value of
$\gamma _{\mathrm {Frob}}(f,z)$
, computed by the GammaProb subroutines, yielded a result that is smaller than the actual value of
![]() $\gamma _{\mathrm {Frob}}(f, z)$
. There are at most
$\gamma _{\mathrm {Frob}}(f, z)$
. There are at most
![]() $n K_{\max }$
such estimations, so by Theorem 3.3, this happens with probability at most
$n K_{\max }$
such estimations, so by Theorem 3.3, this happens with probability at most
![]() $n K_{\max } \eta $
, which by choice of
$n K_{\max } \eta $
, which by choice of
![]() $\eta $
is exactly
$\eta $
is exactly
![]() $\varepsilon $
.
$\varepsilon $
.
The total number of operations is bounded by
![]() $K_{\max }$
times the cost of an iteration. After computing the derivative at z of
$K_{\max }$
times the cost of an iteration. After computing the derivative at z of
![]() ${\mathbf w}_t\cdot F$
, in
${\mathbf w}_t\cdot F$
, in
![]() $\operatorname {poly}(n, {D})L(F)$
operations, we can compute an approximation of the number
$\operatorname {poly}(n, {D})L(F)$
operations, we can compute an approximation of the number
![]() $\kappa ({\mathbf w}_t\cdot F, z)$
within a factor of 2, which is good enough for our purpose. We do so with
$\kappa ({\mathbf w}_t\cdot F, z)$
within a factor of 2, which is good enough for our purpose. We do so with
![]() $O(n^3)$
operations using tridiagonalisation with Householder’s reflections and a result by [Reference Kahan27] (the same argument is used in Corollary I.33). So the cost of an iteration is dominated by the evaluation of the
$O(n^3)$
operations using tridiagonalisation with Householder’s reflections and a result by [Reference Kahan27] (the same argument is used in Corollary I.33). So the cost of an iteration is dominated by the evaluation of the
![]() $g_i$
, which is bounded by
$g_i$
, which is bounded by
![]() $O({D} \log ({D} n K_{\max } \varepsilon ^{-1}) (L(F) + n +\log {D} ) )$
by Theorem 3.3 and the choice of
$O({D} \log ({D} n K_{\max } \varepsilon ^{-1}) (L(F) + n +\log {D} ) )$
by Theorem 3.3 and the choice of
![]() $\eta $
, and Newton iteration, which costs
$\eta $
, and Newton iteration, which costs
![]() $\operatorname {poly}(n,{D}) L(F)$
.
$\operatorname {poly}(n,{D}) L(F)$
.
In case Algorithm 3 fails, it is natural to restart the computation with a higher iteration limit. This is Algorithm 4. We can compare its complexity to that of Algorithm 1, which assumes an exact computation of
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $K(F, {\mathbf u}, {\mathbf v}, \zeta )$
be a bound for the number of iterations performed by Algorithm 1 on input F,
$K(F, {\mathbf u}, {\mathbf v}, \zeta )$
be a bound for the number of iterations performed by Algorithm 1 on input F,
![]() ${\mathbf u}$
,
${\mathbf u}$
,
![]() ${\mathbf v}$
and
${\mathbf v}$
and
![]() $\zeta $
, allowing an overestimation of the step length up to a factor
$\zeta $
, allowing an overestimation of the step length up to a factor
![]() $192 n^2{D}$
(in view of Theorem 3.3).
$192 n^2{D}$
(in view of Theorem 3.3).

Proposition 3.10. On input F,
![]() ${\mathbf u}$
,
${\mathbf u}$
,
![]() ${\mathbf v}$
,
${\mathbf v}$
,
![]() $\zeta $
and
$\zeta $
and
![]() $\varepsilon \in (0,\frac 14 \rbrack $
, such that
$\varepsilon \in (0,\frac 14 \rbrack $
, such that
![]() $\zeta $
is a zero of
$\zeta $
is a zero of
![]() ${\mathbf v} \cdot F$
, and
${\mathbf v} \cdot F$
, and
![]() $K(F, {\mathbf u}, {\mathbf v}, \zeta ) < \infty $
, the randomised Algorithm BlackBoxNC (Algorithm 4) terminates almost surely and returns an approximate zero of
$K(F, {\mathbf u}, {\mathbf v}, \zeta ) < \infty $
, the randomised Algorithm BlackBoxNC (Algorithm 4) terminates almost surely and returns an approximate zero of
![]() ${\mathbf u} \cdot F$
with probability at least
${\mathbf u} \cdot F$
with probability at least
![]() $1-\varepsilon $
. The average total number of operations is
$1-\varepsilon $
. The average total number of operations is
![]() $\operatorname {poly}(n, {D}) \cdot L(F) \cdot K \log \left ( K \varepsilon ^{-1} \right )$
, with
$\operatorname {poly}(n, {D}) \cdot L(F) \cdot K \log \left ( K \varepsilon ^{-1} \right )$
, with
![]() $K = K(F, {\mathbf u}, {\mathbf v}, \zeta )$
(NB: The only source of randomness is the probabilistic evaluation of
$K = K(F, {\mathbf u}, {\mathbf v}, \zeta )$
(NB: The only source of randomness is the probabilistic evaluation of
![]() $\gamma _{\mathrm {Frob}}$
).
$\gamma _{\mathrm {Frob}}$
).
Proof. Let
![]() $K\,{\stackrel {.}{=}}\, K(F, {\mathbf u}, {\mathbf v}, \zeta )$
. By definition of K, if all approximations lie in the desired confidence interval, then BoundedBlackBoxNC terminates after at most K iterations. So as soon as
$K\,{\stackrel {.}{=}}\, K(F, {\mathbf u}, {\mathbf v}, \zeta )$
. By definition of K, if all approximations lie in the desired confidence interval, then BoundedBlackBoxNC terminates after at most K iterations. So as soon as
![]() ${K_{\mathrm {max}}} \geqslant K$
, BoundedBlackBoxNC may return Fail only if the approximation of some
${K_{\mathrm {max}}} \geqslant K$
, BoundedBlackBoxNC may return Fail only if the approximation of some
![]() $\gamma _{\mathrm {Frob}}$
is not correct. This happens with probability at most
$\gamma _{\mathrm {Frob}}$
is not correct. This happens with probability at most
![]() $\varepsilon $
at each iteration of the main loop in Algorithm 4, independently. So the number of iterations is finite, almost surely. That the result is correct with probability at least
$\varepsilon $
at each iteration of the main loop in Algorithm 4, independently. So the number of iterations is finite, almost surely. That the result is correct with probability at least
![]() $1-\varepsilon $
follows from Proposition 3.9.
$1-\varepsilon $
follows from Proposition 3.9.
We now consider the total cost. At the mth iteration, we have
![]() ${K_{\mathrm {max}}}=2^m$
, so the cost of the mth iteration is
${K_{\mathrm {max}}}=2^m$
, so the cost of the mth iteration is
![]() $\operatorname {poly}(n, {D}) \cdot 2^m \log (2^m \varepsilon ^{-1}) \cdot L(f)$
, by Proposition 3.9. Put
$\operatorname {poly}(n, {D}) \cdot 2^m \log (2^m \varepsilon ^{-1}) \cdot L(f)$
, by Proposition 3.9. Put
![]() $\ell \,{\stackrel {.}{=}}\, \lceil \log _2 K \rceil $
. If the mth iteration is reached for some
$\ell \,{\stackrel {.}{=}}\, \lceil \log _2 K \rceil $
. If the mth iteration is reached for some
![]() $m> \ell $
, then all the iterations from
$m> \ell $
, then all the iterations from
![]() $\ell $
to
$\ell $
to
![]() $m-1$
have failed. This has a probability
$m-1$
have failed. This has a probability
![]() $\leqslant \varepsilon ^{m - \ell }$
to happen, so, if I denotes the number of iterations, we have
$\leqslant \varepsilon ^{m - \ell }$
to happen, so, if I denotes the number of iterations, we have
The total expected cost is, therefore, bounded by
 $$ \begin{align} \mathbb{E}[\mathrm{cost}] &\leqslant \operatorname{poly}(n, {D}) L(f)\sum_{m=1}^\infty 2^m \log(2^m \varepsilon ^{-1}) \mathbb{P}[I \geqslant m] \end{align} $$
$$ \begin{align} \mathbb{E}[\mathrm{cost}] &\leqslant \operatorname{poly}(n, {D}) L(f)\sum_{m=1}^\infty 2^m \log(2^m \varepsilon ^{-1}) \mathbb{P}[I \geqslant m] \end{align} $$
 $$ \begin{align} &\leqslant \operatorname{poly}(n, {D}) L(f)\sum_{m=1}^\infty 2^m \log (2^m \varepsilon ^{-1}) \min\left(1, \varepsilon ^{m-\ell}\right). \\[-15pt]\nonumber\end{align} $$
$$ \begin{align} &\leqslant \operatorname{poly}(n, {D}) L(f)\sum_{m=1}^\infty 2^m \log (2^m \varepsilon ^{-1}) \min\left(1, \varepsilon ^{m-\ell}\right). \\[-15pt]\nonumber\end{align} $$
The claim follows easily from splitting the sum into two parts,
![]() $1\leqslant m < \ell $
and
$1\leqslant m < \ell $
and
![]() $m> \ell $
, and applying the bounds (with
$m> \ell $
, and applying the bounds (with
![]() $c=\log \varepsilon ^{-1}$
)
$c=\log \varepsilon ^{-1}$
)
 $$ \begin{align} \sum_{m=1}^{\ell-1} 2^m (m + c) \leqslant (\ell+c)2^\ell \\[-15pt]\nonumber\end{align} $$
$$ \begin{align} \sum_{m=1}^{\ell-1} 2^m (m + c) \leqslant (\ell+c)2^\ell \\[-15pt]\nonumber\end{align} $$
and, for
![]() $\varepsilon \in (0,\frac 14)$
,
$\varepsilon \in (0,\frac 14)$
,
 $$ \begin{align} \sum_{m=\ell}^\infty 2^m (m+c) \varepsilon ^{m-\ell} \leqslant \frac{(\ell+c) 2^\ell}{(1-2\varepsilon )^2} \leqslant 4 (\ell+c) 2^\ell. \end{align} $$
$$ \begin{align} \sum_{m=\ell}^\infty 2^m (m+c) \varepsilon ^{m-\ell} \leqslant \frac{(\ell+c) 2^\ell}{(1-2\varepsilon )^2} \leqslant 4 (\ell+c) 2^\ell. \end{align} $$
4 Condition-based complexity analysis
We recall from Part I (Section 2) the rigid solution variety corresponding to a polynomial system
![]() $F = (f_1,\dotsc ,f_n)$
, which consists of the pairs
$F = (f_1,\dotsc ,f_n)$
, which consists of the pairs
![]() $({\mathbf v},\zeta ) \in {\mathcal {U}}\times {\mathbb {P}}^n$
, such that
$({\mathbf v},\zeta ) \in {\mathcal {U}}\times {\mathbb {P}}^n$
, such that
![]() $({\mathbf v}\cdot F)(\zeta )=0$
, which means
$({\mathbf v}\cdot F)(\zeta )=0$
, which means
![]() $f_1(v_1^{-1}\zeta ) =0,\ldots ,f_n(v_n^{-1}\zeta )=0$
. To solve a given polynomial system
$f_1(v_1^{-1}\zeta ) =0,\ldots ,f_n(v_n^{-1}\zeta )=0$
. To solve a given polynomial system
![]() $F \in {\mathcal {H}}$
, we sample an initial pair in the rigid solution variety corresponding to F (Algorithm I.1) and perform a numerical continuation using Algorithm 4. This gives Algorithm 5 (recall that
$F \in {\mathcal {H}}$
, we sample an initial pair in the rigid solution variety corresponding to F (Algorithm I.1) and perform a numerical continuation using Algorithm 4. This gives Algorithm 5 (recall that
![]() $\mathbf {1}_{{\mathcal {U}}}$
denotes the unit in the group
$\mathbf {1}_{{\mathcal {U}}}$
denotes the unit in the group
![]() ${\mathcal {U}}$
).
${\mathcal {U}}$
).

Proposition 4.1 (Termination and correctness)
Let
![]() $F=(f_1,\ldots ,f_n)$
be a homogeneous polynomial system with only regular zeros. On input F, given as a black-box evaluation program, and
$F=(f_1,\ldots ,f_n)$
be a homogeneous polynomial system with only regular zeros. On input F, given as a black-box evaluation program, and
![]() $\varepsilon \in (0,\frac 14\rbrack $
, Algorithm BlackBoxSolve terminates almost surely and returns a point
$\varepsilon \in (0,\frac 14\rbrack $
, Algorithm BlackBoxSolve terminates almost surely and returns a point
![]() $z^*\in \mathbb {P}^n$
which is an approximate zero of F with probability
$z^*\in \mathbb {P}^n$
which is an approximate zero of F with probability
![]() $1-\varepsilon $
.
$1-\varepsilon $
.
Proof. Termination and correctness directly follow from Proposition 3.10.
We now analyse the cost of Algorithm 5.
Theorem 4.2 (Complexity)
Let
![]() $F=(f_1,\ldots ,f_n)$
be a homogeneous square-free polynomial system with degrees at most
$F=(f_1,\ldots ,f_n)$
be a homogeneous square-free polynomial system with degrees at most
![]() ${D}$
in
${D}$
in
![]() $n+1$
variables given by a black-box evaluation program. Let
$n+1$
variables given by a black-box evaluation program. Let
![]() ${\mathbf u} \in {\mathcal {U}}$
be uniformly distributed, and let
${\mathbf u} \in {\mathcal {U}}$
be uniformly distributed, and let
![]() $H = {\mathbf u} \cdot F$
. Then, on input H, given as a black-box evaluation program, and
$H = {\mathbf u} \cdot F$
. Then, on input H, given as a black-box evaluation program, and
![]() $\varepsilon \in (0,\frac 14\rbrack $
, Algorithm BlackBoxSolve terminates after
$\varepsilon \in (0,\frac 14\rbrack $
, Algorithm BlackBoxSolve terminates after
operations on average. ‘On average’ refers to expectation with respect to both the random draws made by the algorithm and the random variable
![]() ${\mathbf u}$
, but F is fixed.
${\mathbf u}$
, but F is fixed.
We next focus on proving the complexity bound. Note that the statement of Theorem 4.2 is similar to that of Theorem 1.2. The only difference lies in the complexity bound, whose dependence on
![]() $\varepsilon ^{-1}$
is logarithmic in the former and doubly logarithmic in the latter. In Section 4.3 below, we will use BlackBoxSolve with
$\varepsilon ^{-1}$
is logarithmic in the former and doubly logarithmic in the latter. In Section 4.3 below, we will use BlackBoxSolve with
![]() $\varepsilon =\frac 14$
as a routine within a boosting procedure to achieve this cost reduction.
$\varepsilon =\frac 14$
as a routine within a boosting procedure to achieve this cost reduction.
4.1 Complexity of sampling the rigid solution variety
Towards the proof of Theorems 1.2 and 4.2, we first review the complexity of sampling the initial pair for the numerical continuation. In the rigid setting, this sampling boils down to sampling hypersurfaces, which, in turn, amounts to computing roots of univariate polynomials (see Part I, Section 2.4). Some technicalities are required to connect known results about root-finding algorithms to our setting, and especially the parameter
![]() $\Gamma (F)$
, but the material is very classical. Below,
$\Gamma (F)$
, but the material is very classical. Below,
![]() $\log \log (x)$
is to be interpreted as the function
$\log \log (x)$
is to be interpreted as the function
![]() $\log _2\log _2(x+2)$
which is defined for all positive x. Since our statements are asymptotic, this does not change anything.
$\log _2\log _2(x+2)$
which is defined for all positive x. Since our statements are asymptotic, this does not change anything.
Proposition 4.3. Given
![]() $F \in {\mathcal {H}}$
as a black-box evaluation program, we can sample
$F \in {\mathcal {H}}$
as a black-box evaluation program, we can sample
![]() ${\mathbf v} \in {\mathcal {U}}$
and
${\mathbf v} \in {\mathcal {U}}$
and
![]() $\zeta \in \mathbb {P}^n$
, such that
$\zeta \in \mathbb {P}^n$
, such that
![]() ${\mathbf v}$
is uniformly distributed and
${\mathbf v}$
is uniformly distributed and
![]() $\zeta $
is a uniformly distributed zero of
$\zeta $
is a uniformly distributed zero of
![]() ${\mathbf v} \cdot F$
, with
${\mathbf v} \cdot F$
, with
![]() $\operatorname {poly}(n, {D}) \cdot ( L(F) + \log \log \Gamma (F) )$
operations on average.
$\operatorname {poly}(n, {D}) \cdot ( L(F) + \log \log \Gamma (F) )$
operations on average.
Proof. This follows from Proposition I.10 and Proposition 4.4 below.
Proposition 4.4. For any
![]() $f \in \mathbb {C}[z_0,\dotsc ,z_n]$
homogeneous of degree
$f \in \mathbb {C}[z_0,\dotsc ,z_n]$
homogeneous of degree
![]() ${D}\ge 2$
, given as a black-box evaluation program, one can sample a uniformly distributed point in the zero set
${D}\ge 2$
, given as a black-box evaluation program, one can sample a uniformly distributed point in the zero set
![]() $V(f)$
of f by a probabilistic algorithm with
$V(f)$
of f by a probabilistic algorithm with
![]() $\operatorname {poly}(n, {D}) \cdot ( L(f) + \log \log \Gamma (f) )$
operations on average.
$\operatorname {poly}(n, {D}) \cdot ( L(f) + \log \log \Gamma (f) )$
operations on average.
Proof. Following Corollary I.9, we can compute a uniformly distributed zero of f by first sampling a line
![]() $\ell \subset \mathbb {P}^n$
uniformly distributed in the Grasmannian of lines, and then sampling a uniformly distributed point in the finite set
$\ell \subset \mathbb {P}^n$
uniformly distributed in the Grasmannian of lines, and then sampling a uniformly distributed point in the finite set
![]() $\ell \cap V(f)$
. To do this, we consider the restriction
$\ell \cap V(f)$
. To do this, we consider the restriction
![]() $f|_\ell $
, which, after choosing an orthonormal basis of
$f|_\ell $
, which, after choosing an orthonormal basis of
![]() $\ell $
, is a bivariate homogeneous polynomial, and compute its roots. The representation of
$\ell $
, is a bivariate homogeneous polynomial, and compute its roots. The representation of
![]() $f|_\ell $
in a monomial basis can be computed by
$f|_\ell $
in a monomial basis can be computed by
![]() ${D}+1$
evaluations of f and interpolation, at a cost
${D}+1$
evaluations of f and interpolation, at a cost
![]() $O \left ( {D} (L(f) + n + \log {D}) \right )$
, as in Lemma 3.4. By Lemma 4.5 below, computing the roots takes
$O \left ( {D} (L(f) + n + \log {D}) \right )$
, as in Lemma 3.4. By Lemma 4.5 below, computing the roots takes
 $$ \begin{align} \operatorname{poly}({D}) \log\log \left(\max_{\zeta \in \ell\cap V(f)} \gamma(f|_\ell, \zeta)\right) \end{align} $$
$$ \begin{align} \operatorname{poly}({D}) \log\log \left(\max_{\zeta \in \ell\cap V(f)} \gamma(f|_\ell, \zeta)\right) \end{align} $$
operations on average. We assume a 6th type of node to refine approximate roots into exact roots (recall the discussion in Section 1.3). Then we have, by the definition (1.5) of
![]() $\Gamma (f|_\ell )$
,
$\Gamma (f|_\ell )$
,

By Jensen’s inequality [Reference Bürgisser and Cucker15, Proposition 2.28], using the concavity of
![]() $\log _2\log _2(x)$
on
$\log _2\log _2(x)$
on
![]() $\lbrack 2,\infty )$
, we obtain
$\lbrack 2,\infty )$
, we obtain
Finally, Lemma 4.6 below gives
and the claim follows.
Lemma 4.5. Let
![]() $g \in \mathbb {C}[{z_0,z_1}]$
be a homogeneous polynomial of degree
$g \in \mathbb {C}[{z_0,z_1}]$
be a homogeneous polynomial of degree
![]() ${D}$
without multiple zeros. One can compute, with a probabilistic algorithm,
${D}$
without multiple zeros. One can compute, with a probabilistic algorithm,
![]() ${D}$
approximate zeros of g, one for each zero of g, with
${D}$
approximate zeros of g, one for each zero of g, with
![]() $\operatorname {poly}({D}) \log \log \gamma _{\max }$
operations on average, where
$\operatorname {poly}({D}) \log \log \gamma _{\max }$
operations on average, where
![]() $\gamma _{\max }\, {\stackrel {.}{=}} \,\max _{\zeta \in V(g)} \gamma (g, \zeta )$
.
$\gamma _{\max }\, {\stackrel {.}{=}} \,\max _{\zeta \in V(g)} \gamma (g, \zeta )$
.
Proof. The proof essentially relies on the following known fact due to [Reference Renegar35] (see also [Reference Pan33, Thm. 2.1.1 and Cor. 2.1.2], for tighter bounds). Let
![]() $f \in \mathbb {C}[t]$
be a given polynomial of degree
$f \in \mathbb {C}[t]$
be a given polynomial of degree
![]() ${D}$
,
${D}$
,
![]() $R> 0$
be a known upper bound on the modulus of the roots
$R> 0$
be a known upper bound on the modulus of the roots
![]() $\xi _1,\dotsc ,\xi _{D} \in \mathbb {C}$
of f and
$\xi _1,\dotsc ,\xi _{D} \in \mathbb {C}$
of f and
![]() $\varepsilon>0$
. We can compute from these data with
$\varepsilon>0$
. We can compute from these data with
![]() $\operatorname {poly}({D}) \log \log \frac R\varepsilon $
operations approximations
$\operatorname {poly}({D}) \log \log \frac R\varepsilon $
operations approximations
![]() $x_1,\dotsc ,x_n \in \mathbb {C}$
of the zeros, such that
$x_1,\dotsc ,x_n \in \mathbb {C}$
of the zeros, such that
![]() ${\left | {\xi _i - x_i} \right |} \leqslant \varepsilon $
.
${\left | {\xi _i - x_i} \right |} \leqslant \varepsilon $
.
To apply this result to the given homogeneous polynomial g, we first apply a uniformly random unitary transformation
![]() $u\in U(2)$
to the given g and dehomogenise
$u\in U(2)$
to the given g and dehomogenise
![]() $u\cdot g$
, obtaining the univariate polynomial
$u\cdot g$
, obtaining the univariate polynomial
![]() $f\in {\mathbb {C}}[t]$
.
$f\in {\mathbb {C}}[t]$
.
We first claim that, with probability at least
![]() $3/4$
, we have: (
$3/4$
, we have: (
![]() $*$
)
$*$
)
![]() $|\xi _i| \le 2 \sqrt {{D}}$
for all zeros
$|\xi _i| \le 2 \sqrt {{D}}$
for all zeros
![]() $\xi _i\in {\mathbb {C}}$
of f. This can be seen as follows. We measure distances in
$\xi _i\in {\mathbb {C}}$
of f. This can be seen as follows. We measure distances in
![]() ${\mathbb {P}}^1$
with respect to the projective (angular) distance. The disk of radius
${\mathbb {P}}^1$
with respect to the projective (angular) distance. The disk of radius
![]() $\theta $
around a point in
$\theta $
around a point in
![]() ${\mathbb {P}}^1$
, has measure at most
${\mathbb {P}}^1$
, has measure at most
![]() $\pi (\sin \theta )^2$
[Reference Bürgisser and Cucker15, Lemma 20.8]. Let
$\pi (\sin \theta )^2$
[Reference Bürgisser and Cucker15, Lemma 20.8]. Let
![]() $\sin \theta =(2\sqrt {{D}})^{-1}$
. Then a uniformly random point p in
$\sin \theta =(2\sqrt {{D}})^{-1}$
. Then a uniformly random point p in
![]() ${\mathbb {P}}^1$
lies in a disk of radius
${\mathbb {P}}^1$
lies in a disk of radius
![]() $\theta $
around a root of f with probability at most
$\theta $
around a root of f with probability at most
![]() ${D} (\sin \theta )^2 \le 1/4$
. Write
${D} (\sin \theta )^2 \le 1/4$
. Write
![]() $0\,{\stackrel {.}{=}} \,[1:0]$
and
$0\,{\stackrel {.}{=}} \,[1:0]$
and
![]() $\infty \,{\stackrel {.}{=}}], [0:1]$
, and note that
$\infty \,{\stackrel {.}{=}}], [0:1]$
, and note that
![]() $\operatorname {dist}(0,p) + \operatorname {dist}(p, \infty ) =\pi /2$
for any
$\operatorname {dist}(0,p) + \operatorname {dist}(p, \infty ) =\pi /2$
for any
![]() $p\in {\mathbb {P}}^1$
. Since
$p\in {\mathbb {P}}^1$
. Since
![]() $u^{-1}(\infty )$
is uniformly distributed, we conclude that with probability at least
$u^{-1}(\infty )$
is uniformly distributed, we conclude that with probability at least
![]() $3/4$
, each zero
$3/4$
, each zero
![]() $\zeta \in {\mathbb {P}}^1$
of g satisfies
$\zeta \in {\mathbb {P}}^1$
of g satisfies
![]() $\operatorname {dist}(\zeta , u^{-1}(\infty )) \ge \theta $
, which means
$\operatorname {dist}(\zeta , u^{-1}(\infty )) \ge \theta $
, which means
![]() $\operatorname {dist}(\zeta , u^{-1}( 0)) \le \pi /2 -\theta $
. The latter easily implies for the corresponding affine root
$\operatorname {dist}(\zeta , u^{-1}( 0)) \le \pi /2 -\theta $
. The latter easily implies for the corresponding affine root
![]() $\xi =\zeta _1/\zeta _0$
of f that
$\xi =\zeta _1/\zeta _0$
of f that
![]() $|\xi | \le (\tan \theta )^{-1} \le (\sin \theta )^{-1}= 2\sqrt {{D}}$
, hence, (
$|\xi | \le (\tan \theta )^{-1} \le (\sin \theta )^{-1}= 2\sqrt {{D}}$
, hence, (
![]() $*$
) holds.
$*$
) holds.
The maximum norm of a zero of
![]() $f\in {\mathbb {C}}[{t}]$
can be computed with a small relative error with
$f\in {\mathbb {C}}[{t}]$
can be computed with a small relative error with
![]() $O({D} \log {D})$
operations [Reference Pan34, Fact 2.2(b)], so we can test the property (
$O({D} \log {D})$
operations [Reference Pan34, Fact 2.2(b)], so we can test the property (
![]() $*$
). We repeatedly sample a new
$*$
). We repeatedly sample a new
![]() $u \in U(2)$
until (
$u \in U(2)$
until (
![]() $*$
) holds. Each iteration succeeds with probability at least
$*$
) holds. Each iteration succeeds with probability at least
![]() $\frac 34$
of success, so there are at most two iterations on average.
$\frac 34$
of success, so there are at most two iterations on average.
For a chosen
![]() $\varepsilon>0$
, we can now compute with Renegar’s algorithm the roots of f, up to precision
$\varepsilon>0$
, we can now compute with Renegar’s algorithm the roots of f, up to precision
![]() $\varepsilon $
with
$\varepsilon $
with
![]() $\operatorname {poly}({D}) \log \log \frac {1}{\varepsilon }$
operations (where the
$\operatorname {poly}({D}) \log \log \frac {1}{\varepsilon }$
operations (where the
![]() $\log \log 2\sqrt {{D}}$
is absorbed by
$\log \log 2\sqrt {{D}}$
is absorbed by
![]() $\operatorname {poly}({D})$
). By homogenising and transforming back with
$\operatorname {poly}({D})$
). By homogenising and transforming back with
![]() $u^{-1}$
, we obtain approximations
$u^{-1}$
, we obtain approximations
![]() $p_1,\dotsc ,p_{D}$
of the projective roots
$p_1,\dotsc ,p_{D}$
of the projective roots
![]() $\zeta _1,\ldots ,\zeta _{D}$
of g up to precision
$\zeta _1,\ldots ,\zeta _{D}$
of g up to precision
![]() $\varepsilon $
, measured in projective distance.
$\varepsilon $
, measured in projective distance.
The remaining difficulty is that the
![]() $p_i$
might not be approximate roots of g, in the sense of Smale. However, suppose that for all i we have
$p_i$
might not be approximate roots of g, in the sense of Smale. However, suppose that for all i we have
Using that
![]() $z \mapsto \gamma (g,z)^{-1}$
is 5-Lipschitz continuous on
$z \mapsto \gamma (g,z)^{-1}$
is 5-Lipschitz continuous on
![]() $\mathbb {P}^1$
(by Lemma I.31), we see that
$\mathbb {P}^1$
(by Lemma I.31), we see that
![]() $\varepsilon \gamma (g, \zeta _i) \leqslant \frac 16$
for all i. This is known to imply that
$\varepsilon \gamma (g, \zeta _i) \leqslant \frac 16$
for all i. This is known to imply that
![]() $p_i$
is an approximate zero of
$p_i$
is an approximate zero of
![]() $p_i$
([Reference Shub and Smale40], and Theorem I.12 for the constant). On the other hand, using again the Lipschitz property, we are sure that Condition (4.5) is met as soon as
$p_i$
([Reference Shub and Smale40], and Theorem I.12 for the constant). On the other hand, using again the Lipschitz property, we are sure that Condition (4.5) is met as soon as
![]() $\varepsilon \gamma _{\max } \leqslant \tfrac {1}{16}$
.
$\varepsilon \gamma _{\max } \leqslant \tfrac {1}{16}$
.
So starting with
![]() $\varepsilon = \frac 12$
, we compute points
$\varepsilon = \frac 12$
, we compute points
![]() $p_1,\dotsc ,p_{D}$
approximating
$p_1,\dotsc ,p_{D}$
approximating
![]() $\zeta _1,\dotsc ,\zeta _{D}$
up to precision
$\zeta _1,\dotsc ,\zeta _{D}$
up to precision
![]() $\varepsilon $
until (4.5) is met for all
$\varepsilon $
until (4.5) is met for all
![]() $p_i$
, squaring
$p_i$
, squaring
![]() $\varepsilon $
after each unsuccessful iteration. Note that Renegar’s algorithm need not be restarted when
$\varepsilon $
after each unsuccessful iteration. Note that Renegar’s algorithm need not be restarted when
![]() $\varepsilon $
is refined. We have
$\varepsilon $
is refined. We have
![]() $\varepsilon \gamma _{\max } \leqslant \tfrac {1}{16}$
after at most
$\varepsilon \gamma _{\max } \leqslant \tfrac {1}{16}$
after at most
![]() $\log \log ( 16\gamma _{\max } )$
iterations. Finally, note that we do not need to compute exactly
$\log \log ( 16\gamma _{\max } )$
iterations. Finally, note that we do not need to compute exactly
![]() $\gamma $
, an approximation within factor 2 is enough, with appropriate modifications of the constants, and this is achieved by
$\gamma $
, an approximation within factor 2 is enough, with appropriate modifications of the constants, and this is achieved by
![]() $\gamma _{\mathrm {Frob}}$
, see (1.4), which we can compute in
$\gamma _{\mathrm {Frob}}$
, see (1.4), which we can compute in
![]() $\operatorname {poly}({D})$
operations.
$\operatorname {poly}({D})$
operations.
Lemma 4.6. Let
![]() $f \in {\mathbb {C}}[z_0,\ldots ,z_n]$
be homogeneous of degree
$f \in {\mathbb {C}}[z_0,\ldots ,z_n]$
be homogeneous of degree
![]() ${D}$
, and let
${D}$
, and let
![]() $\ell \subseteq \mathbb {P}^n$
be a uniformly distributed random projective line. Then
$\ell \subseteq \mathbb {P}^n$
be a uniformly distributed random projective line. Then
![]() ${\mathbb {E}}_{\ell } \left [ \Gamma (f|_\ell )^2 \right ] \leqslant 2n\; \Gamma (f)^2$
.
${\mathbb {E}}_{\ell } \left [ \Gamma (f|_\ell )^2 \right ] \leqslant 2n\; \Gamma (f)^2$
.
Proof. Let
![]() $\ell \subseteq \mathbb {P}^n$
be a uniformly distributed random projective line, and let
$\ell \subseteq \mathbb {P}^n$
be a uniformly distributed random projective line, and let
![]() $\zeta \in \ell $
be uniformly distributed among the zeros of
$\zeta \in \ell $
be uniformly distributed among the zeros of
![]() $f|_\ell $
. Then
$f|_\ell $
. Then
![]() $\zeta $
is also a uniformly distributed zero of f (see Corollary I.9). Let
$\zeta $
is also a uniformly distributed zero of f (see Corollary I.9). Let
![]() $\theta $
denote the angle between the tangent line
$\theta $
denote the angle between the tangent line
![]() $T_{\zeta } \ell $
and the line
$T_{\zeta } \ell $
and the line
![]() $T_{\zeta } V(f)^{\perp }$
normal to
$T_{\zeta } V(f)^{\perp }$
normal to
![]() $V(f)$
at
$V(f)$
at
![]() $\zeta $
. By an elementary geometric reasoning, we have
$\zeta $
. By an elementary geometric reasoning, we have
![]() $\|\mathrm {d} _{\zeta } f|_\ell \| = \|\mathrm {d} _{\zeta } f\| \cos \theta $
. Moreover,
$\|\mathrm {d} _{\zeta } f|_\ell \| = \|\mathrm {d} _{\zeta } f\| \cos \theta $
. Moreover,
![]() $\| \mathrm {d} _{\zeta }^k f|_\ell \|_{\mathrm {Frob}} \leqslant \| \mathrm {d} ^k_{\zeta } f\|_{\mathrm {Frob}}$
. So it follows that
$\| \mathrm {d} _{\zeta }^k f|_\ell \|_{\mathrm {Frob}} \leqslant \| \mathrm {d} ^k_{\zeta } f\|_{\mathrm {Frob}}$
. So it follows that
In order to bound this, we consider now a related but different distribution. As above, let
![]() $\zeta $
be a uniformly distributed zero of f. Consider now a uniformly distributed random projective line
$\zeta $
be a uniformly distributed zero of f. Consider now a uniformly distributed random projective line
![]() $\ell '$
passing through
$\ell '$
passing through
![]() $\zeta $
. The two distributions
$\zeta $
. The two distributions
![]() $(\ell ,\zeta )$
and
$(\ell ,\zeta )$
and
![]() $(\zeta ,\ell ')$
are related by Lemma I.5 as follows: for any integrable function h of
$(\zeta ,\ell ')$
are related by Lemma I.5 as follows: for any integrable function h of
![]() $\ell $
and
$\ell $
and
![]() $\zeta $
, we have
$\zeta $
, we have
where c is some normalisation constant and where
![]() ${\operatorname {det}\nolimits }^\perp ({T}_{\zeta } \ell ', {T}_{\zeta } V(f))$
is defined in I, Section 2.1. It is only a matter of unfolding definitions to see that it is equal to
${\operatorname {det}\nolimits }^\perp ({T}_{\zeta } \ell ', {T}_{\zeta } V(f))$
is defined in I, Section 2.1. It is only a matter of unfolding definitions to see that it is equal to
![]() $\cos \theta '$
, where
$\cos \theta '$
, where
![]() $\theta '$
denotes the angle between
$\theta '$
denotes the angle between
![]() $T_{\zeta } \ell '$
and
$T_{\zeta } \ell '$
and
![]() $T_{\zeta } V(f)^\perp $
. With
$T_{\zeta } V(f)^\perp $
. With
![]() $h = 1$
, we obtain
$h = 1$
, we obtain
![]() $c = \mathbb {E} \left [ \cos \theta ' \right ]^{-1}$
and, therefore, we get
$c = \mathbb {E} \left [ \cos \theta ' \right ]^{-1}$
and, therefore, we get
We analyse now the distribution of
![]() $\theta '$
:
$\theta '$
:
![]() $\cos (\theta ')^2$
is a beta-distributed variable with parameters
$\cos (\theta ')^2$
is a beta-distributed variable with parameters
![]() $1$
and
$1$
and
![]() $n-1$
: indeed,
$n-1$
: indeed,
![]() $\cos (\theta ')^2 = {\left | {u_1} \right |}^2 / \|u\|^2$
where
$\cos (\theta ')^2 = {\left | {u_1} \right |}^2 / \|u\|^2$
where
![]() $u\in \mathbb {C}^n$
is a Gaussian random vector, and it is well known that the distribution of this quotient of
$u\in \mathbb {C}^n$
is a Gaussian random vector, and it is well known that the distribution of this quotient of
![]() $\chi ^2$
-distributed random variables is a beta-distributed variable. Generally, the moments of a beta-distributed random variable Z with parameters
$\chi ^2$
-distributed random variables is a beta-distributed variable. Generally, the moments of a beta-distributed random variable Z with parameters
![]() $\alpha ,\beta $
satisfy
$\alpha ,\beta $
satisfy
where B is the Beta function and
![]() $r>-\alpha $
. In particular, for
$r>-\alpha $
. In particular, for
![]() $r> -1$
,
$r> -1$
,
and, hence
 $$ \begin{align} \mathbb{E} \left[ \cos(\theta')^{-1} \right] \mathbb{E} \left[ \cos(\theta') \right]^{-1} = \frac{B(\frac12, n-1)}{B(\frac32, n-1)} = 2n - 1. \end{align} $$
$$ \begin{align} \mathbb{E} \left[ \cos(\theta')^{-1} \right] \mathbb{E} \left[ \cos(\theta') \right]^{-1} = \frac{B(\frac12, n-1)}{B(\frac32, n-1)} = 2n - 1. \end{align} $$
Continuing with (4.8), we obtain
the second last equality (4.15) since the random variable
![]() $\theta '$
is independent from
$\theta '$
is independent from
![]() $\zeta $
. This concludes the proof.
$\zeta $
. This concludes the proof.
4.2 Proof of Theorem 4.2
We now study the average complexity of the Algorithm
![]() , where
, where
![]() ${\mathbf u} \in {\mathcal {U}}$
is uniformly distributed. Recall that
${\mathbf u} \in {\mathcal {U}}$
is uniformly distributed. Recall that
![]() $\Gamma ({\mathbf u}\cdot F)= \Gamma (F)$
, by unitary invariance of
$\Gamma ({\mathbf u}\cdot F)= \Gamma (F)$
, by unitary invariance of
![]() $\gamma _{\mathrm {Frob}}$
, and
$\gamma _{\mathrm {Frob}}$
, and
![]() $L({\mathbf u} \cdot F) = L(F) + O(n^3)$
.
$L({\mathbf u} \cdot F) = L(F) + O(n^3)$
.
The sampling operation costs at most
![]() $\operatorname {poly}(n, {D}) \cdot L(F) \cdot \log \log \Gamma (F)$
on average, by Proposition 4.3. The expected cost of the continuation phase is
$\operatorname {poly}(n, {D}) \cdot L(F) \cdot \log \log \Gamma (F)$
on average, by Proposition 4.3. The expected cost of the continuation phase is
![]() $\operatorname {poly}(n, {D}) \cdot L(F) \cdot K (\log K +\log \varepsilon ^{-1})$
, by Proposition 3.10, where
$\operatorname {poly}(n, {D}) \cdot L(F) \cdot K (\log K +\log \varepsilon ^{-1})$
, by Proposition 3.10, where
![]() $K=K({\mathbf u} \cdot F, \mathbf {1}_{{\mathcal {U}}}, {\mathbf v}, \zeta )$
and
$K=K({\mathbf u} \cdot F, \mathbf {1}_{{\mathcal {U}}}, {\mathbf v}, \zeta )$
and
![]() $({\mathbf v}, \zeta )$
is the sampled initial pair. By unitary invariance,
$({\mathbf v}, \zeta )$
is the sampled initial pair. By unitary invariance,
where
![]() ${\mathbf v}' = {\mathbf v}{\mathbf u}$
. Moreover, since
${\mathbf v}' = {\mathbf v}{\mathbf u}$
. Moreover, since
![]() ${\mathbf v}$
is uniformly distributed and independent from
${\mathbf v}$
is uniformly distributed and independent from
![]() ${\mathbf u}$
,
${\mathbf u}$
,
![]() ${\mathbf v}'$
is also uniformly distributed and independent from
${\mathbf v}'$
is also uniformly distributed and independent from
![]() ${\mathbf u}$
, and
${\mathbf u}$
, and
![]() $\zeta $
is a uniformly distributed zero of
$\zeta $
is a uniformly distributed zero of
![]() ${\mathbf v}' \cdot F$
. So the following proposition concludes the proof of Theorem 4.2.
${\mathbf v}' \cdot F$
. So the following proposition concludes the proof of Theorem 4.2.
Proposition 4.7. Let
![]() ${\mathbf u}, {\mathbf v} \in {\mathcal {U}}$
be independent and uniformly distributed random variables, let
${\mathbf u}, {\mathbf v} \in {\mathcal {U}}$
be independent and uniformly distributed random variables, let
![]() $\zeta $
be a uniformly distributed zero of
$\zeta $
be a uniformly distributed zero of
![]() ${\mathbf v}\cdot F$
and let
${\mathbf v}\cdot F$
and let
![]() $K = K(F, {\mathbf u}, {\mathbf v}, \zeta )$
. Then we have
$K = K(F, {\mathbf u}, {\mathbf v}, \zeta )$
. Then we have
![]() ${\mathbb {E}} \left [ K \right ] \leqslant \operatorname {poly}(n, {D}) \Gamma (F)$
and
${\mathbb {E}} \left [ K \right ] \leqslant \operatorname {poly}(n, {D}) \Gamma (F)$
and
![]() ${\mathbb {E}} \left [ K \log K \right ] \leqslant \operatorname {poly}(n, {D}) \cdot \Gamma (F) \log \Gamma (F)$
.
${\mathbb {E}} \left [ K \log K \right ] \leqslant \operatorname {poly}(n, {D}) \cdot \Gamma (F) \log \Gamma (F)$
.
Sketch of proof
The first bound
![]() ${\mathbb {E}} \left [ K \right ] \leqslant \operatorname {poly}(n, {D}) \Gamma (F)$
was shown in Theorem I.27. Following mutatis mutandis the proof of Theorem I.27 (the only additional fact needed is Proposition 4.8 below for
${\mathbb {E}} \left [ K \right ] \leqslant \operatorname {poly}(n, {D}) \Gamma (F)$
was shown in Theorem I.27. Following mutatis mutandis the proof of Theorem I.27 (the only additional fact needed is Proposition 4.8 below for
![]() $a=3/2$
), we obtain that
$a=3/2$
), we obtain that
Next, we observe that the function
![]() $h : x \mapsto x^{\frac 23} (1+ \log x^{\frac 23})$
is concave on
$h : x \mapsto x^{\frac 23} (1+ \log x^{\frac 23})$
is concave on
![]() $[1,\infty )$
. By Jensen’s inequalities, it follows that
$[1,\infty )$
. By Jensen’s inequalities, it follows that
which gives the claim.
The following statement extends Proposition I.17 to more general exponents. The proof technique is more elementary, and the result, although not as tight, good enough for our purpose.
Proposition 4.8. Let
![]() $M \in \mathbb {C}^{n\times (n+1)}$
be a random matrix whose rows are independent uniformly distributed vectors in
$M \in \mathbb {C}^{n\times (n+1)}$
be a random matrix whose rows are independent uniformly distributed vectors in
![]() $\mathbb {S}(\mathbb {C}^{n+1})$
, and let
$\mathbb {S}(\mathbb {C}^{n+1})$
, and let
![]() $\sigma _{\min }(M)$
be the smallest singular value of M. For all
$\sigma _{\min }(M)$
be the smallest singular value of M. For all
![]() $a \in [1,2)$
,
$a \in [1,2)$
,
and, equivalently with the notations of Proposition I.17,
Proof. For short, let
![]() $\sigma $
denote
$\sigma $
denote
![]() $\sigma _{\min }(M)$
. Let
$\sigma _{\min }(M)$
. Let
![]() $u_1,\dotsc ,u_n$
be the rows of M. By definition, there is a unit vector
$u_1,\dotsc ,u_n$
be the rows of M. By definition, there is a unit vector
![]() $x \in \mathbb {C}^n$
, such that
$x \in \mathbb {C}^n$
, such that
If
![]() $V_i$
denotes the subspace of
$V_i$
denotes the subspace of
![]() $\mathbb {C}^{n+1}$
spanned by all
$\mathbb {C}^{n+1}$
spanned by all
![]() $u_j$
except
$u_j$
except
![]() $u_i$
, and
$u_i$
, and
![]() $b_i$
denotes the squared Euclidean distance of
$b_i$
denotes the squared Euclidean distance of
![]() $u_i$
to
$u_i$
to
![]() $V_i$
, then (4.20) implies
$V_i$
, then (4.20) implies
![]() $b_i \leqslant {\left | {x_i} \right |}^{-2} \sigma ^2$
for all i. Moreover, since x is a unit vector, there is at least one i, such that
$b_i \leqslant {\left | {x_i} \right |}^{-2} \sigma ^2$
for all i. Moreover, since x is a unit vector, there is at least one i, such that
![]() ${\left | {x_i} \right |}^2 \geqslant \frac {1}{n}$
. Hence,
${\left | {x_i} \right |}^2 \geqslant \frac {1}{n}$
. Hence,
![]() $n \sigma ^2 \geqslant \min _i b_i$
and, therefore
$n \sigma ^2 \geqslant \min _i b_i$
and, therefore
 $$ \begin{align} {\mathbb{E}} \left[ \sigma^{-2a} \right] \leqslant {n^a \mathbb{E} \left[\max_i b_i^{-a} \right]} \leqslant n^a \sum_{i=1}^n \mathbb{E}\left[b_i^{-a}\right]. \end{align} $$
$$ \begin{align} {\mathbb{E}} \left[ \sigma^{-2a} \right] \leqslant {n^a \mathbb{E} \left[\max_i b_i^{-a} \right]} \leqslant n^a \sum_{i=1}^n \mathbb{E}\left[b_i^{-a}\right]. \end{align} $$
To analyse the distribution of
![]() $b_i$
consider, for fixed
$b_i$
consider, for fixed
![]() $V_i$
, a standard Gaussian vector
$V_i$
, a standard Gaussian vector
![]() $p_i$
in
$p_i$
in
![]() $V_i$
, and an independent standard Gaussian vector
$V_i$
, and an independent standard Gaussian vector
![]() $q_i$
in
$q_i$
in
![]() $V_i^\perp $
(note
$V_i^\perp $
(note
![]() $\dim V_i^\perp =4$
). Since
$\dim V_i^\perp =4$
). Since
![]() $u_i$
is uniformly distributed in the sphere, it has the same distribution as
$u_i$
is uniformly distributed in the sphere, it has the same distribution as
![]() $(p_i+q_i)/\sqrt {\|p_i\|^2 + \|q_i\|^2}$
. In particular,
$(p_i+q_i)/\sqrt {\|p_i\|^2 + \|q_i\|^2}$
. In particular,
![]() $b_i$
has the same distribution as
$b_i$
has the same distribution as
![]() $\|q_i\|^2/(\|p_i\|^2 + \|q_i\|^2)$
, which is a Beta distribution with parameters
$\|q_i\|^2/(\|p_i\|^2 + \|q_i\|^2)$
, which is a Beta distribution with parameters
![]() $2, n-1$
, since
$2, n-1$
, since
![]() $\|p_i\|^2$
and
$\|p_i\|^2$
and
![]() $\|q_i\|^2$
are independent
$\|q_i\|^2$
are independent
![]() $\chi ^2$
-distributed random variables with
$\chi ^2$
-distributed random variables with
![]() $2n-2$
and
$2n-2$
and
![]() $4$
degrees of freedom, respectively. By (4.9), we have for the moments, using
$4$
degrees of freedom, respectively. By (4.9), we have for the moments, using
![]() $a<2$
,
$a<2$
,
We obtain
In combination with (4.21), this gives the result.
4.3 Confidence boosting and proof of Theorem 1.2
We may leverage the quadratic convergence of Newton’s iteration to increase the confidence in the result of Algorithm 5 and reduce the dependence on
![]() $\varepsilon $
(the maximum probability of failure) from
$\varepsilon $
(the maximum probability of failure) from
![]() $\log \frac 1\varepsilon $
down to
$\log \frac 1\varepsilon $
down to
![]() $\log \log \frac 1\varepsilon $
, so that we can choose
$\log \log \frac 1\varepsilon $
, so that we can choose
![]() $\varepsilon = \smash {10^{-10^{100}}}$
without afterthoughts, at least in the BSS model. On a physical computer, the working precision should be comparable with
$\varepsilon = \smash {10^{-10^{100}}}$
without afterthoughts, at least in the BSS model. On a physical computer, the working precision should be comparable with
![]() $\varepsilon $
, which imposes some limitations. A complete certification, without possibility of error, with
$\varepsilon $
, which imposes some limitations. A complete certification, without possibility of error, with
![]() $\operatorname {poly}(n,{D})$
evaluations of F, seems difficult to reach in the black-box model: with only
$\operatorname {poly}(n,{D})$
evaluations of F, seems difficult to reach in the black-box model: with only
![]() $\operatorname {poly}(n,{D})$
evaluations, we cannot distinguish a polynomial system F from the infinitely many other systems with the same evaluations.
$\operatorname {poly}(n,{D})$
evaluations, we cannot distinguish a polynomial system F from the infinitely many other systems with the same evaluations.
To describe this boosting procedure, we first recall some details about
![]() $\alpha $
-theory and Part I. Let
$\alpha $
-theory and Part I. Let
![]() $F\in {\mathcal {H}}$
be a polynomial system and
$F\in {\mathcal {H}}$
be a polynomial system and
![]() $z\in \mathbb {P}^n$
be a projective point. Let
$z\in \mathbb {P}^n$
be a projective point. Let
![]() ${\mathcal {N}}_F(z)$
denote the projective Newton iteration (and
${\mathcal {N}}_F(z)$
denote the projective Newton iteration (and
![]() ${\mathcal {N}}^k_F(z)$
denote the composition of k projective Newton iterations). Let
${\mathcal {N}}^k_F(z)$
denote the composition of k projective Newton iterations). Let
There is an absolute constant
![]() $\alpha _0$
, such that for any
$\alpha _0$
, such that for any
![]() $z\in \mathbb {P}^n$
, if
$z\in \mathbb {P}^n$
, if
![]() $\beta (F, z) \gamma (F, z) \leqslant \alpha _0$
, then z is an approximate zero of F [Reference Dedieu and Shub17, Theorem 1] (one may take
$\beta (F, z) \gamma (F, z) \leqslant \alpha _0$
, then z is an approximate zero of F [Reference Dedieu and Shub17, Theorem 1] (one may take
![]() $\alpha _0= 1/137$
). This is one of many variants of the
$\alpha _0= 1/137$
). This is one of many variants of the
![]() $\alpha $
-theorem of [Reference Smale45]. There may be differences in the definition of
$\alpha $
-theorem of [Reference Smale45]. There may be differences in the definition of
![]() $\gamma $
or
$\gamma $
or
![]() $\beta $
, or even the precise definition of approximate zero, but they only change the constant
$\beta $
, or even the precise definition of approximate zero, but they only change the constant
![]() $\alpha _0$
.
$\alpha _0$
.
It is important to be slightly more precise about the output of Algorithm 5 (when all
![]() $\gamma $
’s are correctly estimated, naturally, and hence, the output is an approximate zero of F): by the design of the numerical continuation (see Proposition I.22 with
$\gamma $
’s are correctly estimated, naturally, and hence, the output is an approximate zero of F): by the design of the numerical continuation (see Proposition I.22 with
![]() $C=15$
and
$C=15$
and
![]() $A=\frac {1}{4C}$
), the output point
$A=\frac {1}{4C}$
), the output point
![]() $z^*\in \mathbb {P}^n$
satisfies
$z^*\in \mathbb {P}^n$
satisfies
for some zero
![]() $\zeta $
of F, where
$\zeta $
of F, where
![]() $\hat {\gamma }_{\mathrm {Frob}}$
is the split Frobenius
$\hat {\gamma }_{\mathrm {Frob}}$
is the split Frobenius
![]() $\gamma $
number (see Section 2.3). This implies (see Theorem I.12), using
$\gamma $
number (see Section 2.3). This implies (see Theorem I.12), using
![]() $\gamma \leqslant \hat {\gamma }_{\mathrm {Frob}}$
, that
$\gamma \leqslant \hat {\gamma }_{\mathrm {Frob}}$
, that
The last important property we recall is the 15-Lipschitz continuity of the function
![]() $z\in \mathbb {P}^n \mapsto \hat {\gamma }_{\mathrm {Frob}}(F, z)^{-1}$
(Lemmas I.26 and I.31).
$z\in \mathbb {P}^n \mapsto \hat {\gamma }_{\mathrm {Frob}}(F, z)^{-1}$
(Lemmas I.26 and I.31).
Algorithm 6 checks the criterion
![]() $\beta (F, z^*) \gamma (F, z^*) \leqslant \alpha _0$
after having refined to
$\beta (F, z^*) \gamma (F, z^*) \leqslant \alpha _0$
after having refined to
![]() $z^*$
a presumed approximate zero z with a few Newton iterations. If the input point z is indeed an approximate zero, then
$z^*$
a presumed approximate zero z with a few Newton iterations. If the input point z is indeed an approximate zero, then
![]() $\beta (F, z^*)$
will be very small, and it will satisfy the criterion above even with a very gross approximation of
$\beta (F, z^*)$
will be very small, and it will satisfy the criterion above even with a very gross approximation of
![]() $\gamma (F,z^*)$
.
$\gamma (F,z^*)$
.

Proposition 4.9. On input
![]() $F\in {\mathcal {H}}$
,
$F\in {\mathcal {H}}$
,
![]() $z\in \mathbb {P}^n$
and
$z\in \mathbb {P}^n$
and
![]() $\varepsilon \in (0,\frac 14)$
, Algorithm Boost outputs some
$\varepsilon \in (0,\frac 14)$
, Algorithm Boost outputs some
![]() $z^*\in \mathbb {P}^n$
(succeeds) or fails after
$z^*\in \mathbb {P}^n$
(succeeds) or fails after
![]() $\operatorname {poly}(n, {D})L(F) \log \log \varepsilon ^{-1}$
operations. If z satisfies (4.26), then it succeeds with probability at least
$\operatorname {poly}(n, {D})L(F) \log \log \varepsilon ^{-1}$
operations. If z satisfies (4.26), then it succeeds with probability at least
![]() $\frac 34$
. If it succeeds, then the output point is an approximate zero of F with probability at least
$\frac 34$
. If it succeeds, then the output point is an approximate zero of F with probability at least
![]() $1-\varepsilon $
.
$1-\varepsilon $
.
Proof. We use the notations (k,
![]() $z^*$
and c) of Algorithm 6. Assume first that (4.26) holds for z and some zero
$z^*$
and c) of Algorithm 6. Assume first that (4.26) holds for z and some zero
![]() $\zeta $
of F. By (4.27) and (4.26),
$\zeta $
of F. By (4.27) and (4.26),
Using the Lipschitz continuity and (4.28),
and it follows from (4.27) and (4.26), again, that
Besides, by Theorem 3.3, we have with probability at least
![]() $\frac 34$
,
$\frac 34$
,
(note that the computation of c involves n calls to GammaProb, each returning a result outside the specified range with probability at most
![]() $\frac {1}{4n}$
. So the n computations are correct with probability at least
$\frac {1}{4n}$
. So the n computations are correct with probability at least
![]() $\frac 34$
). It follows from (4.32) and (4.33), along with the choice of k, that
$\frac 34$
). It follows from (4.32) and (4.33), along with the choice of k, that
with probability at least
![]() $\frac 34$
. We conclude, assuming (4.26), that Algorithm BlackBoxSolve succeeds with probability at least
$\frac 34$
. We conclude, assuming (4.26), that Algorithm BlackBoxSolve succeeds with probability at least
![]() $\frac 34$
.
$\frac 34$
.
Assume now that the algorithm succeeds, but
![]() $z^*$
, the output point, is not an approximate zero of F. On the one hand,
$z^*$
, the output point, is not an approximate zero of F. On the one hand,
![]() $z^*$
is not an approximate zero, so
$z^*$
is not an approximate zero, so
and on the other hand, the algorithm succeeds, so
![]() $2^{2^{k-1}} \beta (F, z^*) c \leqslant \alpha _0$
, and then
$2^{2^{k-1}} \beta (F, z^*) c \leqslant \alpha _0$
, and then
By definition (2.16) of
![]() $\hat {\gamma }_{\mathrm {Frob}}(F, z^*)$
, and since
$\hat {\gamma }_{\mathrm {Frob}}(F, z^*)$
, and since
![]() $c = \kappa (F,z) (\Gamma _1^2 + \cdots +\Gamma _n^2)^{\frac 12}$
, where
$c = \kappa (F,z) (\Gamma _1^2 + \cdots +\Gamma _n^2)^{\frac 12}$
, where
![]() $\Gamma _i$
denotes the value returned by the call to
$\Gamma _i$
denotes the value returned by the call to
![]() , we get
, we get
This implies that, for some i,
By the choice of k,
![]() $2^{2^{k-1}} \geqslant \varepsilon ^{-1}$
, and using the tail bound in Theorem 3.3, with
$2^{2^{k-1}} \geqslant \varepsilon ^{-1}$
, and using the tail bound in Theorem 3.3, with
![]() $t=\varepsilon ^{-1}$
, (4.38) may only happen with probability at most
$t=\varepsilon ^{-1}$
, (4.38) may only happen with probability at most
 $$ \begin{align} \frac{1}{4n}\Big(\frac{1}{4n}\Big)^{\frac12 \log_2 t} \le \left(\frac{1}{4}\right)^{\frac12 \log_2 t} = 2^{- \log_2 t} = \varepsilon. \end{align} $$
$$ \begin{align} \frac{1}{4n}\Big(\frac{1}{4n}\Big)^{\frac12 \log_2 t} \le \left(\frac{1}{4}\right)^{\frac12 \log_2 t} = 2^{- \log_2 t} = \varepsilon. \end{align} $$
The complexity bound is clear, since a Newton’s iteration requires only
![]() $\operatorname {poly}(n, {D}) L(F)$
operations.
$\operatorname {poly}(n, {D}) L(F)$
operations.
The combination of BlackBoxSolve and Boost leads to Algorithm 7, BoostBlackBoxSolve.

Proof of Theorem 1.2
The correctness, with probability at least
![]() $1-\varepsilon $
, is clear, by the correctness of Boost. An iteration of Algorithm 7 succeeds if and only if Boost succeeds. If (4.26) holds (which it does with probability at least
$1-\varepsilon $
, is clear, by the correctness of Boost. An iteration of Algorithm 7 succeeds if and only if Boost succeeds. If (4.26) holds (which it does with probability at least
![]() $\frac 34$
), then Boost succeeds with probability at least
$\frac 34$
), then Boost succeeds with probability at least
![]() $\frac 34$
. So each iteration of Algorithm 7 succeeds with probability at least
$\frac 34$
. So each iteration of Algorithm 7 succeeds with probability at least
![]() $\frac 12$
, and the expected number of iterations is, therefore, at most two. Furthermore, on input
$\frac 12$
, and the expected number of iterations is, therefore, at most two. Furthermore, on input
![]() ${\mathbf u} \cdot F$
, the average cost of each iteration is
${\mathbf u} \cdot F$
, the average cost of each iteration is
![]() $\operatorname {poly}(n,{D}) L(F) \Gamma (F) \log \Gamma (F)$
for BlackBoxSolve and
$\operatorname {poly}(n,{D}) L(F) \Gamma (F) \log \Gamma (F)$
for BlackBoxSolve and
![]() $\operatorname {poly}(n,{D}) L(F) \log \log \varepsilon ^{-1}$
for Boost.
$\operatorname {poly}(n,{D}) L(F) \log \log \varepsilon ^{-1}$
for Boost.
Proof of Corollary 1.3
Let
![]() ${\mathbf u}\in {\mathcal {U}}$
be uniformly distributed and independent from F. By hypothesis,
${\mathbf u}\in {\mathcal {U}}$
be uniformly distributed and independent from F. By hypothesis,
![]() ${\mathbf u}\cdot F$
and F have the same distribution, so we study
${\mathbf u}\cdot F$
and F have the same distribution, so we study
![]() ${\mathbf u}\cdot F$
instead. Then Theorem 1.2 applies, and we obtain, for fixed
${\mathbf u}\cdot F$
instead. Then Theorem 1.2 applies, and we obtain, for fixed
![]() $F\in {\mathcal {H}}$
and random
$F\in {\mathcal {H}}$
and random
![]() $u\in {\mathcal {U}}$
, that BoostBlackBoxSolve terminates after
$u\in {\mathcal {U}}$
, that BoostBlackBoxSolve terminates after
operations on average. With the concavity on
![]() $[1,\infty )$
of the function
$[1,\infty )$
of the function
![]() $h:x\mapsto x^{\frac 12} \log x^{\frac 12}$
, Jensen’s inequality ensures that
$h:x\mapsto x^{\frac 12} \log x^{\frac 12}$
, Jensen’s inequality ensures that
which gives the complexity bound.
5 Probabilistic analysis of algebraic branching programs
The goal of this section is to prove our second main result, Theorem 1.5. Recall from Section 1.7 the notion of a Gaussian random ABP. We first state a result that connects the notions of irreducible Gaussian random ABPs with that of irreducible polynomials.
Lemma 5.1. Let f be the homogeneous polynomial computed by an irreducible Gaussian random ABP in the variables
![]() $z_0,\dotsc ,z_n$
. If
$z_0,\dotsc ,z_n$
. If
![]() $n\geqslant 2$
, then f is almost surely irreducible.
$n\geqslant 2$
, then f is almost surely irreducible.
Proof. The proof is by induction on the degree
![]() ${D}$
, the base case
${D}$
, the base case
![]() ${D}=1$
being clear. So suppose
${D}=1$
being clear. So suppose
![]() ${D}\ge 2$
. In the given ABP, replace the label of each edge e by a new variable
${D}\ge 2$
. In the given ABP, replace the label of each edge e by a new variable
![]() $y_e$
. Let G denote the modified ABP and g the polynomial computed by G. The polynomial f is obtained as a restriction of g to a generic linear subspace, so, by Bertini’s theorem, it suffices to prove that g is irreducible (recall
$y_e$
. Let G denote the modified ABP and g the polynomial computed by G. The polynomial f is obtained as a restriction of g to a generic linear subspace, so, by Bertini’s theorem, it suffices to prove that g is irreducible (recall
![]() $n\ge 2$
).
$n\ge 2$
).
Let s denote the source vertex and t the target vertex of G. There is a path from s to t: let
![]() $e = (s,v)$
be its first edge. We remove s and all vertices in the first layer different from v, making v the source vertex of a new ABP denoted H. It is irreducible: if the layers of G have the sizes
$e = (s,v)$
be its first edge. We remove s and all vertices in the first layer different from v, making v the source vertex of a new ABP denoted H. It is irreducible: if the layers of G have the sizes
![]() $1, r_1,\dotsc , r_{{D}-1}, 1$
, then the layers of H have the sizes
$1, r_1,\dotsc , r_{{D}-1}, 1$
, then the layers of H have the sizes
![]() $1,r_2,\dotsc ,r_{{D}-1}, 1$
. The paths of H from source to target are in bijective correspondence with the paths of G from v to t. Therefore,
$1,r_2,\dotsc ,r_{{D}-1}, 1$
. The paths of H from source to target are in bijective correspondence with the paths of G from v to t. Therefore,
![]() $g = y_e p + q$
, where p is the polynomial computed by H, and q corresponds to the paths from s to t which avoid v. By induction hypothesis, p is irreducible. Clearly,
$g = y_e p + q$
, where p is the polynomial computed by H, and q corresponds to the paths from s to t which avoid v. By induction hypothesis, p is irreducible. Clearly,
![]() $q\neq 0$
because
$q\neq 0$
because
![]() $r_1> 0$
, and p does not divide q since the variable corresponding to an edge leaving v does not appear in q (such edge exists due to
$r_1> 0$
, and p does not divide q since the variable corresponding to an edge leaving v does not appear in q (such edge exists due to
![]() ${D}\ge 2$
). We conclude that p and q are relatively prime. Moreover, the variable
${D}\ge 2$
). We conclude that p and q are relatively prime. Moreover, the variable
![]() $y_e$
does neither appear in p nor in q, so it follows that g is irreducible.
$y_e$
does neither appear in p nor in q, so it follows that g is irreducible.
We also remark that a random polynomial computed by a Gaussian random ABP may define a random hypersurface in
![]() $\mathbb {P}^n$
that is always singular. It is rather uncommon in our field to be able to study stochastic models featuring singularities almost surely, so it is worth a lemma.
$\mathbb {P}^n$
that is always singular. It is rather uncommon in our field to be able to study stochastic models featuring singularities almost surely, so it is worth a lemma.
Lemma 5.2. If
![]() $f \in \mathbb {C}[z_0,\dotsc ,z_n]$
is the polynomial computed by a algebraic branching program with at most n edges, then the hypersurface
$f \in \mathbb {C}[z_0,\dotsc ,z_n]$
is the polynomial computed by a algebraic branching program with at most n edges, then the hypersurface
![]() $V(f) \subseteq \mathbb {P}^n$
is singular.
$V(f) \subseteq \mathbb {P}^n$
is singular.
Proof. Let e be the number of edges of the algebraic branching program computing f. After a linear change of variables, we may assume that f depends only on
![]() $z_0,\dotsc ,z_{e-1}$
. The singular locus of
$z_0,\dotsc ,z_{e-1}$
. The singular locus of
![]() $V(f)$
is defined by the vanishing of the partial derivatives
$V(f)$
is defined by the vanishing of the partial derivatives
![]() $\frac {\partial }{\partial z_i} f$
. But these derivatives are identically 0 for
$\frac {\partial }{\partial z_i} f$
. But these derivatives are identically 0 for
![]() $i\geqslant e$
, so that the singular locus is defined by at most e equations. So it is nonempty.
$i\geqslant e$
, so that the singular locus is defined by at most e equations. So it is nonempty.
As already mentioned before, the distribution of a polynomial computed by a Gaussian random ABP is best understood in terms of matrices. This calls for the introduction of some terminology. For any
![]() ${D}$
-tuple
${D}$
-tuple
![]() ${\mathbf r} =(r_1,\dotsc ,r_{D})$
, let
${\mathbf r} =(r_1,\dotsc ,r_{D})$
, let
![]() $M_{\mathbf r}(n+1)$
(and
$M_{\mathbf r}(n+1)$
(and
![]() $M_{\mathbf r}$
for short) denote the space of all
$M_{\mathbf r}$
for short) denote the space of all
![]() ${D}$
-tuples of matrices
${D}$
-tuples of matrices
![]() $(A_1(z),\dotsc ,A_{D}(z))$
, of respective size
$(A_1(z),\dotsc ,A_{D}(z))$
, of respective size
![]() $r_{D}\times r_1$
,
$r_{D}\times r_1$
,
![]() $r_1\times r_2$
, …,
$r_1\times r_2$
, …,
![]() $r_{{D}-1}\times r_{D}$
, with degree one homogeneous entries in
$r_{{D}-1}\times r_{D}$
, with degree one homogeneous entries in
![]() $z=(z_0,\ldots ,z_n)$
(it is convenient to think of
$z=(z_0,\ldots ,z_n)$
(it is convenient to think of
![]() $r_0=r_{D}$
). We have
$r_0=r_{D}$
). We have
![]() $\dim _{{\mathbb {C}}}M_{{\mathbf r}}=(n+1)\sum _{i=1}^{D} r_{i-1}r_i$
. For
$\dim _{{\mathbb {C}}}M_{{\mathbf r}}=(n+1)\sum _{i=1}^{D} r_{i-1}r_i$
. For
![]() $A \in M_{\mathbf r}$
, we define the degree
$A \in M_{\mathbf r}$
, we define the degree
![]() ${D}$
homogeneous polynomial
${D}$
homogeneous polynomial
A Hermitian norm is defined on
![]() $M_{\mathbf r}$
by
$M_{\mathbf r}$
by
 $$ \begin{align*} \|A\|^2 \,{\stackrel{.}{=}}\, \sum_{i=1}^{D} \sum_{j=0}^n \|A_i(e_j)\|^2_{\mathrm{Frob}}, \end{align*} $$
$$ \begin{align*} \|A\|^2 \,{\stackrel{.}{=}}\, \sum_{i=1}^{D} \sum_{j=0}^n \|A_i(e_j)\|^2_{\mathrm{Frob}}, \end{align*} $$
where
![]() $e_j = (0,\dotsc ,0,1,0,\dotsc ,0)\in {\mathbb {C}}^{n+1}$
, with a 1 at index j (
$e_j = (0,\dotsc ,0,1,0,\dotsc ,0)\in {\mathbb {C}}^{n+1}$
, with a 1 at index j (
![]() $0\leqslant j \leqslant n$
). The standard Gaussian probability on
$0\leqslant j \leqslant n$
). The standard Gaussian probability on
![]() $M_{{\mathbf r}}$
is defined by the density
$M_{{\mathbf r}}$
is defined by the density
![]() $\pi ^{-\dim _{{\mathbb {C}}} M_{{\mathbf r}}} \exp (-\|A\|^2) \mathrm {d} A$
. The distribution of the polynomial computed by a Gaussian random ABP with layer sizes
$\pi ^{-\dim _{{\mathbb {C}}} M_{{\mathbf r}}} \exp (-\|A\|^2) \mathrm {d} A$
. The distribution of the polynomial computed by a Gaussian random ABP with layer sizes
![]() $(r_1,\dotsc ,r_{{D}-1})$
is the distribution of
$(r_1,\dotsc ,r_{{D}-1})$
is the distribution of
![]() $f_A$
, where A is standard Gaussian in
$f_A$
, where A is standard Gaussian in
![]() $M_{(r_1,\dotsc ,r_{{D}-1},1)}$
.
$M_{(r_1,\dotsc ,r_{{D}-1},1)}$
.
The following statement is the main ingredient of the proof of Theorem 1.5. It can be seen as an analogue of Lemma I.37. Note that the case
![]() $r_{D}=1$
is the case of ABPs.
$r_{D}=1$
is the case of ABPs.
Proposition 5.3. Let
![]() $r_1,\dotsc ,r_{{D}-1}\geqslant 2$
, and
$r_1,\dotsc ,r_{{D}-1}\geqslant 2$
, and
![]() $r_{D} \geqslant 1$
. Let
$r_{D} \geqslant 1$
. Let
![]() $A \in M_{{\mathbf r}}$
be standard Gaussian, and let
$A \in M_{{\mathbf r}}$
be standard Gaussian, and let
![]() $\zeta \in \mathbb {P}^n$
be a uniformly distributed projective zero of
$\zeta \in \mathbb {P}^n$
be a uniformly distributed projective zero of
![]() $f_A$
. For any
$f_A$
. For any
![]() $k \geqslant 2$
, we have
$k \geqslant 2$
, we have
 $$ \begin{align*} {\mathbb{E}}_{A,\zeta} \left[ \left\| \mathrm{d} _{\zeta} f_A \right\|^{-2} \left\|{\frac{1}{k!}} \mathrm{d} _{\zeta}^k f_A \right\|_{{{\mathrm{Frob}}}}^2 \right] &\leqslant \frac{1}{n {D}} \binom{{D}}{k} \binom{{D} + n}{k} \left( 1+\frac{{D}-1}{k-1} \right)^{k-1} \\ &\leqslant \left[\tfrac14 {D}^2 ({D}+n) \left( 1+\frac{{D}-1}{k-1} \right)\right]^{k-1}. \end{align*} $$
$$ \begin{align*} {\mathbb{E}}_{A,\zeta} \left[ \left\| \mathrm{d} _{\zeta} f_A \right\|^{-2} \left\|{\frac{1}{k!}} \mathrm{d} _{\zeta}^k f_A \right\|_{{{\mathrm{Frob}}}}^2 \right] &\leqslant \frac{1}{n {D}} \binom{{D}}{k} \binom{{D} + n}{k} \left( 1+\frac{{D}-1}{k-1} \right)^{k-1} \\ &\leqslant \left[\tfrac14 {D}^2 ({D}+n) \left( 1+\frac{{D}-1}{k-1} \right)\right]^{k-1}. \end{align*} $$
Theorem 1.5 easily follows from Proposition 5.3.
Proof of Theorem 1.5
Let
![]() $A \in M_{\mathbf r}$
be standard Gaussian so that
$A \in M_{\mathbf r}$
be standard Gaussian so that
![]() $f =f_A$
. The proof follows exactly the lines of the proof of Lemma I.38 and the intermediate Lemma I.37. We bound the supremum in the definition (1.3) of
$f =f_A$
. The proof follows exactly the lines of the proof of Lemma I.38 and the intermediate Lemma I.37. We bound the supremum in the definition (1.3) of
![]() $\gamma _{\mathrm {Frob}}$
by a sum:
$\gamma _{\mathrm {Frob}}$
by a sum:
 $$ \begin{align} {\mathbb{E}} \left[ \gamma_{\mathrm{Frob}}(f_A,\zeta)^2 \right] &\leqslant \sum_{k = 2}^{D} {\mathbb{E}} \left[ \left( \left\| \mathrm{d} _{\zeta} f_A \right\|^{-1} \left\| \tfrac{1}{k!} \mathrm{d} ^k_{\zeta} f_A \right\|_{\mathrm{Frob}} \right)^{\frac{2}{k-1}} \right] \end{align} $$
$$ \begin{align} {\mathbb{E}} \left[ \gamma_{\mathrm{Frob}}(f_A,\zeta)^2 \right] &\leqslant \sum_{k = 2}^{D} {\mathbb{E}} \left[ \left( \left\| \mathrm{d} _{\zeta} f_A \right\|^{-1} \left\| \tfrac{1}{k!} \mathrm{d} ^k_{\zeta} f_A \right\|_{\mathrm{Frob}} \right)^{\frac{2}{k-1}} \right] \end{align} $$
 $$ \begin{align} &\leqslant \sum_{k = 2}^{D} {\mathbb{E}} \left[\left\| \mathrm{d} _{\zeta} f_A \right\|^{-2} \left\| \tfrac{1}{k!} \mathrm{d} ^k_{\zeta} f_A \right\|_{\mathrm{Frob}}^{2} \right]^{\frac{1}{k-1}} \end{align} $$
$$ \begin{align} &\leqslant \sum_{k = 2}^{D} {\mathbb{E}} \left[\left\| \mathrm{d} _{\zeta} f_A \right\|^{-2} \left\| \tfrac{1}{k!} \mathrm{d} ^k_{\zeta} f_A \right\|_{\mathrm{Frob}}^{2} \right]^{\frac{1}{k-1}} \end{align} $$
 $$ \begin{align} &\leqslant \sum_{k=2}^{D} \tfrac14 {D}^2 ({D}+n) \left( 1+\frac{{D}-1}{k-1} \right), \text{ by Proposition~5.3,} \end{align} $$
$$ \begin{align} &\leqslant \sum_{k=2}^{D} \tfrac14 {D}^2 ({D}+n) \left( 1+\frac{{D}-1}{k-1} \right), \text{ by Proposition~5.3,} \end{align} $$
using Jensen’s inequality for (5.3) and
![]() $1 +\sum _{k=2}^{D} \frac {1}{k-1} \leqslant 2 +\log ({D}-1) \le 3 \log {D}$
for (5.5).
$1 +\sum _{k=2}^{D} \frac {1}{k-1} \leqslant 2 +\log ({D}-1) \le 3 \log {D}$
for (5.5).
The remainder of this article is devoted to the proof of Proposition 5.3.
5.1 A coarea formula
The goal of this subsection is to establish a consequence of the coarea formula [Reference Federer19, Theorem 3.1] that is especially useful to estimate
![]() $\Gamma (f)$
for a random polynomial f. This involves a certain identity of normal Jacobians of projections that appears so frequently that it is worthwhile to provide the statement in some generality. Let us first introduce some useful notations. For a linear map
$\Gamma (f)$
for a random polynomial f. This involves a certain identity of normal Jacobians of projections that appears so frequently that it is worthwhile to provide the statement in some generality. Let us first introduce some useful notations. For a linear map
![]() $h : E \to F$
between two real Euclidean spaces, we define its Euclidean determinant as
$h : E \to F$
between two real Euclidean spaces, we define its Euclidean determinant as
where
![]() $h^* : F\to E$
is the adjoint operator of h and the notation
$h^* : F\to E$
is the adjoint operator of h and the notation
![]() ${\operatorname {det}\nolimits }_{\mathbb {R}}$
simply recalls that the base field is
${\operatorname {det}\nolimits }_{\mathbb {R}}$
simply recalls that the base field is
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
If
![]() $p : U\to V$
is a linear map between complex Hermitian spaces, then
$p : U\to V$
is a linear map between complex Hermitian spaces, then
![]() $\operatorname {Edet}(p)$
is defined by the induced real Euclidean structures on U and V, and it is well known that
$\operatorname {Edet}(p)$
is defined by the induced real Euclidean structures on U and V, and it is well known that
and
![]() ${\operatorname {det}\nolimits }_{\mathbb {C}}$
is the determinant over
${\operatorname {det}\nolimits }_{\mathbb {C}}$
is the determinant over
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
The normal Jacobian of a smooth map
![]() $\varphi $
between Riemannian manifolds at a given point x is defined as the Euclidean determinant of the derivative of the map at that point:
$\varphi $
between Riemannian manifolds at a given point x is defined as the Euclidean determinant of the derivative of the map at that point:
Lemma 5.4. Let E and F be Euclidean (respectively, Hermitian) spaces, let V be a subspace of
![]() $E\times F$
and let
$E\times F$
and let
![]() $p:E\times F \to E$
and
$p:E\times F \to E$
and
![]() $q:E\times F\to F$
be the canonical projections. Then
$q:E\times F\to F$
be the canonical projections. Then
![]() $\operatorname {Edet}(p|_V) = \operatorname {Edet}((q|_{V^\perp })^*)$
and
$\operatorname {Edet}(p|_V) = \operatorname {Edet}((q|_{V^\perp })^*)$
and
![]() $\operatorname {Edet}(q|_V) = \operatorname {Edet}((p|_{V^\perp })^*)$
.
$\operatorname {Edet}(q|_V) = \operatorname {Edet}((p|_{V^\perp })^*)$
.
Proof. By symmetry, it suffices to show the first equality. Let
![]() $v_1,\dotsc ,v_r, w_1,\dotsc ,w_s$
be an orthonormal basis of
$v_1,\dotsc ,v_r, w_1,\dotsc ,w_s$
be an orthonormal basis of
![]() $E\times F$
, such that
$E\times F$
, such that
![]() $v_1,\dotsc ,v_r$
is a basis of V and
$v_1,\dotsc ,v_r$
is a basis of V and
![]() $w_1,\dotsc ,w_s$
is a basis of
$w_1,\dotsc ,w_s$
is a basis of
![]() $V^\perp $
. After fixing orthonormal bases for E and F (and the corresponding basis of
$V^\perp $
. After fixing orthonormal bases for E and F (and the corresponding basis of
![]() $E\times F$
), consider the orthogonal (respectively, unitary) matrix U with columns
$E\times F$
), consider the orthogonal (respectively, unitary) matrix U with columns
![]() $v_1,\dotsc ,v_r, w_1,\dotsc ,w_s$
. We decompose U as a block matrix
$v_1,\dotsc ,v_r, w_1,\dotsc ,w_s$
. We decompose U as a block matrix

Using
![]() $U U^*=I$
and
$U U^*=I$
and
![]() $U^* U = I$
, we see that
$U^* U = I$
, we see that
![]() $V_E^{\phantom {*}} V_E^* + W_E^{\phantom {*}} W_E^* = I$
and
$V_E^{\phantom {*}} V_E^* + W_E^{\phantom {*}} W_E^* = I$
and
![]() $W^*_E W^{\phantom {*}}_E + W_F^* W_F^{\phantom {*}} = I$
. It follows from Sylvester’s determinant identity
$W^*_E W^{\phantom {*}}_E + W_F^* W_F^{\phantom {*}} = I$
. It follows from Sylvester’s determinant identity
![]() ${\operatorname {det}\nolimits }(I+AB)={\operatorname {det}\nolimits }(I+BA)$
that
${\operatorname {det}\nolimits }(I+AB)={\operatorname {det}\nolimits }(I+BA)$
that
By definition, we have
![]() $\operatorname {Edet}(p|_V) = {\operatorname {det}\nolimits }(V_E^{\phantom {*}} V^*_E )^{\frac {\eta }{2}}$
with
$\operatorname {Edet}(p|_V) = {\operatorname {det}\nolimits }(V_E^{\phantom {*}} V^*_E )^{\frac {\eta }{2}}$
with
![]() $\eta =1$
in the Euclidean situation and
$\eta =1$
in the Euclidean situation and
![]() $\eta =2$
in the Hermitian situation. Similarly,
$\eta =2$
in the Hermitian situation. Similarly,
![]() $\operatorname {Edet}((q|_{V^\perp })^*) = {\operatorname {det}\nolimits }(W_F^* W_F^{\phantom {*}})^{\frac \eta 2}$
. Therefore, we have
$\operatorname {Edet}((q|_{V^\perp })^*) = {\operatorname {det}\nolimits }(W_F^* W_F^{\phantom {*}})^{\frac \eta 2}$
. Therefore, we have
![]() $\operatorname {Edet}(p|_V) = \operatorname {Edet}((q|_{V^\perp })^*)$
.
$\operatorname {Edet}(p|_V) = \operatorname {Edet}((q|_{V^\perp })^*)$
.
Corollary 5.5. In the setting of Lemma 5.4, suppose V is a real (or complex) hyperplane in
![]() $E\times F$
with nonzero normal vector
$E\times F$
with nonzero normal vector
![]() $(v,w)\in E \times F$
. Then
$(v,w)\in E \times F$
. Then
 $$\begin{align*}\frac{\operatorname{Edet}(p|_{V})}{\operatorname{Edet}(q|_{V})} = \left(\frac{\|w\|}{\|v\|}\right)^\eta, \end{align*}$$
$$\begin{align*}\frac{\operatorname{Edet}(p|_{V})}{\operatorname{Edet}(q|_{V})} = \left(\frac{\|w\|}{\|v\|}\right)^\eta, \end{align*}$$
where
![]() $\eta =1$
in the Euclidean situation and
$\eta =1$
in the Euclidean situation and
![]() $\eta =2$
in the Hermitian situation.
$\eta =2$
in the Hermitian situation.
Proof.
![]() $V^\perp $
is spanned by
$V^\perp $
is spanned by
![]() $(v,w)$
. Without loss of generality, we may scale
$(v,w)$
. Without loss of generality, we may scale
![]() $(v, w)$
so that
$(v, w)$
so that
![]() $\|v\|^2 + \|w\|^2 = 1$
. The vector
$\|v\|^2 + \|w\|^2 = 1$
. The vector
![]() $(v, w)$
forms a unitary basis of
$(v, w)$
forms a unitary basis of
![]() $V^\perp $
, in which the matrix of
$V^\perp $
, in which the matrix of
![]() $p|_{V^\perp }$
is given by v, as a column vector. Therefore,
$p|_{V^\perp }$
is given by v, as a column vector. Therefore,
![]() $\operatorname {Edet}((p_{V^\perp })^*) = {\operatorname {det}\nolimits }(v^* v)^{\frac {\eta }{2}} = \|v\|^\eta $
. Similarly,
$\operatorname {Edet}((p_{V^\perp })^*) = {\operatorname {det}\nolimits }(v^* v)^{\frac {\eta }{2}} = \|v\|^\eta $
. Similarly,
![]() $\operatorname {Edet}((q|_{V^\perp })^*)= {\operatorname {det}\nolimits }(w^* w)^{\frac {\eta }{2}} = \|w\|^\eta $
. Now apply Lemma 5.4.
$\operatorname {Edet}((q|_{V^\perp })^*)= {\operatorname {det}\nolimits }(w^* w)^{\frac {\eta }{2}} = \|w\|^\eta $
. Now apply Lemma 5.4.
We consider now the abstract setting of a family
![]() $(f_A)$
of homogeneous polynomials of degree
$(f_A)$
of homogeneous polynomials of degree
![]() ${D}$
in the variables
${D}$
in the variables
![]() $z_0,\dotsc ,z_n$
, parameterised by elements A of a Hermitian manifold M through a holomorphic map
$z_0,\dotsc ,z_n$
, parameterised by elements A of a Hermitian manifold M through a holomorphic map
![]() $A \in M\mapsto f_A$
. Let
$A \in M\mapsto f_A$
. Let
![]() ${\mathcal {V}}$
be the solution variety
${\mathcal {V}}$
be the solution variety
![]() $\left \{ (A,\zeta )\in M\times {{\mathbb {P}}^n} \mathrel {}\middle |\mathrel {} f_A(\zeta ) = 0 \right \}$
and
$\left \{ (A,\zeta )\in M\times {{\mathbb {P}}^n} \mathrel {}\middle |\mathrel {} f_A(\zeta ) = 0 \right \}$
and
![]() $\pi _1 : {\mathcal {V}}\to M$
and
$\pi _1 : {\mathcal {V}}\to M$
and
![]() $\pi _2 : {\mathcal {V}} \to {\mathbb {P}}^n$
be the restrictions of the canonical projections. We can identify the fibre
$\pi _2 : {\mathcal {V}} \to {\mathbb {P}}^n$
be the restrictions of the canonical projections. We can identify the fibre
![]() $\pi _1^{-1}(A)$
with the zero set
$\pi _1^{-1}(A)$
with the zero set
![]() $V(f_A)$
in
$V(f_A)$
in
![]() ${{\mathbb {P}}^n}$
. Moreover, the fibre
${{\mathbb {P}}^n}$
. Moreover, the fibre
![]() $\pi _2^{-1}(\zeta )$
can be identified with
$\pi _2^{-1}(\zeta )$
can be identified with
![]() $M_{\zeta } \,{\stackrel {.}{=}}\, \left \{ A\in M\mathrel {}\middle |\mathrel {} f_A(\zeta ) = 0 \right \}$
. For fixed
$M_{\zeta } \,{\stackrel {.}{=}}\, \left \{ A\in M\mathrel {}\middle |\mathrel {} f_A(\zeta ) = 0 \right \}$
. For fixed
![]() $\zeta \in {\mathbb {C}}^{n+1}$
, such that
$\zeta \in {\mathbb {C}}^{n+1}$
, such that
![]() $\|\zeta \|=1$
, we consider the map
$\|\zeta \|=1$
, we consider the map
![]() $M\to {\mathbb {C}},\, A \mapsto f_A(\zeta )$
and its derivative at A,
$M\to {\mathbb {C}},\, A \mapsto f_A(\zeta )$
and its derivative at A,
Moreover, for fixed
![]() $A\in M$
, we consider the map
$A\in M$
, we consider the map
![]() $f_A\colon {\mathbb {C}}^{n+1}\to {\mathbb {C}}$
and its derivative at
$f_A\colon {\mathbb {C}}^{n+1}\to {\mathbb {C}}$
and its derivative at
![]() $\zeta $
,
$\zeta $
,
restricted to the tangent space
![]() $T_{\zeta }{{\mathbb {P}}^n}$
, that we identify with the orthogonal complement of
$T_{\zeta }{{\mathbb {P}}^n}$
, that we identify with the orthogonal complement of
![]() ${\mathbb {C}}\zeta $
in
${\mathbb {C}}\zeta $
in
![]() ${\mathbb {C}}^{n+1}$
with respect to the standard Hermitian inner product. Below, it will be convenient to write
${\mathbb {C}}^{n+1}$
with respect to the standard Hermitian inner product. Below, it will be convenient to write
![]() $\partial _A f(\zeta )$
and
$\partial _A f(\zeta )$
and
![]() $\mathrm {d} _{\zeta } f_A$
for
$\mathrm {d} _{\zeta } f_A$
for
![]() $\zeta \in \mathbb {P}^n$
, meaning that
$\zeta \in \mathbb {P}^n$
, meaning that
![]() $\zeta $
stands for a representative in
$\zeta $
stands for a representative in
![]() $\mathbb {C}^{n+1}$
(due to
$\mathbb {C}^{n+1}$
(due to
![]() $\partial _A f(t \zeta ) = t^{D} \partial _A f(\zeta )$
and
$\partial _A f(t \zeta ) = t^{D} \partial _A f(\zeta )$
and
![]() $\mathrm {d} _{t\zeta } f_A = t^{D} \mathrm {d} _{\zeta } f_A$
, the statements do not depend on the scaling).
$\mathrm {d} _{t\zeta } f_A = t^{D} \mathrm {d} _{\zeta } f_A$
, the statements do not depend on the scaling).
Proposition 5.6. For any measurable function
![]() $\Theta : {\mathcal {V}}\to [0,\infty )$
, we have
$\Theta : {\mathcal {V}}\to [0,\infty )$
, we have

Here,
![]() $\mathrm {d} A$
denotes the Riemannian volume measure on M and
$\mathrm {d} A$
denotes the Riemannian volume measure on M and
![]() $M_{\zeta }$
, respectively.
$M_{\zeta }$
, respectively.
Proof. As in [Reference Bürgisser and Cucker15, Lemma 16.9], the tangent space of
![]() ${\mathcal {V}}$
at
${\mathcal {V}}$
at
![]() $(A,\zeta ) \in {\mathcal {V}}$
can be expressed as
$(A,\zeta ) \in {\mathcal {V}}$
can be expressed as
If
![]() $\partial _A f(\zeta )$
and
$\partial _A f(\zeta )$
and
![]() $\mathrm {d} _{\zeta } f_A$
are not both zero, then V is a hyperplane in the product
$\mathrm {d} _{\zeta } f_A$
are not both zero, then V is a hyperplane in the product
![]() $E\times F \,{\stackrel {.}{=}}\, T_A M \times T_{\zeta }{{\mathbb {P}}^n}$
of Hermitian spaces and V has the normal vector
$E\times F \,{\stackrel {.}{=}}\, T_A M \times T_{\zeta }{{\mathbb {P}}^n}$
of Hermitian spaces and V has the normal vector
![]() $((\partial _A f(\zeta ))^*, (\mathrm {d} _{\zeta } f_A)^*)$
, where
$((\partial _A f(\zeta ))^*, (\mathrm {d} _{\zeta } f_A)^*)$
, where
![]() ${}^*$
denotes the Hermitian adjoint. If we denote by p and q the canonical projections of V onto E and F, then
${}^*$
denotes the Hermitian adjoint. If we denote by p and q the canonical projections of V onto E and F, then
![]() $\mathrm {d} _{A,\zeta } \pi _1 = p|_V$
and
$\mathrm {d} _{A,\zeta } \pi _1 = p|_V$
and
![]() $\mathrm {d} _{A,\zeta } \pi _2 = q|_V $
, hence
$\mathrm {d} _{A,\zeta } \pi _2 = q|_V $
, hence
By Corollary 5.5, we, therefore, have
 $$ \begin{align} \frac{\operatorname{NJ}_{A,\zeta}(\pi_1)}{\operatorname{NJ}_{A,\zeta}(\pi_2)} = \frac{\operatorname{Edet}(p|_V)}{\operatorname{Edet}(q|_V)} = \frac{\|(\mathrm{d} _{\zeta} f_A)^*\|^2}{\|(\partial_A f(\zeta))^*\|^2} = \frac{\|\mathrm{d} _{\zeta} f_A\|^2}{\|\partial_A f(\zeta)\|^2}. \end{align} $$
$$ \begin{align} \frac{\operatorname{NJ}_{A,\zeta}(\pi_1)}{\operatorname{NJ}_{A,\zeta}(\pi_2)} = \frac{\operatorname{Edet}(p|_V)}{\operatorname{Edet}(q|_V)} = \frac{\|(\mathrm{d} _{\zeta} f_A)^*\|^2}{\|(\partial_A f(\zeta))^*\|^2} = \frac{\|\mathrm{d} _{\zeta} f_A\|^2}{\|\partial_A f(\zeta)\|^2}. \end{align} $$
The coarea formula [Reference Federer19, Theorem 3.1], applied to
![]() $\pi _1 : \mathcal {V}\to M$
asserts,
$\pi _1 : \mathcal {V}\to M$
asserts,

(note that
![]() ${\mathcal {V}}$
may have singularities, so we actually apply the coarea formula to its smooth locus. The Lipschitz-continuity hypothesis required by Federer is satisfied:
${\mathcal {V}}$
may have singularities, so we actually apply the coarea formula to its smooth locus. The Lipschitz-continuity hypothesis required by Federer is satisfied:
![]() $\pi _1$
is 1-Lipschitz continuous, since it is the restriction to
$\pi _1$
is 1-Lipschitz continuous, since it is the restriction to
![]() ${\mathcal {V}}$
of the projection
${\mathcal {V}}$
of the projection
![]() $M\times \mathbb {P}^n\to M$
). On the other hand, the coarea formula applied to
$M\times \mathbb {P}^n\to M$
). On the other hand, the coarea formula applied to
![]() $\pi _2:{\mathcal {V}} \to \mathbb {P}^n$
gives
$\pi _2:{\mathcal {V}} \to \mathbb {P}^n$
gives

By (5.15), we have
so all the four integrals above are equal.
5.2 A few lemmas on Gaussian random matrices
We present, here, some auxiliary results on Gaussian random matrices, centring around the new notion of the anomaly of a matrix. This will be crucial for the proof of Theorem 1.5.
We endow the space
![]() $\mathbb {C}^r$
with the probability density
$\mathbb {C}^r$
with the probability density
![]() $\pi ^{-r} e^{-\|x\|^2} \mathrm {d} x$
, where
$\pi ^{-r} e^{-\|x\|^2} \mathrm {d} x$
, where
![]() $\|x\|$
is the usual Hermitian norm, and call a random vector
$\|x\|$
is the usual Hermitian norm, and call a random vector
![]() $x\in \mathbb {C}^r$
with this probability distribution standard Gaussian. This amounts to say that the real and imaginary parts of x are independent centred Gaussian with variance
$x\in \mathbb {C}^r$
with this probability distribution standard Gaussian. This amounts to say that the real and imaginary parts of x are independent centred Gaussian with variance
![]() $\frac 12$
. We note that
$\frac 12$
. We note that
![]() ${\mathbb {E}}_x \left [\|x\|^2\right ] = r$
. This convention slightly differs from some previous writings with a different scaling, where the distribution used is
${\mathbb {E}}_x \left [\|x\|^2\right ] = r$
. This convention slightly differs from some previous writings with a different scaling, where the distribution used is
![]() $(2\pi )^{-r} e^{-\frac 12\|x\|^2} \mathrm {d} x$
. This choice seems more natural since it avoids many spurious factors. Similarly, the matrix space
$(2\pi )^{-r} e^{-\frac 12\|x\|^2} \mathrm {d} x$
. This choice seems more natural since it avoids many spurious factors. Similarly, the matrix space
![]() $\mathbb {C}^{r\times s}$
is endowed with the probability density
$\mathbb {C}^{r\times s}$
is endowed with the probability density
![]() $\pi ^{-rs} \exp (-\|R\|_{\mathrm {Frob}}^2) \mathrm {d} R$
, and we call a random matrix with this probability distribution standard Gaussian as well (in the random matrix literature, this is called complex Ginibre ensemble).
$\pi ^{-rs} \exp (-\|R\|_{\mathrm {Frob}}^2) \mathrm {d} R$
, and we call a random matrix with this probability distribution standard Gaussian as well (in the random matrix literature, this is called complex Ginibre ensemble).
Lemma 5.7. For
![]() $P\in \mathbb {C}^{r\times s}$
fixed and
$P\in \mathbb {C}^{r\times s}$
fixed and
![]() $x \in \mathbb {C}^s$
standard Gaussian, we have
$x \in \mathbb {C}^s$
standard Gaussian, we have
Proof. By the singular value decomposition and unitary invariance, we may assume that P equals
![]() $\mathrm {diag}(\sigma _1,\ldots ,\sigma _{\min (r, s)})$
, with zero columns or zero rows appended. Then
$\mathrm {diag}(\sigma _1,\ldots ,\sigma _{\min (r, s)})$
, with zero columns or zero rows appended. Then
![]() $\|Px\|^2 = \sum _i \sigma _i^2 |x_i|^2 $
, hence,
$\|Px\|^2 = \sum _i \sigma _i^2 |x_i|^2 $
, hence,
![]() ${\mathbb {E}}_x \left [\|P x\|^2\right ] = \sum _i \sigma _i^2 {\mathbb {E}}_{x_i} \left [\|x_i\|^2\right ] = \sum _i \sigma _i^2 = \|P\|_{\mathrm {Frob}}^2$
.
${\mathbb {E}}_x \left [\|P x\|^2\right ] = \sum _i \sigma _i^2 {\mathbb {E}}_{x_i} \left [\|x_i\|^2\right ] = \sum _i \sigma _i^2 = \|P\|_{\mathrm {Frob}}^2$
.
For the second assertion, we note that for a nonnegative random variable Z, we have by Jensen’s inequality that
![]() ${\mathbb {E}}\left [Z\right ]^{-1} \le {\mathbb {E}}\left [Z^{-1}\right ]$
, since
${\mathbb {E}}\left [Z\right ]^{-1} \le {\mathbb {E}}\left [Z^{-1}\right ]$
, since
![]() $x\mapsto x^{-1}$
is convex on
$x\mapsto x^{-1}$
is convex on
![]() $(0,\infty )$
. The second assertion follows by applying this to
$(0,\infty )$
. The second assertion follows by applying this to
![]() $Z \,{\stackrel {.}{=}}\, \|Px\|^2$
and using the first assertion.
$Z \,{\stackrel {.}{=}}\, \|Px\|^2$
and using the first assertion.
For the third assertion, we note
![]() $\|x\|^2 = \frac 12 \chi _{2s}^2$
, where
$\|x\|^2 = \frac 12 \chi _{2s}^2$
, where
![]() $\chi _{2s}^2$
stands for a chi-square distribution with
$\chi _{2s}^2$
stands for a chi-square distribution with
![]() $2s$
degrees of freedom. Hence,
$2s$
degrees of freedom. Hence,
![]() $\chi _{2s}^{-2}$
is an inverse chi-square and
$\chi _{2s}^{-2}$
is an inverse chi-square and
![]() ${\mathbb {E}} [ \chi _{2s}^{-2} ] = 1/(2s-2)$
[Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin20, §A.1, Table A.1].
${\mathbb {E}} [ \chi _{2s}^{-2} ] = 1/(2s-2)$
[Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin20, §A.1, Table A.1].
We define the anomaly of a matrix
![]() $P \in \mathbb {C}^{r\times s}$
as the quantity
$P \in \mathbb {C}^{r\times s}$
as the quantity
 $$ \begin{align} \theta(P) \,{\stackrel{.}{=}}\, {\mathbb{E}}_x \left[ \frac{\|P\|_{\mathrm{Frob}}^2}{\|P x\|^2} \right] \in [1,\infty) , \end{align} $$
$$ \begin{align} \theta(P) \,{\stackrel{.}{=}}\, {\mathbb{E}}_x \left[ \frac{\|P\|_{\mathrm{Frob}}^2}{\|P x\|^2} \right] \in [1,\infty) , \end{align} $$
where
![]() $x \in \mathbb {C}^s$
is a standard Gaussian random vector. Note that
$x \in \mathbb {C}^s$
is a standard Gaussian random vector. Note that
![]() $\theta (P) \ge 1$
by Lemma 5.7. Moreover, by the same lemma,
$\theta (P) \ge 1$
by Lemma 5.7. Moreover, by the same lemma,
![]() $\theta (I_r) = r/(r-1)$
. This quantity
$\theta (I_r) = r/(r-1)$
. This quantity
![]() $\theta (P)$
is easily seen to be finite if
$\theta (P)$
is easily seen to be finite if
![]() $\operatorname {rk} P> 1$
; it grows logarithmically to infinity as P approaches a rank 1 matrix.
$\operatorname {rk} P> 1$
; it grows logarithmically to infinity as P approaches a rank 1 matrix.
Lemma 5.8. Let
![]() $P \in \mathbb {C}^{r\times s}$
and
$P \in \mathbb {C}^{r\times s}$
and
![]() $Q \in \mathbb {C}^{t\times u}$
be fixed matrices and
$Q \in \mathbb {C}^{t\times u}$
be fixed matrices and
![]() $X \in {\mathbb {C}^{s\times t}}$
be a standard Gaussian random matrix. Then
$X \in {\mathbb {C}^{s\times t}}$
be a standard Gaussian random matrix. Then
 $$\begin{align*}{\mathbb{E}}_X \left[ \frac{\|P\|_{\mathrm{Frob}}^2 \|Q\|_{\mathrm{Frob}}^2}{\|P X Q\|_{\mathrm{Frob}}^2} \right] \leqslant \theta(P). \end{align*}$$
$$\begin{align*}{\mathbb{E}}_X \left[ \frac{\|P\|_{\mathrm{Frob}}^2 \|Q\|_{\mathrm{Frob}}^2}{\|P X Q\|_{\mathrm{Frob}}^2} \right] \leqslant \theta(P). \end{align*}$$
Proof. Up to left and right multiplications of Q by unitary matrices, we may assume that Q is diagonal, with nonnegative real numbers
![]() $\sigma _1,\dotsc ,\sigma _{\min (t, u)}$
on the diagonal (and we define
$\sigma _1,\dotsc ,\sigma _{\min (t, u)}$
on the diagonal (and we define
![]() $\sigma _ i=0$
for
$\sigma _ i=0$
for
![]() $i> \min (t, u)$
). This does not change the left-hand side because the Frobenius norm is invariant by left and right multiplications with unitary matrices, and the distribution of X is unitarily invariant as well.
$i> \min (t, u)$
). This does not change the left-hand side because the Frobenius norm is invariant by left and right multiplications with unitary matrices, and the distribution of X is unitarily invariant as well.
Let
![]() $e^u_1,\dotsc ,e^u_u$
(reps.
$e^u_1,\dotsc ,e^u_u$
(reps.
![]() $e_1^t, \dotsc , e_t^t)$
be the canonical basis of
$e_1^t, \dotsc , e_t^t)$
be the canonical basis of
![]() $\mathbb {C}^u$
(respectively,
$\mathbb {C}^u$
(respectively,
![]() $\mathbb {C}^t$
). Observe that
$\mathbb {C}^t$
). Observe that
 $$ \begin{align} \|PXQ\|_{\mathrm{Frob}}^2 = \sum_{i=1}^u \|PXQ e^u_i\|^2 = \sum_{i=1}^{t} \sigma_i^2 \|PX e^{t}_i \|^2. \end{align} $$
$$ \begin{align} \|PXQ\|_{\mathrm{Frob}}^2 = \sum_{i=1}^u \|PXQ e^u_i\|^2 = \sum_{i=1}^{t} \sigma_i^2 \|PX e^{t}_i \|^2. \end{align} $$
Noting that
![]() $\|Q\|_{\mathrm {Frob}}^2 = \sigma _1^2 + \dotsb + \sigma _{t}^2$
, the convexity of
$\|Q\|_{\mathrm {Frob}}^2 = \sigma _1^2 + \dotsb + \sigma _{t}^2$
, the convexity of
![]() $x \mapsto x^{-1}$
on
$x \mapsto x^{-1}$
on
![]() $(0,\infty )$
gives
$(0,\infty )$
gives
 $$ \begin{align} \left( \frac{1}{\|Q\|_{\mathrm{Frob}}^2} \sum_{i=1}^{t} \sigma_i^2 \|P X e^{t}_i \|^2 \right)^{-1} \leqslant \frac{1}{\|Q\|_{\mathrm{Frob}}^2} \sum_{i=1}^{t} \frac{\sigma_i^2}{\|P Xe^{t}_i\|^2}. \end{align} $$
$$ \begin{align} \left( \frac{1}{\|Q\|_{\mathrm{Frob}}^2} \sum_{i=1}^{t} \sigma_i^2 \|P X e^{t}_i \|^2 \right)^{-1} \leqslant \frac{1}{\|Q\|_{\mathrm{Frob}}^2} \sum_{i=1}^{t} \frac{\sigma_i^2}{\|P Xe^{t}_i\|^2}. \end{align} $$
Since X is standard Gaussian,
![]() $X e^{t}_i \in \mathbb {C}^s$
is also standard Gaussian. Therefore, by definition of
$X e^{t}_i \in \mathbb {C}^s$
is also standard Gaussian. Therefore, by definition of
![]() $\theta $
, we have for any
$\theta $
, we have for any
![]() $1\leqslant i\leqslant t$
,
$1\leqslant i\leqslant t$
,
 $$ \begin{align} {\mathbb{E}}_X \left[ \frac{\|P\|_{\mathrm{Frob}}^2}{\|P X e^{t}_i\|^2} \right] = \theta(P). \end{align} $$
$$ \begin{align} {\mathbb{E}}_X \left[ \frac{\|P\|_{\mathrm{Frob}}^2}{\|P X e^{t}_i\|^2} \right] = \theta(P). \end{align} $$
It follows that
 $$ \begin{align*} {\mathbb{E}}_X \left[ \frac{\|P\|_{\mathrm{Frob}}^2 \|Q\|_{\mathrm{Frob}}^2}{\|P X Q\|_{\mathrm{Frob}}^2} \right] &\leqslant \frac{1}{\|Q\|_{\mathrm{Frob}}^2} \sum_{i=1}^t \sigma_i^2 {\mathbb{E}} \left[ \frac{\|P\|_{\mathrm{Frob}}^2}{\|P Xe^{t}_i\|^2} \right], && \text{by~(5.20) and (5.21),}\\ &= \frac{1}{\|Q\|_{\mathrm{Frob}}^2} \sum_{i=1}^t \sigma_i^2 \theta(P), &&\text{by (5.22),} \\ & = \theta(P), \end{align*} $$
$$ \begin{align*} {\mathbb{E}}_X \left[ \frac{\|P\|_{\mathrm{Frob}}^2 \|Q\|_{\mathrm{Frob}}^2}{\|P X Q\|_{\mathrm{Frob}}^2} \right] &\leqslant \frac{1}{\|Q\|_{\mathrm{Frob}}^2} \sum_{i=1}^t \sigma_i^2 {\mathbb{E}} \left[ \frac{\|P\|_{\mathrm{Frob}}^2}{\|P Xe^{t}_i\|^2} \right], && \text{by~(5.20) and (5.21),}\\ &= \frac{1}{\|Q\|_{\mathrm{Frob}}^2} \sum_{i=1}^t \sigma_i^2 \theta(P), &&\text{by (5.22),} \\ & = \theta(P), \end{align*} $$
which concludes the proof.
Lemma 5.9. Let
![]() $P \in \mathbb {C}^{r\times s}$
be fixed,
$P \in \mathbb {C}^{r\times s}$
be fixed,
![]() $t>1$
and
$t>1$
and
![]() $X\in \mathbb {C}^{s\times t}$
be a standard Gaussian random matrix. Then
$X\in \mathbb {C}^{s\times t}$
be a standard Gaussian random matrix. Then
Furthermore, if
![]() $X_1,\dotsc ,X_m$
are standard Gaussian matrices of size
$X_1,\dotsc ,X_m$
are standard Gaussian matrices of size
![]() $r_{0}\times r_1$
,
$r_{0}\times r_1$
,
![]() $r_1\times r_2, \ldots , r_{m-1}\times r_m$
, respectively, where
$r_1\times r_2, \ldots , r_{m-1}\times r_m$
, respectively, where
![]() $r_0,\ldots ,r_m>1$
, then
$r_0,\ldots ,r_m>1$
, then
 $$\begin{align*}{\mathbb{E}}_{X_1,\ldots,X_m} \left[ \theta(X_1 \dotsb X_m ) \right] = 1 + \sum_{i=0}^m \frac{1}{r_i-1}. \end{align*}$$
$$\begin{align*}{\mathbb{E}}_{X_1,\ldots,X_m} \left[ \theta(X_1 \dotsb X_m ) \right] = 1 + \sum_{i=0}^m \frac{1}{r_i-1}. \end{align*}$$
Proof. Let
![]() $x \in \mathbb {C}^t$
be a standard Gaussian random vector, so that
$x \in \mathbb {C}^t$
be a standard Gaussian random vector, so that
 $$ \begin{align} {\mathbb{E}}_X \left[ \theta(PX) \right] = {\mathbb{E}}_{X,x} \left[ \frac{\|P X\|_{\mathrm{Frob}}^2}{\|P X x\|^2} \right]. \end{align} $$
$$ \begin{align} {\mathbb{E}}_X \left[ \theta(PX) \right] = {\mathbb{E}}_{X,x} \left[ \frac{\|P X\|_{\mathrm{Frob}}^2}{\|P X x\|^2} \right]. \end{align} $$
We first compute the expectation conditionally on x. So we fix x and write
![]() $x = \|x\| u_1$
for some unit vector
$x = \|x\| u_1$
for some unit vector
![]() $u_1$
. We choose other unit vectors
$u_1$
. We choose other unit vectors
![]() $u_2,\dotsc ,u_t$
to form an orthonormal basis of
$u_2,\dotsc ,u_t$
to form an orthonormal basis of
![]() $\mathbb {C}^t$
. Since
$\mathbb {C}^t$
. Since
![]() $\|PX\|_{\mathrm {Frob}}^2 = \sum _{i=1}^t \|PXu_i\|^2$
, we obtain
$\|PX\|_{\mathrm {Frob}}^2 = \sum _{i=1}^t \|PXu_i\|^2$
, we obtain
 $$ \begin{align} \frac{\|PX\|_{\mathrm{Frob}}^2}{\|PXx\|^2} = \frac{1}{\|x\|^2} + \sum_{i=2}^t \frac{\|PX u_i\|^2}{\|PXu_1\|^2 \|x\|^2}. \end{align} $$
$$ \begin{align} \frac{\|PX\|_{\mathrm{Frob}}^2}{\|PXx\|^2} = \frac{1}{\|x\|^2} + \sum_{i=2}^t \frac{\|PX u_i\|^2}{\|PXu_1\|^2 \|x\|^2}. \end{align} $$
Since X is standard Gaussian, the vectors
![]() $X u_i$
are standard Gaussian and independent. So we obtain, using Lemma 5.7,
$X u_i$
are standard Gaussian and independent. So we obtain, using Lemma 5.7,
 $$ \begin{align} {\mathbb{E}}_X \left[ \frac{\|PX u_i\|^2}{\|PXu_1\|^2} \right] &= {\mathbb{E}}_X [ \|PXu_i\|^2 ] \, {\mathbb{E}}_X \left[ \frac{1}{\|PX u_1\|^2} \right] \end{align} $$
$$ \begin{align} {\mathbb{E}}_X \left[ \frac{\|PX u_i\|^2}{\|PXu_1\|^2} \right] &= {\mathbb{E}}_X [ \|PXu_i\|^2 ] \, {\mathbb{E}}_X \left[ \frac{1}{\|PX u_1\|^2} \right] \end{align} $$
 $$ \begin{align} &= \|P\|_{\mathrm{Frob}}^2 \, {\mathbb{E}}_X \left[ \frac{1}{\|PX u_1\|^2} \right] = \theta(P). \end{align} $$
$$ \begin{align} &= \|P\|_{\mathrm{Frob}}^2 \, {\mathbb{E}}_X \left[ \frac{1}{\|PX u_1\|^2} \right] = \theta(P). \end{align} $$
Combining with (5.24), we obtain
 $$ \begin{align} {\mathbb{E}}_{X} \left[ \frac{\|P X\|_{\mathrm{Frob}}^2}{\|P X x\|^2} \right] = \frac{1}{\|x\|^2} + \sum_{i=2}^t \frac{\theta(P)}{\|x\|^2} = \frac{1}{\|x\|^2} \big(1+ (t-1) \theta(P)\big). \end{align} $$
$$ \begin{align} {\mathbb{E}}_{X} \left[ \frac{\|P X\|_{\mathrm{Frob}}^2}{\|P X x\|^2} \right] = \frac{1}{\|x\|^2} + \sum_{i=2}^t \frac{\theta(P)}{\|x\|^2} = \frac{1}{\|x\|^2} \big(1+ (t-1) \theta(P)\big). \end{align} $$
When we take the expectation over x, the first claim follows with the third statement of Lemma 5.7.
The second claim follows by induction on m. The base case
![]() $m=1$
follows from writing
$m=1$
follows from writing
![]() ${\mathbb {E}}_{X_1} \left [ \theta (X_1) \right ]={\mathbb {E}}_{X_1} \left [ \theta (I_{r_0}X_1) \right ]$
, the first part of Lemma 5.7 and
${\mathbb {E}}_{X_1} \left [ \theta (X_1) \right ]={\mathbb {E}}_{X_1} \left [ \theta (I_{r_0}X_1) \right ]$
, the first part of Lemma 5.7 and
![]() $\theta ( I_{r_0} ) = 1+\frac {1}{r_0-1}$
. For the induction step
$\theta ( I_{r_0} ) = 1+\frac {1}{r_0-1}$
. For the induction step
![]() $m>1$
, we first fix
$m>1$
, we first fix
![]() $X_1,\ldots ,X_{m-1}$
and obtain from the first assertion
$X_1,\ldots ,X_{m-1}$
and obtain from the first assertion
Taking the expectation over
![]() $X_1,\ldots ,\dotsb , X_{m-1}$
and applying the induction hypothesis implies the claim.
$X_1,\ldots ,\dotsb , X_{m-1}$
and applying the induction hypothesis implies the claim.
Lemma 5.10. For any fixed
![]() $P, Q \in \mathbb {C}^{r\times r}$
and
$P, Q \in \mathbb {C}^{r\times r}$
and
![]() $X \in \mathbb {C}^{r\times r}$
standard Gaussian, we have
$X \in \mathbb {C}^{r\times r}$
standard Gaussian, we have
-
(i)
 $\mathbb {E} \left [ \left | \operatorname {tr} (XQ) \right |{}^2 \right ] = \left \| Q \right \|_{\mathrm {Frob}}^2$
,
$\mathbb {E} \left [ \left | \operatorname {tr} (XQ) \right |{}^2 \right ] = \left \| Q \right \|_{\mathrm {Frob}}^2$
, -
(ii)
 $\mathbb {E} \left [ \left \| PXQ \right \|_{\mathrm {Frob}}^2 \right ] = \left \| P \right \|_{\mathrm {Frob}}^2 \left \| Q \right \|_{\mathrm {Frob}}^2$
.
$\mathbb {E} \left [ \left \| PXQ \right \|_{\mathrm {Frob}}^2 \right ] = \left \| P \right \|_{\mathrm {Frob}}^2 \left \| Q \right \|_{\mathrm {Frob}}^2$
.
Proof. By unitary invariance of the distribution of X and the Frobenius norm, we can assume that P and Q are diagonal matrices. Then the claims reduce to easy computations.
5.3 Proof of Proposition 5.3
We now carry out the estimation of
 $$ \begin{align} {\mathbb{E}} \left[ \left\| \mathrm{d} _{\zeta} f_{A} \right\|^{-2} \left\|{\tfrac{1}{k!}}\mathrm{d} _{\zeta}^{k}f_{A}\right\|_{\mathrm{Frob}}^{2} \right], \end{align} $$
$$ \begin{align} {\mathbb{E}} \left[ \left\| \mathrm{d} _{\zeta} f_{A} \right\|^{-2} \left\|{\tfrac{1}{k!}}\mathrm{d} _{\zeta}^{k}f_{A}\right\|_{\mathrm{Frob}}^{2} \right], \end{align} $$
where
![]() $A \in M_{\mathbf r}$
is standard Gaussian and
$A \in M_{\mathbf r}$
is standard Gaussian and
![]() $\zeta \in \mathbb {P}^n$
is a uniformly distributed zero of
$\zeta \in \mathbb {P}^n$
is a uniformly distributed zero of
![]() $f_{A}$
. The computation is lengthy, but the different ingredients arrange elegantly.
$f_{A}$
. The computation is lengthy, but the different ingredients arrange elegantly.
5.3.1 Conditioning
 $A $
on
$A $
on
 $\zeta $
$\zeta $
As often in this kind of average analysis, the first step is to consider the conditional distribution of A given
![]() $\zeta $
, reversing the natural definition where
$\zeta $
, reversing the natural definition where
![]() $\zeta $
is defined conditionally on A. This is of course the main purpose of Proposition 5.6. Consider the Hermitian vector space
$\zeta $
is defined conditionally on A. This is of course the main purpose of Proposition 5.6. Consider the Hermitian vector space
![]() $M \,{\stackrel {.}{=}}\, M_{{\mathbf r}}$
, and let
$M \,{\stackrel {.}{=}}\, M_{{\mathbf r}}$
, and let
![]() $\mathrm {d} ' A = \pi ^{-\dim _{\mathbb {C}} M_{\mathbf r}} e^{-\sum _i \left \| A_i \right \|^2} \mathrm {d} A$
denote the Gaussian probability measure on
$\mathrm {d} ' A = \pi ^{-\dim _{\mathbb {C}} M_{\mathbf r}} e^{-\sum _i \left \| A_i \right \|^2} \mathrm {d} A$
denote the Gaussian probability measure on
![]() $M_{\mathbf r}$
. It is a classical fact (e.g., [Reference Howard25, p. 20]), that the volume of a hypersurface of degree
$M_{\mathbf r}$
. It is a classical fact (e.g., [Reference Howard25, p. 20]), that the volume of a hypersurface of degree
![]() ${D}$
in
${D}$
in
![]() $\mathbb {P}^n$
equals
$\mathbb {P}^n$
equals
![]() ${D} \operatorname {vol} \mathbb {P}^{n-1}$
, this applies, in particular, to
${D} \operatorname {vol} \mathbb {P}^{n-1}$
, this applies, in particular, to
![]() $V(f_{A})$
. By Proposition 5.6, we have
$V(f_{A})$
. By Proposition 5.6, we have


Here,
![]() $\mathrm {d}'A$
denotes the Gaussian measure on M and
$\mathrm {d}'A$
denotes the Gaussian measure on M and
![]() $M_{\zeta }$
, respectively. We focus on the inner integral over
$M_{\zeta }$
, respectively. We focus on the inner integral over
![]() $M_{\zeta }$
for some fixed
$M_{\zeta }$
for some fixed
![]() $\zeta $
. Everything being unitarily invariant, this integral actually does not depend on
$\zeta $
. Everything being unitarily invariant, this integral actually does not depend on
![]() $\zeta $
. So we fix
$\zeta $
. So we fix
![]() $\zeta \,{\stackrel {.}{=}}\, [1:0:\dotsb :0]$
. We next note that
$\zeta \,{\stackrel {.}{=}}\, [1:0:\dotsb :0]$
. We next note that
![]() $\operatorname {vol} \mathbb {P}^n =\frac {\pi }n\operatorname {vol}\mathbb {P}^{n-1}$
, and we obtain
$\operatorname {vol} \mathbb {P}^n =\frac {\pi }n\operatorname {vol}\mathbb {P}^{n-1}$
, and we obtain

Recall that the entries of
![]() $A_{i} = A_i(z)$
are linear forms in
$A_{i} = A_i(z)$
are linear forms in
![]() $z_0,z_{1},\dotsc ,z_{n}$
. We define
$z_0,z_{1},\dotsc ,z_{n}$
. We define
where the entries of the matrix
![]() $C_i(z_{1},\dotsc ,z_{n})$
are linear forms
$C_i(z_{1},\dotsc ,z_{n})$
are linear forms
![]() $z_{1},\dotsc ,z_{n}$
. This yields an orthogonal decomposition
$z_{1},\dotsc ,z_{n}$
. This yields an orthogonal decomposition
![]() $M_{{\mathbf r}}(n+1)\simeq M_{{\mathbf r}}(1)\oplus M_{{\mathbf r}}(n)$
with respect to the Hermitian norm on
$M_{{\mathbf r}}(n+1)\simeq M_{{\mathbf r}}(1)\oplus M_{{\mathbf r}}(n)$
with respect to the Hermitian norm on
![]() $M_{\mathbf r}$
, where
$M_{\mathbf r}$
, where
![]() $A=B+C$
with
$A=B+C$
with
 $$ \begin{align} B=(B_1,\ldots,B_{{D}})\in\prod_{i=1}^{{D}}{\mathbb{C}}^{r_{i-1}\times r_i}\simeq M_{{\mathbf r}}(1) ,\quad C=(C_1,\ldots,C_{D})\in M_{{\mathbf r}}(n).\\[-9pt]\nonumber \end{align} $$
$$ \begin{align} B=(B_1,\ldots,B_{{D}})\in\prod_{i=1}^{{D}}{\mathbb{C}}^{r_{i-1}\times r_i}\simeq M_{{\mathbf r}}(1) ,\quad C=(C_1,\ldots,C_{D})\in M_{{\mathbf r}}(n).\\[-9pt]\nonumber \end{align} $$
Consider the function
![]() $f(\zeta ):M_{{\mathbf r}}(n+1) \to {\mathbb {C}}$
,
$f(\zeta ):M_{{\mathbf r}}(n+1) \to {\mathbb {C}}$
,
![]() $A\mapsto f_A(\zeta )$
. By (5.1), we have
$A\mapsto f_A(\zeta )$
. By (5.1), we have
![]() $f_A(\zeta ) =\operatorname {tr}(A_1(\zeta ),\ldots ,A_{D}(\zeta ))= \operatorname {tr}(B_1\dotsb B_{D})$
. The derivative of
$f_A(\zeta ) =\operatorname {tr}(A_1(\zeta ),\ldots ,A_{D}(\zeta ))= \operatorname {tr}(B_1\dotsb B_{D})$
. The derivative of
![]() $f(\zeta )$
is given by
$f(\zeta )$
is given by
 $$ \begin{align} \partial_A f(\zeta) (\dot A) = \sum_{i=1}^{D} \operatorname{tr} \left( B_1 \dotsb B_{i-1} \dot B_i B_{i+1} \dotsb B_{D} \right) = \sum_{i=1}^{D} \operatorname{tr}( \dot B_i \hat B_i),\\[-9pt]\nonumber \end{align} $$
$$ \begin{align} \partial_A f(\zeta) (\dot A) = \sum_{i=1}^{D} \operatorname{tr} \left( B_1 \dotsb B_{i-1} \dot B_i B_{i+1} \dotsb B_{D} \right) = \sum_{i=1}^{D} \operatorname{tr}( \dot B_i \hat B_i),\\[-9pt]\nonumber \end{align} $$
where
![]() $\dot {A}=\dot {B}+\dot {C}$
and (invariance of the trace under cyclic permutations)
$\dot {A}=\dot {B}+\dot {C}$
and (invariance of the trace under cyclic permutations)
Hence, the induced norm of the linear form
![]() $\partial _A f(\zeta )$
on the Hermitian space
$\partial _A f(\zeta )$
on the Hermitian space
![]() $M_{\mathbf r}$
satisfies
$M_{\mathbf r}$
satisfies
 $$ \begin{align} \| \partial_A f(\zeta) \|^2 = \sum_{i=1}^{D} \|\hat B_i\|^2_{\mathrm{Frob}}.\\[-9pt]\nonumber \end{align} $$
$$ \begin{align} \| \partial_A f(\zeta) \|^2 = \sum_{i=1}^{D} \|\hat B_i\|^2_{\mathrm{Frob}}.\\[-9pt]\nonumber \end{align} $$
The equation defining the fibre
![]() $M_{\zeta }$
can be written as
$M_{\zeta }$
can be written as
![]() $\operatorname {tr} \left ( B_{1} \dotsb B_{{D}} \right ) = 0$
. We have
$\operatorname {tr} \left ( B_{1} \dotsb B_{{D}} \right ) = 0$
. We have
![]() $M_{\zeta } \simeq W \times M_{\mathbf r}(n)$
, where W denotes the space of
$M_{\zeta } \simeq W \times M_{\mathbf r}(n)$
, where W denotes the space of
![]() ${D}$
-tuples of complex matrices (of respective size
${D}$
-tuples of complex matrices (of respective size
![]() $r_0\times r_1$
,
$r_0\times r_1$
,
![]() $r_1\times r_2$
, etc.) that satisfy this condition. Using this identification, the projection
$r_1\times r_2$
, etc.) that satisfy this condition. Using this identification, the projection
is given by evaluation at
![]() $\zeta $
. With (5.37), this implies that
$\zeta $
. With (5.37), this implies that


As before, we denote by
![]() $\mathrm {d} 'B$
and
$\mathrm {d} 'B$
and
![]() $\mathrm {d} 'C$
the Gaussian probability measures on the respective spaces.
$\mathrm {d} 'C$
the Gaussian probability measures on the respective spaces.
5.3.2 Computation of the inner integral
We now study
![]() $ \| \mathrm {d} _{\zeta }^{k} f_A \|_{\mathrm {Frob}}^2$
to obtain an expression for the integral
$ \| \mathrm {d} _{\zeta }^{k} f_A \|_{\mathrm {Frob}}^2$
to obtain an expression for the integral
![]() $\int \mathrm {d} ' C \|{\tfrac {1}{k!}}\mathrm {d} _{\zeta }^{k} f_{A}\|_{\mathrm {Frob}}^{2}$
that appears in (5.40). The goal is Equation (5.56).
$\int \mathrm {d} ' C \|{\tfrac {1}{k!}}\mathrm {d} _{\zeta }^{k} f_{A}\|_{\mathrm {Frob}}^{2}$
that appears in (5.40). The goal is Equation (5.56).
Recall that
![]() $\zeta =(1,0,\ldots ,0)$
. Let
$\zeta =(1,0,\ldots ,0)$
. Let
![]() $g(z) \,{\stackrel {.}{=}}\, f_A(\zeta + z)$
, and write
$g(z) \,{\stackrel {.}{=}}\, f_A(\zeta + z)$
, and write
![]() $g_{k}$
for the kth homogeneous component of g. By Lemma I.30, we have
$g_{k}$
for the kth homogeneous component of g. By Lemma I.30, we have
By expanding a multilinear product, we compute with (5.33) that
where
![]() $h_I(z_1,\dotsc ,z_n) \,{\stackrel {.}{=}}\, \operatorname {tr} \left ( U^{I}_{1} \dotsb U^{I}_{{D}} \right )$
with
$h_I(z_1,\dotsc ,z_n) \,{\stackrel {.}{=}}\, \operatorname {tr} \left ( U^{I}_{1} \dotsb U^{I}_{{D}} \right )$
with
 $$ \begin{align} U_{i}^{I} \,{\stackrel{.}{=}}\, \begin{cases} C_{i}(z_{1},\dotsc,z_{n}) & \mbox{if } i \in I\\ B_{i} & \mbox{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} U_{i}^{I} \,{\stackrel{.}{=}}\, \begin{cases} C_{i}(z_{1},\dotsc,z_{n}) & \mbox{if } i \in I\\ B_{i} & \mbox{otherwise}. \end{cases} \end{align} $$
Note that
![]() $h_I$
is of degree
$h_I$
is of degree
![]() $\# I$
in
$\# I$
in
![]() $z_1,\ldots ,z_n$
. Hence, the homogeneous part
$z_1,\ldots ,z_n$
. Hence, the homogeneous part
![]() $g_k$
satisfies
$g_k$
satisfies
 $$ \begin{align} g_{k}(z_{0},\dotsc,z_{{D}}) = \sum_{m = 1}^k \binom{{D} - m}{k-m}z_{0}^{k-m} \sum_{\# I = m} h_I(z_1,\dotsc,z_n). \end{align} $$
$$ \begin{align} g_{k}(z_{0},\dotsc,z_{{D}}) = \sum_{m = 1}^k \binom{{D} - m}{k-m}z_{0}^{k-m} \sum_{\# I = m} h_I(z_1,\dotsc,z_n). \end{align} $$
The contribution for
![]() $m=0$
vanishes by assumption:
$m=0$
vanishes by assumption:
 $$ \begin{align} \binom{{D} }{k}z_{0}^{k} h_\varnothing = \binom{{D} }{k}z_{0}^{k} \operatorname{tr} (B_1\dotsb B_k) = 0. \end{align} $$
$$ \begin{align} \binom{{D} }{k}z_{0}^{k} h_\varnothing = \binom{{D} }{k}z_{0}^{k} \operatorname{tr} (B_1\dotsb B_k) = 0. \end{align} $$
All the terms of the outer sum in (5.45) over m have disjoint monomial support, so they are orthogonal for the Weyl inner product (see Section 3.1). Moreover, for any homogeneous polynomial
![]() $p(z_1,\dotsc ,z_n)$
of degree
$p(z_1,\dotsc ,z_n)$
of degree
![]() $m\leqslant k$
, the definition of the Weyl norm easily implies
$m\leqslant k$
, the definition of the Weyl norm easily implies
![]() $\binom {k}{m}\|z_0^{k-m} p\|^2_W = \| p \|_W^2$
. It follows that
$\binom {k}{m}\|z_0^{k-m} p\|^2_W = \| p \|_W^2$
. It follows that
 $$ \begin{align} \left\| g_k \right\|_W^2 = \sum_{m=1}^k \binom{{D} - m}{k-m}^2 \binom{k}{m}^{-1} \left\|\sum_{\# I = m} h_I \right\|^2_W. \end{align} $$
$$ \begin{align} \left\| g_k \right\|_W^2 = \sum_{m=1}^k \binom{{D} - m}{k-m}^2 \binom{k}{m}^{-1} \left\|\sum_{\# I = m} h_I \right\|^2_W. \end{align} $$
For two different subsets
![]() $I,I'\subseteq \{1,\dotsc ,{D}\}$
, there is at least one index i, such that
$I,I'\subseteq \{1,\dotsc ,{D}\}$
, there is at least one index i, such that
![]() $C_i$
occurs in
$C_i$
occurs in
![]() $h_I$
and not in
$h_I$
and not in
![]() $h_{I'}$
, so that the Weyl inner product
$h_{I'}$
, so that the Weyl inner product
![]() $\langle h_I, h_{I'} \rangle _{{W}}$
depends linearly on
$\langle h_I, h_{I'} \rangle _{{W}}$
depends linearly on
![]() $C_i$
and then, by symmetry,
$C_i$
and then, by symmetry,
![]() $\int \mathrm {d} ' C \left \langle h_I, h_{I'}\right \rangle _W = 0$
. It follows that
$\int \mathrm {d} ' C \left \langle h_I, h_{I'}\right \rangle _W = 0$
. It follows that
 $$ \begin{align} \int \mathrm{d} 'C \ \left\| g_k \right\|_W^2 = \sum_{m=1}^k \binom{{D} - m}{k-m}^2 \binom{k}{m}^{-1} \sum_{\# I = m} \int \mathrm{d} 'C \left\| h_I \right\|^2_W. \end{align} $$
$$ \begin{align} \int \mathrm{d} 'C \ \left\| g_k \right\|_W^2 = \sum_{m=1}^k \binom{{D} - m}{k-m}^2 \binom{k}{m}^{-1} \sum_{\# I = m} \int \mathrm{d} 'C \left\| h_I \right\|^2_W. \end{align} $$
For computing
![]() $\int \mathrm {d} ' C \left \| h_I \right \|^2_W$
, with
$\int \mathrm {d} ' C \left \| h_I \right \|^2_W$
, with
![]() $\# I = m> 0$
, we proceed as follows. From Lemma 3.1 (
$\# I = m> 0$
, we proceed as follows. From Lemma 3.1 (
![]() $h_I$
is a homogeneous polynomial in n variables of degree m), we obtain that
$h_I$
is a homogeneous polynomial in n variables of degree m), we obtain that
 $$ \begin{align} \left\| h_I \right\|_W^2 = \binom{m+n-1}{m} \frac{1}{\operatorname{vol} \mathbb{S}(\mathbb{C}^{n})} \int_{\mathbb{S}(\mathbb{C}^n)} \mathrm{d} z \left| h_I(z) \right|{}^2. \end{align} $$
$$ \begin{align} \left\| h_I \right\|_W^2 = \binom{m+n-1}{m} \frac{1}{\operatorname{vol} \mathbb{S}(\mathbb{C}^{n})} \int_{\mathbb{S}(\mathbb{C}^n)} \mathrm{d} z \left| h_I(z) \right|{}^2. \end{align} $$
Then, given that the tuple
![]() $(C_1,\dotsc ,C_{D})$
is standard Gaussian in
$(C_1,\dotsc ,C_{D})$
is standard Gaussian in
![]() $M_{\mathbf r}(n)$
, the matrices
$M_{\mathbf r}(n)$
, the matrices
![]() $C_1(z), \dotsc , C_{D}(z)$
are independent standard Gaussian random matrices, for any
$C_1(z), \dotsc , C_{D}(z)$
are independent standard Gaussian random matrices, for any
![]() $z \in \mathbb {S}(\mathbb {C}^r)$
. Let
$z \in \mathbb {S}(\mathbb {C}^r)$
. Let
![]() $I\subseteq \{1,\dotsc ,{D}\}$
be such that
$I\subseteq \{1,\dotsc ,{D}\}$
be such that
![]() $1 \in I$
(without loss of generality, because the indices are defined up to cyclic permutation). Then we have
$1 \in I$
(without loss of generality, because the indices are defined up to cyclic permutation). Then we have
![]() $h_I(z_1,\dotsc ,z_n) = \operatorname {tr} \left ( C_1(z) U^{I}_{2} \dotsb U^{I}_{{D}} \right )$
. Integrating over
$h_I(z_1,\dotsc ,z_n) = \operatorname {tr} \left ( C_1(z) U^{I}_{2} \dotsb U^{I}_{{D}} \right )$
. Integrating over
![]() $C_1$
, Lemma 5.10
1 shows for a fixed
$C_1$
, Lemma 5.10
1 shows for a fixed
![]() $z\in \mathbb {S}(\mathbb {C}^{n+1})$
that
$z\in \mathbb {S}(\mathbb {C}^{n+1})$
that
Integrating further with respect to
![]() $C_i$
with
$C_i$
with
![]() $i \not \in I$
is trivial since
$i \not \in I$
is trivial since
![]() $\|U_2^I\dotsm U_{D}^I\|^2_{\mathrm {Frob}}$
does not depend on these
$\|U_2^I\dotsm U_{D}^I\|^2_{\mathrm {Frob}}$
does not depend on these
![]() $C_i$
. To integrate with respect to
$C_i$
. To integrate with respect to
![]() $C_i$
with
$C_i$
with
![]() $i \in I$
, we use Lemma 5.10
(ii) to obtain
$i \in I$
, we use Lemma 5.10
(ii) to obtain
After integrating with respect to the remaining
![]() $C_i$
in the same way, we obtain
$C_i$
in the same way, we obtain
where
![]() $P_I(B)$
does not depend on z and is defined as follows. Let
$P_I(B)$
does not depend on z and is defined as follows. Let
![]() $I=\{i_1,\dotsc ,i_m\}$
, with
$I=\{i_1,\dotsc ,i_m\}$
, with
![]() $1=i_1<\dotsb <i_m$
. Then
$1=i_1<\dotsb <i_m$
. Then
More generally, if
![]() $i_1 \neq 1$
,
$i_1 \neq 1$
,
![]() $P_I(B)$
is defined as above with the first and last factors replaced, respectively, by
$P_I(B)$
is defined as above with the first and last factors replaced, respectively, by
and (5.52) still holds. Averaging (5.52) with respect to
![]() $z\in {\mathbb S}({\mathbb {C}}^{n})$
, we obtain with (5.49)
$z\in {\mathbb S}({\mathbb {C}}^{n})$
, we obtain with (5.49)
 $$ \begin{align} \int \mathrm{d} 'C \ \|h_I\|_W^2 = \binom{m + n-1}{m} P_I(B).\\[-17pt]\nonumber \end{align} $$
$$ \begin{align} \int \mathrm{d} 'C \ \|h_I\|_W^2 = \binom{m + n-1}{m} P_I(B).\\[-17pt]\nonumber \end{align} $$
Combining further with (5.41) and (5.48), we obtain
 $$ \begin{align} \int \mathrm{d} ' C\ \left\|{\tfrac{1}{k!}}\mathrm{d} _{\zeta}^k f_A \right\|_{\mathrm{Frob}}^2 = \sum_{m=1}^k \binom{{D} - m}{k-m}^2 \binom{k}{m}^{-1} \binom{m+n-1}{m} \sum_{\# I = m} P_I(B).\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} \int \mathrm{d} ' C\ \left\|{\tfrac{1}{k!}}\mathrm{d} _{\zeta}^k f_A \right\|_{\mathrm{Frob}}^2 = \sum_{m=1}^k \binom{{D} - m}{k-m}^2 \binom{k}{m}^{-1} \binom{m+n-1}{m} \sum_{\# I = m} P_I(B).\\[-16pt]\nonumber \end{align} $$
Combining with (5.40), this leads to

Recall that
![]() $\hat B_i = B_{i+1}\dotsb B_{D} B_1 \dotsb B_{i-1}$
.
$\hat B_i = B_{i+1}\dotsb B_{D} B_1 \dotsb B_{i-1}$
.
5.3.3 Computation of the integral over W
We now consider the integral

which appears in the right-hand side of (5.57). The goal is the bound (5.68). To simplify notation, we assume
![]() $1\in I$
, but this does not change anything, up to cyclic permutation of the indices. We apply the coarea formula to the projection
$1\in I$
, but this does not change anything, up to cyclic permutation of the indices. We apply the coarea formula to the projection
![]() $q\colon W\to F,\, B \mapsto (B_2,\dotsc ,B_{D})$
, where
$q\colon W\to F,\, B \mapsto (B_2,\dotsc ,B_{D})$
, where
![]() $F \,{\stackrel {.}{=}}\, \mathbb {C}^{r_1\times r_2}\times \dotsb \times \mathbb {C}^{r_{{D}-1}\times r_{D}}$
. Since the complex hypersurface W is defined by the condition
$F \,{\stackrel {.}{=}}\, \mathbb {C}^{r_1\times r_2}\times \dotsb \times \mathbb {C}^{r_{{D}-1}\times r_{D}}$
. Since the complex hypersurface W is defined by the condition
![]() $\operatorname {tr}(B_1\dotsb B_{D})=0$
, we have
$\operatorname {tr}(B_1\dotsb B_{D})=0$
, we have
 $$ \begin{align} T_{B} W = \left\{ (\dot B_1,\dotsc,\dot B_{D}) \mathrel{}\middle|\mathrel{} \sum_{i=1}^{D} \operatorname{tr}(\dot B_i \hat B_i) =0 \right\} \subseteq {\mathbb{C}}^{r_{D}\times r_1} \times F ,\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} T_{B} W = \left\{ (\dot B_1,\dotsc,\dot B_{D}) \mathrel{}\middle|\mathrel{} \sum_{i=1}^{D} \operatorname{tr}(\dot B_i \hat B_i) =0 \right\} \subseteq {\mathbb{C}}^{r_{D}\times r_1} \times F ,\\[-16pt]\nonumber \end{align} $$
this is the same computation as for (5.35).
In particular, the normal space of W is spanned by
![]() $(\hat B_1^*,\dotsc ,\hat B_{D}^*)$
, where
$(\hat B_1^*,\dotsc ,\hat B_{D}^*)$
, where
![]() ${}^*$
denotes the Hermitian transpose. It follows from Lemma 5.4 (used as in Corollary 5.5) that the normal Jacobian
${}^*$
denotes the Hermitian transpose. It follows from Lemma 5.4 (used as in Corollary 5.5) that the normal Jacobian
![]() $\operatorname {NJ}_B(q)$
of q at some
$\operatorname {NJ}_B(q)$
of q at some
![]() $B\in W$
is given by
$B\in W$
is given by
 $$ \begin{align} \operatorname{NJ}_B(q) = \frac{\|\hat B_1\|^2}{\|\hat B_1\|^2_{\mathrm{Frob}} + \dotsb + \|\hat B_{D}\|^2_{\mathrm{Frob}}}. \end{align} $$
$$ \begin{align} \operatorname{NJ}_B(q) = \frac{\|\hat B_1\|^2}{\|\hat B_1\|^2_{\mathrm{Frob}} + \dotsb + \|\hat B_{D}\|^2_{\mathrm{Frob}}}. \end{align} $$
The coarea formula then gives

Note that the inner integrand does not depend on
![]() $B_1$
. Moreover, for fixed
$B_1$
. Moreover, for fixed
![]() $B_2,\ldots ,B_{D}$
, the condition
$B_2,\ldots ,B_{D}$
, the condition
![]() $\operatorname {tr}(B_1\dotsb B_{D})=0$
restricts
$\operatorname {tr}(B_1\dotsb B_{D})=0$
restricts
![]() $B_1$
to a hyperplane in
$B_1$
to a hyperplane in
![]() $\mathbb {C}^{r_0\times r_1}$
. Due to the unitary invariance of the standard Gaussian measure, the position of the hyperplane does not matter, and we obtain
$\mathbb {C}^{r_0\times r_1}$
. Due to the unitary invariance of the standard Gaussian measure, the position of the hyperplane does not matter, and we obtain
It follows that


where
![]() $I= \left \{ i_1,\dotsc ,i_m \right \}$
with
$I= \left \{ i_1,\dotsc ,i_m \right \}$
with
![]() $i_1=1$
. If
$i_1=1$
. If
![]() $m= 1$
, that is
$m= 1$
, that is
![]() $I= \left \{ 1 \right \}$
, then the integrand simplifies to
$I= \left \{ 1 \right \}$
, then the integrand simplifies to
![]() $1$
.
$1$
.
Recall the anomaly
![]() $\theta (A)$
of a matrix defined in (5.19). When
$\theta (A)$
of a matrix defined in (5.19). When
![]() $m> 1$
, we take expectations over
$m> 1$
, we take expectations over
![]() $B_{i_2},\ldots ,B_{i_m}$
and repeatedly apply Lemma 5.8, to obtainFootnote
7
$B_{i_2},\ldots ,B_{i_m}$
and repeatedly apply Lemma 5.8, to obtainFootnote
7

Every block
![]() $B_{i_k+1}\dotsb B_{i_{k+1}-1}$
appears except the last block
$B_{i_k+1}\dotsb B_{i_{k+1}-1}$
appears except the last block
![]() $B_{i_m+1}\dotsb B_{D}$
. If one of the parameters
$B_{i_m+1}\dotsb B_{D}$
. If one of the parameters
![]() $r_i$
is 1, then, by cyclic permutation of the indices, we may assume that it appears in the last block (indeed, by the hypothesis
$r_i$
is 1, then, by cyclic permutation of the indices, we may assume that it appears in the last block (indeed, by the hypothesis
![]() $r_1,\ldots ,r_{{D}-1} \ge 2$
, there is at most one i with
$r_1,\ldots ,r_{{D}-1} \ge 2$
, there is at most one i with
![]() $r_i=1$
).
$r_i=1$
).
So we can apply Lemma 5.9 and obtain

 $$ \begin{align} &\leqslant \left( 1 + \frac{1}{m-1} \sum_{j=i_1}^{i_m-1} \frac{1}{r_j-1} \right)^{m-1} , \end{align} $$
$$ \begin{align} &\leqslant \left( 1 + \frac{1}{m-1} \sum_{j=i_1}^{i_m-1} \frac{1}{r_j-1} \right)^{m-1} , \end{align} $$
using the inequality of arithmetic and geometric means. Since
![]() $r_j> 1$
for
$r_j> 1$
for
![]() $j\leqslant i_m-1$
, we further obtain
$j\leqslant i_m-1$
, we further obtain

5.3.4 Conclusion
Combining (5.32), (5.57), (5.63) and (5.68), we obtain (note the cancellation of
![]() $\pi $
),
$\pi $
),
 $$ \begin{align} &\mathbb{E} \left[ \left\| \mathrm{d} _{\zeta} f_{A} \right\|^{-2} \left\|{\tfrac{1}{k!}}\mathrm{d} _{\zeta}^{k} f_{A}\right\|_{\mathrm{Frob}}^{2}\right] \notag\\ &\qquad\qquad\qquad \leqslant \frac{1}{{D} n} \sum_{m=1}^k \binom{{D} - m}{k-m}^2 \binom{k}{m}^{-1} \binom{m+n-1}{m} \binom{{D}}{m} \left( 1 + \frac{{D}-1}{m-1} \right)^{m-1}. \end{align} $$
$$ \begin{align} &\mathbb{E} \left[ \left\| \mathrm{d} _{\zeta} f_{A} \right\|^{-2} \left\|{\tfrac{1}{k!}}\mathrm{d} _{\zeta}^{k} f_{A}\right\|_{\mathrm{Frob}}^{2}\right] \notag\\ &\qquad\qquad\qquad \leqslant \frac{1}{{D} n} \sum_{m=1}^k \binom{{D} - m}{k-m}^2 \binom{k}{m}^{-1} \binom{m+n-1}{m} \binom{{D}}{m} \left( 1 + \frac{{D}-1}{m-1} \right)^{m-1}. \end{align} $$
By reordering the factorials, we have
 $$ \begin{align} \binom{{D}-m}{k-m}^2 \binom{k}{m}^{-1} \binom{{D}}{m} = \binom{{D}-m}{k-m} \binom{{D}}{k}. \end{align} $$
$$ \begin{align} \binom{{D}-m}{k-m}^2 \binom{k}{m}^{-1} \binom{{D}}{m} = \binom{{D}-m}{k-m} \binom{{D}}{k}. \end{align} $$
As in the proof of Lemma I.37, we observe the identity
 $$ \begin{align} \sum_{m=0}^k \binom{{D}-m}{k-m} \binom{m+n-1}{m} = \binom{{D}+n}{k}. \end{align} $$
$$ \begin{align} \sum_{m=0}^k \binom{{D}-m}{k-m} \binom{m+n-1}{m} = \binom{{D}+n}{k}. \end{align} $$
Moreover, since
![]() $m \leqslant k$
,
$m \leqslant k$
,
 $$ \begin{align} \left( 1 + \frac{{D}-1}{m-1} \right)^{m-1} \leqslant \left( 1 + \frac{{D}-1}{k-1} \right)^{k-1} \end{align} $$
$$ \begin{align} \left( 1 + \frac{{D}-1}{m-1} \right)^{m-1} \leqslant \left( 1 + \frac{{D}-1}{k-1} \right)^{k-1} \end{align} $$
(including
![]() $m=1$
, where the left-hand side is 1). Equations (5.69), (5.70), (5.71) and (5.72) give
$m=1$
, where the left-hand side is 1). Equations (5.69), (5.70), (5.71) and (5.72) give
 $$ \begin{align} \mathbb{E} \left[ \left\| \mathrm{d} _{\zeta} f_{A} \right\|^{-2} \left\|{\tfrac{1}{k!}}\mathrm{d} _{\zeta}^{k} f_{A}\right\|_{\mathrm{Frob}}^{2}\right] \leqslant \frac{1}{n{D}} \binom{{D}}{k} \binom{{D}+n}{k} \left( 1 + \frac{{D}-1}{k-1} \right)^{k-1}. \end{align} $$
$$ \begin{align} \mathbb{E} \left[ \left\| \mathrm{d} _{\zeta} f_{A} \right\|^{-2} \left\|{\tfrac{1}{k!}}\mathrm{d} _{\zeta}^{k} f_{A}\right\|_{\mathrm{Frob}}^{2}\right] \leqslant \frac{1}{n{D}} \binom{{D}}{k} \binom{{D}+n}{k} \left( 1 + \frac{{D}-1}{k-1} \right)^{k-1}. \end{align} $$
This gives the first inequality of Proposition 5.3. For the second, we argue as in the proof of Lemma I.37: the maximum value of
![]() $\left [\frac {1}{n{D}} \binom {{D}}{k} \binom {{D}+n}{k}\right ]^{\frac {1}{k-1}}$
with
$\left [\frac {1}{n{D}} \binom {{D}}{k} \binom {{D}+n}{k}\right ]^{\frac {1}{k-1}}$
with
![]() $k\ge 2$
is reached at
$k\ge 2$
is reached at
![]() $k=2$
. Hence, for any
$k=2$
. Hence, for any
![]() $k\ge 2$
,
$k\ge 2$
,
 $$ \begin{align} \left[\frac{1}{n{D}} \binom{{D}}{k} \binom{{D}+n}{k}\right]^{\frac{1}{k-1}} \le \left[\frac{1}{n{D}} \binom{{D}}{2} \binom{{D}+n}{2}\right]^{\frac{1}{k-1}} \le \left[\frac{1}{4} {D}^2 ({D}+n) \right]^{\frac{1}{k-1}}. \end{align} $$
$$ \begin{align} \left[\frac{1}{n{D}} \binom{{D}}{k} \binom{{D}+n}{k}\right]^{\frac{1}{k-1}} \le \left[\frac{1}{n{D}} \binom{{D}}{2} \binom{{D}+n}{2}\right]^{\frac{1}{k-1}} \le \left[\frac{1}{4} {D}^2 ({D}+n) \right]^{\frac{1}{k-1}}. \end{align} $$
This concludes the proof of Proposition 5.3.
Acknowledgments
We are grateful to the referees for a very accurate work. This research was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 787840); a GRF grant from the Research Grants Council of the Hong Kong SAR (project number CityU 11302321); and the projet De Rerum Natura ANR-19-CE40-0018 of the French National Research Agency (ANR).
Conflicts of Interest
The authors have no conflicts of interest to declare.