Introduction
Evans Ice Stream is a large ice stream with five tributaries, draining a 104 000 km2 catchment of the West Antarctic ice sheet (WAIS) (Reference Bamber, Vaughan and JoughinBamber and others, 2000; Reference Joughin and BamberJoughin and Bamber, 2005). The WAIS is a marine ice sheet with much of its bed below sea level, containing ∼6m of potential sea-level rise. The grounding zone, which marks the transition between an ice sheet and an ice shelf, is an important control on ice-sheet stability as it determines the ice discharge from the grounded ice sheet (e.g. Reference WeertmanWeertman, 1974; Reference SchoofSchoof, 2007). Longitudinal stress in this area prevents a large increase in velocity when basal drag is reduced to zero as the ice starts to float (Reference BindschadlerBindschadler, 2006). However, grounding lines are often modelled inadequately, due to both coarse ice-sheet model resolution and the use of approximations in models of marine ice sheets, which leads to ice sheets being modelled separately from ice shelves, with boundary conditions imposed at the grounding line (Reference Vieli and PayneVieli and Payne, 2005; Reference SchoofSchoof, 2007).
It is now widely recognized that the previously held view of an ice-sheet ’grounding line’ is an oversimplification, which has been used to refer to several locations (Fig. 1): the landward limit of tidal flexing of the grounded ice stream, also known as the hinge line (F in figure); the limit of flotation (G), which will migrate with the tide, leading to areas between its furthest landward and seaward locations being intermittently grounded at different points in the tidal cycle; the inflexion point (I) and the seaward limit of tidal flexing, which is also the landward limit of the ice-shelf hydrostatic zone (H) (Reference SmithSmith, 1991; Reference VaughanVaughan, 1994; Reference Fricker and PadmanFricker and Padman, 2006). The grounding zone, or hinge zone, may be defined as the area between F and H, and may be up to several kilometres wide, depending on ice thickness and bed topography.

Fig. 1. An ice-shelf grounding zone. F and H mark the landward and seaward limits of tidal flexure, G the limit of flotation and I the inflexion point (after Reference SmithSmith, 1991; Reference VaughanVaughan, 1994; Reference Fricker and PadmanFricker and Padman, 2006).
Locating the grounding zone correctly is important for the interpretation of velocity data, which contain tidal modulation of the signal downstream of F, where Reference Jenkins, Corr, Nicholls, Stewart and DoakeJenkins and others (2006) also found tidal modulation of vertical strain rates and ice thickness on nearby Rutford Ice Stream. More subdued tidal modulation of velocity may also occur considerable distances upstream of F (Reference Anandakrishnan, Voigt, Alley and KingAnandakrishnan and others, 2003; Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003; Reference GudmundssonGudmundsson, 2006). Grounding zone migration is monitored to assess the overall stability of the WAIS, but is reliant on the initial location of the grounding zone being correctly identified, as is the accuracy of models using grounding line location as a boundary condition. However, three previously published locations of the Evans Ice Stream grounding line disagree by as much as 93 km (Fig. 2).

Fig. 2. Previous versions of the grounding line of Evans Ice Stream reported by T. Haran and others (http://nsidc.org/data/nsidc-0280.html), Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyealJoughin and others (2006), Reference Lythe and VaughanLythe and others (2001) and Reference Vaughan, Smith, Nath and Le MeurVaughan and others (2003). The grounding zone mapped in the present study is marked in white. SAR frames are shown and marked with track numbers (Table 1). The white star is the location where tidal components were extracted from the CATS02.01 model. White triangles represent where the CATS02.01 model would run, and white circles indicate locations where it would not, due to its bathymetry grid. The projection is polar stereographic.
Knowledge of the behaviour of the ice streams draining the WAIS is necessary for an accurate assessment of its present and future mass balance and contribution to sea-level rise. Although Evans Ice Stream has the largest discharge of any ice stream feeding the Filchner–Ronne Ice Shelf (FRIS), estimated at 35.7 ± 3.6Gt a−1 (Reference Joughin and BamberJoughin and Bamber, 2005), it is the subject of surprisingly little published work. Field expeditions there are hampered by adverse conditions such as crevasse fields and poor visibility (personal communications from E. King, 2006 and E. Morris, 2007). Valuable insight into its dynamics is therefore provided by modelling and by remote-sensing methods, particularly active microwave systems such as synthetic aperture radar (SAR), which is not affected by the presence of cloud and can image through the polar night.
Methods
Synthetic aperture radar interferometry
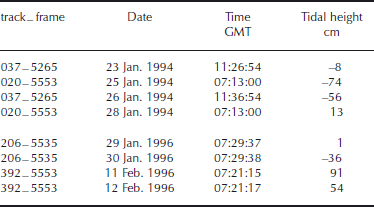
SAR interferometry uses the phase difference between successive active microwave satellite scenes to show displacement in the line-of-sight (LOS) direction of the satellite (including both horizontal and vertical displacement) and topography. Scenes from the European Remote-sensing Satellites, ERS-1 and ERS-2, were selected for the ’second ice phase’ in 1994, and the ’second multidisciplinary phase’ in 1996 (Table 1), both of which had short enough orbital repeat periods to maintain coherence, or correlation, between successive scenes, which is a requirement for interferometry.
Table 1. Tidal height change from the CATS02.01 and t−tide models and as shown by interferograms, for ERS SAR scenes used to map the grounding zone of Evans Ice Stream

The phase difference between co-registered scenes of the same frame is calculated for each pixel by multiplying the complex pixel value of one image by the complex conjugate of the other. Phase differences are scaled from 0 to 2π radians. Complete phase cycles are displayed in cycles of colour known as fringes, which are the result of scene topography, LOS displacement and the perpendicular baseline, which is the separation between paired images in the across-track direction. The topographic elevation represented by one fringe is known as the altitude of ambiguity, and for the ERS satellites is calculated by dividing 9416 by the perpendicular baseline (Table 1; NPA Group, http://www.npagroup.com/insar/whatisinsar/insar−simple.htm).
Interferometry, like most methods used to map the grounding zone, identifies F and H (Fig. 1). The high phase gradient in the grounding zone, which occurs because of the change in vertical motion where the ice adjusts to hydrostatic equilibrium at H, means the grounding zone is easily identifiable by its many closely spaced fringes (Reference RignotRignot, 1998). We digitized the shape and width of the grounding zone in ArcMap from georeferenced interferograms created by the Gamma tools (Fig. 3). Both single- and double-difference interferograms were used; the double-difference interferograms (Reference Zebker, Rosen, R.M. Goldstein, Gabriel and WernerZebker and others, 1994), which have had the effects of motion common to two single-difference interferograms removed, proved particularly effective in mapping the grounding zone as they show only differential tidal displacement and scene topography.

Fig. 3. Grounding zone width of Evans Ice Stream mapped from interferograms. (a) Mosaicked interferograms of tracks 206 and 392. (b) Zoom of the grounding zone in the track 206 interferogram. (c) The grounding zone as mapped from SAR interferometry. Dotted curves indicate mapping from track 206, which also fitted interferograms from tracks 020 and 037; solid curves indicate mapping from a double-difference interferogram of track 392 further upstream. The locations of ice thicknesses used in the elastic beam model are marked as black triangles. SAR frames are shown in black. The dashed grey curve indicates a major flowline. Coordinates are polar stereographic.
The ERS satellites are 2.4 times more sensitive to vertical displacement than horizontal displacement due to their steep look angle, 23◦, and each fringe represents ∼2.6 cm of vertical displacement if it is assumed all displacement was vertical. Fringes in the grounding zone were counted and the total vertical displacement compared to the tidal change between scenes as predicted by the model (Table 1).
Tidal model
At any given location, the tidal signal can be described as the sum of a number of sine functions representing different diurnal, semi-diurnal and longer-term components, each of which is caused by the gravitational forces between the Sun, the Moon and the Earth. The components of the tidal signal are described according to Doodson numbers, which are integers representing six astronomical phenomena: the Earth’s rotation; the Earth’s orbit; the Moon’s orbit; the periodicity of lunar perigee; lunar orbital tilt; and the location of perihelion in the Earth’s orbit (Reference Pawlowicz, Beardsley and LentzPawlowicz and others, 2002). These numbers predict the phase and amplitude of the tidal signal were the Earth’s response fast enough for the ocean to be in equilibrium with its forcing. Table 2 shows the frequencies of the ten principal tidal components.
Table 2. Principal tidal coefficients
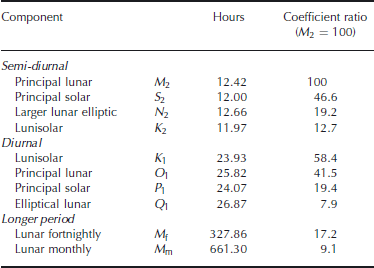
The ten principal tidal components for the Evans Ice Stream grounding zone were extracted from the CATS02.01 Circum-Antarctic Tidal Simulation model (Reference Padman, Fricker, Coleman, Howard and ErofeevaPadman and others, 2002) and usedwith the t−tide model (Reference Pawlowicz, Beardsley and LentzPawlowicz and others, 2002) to reconstruct the tidal signal through the time periods covered by the SAR images (Table 3). The tidal heights at the time of acquisition of each image were used to calculate the difference in tidal height for each interferogram (Table 1).
Table 3. Tidal heights at the time of acquisition of each SAR image of Evans Ice Stream
Elastic beam model
The width of the grounding zone was modelled using an elastic beam model (Reference VaughanVaughan, 1995). The vertical displacement of the ice shelf from its mean position, w(x), was modelled along an x axis perpendicular to and downstream of the grounding line, which, in the model, was clamped in place at x = 0. The beam was of uniform thickness. The hinge zone lies between the conditions where w, ∂w/∂x and x = 0 (at the grounding line, in this case meaning F), and w = A0(t), where A0(t) is the deviation from mean sea level at a given time, and is given by:
In this equation A0(t) would be the height of the ice-shelf surface were it floating in hydrostatic equilibrium, and is equivalent to half the tidal range (Reference SmithSmith, 1991). The spatial wavenumber, β, is given by the following equation:
where ρsea is the sea-water density (taken as 1030 kgm−3; Reference SmithSmith, 1991), g is gravitational acceleration, E is the elastic (Young’s) modulus, v is Poisson’s ratio and h is the ice-shelf thickness. The spatial wavenumber, β, has a non-linear dependence on h, because changing the ice thickness changes the rigidity of the beam, but β is relatively insensitive to changes in E and v (Reference VaughanVaughan, 1995; Reference Reeh, Lintz Christensen, Mayer and OlesenReeh and others, 2003).
Three different values of E were used: 1.1GPa, as used by Reference SmithSmith (1991); 0.88 GPa, derived empirically by Reference VaughanVaughan (1995) from analysis of tiltmeter data for several sites in Antarctica; and 9GPa, as used by Reference StephensonStephenson (1984), which is close to laboratory-derived values of E for ice of 9.3 GPa (Reference Reeh, Lintz Christensen, Mayer and OlesenReeh and others, 2003). However, ice thickness about half the real value had to be used with this highest value of E by Reference StephensonStephenson (1984), and these were the data that were revisited by Reference SmithSmith (1991).
Two different values of v, which is a measure of how much a material which is being stretched in one dimension contracts in the other two dimensions, were used. The usual value of v given for ice and used by Reference StephensonStephenson (1984), Reference SmithSmith (1991) and Reference VaughanVaughan (1995) is 0.3. However, Reference Jenkins, Corr, Nicholls, Stewart and DoakeJenkins and others (2006) found a value of v close to 0.5 fitted their measured horizontal and vertical strains downstream of the grounding line of nearby Rutford Ice Stream, and which, interestingly, is the theoretical maximum, and as such assumes that the ice shelf is incompressible.
Values of A0(t) came from the results of the t−tide model, discussed below, and were taken as half the typical maximum tidal amplitude at both spring and neap tides for the study period: 2.35 and 0.62 m, respectively. The model was run for two different ice thicknesses, both taken from BEDMAP (Reference Lythe and VaughanLythe and others, 2001): 1017 m, at the location where the CATS02.01 model was run, and 1913 m, the largest value of ice thickness at the grounding zone as mapped from interferometry (Fig. 3). The elastic beam and tidal models were run in MatlabTM, and the hinge zone width calculated to the nearest 100 m.
Results
SAR interferometry showed vertical motion in a clearly defined grounding zone (Fig. 3). The grounding zone was mapped fromfour SAR frames, and found to match where the frames overlapped, although the fringe rate in the grounding zone differed between flattened interferograms of different scenes, due to their different vertical tidal displacements. The grounding line has a complex shape, and runs parallel to the direction of the main trunk for ∼120 km on the east side of the ice stream. The upstream end of this part of the grounding zone lies adjacent to an area of slow-moving ice, probably frozen to its bed, which divides the eastern and western groups of tributaries. A major flowline, visible in both SAR intensity images and interferograms, extends downstream from here, dividing the flow regimes from the two groups of tributaries (Fig. 3). The grounding zone to the west of this flowline is perpendicular to the direction of the main trunk and considerably wider than that on the east side. Thus, for much of the length of the main trunk, the east side of the ice stream is grounded and the west side floating.
Tidal modelling showed that the maximum tidal range for the Evans Ice Stream grounding zone is >5m. This is well above the usual 1–2m range for the ice shelves surrounding Antarctica, and greater than the 3 m range for the FRIS. However, Evans Ice Stream does not have as high a tidal range as the 6m at the grounding line of nearby Rutford Ice Stream (Reference DoakeDoake, 1992; Reference Padman, Fricker, Coleman, Howard and ErofeevaPadman and others, 2002).
Vertical displacement observed in the interferograms was compared to the modelled tidal height differences. On the flat topography of the ice shelf, fringes due to the perpendicular baseline could be discounted because of the relatively high altitudes of ambiguity (Table 1). Although some fringes can be accounted for by LOS displacement, the changing orientation of the grounding zone and range of flow directions from the tributaries means that for most of the area the flow direction is orientated approximately perpendicular to the LOS, meaning the majority of the fringes can be explained by vertical motion. Table 1 shows vertical change in the grounding zone as calculated from the number of fringes. This is a closer match to that predicted by the tidal model for tracks 020 and 206, which are ascending frames located in similar places in 1994 and 1996, respectively, and have look directions perpendicular to the ice-stream flow direction, making them especially insensitive to horizontal displacement. In the case of the track 020 interferogram, additional fringes may have been present in the grounding zone had the scene extended further north. It is clear that the ice shelf is being affected by vertical motion proportional to changing tidal height.
The width of the grounding zone calculated using the elastic beam model was compared to the mapped values, which were measured using tools in ArcGIS both parallel to the ice-flow direction and perpendicular to both F and H (Table 4; Fig. 4). The choice of A 0(t) does not affect the modelled width of the grounding zone, which is consequently the same for spring and neap tides (Fig. 4). Increasing values of E and v lead to an increase in the modelled width. Using v = 0.5 and E = 0.88 produced very similar results to using v = 0.3 and E = 1.1. The grounding zone nearest to where the tidal model was run, where the ice thickness was 1017 m, was found to best fit a model using E = 0.88 and v = 0.3. This was the case for most of the rest of the grounding zone. However, much further upstream, at the mapped grounding zone where the maximum ice thickness was 1913 m, the mapped width best fits a model with E = 1.1 and v between 0.3 and 0.5. Using values of v for ice other than 0.3 should therefore be considered in future work. As suspected, using E = 9 vastly overestimates the width of the grounding zone and thus laboratory-derived values of E for ice are unsuitable for use in this type of work.

Fig. 4. Grounding zone widthmodelled by an elastic beam for Evans Ice Stream using ice thicknesses of 1017 and 1913 m and E of 0.88, 1.1 and 9. Solid and dashed curves indicate Poisson’s ratios of 0.3 and 0.5, respectively.
Table 4. The width of the grounding zone of Evans Ice Stream as modelled using an elastic beam

Discussion
Inconsistencies between previously published versions of the Evans grounding line were noted prior to this study. Grounding lines by Reference Vaughan, Smith, Nath and Le MeurVaughan and others (2003) and Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyealJoughin and others (2006) overlap with the grounding zone derived here, although they differ by up to 9 km, but the grounding line derived from theMODIS (moderate-resolution imaging spectroradiometer) Mosaic of Antarctica (MOA) (T.Haran and others, http://nsidc.org/data/nsidc-0280.html) is as much as 93 km downstream of these and clearly on the floating ice shelf (Fig. 2).
Vaughan’s grounding line, and probably also Joughin’s, were digitized from interferograms, although whether they defined F or H is unknown, and the MOA grounding line was identified from the break in slope between grounded and floating ice (personal communication from NSIDC, 2007). It is not the case that the three grounding lines differ due to picking out different combinations of F, G, I and H, as interferometry maps the zone between F and H, so methods locating either G or I would locate their grounding lines within the hinge zone as mapped from interferometry. It is more useful to map the grounding zone, rather than a line, as this provides additional information by showing its shape and width.
Several widely used datasets of Antarctica also position the grounding line of Evans Ice Stream considerably further downstream than observed in SAR interferometry of 1994 and 1996. The Reference Vaughan, Smith, Nath and Le MeurVaughan and others (2003) and Reference Joughin, Bamber, Scambos, Tulaczyk, Fahnestock and MacAyealJoughin and others (2006) grounding lines, although close to the grounding zone derived in this study, are not part of widely used datasets. The BEDMAP dataset (Reference Lythe and VaughanLythe and others, 2001), for example, defines the grounding line as far as 37 km further downstream than even the MOA grounding line, or up to 100 km from the grounding zone as mapped in this study, as shown by the seaward limit of the grounded bed layer and the landward limit of the water depth layer. This imprecision clearly affects any work using the BEDMAP dataset as an input. Similarly, the landward limit of the bathymetry grid in the CATS02.01 model, which is in a similar place to the grounding line of Reference Lythe and VaughanLythe and others (2001), meant that tidal components used in this study were extracted from the CATS02.01 model at a latitude of –76.75◦ and a longitude of –76.00◦ (Fig. 2), rather than for a coordinate closer to the mapped grounding zone. Whether the ice thickness used for the elastic beam model came from this location or from the mapped grounding zone made a difference of up to 9 km in the modelled width of the hinge zone, for realistic values of E.
Although ice thickness and basal topography are known to affect grounding zone width (Reference Fricker and PadmanFricker and Padman, 2006), in the case of Evans Ice Stream this may also apply to its shape. On the eastern side of the main trunk, where the hinge zone is further downstream, the bed is shallower than on the western side, with depths of, for example, 1249 m compared to 1546 m. The ice-surface elevation is only slightly higher on the eastern side, for example, 235m compared to 201 m, and as such ice on the western side is thicker, for example, 1787 m compared to 1475 m (Reference Lythe and VaughanLythe and others, 2001), leading to a wider grounding zone.
As well as the shape of the grounding zone, tidal conditions are also an important regulator of ice-stream flow. Reference GudmundssonGudmundsson (2007) expected Evans Ice Stream to show fortnightly tidal variations in velocity similar to those of nearby Rutford Ice Stream, and as the tidal range at the Evans grounding line is almost as high, this is clearly worthy of further investigation.
Summary
Evans Ice Stream has a grounding zone with a complex shape, which may be governed by its bed topography and the flow of its five tributaries. SAR interferometry maps the grounding zone up to 100 km upstream of its location in some widely used datasets, and the grounding zone is 6–23 km wide. Evans Ice Stream has a significant tidal range, 5m, and vertical motion of the ice stream due to tidal forcing is clearly taking place. Finally, it is clear that remote-sensing and modelling methods allow much to be learnt about ice streams where adverse conditions hamper extensive field campaigns, although further work is required to resolve discrepancies between datasets.
Acknowledgements
Thanks to G. AðalgeirsdÓttir, M. King and K. Makinson for valuable advice on the tidal model. SAR data were obtained through the VECTRA project. Helpful and constructive comments from C. Clark and from two anonymous reviewers are much appreciated.







