1. Introduction
Analytical models of various fluid mechanical phenomena in wind energy play an important role for basic understanding and for design and control of wind farms. Prime examples are models for the wind turbine wake velocity defect and its downstream evolution commonly used in wind farm layout optimization (Jensen Reference Jensen1983; Stevens & Meneveau Reference Stevens and Meneveau2017; Porté-Agel, Bastankhah & Shamsoddin Reference Porté-Agel, Bastankhah and Shamsoddin2020). In the classic Jensen model, for instance, a linearly expanding wake with a top-hat shape is assumed. More recent models allow for more realistic wake cross-sections with a Gaussian distribution (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2014), and cross-sections that transition from top hat near the turbine to Gaussian further downstream have also been proposed (Shapiro et al. Reference Shapiro, Starke, Meneveau and Gayme2019).
Analytical wake models can be particularly useful in implementation of wake mitigation strategies such as wake steering, which has been receiving growing attention as an important control approach for increasing wind farm power output (Fleming et al. Reference Fleming, Gebraad, Lee, van Wingerden, Johnson, Churchfield, Michalakes, Spalart and Moriarty2014; Gebraad et al. Reference Gebraad, Teeuwisse, Wingerden, Fleming, Ruben, Marden and Pao2014; Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2015; Campagnolo et al. Reference Campagnolo, Petrović, Schreiber, Nanos, Croce and Bottasso2016; Howland et al. Reference Howland, Bossuyt, Martínez-Tossas, Meyers and Meneveau2016; Schottler et al. Reference Schottler, Mühle, Bartl, Peinke, Adaramola, Sætran and Hölling2017; Bartl et al. Reference Bartl, Mühle, Schottler, Sætran, Peinke, Adaramola and Hölling2018; Lin & Porté-Agel Reference Lin and Porté-Agel2019; Kleusberg, Schlatter & Henningson Reference Kleusberg, Schlatter and Henningson2020; Speakman et al. Reference Speakman, Abkar, Martínez-Tossas and Bastankhah2021). Achieving increased power output through wake steering involves turbines, often in the front rows of wind farms, being intentionally operated in yawed conditions to redirect their wakes away from downwind turbines. Although this reduces the power produced by the yawed turbines, research has shown that the total wind farm efficiency can improve as a result of more power generated by downwind turbines (Park & Law Reference Park and Law2016; Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2019; Fleming et al. Reference Fleming2019; Howland, Lele & Dabiri Reference Howland, Lele and Dabiri2019; King et al. Reference King, Fleming, King, Martínez-Tossas, Bay, Mudafort and Simley2021). Yawed turbine wake flows are known to exhibit complex features which makes their modelling more challenging than their unyawed counterparts. The most striking fluid-dynamic feature of a yawed turbine wake is arguably its curled cross-sectional shape (i.e. a kidney-shaped cross-section). This shape arises due to the action of a counter-rotating vortex pair (CVP) as detailed in Howland et al. (Reference Howland, Bossuyt, Martínez-Tossas, Meyers and Meneveau2016). Counter-rotating vortex pairs are typically generated when forcing with spatial cross-stream variations is applied perpendicular to the flow direction. One of the most notable examples are vortices trailing from finite-span wings that roll-up and lead to the formation of a CVP, i.e. wingtip vortices or wake vortices in the aerodynamics literature. The formation and evolution of these vortical structures has been the subject of numerous studies since seminal works of Prandtl and Lancaster (see Anderson (Reference Anderson2011), and references therein). As noted in Bastankhah & Porté-Agel (Reference Bastankhah and Porté-Agel2016), the CVP observed in yawed turbine wakes is also similar to those formed in many other free shear flows with strong spanwise variations of cross-wind velocity such as cross-flow jets (see, e.g. the review of Mahesh Reference Mahesh2013).
In order to exploit the basic understanding of induced velocity and circulation of CVPs generated by finite-span wings, Shapiro, Gayme & Meneveau (Reference Shapiro, Gayme and Meneveau2018) proposed to regard a yawed turbine as a lifting surface with an elliptical planform. Based on this approach, the lateral component of the thrust force can be regarded as the transverse lift force. This analogy made it possible to determine: (i) the distribution of circulation at the yawed rotor modelled as a lifting line, and (ii) the transverse velocity (equivalent to downwash velocity for finite-span wings) at the rotor disk due to the yaw offset. The latter enabled modelling of the transverse displacement of the wake but the wake itself was still assumed to retain a circular cross-sectional shape rather than the curled shape observed in practice. The associated vorticity distribution was later used by Martínez-Tossas et al. (Reference Martínez-Tossas, Annoni, Fleming and Churchfield2019, Reference Martínez-Tossas, King, Quon, Bay, Mudafort, Hamilton, Howland and Fleming2021) to develop a Lagrangian vorticity transport model that can predict the curled shape of the wake after numerical integration. Recently, Martinez-Tossas & Branlard (Reference Martinez-Tossas and Branlard2020) and Zong & Porté-Agel (Reference Zong and Porté-Agel2020) have instead expressed rates of vorticity shedding at rotor blade tips using vortex cylinder theory (Coleman, Feingold & Stempin Reference Coleman, Feingold and Stempin1945; Burton et al. Reference Burton, Sharpe, Jenkins and Bossanyi1995; Branlard & Gaunaa Reference Branlard and Gaunaa2016) to determine the trailing vorticity distribution behind a yawed rotor. The numerical model developed by Zong & Porté-Agel (Reference Zong and Porté-Agel2020) also takes into account the redistribution of point vortices in the wake due to their self-induced velocities. More recently, Shapiro, Gayme & Meneveau (Reference Shapiro, Gayme and Meneveau2020) have solved the linearised mean streamwise vorticity transport equation to develop an analytical expression that can predict the decay of the CVP due to atmospheric turbulence. Bossuyt et al. (Reference Bossuyt, Scott, Ali and Cal2021) have also experimentally demonstrated the impact of vortical structures shedding from a misaligned (either tilted or yawed) rotor on the curled shape of the wake downstream.
Capturing the curled shape of the wake for yawed turbines is of great importance since curling affects how much the wake will effectively overlap with downstream wind turbines, thus affecting the predicted power generation. However, models of the curled wake shape in the literature require numerical integration, and existing analytical wake models (e.g. Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016; Qian & Ishihara Reference Qian and Ishihara2018; Shapiro et al. Reference Shapiro, Gayme and Meneveau2018; Blondel et al. Reference Blondel, Cathelain, Joulin and Bozonnet2020; King et al. Reference King, Fleming, King, Martínez-Tossas, Bay, Mudafort and Simley2021) cannot capture this deformation of the wake shape. There are several advantages to analytically expressed models that represent the trends in simple and explicit forms. Apart from their low computational cost, analytical flow models (Meneveau Reference Meneveau2019) often prove to be useful in revealing additional insights on flow physics that may not be evident using numerical simulation tools. Therefore, the current study aims at developing an analytical model to predict displacement and shape deformation of the wake behind a yawed turbine. The proposed model is inspired by prior works on two-dimensional vortex sheets (e.g. Rottman, Simpson & Stansby Reference Rottman, Simpson and Stansby1987; Coelho & Hunt Reference Coelho and Hunt1989). The proposed analytical model predicts displacement and deformation of a vortex sheet, shedding from the circumference of a yawed rotor, as it is convected downstream. The vortex sheet model is then combined with a model for downstream evolution of wake velocity deficit to predict the shape of the curled wake and velocity distribution downwind of a yawed turbine.
The remainder of the paper is organised as follows. Section 2 derives the vortex sheet, truncated power series solution for the yawed turbine wake in uniform, ideal flow, and model predictions are compared with numerical simulation under laminar uniform inflow. In § 3 the model is extended to cases with turbulent boundary layer inflow, and the results are compared with corresponding large-eddy simulation (LES) data. Finally, § 4 provides a summary of the developed model and our main conclusions.
2. Vortex sheet evolution in uniform, ideal flow
2.1. Evolving vortex sheet governing equations
As shown in Shapiro et al. (Reference Shapiro, Gayme and Meneveau2020), among others, vortices shedding from the circumference of the yawed rotor represented as an actuator disk form a tubular vortex sheet. The objective of this section is to model the shape evolution of this vortex sheet with downstream distance or, equivalently, with time. Only the streamwise component of the shedding vorticity is modelled in this work because the lateral wake deflection and the deformation of the wake cross-section are mainly due to the velocities induced by the streamwise component of shedding vorticity (Martinez-Tossas & Branlard Reference Martinez-Tossas and Branlard2020). The vortex sheet consists of semi-infinite streamwise vortex lines. In order to enable solving the governing equations analytically, following Coelho & Hunt (Reference Coelho and Hunt1989) and Rottman et al. (Reference Rottman, Simpson and Stansby1987), we assume that the vortex sheet is planar and that its constituent vortex lines are infinite instead of semi-infinite, an approximation that improves at increasing distances from the origin.
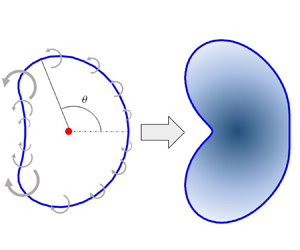
Figure 1 shows a schematic of the vortex sheet in the plane normal to the incoming flow. The ![]() $(x,y,z)$ coordinate system is defined with an origin at the rotor centre and with
$(x,y,z)$ coordinate system is defined with an origin at the rotor centre and with ![]() $x$ in the streamwise direction (i.e. parallel to the incoming flow) and
$x$ in the streamwise direction (i.e. parallel to the incoming flow) and ![]() $y$ and
$y$ and ![]() $z$ in the spanwise and vertical directions, respectively. Alongside this Cartesian system, we define a polar coordinate system of
$z$ in the spanwise and vertical directions, respectively. Alongside this Cartesian system, we define a polar coordinate system of ![]() $(r,\theta )$ in the
$(r,\theta )$ in the ![]() $yz$-plane (i.e. plane normal to the incoming flow). This polar coordinate system is attached to the centre of the vortex sheet, denoted by
$yz$-plane (i.e. plane normal to the incoming flow). This polar coordinate system is attached to the centre of the vortex sheet, denoted by ![]() $C$. The position of
$C$. The position of ![]() $C$ in the
$C$ in the ![]() $(x,y,z)$ coordinate system is denoted by
$(x,y,z)$ coordinate system is denoted by ![]() $(x_c,y_c,z_c)$. As
$(x_c,y_c,z_c)$. As ![]() $r$ is the radial distance from
$r$ is the radial distance from ![]() $C$, one can write
$C$, one can write ![]() $r^{2}=(y-y_c)^{2}+(z-z_c)^{2}$. The polar angle
$r^{2}=(y-y_c)^{2}+(z-z_c)^{2}$. The polar angle ![]() $\theta$ is measured from the positive
$\theta$ is measured from the positive ![]() $y$-axis toward the positive
$y$-axis toward the positive ![]() $z$-axis such that
$z$-axis such that ![]() $\tan \theta =(z-z_c)/(y-y_c)$. The shape of the vortex sheet is represented by the polar function
$\tan \theta =(z-z_c)/(y-y_c)$. The shape of the vortex sheet is represented by the polar function ![]() $\xi (\theta,t)$ that measures the distance of the vortex sheet from the centre, where
$\xi (\theta,t)$ that measures the distance of the vortex sheet from the centre, where ![]() $t$ is time. Our main objective is to describe the evolution of the vortex sheet as a function of time
$t$ is time. Our main objective is to describe the evolution of the vortex sheet as a function of time ![]() $t$ in a frame moving downstream with the convection velocity
$t$ in a frame moving downstream with the convection velocity ![]() $U_{con}$, i.e. determine
$U_{con}$, i.e. determine ![]() $\xi (\theta,t)$. This is equivalent to determining the downstream spatial evolution of the vortex sheet, with
$\xi (\theta,t)$. This is equivalent to determining the downstream spatial evolution of the vortex sheet, with ![]() $x=U_{con} t$. The sheet location
$x=U_{con} t$. The sheet location ![]() $\xi (\theta,t)$ obeys
$\xi (\theta,t)$ obeys
where ![]() $\xi _0=\xi (\theta,0)$ and
$\xi _0=\xi (\theta,0)$ and ![]() $u_r(\theta,t)$ denotes the radial velocity of the vortex sheet, which is affected by the strength of the evolving vortex sheet, whose evolution is treated next.
$u_r(\theta,t)$ denotes the radial velocity of the vortex sheet, which is affected by the strength of the evolving vortex sheet, whose evolution is treated next.

Figure 1. Schematic of the vortex sheet and different velocity terms on the right-hand side of (2.4). (a) Self-induced vortex sheet velocity, ![]() $\boldsymbol {u}_I$. (b) Vortex sheet velocity induced by the point vortex at the vortex sheet centre,
$\boldsymbol {u}_I$. (b) Vortex sheet velocity induced by the point vortex at the vortex sheet centre, ![]() $\boldsymbol {u}_{I\!I}$. (c) Velocity of the vortex sheet centre,
$\boldsymbol {u}_{I\!I}$. (c) Velocity of the vortex sheet centre, ![]() $\boldsymbol {u}_{c}$.
$\boldsymbol {u}_{c}$.
Let us denote the strength of the vortex sheet by ![]() $\gamma =\gamma (\theta,t)$, where the vortex strength
$\gamma =\gamma (\theta,t)$, where the vortex strength ![]() $\gamma$ is defined as the amount of circulation per unit length. In addition to the vortex sheet, there is a point vortex at
$\gamma$ is defined as the amount of circulation per unit length. In addition to the vortex sheet, there is a point vortex at ![]() $C$ with a circulation of
$C$ with a circulation of ![]() $\varGamma _r$ (see figure 1b) to model the rotor root vortex, which is elaborated later in § 2.3. We will show in § 2.3 that the initial condition for the strength can be written as
$\varGamma _r$ (see figure 1b) to model the rotor root vortex, which is elaborated later in § 2.3. We will show in § 2.3 that the initial condition for the strength can be written as
where ![]() $\gamma _r$ and
$\gamma _r$ and ![]() $\gamma _b$ are constants depending on turbine operating conditions. Later in § 2.3, we show that
$\gamma _b$ are constants depending on turbine operating conditions. Later in § 2.3, we show that ![]() $\gamma _b$ is related to the vorticity generated due to turbine yaw, while
$\gamma _b$ is related to the vorticity generated due to turbine yaw, while ![]() $\gamma _r$ and
$\gamma _r$ and ![]() $\varGamma _r$ are related to the vorticity generated by turbine rotating blades. Our focus now is to predict the deformation of the vortex sheet provided that the initial conditions are given by (2.2)–(2.3).
$\varGamma _r$ are related to the vorticity generated by turbine rotating blades. Our focus now is to predict the deformation of the vortex sheet provided that the initial conditions are given by (2.2)–(2.3).
The velocity of the vortex sheet ![]() $\boldsymbol{u}(\theta,t)$ with respect to a coordinate system attached to the centre
$\boldsymbol{u}(\theta,t)$ with respect to a coordinate system attached to the centre ![]() $C$ is given by
$C$ is given by
 \begin{equation} \underbrace{\boldsymbol{u}(\theta,t)}_{\substack{\text{vortex sheet velocity} \\ \text{with respect to C}}}=\underbrace{\boldsymbol{u}_{I}}_{\substack{\text{self-induced} \\ \text{vortex sheet velocity}}}+\underbrace{\boldsymbol{u}_{II}}_{\substack{\text{vortex sheet velocity induced} \\ \text{by point vortex at C}}}-\underbrace{\boldsymbol{u}_{c}}_{\substack{\text{velocity} \\ \text{of C}}}. \end{equation}
\begin{equation} \underbrace{\boldsymbol{u}(\theta,t)}_{\substack{\text{vortex sheet velocity} \\ \text{with respect to C}}}=\underbrace{\boldsymbol{u}_{I}}_{\substack{\text{self-induced} \\ \text{vortex sheet velocity}}}+\underbrace{\boldsymbol{u}_{II}}_{\substack{\text{vortex sheet velocity induced} \\ \text{by point vortex at C}}}-\underbrace{\boldsymbol{u}_{c}}_{\substack{\text{velocity} \\ \text{of C}}}. \end{equation}
In (2.4) and hereafter, bold letters denote vectors. Next, we employ the Biot–Savart law to determine the three velocity terms on the right-hand side of (2.4), starting with the self-induced velocity ![]() $\boldsymbol {u}_{I}=u_{{I},r}\boldsymbol {e}_r+u_{{I},\theta }\boldsymbol {e}_{\theta }$, where
$\boldsymbol {u}_{I}=u_{{I},r}\boldsymbol {e}_r+u_{{I},\theta }\boldsymbol {e}_{\theta }$, where ![]() $\boldsymbol {e}_r$ and
$\boldsymbol {e}_r$ and ![]() $\boldsymbol {e}_{\theta }$ are unit vectors in the radial and tangential directions, respectively. The radial
$\boldsymbol {e}_{\theta }$ are unit vectors in the radial and tangential directions, respectively. The radial ![]() $u_{{I},r}$ and tangential
$u_{{I},r}$ and tangential ![]() $u_{{I},\theta }$ components of the self-induced velocity at a given polar angle of
$u_{{I},\theta }$ components of the self-induced velocity at a given polar angle of ![]() $\theta$ are respectively given by
$\theta$ are respectively given by
where ![]() $l$ and
$l$ and ![]() $\alpha$ are defined in figure 1(a),
$\alpha$ are defined in figure 1(a), ![]() $\theta '$ is a dummy integration variable, and
$\theta '$ is a dummy integration variable, and ![]() $\xi '=\xi (\theta ',t)$. According to the law of cosines,
$\xi '=\xi (\theta ',t)$. According to the law of cosines, ![]() $l^{2}=\xi ^{2}+\xi ^{'2}-2\xi \xi '\cos {(\theta '-\theta )}.$ The angle
$l^{2}=\xi ^{2}+\xi ^{'2}-2\xi \xi '\cos {(\theta '-\theta )}.$ The angle ![]() $\alpha$ shown in the figure 1(a) can be related to
$\alpha$ shown in the figure 1(a) can be related to ![]() $l$ based on the law of sines for the drawn triangle, which results in
$l$ based on the law of sines for the drawn triangle, which results in ![]() $\sin {\alpha }=(\xi '/l)\sin {(\theta '-\theta )}.$ For small values of time
$\sin {\alpha }=(\xi '/l)\sin {(\theta '-\theta )}.$ For small values of time ![]() $t$ and yaw angle
$t$ and yaw angle ![]() $\beta$, we can assume that the vortex sheet is approximately circular and, thus,
$\beta$, we can assume that the vortex sheet is approximately circular and, thus, ![]() $\xi \approx \xi '$. After some trigonometric manipulations, (2.5) and (2.6) can be simplified to
$\xi \approx \xi '$. After some trigonometric manipulations, (2.5) and (2.6) can be simplified to
Both integrals in (2.7) and (2.8) have singularities at ![]() $\theta '=\theta$ and, thus, we use the Cauchy principal values of these two integrals. While the principal value (p.v.) of the latter can be simply obtained by removing
$\theta '=\theta$ and, thus, we use the Cauchy principal values of these two integrals. While the principal value (p.v.) of the latter can be simply obtained by removing ![]() $\sin [(\theta '-\theta )/2]$ from the numerator and the denominator, the p.v. of the former needs to be determined for a given
$\sin [(\theta '-\theta )/2]$ from the numerator and the denominator, the p.v. of the former needs to be determined for a given ![]() $\gamma (\theta,t)$.
$\gamma (\theta,t)$.
Next, we determine the velocity of the vortex sheet induced by the point vortex at C as shown in figure 1(b). We obtain
Finally, we determine ![]() $\boldsymbol {u}_c$, which is the velocity of
$\boldsymbol {u}_c$, which is the velocity of ![]() $C$ induced by the vortex sheet, shown in figure 1(c). It can be readily shown that
$C$ induced by the vortex sheet, shown in figure 1(c). It can be readily shown that ![]() $\boldsymbol {u}_c$ is given by
$\boldsymbol {u}_c$ is given by
If we neglect streamwise (![]() $x$-direction) straining, vorticity is a conserved quantity, so the vorticity transport equation for the vortex sheet strength
$x$-direction) straining, vorticity is a conserved quantity, so the vorticity transport equation for the vortex sheet strength ![]() $\gamma (\theta,t)$ provides the additional required evolution equation (Moore Reference Moore1978)
$\gamma (\theta,t)$ provides the additional required evolution equation (Moore Reference Moore1978)
where ![]() $s$ is the arclength along the vortex sheet. At small values of time
$s$ is the arclength along the vortex sheet. At small values of time ![]() $t$ and yaw angle
$t$ and yaw angle ![]() $\beta$, the vortex sheet remains approximately circular, so
$\beta$, the vortex sheet remains approximately circular, so ![]() $u_s$ and
$u_s$ and ![]() $\partial s$ can be respectively replaced with
$\partial s$ can be respectively replaced with ![]() $u_{\theta }$ and
$u_{\theta }$ and ![]() $\xi \partial \theta$. Therefore, (2.13) is simplified to
$\xi \partial \theta$. Therefore, (2.13) is simplified to
Next, we use ![]() $\gamma _b$ and
$\gamma _b$ and ![]() $\xi _0$ to non-dimensionalise variables in (2.4) and (2.14). This leads to the following set of dimensionless equations:
$\xi _0$ to non-dimensionalise variables in (2.4) and (2.14). This leads to the following set of dimensionless equations:
Here ![]() $\hat {t}=t\gamma _b/\xi _0$,
$\hat {t}=t\gamma _b/\xi _0$, ![]() $\hat {u}=u/\gamma _b$,
$\hat {u}=u/\gamma _b$, ![]() $\hat {\gamma }=\gamma /\gamma _b$,
$\hat {\gamma }=\gamma /\gamma _b$, ![]() $\hat {\xi }=\xi /\xi _0$ and
$\hat {\xi }=\xi /\xi _0$ and ![]() $\chi =\gamma _r/\gamma _b$. Note that the dimensionless time
$\chi =\gamma _r/\gamma _b$. Note that the dimensionless time ![]() $\hat {t}$ becomes negative for negative values of
$\hat {t}$ becomes negative for negative values of ![]() $\gamma _b$. In the following, we solve (2.15)–(2.17) using the power series method.
$\gamma _b$. In the following, we solve (2.15)–(2.17) using the power series method.
2.2. Analytical solution using power series approximation
We write ![]() $\hat {\gamma }(\theta,t)$,
$\hat {\gamma }(\theta,t)$, ![]() $\hat {u}_r(\theta,t)$ and
$\hat {u}_r(\theta,t)$ and ![]() $\hat {u}_{\theta }(\theta,t)$ as power series in the form of
$\hat {u}_{\theta }(\theta,t)$ as power series in the form of
 \begin{equation} \hat{\gamma}(\theta,\hat{t}) = \sum _{n=0}^{\infty} \hat{\gamma}_{n}(\theta)\hat{t}^{n}; \quad \hat{u}_r(\theta,\hat{t}) = \sum _{n=0}^{\infty} \hat{u}_{r n}(\theta)\hat{t}^{n}, \quad \hat{u}_{\theta}(\theta,\hat{t}) =\sum _{n=0}^{\infty} \hat{u}_{\theta n}(\theta)\hat{t}^{n}. \end{equation}
\begin{equation} \hat{\gamma}(\theta,\hat{t}) = \sum _{n=0}^{\infty} \hat{\gamma}_{n}(\theta)\hat{t}^{n}; \quad \hat{u}_r(\theta,\hat{t}) = \sum _{n=0}^{\infty} \hat{u}_{r n}(\theta)\hat{t}^{n}, \quad \hat{u}_{\theta}(\theta,\hat{t}) =\sum _{n=0}^{\infty} \hat{u}_{\theta n}(\theta)\hat{t}^{n}. \end{equation} According to (2.1), for ![]() $\hat {\xi }$ and the factor
$\hat {\xi }$ and the factor ![]() ${1}/{\hat {\xi }}$ in (2.17), we have
${1}/{\hat {\xi }}$ in (2.17), we have
 $$\begin{gather} \hat{\xi}=1+\int \hat{u}_r\,\textrm{d}\hat{t}=1+\sum _{n=0}^{\infty} \frac{1}{n+1} \hat{u}_{r n} \hat{t}^{n+1}, \end{gather}$$
$$\begin{gather} \hat{\xi}=1+\int \hat{u}_r\,\textrm{d}\hat{t}=1+\sum _{n=0}^{\infty} \frac{1}{n+1} \hat{u}_{r n} \hat{t}^{n+1}, \end{gather}$$ $$\begin{gather}\frac{1}{\hat{\xi}} = \sum _{n=0}^{\infty} f_{n}(\theta)\hat{t}^{n}, \end{gather}$$
$$\begin{gather}\frac{1}{\hat{\xi}} = \sum _{n=0}^{\infty} f_{n}(\theta)\hat{t}^{n}, \end{gather}$$
where ![]() $f_n$s are Taylor series expansion coefficients of
$f_n$s are Taylor series expansion coefficients of ![]() ${1}/{\hat {\xi }}$. For example, the first three coefficients, which are used in the final solution of this paper, can be shown to be
${1}/{\hat {\xi }}$. For example, the first three coefficients, which are used in the final solution of this paper, can be shown to be ![]() $f_{0}=1$,
$f_{0}=1$, ![]() $f_{1}=-\hat {u}_{r 0}$ and
$f_{1}=-\hat {u}_{r 0}$ and ![]() $f_{2} =\hat {u}^{2}_{r 0} -\frac {1}{2} \hat {u}_{r 1}$. We insert the power series (2.18a–c) and (2.20) into (2.15)–(2.17) and equating coefficients we obtain
$f_{2} =\hat {u}^{2}_{r 0} -\frac {1}{2} \hat {u}_{r 1}$. We insert the power series (2.18a–c) and (2.20) into (2.15)–(2.17) and equating coefficients we obtain
 $$\begin{gather}\hat{u}_{\theta n}(\theta)\approx\frac{1}{4{\rm \pi}} \int_{0}^{2{\rm \pi}}\hat{\gamma}_n(\theta')\,\textrm{d}\theta'+\frac{1}{2{\rm \pi}} \int_0^{2{\rm \pi}}\hat{\gamma}_n(\theta')\cos\left({\theta'-\theta}\right)\textrm{d}\theta'- \begin{cases} \chi, & \text{if } n=0, \\ 0, & \text{if } n>0, \end{cases} \end{gather}$$
$$\begin{gather}\hat{u}_{\theta n}(\theta)\approx\frac{1}{4{\rm \pi}} \int_{0}^{2{\rm \pi}}\hat{\gamma}_n(\theta')\,\textrm{d}\theta'+\frac{1}{2{\rm \pi}} \int_0^{2{\rm \pi}}\hat{\gamma}_n(\theta')\cos\left({\theta'-\theta}\right)\textrm{d}\theta'- \begin{cases} \chi, & \text{if } n=0, \\ 0, & \text{if } n>0, \end{cases} \end{gather}$$ $$\begin{gather}\hat{\gamma}_{n+1} \approx{-}\frac{1}{(n+1)} \left(\sum_{j=0}^{n}f_{j} \sum_{i=0}^{n-j} \frac{\partial (\hat{\gamma}_i \hat{u}_{\theta (n-j-i)})}{\partial \theta}\right). \end{gather}$$
$$\begin{gather}\hat{\gamma}_{n+1} \approx{-}\frac{1}{(n+1)} \left(\sum_{j=0}^{n}f_{j} \sum_{i=0}^{n-j} \frac{\partial (\hat{\gamma}_i \hat{u}_{\theta (n-j-i)})}{\partial \theta}\right). \end{gather}$$The first term on the right-hand side of (2.21) is a Cauchy p.v. of an improper integral. The following identities are useful to solve this integral:
Here ![]() $n\in \{1,2,\ldots \}$,
$n\in \{1,2,\ldots \}$, ![]() $m\in \{0,1,2,\ldots \}$ and
$m\in \{0,1,2,\ldots \}$ and ![]() $b\in [0,2{\rm \pi} ]$. The complete derivation of these integrals can be found in the Appendix A.
$b\in [0,2{\rm \pi} ]$. The complete derivation of these integrals can be found in the Appendix A.
From (2.2), ![]() $\hat {\gamma }_0(\theta )=\sin \theta +\chi$. One can insert
$\hat {\gamma }_0(\theta )=\sin \theta +\chi$. One can insert ![]() $\hat {\gamma }_0$ into (2.21) and (2.22) to respectively find
$\hat {\gamma }_0$ into (2.21) and (2.22) to respectively find ![]() $\hat {u}_{r0}(\theta )$ and
$\hat {u}_{r0}(\theta )$ and ![]() $\hat {u}_{\theta 0}(\theta )$. Values of
$\hat {u}_{\theta 0}(\theta )$. Values of ![]() $\hat {u}_{r0}(\theta )$,
$\hat {u}_{r0}(\theta )$, ![]() $\hat {u}_{\theta 0}(\theta )$ and
$\hat {u}_{\theta 0}(\theta )$ and ![]() $f_0$ can be then inserted into (2.23) to find
$f_0$ can be then inserted into (2.23) to find ![]() $\hat {\gamma }_1(\theta )$. This recursive process is repeated until reaching the desired order of evaluation for the power series of (2.18a–c). After
$\hat {\gamma }_1(\theta )$. This recursive process is repeated until reaching the desired order of evaluation for the power series of (2.18a–c). After ![]() $\hat {u}_{r}(\theta,\hat {t})$ is obtained using the developed recursive relations, the dimensionless shape of the vortex sheet
$\hat {u}_{r}(\theta,\hat {t})$ is obtained using the developed recursive relations, the dimensionless shape of the vortex sheet ![]() $\hat {\xi }(\theta,\hat {t})$ is evaluated from (2.19). The solutions for
$\hat {\xi }(\theta,\hat {t})$ is evaluated from (2.19). The solutions for ![]() $\hat {\gamma }$,
$\hat {\gamma }$, ![]() $\hat{u}_r$ and
$\hat{u}_r$ and ![]() $\hat{u}_{\theta}$ up to
$\hat{u}_{\theta}$ up to ![]() ${O}(\hat {t}^{3})$ and for
${O}(\hat {t}^{3})$ and for ![]() $\hat {\xi }$ up to
$\hat {\xi }$ up to ![]() ${O}(\hat {t}^{4})$ are written below,
${O}(\hat {t}^{4})$ are written below,
 \begin{align} \hat{\gamma}(\theta,\hat{t}) &= \sin (\theta ) + \chi -\frac{1}{2} \hat{t} \sin (2 \theta ) +\hat{t}^{2} \left(-\frac{1}{4} \chi \cos (2 \theta )+\frac{3}{16} \sin (3 \theta )-\frac{\sin (\theta )}{16}\right) \nonumber\\ &\quad +\hat{t}^{3} \left(\frac{1}{12} \chi ^{2} \sin (2 \theta )-\frac{1}{48} \chi \cos (\theta )+\frac{5}{32} \chi \cos (3 \theta ) \right.\nonumber\\ &\quad \left.+\frac{5}{96} \sin (2\theta )-\frac{7}{96} \sin (4 \theta )\right), \end{align}
\begin{align} \hat{\gamma}(\theta,\hat{t}) &= \sin (\theta ) + \chi -\frac{1}{2} \hat{t} \sin (2 \theta ) +\hat{t}^{2} \left(-\frac{1}{4} \chi \cos (2 \theta )+\frac{3}{16} \sin (3 \theta )-\frac{\sin (\theta )}{16}\right) \nonumber\\ &\quad +\hat{t}^{3} \left(\frac{1}{12} \chi ^{2} \sin (2 \theta )-\frac{1}{48} \chi \cos (\theta )+\frac{5}{32} \chi \cos (3 \theta ) \right.\nonumber\\ &\quad \left.+\frac{5}{96} \sin (2\theta )-\frac{7}{96} \sin (4 \theta )\right), \end{align} \begin{align} \hat{u}_r(\theta,\hat{t}) &={-}\frac{1}{4} \hat{t} \cos (2 \theta )+ \hat{t}^{2} \left(\frac{1}{8} \chi \sin (2 \theta )+\frac{3}{32} \cos (3 \theta )\right) \nonumber\\ &\quad + \hat{t}^{3} \left(\frac{1}{24} \chi ^{2} \cos (2 \theta )-\frac{5}{64} \chi \sin (3 \theta )+\frac{5}{192} \cos (2 \theta )-\frac{7}{192} \cos (4 \theta )\right), \end{align}
\begin{align} \hat{u}_r(\theta,\hat{t}) &={-}\frac{1}{4} \hat{t} \cos (2 \theta )+ \hat{t}^{2} \left(\frac{1}{8} \chi \sin (2 \theta )+\frac{3}{32} \cos (3 \theta )\right) \nonumber\\ &\quad + \hat{t}^{3} \left(\frac{1}{24} \chi ^{2} \cos (2 \theta )-\frac{5}{64} \chi \sin (3 \theta )+\frac{5}{192} \cos (2 \theta )-\frac{7}{192} \cos (4 \theta )\right), \end{align} \begin{align} \hat{\xi}(\theta,\hat{t}) &= 1 -\frac{1}{8} \hat{t}^{2} \cos (2 \theta )+\hat{t}^{3} \left(\frac{1}{24} \chi \sin (2 \theta )+\frac{1}{32} \cos (3 \theta )\right)\nonumber\\ &\quad +\hat{t}^{4} \left(\frac{1}{96} \chi ^{2} \cos (2 \theta)-\frac{5}{256} \chi \sin (3 \theta )+\frac{5}{768} \cos (2 \theta)-\frac{7}{768} \cos (4 \theta )\right). \end{align}
\begin{align} \hat{\xi}(\theta,\hat{t}) &= 1 -\frac{1}{8} \hat{t}^{2} \cos (2 \theta )+\hat{t}^{3} \left(\frac{1}{24} \chi \sin (2 \theta )+\frac{1}{32} \cos (3 \theta )\right)\nonumber\\ &\quad +\hat{t}^{4} \left(\frac{1}{96} \chi ^{2} \cos (2 \theta)-\frac{5}{256} \chi \sin (3 \theta )+\frac{5}{768} \cos (2 \theta)-\frac{7}{768} \cos (4 \theta )\right). \end{align}
One can compute higher-order terms of (2.26)–(2.29), which may become relevant at increasing values of ![]() $\hat {t}$. However, since the above solution is developed based on the assumption that the vortex sheet remains approximately circular, increasing deformation of the vortex sheet makes the solution inaccurate at large values of
$\hat {t}$. However, since the above solution is developed based on the assumption that the vortex sheet remains approximately circular, increasing deformation of the vortex sheet makes the solution inaccurate at large values of ![]() $\hat {t}$. For practical applications at large
$\hat {t}$. For practical applications at large ![]() $\hat {t}$, in Appendix B we propose an empirical formula that merges smoothly with the theoretical expression at small
$\hat {t}$, in Appendix B we propose an empirical formula that merges smoothly with the theoretical expression at small ![]() $\hat {t}$ (i.e.
$\hat {t}$ (i.e. ![]() $|\hat {t}|\leq$2), while it has desired reasonable properties at large times (i.e.
$|\hat {t}|\leq$2), while it has desired reasonable properties at large times (i.e. ![]() $|\hat {t}|>$2). In the next section we prove the validity of the initial conditions in (2.2) and (2.3). Moreover, values of
$|\hat {t}|>$2). In the next section we prove the validity of the initial conditions in (2.2) and (2.3). Moreover, values of ![]() $\xi _0$,
$\xi _0$, ![]() $\gamma _b$ and
$\gamma _b$ and ![]() $\gamma _r$ are determined as functions of turbine operating conditions.
$\gamma _r$ are determined as functions of turbine operating conditions.
2.3. Setting vortex sheet initial conditions at yawed turbine location
In this section we determine the vorticity shedding from a yawed rotor disk (i.e. ![]() $\gamma _0(\theta )=\gamma (\theta,0)$). According to the Kutta–Joukowsky theorem, lift force is proportional to the amount of circulation around a lifting airfoil. This means that an airfoil can be replaced with a bound vortex. Also, for any airfoil with finite span, free vortices must trail downstream from both sides of the bound vortex to infinity, forming a horseshoe vortex (Anderson Reference Anderson2011). Turbine blades rotate and produce power due to their generated lift force, and vorticity is shed from the root and the tip of rotor blades. In addition, the whole yawed rotor can be assumed as a big finite-span airfoil with the lateral component of the thrust force regarded as the lift force. Therefore, in order to find the total shedding vorticity at the rotor disk, we need to determine those due to both yaw offset and rotating blades. In the following, we assume that the yawed rotor can be modelled as a rotating actuator disk.
$\gamma _0(\theta )=\gamma (\theta,0)$). According to the Kutta–Joukowsky theorem, lift force is proportional to the amount of circulation around a lifting airfoil. This means that an airfoil can be replaced with a bound vortex. Also, for any airfoil with finite span, free vortices must trail downstream from both sides of the bound vortex to infinity, forming a horseshoe vortex (Anderson Reference Anderson2011). Turbine blades rotate and produce power due to their generated lift force, and vorticity is shed from the root and the tip of rotor blades. In addition, the whole yawed rotor can be assumed as a big finite-span airfoil with the lateral component of the thrust force regarded as the lift force. Therefore, in order to find the total shedding vorticity at the rotor disk, we need to determine those due to both yaw offset and rotating blades. In the following, we assume that the yawed rotor can be modelled as a rotating actuator disk.
2.3.1. Vorticity shedding due to turbine yaw
Prior studies have suggested two different approaches to model the distribution of circulation at a yawed disk. By modelling a yawed disk as a lifting line, the circulation is concentrated on a vertical line at the centre of the rotor with an elliptical distribution spanning from the bottom tip to the top tip of the rotor (Shapiro et al. Reference Shapiro, Gayme and Meneveau2018). Alternatively, vorticity due to yaw offset can be assumed to shed from the circumference of the rotor (Zong & Porté-Agel Reference Zong and Porté-Agel2020). Martinez-Tossas & Branlard (Reference Martinez-Tossas and Branlard2020) used vortex cylinder theory to state the equivalency of these two methods. Shapiro et al. (Reference Shapiro, Gayme and Meneveau2020) proved that both vorticity distributions yield the same induced velocity inside the radius of the rotor disk. To determine the reference circulation density ![]() $\gamma _b$ needed in (2.2) and to provide more physical insight, we build upon the literature to show that the equivalency of these two vorticity distributions can be also verified simply by rearranging the position of horseshoe vortices over a yawed disk.
$\gamma _b$ needed in (2.2) and to provide more physical insight, we build upon the literature to show that the equivalency of these two vorticity distributions can be also verified simply by rearranging the position of horseshoe vortices over a yawed disk.
Figure 2(a) shows a schematic of a yawed actuator disk modelled as a lifting surface with a constant vortex strength of ![]() $\gamma _b$ in the
$\gamma _b$ in the ![]() $\bar {z}$-direction. The coordinate system
$\bar {z}$-direction. The coordinate system ![]() $(\bar {x},\bar {y},\bar {z})$ is defined based on the rotor plane as shown in figure 2(c), and its respective polar coordinate system (
$(\bar {x},\bar {y},\bar {z})$ is defined based on the rotor plane as shown in figure 2(c), and its respective polar coordinate system (![]() $\bar {r},\bar {\theta }$) is defined such that
$\bar {r},\bar {\theta }$) is defined such that ![]() $\bar {r}=\sqrt {\bar {y}^{2}+\bar {z}^{2}}$ and
$\bar {r}=\sqrt {\bar {y}^{2}+\bar {z}^{2}}$ and ![]() $\tan \bar {\theta }=\bar {z}/\bar {y}$. The lifting surface shown in figure 2(a) can be envisaged as a surface with an infinite number of horseshoe vortices uniformly distributed across the yawed disk. The bound circulation at a given vertical position
$\tan \bar {\theta }=\bar {z}/\bar {y}$. The lifting surface shown in figure 2(a) can be envisaged as a surface with an infinite number of horseshoe vortices uniformly distributed across the yawed disk. The bound circulation at a given vertical position ![]() $z$ is given by
$z$ is given by
 \begin{equation} \varGamma(\bar{z})=\int_{-\sqrt{R^{2}-\bar{z}^{2}}}^{\sqrt{R^{2}-\bar{z}^{2}}} \gamma_b\,\mathrm{d}\bar{y}=2\gamma_b\sqrt{R^{2}-\bar{z}^{2}}, \end{equation}
\begin{equation} \varGamma(\bar{z})=\int_{-\sqrt{R^{2}-\bar{z}^{2}}}^{\sqrt{R^{2}-\bar{z}^{2}}} \gamma_b\,\mathrm{d}\bar{y}=2\gamma_b\sqrt{R^{2}-\bar{z}^{2}}, \end{equation}
where ![]() $R$ is the rotor radius. Note that according to (2.30), the vertical distribution of the bound circulation for the lifting surface with a constant vortex strength
$R$ is the rotor radius. Note that according to (2.30), the vertical distribution of the bound circulation for the lifting surface with a constant vortex strength ![]() $\gamma _b$ is elliptical. This means that if we concentrate all these horseshoe vortices on a vertical line at the centre of the disk, the lifting surface is transformed to a lifting line with an elliptical distribution of circulation, like the one used by Shapiro et al. (Reference Shapiro, Gayme and Meneveau2018), as shown in figure 2(b). In this case, trailing vortices shed from all along the lifting line, because it consists of horseshoe vortices that vary in size. From (2.30), the maximum value of bound circulation for the lifting line, denoted by
$\gamma _b$ is elliptical. This means that if we concentrate all these horseshoe vortices on a vertical line at the centre of the disk, the lifting surface is transformed to a lifting line with an elliptical distribution of circulation, like the one used by Shapiro et al. (Reference Shapiro, Gayme and Meneveau2018), as shown in figure 2(b). In this case, trailing vortices shed from all along the lifting line, because it consists of horseshoe vortices that vary in size. From (2.30), the maximum value of bound circulation for the lifting line, denoted by ![]() $\varGamma _b$, occurs at
$\varGamma _b$, occurs at ![]() $\bar {z}=0$, and its value is equal to
$\bar {z}=0$, and its value is equal to ![]() $2R\gamma _b$. From the lifting line theory, we know that
$2R\gamma _b$. From the lifting line theory, we know that ![]() $\varGamma _b=-U_{h} C_T R \cos ^{2}{\beta }\sin {\beta }$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2018), where
$\varGamma _b=-U_{h} C_T R \cos ^{2}{\beta }\sin {\beta }$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2018), where ![]() $C_T$ is the turbine thrust coefficient. The value of
$C_T$ is the turbine thrust coefficient. The value of ![]() $C_T$ is given by
$C_T$ is given by
where ![]() $T$ is the total magnitude of the turbine thrust force,
$T$ is the total magnitude of the turbine thrust force, ![]() $\rho$ is the air density and
$\rho$ is the air density and ![]() $U_{h}$ is the inflow velocity at the hub height. Note that this definition is the same as the one used in Shapiro et al. (Reference Shapiro, Gayme and Meneveau2018), but it is different from the one used in some other prior studies (e.g. Burton et al. Reference Burton, Sharpe, Jenkins and Bossanyi1995; Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016). Since
$U_{h}$ is the inflow velocity at the hub height. Note that this definition is the same as the one used in Shapiro et al. (Reference Shapiro, Gayme and Meneveau2018), but it is different from the one used in some other prior studies (e.g. Burton et al. Reference Burton, Sharpe, Jenkins and Bossanyi1995; Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016). Since ![]() $\gamma _b=\varGamma _b/2R$, the value of
$\gamma _b=\varGamma _b/2R$, the value of ![]() $\gamma _b$ is given by
$\gamma _b$ is given by

Figure 2. Vorticity shedding from a yawed actuator disk, modelled (a) as a lifting surface, and (b) as a lifting line. (c) A schematic of different coordinate systems used in this paper.
Next, we determine the distribution of trailing vortices shedding from the circumference of the lifting surface. The circulation of the vortex shedding from an infinitesimal circumferential element ![]() $\mathrm {d}s$, where
$\mathrm {d}s$, where ![]() $\mathrm {d}\bar {s}=R\,\mathrm {d}\bar {\theta }$, is
$\mathrm {d}\bar {s}=R\,\mathrm {d}\bar {\theta }$, is ![]() $\mathrm {d}\varGamma _{shed,yaw}=\gamma _b \,\mathrm {d}\bar {y}$. Given that
$\mathrm {d}\varGamma _{shed,yaw}=\gamma _b \,\mathrm {d}\bar {y}$. Given that ![]() $\mathrm {d}\bar {y}=\mathrm {d}\bar {s}\sin {\bar {\theta }}$, we obtain
$\mathrm {d}\bar {y}=\mathrm {d}\bar {s}\sin {\bar {\theta }}$, we obtain
For the lifting line, on the other hand, the magnitude of circulation of trailing vortex over the segment ![]() $\mathrm {d}\bar {z}$ is equal to -
$\mathrm {d}\bar {z}$ is equal to -![]() $(\mathrm {d}\varGamma /\mathrm {d}\bar {z})\,\mathrm {d}\bar {z}$ (Anderson Reference Anderson2011). From (2.30) and
$(\mathrm {d}\varGamma /\mathrm {d}\bar {z})\,\mathrm {d}\bar {z}$ (Anderson Reference Anderson2011). From (2.30) and ![]() $\varGamma _b=2R\gamma _b$, we obtain
$\varGamma _b=2R\gamma _b$, we obtain
Using the variable change ![]() $\bar {z}=R\sin {\bar {\theta }}$, one can easily show that
$\bar {z}=R\sin {\bar {\theta }}$, one can easily show that ![]() $\mathrm {d}\varGamma _{shed}$ for the lifting surface at any
$\mathrm {d}\varGamma _{shed}$ for the lifting surface at any ![]() $\bar {\theta }$ (2.33) is half of that of the lifting line (2.34) at the respective height
$\bar {\theta }$ (2.33) is half of that of the lifting line (2.34) at the respective height ![]() $\bar {z}$. Note that for the lifting surface, at a given height, trailing vortices shed at both angles of
$\bar {z}$. Note that for the lifting surface, at a given height, trailing vortices shed at both angles of ![]() $\bar {\theta }$ and
$\bar {\theta }$ and ![]() $({\rm \pi} - \bar {\theta })$ with the same magnitude of circulation. Therefore, trailing vortices shedding from the lifting line and the lifting surface vary with height in a similar manner. It is also worth mentioning that the results presented here are in agreement with those obtained from the skewed vortex cylinder theory (Coleman et al. Reference Coleman, Feingold and Stempin1945; Branlard & Gaunaa Reference Branlard and Gaunaa2016). By modelling a yawed turbine wake as a skewed vortex cylinder, Martinez-Tossas & Branlard (Reference Martinez-Tossas and Branlard2020) stated that the dominant vorticity shedding from the rotor is the tangential vorticity vector, which lies in the rotor plane. The streamwise projection of this tangential vorticity is equal to the one found in the present work (2.33) (c.f. (9) in Martinez-Tossas & Branlard Reference Martinez-Tossas and Branlard2020).
$({\rm \pi} - \bar {\theta })$ with the same magnitude of circulation. Therefore, trailing vortices shedding from the lifting line and the lifting surface vary with height in a similar manner. It is also worth mentioning that the results presented here are in agreement with those obtained from the skewed vortex cylinder theory (Coleman et al. Reference Coleman, Feingold and Stempin1945; Branlard & Gaunaa Reference Branlard and Gaunaa2016). By modelling a yawed turbine wake as a skewed vortex cylinder, Martinez-Tossas & Branlard (Reference Martinez-Tossas and Branlard2020) stated that the dominant vorticity shedding from the rotor is the tangential vorticity vector, which lies in the rotor plane. The streamwise projection of this tangential vorticity is equal to the one found in the present work (2.33) (c.f. (9) in Martinez-Tossas & Branlard Reference Martinez-Tossas and Branlard2020).
2.3.2. Inclusion of wake angular momentum effects
In this section we determine the value of ![]() $\gamma _r$ required in (2.2) and (2.3). Based on the method of Joukowsky that models a turbine blade as one single horseshoe vortex with constant bound circulation (see Okulov & Van Kuik (Reference Okulov and Van Kuik2012) for historical background), two free trailing vortices with the same magnitude of circulation are shed from both root and tip ends of each turbine blade. Under the assumption of a large number of blades, this creates a vortex system consisting of a bound vortex disk, an axial root vortex and a tubular vortex sheet as shown in figure 3(a). Let us denote the circulation of the root trailing vortex with
$\gamma _r$ required in (2.2) and (2.3). Based on the method of Joukowsky that models a turbine blade as one single horseshoe vortex with constant bound circulation (see Okulov & Van Kuik (Reference Okulov and Van Kuik2012) for historical background), two free trailing vortices with the same magnitude of circulation are shed from both root and tip ends of each turbine blade. Under the assumption of a large number of blades, this creates a vortex system consisting of a bound vortex disk, an axial root vortex and a tubular vortex sheet as shown in figure 3(a). Let us denote the circulation of the root trailing vortex with ![]() $\varGamma _r$. As the amount of circulation along any horseshoe vortice remains constant, the bound circulation on the rotor disk at any radial position should be the same as
$\varGamma _r$. As the amount of circulation along any horseshoe vortice remains constant, the bound circulation on the rotor disk at any radial position should be the same as ![]() $\varGamma _r$. According to the Kutta–Joukowsky theorem, the bound circulation over an annular ring at a radial position
$\varGamma _r$. According to the Kutta–Joukowsky theorem, the bound circulation over an annular ring at a radial position ![]() $\bar {r}$ and thickness of
$\bar {r}$ and thickness of ![]() $\textrm {d}\bar {r}$ on the rotor disk generates a lift force
$\textrm {d}\bar {r}$ on the rotor disk generates a lift force ![]() $\textrm {d}\boldsymbol {L}$, which amounts to (Okulov & Sørensen Reference Okulov and Sørensen2010)
$\textrm {d}\boldsymbol {L}$, which amounts to (Okulov & Sørensen Reference Okulov and Sørensen2010)
where ![]() $\boldsymbol {V_0}$ is the resultant relative wind velocity experienced by the blade element as shown in figure 3(b). In this figure,
$\boldsymbol {V_0}$ is the resultant relative wind velocity experienced by the blade element as shown in figure 3(b). In this figure, ![]() $\phi$ denotes the angle between
$\phi$ denotes the angle between ![]() $\boldsymbol {V_0}$ and
$\boldsymbol {V_0}$ and ![]() $\bar {\theta }$-direction, and
$\bar {\theta }$-direction, and ![]() $U_d$ is the component of
$U_d$ is the component of ![]() $\boldsymbol {V_0}$ in the
$\boldsymbol {V_0}$ in the ![]() $\bar {x}$-direction. The tangential component of
$\bar {x}$-direction. The tangential component of ![]() $\textrm {d}\boldsymbol {L}$ produces power
$\textrm {d}\boldsymbol {L}$ produces power ![]() $P$, which is given by
$P$, which is given by
where ![]() $\varOmega$ is the turbine rotational velocity and
$\varOmega$ is the turbine rotational velocity and ![]() $\textrm {d}Q$ is the torque generated by the given annular ring. From the axial momentum theory, the power generated by the annular ring can be written as the product of
$\textrm {d}Q$ is the torque generated by the given annular ring. From the axial momentum theory, the power generated by the annular ring can be written as the product of ![]() $U_d$ and
$U_d$ and ![]() $\textrm {d}T$, where
$\textrm {d}T$, where ![]() $\textrm {d}T$ is the thrust force exerted on the annular ring. Therefore, we obtain an additional equation for
$\textrm {d}T$ is the thrust force exerted on the annular ring. Therefore, we obtain an additional equation for ![]() $\textrm {d}P$ as
$\textrm {d}P$ as
Note that to derive (2.37), the local thrust coefficient for a given annular ring is assumed to be the same as its value for the whole rotor defined in (2.31). This is a correct assumption for the Joukowsky vortex model (Van Kuik, Sørensen & Okulov Reference Van Kuik, Sørensen and Okulov2015). Equating (2.36) and (2.37) leads to
where ![]() $\lambda$ is the tip-speed ratio and defined as
$\lambda$ is the tip-speed ratio and defined as ![]() $\varOmega R/U_{h}$.
$\varOmega R/U_{h}$.

Figure 3. (a) Modelling a turbine rotor as a rotating actuator disk. (b) The velocity triangle for a rotor blade element.
As seen in figure 3(a), the trailing vorticity sheds over the circumference of the rotor disk. It is evident that the value of circulation for the vorticity shedding over the circumferential element ![]() $\mathrm {d}\bar {s}$ is given by
$\mathrm {d}\bar {s}$ is given by
where ![]() $\gamma _r=-\varGamma _r/(2{\rm \pi} R)$. The variable
$\gamma _r=-\varGamma _r/(2{\rm \pi} R)$. The variable ![]() $\gamma _r$ denotes the strength of the shedding tubular vortex sheet, and from (2.38),
$\gamma _r$ denotes the strength of the shedding tubular vortex sheet, and from (2.38),
It is important to note that as discussed by Branlard & Gaunaa (Reference Branlard and Gaunaa2016), the above-mentioned shedding vortices are actually in the direction of the wake centreline axis that forms an angle with the streamwise coordinate ![]() $x$. Prior studies (e.g. Coleman et al. Reference Coleman, Feingold and Stempin1945) however showed that the angle between the wake centreline and the
$x$. Prior studies (e.g. Coleman et al. Reference Coleman, Feingold and Stempin1945) however showed that the angle between the wake centreline and the ![]() $x$-coordinate is expected to be much smaller than the turbine yaw angle. Therefore, we assume that both axial root and tip shedding vortices are in the
$x$-coordinate is expected to be much smaller than the turbine yaw angle. Therefore, we assume that both axial root and tip shedding vortices are in the ![]() $x$-direction for simplicity.
$x$-direction for simplicity.
2.3.3. Total vorticity shedding from a yawed turbine
From findings of §§ 2.3.1 and 2.3.2, we can determine the total vorticity shedding from a yawed rotor due to both yaw offset and rotating blades as a function of turbine operating conditions. From (2.33) and (2.39), the value of the dimensionless initial vortex strength ![]() $\hat {\gamma }_0$ in the
$\hat {\gamma }_0$ in the ![]() $(r,\theta )$ polar coordinate system is given by
$(r,\theta )$ polar coordinate system is given by
The variable ![]() $\chi$, called the rotation rate, is the ratio of the strength of vortex generation due to rotating blades to the one generated due to yaw offset. For the limiting cases of
$\chi$, called the rotation rate, is the ratio of the strength of vortex generation due to rotating blades to the one generated due to yaw offset. For the limiting cases of ![]() $\lambda =\pm \infty$,
$\lambda =\pm \infty$, ![]() $\chi$ is equal to zero, and the shedding vorticity is only due to the yaw offset. As the tip-speed ratio
$\chi$ is equal to zero, and the shedding vorticity is only due to the yaw offset. As the tip-speed ratio ![]() $\lambda$ goes to infinity, the amount of torque generated by the turbine goes to zero. Therefore, according to the conservation of angular momentum, there should be no wake rotation downwind of the actuator disk in the limiting cases of
$\lambda$ goes to infinity, the amount of torque generated by the turbine goes to zero. Therefore, according to the conservation of angular momentum, there should be no wake rotation downwind of the actuator disk in the limiting cases of ![]() $\lambda =\pm \infty$. Hereafter, the term non-rotating wake refers to the wake of an actuator disk with an infinite tip-speed ratio
$\lambda =\pm \infty$. Hereafter, the term non-rotating wake refers to the wake of an actuator disk with an infinite tip-speed ratio ![]() $\lambda$, while rotating wake refers to the wake of an actuator disk with a finite value of
$\lambda$, while rotating wake refers to the wake of an actuator disk with a finite value of ![]() $\lambda$.
$\lambda$.
2.3.4. Initial shape of the vortex sheet
The vortex sheet sheds from the circumference of the rotor, so it initially has a shape similar to the projected frontal area of the yawed disk, which is an ellipse with a semi-major axis of ![]() $R$ in the
$R$ in the ![]() $z$-direction, and a semi-minor axis of
$z$-direction, and a semi-minor axis of ![]() $R\cos \beta$ in the
$R\cos \beta$ in the ![]() $y$-direction. The disk-averaged velocity normal to the rotor
$y$-direction. The disk-averaged velocity normal to the rotor ![]() $U_d$ is equal to
$U_d$ is equal to ![]() $U_{\infty }\cos \beta (1-a)$, where
$U_{\infty }\cos \beta (1-a)$, where ![]() $a$ is the turbine induction factor, and it is given by
$a$ is the turbine induction factor, and it is given by ![]() $0.5(1-\sqrt {1-C_T\cos ^{2}\beta })$ (Burton et al. Reference Burton, Sharpe, Jenkins and Bossanyi1995). Behind the turbine, the rotor streamtube area expands further as pressure recovers to the background value (Manwell, McGowan & Rogers Reference Manwell, McGowan and Rogers2010). At this location, the streamwise velocity is given by
$0.5(1-\sqrt {1-C_T\cos ^{2}\beta })$ (Burton et al. Reference Burton, Sharpe, Jenkins and Bossanyi1995). Behind the turbine, the rotor streamtube area expands further as pressure recovers to the background value (Manwell, McGowan & Rogers Reference Manwell, McGowan and Rogers2010). At this location, the streamwise velocity is given by ![]() $U_{\infty }(1-2a)$ (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016; Shapiro et al. Reference Shapiro, Gayme and Meneveau2018). From continuity,
$U_{\infty }(1-2a)$ (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016; Shapiro et al. Reference Shapiro, Gayme and Meneveau2018). From continuity, ![]() $A_*$, the ratio of the expanded streamtube area to the projected frontal area of the rotor is therefore given by
$A_*$, the ratio of the expanded streamtube area to the projected frontal area of the rotor is therefore given by
 \begin{equation} A_*=\frac{\left(1-a\right)\cos\beta}{1-2a}\frac{1}{\cos\beta}= \frac{1+\sqrt{1-C_T\cos^{2}\beta}}{2\sqrt{1-C_T\cos^{2}\beta}}. \end{equation}
\begin{equation} A_*=\frac{\left(1-a\right)\cos\beta}{1-2a}\frac{1}{\cos\beta}= \frac{1+\sqrt{1-C_T\cos^{2}\beta}}{2\sqrt{1-C_T\cos^{2}\beta}}. \end{equation}
Neglecting the distance between the rotor and the end of the streamtube expansion, we set the initial wake area enclosed by the vortex sheet at ![]() $t=0$ to be the projected frontal area of the rotor times
$t=0$ to be the projected frontal area of the rotor times ![]() $A_*$. Therefore,
$A_*$. Therefore, ![]() $\xi _0(\theta )$ has an elliptical shape expressed by
$\xi _0(\theta )$ has an elliptical shape expressed by
For a small yaw angle ![]() $\beta$, the vortex sheet initially has an approximately circular shape. Therefore, one can approximate
$\beta$, the vortex sheet initially has an approximately circular shape. Therefore, one can approximate ![]() $\xi _0$ with
$\xi _0$ with ![]() $\tilde {\xi }_0$ given by
$\tilde {\xi }_0$ given by
2.4. Vortex sheet lateral deflection
The analytical solutions of the vortex sheet shape developed earlier are represented in the ![]() $(r,\theta )$ polar coordinate system, which is attached to the vortex sheet centre
$(r,\theta )$ polar coordinate system, which is attached to the vortex sheet centre ![]() $C$. Therefore, in order to fully determine the locus of the vortex sheet with respect to a stationary coordinate system, we also need to compute how
$C$. Therefore, in order to fully determine the locus of the vortex sheet with respect to a stationary coordinate system, we also need to compute how ![]() $y_c$ and
$y_c$ and ![]() $z_c$ vary with time or downstream distance (i.e. wake deflection). From figure 1(c), the Kutta–Joukowsky theorem can be used to obtain
$z_c$ vary with time or downstream distance (i.e. wake deflection). From figure 1(c), the Kutta–Joukowsky theorem can be used to obtain
 $$\begin{gather} \hat{y}_c=\frac{1}{2{\rm \pi}}\int_0^{\hat{t}} \int_0^{2{\rm \pi}}\hat{\gamma}(\theta',\hat{t})\sin\theta'\,\textrm{d}\theta'\,\textrm{d}\hat{t}, \end{gather}$$
$$\begin{gather} \hat{y}_c=\frac{1}{2{\rm \pi}}\int_0^{\hat{t}} \int_0^{2{\rm \pi}}\hat{\gamma}(\theta',\hat{t})\sin\theta'\,\textrm{d}\theta'\,\textrm{d}\hat{t}, \end{gather}$$ $$\begin{gather}\hat{z}_c=\frac{-1}{2{\rm \pi}}\int_0^{\hat{t}}\int_0^{2{\rm \pi}} \hat{\gamma}(\theta',\hat{t})\cos\theta'\,\textrm{d}\theta'\,\textrm{d}\hat{t}, \end{gather}$$
$$\begin{gather}\hat{z}_c=\frac{-1}{2{\rm \pi}}\int_0^{\hat{t}}\int_0^{2{\rm \pi}} \hat{\gamma}(\theta',\hat{t})\cos\theta'\,\textrm{d}\theta'\,\textrm{d}\hat{t}, \end{gather}$$
where ![]() $\hat {y}_c=y_c/\xi _0$ and
$\hat {y}_c=y_c/\xi _0$ and ![]() $\hat {z}_c=z_c/\xi _0$. Inserting
$\hat {z}_c=z_c/\xi _0$. Inserting ![]() $\hat {\gamma }(\theta,\hat {t})$ from (2.26) into (2.46) and (2.47) and performing the integration lead to
$\hat {\gamma }(\theta,\hat {t})$ from (2.26) into (2.46) and (2.47) and performing the integration lead to
From (2.49), the vertical displacement of ![]() $C$ is zero when
$C$ is zero when ![]() $\chi =0$ (i.e. actuator disks with non-rotating wake) as expected from symmetry and consistent with prior experimental and numerical works (e.g. Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016; Howland et al. Reference Howland, Bossuyt, Martínez-Tossas, Meyers and Meneveau2016; Bartl et al. Reference Bartl, Mühle, Schottler, Sætran, Peinke, Adaramola and Hölling2018). Comparison of (2.48) and (2.49) for non-zero values of
$\chi =0$ (i.e. actuator disks with non-rotating wake) as expected from symmetry and consistent with prior experimental and numerical works (e.g. Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016; Howland et al. Reference Howland, Bossuyt, Martínez-Tossas, Meyers and Meneveau2016; Bartl et al. Reference Bartl, Mühle, Schottler, Sætran, Peinke, Adaramola and Hölling2018). Comparison of (2.48) and (2.49) for non-zero values of ![]() $\chi$ shows that
$\chi$ shows that ![]() $\hat {z}_c$ is non-zero but still considerably smaller than
$\hat {z}_c$ is non-zero but still considerably smaller than ![]() $\hat {y}_c$ for small values of
$\hat {y}_c$ for small values of ![]() $\hat {t}$. Therefore, we neglect
$\hat {t}$. Therefore, we neglect ![]() $\hat {z}_c$ in this work for simplicity.
$\hat {z}_c$ in this work for simplicity.
It is worth remembering that to derive the analytical solution for the deformation of the vortex sheet, we assumed that the shape of the vortex sheet does not largely deviate from a circle. Although this is an acceptable assumption for small values of yaw angle and time, it is less accurate for large values of time, when the vortex sheet rolls up and forms a CVP. As shown in figure 4(a), based on (2.48), the value of ![]() $\hat {y}_c$ may even decrease with an increase of
$\hat {y}_c$ may even decrease with an increase of ![]() $\hat {t}$, which is clearly unphysical. Since we expect that at large times (or downstream distances) a CVP can more realistically represent the vorticity shedding from the yawed rotor, we enhance our model for
$\hat {t}$, which is clearly unphysical. Since we expect that at large times (or downstream distances) a CVP can more realistically represent the vorticity shedding from the yawed rotor, we enhance our model for ![]() $\hat {y}_c$ so that at large distances it tends to the situation of a CVP instead of using the truncated series vortex sheet solution.
$\hat {y}_c$ so that at large distances it tends to the situation of a CVP instead of using the truncated series vortex sheet solution.

Figure 4. (a) Lateral deflection of the vortex sheet centre ![]() $y_c$ based on modelling the shed vorticity either as an approximately circular vortex sheet (2.48) or a CVP (2.53). The empirical relation (2.55) provides predictions similar to the former approach at small
$y_c$ based on modelling the shed vorticity either as an approximately circular vortex sheet (2.48) or a CVP (2.53). The empirical relation (2.55) provides predictions similar to the former approach at small ![]() $\hat {t}$, while it tends to the latter solution at large times. (b) Schematic of modelling the CVP shedding from a yawed rotor.
$\hat {t}$, while it tends to the latter solution at large times. (b) Schematic of modelling the CVP shedding from a yawed rotor.
Figure 4(b) shows a schematic of a CVP. The CVP has the circulation of ![]() $\varGamma _b$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2018) as shown in figure 4(b). The lateral position of the CVP is denoted by
$\varGamma _b$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2018) as shown in figure 4(b). The lateral position of the CVP is denoted by ![]() $y_{cvp}$, and the lateral distance between the wake centre
$y_{cvp}$, and the lateral distance between the wake centre ![]() $C$ and the CVP is denoted by
$C$ and the CVP is denoted by ![]() $\delta _c$ in the figure. The vertical spacing between counter-rotating vortices is equal to
$\delta _c$ in the figure. The vertical spacing between counter-rotating vortices is equal to ![]() $2\xi _0$ and it is assumed to remain constant. Initial values of
$2\xi _0$ and it is assumed to remain constant. Initial values of ![]() $y_c$,
$y_c$, ![]() $y_{cvp}$ and
$y_{cvp}$ and ![]() $\delta _c$ are zero. In this analysis, only the vorticity shed due to the yaw offset is considered as the effect of shed vorticity due to rotating blades on the wake deflection is expected to be small. Our objective is to find the variation of
$\delta _c$ are zero. In this analysis, only the vorticity shed due to the yaw offset is considered as the effect of shed vorticity due to rotating blades on the wake deflection is expected to be small. Our objective is to find the variation of ![]() $y_c$ with time (or downstream distance), but let us first determine how
$y_c$ with time (or downstream distance), but let us first determine how ![]() $\delta _c$ varies with time. According to the Biot–Savart law,
$\delta _c$ varies with time. According to the Biot–Savart law,
where ![]() $v_c$ is the lateral velocity of
$v_c$ is the lateral velocity of ![]() $C$ induced by the CVP, and
$C$ induced by the CVP, and ![]() $L$ and
$L$ and ![]() $\alpha$ are defined in figure 4(b). The CVP also moves with a lateral velocity of
$\alpha$ are defined in figure 4(b). The CVP also moves with a lateral velocity of ![]() $v_{cvp}=\varGamma _b/(4{\rm \pi} \xi _0)$ due to its self-induced velocity. Therefore, one can write
$v_{cvp}=\varGamma _b/(4{\rm \pi} \xi _0)$ due to its self-induced velocity. Therefore, one can write
It is interesting to note that, according to (2.51), ![]() $\delta _c$ increases until
$\delta _c$ increases until ![]() $\delta _c$ approaches
$\delta _c$ approaches ![]() $\sqrt {3}\xi _0$. At this time
$\sqrt {3}\xi _0$. At this time ![]() $v_c=v_{cvp}$ and, therefore, the relative position of C with respect to the CVP does not change anymore, and
$v_c=v_{cvp}$ and, therefore, the relative position of C with respect to the CVP does not change anymore, and ![]() $\delta _c$ remains equal to
$\delta _c$ remains equal to ![]() $\sqrt {3}\xi _0$ afterwards.
$\sqrt {3}\xi _0$ afterwards.
Next, we approximate ![]() $\varGamma _b \approx 2\xi _0\gamma _b$ in (2.51). We then integrate (2.51) (with separation of variables,
$\varGamma _b \approx 2\xi _0\gamma _b$ in (2.51). We then integrate (2.51) (with separation of variables, ![]() $\delta _c$ and
$\delta _c$ and ![]() $t$) and write the solution in the dimensionless form. This yields an implicit expression for
$t$) and write the solution in the dimensionless form. This yields an implicit expression for ![]() $\hat {\delta }_c(\hat {t})$ (it will be later expressed explicitly using an empirical formula),
$\hat {\delta }_c(\hat {t})$ (it will be later expressed explicitly using an empirical formula),
 \begin{equation} \frac{\hat{t}}{2{\rm \pi}}=\frac{-2}{\sqrt{3}}\ln{\left(\frac{\sqrt{3}-\hat{\delta}_c}{\sqrt{3}+ \hat{\delta}_c}\right)}-\hat{\delta}_c, \end{equation}
\begin{equation} \frac{\hat{t}}{2{\rm \pi}}=\frac{-2}{\sqrt{3}}\ln{\left(\frac{\sqrt{3}-\hat{\delta}_c}{\sqrt{3}+ \hat{\delta}_c}\right)}-\hat{\delta}_c, \end{equation}
where ![]() $\hat {\delta }_c=\delta _c/\xi _0$. Note that to derive (2.52), we assume that
$\hat {\delta }_c=\delta _c/\xi _0$. Note that to derive (2.52), we assume that ![]() $\hat {\delta }_c < \sqrt {3}$. Given that
$\hat {\delta }_c < \sqrt {3}$. Given that ![]() $\hat {y}_c=\hat {\delta }_c+\hat {y}_{cvp}$, we have
$\hat {y}_c=\hat {\delta }_c+\hat {y}_{cvp}$, we have
Predictions of ![]() $\hat {y}_c$ based on modelling the vortex sheet as a CVP using (2.52) and (2.53) are shown in figure 4(a). As discussed earlier, the solution for
$\hat {y}_c$ based on modelling the vortex sheet as a CVP using (2.52) and (2.53) are shown in figure 4(a). As discussed earlier, the solution for ![]() $\hat {y}_c$ based on the CVP is expected to provide acceptable predictions at large values of
$\hat {y}_c$ based on the CVP is expected to provide acceptable predictions at large values of ![]() $\hat {t}$, while the solution based on an approximately circular vortex sheet (2.48) works better at short values of
$\hat {t}$, while the solution based on an approximately circular vortex sheet (2.48) works better at short values of ![]() $\hat {t}$. An empirical formula that merges these two behaviours to leading order in both limits can be written as
$\hat {t}$. An empirical formula that merges these two behaviours to leading order in both limits can be written as
where ![]() $\textrm {sgn}(x)$ is the sign function of
$\textrm {sgn}(x)$ is the sign function of ![]() $x$, and
$x$, and ![]() $c_1,\ldots,c_6$ are polynomial coefficients, which need to be determined. Note that, similar to the vortex sheet and CVP solutions, the empirical relation is an odd function, so the wake deflection is opposite for turbines with opposite yaw angles. To find suitable values of polynomial coefficients (
$c_1,\ldots,c_6$ are polynomial coefficients, which need to be determined. Note that, similar to the vortex sheet and CVP solutions, the empirical relation is an odd function, so the wake deflection is opposite for turbines with opposite yaw angles. To find suitable values of polynomial coefficients (![]() $c_1,\ldots,c_6$), we match the series expansion of (2.54) at
$c_1,\ldots,c_6$), we match the series expansion of (2.54) at ![]() $\hat {t}\to 0$ and
$\hat {t}\to 0$ and ![]() $\hat {t}\to \infty$ with
$\hat {t}\to \infty$ with ![]() $\hat {t}/2-\hat {t}^{3}/96$ and
$\hat {t}/2-\hat {t}^{3}/96$ and ![]() $\hat {t}/(2{\rm \pi} )+\sqrt {3}$, respectively. This leads to a system of equations that needs to be solved. So we obtain
$\hat {t}/(2{\rm \pi} )+\sqrt {3}$, respectively. This leads to a system of equations that needs to be solved. So we obtain
Equation (2.55) provides predictions similar to (2.48) at small values of ![]() $\hat {t}$ and approaches (2.53) at large values of
$\hat {t}$ and approaches (2.53) at large values of ![]() $\hat {t}$ as shown in figure 4(a).
$\hat {t}$ as shown in figure 4(a).
2.5. Comparison with numerical simulations
In this section we compare predictions of the vortex sheet (i.e. wake edge) shape ![]() $\xi (\theta,t)$ based on the new proposed model with numerical simulation data. For simulations, the pseudo-spectral LES code LESGO is applied. The LESGO code has been used in prior works (Calaf, Meneveau & Meyers Reference Calaf, Meneveau and Meyers2010; Stevens, Graham & Meneveau Reference Stevens, Graham and Meneveau2014; VerHulst & Meneveau Reference VerHulst and Meneveau2015; Martínez-Tossas et al. Reference Martínez-Tossas, Churchfield, Yilmaz, Sarlak, Johnson, Sørensen, Meyers and Meneveau2018; Shapiro et al. Reference Shapiro, Gayme and Meneveau2018; Stevens, Martınez-Tossas & Meneveau Reference Stevens, Martınez-Tossas and Meneveau2018) to simulate flow past wind turbines and wind farms. It has been validated by detailed comparisons with several other LES codes (Martínez-Tossas et al. Reference Martínez-Tossas, Churchfield, Yilmaz, Sarlak, Johnson, Sørensen, Meyers and Meneveau2018). Turbines are simulated using the actuator disk model with rotation (ADM-R). See the Appendix C for more information about the LESGO code and the LES set-up of this study. Under uniform inflow conditions the role of turbulence is minimal, and the code runs mostly as an inviscid solver with regularization, as it was also used in Shapiro et al. (Reference Shapiro, Gayme and Meneveau2018). Simulations are performed for a range of local thrust coefficients
$\xi (\theta,t)$ based on the new proposed model with numerical simulation data. For simulations, the pseudo-spectral LES code LESGO is applied. The LESGO code has been used in prior works (Calaf, Meneveau & Meyers Reference Calaf, Meneveau and Meyers2010; Stevens, Graham & Meneveau Reference Stevens, Graham and Meneveau2014; VerHulst & Meneveau Reference VerHulst and Meneveau2015; Martínez-Tossas et al. Reference Martínez-Tossas, Churchfield, Yilmaz, Sarlak, Johnson, Sørensen, Meyers and Meneveau2018; Shapiro et al. Reference Shapiro, Gayme and Meneveau2018; Stevens, Martınez-Tossas & Meneveau Reference Stevens, Martınez-Tossas and Meneveau2018) to simulate flow past wind turbines and wind farms. It has been validated by detailed comparisons with several other LES codes (Martínez-Tossas et al. Reference Martínez-Tossas, Churchfield, Yilmaz, Sarlak, Johnson, Sørensen, Meyers and Meneveau2018). Turbines are simulated using the actuator disk model with rotation (ADM-R). See the Appendix C for more information about the LESGO code and the LES set-up of this study. Under uniform inflow conditions the role of turbulence is minimal, and the code runs mostly as an inviscid solver with regularization, as it was also used in Shapiro et al. (Reference Shapiro, Gayme and Meneveau2018). Simulations are performed for a range of local thrust coefficients ![]() $C_T'= 0.8, 1.0$ and
$C_T'= 0.8, 1.0$ and ![]() $1.33$, yaw angles
$1.33$, yaw angles ![]() $\beta = 10^{\circ }$,
$\beta = 10^{\circ }$, ![]() $20^{\circ }$ and
$20^{\circ }$ and ![]() $30^{\circ }$, and rotation rates
$30^{\circ }$, and rotation rates ![]() $\chi = 0$, 0.25 and 0.5. Note that according to (2.32) this means that
$\chi = 0$, 0.25 and 0.5. Note that according to (2.32) this means that ![]() $\gamma _b$ and
$\gamma _b$ and ![]() $\hat {t}$ are negative and the curling is expected to be in the opposite direction of that shown in the sketch in figure 1, i.e. in the LES the wake is being deflected in the negative
$\hat {t}$ are negative and the curling is expected to be in the opposite direction of that shown in the sketch in figure 1, i.e. in the LES the wake is being deflected in the negative ![]() $y$-direction. Also, it is worth remembering that the rotation rate
$y$-direction. Also, it is worth remembering that the rotation rate ![]() $\chi$ depends on both yaw angle
$\chi$ depends on both yaw angle ![]() $\beta$ and tip-speed ratio
$\beta$ and tip-speed ratio ![]() $\lambda$. According to (2.42), for a utility-scale wind turbine with a tip-speed ratio
$\lambda$. According to (2.42), for a utility-scale wind turbine with a tip-speed ratio ![]() $\lambda =8$ and yaw angle
$\lambda =8$ and yaw angle ![]() $\beta =15^{\circ } - 30^{\circ }$, rotation rate
$\beta =15^{\circ } - 30^{\circ }$, rotation rate ![]() $\chi$ varies between 0.25–0.5. The non-rotating case commonly used in the LES corresponds to an infinite tip-speed ratio and reduces to the standard actuator disk model (ADM) without rotation. The local thrust coefficient
$\chi$ varies between 0.25–0.5. The non-rotating case commonly used in the LES corresponds to an infinite tip-speed ratio and reduces to the standard actuator disk model (ADM) without rotation. The local thrust coefficient ![]() $C_T'$ is related to the thrust coefficient
$C_T'$ is related to the thrust coefficient ![]() $C_T$ through
$C_T$ through ![]() $C_T=16C_T'/(4+C_T'\cos ^{2}\beta )^{2}$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2018). A fringe forcing region is used to force the flow back to laminar inflow when using periodic boundary conditions in the
$C_T=16C_T'/(4+C_T'\cos ^{2}\beta )^{2}$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2018). A fringe forcing region is used to force the flow back to laminar inflow when using periodic boundary conditions in the ![]() $x$-direction. Excluding this fringe region the effective domain has sides that are
$x$-direction. Excluding this fringe region the effective domain has sides that are ![]() $L_x = 15.12D$,
$L_x = 15.12D$, ![]() $L_y = 5.76D$ and
$L_y = 5.76D$ and ![]() $L_z = 5.76D$ long. A uniform grid with
$L_z = 5.76D$ long. A uniform grid with ![]() $N_x = 384$ effective grid points in the streamwise direction and
$N_x = 384$ effective grid points in the streamwise direction and ![]() $N_y = N_z = 192$ grid points in the spanwise and vertical directions are used. The centre of the actuator disk is placed 3.6D from the inlet of the domain.
$N_y = N_z = 192$ grid points in the spanwise and vertical directions are used. The centre of the actuator disk is placed 3.6D from the inlet of the domain.
In order to determine the shape of the wake edge based on the developed model, we need to first compute the value of ![]() $\hat {t}=\gamma _bt/\xi _0$, where
$\hat {t}=\gamma _bt/\xi _0$, where ![]() $\xi _0$ can be approximated with
$\xi _0$ can be approximated with ![]() $\tilde {\xi }_0$ (2.45) and
$\tilde {\xi }_0$ (2.45) and ![]() $t=x/U_{con}$. Although the convection velocity
$t=x/U_{con}$. Although the convection velocity ![]() $U_{con}$ in turbine wakes changes with the streamwise distance, it is approximated with a constant value in this study, as done in prior studies (e.g. Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). For cases with no incoming turbulence, the turbine wake does not significantly interact with the surrounding flow, and it experiences a slow recovery. In this case, the streamwise velocity profile in the central part of the wake can be modelled as a top-hat core (i.e. potential core) with a constant velocity
$U_{con}$ in turbine wakes changes with the streamwise distance, it is approximated with a constant value in this study, as done in prior studies (e.g. Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). For cases with no incoming turbulence, the turbine wake does not significantly interact with the surrounding flow, and it experiences a slow recovery. In this case, the streamwise velocity profile in the central part of the wake can be modelled as a top-hat core (i.e. potential core) with a constant velocity ![]() $U_0$ equal to
$U_0$ equal to ![]() $U_{{in}}\sqrt {1-C_T\cos ^{2}\beta }$ (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016; Shapiro et al. Reference Shapiro, Gayme and Meneveau2018), where
$U_{{in}}\sqrt {1-C_T\cos ^{2}\beta }$ (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016; Shapiro et al. Reference Shapiro, Gayme and Meneveau2018), where ![]() $U_{{in}}$ is the incoming velocity. The top-hat core is surrounded by a shear layer in which the velocity changes from
$U_{{in}}$ is the incoming velocity. The top-hat core is surrounded by a shear layer in which the velocity changes from ![]() $U_0$ to
$U_0$ to ![]() $U_{{in}}$. Therefore, we approximate the convection velocity with
$U_{{in}}$. Therefore, we approximate the convection velocity with ![]() $U_{con}=0.5(U_0+U_{{in}})$. For instance, based on this definition,
$U_{con}=0.5(U_0+U_{{in}})$. For instance, based on this definition, ![]() $|\hat {t}|=2$ (i.e. limiting value for using the analytical model) corresponds to a streamwise distance in the range of
$|\hat {t}|=2$ (i.e. limiting value for using the analytical model) corresponds to a streamwise distance in the range of ![]() $12R-29R$ for a turbine with
$12R-29R$ for a turbine with ![]() $C_T'=1.33$ (i.e.
$C_T'=1.33$ (i.e. ![]() $C_T\approx 0.75$ for
$C_T\approx 0.75$ for ![]() $\beta =0$), and
$\beta =0$), and ![]() $\beta =30^{\circ } - 10^{\circ }$.
$\beta =30^{\circ } - 10^{\circ }$.
The analysis presented in § 2 suggests that the wake shape, non-dimensionalised by ![]() $\xi _0(\theta )$, only depends on the dimensionless time
$\xi _0(\theta )$, only depends on the dimensionless time ![]() $\hat {t}$, and the rotation rate
$\hat {t}$, and the rotation rate ![]() $\chi =1/\lambda \sin \beta$. As a first test of the model, we compare the dimensionless model predictions with LES results normalised such that they can be presented as function of
$\chi =1/\lambda \sin \beta$. As a first test of the model, we compare the dimensionless model predictions with LES results normalised such that they can be presented as function of ![]() $\hat {t}$ and
$\hat {t}$ and ![]() $\chi$. For the LES data, the edges of the wake are identified by tracking the edge of the streamtube that passes through the face of the actuator disk which is appropriate in this case due to the lack of turbulent mixing. Results are shown in figure 5, which shows that the LES data for turbines with different operating conditions approximately collapse onto the same wake profile curve for given values of
$\chi$. For the LES data, the edges of the wake are identified by tracking the edge of the streamtube that passes through the face of the actuator disk which is appropriate in this case due to the lack of turbulent mixing. Results are shown in figure 5, which shows that the LES data for turbines with different operating conditions approximately collapse onto the same wake profile curve for given values of ![]() $\hat {t}$ and
$\hat {t}$ and ![]() $\chi$, in agreement with the proposed theory. The figure also shows that the proposed analytical model is able to capture the scaled wake shape. At larger time magnitudes and large rotation rates some discrepancies appear, especially in the bottom right quadrant. The governing equations are developed by assuming small deviations of the vortex sheet from its initial shape. In addition, a severely truncated series expansion is used to solve governing equations. Therefore, the model cannot fully capture the vortex roll-up and transition of the vortex sheet to a CVP at large times, and some discrepancies are noticeable. For non-zero values of rotation rate, an additional level of vorticity
$\chi$, in agreement with the proposed theory. The figure also shows that the proposed analytical model is able to capture the scaled wake shape. At larger time magnitudes and large rotation rates some discrepancies appear, especially in the bottom right quadrant. The governing equations are developed by assuming small deviations of the vortex sheet from its initial shape. In addition, a severely truncated series expansion is used to solve governing equations. Therefore, the model cannot fully capture the vortex roll-up and transition of the vortex sheet to a CVP at large times, and some discrepancies are noticeable. For non-zero values of rotation rate, an additional level of vorticity ![]() $\gamma _r$ sheds from the rotor circumference due to blade rotation. Given the sinusoidal nature of vorticity due to yaw offset (2.33), the additional shedding vorticity due to rotation increases the vorticity magnitude on either bottom or top halves of the wake (e.g. bottom half for the data shown in figure 5), which in turn accelerates the vortex roll-up. At larger values of rotation rate, discrepancy is thus expected to be higher due to the earlier occurrence of vortex roll-up. This is confirmed in figure 5 by comparing model predictions at the same dimensionless time (e.g.
$\gamma _r$ sheds from the rotor circumference due to blade rotation. Given the sinusoidal nature of vorticity due to yaw offset (2.33), the additional shedding vorticity due to rotation increases the vorticity magnitude on either bottom or top halves of the wake (e.g. bottom half for the data shown in figure 5), which in turn accelerates the vortex roll-up. At larger values of rotation rate, discrepancy is thus expected to be higher due to the earlier occurrence of vortex roll-up. This is confirmed in figure 5 by comparing model predictions at the same dimensionless time (e.g. ![]() $\hat {t}=-1.6$), but different values of rotation rate.
$\hat {t}=-1.6$), but different values of rotation rate.

Figure 5. Dimensionless shape of the wake of yawed wind turbines in uniform inflow for ![]() $C_T' = 0.8$ (
$C_T' = 0.8$ (![]() $\circ$),
$\circ$), ![]() $C_T' = 1$ (
$C_T' = 1$ (![]() $\square$) and
$\square$) and ![]() $C_T' = 1.33$ (
$C_T' = 1.33$ (![]() $\triangle$) and yaw angles
$\triangle$) and yaw angles ![]() $\beta =10^{\circ }$ (red),
$\beta =10^{\circ }$ (red), ![]() $\beta =20^{\circ }$ (blue),
$\beta =20^{\circ }$ (blue), ![]() $\beta =30^{\circ }$ (green) at various evolution times
$\beta =30^{\circ }$ (green) at various evolution times ![]() $\hat {t}$ and rotation rates
$\hat {t}$ and rotation rates ![]() $\chi$. The analytical model (black solid line) is shown for comparison. Note that results of
$\chi$. The analytical model (black solid line) is shown for comparison. Note that results of ![]() $\beta =10^{\circ }$ are not shown for
$\beta =10^{\circ }$ are not shown for ![]() $\hat {t}=-1.6$ and
$\hat {t}=-1.6$ and ![]() $-2.0$ because for this yaw angle they correspond to downwind distances that exceed the computational domain.
$-2.0$ because for this yaw angle they correspond to downwind distances that exceed the computational domain.
Next, we expand the comparison and plot the results in terms of physical parameters that are more directly related to the flow configuration: downstream distance ![]() $x/R$, local thrust coefficient
$x/R$, local thrust coefficient ![]() $C_T^{\prime }$, yaw angle
$C_T^{\prime }$, yaw angle ![]() $\beta$ and dimensionless rotation rate
$\beta$ and dimensionless rotation rate ![]() $\chi$. Figure 6 shows wake edge predictions of the analytical model together with the LES data for different values of
$\chi$. Figure 6 shows wake edge predictions of the analytical model together with the LES data for different values of ![]() $C_T'$,
$C_T'$, ![]() $\beta$ and
$\beta$ and ![]() $\chi$, at several downwind locations. The figure shows that the degree of wake curling increases with yaw angle, thrust coefficient and streamwise distance, as expected from the analysis presented in § 2. Moreover, wake rotation breaks the vertical symmetry of the wake. The results presented in figure 6 show that the wake shape depends strongly on all of the varied parameters: thrust coefficient, yaw angle and rotation rate. The analytical model developed is seen to agree well with the LES results, up to intermediate levels of wake curling. The analytical model successfully predicts the shape of the wake for various operating conditions. As the wake deformation grows further downstream or at increasing
$\chi$, at several downwind locations. The figure shows that the degree of wake curling increases with yaw angle, thrust coefficient and streamwise distance, as expected from the analysis presented in § 2. Moreover, wake rotation breaks the vertical symmetry of the wake. The results presented in figure 6 show that the wake shape depends strongly on all of the varied parameters: thrust coefficient, yaw angle and rotation rate. The analytical model developed is seen to agree well with the LES results, up to intermediate levels of wake curling. The analytical model successfully predicts the shape of the wake for various operating conditions. As the wake deformation grows further downstream or at increasing ![]() $C_T^{\prime }$, differences appear, as mentioned before due to the limitations of the model that is based on a severely truncated series expansion. It is clear that there is reduced agreement in the lower half of the wake for cases with large values of yaw angle and rotation rate. As discussed earlier, for these cases, the lower half of the wake cross-section is subject to a strong vortex roll-up caused by the cumulative vorticity due to both yaw offset and rotation. Still, the model is able to predict many qualitative features of the wake shape, including its vertical asymmetry for cases with rotation. In addition, the sideways displacement of the entire wake is also captured quite well in all cases.
$C_T^{\prime }$, differences appear, as mentioned before due to the limitations of the model that is based on a severely truncated series expansion. It is clear that there is reduced agreement in the lower half of the wake for cases with large values of yaw angle and rotation rate. As discussed earlier, for these cases, the lower half of the wake cross-section is subject to a strong vortex roll-up caused by the cumulative vorticity due to both yaw offset and rotation. Still, the model is able to predict many qualitative features of the wake shape, including its vertical asymmetry for cases with rotation. In addition, the sideways displacement of the entire wake is also captured quite well in all cases.

Figure 6. Wake of yawed wind turbines in uniform inflow for yaw angles ![]() $\beta =10^{\circ }$ (red),
$\beta =10^{\circ }$ (red), ![]() $\beta =20^{\circ }$ (blue),
$\beta =20^{\circ }$ (blue), ![]() $\beta =30^{\circ }$ (green) at various downstream locations
$\beta =30^{\circ }$ (green) at various downstream locations ![]() $x/R$ and rotation rates
$x/R$ and rotation rates ![]() $\chi$. Large-eddy simulation measurements are shown with symbols and modelled wake locations are shown with solid lines.
$\chi$. Large-eddy simulation measurements are shown with symbols and modelled wake locations are shown with solid lines.
3. Vortex sheet evolution in turbulent atmospheric boundary layer
In this section we generalize the prior analytical model of a yawed wind turbine wake that is applicable for ideal non-turbulent flow to the case of a wake with a turbulent atmospheric boundary layer background flow. Here we seek a model for the entire mean velocity distribution as a function of downstream distance as well as cross-stream position, accounting for the fact that the wake will be curling due to turbine yaw.
3.1. Vortex sheet evolution in turbulent atmospheric boundary layer
For the ideal flow case, we assumed that the vortex sheet does not decay as it moves downstream, and the strength of the streamwise vorticity only evolves along the vortex sheet in time following idealised vortex dynamics. Although this may be an acceptable assumption for turbines with uniform non-turbulent inflows, it is not expected to be valid for turbines immersed in turbulent environments such as the atmospheric boundary layer (ABL). The vertically varying mean inflow velocity in the ABL can be approximated as ![]() $U_\textrm {in}(z) = (u_*/\kappa )\ln (z/z_0)$, where
$U_\textrm {in}(z) = (u_*/\kappa )\ln (z/z_0)$, where ![]() $u_*$ is the friction velocity,
$u_*$ is the friction velocity, ![]() $\kappa$ is the von-Kàrmàn constant and
$\kappa$ is the von-Kàrmàn constant and ![]() $z_0$ is the roughness height. As discussed in Shapiro et al. (Reference Shapiro, Gayme and Meneveau2020), the vorticity shedding from a yawed rotor decays due to the turbulent diffusion; i.e.
$z_0$ is the roughness height. As discussed in Shapiro et al. (Reference Shapiro, Gayme and Meneveau2020), the vorticity shedding from a yawed rotor decays due to the turbulent diffusion; i.e. ![]() $\gamma _b(t)$ and
$\gamma _b(t)$ and ![]() $\gamma _r(t)$ are functions of time. Instead of solving the full governing equations for a diffusing vortex sheet, we approximate the effects of diffusion by scaling
$\gamma _r(t)$ are functions of time. Instead of solving the full governing equations for a diffusing vortex sheet, we approximate the effects of diffusion by scaling ![]() $\gamma$ and the velocities by the circulation
$\gamma$ and the velocities by the circulation ![]() $\gamma _b(t)$ that is decaying according to a previously obtained analytical solution for the decay of CVP in a turbulent boundary layer (Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). Specifically, we define new scaled variables
$\gamma _b(t)$ that is decaying according to a previously obtained analytical solution for the decay of CVP in a turbulent boundary layer (Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). Specifically, we define new scaled variables ![]() $\hat {\gamma }$,
$\hat {\gamma }$, ![]() $\hat {u}_r$ and
$\hat {u}_r$ and ![]() $\hat {u}_\theta$ such that
$\hat {u}_\theta$ such that
If one defines scaled displacement and time according to
one recovers the original governing equations (2.15), (2.16) and (2.55) for the new definition of variables ![]() $\hat {\gamma }, \hat {u}_r, \hat {u}_\theta, \hat {\xi }$ and
$\hat {\gamma }, \hat {u}_r, \hat {u}_\theta, \hat {\xi }$ and ![]() $\hat {t}$. An additional term is however introduced in (2.17), so
$\hat {t}$. An additional term is however introduced in (2.17), so
It will be shown later in (3.8) that ![]() $\int (\gamma _b/\gamma _{b0})\,\textrm {d} t \propto c(1-\textrm {exp}(k_vt/c))$, where
$\int (\gamma _b/\gamma _{b0})\,\textrm {d} t \propto c(1-\textrm {exp}(k_vt/c))$, where ![]() $\gamma _{b0}=\gamma _b(t=0)$,
$\gamma _{b0}=\gamma _b(t=0)$, ![]() $c$ is a constant and
$c$ is a constant and ![]() $k_v$ is the expansion rate of the turbulent diffusive scale, and it is modelled as
$k_v$ is the expansion rate of the turbulent diffusive scale, and it is modelled as ![]() $u_*/U_{in}(z)$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). So the Taylor expansion of
$u_*/U_{in}(z)$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). So the Taylor expansion of ![]() $\gamma _b(t)$ is given by
$\gamma _b(t)$ is given by
For atmospheric flows, the value of ![]() $k_v$ at the hub height is equal to
$k_v$ at the hub height is equal to ![]() $u_*/U_h<\!<1$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). Therefore,
$u_*/U_h<\!<1$ (Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). Therefore, ![]() $\gamma _b$ is a slow varying reference quantity, and the additional term on the right-hand side of (3.4) is neglected for simplicity. This means that the solution already developed in § 2.2 will still be used as a model for the decaying vortex sheet once rescaled by the prescribed
$\gamma _b$ is a slow varying reference quantity, and the additional term on the right-hand side of (3.4) is neglected for simplicity. This means that the solution already developed in § 2.2 will still be used as a model for the decaying vortex sheet once rescaled by the prescribed ![]() $\gamma _b(t)$ evolution and using the modified time
$\gamma _b(t)$ evolution and using the modified time ![]() $\hat {t}$. Note that for a constant
$\hat {t}$. Note that for a constant ![]() $\gamma _b$, (3.1a–c)–(3.3) become the same as dimensionless variables defined earlier for a non-decaying vortex sheet.
$\gamma _b$, (3.1a–c)–(3.3) become the same as dimensionless variables defined earlier for a non-decaying vortex sheet.
Next, in order to evaluate the integral of (3.3) and derive a relationship for ![]() $\hat {t}$ under turbulent inflow conditions we need to specify a convection velocity under turbulent inflow conditions. Due to atmospheric turbulence, the wake mixes and recovers more quickly than in the laminar inflow case, and, thus, the mean velocity at the wake edge is comparable to the incoming velocity. We therefore assume that in this case the vortex sheet at a height
$\hat {t}$ under turbulent inflow conditions we need to specify a convection velocity under turbulent inflow conditions. Due to atmospheric turbulence, the wake mixes and recovers more quickly than in the laminar inflow case, and, thus, the mean velocity at the wake edge is comparable to the incoming velocity. We therefore assume that in this case the vortex sheet at a height ![]() $z$ is convected downstream with the incoming velocity at that height
$z$ is convected downstream with the incoming velocity at that height ![]() $U_{{in}}(z)$; thus,
$U_{{in}}(z)$; thus, ![]() $U_{con}=U_{{in}}(z)$ and
$U_{con}=U_{{in}}(z)$ and ![]() $t \approx x/U_{{in}}(z)$.
$t \approx x/U_{{in}}(z)$.
To evaluate (3.3), we must specify the decay of vorticity, i.e. of ![]() $\gamma _b$ with streamwise distance. In Shapiro et al. (Reference Shapiro, Gayme and Meneveau2020) the decay of the total vortex circulation
$\gamma _b$ with streamwise distance. In Shapiro et al. (Reference Shapiro, Gayme and Meneveau2020) the decay of the total vortex circulation ![]() $\varGamma _b(x)$ was studied, its relationship with the density
$\varGamma _b(x)$ was studied, its relationship with the density ![]() $\gamma _b$ being
$\gamma _b$ being ![]() $\gamma _b=\varGamma _b/2R$. The resulting derived model for the total vortex circulation
$\gamma _b=\varGamma _b/2R$. The resulting derived model for the total vortex circulation ![]() $\varGamma _b(x)$ as a function of downstream distance
$\varGamma _b(x)$ as a function of downstream distance ![]() $x$ is given by
$x$ is given by
where ![]() $\varGamma _{b0}=\varGamma _{b}(x=0)$,
$\varGamma _{b0}=\varGamma _{b}(x=0)$, ![]() $I_n$ is the modified Bessel function of the first kind with order
$I_n$ is the modified Bessel function of the first kind with order ![]() $n$,
$n$, ![]() $\eta (x)=k_{\nu }(x-x_0)/24^{1/4}$ is the turbulent diffusive scale, and
$\eta (x)=k_{\nu }(x-x_0)/24^{1/4}$ is the turbulent diffusive scale, and ![]() $x_0$ is the virtual origin assumed to be zero in the current work for simplicity.
$x_0$ is the virtual origin assumed to be zero in the current work for simplicity.
One can use ![]() $\gamma _b=\varGamma _b/2R$,
$\gamma _b=\varGamma _b/2R$, ![]() $t\approx x/U_\textrm {in}(z)$ and
$t\approx x/U_\textrm {in}(z)$ and ![]() $\eta (x)\approx k_{\nu }x/24^{1/4}$ to rewrite (3.3) as
$\eta (x)\approx k_{\nu }x/24^{1/4}$ to rewrite (3.3) as
Numerical integration of ![]() $\varGamma _b$, expressed by (3.6), yields results that can be conveniently approximated by the following (fitted) expression:
$\varGamma _b$, expressed by (3.6), yields results that can be conveniently approximated by the following (fitted) expression:
We then use (2.32) to express ![]() $\varGamma _{b0}$ as a function of operating conditions, approximate
$\varGamma _{b0}$ as a function of operating conditions, approximate ![]() $\xi _0(\theta )$ with
$\xi _0(\theta )$ with ![]() $\tilde {\xi }_0$ given by (2.45), and insert (3.8) into (3.7) to obtain
$\tilde {\xi }_0$ given by (2.45), and insert (3.8) into (3.7) to obtain
Due to vorticity decay, ![]() $\hat {t}$ for turbulent inflow cases increases at a slower rate than the one for laminar inflow cases. For instance, according to (3.9), for a turbine with
$\hat {t}$ for turbulent inflow cases increases at a slower rate than the one for laminar inflow cases. For instance, according to (3.9), for a turbine with ![]() $C_T'=1.33$ subject to an ABL with
$C_T'=1.33$ subject to an ABL with ![]() $k_\nu = 0.05$, the streamwise position associated with
$k_\nu = 0.05$, the streamwise position associated with ![]() $|\hat {t}|=2$ varies between
$|\hat {t}|=2$ varies between ![]() $17R$ and
$17R$ and ![]() $61R$ for
$61R$ for ![]() $\beta =30^{\circ } - 10^{\circ }$. As mentioned in § 2.5, for the same turbine with
$\beta =30^{\circ } - 10^{\circ }$. As mentioned in § 2.5, for the same turbine with ![]() $\beta =30^{\circ } - 10^{\circ }$ subject to a laminar flow,
$\beta =30^{\circ } - 10^{\circ }$ subject to a laminar flow, ![]() $|\hat {t}|=2$ at
$|\hat {t}|=2$ at ![]() $x=12R-29R$. It is also worth noting that the above definition of
$x=12R-29R$. It is also worth noting that the above definition of ![]() $\hat {t}$, (3.9), is reduced to the one used for non-decaying vortex sheets (i.e.
$\hat {t}$, (3.9), is reduced to the one used for non-decaying vortex sheets (i.e. ![]() $\hat {t}=\gamma _{b0}t/\tilde {\xi }_0$) as
$\hat {t}=\gamma _{b0}t/\tilde {\xi }_0$) as ![]() $u_*$ tends to zero.
$u_*$ tends to zero.
The effect of the ground on the wake deflection was not modelled in the uniform inflow cases. To model the effect of the ground, we use an image technique to modify the wake centre location ![]() $y_c$, as shown in figure 7. Modelling the vortex sheet as a CVP, the image CVP induces a lateral velocity in the opposite direction, termed as
$y_c$, as shown in figure 7. Modelling the vortex sheet as a CVP, the image CVP induces a lateral velocity in the opposite direction, termed as ![]() $v_g$ given by
$v_g$ given by
Therefore, the lateral wake deflection caused by the ground is given by
 \begin{equation} y_g(z) = \int_0^{t} v_g(z,t') \,\textrm{d} t' = \frac{\xi_0 \displaystyle\int_0^{t} \varGamma_b(t') \,\textrm{d} t}{{\rm \pi} \left[(z+z_h)^{2}-\xi_0^{2}\right]}. \end{equation}
\begin{equation} y_g(z) = \int_0^{t} v_g(z,t') \,\textrm{d} t' = \frac{\xi_0 \displaystyle\int_0^{t} \varGamma_b(t') \,\textrm{d} t}{{\rm \pi} \left[(z+z_h)^{2}-\xi_0^{2}\right]}. \end{equation}
Approximating ![]() $\varGamma _b \approx 2\xi _0\gamma _b$ and using
$\varGamma _b \approx 2\xi _0\gamma _b$ and using ![]() $\hat {t} = \int _0^{t} \gamma _b(t') / \xi _0 \,\textrm {d} t'$, we find that
$\hat {t} = \int _0^{t} \gamma _b(t') / \xi _0 \,\textrm {d} t'$, we find that
 \begin{equation} \hat{y}_g = \frac{2}{\rm \pi} \frac{\hat{t}}{\left[ ({z+z_h)}/{\xi_0}\right]^{2}-1}, \end{equation}
\begin{equation} \hat{y}_g = \frac{2}{\rm \pi} \frac{\hat{t}}{\left[ ({z+z_h)}/{\xi_0}\right]^{2}-1}, \end{equation}
where ![]() $\hat {y}_g=y_g/\xi _0$. Substituting
$\hat {y}_g=y_g/\xi _0$. Substituting ![]() $\xi _0$ with
$\xi _0$ with ![]() $\tilde {\xi }_0$ in (3.12) for simplicity and subtracting this result from (2.55) yields
$\tilde {\xi }_0$ in (3.12) for simplicity and subtracting this result from (2.55) yields
 \begin{equation} \hat{y}_c = \frac{({\rm \pi}-1)|\hat{t}|^{3}+2\sqrt{3}{\rm \pi}^{2}\hat{t}^{2}+48 ({\rm \pi}-1)^{2}|\hat{t}|}{2{\rm \pi}({\rm \pi}-1)\hat{t}^{2}+4\sqrt{3}{\rm \pi}^{2}|\hat{t}|+96({\rm \pi}-1)^{2}} \textrm{sgn}(\hat{t}) - \frac{2}{\rm \pi}\frac{\hat{t}}{[({z+z_h})/{\tilde{\xi}_0}]^{2}-1}. \end{equation}
\begin{equation} \hat{y}_c = \frac{({\rm \pi}-1)|\hat{t}|^{3}+2\sqrt{3}{\rm \pi}^{2}\hat{t}^{2}+48 ({\rm \pi}-1)^{2}|\hat{t}|}{2{\rm \pi}({\rm \pi}-1)\hat{t}^{2}+4\sqrt{3}{\rm \pi}^{2}|\hat{t}|+96({\rm \pi}-1)^{2}} \textrm{sgn}(\hat{t}) - \frac{2}{\rm \pi}\frac{\hat{t}}{[({z+z_h})/{\tilde{\xi}_0}]^{2}-1}. \end{equation}
It is worth mentioning that for ![]() $z_h\to \infty$, the second term on the right-hand side of (3.13) vanishes, and, thus, the equation is reduced to (2.55).
$z_h\to \infty$, the second term on the right-hand side of (3.13) vanishes, and, thus, the equation is reduced to (2.55).

Figure 7. Schematic of modelling the effect of ground using an image technique.
3.2. Analytical model for mean velocity distribution
The shape of the wake edge predicted earlier can now be used to model the spatial distribution of the velocity deficit in the curled wake at each streamwise position. For non-curled (i.e. non-yawed) wakes, a number of wake profiles have already been proposed in the literature, including top hat (Katić, Højstrup & Jensen Reference Katić, Højstrup and Jensen1986; Frandsen et al. Reference Frandsen, Barthelmie, Pryor, Rathmann, Larsen, Højstrup and Thøgersen2006), Gaussian (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2014; Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016), double Gaussian (Schreiber, Balbaa & Bottasso Reference Schreiber, Balbaa and Bottasso2020) and super-Gaussian (Shapiro et al. Reference Shapiro, Starke, Meneveau and Gayme2019; Blondel & Cathelain Reference Blondel and Cathelain2020). Most of these conserve flux of momentum deficit only in its linearised version valid far downstream; see discussion in Bastankhah & Porté-Agel (Reference Bastankhah and Porté-Agel2014). Here we demonstrate the use of the shape deformation for an analytical model in the context of the Gaussian wake model (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2014; Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016), but it could be implemented in other wake models as well.
The modelled streamwise mean velocity,
is defined based on the incoming velocity field ![]() $U_{{in}}(z)$ and the modelled velocity deficit in the wake,
$U_{{in}}(z)$ and the modelled velocity deficit in the wake, ![]() $\Delta U(\boldsymbol {x})$. In the Gaussian model, the velocity deficit profile is modelled as
$\Delta U(\boldsymbol {x})$. In the Gaussian model, the velocity deficit profile is modelled as
where ![]() $C(x)$ is the normalised maximum velocity deficit at each streamwise location and
$C(x)$ is the normalised maximum velocity deficit at each streamwise location and ![]() $\sigma$ is the characteristic wake width. In (3.15) the wake centre location is
$\sigma$ is the characteristic wake width. In (3.15) the wake centre location is ![]() $y_c=\hat {y}_c\xi _0$, where
$y_c=\hat {y}_c\xi _0$, where ![]() $\hat {y}_c$ is obtained from (3.13) and
$\hat {y}_c$ is obtained from (3.13) and ![]() $\xi _0$ is approximated with
$\xi _0$ is approximated with ![]() $\tilde {\xi }_0$ given in (2.45). In prior versions of the Gaussian wake model, it is assumed that the characteristic wake width depends only on downstream distance. Moreover, it is assumed that it grows linearly downstream at a rate
$\tilde {\xi }_0$ given in (2.45). In prior versions of the Gaussian wake model, it is assumed that the characteristic wake width depends only on downstream distance. Moreover, it is assumed that it grows linearly downstream at a rate ![]() $k$. The linear growth of the wake arises from the similarity solution when eddy viscosity is assumed to scale with a constant velocity, friction velocity
$k$. The linear growth of the wake arises from the similarity solution when eddy viscosity is assumed to scale with a constant velocity, friction velocity ![]() $u^{*}$ and the wake scale
$u^{*}$ and the wake scale ![]() $\sigma$ itself (Shapiro et al. Reference Shapiro, Starke, Meneveau and Gayme2019), i.e.
$\sigma$ itself (Shapiro et al. Reference Shapiro, Starke, Meneveau and Gayme2019), i.e.
where ![]() $k$ is the wake expansion rate and
$k$ is the wake expansion rate and ![]() $\sigma _0$ the initial wake size. We now propose to include wake curling and deformation by making
$\sigma _0$ the initial wake size. We now propose to include wake curling and deformation by making ![]() $\sigma$ dependent also on the angle
$\sigma$ dependent also on the angle ![]() $\theta$ according to
$\theta$ according to
where ![]() $\xi (x,\theta )=\xi _0(\theta )\hat {\xi }(\theta,\hat {t})$, and
$\xi (x,\theta )=\xi _0(\theta )\hat {\xi }(\theta,\hat {t})$, and ![]() $\xi _0(\theta )$ is given by (2.44), and the dimensionless wake shape
$\xi _0(\theta )$ is given by (2.44), and the dimensionless wake shape ![]() $\hat {\xi }(\theta,\hat {t})$ is given by either the analytical relation of (2.29) for
$\hat {\xi }(\theta,\hat {t})$ is given by either the analytical relation of (2.29) for ![]() $|\hat {t}|\leq 2$ or the empirical relation (B1) for given values of polar angle
$|\hat {t}|\leq 2$ or the empirical relation (B1) for given values of polar angle ![]() $\theta$ and dimensionless time
$\theta$ and dimensionless time ![]() $\hat {t}$. The polar angle is determined at each position from
$\hat {t}$. The polar angle is determined at each position from ![]() $\tan \theta =(z-z_h)/(y-y_c)$, and
$\tan \theta =(z-z_h)/(y-y_c)$, and ![]() $\hat {t}$ is given by (3.9). In (3.17) the first term on the right-hand side of the equation expands the wake in all radial directions due to turbulent mixing, while the second term deforms the wake cross-section according to the vortex sheet solution derived earlier. According to (3.17), for an unyawed turbine, the initial characteristic wake width is reduced to
$\hat {t}$ is given by (3.9). In (3.17) the first term on the right-hand side of the equation expands the wake in all radial directions due to turbulent mixing, while the second term deforms the wake cross-section according to the vortex sheet solution derived earlier. According to (3.17), for an unyawed turbine, the initial characteristic wake width is reduced to ![]() $0.4R\sqrt {A_*}$, which is the same as the one suggested by Bastankhah & Porté-Agel (Reference Bastankhah and Porté-Agel2014). For the wake expansion rate, we assume that
$0.4R\sqrt {A_*}$, which is the same as the one suggested by Bastankhah & Porté-Agel (Reference Bastankhah and Porté-Agel2014). For the wake expansion rate, we assume that ![]() $k = \alpha u_*/U_{{in}}(z)$ (Shapiro et al. Reference Shapiro, Starke, Meneveau and Gayme2019), where
$k = \alpha u_*/U_{{in}}(z)$ (Shapiro et al. Reference Shapiro, Starke, Meneveau and Gayme2019), where ![]() $\alpha$ is an empirical constant. Alternatively,
$\alpha$ is an empirical constant. Alternatively, ![]() $k$ can be estimated based on the turbulence intensity
$k$ can be estimated based on the turbulence intensity ![]() $I$ of the incoming boundary layer flow (i.e.
$I$ of the incoming boundary layer flow (i.e. ![]() $k=\alpha ' I$, where
$k=\alpha ' I$, where ![]() $\alpha '$ is an empirical constant) as suggested in prior studies (see Niayifar & Porté-Agel (Reference Niayifar and Porté-Agel2016), Carbajo Fuertes, Markfort & Porté-Agel (Reference Carbajo Fuertes, Markfort and Porté-Agel2018), Zhan, Letizia & Iungo (Reference Zhan, Letizia and Iungo2020), among others). At each height
$\alpha '$ is an empirical constant) as suggested in prior studies (see Niayifar & Porté-Agel (Reference Niayifar and Porté-Agel2016), Carbajo Fuertes, Markfort & Porté-Agel (Reference Carbajo Fuertes, Markfort and Porté-Agel2018), Zhan, Letizia & Iungo (Reference Zhan, Letizia and Iungo2020), among others). At each height ![]() $z$, turbulence intensity
$z$, turbulence intensity ![]() $I(z)$ is defined as
$I(z)$ is defined as ![]() $\sqrt {\overline {u^{'2}}}/U_{in}(z)$, where
$\sqrt {\overline {u^{'2}}}/U_{in}(z)$, where ![]() $u'$ is the turbulent fluctuation of streamwise velocity and the overbar denotes time averaging. Note that by invoking the logarithmic law for the fluctuating velocity variance in high-Reynolds-number turbulent boundary layers (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013; Meneveau & Marusic Reference Meneveau and Marusic2013), one can show that
$u'$ is the turbulent fluctuation of streamwise velocity and the overbar denotes time averaging. Note that by invoking the logarithmic law for the fluctuating velocity variance in high-Reynolds-number turbulent boundary layers (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013; Meneveau & Marusic Reference Meneveau and Marusic2013), one can show that ![]() $u_*/U_{in}$ and
$u_*/U_{in}$ and ![]() $I$ are related to each other by
$I$ are related to each other by ![]() $I=(u_*/U_{in}) [B_1-A_1\ln (z/\delta )]^{1/2}$, where
$I=(u_*/U_{in}) [B_1-A_1\ln (z/\delta )]^{1/2}$, where ![]() $\delta$ is the boundary layer thickness, and
$\delta$ is the boundary layer thickness, and ![]() $A_1$ and
$A_1$ and ![]() $B_1$ are constants.
$B_1$ are constants.
The maximum velocity deficit ![]() $C(x)$ in (3.15) is obtained by enforcing the conservation of streamwise momentum deficit flux
$C(x)$ in (3.15) is obtained by enforcing the conservation of streamwise momentum deficit flux ![]() $\rho \int \Delta U (U_h - \Delta U) \,\textrm {d} A \approx T \cos \beta$. To simplify the integration and avoid dependence on
$\rho \int \Delta U (U_h - \Delta U) \,\textrm {d} A \approx T \cos \beta$. To simplify the integration and avoid dependence on ![]() $\theta$, we approximate
$\theta$, we approximate ![]() $\sigma ^{2}(x,\theta )$ with
$\sigma ^{2}(x,\theta )$ with ![]() $\tilde {\sigma }^{2}(x)$ where the latter is given by
$\tilde {\sigma }^{2}(x)$ where the latter is given by
In this expression, ![]() $\tilde {\xi }_0$ is given by (2.45) and
$\tilde {\xi }_0$ is given by (2.45) and ![]() $k=\alpha u_*/U_h$ is the wake expansion rate at
$k=\alpha u_*/U_h$ is the wake expansion rate at ![]() $z=z_h$. This yields
$z=z_h$. This yields
 \begin{equation} C(x) = 1 - \sqrt{1 - \frac{C_T \cos^{3} \beta}{2 \tilde{\sigma}^{2}(x)/R^{2}}}. \end{equation}
\begin{equation} C(x) = 1 - \sqrt{1 - \frac{C_T \cos^{3} \beta}{2 \tilde{\sigma}^{2}(x)/R^{2}}}. \end{equation}Note that in stating conservation of flux of streamwise momentum deficit, pressure and turbulent and viscous shear stress effects are assumed to be negligible. This may be a questionable assumption in the near wake region as well as far wake of turbines deep inside a wind farm (Bastankhah et al. Reference Bastankhah, Welch, Martínez-Tossas, King and Fleming2021).
For the sake of completeness, a summary of the steps required to implement the proposed model and predict wake velocity deficit distributions at a given downwind location ![]() $\boldsymbol {x}=(x,y,z)$ is provided below.
$\boldsymbol {x}=(x,y,z)$ is provided below.
(1) Compute the approximate form of the initial wake shape
 $\tilde {\xi }_0$ (2.45).
$\tilde {\xi }_0$ (2.45).(2) Determine the dimensionless time
 $\hat {t}$ from (3.9).
$\hat {t}$ from (3.9).(3) Find the wake centre location
 $y_c\approx \hat {y}_c\tilde {\xi }_0$, where
$y_c\approx \hat {y}_c\tilde {\xi }_0$, where  $\hat {y}_c$ is given by (3.13).
$\hat {y}_c$ is given by (3.13).(4) Find the polar angle
 $\theta$, which is measured from the positive
$\theta$, which is measured from the positive  $y$-axis toward the positive
$y$-axis toward the positive  $z$-axis such that
$z$-axis such that  $\tan \theta =(z-z_h)/(y-y_c)$.
$\tan \theta =(z-z_h)/(y-y_c)$.(5) Evaluate the initial wake shape
 $\xi _0(\theta )$ (2.44).
$\xi _0(\theta )$ (2.44).(6) Calculate the wake shape function
 $\xi (\theta,x)=\xi _0(\theta )\hat {\xi }(\theta,\hat {t})$, where
$\xi (\theta,x)=\xi _0(\theta )\hat {\xi }(\theta,\hat {t})$, where  $\hat {\xi }(\theta,\hat {t})$ can be estimated either from the analytical solution (2.29) (if
$\hat {\xi }(\theta,\hat {t})$ can be estimated either from the analytical solution (2.29) (if  $|\hat {t}|<2$) or the empirical one (B1), and
$|\hat {t}|<2$) or the empirical one (B1), and  $\chi$ is given by (2.42).
$\chi$ is given by (2.42).(7) Find the wake width
 $\sigma (x,\theta )$ based on (3.17).
$\sigma (x,\theta )$ based on (3.17).(8) Evaluate the maximum velocity deficit
 $C(x)$ from (3.19), where
$C(x)$ from (3.19), where  $\tilde {\sigma }^{2}(x)$ is given by (3.18).
$\tilde {\sigma }^{2}(x)$ is given by (3.18).(9) Determine the wake velocity deficit
 $\Delta U$ according to (3.15), where
$\Delta U$ according to (3.15), where  $\sigma$ obtained in step (7) is used.
$\sigma$ obtained in step (7) is used.
3.3. Comparison with LES
In the following, the streamwise mean velocity distribution based on the proposed model is compared with the LES data for turbulent ABL inflow cases. Simulations of yawed wind turbines represented as rotating actuator disks (ADM-R) are performed using ![]() $C_T' = 1.33$ and a local tip-speed ratio of
$C_T' = 1.33$ and a local tip-speed ratio of ![]() $\lambda '=10.67$ at yaw angles of
$\lambda '=10.67$ at yaw angles of ![]() $\beta = 15^{\circ }$,
$\beta = 15^{\circ }$, ![]() $20^{\circ }$,
$20^{\circ }$, ![]() $25^{\circ }$ and
$25^{\circ }$ and ![]() $30^{\circ }$, where the local tip-speed ratio is defined as
$30^{\circ }$, where the local tip-speed ratio is defined as ![]() $\lambda '=\varOmega R/U_d$. In unyawed conditions the selection of local thrust coefficient and tip-speed ratio corresponds to
$\lambda '=\varOmega R/U_d$. In unyawed conditions the selection of local thrust coefficient and tip-speed ratio corresponds to ![]() $C_T = 0.75$ and
$C_T = 0.75$ and ![]() $\lambda =8$, which are realistic of modern utility-scale turbines. The actuator disk with diameter
$\lambda =8$, which are realistic of modern utility-scale turbines. The actuator disk with diameter ![]() $D = 100$ m and a hub height of
$D = 100$ m and a hub height of ![]() $z_h = 100$ m is placed 500 m from the inlet of a domain with an effective size of
$z_h = 100$ m is placed 500 m from the inlet of a domain with an effective size of ![]() $L_x = 3.75$,
$L_x = 3.75$, ![]() $L_y = 3$ and
$L_y = 3$ and ![]() $L_z = 1$ km. The domain is divided into
$L_z = 1$ km. The domain is divided into ![]() $N_x = 360$,
$N_x = 360$, ![]() $N_y = 288$ and
$N_y = 288$ and ![]() $N_z = 432$ grid points. The velocity field is averaged for a time
$N_z = 432$ grid points. The velocity field is averaged for a time ![]() $\mathcal {T} u_*/L_z \approx 8$, where
$\mathcal {T} u_*/L_z \approx 8$, where ![]() $u_* = 0.45$ m s
$u_* = 0.45$ m s![]() $^{-1}$. A
$^{-1}$. A ![]() $0.49L_z$ shift is used to reduce streamwise streaks in the time-averaged velocity field. The roughness height is
$0.49L_z$ shift is used to reduce streamwise streaks in the time-averaged velocity field. The roughness height is ![]() $z_0 = 0.1$ m.
$z_0 = 0.1$ m.
Figures 8 show contour maps of streamwise velocity on representative planes across the LES domain. It shows the streaks in the turbulent ABL at the turbine hub height and the generated wake behind the yawed wind turbine, which is shown as a black circle. At downstream locations, the effect of the curled yawed wind turbine wake on the cross-plane velocity field is shown at downstream locations of ![]() $x/R = 8$,
$x/R = 8$, ![]() $24$ and
$24$ and ![]() $40$.
$40$.

Figure 8. Contour plots of instantaneous streamwise velocity including a wind turbine with turbulent boundary layer inflow from LES. Turbine operating parameters are ![]() $C_T' = 1.33$ and yaw angle
$C_T' = 1.33$ and yaw angle ![]() $\beta =25^{\circ }$. Contours are shown through the turbine centre at
$\beta =25^{\circ }$. Contours are shown through the turbine centre at ![]() $z=z_h$, at the back of the domain at
$z=z_h$, at the back of the domain at ![]() $y=L_y$ and
$y=L_y$ and ![]() $x=L_x$ and at cross-planes of
$x=L_x$ and at cross-planes of ![]() $x/R=8$,
$x/R=8$, ![]() $24$ and
$24$ and ![]() $40$. The swept area of the rotor is denoted as a black circle. A zoomed in flow field around the turbine (red box) is also shown and white arrows highlight the sense of rotation of the induced CVP.
$40$. The swept area of the rotor is denoted as a black circle. A zoomed in flow field around the turbine (red box) is also shown and white arrows highlight the sense of rotation of the induced CVP.
Figures 9 and 10 show the wake mean velocity distributions based on the LES results and the analytical model for ![]() $\beta = 15^{\circ }$ and
$\beta = 15^{\circ }$ and ![]() $25^{\circ }$ at various downstream locations. Top panels show the normalised velocity deficit
$25^{\circ }$ at various downstream locations. Top panels show the normalised velocity deficit ![]() $\Delta U/U_h$ and bottom panels show the normalised streamwise velocity distribution.
$\Delta U/U_h$ and bottom panels show the normalised streamwise velocity distribution.

Figure 9. (a) Contour plots of normalised wake velocity deficit behind a wind turbine in turbulent inflow with a thrust coefficient of ![]() $C_T' = 1.33$ and local tip-speed ratio
$C_T' = 1.33$ and local tip-speed ratio ![]() $\lambda '=10.67$ at a yaw angle of
$\lambda '=10.67$ at a yaw angle of ![]() $\beta =15^{\circ }$. White circles indicate the frontal area of wind turbines. (b) Contour plots of normalised streamwise velocity behind the same turbine.
$\beta =15^{\circ }$. White circles indicate the frontal area of wind turbines. (b) Contour plots of normalised streamwise velocity behind the same turbine.

Figure 10. Same as figure 9 but for a yaw angle of ![]() $\beta =25^{\circ }$.
$\beta =25^{\circ }$.
As in past studies (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016; Shapiro et al. Reference Shapiro, Gayme and Meneveau2018), the wake recovery rate ![]() $k$ in the analytical model is calculated by fitting a Gaussian profile to the downstream wake profiles at
$k$ in the analytical model is calculated by fitting a Gaussian profile to the downstream wake profiles at ![]() $z=z_h$. This gives the resulting wake expansion rate as
$z=z_h$. This gives the resulting wake expansion rate as ![]() $k=0.6 u_*/U_{in}$. As seen in figures 9 and 10, the model captures the curling and deflection of the wake as well as some variation in the wake deflection as a function of vertical distance due to ground effects. The LES results display slightly less curling than the model as well as more noticeable wake deflection towards the ground that is opposite to the deflection of the bulk of the wake. Also, the analytical model does not predict small vertical wake deflections observed in the LES data. According to the vortex sheet analysis performed in the current study (see (2.49)), this vertical deflection is due to rotation effects (i.e. non-zero values of rotation rate
$k=0.6 u_*/U_{in}$. As seen in figures 9 and 10, the model captures the curling and deflection of the wake as well as some variation in the wake deflection as a function of vertical distance due to ground effects. The LES results display slightly less curling than the model as well as more noticeable wake deflection towards the ground that is opposite to the deflection of the bulk of the wake. Also, the analytical model does not predict small vertical wake deflections observed in the LES data. According to the vortex sheet analysis performed in the current study (see (2.49)), this vertical deflection is due to rotation effects (i.e. non-zero values of rotation rate ![]() $\chi$). As mentioned in § 2.4, for simplicity, we did not include the vertical wake deflection in the final version of the model. Despite these small differences, figures 9 and 10 show that overall model predictions are in acceptable agreement with the LES data.
$\chi$). As mentioned in § 2.4, for simplicity, we did not include the vertical wake deflection in the final version of the model. Despite these small differences, figures 9 and 10 show that overall model predictions are in acceptable agreement with the LES data.
Wake flow results are also used to compute the power of a downwind turbine based on both the proposed analytical model and the LES data. In both cases, a virtual wind turbine is placed in the flow field at different distances downstream of the yawed turbine. The idea is that as yawing increases, the downstream turbine will overlap less and less with the wake due both to the sideways displacement of the wake and to the curled crescent shaped wake that creates lower velocity deficit at the centre of the hypothetical downstream turbine.
In order to evaluate the power generated by the downwind turbine, we require the disk-averaged streamwise velocity defined according to
where ![]() $U(x_T,y,z)$ is the mean velocity in the flow at the turbine location
$U(x_T,y,z)$ is the mean velocity in the flow at the turbine location ![]() $x_T$ computed from the model or from the LES and the integration covers the turbine disk area. For the latter case, we evaluate the mean velocity by time averaging
$x_T$ computed from the model or from the LES and the integration covers the turbine disk area. For the latter case, we evaluate the mean velocity by time averaging ![]() $U(x_T,y,z)=\langle \tilde {u}_1(x_T,y,z)\rangle$. Since the turbine is not included in the simulation, the turbine disk velocity that would occur there includes the
$U(x_T,y,z)=\langle \tilde {u}_1(x_T,y,z)\rangle$. Since the turbine is not included in the simulation, the turbine disk velocity that would occur there includes the ![]() $(1-a)$ prefactor, where
$(1-a)$ prefactor, where ![]() $a$ is the turbine's assumed induction factor. The power is subsequently calculated as
$a$ is the turbine's assumed induction factor. The power is subsequently calculated as
and it is normalised by the power that an unyawed free-standing turbine would generate under similar conditions, ![]() $P_0 = (1/2) \rho {\rm \pi}R^{2} C_T'(1-a)^{3} U_h^{3}$ (thus making the result independent of assumed
$P_0 = (1/2) \rho {\rm \pi}R^{2} C_T'(1-a)^{3} U_h^{3}$ (thus making the result independent of assumed ![]() $C_T'$, etc.).
$C_T'$, etc.).
Figure 11 shows the normalised power of this hypothetical turbine as a function of streamwise spacing for different yaw angles of the upwind turbine. The figure demonstrates good agreement between the analytical model and the LES results for a broad range of streamwise spacings and yaw angles.

Figure 11. (a) Sketch of a hypothetical turbine placed at various locations downstream of the yawed turbine in the LES field. (b) Normalised power of the hypothetical turbine operating at ![]() $C_T' = 1.33$. Different yaw angles in LES are
$C_T' = 1.33$. Different yaw angles in LES are ![]() $\beta =15^{\circ }$ (
$\beta =15^{\circ }$ (![]() $\circ$, red),
$\circ$, red), ![]() $\beta =20^{\circ }$ (
$\beta =20^{\circ }$ (![]() $\square$, green),
$\square$, green), ![]() $\beta =25^{\circ }$ (
$\beta =25^{\circ }$ (![]() $\triangle$, blue) and
$\triangle$, blue) and ![]() $\beta =30^{\circ }$ (
$\beta =30^{\circ }$ ( , purple). The predictions based on the analytical curled wake model are shown as solid lines.
, purple). The predictions based on the analytical curled wake model are shown as solid lines.
3.4. Comparison with experimental data
Model predictions are also compared with wind-tunnel experiments by Bastankhah & Porté-Agel (Reference Bastankhah and Porté-Agel2016). Flow measurements were performed to quantify the wake of a yawed wind turbine with a diameter of ![]() $15$ cm and hub height of
$15$ cm and hub height of ![]() $12.5$ cm, and the turbine is subject to a turbulent boundary layer, naturally developed over the smooth surface of the wind-tunnel floor. Additional information on turbine properties (
$12.5$ cm, and the turbine is subject to a turbulent boundary layer, naturally developed over the smooth surface of the wind-tunnel floor. Additional information on turbine properties (![]() $C_T$,
$C_T$, ![]() $\lambda$, etc.) and inflow conditions (
$\lambda$, etc.) and inflow conditions (![]() $U_h$,
$U_h$, ![]() $I$, etc.) may be found in Bastankhah & Porté-Agel (Reference Bastankhah and Porté-Agel2016). The wake recovery rate
$I$, etc.) may be found in Bastankhah & Porté-Agel (Reference Bastankhah and Porté-Agel2016). The wake recovery rate ![]() $k$ for the analytical model is estimated based on
$k$ for the analytical model is estimated based on ![]() $k=0.35I$ (Carbajo Fuertes et al. Reference Carbajo Fuertes, Markfort and Porté-Agel2018). Figure 12 shows contours of normalised velocity deficit in
$k=0.35I$ (Carbajo Fuertes et al. Reference Carbajo Fuertes, Markfort and Porté-Agel2018). Figure 12 shows contours of normalised velocity deficit in ![]() $yz$-planes at different downwind locations and different yaw angles based on both experiments and model predictions. Overall the figure shows that the proposed model is able to successfully predict the complex curled shape of the wake and its lateral deflection. The opposite wake deflection close to the ground is also well captured by the model. While the overall trends and qualitative features of the velocity defect distribution of the curled wake are reproduced by the analytical model, some differences between measurements and model can still be discerned. The figure shows that the vertical extent of the lower half of the wake is underestimated by the analytical model, which is mainly due to neglecting the wake of the turbine tower in the analytical model. Tower wake effects are however expected to be less significant for utility-scale wind turbines which tend to have less bulky towers (with respect to the rotor diameter).
$yz$-planes at different downwind locations and different yaw angles based on both experiments and model predictions. Overall the figure shows that the proposed model is able to successfully predict the complex curled shape of the wake and its lateral deflection. The opposite wake deflection close to the ground is also well captured by the model. While the overall trends and qualitative features of the velocity defect distribution of the curled wake are reproduced by the analytical model, some differences between measurements and model can still be discerned. The figure shows that the vertical extent of the lower half of the wake is underestimated by the analytical model, which is mainly due to neglecting the wake of the turbine tower in the analytical model. Tower wake effects are however expected to be less significant for utility-scale wind turbines which tend to have less bulky towers (with respect to the rotor diameter).

Figure 12. Contours of normalised velocity deficit in ![]() $yz$-planes at different downwind locations and different yaw angles based on: wind-tunnel experiments (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016) and the new proposed analytical model. White circles indicate the frontal area of wind turbine.
$yz$-planes at different downwind locations and different yaw angles based on: wind-tunnel experiments (Bastankhah & Porté-Agel Reference Bastankhah and Porté-Agel2016) and the new proposed analytical model. White circles indicate the frontal area of wind turbine.
4. Summary and conclusions
A curled shape is a typical aerodynamic feature of wakes behind yawed turbines. In this study we develop an analytical model to describe the wake shape and its downstream evolution for both uniform ideal inflow and turbulent boundary layer background flow. The predicted wake shape is then used in a wake model to describe analytically the mean velocity deficit distribution behind a yawed wind turbine.
To model the curled shape of the wake, we represent the wake edge as a vortex sheet shedding from the rotor disk circumference due to both yaw offset and rotation. A simple relationship is developed to estimate the initial distribution of vorticity along this vortex sheet as a function of turbine operating conditions such as thrust coefficient, yaw angle and tip-speed ratio. The goal is to obtain the evolution of the locus of this vortex sheet with time. The governing equations for the deformation of the vortex sheet are developed based on the Biot–Savart law and the vorticity transport equation. After non-dimensionalising the equations, they are solved using a power series expansion method. Subsequently, assuming a given downstream convection velocity, we map the time evolution to a spatial one in the streamwise direction. The developed solution is only valid for a limited range of dimensionless times (![]() $|\hat {t}|< 2$) or equivalent distances. For larger values of
$|\hat {t}|< 2$) or equivalent distances. For larger values of ![]() $|\hat {t}|$, an empirical expression is also proposed, which complies with the derived analytical solution for smaller times but is also realistic for larger times.
$|\hat {t}|$, an empirical expression is also proposed, which complies with the derived analytical solution for smaller times but is also realistic for larger times.
Apart from deforming to a curled shape, the vortex sheet is also deflected laterally behind a yawed turbine. This deflection is modelled with an equation combining analytically derived deflections using two approaches: considering an approximately circular vortex sheet (valid for small times) and considering self-induced motion of a CVP (valid for larger times). Moreover, close to the ground the wake is deflected in the opposite direction. This ground effect is modelled using image flow that introduces an additional deflection term to account for the velocity induced by the image CVP.
Wake shape predictions are first compared with numerical simulation data for a yawed turbine placed in a uniform, non-turbulent inflow. Several cases with different values of thrust coefficients, yaw angles and tip-speed ratios are considered. It is shown that the analytical model predictions agree well with LES results at moderate times. Also in agreement with the theory, we show that the numerical simulation results can be collapsed into a common wake shape when the problem variables are normalised using the scaling as suggested by the theoretical model.
The theory is then adapted to the case of turbulent ABL inflow for applications to real wind turbine flows. It is known that, unlike the case of ideal flow, turbulent diffusion plays a central role in weakening the streamwise vortices during their downstream evolution. This phenomenon is modelled by non-dimensionalising the governing equations using a time-varying reference vortex sheet strength. Finally, we modify the Gaussian wake model to incorporate the predicted shape ![]() $\xi (\theta,\hat {t})$ and lateral deflection
$\xi (\theta,\hat {t})$ and lateral deflection ![]() $y_c$ of the curled wake. The analytical curled wake model thus describes the full spatial distribution of mean streamwise velocity downstream of a yawed turbine. To validate the model predictions for the ABL case, wake velocity contours at different downstream positions are compared with LES and wind-tunnel results at various yaw angles. Moreover, the power extracted by a hypothetical wind turbine located at different downwind positions is computed and compared with similar results from the LES-generated mean velocity distributions. A good agreement of the model predictions with the numerical and experimental data is observed, suggesting that the proposed model includes the most relevant fluid mechanical effects governing the mean velocity distribution in wakes downstream of yawed wind turbines. Also, the proposed analytical model should be useful for tasks such as wind farm optimization and control, where numerical simulations tend to be too time consuming and costly. While to our knowledge the developed analytical model is the first of its kind to predict the curled shape of yawed turbine wakes, more research is still needed to shed light on the impact of ABL characteristics such as wind veer on the wake of a yawed turbine. Of special interest is to study the combined effect of yaw offset and wind veer on the wake cross-section in future works. Moreover, the effect of ground and rotation on the wake cross-section needs to be thoroughly studied in future works for turbines with different geometries and operating conditions.
$y_c$ of the curled wake. The analytical curled wake model thus describes the full spatial distribution of mean streamwise velocity downstream of a yawed turbine. To validate the model predictions for the ABL case, wake velocity contours at different downstream positions are compared with LES and wind-tunnel results at various yaw angles. Moreover, the power extracted by a hypothetical wind turbine located at different downwind positions is computed and compared with similar results from the LES-generated mean velocity distributions. A good agreement of the model predictions with the numerical and experimental data is observed, suggesting that the proposed model includes the most relevant fluid mechanical effects governing the mean velocity distribution in wakes downstream of yawed wind turbines. Also, the proposed analytical model should be useful for tasks such as wind farm optimization and control, where numerical simulations tend to be too time consuming and costly. While to our knowledge the developed analytical model is the first of its kind to predict the curled shape of yawed turbine wakes, more research is still needed to shed light on the impact of ABL characteristics such as wind veer on the wake of a yawed turbine. Of special interest is to study the combined effect of yaw offset and wind veer on the wake cross-section in future works. Moreover, the effect of ground and rotation on the wake cross-section needs to be thoroughly studied in future works for turbines with different geometries and operating conditions.
Funding
M.B. acknowledges funding from Innovate UK (grant no. 89640). C.S., D.G. and C.M. acknowledge funding from the National Science Foundation (grant nos. 1949778) and computational resources from MARCC and Cheyenne (doi:10.5065/D6RX99HX). C.S. is an American Association for the Advancement of Science (AAAS) Science & Technology Policy Fellow hosted at the US Department of Energy. All opinions expressed in this article are the authors' and do not necessarily reflect the policies or views of the Department of Energy, Oak Ridge Associated Universities, the Oak Ridge Institute for Science and Education, or AAAS.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Evaluation of p.v. of required integrals
This appendix evaluates the integrals (2.24) and (2.25). Here, we only provide the proof for (2.24), as (2.25) can be solved similarly. First, we define ![]() $I$ as
$I$ as
By defining the complex parameters ![]() $i \colon = \sqrt {-1}$ and
$i \colon = \sqrt {-1}$ and ![]() $a \colon = \textrm {e}^{-\textrm {i}({b}/{2})}$ and the complex variable
$a \colon = \textrm {e}^{-\textrm {i}({b}/{2})}$ and the complex variable ![]() $z \colon = \textrm {e}^{\textrm {i}x}$, and considering that
$z \colon = \textrm {e}^{\textrm {i}x}$, and considering that ![]() $\textrm {d}x=\textrm {d}z/(\textrm {i}z)$,
$\textrm {d}x=\textrm {d}z/(\textrm {i}z)$, ![]() $\sin (n x)={( z^{n} - z^{-n} )}/{(2i)}$ and
$\sin (n x)={( z^{n} - z^{-n} )}/{(2i)}$ and ![]() $\tan [{(x-b)}/{2}]= -\textrm {i} {( a^{2} z-1 )}/{( a^{2} z+1 )}$, the integral
$\tan [{(x-b)}/{2}]= -\textrm {i} {( a^{2} z-1 )}/{( a^{2} z+1 )}$, the integral ![]() $I$ can be written as
$I$ can be written as
where ![]() $C_1$ is the integration path, which is the unit circle,
$C_1$ is the integration path, which is the unit circle, ![]() $|z|=1$, on the complex plane, and
$|z|=1$, on the complex plane, and ![]() $F(z)$ is defined as
$F(z)$ is defined as
 \begin{equation} F(z)\colon = \frac{ (z^{2n} - 1) (a^{2} z+1) }{ a^{2} z^{n+1}\left(z-\dfrac{1}{a^{2}}\right)}. \end{equation}
\begin{equation} F(z)\colon = \frac{ (z^{2n} - 1) (a^{2} z+1) }{ a^{2} z^{n+1}\left(z-\dfrac{1}{a^{2}}\right)}. \end{equation}
In order to evaluate the integral in (A2), we need to calculate the residues of ![]() $F(z)$ at its singularities. Here
$F(z)$ at its singularities. Here ![]() $F(z)$ has two singularities: one at
$F(z)$ has two singularities: one at ![]() $z=0$ (pole of order
$z=0$ (pole of order ![]() $n+1$) and the other at
$n+1$) and the other at ![]() $z=a^{-2}$ (pole of order one). To calculate the residue of
$z=a^{-2}$ (pole of order one). To calculate the residue of ![]() $F(z)$ at
$F(z)$ at ![]() $z=0$, we define a function
$z=0$, we define a function ![]() $\varPhi (z)$ such that (see Ablowitz & Fokas (Reference Ablowitz and Fokas2003), chapter 4)
$\varPhi (z)$ such that (see Ablowitz & Fokas (Reference Ablowitz and Fokas2003), chapter 4)
Therefore, the residue at ![]() $z=0$ is
$z=0$ is
or
 \begin{equation} Res(F(z); 0) = \frac{1}{n!} \left[ \sum_{k=0}^{n} {n \choose k} \frac{\textrm{d}^{n-k}}{\textrm{d}z^{n-k}}(a^{2} z^{2n+1} + z^{2n} -a^{2} z -1) \frac{\textrm{d}^{k}}{\textrm{d}z^{k}} \frac{1}{a^{2} z - 1 } \right]_{z=0}. \end{equation}
\begin{equation} Res(F(z); 0) = \frac{1}{n!} \left[ \sum_{k=0}^{n} {n \choose k} \frac{\textrm{d}^{n-k}}{\textrm{d}z^{n-k}}(a^{2} z^{2n+1} + z^{2n} -a^{2} z -1) \frac{\textrm{d}^{k}}{\textrm{d}z^{k}} \frac{1}{a^{2} z - 1 } \right]_{z=0}. \end{equation}
It can readily be shown that the first derivative term is non-zero only for ![]() $k=n-1$ and
$k=n-1$ and ![]() $k=n$. Also expanding the second derivative, and after some manipulation, we obtain
$k=n$. Also expanding the second derivative, and after some manipulation, we obtain
Now we calculate the residue of ![]() $F(z)$ at
$F(z)$ at ![]() $z=a^{-2}$. To do this, we define a function
$z=a^{-2}$. To do this, we define a function ![]() $\varPhi '(z)$ such that
$\varPhi '(z)$ such that
 \begin{equation} F(z) = \frac{\varPhi'(z)}{\left(z-\dfrac{1}{a^{2}}\right)}. \end{equation}
\begin{equation} F(z) = \frac{\varPhi'(z)}{\left(z-\dfrac{1}{a^{2}}\right)}. \end{equation}
Therefore, the residue at ![]() $z=a^{-2}$ is
$z=a^{-2}$ is
Since the second singularity is located on the integration path, we cannot use the Cauchy residue theorem directly. However, this integral can be regarded as a Cauchy type integral, and we can use the Plemelj formulae to evaluate its Cauchy p.v.. To do this, we assume ![]() $I^{+}$ is the limiting value of the integral
$I^{+}$ is the limiting value of the integral ![]() $I$ when the second singularity of
$I$ when the second singularity of ![]() $F(z)$ (i.e.
$F(z)$ (i.e. ![]() $z=a^{-2}=\textrm {e}^{\textrm {i}b}$) approaches the integration path (
$z=a^{-2}=\textrm {e}^{\textrm {i}b}$) approaches the integration path (![]() $|z|=1$) from inside the unit circle, and
$|z|=1$) from inside the unit circle, and ![]() $I^{-}$ is the limiting value of the integral
$I^{-}$ is the limiting value of the integral ![]() $I$ when the second singularity of
$I$ when the second singularity of ![]() $F(z)$ approaches the integration path from outside the unit circle (see Ablowitz & Fokas (Reference Ablowitz and Fokas2003), chapter 7). Thus,
$F(z)$ approaches the integration path from outside the unit circle (see Ablowitz & Fokas (Reference Ablowitz and Fokas2003), chapter 7). Thus,
and
According to the Plemelj formulae, we have the following for the p.v. of integral ![]() $I$,
$I$,
and (2.24) is proved.
Appendix B. Empirical vortex sheet shape model for large times
The analytical solution for the deformation of the vortex sheet derived earlier is valid only for relatively short times. In fact, ![]() $\xi (\theta,\hat {t})$ can become negative (the vortex sheet crosses itself and becomes non-simple and non-analytic) at dimensionless times with magnitude larger than a critical time denoted by
$\xi (\theta,\hat {t})$ can become negative (the vortex sheet crosses itself and becomes non-simple and non-analytic) at dimensionless times with magnitude larger than a critical time denoted by ![]() $\hat {t}_{c}$. Therefore, the analytical solution should be only used for
$\hat {t}_{c}$. Therefore, the analytical solution should be only used for ![]() $|\hat {t}|<\hat {t}_c$. By setting
$|\hat {t}|<\hat {t}_c$. By setting ![]() $\hat {\xi }=0$ in (2.29), one can find that
$\hat {\xi }=0$ in (2.29), one can find that ![]() $\hat {t}_{c}$ is in the range of 2–2.5. Thus, a limit of
$\hat {t}_{c}$ is in the range of 2–2.5. Thus, a limit of ![]() $|\hat {t}|\leq 2$ is considered in this paper for the analytical solution to be used. Note that the downwind location where
$|\hat {t}|\leq 2$ is considered in this paper for the analytical solution to be used. Note that the downwind location where ![]() $|\hat {t}|=2$ is reached depends on inflow and turbine operating conditions as discussed in §§ 2.5 and 3.
$|\hat {t}|=2$ is reached depends on inflow and turbine operating conditions as discussed in §§ 2.5 and 3.
In the following, we develop an empirical relationship for ![]() $\hat {\xi }(\theta,\hat {t})$. Using the same harmonic terms as those in the analytical solution (2.29), we assume the empirical model is given by
$\hat {\xi }(\theta,\hat {t})$. Using the same harmonic terms as those in the analytical solution (2.29), we assume the empirical model is given by
 \begin{align} \hat{\xi}(\theta,\hat{t})
&= 1 -\alpha[c_1(\hat{t}) \cos 2 \theta +
(c_2(\hat{t}) \chi \sin 2 \theta +c_3(\hat{t}) \cos 3
\theta)\nonumber\\ &\quad +(c_4(\hat{t})\chi^{2} \cos 2
\theta+c_5(\hat{t})\chi\sin 3 \theta +c_6(\hat{t})\cos 2
\theta+c_7(\hat{t}) \cos 4 \theta)],
\end{align}
\begin{align} \hat{\xi}(\theta,\hat{t})
&= 1 -\alpha[c_1(\hat{t}) \cos 2 \theta +
(c_2(\hat{t}) \chi \sin 2 \theta +c_3(\hat{t}) \cos 3
\theta)\nonumber\\ &\quad +(c_4(\hat{t})\chi^{2} \cos 2
\theta+c_5(\hat{t})\chi\sin 3 \theta +c_6(\hat{t})\cos 2
\theta+c_7(\hat{t}) \cos 4 \theta)],
\end{align}
where ![]() $\alpha$ is a constant, and
$\alpha$ is a constant, and ![]() $c_1(\hat {t}),\ldots,c_7(\hat {t})$ are time-dependant coefficients that need to be determined. Equation (B1) must provide predictions similar to the analytical solution (2.29) at small values of
$c_1(\hat {t}),\ldots,c_7(\hat {t})$ are time-dependant coefficients that need to be determined. Equation (B1) must provide predictions similar to the analytical solution (2.29) at small values of ![]() $|\hat {t}|$, but it must provide desirable results for
$|\hat {t}|$, but it must provide desirable results for ![]() $|\hat {t}|$ beyond
$|\hat {t}|$ beyond ![]() $\hat {t}_c$ too. To achieve this goal, we use a hyperbolic tangent function to express
$\hat {t}_c$ too. To achieve this goal, we use a hyperbolic tangent function to express ![]() $c_i(\hat {t})$,
$c_i(\hat {t})$,
where ![]() $i=1,\ldots,7$ and
$i=1,\ldots,7$ and ![]() $a_i$,
$a_i$, ![]() $b_i$ and
$b_i$ and ![]() $n_i$ are constants. As
$n_i$ are constants. As ![]() $\hat {t}\to \infty$, (B1) is reduced to
$\hat {t}\to \infty$, (B1) is reduced to
 \begin{align} \lim_{\hat{t}\to\infty}
\hat{\xi}(\theta,\hat{t}) &= 1 -\alpha[a_1\cos 2
\theta + (a_2\chi \sin 2 \theta +a_3\cos 3
\theta)\nonumber\\ &\quad +(a_4\chi^{2} \cos 2 \theta+a_5\chi\sin 3 \theta
+a_6\cos 2 \theta+a_7\cos 4 \theta)].
\end{align}
\begin{align} \lim_{\hat{t}\to\infty}
\hat{\xi}(\theta,\hat{t}) &= 1 -\alpha[a_1\cos 2
\theta + (a_2\chi \sin 2 \theta +a_3\cos 3
\theta)\nonumber\\ &\quad +(a_4\chi^{2} \cos 2 \theta+a_5\chi\sin 3 \theta
+a_6\cos 2 \theta+a_7\cos 4 \theta)].
\end{align}
In (B3) the overall curled shape of the wake is achieved by a suitable selection of ![]() $a_1,\ldots,a_7$, while the extent of curling is controlled by
$a_1,\ldots,a_7$, while the extent of curling is controlled by ![]() $\alpha$. The constant
$\alpha$. The constant ![]() $\alpha$ is introduced to ensure that the maximum possible curling is obtained as
$\alpha$ is introduced to ensure that the maximum possible curling is obtained as ![]() $\hat {t}\to \infty$. To estimate values of
$\hat {t}\to \infty$. To estimate values of ![]() $a_1,\ldots, a_7$, one can use the analytical solution at an arbitrary dimensionless time which is sufficiently large but still smaller than
$a_1,\ldots, a_7$, one can use the analytical solution at an arbitrary dimensionless time which is sufficiently large but still smaller than ![]() $\hat {t}_c$. By doing so, we construct the curled shape of the wake for
$\hat {t}_c$. By doing so, we construct the curled shape of the wake for ![]() $\hat {t}\to \infty$ from its analytical shape at a finite value of
$\hat {t}\to \infty$ from its analytical shape at a finite value of ![]() $\hat {t}$. The values of
$\hat {t}$. The values of ![]() $a_i$ (
$a_i$ (![]() $i=1,\ldots,7$) are obtained based on the analytical solution (2.29) at
$i=1,\ldots,7$) are obtained based on the analytical solution (2.29) at ![]() $\hat {t}=2$ and are written in table 1, although other values of
$\hat {t}=2$ and are written in table 1, although other values of ![]() $\hat {t}$ could be used.
$\hat {t}$ could be used.
Table 1. Coefficients of the empirical vortex sheet shape model (B1), where ![]() $\alpha =1.263\cos (0.33\chi )$ and
$\alpha =1.263\cos (0.33\chi )$ and ![]() $c_i=a_i\tanh (\hat {t}^{n_i}/b_i)$.
$c_i=a_i\tanh (\hat {t}^{n_i}/b_i)$.

In order to obtain maximum curling as ![]() $\hat {t}\to \infty$,
$\hat {t}\to \infty$, ![]() $\hat {\xi }$ must go to zero at
$\hat {\xi }$ must go to zero at ![]() $\theta =\theta _0$, where
$\theta =\theta _0$, where ![]() $0\leq \theta _0\leq 2{\rm \pi}$, while
$0\leq \theta _0\leq 2{\rm \pi}$, while ![]() $\hat {\xi }$ should be still non-negative for all polar angles. Note that for
$\hat {\xi }$ should be still non-negative for all polar angles. Note that for ![]() $\chi =0$,
$\chi =0$, ![]() $\theta _0$ is a multiple of
$\theta _0$ is a multiple of ![]() ${\rm \pi}$, but it might have a different value if
${\rm \pi}$, but it might have a different value if ![]() $\chi \neq 0$ due to the wake rotation. Based on the values of
$\chi \neq 0$ due to the wake rotation. Based on the values of ![]() $a_i$ written in table 1, one can show that
$a_i$ written in table 1, one can show that ![]() $\hat {\xi }$ given in (B3) is always equal or greater than
$\hat {\xi }$ given in (B3) is always equal or greater than ![]() $1-0.792\alpha \sec ({0.33\chi })$. Therefore,
$1-0.792\alpha \sec ({0.33\chi })$. Therefore, ![]() $\alpha$ must be equal to
$\alpha$ must be equal to ![]() $1.263\cos (0.33\chi )$ to guarantee that (i)
$1.263\cos (0.33\chi )$ to guarantee that (i) ![]() $\hat {\xi }$ never becomes negative, and (ii) maximum possible curling occurs as
$\hat {\xi }$ never becomes negative, and (ii) maximum possible curling occurs as ![]() $\hat {t}\to \infty$.
$\hat {t}\to \infty$.
The asymptotic behaviour of (B1) at ![]() $\hat {t}\to \infty$ was used to find values of
$\hat {t}\to \infty$ was used to find values of ![]() $a_i$ and
$a_i$ and ![]() $\alpha$. Next, we look into the asymptotic behaviour of (B1) at
$\alpha$. Next, we look into the asymptotic behaviour of (B1) at ![]() $\hat {t}\to 0$ to find
$\hat {t}\to 0$ to find ![]() $b_i$ and
$b_i$ and ![]() $n_i$. The function
$n_i$. The function ![]() $a_i\tanh {\hat {t}^{n_i}/b_i}$ asymptotes to
$a_i\tanh {\hat {t}^{n_i}/b_i}$ asymptotes to ![]() $a_i\hat {t}^{n_i}/b_i$ as
$a_i\hat {t}^{n_i}/b_i$ as ![]() $\hat {t}\to 0$. Therefore, we obtain
$\hat {t}\to 0$. Therefore, we obtain
 \begin{align} \lim_{\hat{t}\to 0}\hat{\xi}(\theta,\hat{t}) &= 1 -\alpha\left[\frac{a_1\hat{t}^{n_1}}{b_1}\cos 2 \theta + \left(\frac{a_2\hat{t}^{n_2}}{b_2}\chi \sin 2 \theta +\frac{a_3\hat{t}^{n_3}}{b_3}\cos 3 \theta\right) \right. \nonumber\\ &\quad \left.+\left(\frac{a_4\hat{t}^{n_4}}{b_4}\chi^{2} \cos 2 \theta+\frac{a_5\hat{t}^{n_5}}{b_5}\chi\sin 3 \theta +\frac{a_6\hat{t}^{n_6}}{b_6}\cos 2 \theta+\frac{a_7\hat{t}^{n_7}}{b_7}\cos 4 \theta\right)\right]. \end{align}
\begin{align} \lim_{\hat{t}\to 0}\hat{\xi}(\theta,\hat{t}) &= 1 -\alpha\left[\frac{a_1\hat{t}^{n_1}}{b_1}\cos 2 \theta + \left(\frac{a_2\hat{t}^{n_2}}{b_2}\chi \sin 2 \theta +\frac{a_3\hat{t}^{n_3}}{b_3}\cos 3 \theta\right) \right. \nonumber\\ &\quad \left.+\left(\frac{a_4\hat{t}^{n_4}}{b_4}\chi^{2} \cos 2 \theta+\frac{a_5\hat{t}^{n_5}}{b_5}\chi\sin 3 \theta +\frac{a_6\hat{t}^{n_6}}{b_6}\cos 2 \theta+\frac{a_7\hat{t}^{n_7}}{b_7}\cos 4 \theta\right)\right]. \end{align}
Equation (B4) should match the analytical solution (2.29). Therefore, values of ![]() $n_i$ and
$n_i$ and ![]() $b_i$ can be readily determined, and they are written in table 1. Figure 13 shows predictions of the wake shape based on both the analytical and empirical solutions for different values of dimensionless time
$b_i$ can be readily determined, and they are written in table 1. Figure 13 shows predictions of the wake shape based on both the analytical and empirical solutions for different values of dimensionless time ![]() $\hat {t}$ and rotation rate
$\hat {t}$ and rotation rate ![]() $\chi$. As expected, the empirical relation provides similar results to those of the analytical solution at small values of
$\chi$. As expected, the empirical relation provides similar results to those of the analytical solution at small values of ![]() $\hat {t}$. Moreover, unlike the analytical solution, it provides reasonable predictions for large values of
$\hat {t}$. Moreover, unlike the analytical solution, it provides reasonable predictions for large values of ![]() $\hat {t}$ (i.e.
$\hat {t}$ (i.e. ![]() $|\hat {t}|>2$).
$|\hat {t}|>2$).

Figure 13. The curled shape of the wake for different values of dimensionless time ![]() $\hat {t}$ and rotation rate
$\hat {t}$ and rotation rate ![]() $\chi$. The analytical solution (2.29) is shown by the red colour (solid curves for
$\chi$. The analytical solution (2.29) is shown by the red colour (solid curves for ![]() $\hat {t}\leq 2$ and dotted curves for
$\hat {t}\leq 2$ and dotted curves for ![]() $\hat {t}>2$), and the proposed empirical relation (B1) is shown by black dashed lines.
$\hat {t}>2$), and the proposed empirical relation (B1) is shown by black dashed lines.
Appendix C. Large-eddy simulation code
The numerical code used in this study is the pseudo-spectral LES code LESGO. It solves the filtered Navier–Stokes equations in rotational form
where ![]() $\tilde {u}_i$ is the filtered velocity field,
$\tilde {u}_i$ is the filtered velocity field, ![]() $\tau _{ij}$ is the trace-free part of the subgrid stress tensor,
$\tau _{ij}$ is the trace-free part of the subgrid stress tensor, ![]() $\tilde {p}^{*}$ is the modified pressure,
$\tilde {p}^{*}$ is the modified pressure, ![]() $\partial _x p_\infty$ is the driving streamwise pressure gradient and
$\partial _x p_\infty$ is the driving streamwise pressure gradient and ![]() $f_i$ are the turbine forces. The trace-free part of the subgrid stress tensor is modelled using an eddy viscosity approach
$f_i$ are the turbine forces. The trace-free part of the subgrid stress tensor is modelled using an eddy viscosity approach
where ![]() $\tilde {S}_{ij} = \frac {1}{2}(\partial _j \tilde {u}_i + \partial _i \tilde {u}_j)$ is the filtered strain rate tensor. The LESGO code simulates Cartesian domains using a pseudo-spectral numerical scheme that mixes spectral derivatives in the streamwise direction
$\tilde {S}_{ij} = \frac {1}{2}(\partial _j \tilde {u}_i + \partial _i \tilde {u}_j)$ is the filtered strain rate tensor. The LESGO code simulates Cartesian domains using a pseudo-spectral numerical scheme that mixes spectral derivatives in the streamwise direction ![]() $x$ and spanwise direction
$x$ and spanwise direction ![]() $y$ with second-order finite-differencing in the vertical direction
$y$ with second-order finite-differencing in the vertical direction ![]() $z$. Time integration uses the second-order Adams–Bashforth method.
$z$. Time integration uses the second-order Adams–Bashforth method.
We consider wind turbines under both uniform laminar inflow (Shapiro et al. Reference Shapiro, Gayme and Meneveau2018) and turbulent boundary layer inflows (Shapiro et al. Reference Shapiro, Gayme and Meneveau2020). In the uniform inflow simulations, the Smagorinsky model is used for the eddy viscosity
where ![]() $C_s=0.16$ is the Smagorinsky coefficient. This choice has a negligible effect on the results as the eddy diffusivity is confined to regions of the flow with strong velocity gradients. The inflow conditions are enforced via a fringe region at the end of the domain. This fringe region smoothly transitions to a prescribed inflow velocity
$C_s=0.16$ is the Smagorinsky coefficient. This choice has a negligible effect on the results as the eddy diffusivity is confined to regions of the flow with strong velocity gradients. The inflow conditions are enforced via a fringe region at the end of the domain. This fringe region smoothly transitions to a prescribed inflow velocity ![]() $U_i(0,y,z) = U_{{in}} \delta _{i1}$ (Stevens et al. Reference Stevens, Graham and Meneveau2014). At the top and bottom of the domain, the stress-free boundary conditions for streamwise
$U_i(0,y,z) = U_{{in}} \delta _{i1}$ (Stevens et al. Reference Stevens, Graham and Meneveau2014). At the top and bottom of the domain, the stress-free boundary conditions for streamwise ![]() $u$ and spanwise
$u$ and spanwise ![]() $v$ velocity components are applied and the no-penetration condition is applied for the vertical component
$v$ velocity components are applied and the no-penetration condition is applied for the vertical component ![]() $w$.
$w$.
For the turbulent boundary layer simulations, the Smagorinsky coefficient C s is modelled using the Lagrangian-averaged scale dependent model (Bou-Zeid, Meneveau & Parlange Reference Bou-Zeid, Meneveau and Parlange2005). Turbulent inflow conditions are applied using a fringe region forcing where the inflow condition is sampled from a concurrently running simulation (Stevens et al. Reference Stevens, Graham and Meneveau2014) with shifted periodic boundary conditions (Munters, Meneveau & Meyers Reference Munters, Meneveau and Meyers2016). At the ground, the stress with a roughness height of ![]() $z_0$ is modelled using the equilibrium wall model. The total wall stress is given by
$z_0$ is modelled using the equilibrium wall model. The total wall stress is given by
where ![]() $\Delta z$ is the vertical grid spacing,
$\Delta z$ is the vertical grid spacing, ![]() $\kappa$ is the von-Kármán constant and
$\kappa$ is the von-Kármán constant and ![]() $V$ is the velocity magnitude obtained from
$V$ is the velocity magnitude obtained from ![]() $V^{2} = \tilde {u}(\Delta z/2)^{2} + \tilde {v}(\Delta z/2)^{2}$. The wall stress is then apportioned to each component as
$V^{2} = \tilde {u}(\Delta z/2)^{2} + \tilde {v}(\Delta z/2)^{2}$. The wall stress is then apportioned to each component as
The LESGO code implements the ADM-R using the local formulation for the thrust and angular forces. The thrust force in this formulation is
where ![]() $C_T'$ is the local thrust coefficient and
$C_T'$ is the local thrust coefficient and ![]() $U_d$ is the disk-averaged velocity. The total thrust force is distributed across the swept area of the disk using the filtered indicator function
$U_d$ is the disk-averaged velocity. The total thrust force is distributed across the swept area of the disk using the filtered indicator function ![]() $\mathcal {R}(\boldsymbol {x})$,
$\mathcal {R}(\boldsymbol {x})$,
in the unit normal direction to the disk ![]() $\boldsymbol {n} = \cos \beta \boldsymbol {i} + \sin \beta \boldsymbol {j}$. The filtered indicator function
$\boldsymbol {n} = \cos \beta \boldsymbol {i} + \sin \beta \boldsymbol {j}$. The filtered indicator function
is found by convolving an indicator function ![]() $\mathcal {I}(\boldsymbol {x})$ for the geometric shape of the disk with finite thickness
$\mathcal {I}(\boldsymbol {x})$ for the geometric shape of the disk with finite thickness ![]() $s$ with a Gaussian filtering kernel
$s$ with a Gaussian filtering kernel ![]() $G(\boldsymbol {x})$ with a characteristic width
$G(\boldsymbol {x})$ with a characteristic width ![]() $\sigma _R = 1.5 h / \sqrt {12}$ that is proportional to the mean grid size
$\sigma _R = 1.5 h / \sqrt {12}$ that is proportional to the mean grid size ![]() $h = \sqrt {\Delta x^{2} + \Delta y^{2} + \Delta z^{2}}$.
$h = \sqrt {\Delta x^{2} + \Delta y^{2} + \Delta z^{2}}$.
To define the angular force of the rotation actuator disk in a local formulation, we consider the ADM for unyawed wind turbines. The disk-averaged velocity ![]() $U_d = U_{{in}} (1-a)$, streamwise velocity deficit
$U_d = U_{{in}} (1-a)$, streamwise velocity deficit ![]() $u_x = 2U_\textrm {in} a$ and angular change in velocity
$u_x = 2U_\textrm {in} a$ and angular change in velocity ![]() $u_\theta = 2 a' \varOmega r$ are defined based on the streamwise
$u_\theta = 2 a' \varOmega r$ are defined based on the streamwise ![]() $a$ and tangential
$a$ and tangential ![]() $a'$ induction factors and rotation rate of the disk
$a'$ induction factors and rotation rate of the disk ![]() $\varOmega$. Considering annular rings of the swept area of the rotor, the annular thrust is the product of the annular flow rate and the change in momentum
$\varOmega$. Considering annular rings of the swept area of the rotor, the annular thrust is the product of the annular flow rate and the change in momentum ![]() $\textrm {d}T = U_{{in}} a(1-a) {\rm \pi}r \,\textrm {d}r \,\rho 2 U_{{in}}$. The annular torque is similarly the product of the annular flow rate and the change in angular momentum
$\textrm {d}T = U_{{in}} a(1-a) {\rm \pi}r \,\textrm {d}r \,\rho 2 U_{{in}}$. The annular torque is similarly the product of the annular flow rate and the change in angular momentum ![]() $\textrm {d}Q = U_{{in}} (1-a) {\rm \pi}r \,\textrm {d}r \,\rho 2 a' \varOmega r^{2}$.
$\textrm {d}Q = U_{{in}} (1-a) {\rm \pi}r \,\textrm {d}r \,\rho 2 a' \varOmega r^{2}$.
Since the annular power is equal to the products ![]() $\textrm {d}P = \textrm {d}T\, U_d$ and
$\textrm {d}P = \textrm {d}T\, U_d$ and ![]() $\textrm {d}P = \textrm {d}Q \,\varOmega$, the equality
$\textrm {d}P = \textrm {d}Q \,\varOmega$, the equality
can be solved for the tangential induction factor, so we obtain
The torque can be written in local and standard forms
Defining the tip-speed ratio ![]() $\lambda = \varOmega R/U_{{in}}$ and local tip-speed ratio as
$\lambda = \varOmega R/U_{{in}}$ and local tip-speed ratio as ![]() $\lambda ' = \varOmega R/U_d$ the torque coefficient is
$\lambda ' = \varOmega R/U_d$ the torque coefficient is
For ideal actuator disks, ![]() $C_P' = C_T'$. The tangential force is then found from
$C_P' = C_T'$. The tangential force is then found from ![]() $r \textrm {d} f_\theta = \textrm {d} Q$,
$r \textrm {d} f_\theta = \textrm {d} Q$,
The tangential force applied by the rotating rotor in LESGO is written as
where ![]() $\hat {\boldsymbol {\theta }}$ is the tangential unit vector. In the case of no wake rotation, the tip-speed ratio is infinite and the angular force vanishes.
$\hat {\boldsymbol {\theta }}$ is the tangential unit vector. In the case of no wake rotation, the tip-speed ratio is infinite and the angular force vanishes.