Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T20:51:17.349Z Has data issue: false hasContentIssue false
  • English
  • Français

VARIETIES OF CLASS-THEORETIC POTENTIALISM

Part of: Philosophical aspects of logic and foundations General and miscellaneous specific topics Set theory

Published online by Cambridge University Press:  22 May 2023

NEIL BARTON Open the ORCID record for NEIL BARTON [Opens in a new window]  and
KAMERYN J. WILLIAMS
NEIL BARTON
Affiliation:
IFIKK, UNIVERSITETET I OSLO POSTBOKS 1020, BLINDERN 0315 OSLO, NORWAY E-mail: n.a.barton@ifikk.uio.no URL: https://neilbarton.net/
KAMERYN J. WILLIAMS*
Affiliation:
BARD COLLEGE AT SIMON’S ROCK DIVISION OF SCIENCE, MATHEMATICS, AND COMPUTING 84 ALFORD ROAD GREAT BARRINGTON, MA 01230, USA URL: https://kamerynjw.net
*
E-mail: kwilliams@simons-rock.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We explain and explore class-theoretic potentialism—the view that one can always individuate more classes over a set-theoretic universe. We examine some motivations for class-theoretic potentialism, before proving some results concerning the relevant potentialist systems (in particular exhibiting failures of the 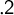$\mathsf {.2}$ and $\mathsf {.3}$ axioms). We then discuss the significance of these results for the different kinds of class-theoretic potentialists.

Keywords

class theorypotentialismtruth predicates

MSC classification

Primary: 00A30: Philosophy of mathematics 03A05: Philosophical and critical 03E70: Nonclassical and second-order set theories
Type
Research Article
Information
The Review of Symbolic Logic , Volume 17 , Issue 1 , March 2024 , pp. 272 - 304
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Arrigoni, T., & Friedman, S.-D. (2013). The hyperuniverse program. Bulletin of Symbolic Logic, 19, 77–96.CrossRefGoogle Scholar
Barton, N. (2021). Indeterminateness and ‘the’ universe of sets: Multiversism, potentialism, and pluralism. In Daghighi, A. S. and Rezus, A., editors. Selected Topics from Contemporary Logics, Landscapes in Logic. Georgia: College Publications, pp. 105–183.Google Scholar
Blackburn, P., de Rijke, M., and Venema, Y. (2002). Modal Logic. Cambridge Tracts in Theoretical Computer Science. Cambridge: Cambridge University Press.Google Scholar
Blass, A. (1984). Existence of bases implies the axiom of choice. In Baumgartner, J. E., Martin, D. A., and Shelah, S., editors. Axiomatic Set Theory (Boulder, CO, 1983), Contemporary Mathematics, vol. 31. Providence: American Mathematical Society, pp. 31–33.CrossRefGoogle Scholar
Cocchiarella, N. B., & Freund, M. A. (2008). Modal Logic: An Introduction to its Syntax and Semantics. Oxford: Oxford University Press.CrossRefGoogle Scholar
Ehrlich, P. (2012). The absolute arithmetic continuum and the unification of all numbers great and small. Bulletin of Symbolic Logic, 18(1), 1–45 CrossRefGoogle Scholar
Feferman, S., & Hellman, G. (1995). Predicative foundations of arithmetic. Journal of Philosophical Logic, 24(1), 1–17.CrossRefGoogle Scholar
Felgner, U. (1971). Comparison of the axioms of local and universal choice. Fundamenta Mathematicae, 71(1), 43–62.CrossRefGoogle Scholar
Fine, K. (2005). Class and membership. Journal of Philosophy, 102(11), 547–572.CrossRefGoogle Scholar
Florio, S., & Linnebo, Ø. (2016). On the innocence and determinacy of plural quantification. Noûs, 50(3), 565–583.CrossRefGoogle Scholar
Fujimoto, K. (2012). Classes and truths in set theory. Annals of Pure & Applied Logic, 163(11), 1484–1523.CrossRefGoogle Scholar
Fujimoto, K. (2019). Predicativism about classes. Journal of Philosophy, 116(4), 206–229.CrossRefGoogle Scholar
Gitman, V. and Hamkins, J. D. (2016). Open determinacy for class games. In Caicedo, A. E., Cummings, J., Koellner, P., and Larson, P., editors. Foundations of Mathematics, Logic at Harvard, Essays in Honor of Hugh Woodin’s 60th Birthday, Contemporary Mathematics, vol. 690. Providence: American Mathematical Society.Google Scholar
Gitman, V. and Hamkins, J. D. (2017). Open determinacy for class games. In Caicedo, A. E., Cummings, J., Koellner, P., and Larson, P. B., editors. Foundations of Mathematics: Logic at Harvard Essays in Honor of W. Hugh Woodin’s 60th Birthday, Contemporary Mathematics, vol. 690. Providence: American Mathematical Society, pp. 121–144.CrossRefGoogle Scholar
Gitman, V., Hamkins, J. D., Holy, P., Schlicht, P., & Williams, K. J. (2020). The exact strength of the class forcing theorem. Journal of Symbolic Logic, 85(3), 869–905.CrossRefGoogle Scholar
Gitman, V., Hamkins, J. D., & Karagila, A. (2019). Kelley–Morse set theory does not prove the class Fodor principle. Fundamenta Mathematicae, 254(2021), 133–154.CrossRefGoogle Scholar
Habič, M. E., Hamkins, J. D., Klausner, L. D., Verner, J., & Williams, K. J. (2019). Set-theoretic blockchains. Archive for Mathematical Logic, 58(7–8), 965–997 CrossRefGoogle Scholar
Hamkins, J., Kirmayer, G., & Perlmutter, N. (2012). Generalizations of the Kunen inconsistency. Annals of Pure and Applied Logic, 163(12), 1972–1890CrossRefGoogle Scholar
Hamkins, J. D. (2003). A simple maximality principle. Journal of Symbolic Logic, 68(2), 527–550 CrossRefGoogle Scholar
Hamkins, J. D. (2012). The set-theoretic multiverse. Review of Symbolic Logic, 5(3), 416–449 CrossRefGoogle Scholar
Hamkins, J. D. (2016). Is the universality of the surreal number line a weak global choice principle? MathOverflow. Available from: https://mathoverflow.net/q/227849 (version: 2017-04-13).Google Scholar
Hamkins, J. D. (2018). The modal logic of arithmetic potentialism and the universal algorithm. Preprint, arXiv:1801.04599, pp. 1–35. Under review.Google Scholar
Hamkins, J. D., Leibman, G., & Löwe, B. (2015). Structural connections between a forcing class and its modal logic. Israel Journal of Mathematics, 207(2), 617–651 CrossRefGoogle Scholar
Hamkins, J. D., Linetsky, D., & Reitz, J. (2013). Pointwise definable models of set theory. Journal of Symbolic Logic, 78(1), 139–156.CrossRefGoogle Scholar
Hamkins, J. D., & Linnebo, O. (2018). The modal logic of set-theoretic potentialism and the potentialist maximality principles. Review of Symbolic Logic, 15, 1–35.CrossRefGoogle Scholar
Hamkins, J. D., & Löwe, B. (2008). The modal logic of forcing. Transactions of the American Mathematical Society, 360(4), 1793–1817 CrossRefGoogle Scholar
Hamkins, J. D. and Williams, K. J. (2021). The ${\varSigma}_1$ -definable universal finite sequence. Journal of Symbolic Logic, 87, 783–801.CrossRefGoogle Scholar
Hamkins, J. D. and Woodin, W. H. (2018). Open class determinacy is preserved by forcing. Preprint, arXiv:1806.11180, pp. 1–14. Under review.Google Scholar
Hellman, G., & Feferman, S. (2000). Challenges to Predicative Foundations of Arithmetic. Cambridge: Cambridge University Press, pp. 317–338.Google Scholar
Holy, P., Krapf, R., Lücke, P., Njegomir, A., & Schlicht, P. (2016). Class forcing, the forcing theorem, and Boolean completions. Journal of Symbolic Logic, 81(4), 1500–1530 CrossRefGoogle Scholar
Holy, P., Krapf, R., & Schlicht, P. (2018). Characterizations of pretameness and the Ord-cc. Annals of Pure and Applied Logic, 169(8), 775–802 CrossRefGoogle Scholar
Hossack, K. (2000). Plurals and complexes. British Journal for the Philosophy of Science, 51(3), 411–443 CrossRefGoogle Scholar
Kunen, K. (1971). Elementary embeddings and infinitary combinatorics. Journal of Symbolic Logic, 36, 407–413.CrossRefGoogle Scholar
Lewis, D. (1991). Parts of Classes. Oxford: Blackwell.Google Scholar
Linnebo, Ø. (2006). Sets, properties, and unrestricted quantification. In Uzquiano, G. and Rayo, A., editors. Absolute Generality. Oxford: Oxford University Press, pp. 149–178.CrossRefGoogle Scholar
Linnebo, Ø. (2013). The potential hierarchy of sets. Review of Symbolic Logic, 6(2), 205–228.CrossRefGoogle Scholar
Maddy, P., & Meadows, T. (2020). A reconstruction of Steel’s multiverse project. Bulletin of Symbolic Logic, 26, 118–169.CrossRefGoogle Scholar
Marek, W., & Mostowski, A. (1975). On Extendability of Models of ZF Set Theory to the Models of Kelley–Morse Theory of Classes. Berlin–Heidelberg: Springer, pp. 460–542.Google Scholar
McAloon, K. (1971). Consistency results about ordinal definability. Annals of Mathematical Logic, 2(4), 449–467 CrossRefGoogle Scholar
Mostowski, A. (1976). A remark on models of the Gödel–Bernays axioms for set theory. In Müller, G. H., editor. Sets and Classes: On the Work by Paul Bernays, Studies in Logic and the Foundations of Mathematics, vol. 84. Amsterdam: North-Holland, pp. 325–340. https://doi.org/10.1016/S0049-237X(09)70288-5 CrossRefGoogle Scholar
Parsons, C. (1974). Sets and classes. Nous, 8(1), 1–12 CrossRefGoogle Scholar
Roberts, S. (MSa). The iterative conception of properties. Unpublished manuscript.Google Scholar
Roberts, S. (MSb). Properties and truth. Unpublished manuscript.Google Scholar
Sato, K. (2014). Relative predicativity and dependent recursion in second-order set theory and higher-order theories. Journal of Symbolic Logic, 79(3), 712–732.Google Scholar
Scambler, C. (2021). Can all things be counted? Journal of Philosophical Logic, 50, 1079–1106.CrossRefGoogle Scholar
Simpson, S. G. (2009). Subsystems of Second Order Arithmetic, Perspectives in Logic. New York: Association for Symbolic Logic.CrossRefGoogle Scholar
Steel, J. (2014). Gödel’s program. In Kennedy, J., editor. Interpreting Gödel. Cambridge: Cambridge University Press.Google Scholar
Suzuki, A. (1999). No elementary embedding from $V$ into $V$ is definable from parameters. Journal of Symbolic Logic, 64(4), 1591–1594.CrossRefGoogle Scholar
Uzquiano, G. (2003). Plural quantification and classes. Philosophia Mathematica, 11(1), 67–81.CrossRefGoogle Scholar
Vickers, J., & Welch, P. (2001). On elementary embeddings from an inner model to the universe. Journal of Symbolic Logic, 66(3), 1090–1116.CrossRefGoogle Scholar
Williams, K. J. (2018). The structure of models of second-order set theory. PhD Thesis, The Graduate Center, CUNY.Google Scholar
Williams, K. J. (2019). Minimum models of second-order set theories. Journal of Symbolic Logic, 8(2), 589–620 CrossRefGoogle Scholar
Zermelo, E. (1930). On boundary numbers and domains of sets. In Ewald, W. B., editor. From Kant to Hilbert: A Source Book in the Foundations of Mathematics, Volume II. Oxford: Oxford University Press, pp. 1208–1233.Google Scholar