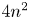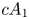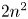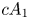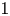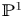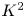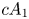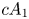1. Introduction
Throughout the paper we work over the field ![]() $\mathbb {C}$ of complex numbers.
$\mathbb {C}$ of complex numbers.
1.1  $2 n^2$-inequality for
$2 n^2$-inequality for  $cA_1$ points
$cA_1$ points
Birational (super)rigidity of a Mori fiber space is roughly an essential uniqueness of the Mori fiber space structure in its birational equivalence class (see Definition 2.3 for the precise definition). Birational non-(super)rigidity of a Mori fiber space implies the existence of a non-biregular birational map to a Mori fiber space, and this further implies the existence of a mobile linear system that is highly singular. In order to prove the birational (super)rigidity of a given Mori fiber space, one has to exclude the possibility of the existence of such a highly singular mobile linear system. The ![]() $4n^2$-inequality, which is stated in the following, is quite useful in this context, and it is one of the most important ingredients in the proofs of birational (super)rigidity of Mori fiber spaces.
$4n^2$-inequality, which is stated in the following, is quite useful in this context, and it is one of the most important ingredients in the proofs of birational (super)rigidity of Mori fiber spaces.
Theorem 1.1 ( $4 n^2$-inequality [Reference PukhlikovPuk13, Theorem 2.1])
$4 n^2$-inequality [Reference PukhlikovPuk13, Theorem 2.1])
Let ![]() $\mathsf {p} \in X$ be the germ of a smooth
$\mathsf {p} \in X$ be the germ of a smooth ![]() $3$-fold. Let
$3$-fold. Let ![]() $\mathcal {M}$ be a mobile linear system on
$\mathcal {M}$ be a mobile linear system on ![]() $X$ and let
$X$ and let ![]() $n$ be a positive rational number. If
$n$ be a positive rational number. If ![]() $\mathsf {p}$ is a center of non-canonical singularities of the pair
$\mathsf {p}$ is a center of non-canonical singularities of the pair ![]() $(X, ({1}/{n}) \mathcal {M})$, then for general members
$(X, ({1}/{n}) \mathcal {M})$, then for general members ![]() $D_1, D_2$ in
$D_1, D_2$ in ![]() $\mathcal {M}$ we have
$\mathcal {M}$ we have
To the best of the authors’ knowledge, there is no known example of a birationally (super)rigid ![]() $3$-dimensional Mori fiber space admitting a singularity other than quotient singularities and ordinary double points. This is mainly because of the lack of a local inequality for singular points that is similar to
$3$-dimensional Mori fiber space admitting a singularity other than quotient singularities and ordinary double points. This is mainly because of the lack of a local inequality for singular points that is similar to ![]() $4 n^2$-inequality.
$4 n^2$-inequality.
In this paper we consider a ![]() $3$-fold terminal singularity
$3$-fold terminal singularity ![]() $\mathsf {p} \in X$ of type
$\mathsf {p} \in X$ of type ![]() $cA_k$ which is, by definition, an isolated hypersurface singularity whose general hyperplane section is the Du Val singularity of type
$cA_k$ which is, by definition, an isolated hypersurface singularity whose general hyperplane section is the Du Val singularity of type ![]() $A_k$. Our first goal is to obtain a similar inequality for singular points of type
$A_k$. Our first goal is to obtain a similar inequality for singular points of type ![]() $cA_1$.
$cA_1$.
Theorem 1.2 ( $2 n^2$-inequality for
$2 n^2$-inequality for  $cA_1$ points)
$cA_1$ points)
Let ![]() $\mathsf {p} \in X$ be the germ of a
$\mathsf {p} \in X$ be the germ of a ![]() $cA_1$ singularity. Let
$cA_1$ singularity. Let ![]() $\mathcal {M}$ be a mobile linear system on
$\mathcal {M}$ be a mobile linear system on ![]() $X$ and let
$X$ and let ![]() $n$ be a positive rational number. If
$n$ be a positive rational number. If ![]() $\mathsf {p}$ is a center of non-canonical singularities of the pair
$\mathsf {p}$ is a center of non-canonical singularities of the pair ![]() $(X, ({1}/{n}) \mathcal {M})$, then for general members
$(X, ({1}/{n}) \mathcal {M})$, then for general members ![]() $D_1, D_2$ in
$D_1, D_2$ in ![]() $\mathcal {M}$ we have
$\mathcal {M}$ we have
As applications, we give first examples of birationally (super)rigid Fano ![]() $3$-folds and del Pezzo fibrations admitting
$3$-folds and del Pezzo fibrations admitting ![]() $cA_1$ points.
$cA_1$ points.
1.2 Applications to birational rigidity
We explain applications of the ![]() $2 n^2$-inequality for
$2 n^2$-inequality for ![]() $cA_1$ points to birational rigidity of some prime Fano
$cA_1$ points to birational rigidity of some prime Fano ![]() $3$-folds and del Pezzo fibrations.
$3$-folds and del Pezzo fibrations.
A Fano ![]() $3$-fold is a normal projective
$3$-fold is a normal projective ![]() $\mathbb {Q}$-factorial variety of dimension
$\mathbb {Q}$-factorial variety of dimension ![]() $3$ with only terminal singularities whose anticanonical divisor is ample. A Fano
$3$ with only terminal singularities whose anticanonical divisor is ample. A Fano ![]() $3$-fold
$3$-fold ![]() $X$ is prime if its class group
$X$ is prime if its class group ![]() $\operatorname {Cl} (X)$ is isomorphic to
$\operatorname {Cl} (X)$ is isomorphic to ![]() $\mathbb {Z}$ and is generated by
$\mathbb {Z}$ and is generated by ![]() $-K_X$.
$-K_X$.
1.2.1 Sextic double solids
A sextic double solid is a normal projective variety which is a double cover of ![]() $\mathbb {P}^3$ branched along a sextic surface. Birational superrigidity of smooth sextic double solids was proved by Iskovskikh [Reference IskovskikhIsk98], and later on, birational superrigidity of
$\mathbb {P}^3$ branched along a sextic surface. Birational superrigidity of smooth sextic double solids was proved by Iskovskikh [Reference IskovskikhIsk98], and later on, birational superrigidity of ![]() $\mathbb {Q}$-factorial sextic double solids with only ordinary double points was proved by Cheltsov and Park [Reference Cheltsov and ParkCP10].
$\mathbb {Q}$-factorial sextic double solids with only ordinary double points was proved by Cheltsov and Park [Reference Cheltsov and ParkCP10].
In [Reference PaemurruPae21], birational geometry of sextic double solids with ![]() $cA_k$ points are investigated, and it is in particular proved that a general sextic double solid with a
$cA_k$ points are investigated, and it is in particular proved that a general sextic double solid with a ![]() $cA_k$ singular point, where
$cA_k$ singular point, where ![]() $k \ge 4$, is not birationally rigid. Moreover, the following expectation (which we pose as a conjecture) is made.
$k \ge 4$, is not birationally rigid. Moreover, the following expectation (which we pose as a conjecture) is made.
Conjecture 1.3 A ![]() $\mathbb {Q}$-factorial sextic double solid with only terminal
$\mathbb {Q}$-factorial sextic double solid with only terminal ![]() $cA_1$ and
$cA_1$ and ![]() $cA_2$ singularities is birationally superrigid, and a
$cA_2$ singularities is birationally superrigid, and a ![]() $\mathbb {Q}$-factorial sextic double solid with only terminal
$\mathbb {Q}$-factorial sextic double solid with only terminal ![]() $cA_1, cA_2$ and
$cA_1, cA_2$ and ![]() $cA_3$ singularities is birationally rigid.
$cA_3$ singularities is birationally rigid.
We generalize the result of Cheltsov and Park [Reference Cheltsov and ParkCP10], and prove the following.
Theorem 1.4 ( $=$ Theorem 4.1)
$=$ Theorem 4.1)
Let ![]() $X$ be a
$X$ be a ![]() $\mathbb {Q}$-factorial sextic double solid with only terminal singularities of type
$\mathbb {Q}$-factorial sextic double solid with only terminal singularities of type ![]() $cA_1$. Then
$cA_1$. Then ![]() $X$ is birationally superrigid.
$X$ is birationally superrigid.
We also consider sextic double solids with a ![]() $cA_3$ point in § 4.4 and construct a Sarkisov self-link under a generality assumption.
$cA_3$ point in § 4.4 and construct a Sarkisov self-link under a generality assumption.
In Theorem 1.4 we are assuming that sextic double solids with ![]() $cA_1$ singularities are
$cA_1$ singularities are ![]() $\mathbb {Q}$-factorial, which is a crucial condition for them to be birationally superrigid. However, it is not a simple problem to determine whether a given singular variety is
$\mathbb {Q}$-factorial, which is a crucial condition for them to be birationally superrigid. However, it is not a simple problem to determine whether a given singular variety is ![]() $\mathbb {Q}$-factorial or not. We provide a criterion for
$\mathbb {Q}$-factorial or not. We provide a criterion for ![]() $\mathbb {Q}$-factoriality of sextic double solids with
$\mathbb {Q}$-factoriality of sextic double solids with ![]() $cA_1$ singularities in § 4.5.
$cA_1$ singularities in § 4.5.
1.2.2 Prime Fano  $3$-fold weighted complete intersections
$3$-fold weighted complete intersections
Quasi-smooth prime Fano ![]() $3$-fold weighted complete intersections are classified under some extra conditions and they consist of
$3$-fold weighted complete intersections are classified under some extra conditions and they consist of ![]() $95$ families of weighted hypersurfaces,
$95$ families of weighted hypersurfaces, ![]() $85$ families of weighted complete intersections of codimension
$85$ families of weighted complete intersections of codimension ![]() $2$, and the family of complete intersections of
$2$, and the family of complete intersections of ![]() $3$ quadrics in
$3$ quadrics in ![]() $\mathbb {P}^6$ (see [Reference Iano-FletcherIan00, 16.6, 16.7] and [Reference Chen, Chen and ChenCCC11, Theorems 1.3, 6.1 and 7.4]). The study of birational (super)rigidity of these objects is almost completed under the assumption of quasi-smoothness.
$\mathbb {P}^6$ (see [Reference Iano-FletcherIan00, 16.6, 16.7] and [Reference Chen, Chen and ChenCCC11, Theorems 1.3, 6.1 and 7.4]). The study of birational (super)rigidity of these objects is almost completed under the assumption of quasi-smoothness.
• It is proved by [Reference Corti, Pukhlikov and ReidCPR00] and [Reference Cheltsov and ParkCP17] that every quasi-smooth prime Fano
 $3$-fold weighted hypersurface is birationally rigid.
$3$-fold weighted hypersurface is birationally rigid.• It is proved by [Reference OkadaOka14] and [Reference Ahmadinezhad and ZucconiAZ16] that a quasi-smooth prime Fano
 $3$-fold weighted complete intersection of codimension
$3$-fold weighted complete intersection of codimension  $2$ other than a complete intersection of a quadric and a cubic in
$2$ other than a complete intersection of a quadric and a cubic in  $\mathbb {P}^5$ is birationally rigid if and only if it belongs to one of the specific
$\mathbb {P}^5$ is birationally rigid if and only if it belongs to one of the specific  $18$ families.
$18$ families.• It is proved by [Reference Iskovskikh and PukhlikovIP96] that a general smooth complete intersection of a quadric and a cubic in
 $\mathbb {P}^5$ is birationally rigid.
$\mathbb {P}^5$ is birationally rigid.
It is known that a quasi-smooth weighted complete intersection has only cyclic quotient singularities [Reference DolgachevDol82, Theorem 3.1.6]. Thus, a quasi-smooth prime Fano ![]() $3$-fold weighted complete intersection has only terminal cyclic quotient singularities. We consider
$3$-fold weighted complete intersection has only terminal cyclic quotient singularities. We consider ![]() $78$ families of prime Fano
$78$ families of prime Fano ![]() $3$-fold weighted hypersurfaces and
$3$-fold weighted hypersurfaces and ![]() $18$ families of prime Fano
$18$ families of prime Fano ![]() $3$-fold weighted complete intersections of codimension
$3$-fold weighted complete intersections of codimension ![]() $2$, and prove birational (super)rigidity of their special members admitting
$2$, and prove birational (super)rigidity of their special members admitting ![]() $cA_1$ points.
$cA_1$ points.
Theorem 1.5 ( $=$ Theorem 5.2)
$=$ Theorem 5.2)
Let ![]() $X$ be a prime Fano
$X$ be a prime Fano ![]() $3$-fold weighted complete intersection which belongs to one of the families listed in Tables 2 and 3. Suppose that
$3$-fold weighted complete intersection which belongs to one of the families listed in Tables 2 and 3. Suppose that ![]() $X$ is quasi-smooth along the singular locus of the ambient weighted projective space, and
$X$ is quasi-smooth along the singular locus of the ambient weighted projective space, and ![]() $X$ has only
$X$ has only ![]() $cA_1$ singularities in addition to terminal quotient singular points. Then
$cA_1$ singularities in addition to terminal quotient singular points. Then ![]() $X$ is birationally rigid.
$X$ is birationally rigid.
1.2.3 Del Pezzo fibrations of degree  $1$
$1$
Let ![]() $\pi \colon X \to \mathbb {P}^1$ be a del Pezzo fibration of degree
$\pi \colon X \to \mathbb {P}^1$ be a del Pezzo fibration of degree ![]() $1$, that is, it is a Mori fiber space and its general fiber is a smooth del Pezzo surface of degree
$1$, that is, it is a Mori fiber space and its general fiber is a smooth del Pezzo surface of degree ![]() $1$. We say that
$1$. We say that ![]() $X/\mathbb {P}^1$ satisfies the
$X/\mathbb {P}^1$ satisfies the ![]() $K^2$-condition if the
$K^2$-condition if the ![]() $1$-cycle
$1$-cycle ![]() $(-K_X)^2$ is not contained in the interior of the cone
$(-K_X)^2$ is not contained in the interior of the cone ![]() $\operatorname {\overline {NE}} (X)$ of effective curves on
$\operatorname {\overline {NE}} (X)$ of effective curves on ![]() $X$, i.e.
$X$, i.e.
We refer the reader to [Reference Brown, Corti and ZucconiBCZ04] for more details on ![]() $K^2$-condition and its related condition.
$K^2$-condition and its related condition.
Pukhlikov [Reference PukhlikovPuk98] proved birational superrigidity of nonsingular del Pezzo fibrations satisfying the ![]() $K^2$-condition. As an application of
$K^2$-condition. As an application of ![]() $2 n^2$-inequality for
$2 n^2$-inequality for ![]() $cA_1$ points, we generalize the Pukhlikov's result and obtain the following.
$cA_1$ points, we generalize the Pukhlikov's result and obtain the following.
Theorem 1.6 Let ![]() $\pi \colon X \to \mathbb {P}^1$ be a del Pezzo fibration of degree
$\pi \colon X \to \mathbb {P}^1$ be a del Pezzo fibration of degree ![]() $1$ with only
$1$ with only ![]() $cA_1$ singularities. If
$cA_1$ singularities. If ![]() $X/\mathbb {P}^1$ satisfies the
$X/\mathbb {P}^1$ satisfies the ![]() $K^2$-condition, then
$K^2$-condition, then ![]() $X$ is birationally superrigid.
$X$ is birationally superrigid.
2. Preliminaries
2.1 Birational (super)rigidity
Definition 2.1 Let ![]() $\pi \colon X \to S$ be a morphism between normal projective varieties. We say that
$\pi \colon X \to S$ be a morphism between normal projective varieties. We say that ![]() $\pi \colon X \to S$ (or simply
$\pi \colon X \to S$ (or simply ![]() $X/S$ if
$X/S$ if ![]() $\pi$ is understood) is a Mori fiber space if:
$\pi$ is understood) is a Mori fiber space if:
•
 $\dim S < \dim X$ and
$\dim S < \dim X$ and  $\pi$ has connected fibers;
$\pi$ has connected fibers;•
 $X$ is
$X$ is  $\mathbb {Q}$-factorial and has only terminal singularities;
$\mathbb {Q}$-factorial and has only terminal singularities;•
 $-K_X$ is
$-K_X$ is  $\pi$-ample and the relative Picard rank is
$\pi$-ample and the relative Picard rank is  $1$.
$1$.
We call ![]() $X/S$ a del Pezzo fibration if
$X/S$ a del Pezzo fibration if ![]() $\dim X - \dim S = 2$.
$\dim X - \dim S = 2$.
Note that Mori fiber spaces over a point are exactly Fano varieties of Picard rank ![]() $1$.
$1$.
Definition 2.2 Let ![]() $\pi _X \colon X \to S$ and
$\pi _X \colon X \to S$ and ![]() $\pi _Y \colon Y \to T$ be Mori fiber spaces. A birational map
$\pi _Y \colon Y \to T$ be Mori fiber spaces. A birational map ![]() $\chi \colon X \dashrightarrow Y$ is called square if it fits into a commutative diagram
$\chi \colon X \dashrightarrow Y$ is called square if it fits into a commutative diagram

where ![]() $\xi$ is birational and in addition the induced map on the generic fibers
$\xi$ is birational and in addition the induced map on the generic fibers ![]() $\chi _{\eta } \colon X_{\eta } \dashrightarrow Y_{\eta }$ is an isomorphism. In this case we say that
$\chi _{\eta } \colon X_{\eta } \dashrightarrow Y_{\eta }$ is an isomorphism. In this case we say that ![]() $X/S$ and
$X/S$ and ![]() $Y/T$ are square birational.
$Y/T$ are square birational.
Definition 2.3 We say that a Mori fiber space ![]() $\pi \colon X \to S$ is birationally rigid if, for any Mori fiber space
$\pi \colon X \to S$ is birationally rigid if, for any Mori fiber space ![]() $Y/T$, the variety
$Y/T$, the variety ![]() $Y$ is birational to
$Y$ is birational to ![]() $X$ if and only if
$X$ if and only if ![]() $X/S$ and
$X/S$ and ![]() $Y/T$ are square birational.
$Y/T$ are square birational.
We say that ![]() $X/S$ is birationally superrigid if, for any Mori fiber space
$X/S$ is birationally superrigid if, for any Mori fiber space ![]() $Y/T$, any birational map
$Y/T$, any birational map ![]() $X \dashrightarrow Y$ (if it exists) is square.
$X \dashrightarrow Y$ (if it exists) is square.
Note that a Fano variety ![]() $X$ of Picard rank
$X$ of Picard rank ![]() $1$ is birationally rigid if the only Mori fiber space it is birational to is itself, for example it is not birational to other Fano varieties. Birationally rigid Fano variety is birationally superrigid if and only if any birational self-map is square and, hence, is an isomorphism.
$1$ is birationally rigid if the only Mori fiber space it is birational to is itself, for example it is not birational to other Fano varieties. Birationally rigid Fano variety is birationally superrigid if and only if any birational self-map is square and, hence, is an isomorphism.
2.2 Maximal singularity
For a normal variety ![]() $V$, a prime divisor
$V$, a prime divisor ![]() $E$ on a normal variety
$E$ on a normal variety ![]() $W$ admitting a projective birational morphism
$W$ admitting a projective birational morphism ![]() $\varphi \colon W \to V$ is called a prime divisor over
$\varphi \colon W \to V$ is called a prime divisor over ![]() $V$. A prime divisor over
$V$. A prime divisor over ![]() $V$ is exceptional if its center on
$V$ is exceptional if its center on ![]() $V$ is a subvariety of codimension greater than
$V$ is a subvariety of codimension greater than ![]() $1$.
$1$.
In the following, let ![]() $\pi \colon X \to S$ be a Mori fiber space. For a mobile linear system
$\pi \colon X \to S$ be a Mori fiber space. For a mobile linear system ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $X$, the rational number
$X$, the rational number ![]() $n \ge 0$ such that
$n \ge 0$ such that ![]() $\mathcal {M} \sim _{\mathbb {Q}} - n K_X + \pi ^*A$ for some
$\mathcal {M} \sim _{\mathbb {Q}} - n K_X + \pi ^*A$ for some ![]() $\mathbb {Q}$-divisor
$\mathbb {Q}$-divisor ![]() $A$ on
$A$ on ![]() $S$ is called the quasi-effective threshold of
$S$ is called the quasi-effective threshold of ![]() $\mathcal {M}$.
$\mathcal {M}$.
Definition 2.4 A prime exceptional divisor ![]() $E$ over
$E$ over ![]() $X$ is a maximal singularity if there exists a mobile linear system
$X$ is a maximal singularity if there exists a mobile linear system ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $X$ such that
$X$ such that
where ![]() $n > 0$ is the quasi-effective threshold of
$n > 0$ is the quasi-effective threshold of ![]() $\mathcal {M}$,
$\mathcal {M}$, ![]() $\varphi \colon Y \to X$ is a projective birational morphism such that
$\varphi \colon Y \to X$ is a projective birational morphism such that ![]() $E \subset Y$ and
$E \subset Y$ and ![]() $a_E (K_X)$ denotes the discrepancy of
$a_E (K_X)$ denotes the discrepancy of ![]() $K_X$ along
$K_X$ along ![]() $E$. The center
$E$. The center ![]() $\Gamma \subset X$ of a maximal singularity is called a maximal center. An extremal divisorial contraction
$\Gamma \subset X$ of a maximal singularity is called a maximal center. An extremal divisorial contraction ![]() $\varphi \colon Y \to X$ is called a maximal extraction if its exceptional divisor is a maximal singularity.
$\varphi \colon Y \to X$ is called a maximal extraction if its exceptional divisor is a maximal singularity.
We have the following characterization of birational superrigidity for Fano ![]() $3$-folds of Picard rank
$3$-folds of Picard rank ![]() $1$.
$1$.
Theorem 2.5 ([Reference Cheltsov and ShramovCS08, Theorem 1.26] and [Reference CortiCor95, (2.10) Proposition-definition])
Let ![]() $X$ be a Fano
$X$ be a Fano ![]() $3$-fold of Picard rank
$3$-fold of Picard rank ![]() $1$. Then the following are equivalent:
$1$. Then the following are equivalent:
(1)
 $X$ is birationally superrigid;
$X$ is birationally superrigid;(2)
 $X$ does not admit a maximal singularity;
$X$ does not admit a maximal singularity;(3)
 $X$ does not admit a maximal extraction.
$X$ does not admit a maximal extraction.
Let ![]() $X$ be a Fano variety of Picard rank
$X$ be a Fano variety of Picard rank ![]() $1$, then we say that an a non-biregular birational map
$1$, then we say that an a non-biregular birational map ![]() $\sigma \colon X \dashrightarrow X'$ to a Fano variety of Picard number
$\sigma \colon X \dashrightarrow X'$ to a Fano variety of Picard number ![]() $1$ is an elementary link of type II if it sits in the commutative diagram
$1$ is an elementary link of type II if it sits in the commutative diagram

where ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi '$ are extremal divisorial contractions and
$\varphi '$ are extremal divisorial contractions and ![]() $\tau$ is a birational map which is an isomorphism in codimension
$\tau$ is a birational map which is an isomorphism in codimension ![]() $1$. An elementary link of type II which is a birational self-map is called an elementary self-link of type II.
$1$. An elementary link of type II which is a birational self-map is called an elementary self-link of type II.
Lemma 2.6 [Reference OkadaOka18, Lemmas 2.34 and 2.22]
Let ![]() $X$ be a Fano
$X$ be a Fano ![]() $3$-fold of Picard number
$3$-fold of Picard number ![]() $1$. If for any maximal extraction
$1$. If for any maximal extraction ![]() $\varphi \colon Y \to X$ there exists a Sarkisov self-link of type II initiated by
$\varphi \colon Y \to X$ there exists a Sarkisov self-link of type II initiated by ![]() $\varphi$, then
$\varphi$, then ![]() $X$ is birationally rigid.
$X$ is birationally rigid.
2.3 Exclusion methods
We explain several methods which are used to exclude maximal centers.
2.3.1 Methods for curves
Lemma 2.7 ([Reference Corti, Pukhlikov and ReidCPR00, Proof of Theorem 5.1.1] and [Reference OkadaOka18, Lemma 2.9])
Let ![]() $X$ be a Fano
$X$ be a Fano ![]() $3$-fold of Picard rank
$3$-fold of Picard rank ![]() $1$ and let
$1$ and let ![]() $\Gamma \subset X$ be an irreducible and reduced curve. If
$\Gamma \subset X$ be an irreducible and reduced curve. If ![]() $(-K_X \cdot \Gamma ) \ge (-K_X)^3$, then
$(-K_X \cdot \Gamma ) \ge (-K_X)^3$, then ![]() $\Gamma$ is not a maximal center.
$\Gamma$ is not a maximal center.
The following is a simplified version of [Reference OkadaOka18, Lemma 2.11], which is enough for the purpose of this paper.
Lemma 2.8 (cf. [Reference OkadaOka18, Lemma 2.11])
Let ![]() $X$ be a Fano
$X$ be a Fano ![]() $3$-fold of Picard rank
$3$-fold of Picard rank ![]() $1$, and let
$1$, and let ![]() $\Gamma \subset X$ be an irreducible and reduced curve. Assume that there is a pencil
$\Gamma \subset X$ be an irreducible and reduced curve. Assume that there is a pencil ![]() $\mathcal {P}$ of divisors on
$\mathcal {P}$ of divisors on ![]() $X$ satisfying the following properties:
$X$ satisfying the following properties:
(1)
 $\mathcal {P} \sim _{\mathbb {Q}} - m K_X$ for some rational number
$\mathcal {P} \sim _{\mathbb {Q}} - m K_X$ for some rational number  $m \ge 1$;
$m \ge 1$;(2) a general member of
 $\mathcal {P}$ is a normal surface;
$\mathcal {P}$ is a normal surface;(3) for distinct general members
 $S, T \in \mathcal {P}$, we have
$S, T \in \mathcal {P}$, we have  $T|_S = \Gamma + \Delta$, where
$T|_S = \Gamma + \Delta$, where  $\Delta$ is an irreducible and reduced curve such that
$\Delta$ is an irreducible and reduced curve such that  $\Delta \ne \Gamma$, and we have
$\Delta \ne \Gamma$, and we have  $(\Gamma \cdot \Delta )_S \ge (-K_X \cdot \Delta )$.
$(\Gamma \cdot \Delta )_S \ge (-K_X \cdot \Delta )$.
Then ![]() $\Gamma$ is not a maximal center.
$\Gamma$ is not a maximal center.
When we apply Lemma 2.8, we need to compute ![]() $(\Gamma \cdot \Delta )_S$, which will follow from the computation of
$(\Gamma \cdot \Delta )_S$, which will follow from the computation of ![]() $(\Gamma ^2)_S$. In this paper we need to consider the case where
$(\Gamma ^2)_S$. In this paper we need to consider the case where ![]() $\Gamma \cong \mathbb {P}^1$ and
$\Gamma \cong \mathbb {P}^1$ and ![]() $S$ has Du Val singular points of type
$S$ has Du Val singular points of type ![]() $A$ along
$A$ along ![]() $\Gamma$, and the computation of
$\Gamma$, and the computation of ![]() $(\Gamma ^2)_S$ will be done by the following method.
$(\Gamma ^2)_S$ will be done by the following method.
Definition 2.9 Let ![]() $\mathsf {p} \in S$ be the germ of a normal surface and
$\mathsf {p} \in S$ be the germ of a normal surface and ![]() $\Gamma$ an irreducible and reduced curve on
$\Gamma$ an irreducible and reduced curve on ![]() $S$. Let
$S$. Let ![]() $\hat {S} \to S$ be the minimal resolution of
$\hat {S} \to S$ be the minimal resolution of ![]() $\mathsf {p} \in S$ and denote by
$\mathsf {p} \in S$ and denote by ![]() $E_1,\ldots,E_m$ the prime exceptional divisors. We define
$E_1,\ldots,E_m$ the prime exceptional divisors. We define ![]() $G (S,\mathsf {p},\Gamma )$ to be the dual graph of
$G (S,\mathsf {p},\Gamma )$ to be the dual graph of ![]() $E_1,\ldots,E_m$ together with the proper transform
$E_1,\ldots,E_m$ together with the proper transform ![]() $\hat {\Gamma }$ of
$\hat {\Gamma }$ of ![]() $\Gamma$ on
$\Gamma$ on ![]() $\hat {S}$: vertices of
$\hat {S}$: vertices of ![]() $G(S,\mathsf {p},\Gamma )$ corresponds to
$G(S,\mathsf {p},\Gamma )$ corresponds to ![]() $E_1,\ldots,E_m$ and
$E_1,\ldots,E_m$ and ![]() $\hat {\Gamma }$, and two vertices corresponding to
$\hat {\Gamma }$, and two vertices corresponding to ![]() $E_i$ and
$E_i$ and ![]() $E_j$ (respectively,
$E_j$ (respectively, ![]() $E_i$ and
$E_i$ and ![]() $\hat {\Gamma }$) are joined by
$\hat {\Gamma }$) are joined by ![]() $(E_i \cdot E_j)$-ple edge (respectively,
$(E_i \cdot E_j)$-ple edge (respectively, ![]() $(E_i \cdot \hat {\Gamma })$-ple edge). We call
$(E_i \cdot \hat {\Gamma })$-ple edge). We call ![]() $G (S,\mathsf {p},\Gamma )$ the extended dual graph of
$G (S,\mathsf {p},\Gamma )$ the extended dual graph of ![]() $(S,\mathsf {p},\Gamma )$.
$(S,\mathsf {p},\Gamma )$.
Definition 2.10 We say that ![]() $G (S,\mathsf {p},\Gamma )$ is of type
$G (S,\mathsf {p},\Gamma )$ is of type ![]() $A_{n,k}$ if it is of the following form.
$A_{n,k}$ if it is of the following form.

Here, ![]() $\circ$ means that the corresponding exceptional divisor is a
$\circ$ means that the corresponding exceptional divisor is a ![]() $(-2)$-curve. In other words,
$(-2)$-curve. In other words, ![]() $G (S,\mathsf {p},\Gamma )$ is of type
$G (S,\mathsf {p},\Gamma )$ is of type ![]() $A_{n,k}$ if
$A_{n,k}$ if ![]() $(S,\mathsf {p})$ is of type
$(S,\mathsf {p})$ is of type ![]() $A_n$,
$A_n$, ![]() $(\hat {\Gamma } \cdot E_i) = 0$ for
$(\hat {\Gamma } \cdot E_i) = 0$ for ![]() $i \ne k$ and
$i \ne k$ and ![]() $(\hat {\Gamma } \cdot E_k) = 1$.
$(\hat {\Gamma } \cdot E_k) = 1$.
Lemma 2.11 Let ![]() $S$ be a normal projective surface, and let
$S$ be a normal projective surface, and let ![]() $\Gamma$ be a smooth rational curve on
$\Gamma$ be a smooth rational curve on ![]() $S$. Let
$S$. Let ![]() $\mathsf {p}_1, \ldots, \mathsf {p}_m$ be points on
$\mathsf {p}_1, \ldots, \mathsf {p}_m$ be points on ![]() $\Gamma$. Suppose that
$\Gamma$. Suppose that ![]() $S$ is smooth along
$S$ is smooth along ![]() $\Gamma \setminus \{\mathsf {p}_1, \ldots, \mathsf {p}_m\}$ and that each extended dual graph
$\Gamma \setminus \{\mathsf {p}_1, \ldots, \mathsf {p}_m\}$ and that each extended dual graph ![]() $G (S, \mathsf {p}_i, \Gamma )$ is of type
$G (S, \mathsf {p}_i, \Gamma )$ is of type ![]() $A_{n_i, k_i}$ for some positive integers
$A_{n_i, k_i}$ for some positive integers ![]() $n_i, k_i$. Then,
$n_i, k_i$. Then,
 \[ (\Gamma^2) = - 2 - (K_S \cdot \Gamma) + \sum_{i=1}^m \frac{k_i (n_i - k_i + 1)}{n_i + 1}. \]
\[ (\Gamma^2) = - 2 - (K_S \cdot \Gamma) + \sum_{i=1}^m \frac{k_i (n_i - k_i + 1)}{n_i + 1}. \]
Proof. This follows from [Reference OkadaOka20b, Lemma 10.7].
3. Local inequalities for  $cA$ points
$cA$ points
Let ![]() $V$ be an
$V$ be an ![]() $n$-dimensional variety. For
$n$-dimensional variety. For ![]() $i = 0, \ldots, n$, we denote by
$i = 0, \ldots, n$, we denote by ![]() $Z_i (V)$ the group of
$Z_i (V)$ the group of ![]() $i$-cycles on
$i$-cycles on ![]() $V$, and by
$V$, and by ![]() $A_i (V) = Z_i (V)/\sim _{\operatorname {rat}}$ the Chow group of
$A_i (V) = Z_i (V)/\sim _{\operatorname {rat}}$ the Chow group of ![]() $i$-cycles on
$i$-cycles on ![]() $V$, where
$V$, where ![]() $\sim _{\operatorname {rat}}$ is the rational equivalence. For Cartier divisors
$\sim _{\operatorname {rat}}$ is the rational equivalence. For Cartier divisors ![]() $D_1, \ldots, D_k$ on
$D_1, \ldots, D_k$ on ![]() $V$ that intersect properly, that is, the irreducible components of
$V$ that intersect properly, that is, the irreducible components of ![]() $\operatorname {Supp} (D_1) \cap \cdots \cap \operatorname {Supp} (D_k)$ all have codimension equal to
$\operatorname {Supp} (D_1) \cap \cdots \cap \operatorname {Supp} (D_k)$ all have codimension equal to ![]() $k$ in
$k$ in ![]() $V$, there is a uniquely defined intersection cycle
$V$, there is a uniquely defined intersection cycle
See [Reference FultonFul98, Definition 2.4.2].
3.1 Blow-ups and degrees of cycles
Let ![]() $X$ be a normal
$X$ be a normal ![]() $3$-fold, and let
$3$-fold, and let ![]() $B \subset X$ be an irreducible subvariety of codimension at least
$B \subset X$ be an irreducible subvariety of codimension at least ![]() $2$. Let
$2$. Let ![]() $\varphi \colon \tilde {X} \to X$ be the blow-up of
$\varphi \colon \tilde {X} \to X$ be the blow-up of ![]() $X$ along
$X$ along ![]() $B$. For a cycle
$B$. For a cycle ![]() $\Gamma \in Z_i(X)$ on
$\Gamma \in Z_i(X)$ on ![]() $X$ such that
$X$ such that ![]() $\operatorname {Supp} \Gamma \not \subset B$, we denote by
$\operatorname {Supp} \Gamma \not \subset B$, we denote by ![]() $\varphi _*^{-1} \Gamma$ the proper transform of
$\varphi _*^{-1} \Gamma$ the proper transform of ![]() $\Gamma$ on
$\Gamma$ on ![]() $\tilde {X}$.
$\tilde {X}$.
Definition 3.1 Under the above setting, suppose that ![]() $B$ is not contained in the singular locus of
$B$ is not contained in the singular locus of ![]() $X$, and let
$X$, and let ![]() $E \subset \tilde {X}$ be the unique exceptional divisor dominating
$E \subset \tilde {X}$ be the unique exceptional divisor dominating ![]() $B$. Let
$B$. Let ![]() $Z = \sum _i m_i Z_i$ be a
$Z = \sum _i m_i Z_i$ be a ![]() $1$-cycle supported on the exceptional set
$1$-cycle supported on the exceptional set ![]() $\varphi ^{-1} (B)$, where
$\varphi ^{-1} (B)$, where ![]() $Z_i \subset \sigma ^{-1} (B)$ is an irreducible curve. We define the degree of
$Z_i \subset \sigma ^{-1} (B)$ is an irreducible curve. We define the degree of ![]() $Z$ with respect to
$Z$ with respect to ![]() $E$ by
$E$ by
where ![]() $\varphi ^{-1} (b) \cong \mathbb {P}^{2 - \dim B}$ is the fiber over a general point
$\varphi ^{-1} (b) \cong \mathbb {P}^{2 - \dim B}$ is the fiber over a general point ![]() $b \in B$.
$b \in B$.
Lemma 3.2 [Reference PukhlikovPuk13, Lemma 2.2]
Let ![]() $X$ be a normal
$X$ be a normal ![]() $3$-fold,
$3$-fold, ![]() $B \subset X$ be an irreducible subvariety of codimension at least
$B \subset X$ be an irreducible subvariety of codimension at least ![]() $2$ such that
$2$ such that ![]() $B \not \subset \operatorname {Sing} X$, and let
$B \not \subset \operatorname {Sing} X$, and let ![]() $D_1, D_2$ be Cartier divisors on
$D_1, D_2$ be Cartier divisors on ![]() $X$ which share no common component.
$X$ which share no common component.
(1) Assume that
 $B$ is a point. Then, for the
$B$ is a point. Then, for the  $1$-cycle
which is supported on
$1$-cycle
which is supported on \[ Z := \varphi_*^{-1} D_1 \cdot \varphi_*^{-1} D_2 - \varphi_*^{-1} (D_1 \cdot D_2), \]
\[ Z := \varphi_*^{-1} D_1 \cdot \varphi_*^{-1} D_2 - \varphi_*^{-1} (D_1 \cdot D_2), \]
 $\varphi ^{-1} (B)$, we have
$\varphi ^{-1} (B)$, we have
 \[ \deg_E Z = \operatorname{mult}_B (D_1 \cdot D_2) - \operatorname{mult}_B D_1 \operatorname{mult}_B D_2. \]
\[ \deg_E Z = \operatorname{mult}_B (D_1 \cdot D_2) - \operatorname{mult}_B D_1 \operatorname{mult}_B D_2. \]
(2) Assume that
 $B$ is a curve. Then, for the decomposition
where
$B$ is a curve. Then, for the decomposition
where \[ \varphi_*^{-1} D_1 \cdot \varphi_*^{-1} D_2 = Z + \Gamma, \]
\[ \varphi_*^{-1} D_1 \cdot \varphi_*^{-1} D_2 = Z + \Gamma, \]
 $\operatorname {Supp} Z \subset \varphi ^{-1} (B)$ and
$\operatorname {Supp} Z \subset \varphi ^{-1} (B)$ and  $\operatorname {Supp} \varphi _* \Gamma$ does not contain
$\operatorname {Supp} \varphi _* \Gamma$ does not contain  $B$, we have
$B$, we have
 \[ D_1 \cdot D_2 = (\operatorname{mult}_B D_1 \operatorname{mult}_B D_2 + \deg_E Z) B + \varphi_* \Gamma. \]
\[ D_1 \cdot D_2 = (\operatorname{mult}_B D_1 \operatorname{mult}_B D_2 + \deg_E Z) B + \varphi_* \Gamma. \]
3.2 Blow-up of a  $cA_1$ point
$cA_1$ point
By [Reference ReidRei83], a ![]() $3$-dimensional singularity is a terminal singularity if and only if it is the quotient of an isolated
$3$-dimensional singularity is a terminal singularity if and only if it is the quotient of an isolated ![]() $cDV$ singularity by a suitable action of a cyclic group (of order
$cDV$ singularity by a suitable action of a cyclic group (of order ![]() $\ge 1$). Note that a
$\ge 1$). Note that a ![]() $cDV$ singularity is a hypersurface singularity whose general hyperplane section is a Du Val singularity. Note also that a
$cDV$ singularity is a hypersurface singularity whose general hyperplane section is a Du Val singularity. Note also that a ![]() $cDV$ singular point is Gorenstein since it is a hypersurface singularity and, hence,
$cDV$ singular point is Gorenstein since it is a hypersurface singularity and, hence, ![]() $3$-dimensional terminal Gorenstein singularities are exactly isolated
$3$-dimensional terminal Gorenstein singularities are exactly isolated ![]() $cDV$ singularities (see also [Reference ReidRei83, Theorem 1.1]). We consider
$cDV$ singularities (see also [Reference ReidRei83, Theorem 1.1]). We consider ![]() $cA_k$ singularities which are particular types of
$cA_k$ singularities which are particular types of ![]() $cDV$ points.
$cDV$ points.
Definition 3.3 Let ![]() $\mathsf {p} \in X$ be the germ of a
$\mathsf {p} \in X$ be the germ of a ![]() $3$-fold singularity. We say that
$3$-fold singularity. We say that ![]() $\mathsf {p} \in X$ is a singularity of type
$\mathsf {p} \in X$ is a singularity of type ![]() $cA_k$ (or simply a
$cA_k$ (or simply a ![]() $cA_k$ point), if the germ is analytically equivalent to the germ of a hypersurface singularity whose general hyperplane section is the Du Val singular point of type
$cA_k$ point), if the germ is analytically equivalent to the germ of a hypersurface singularity whose general hyperplane section is the Du Val singular point of type ![]() $A_k$.
$A_k$.
An example of an isolated ![]() $cA_k$ is a point
$cA_k$ is a point ![]() $o \in (f = 0) \subset \mathbb {A}^4$, where
$o \in (f = 0) \subset \mathbb {A}^4$, where
for some ![]() $M \ge k+1$. It is well known that any isolated
$M \ge k+1$. It is well known that any isolated ![]() $cA_1$-point is analytically equivalent to the above example with
$cA_1$-point is analytically equivalent to the above example with ![]() $k = 1$.
$k = 1$.
Lemma 3.4 Let ![]() $\mathsf {p} \in X$ be an isolated
$\mathsf {p} \in X$ be an isolated ![]() $cA_1$-point, then it is analytically equivalent to
$cA_1$-point, then it is analytically equivalent to
where
for some ![]() $M \ge 2$.
$M \ge 2$.
Proof. By definition, ![]() $\mathsf {p} \in X$ is a hypersurface singularity, therefore without loss of generality we assume that
$\mathsf {p} \in X$ is a hypersurface singularity, therefore without loss of generality we assume that ![]() $X$ is given by
$X$ is given by ![]() $g=0$ in
$g=0$ in ![]() $\mathbb {A}^4$ and
$\mathbb {A}^4$ and ![]() $\mathsf {p} = (0,0,0,0)$. Since general hyperplane section of
$\mathsf {p} = (0,0,0,0)$. Since general hyperplane section of ![]() $X$ has the
$X$ has the ![]() $A_1$-singularity the general form of
$A_1$-singularity the general form of ![]() $g$ is
$g$ is
By the splitting lemma [Reference Greuel, Lossen and ShustinGLS07, Theorem I.2.47] we may change ![]() $g$ into
$g$ into
In the following we identify ![]() $\mathsf {p} \in X$ with the above hypersurface germ, that is, we assume that
$\mathsf {p} \in X$ with the above hypersurface germ, that is, we assume that ![]() $\mathsf {p} \in X$ is the hypersurface germ defined by the vanishing of
$\mathsf {p} \in X$ is the hypersurface germ defined by the vanishing of ![]() $f$ from Lemma 3.4. We set
$f$ from Lemma 3.4. We set ![]() $W = \mathbb {A}^4$. Let
$W = \mathbb {A}^4$. Let ![]() $\varphi _W \colon \tilde {W} \to W$ be the blow-up of
$\varphi _W \colon \tilde {W} \to W$ be the blow-up of ![]() $W$ at the origin
$W$ at the origin ![]() $\mathsf {p}$,
$\mathsf {p}$, ![]() $\tilde {X}$ the proper transform of
$\tilde {X}$ the proper transform of ![]() $X$ in
$X$ in ![]() $\tilde {W}$, and
$\tilde {W}$, and ![]() $\varphi = \varphi _W|_{\tilde {X}} \colon \tilde {X} \to X$ the restriction. We denote by
$\varphi = \varphi _W|_{\tilde {X}} \colon \tilde {X} \to X$ the restriction. We denote by ![]() $E_W \cong \mathbb {P}^3$ the exceptional divisor of
$E_W \cong \mathbb {P}^3$ the exceptional divisor of ![]() $\varphi _W$ and we set
$\varphi _W$ and we set ![]() $E = E_W|_{\tilde {X}}$. The equation of
$E = E_W|_{\tilde {X}}$. The equation of ![]() $E$ in
$E$ in ![]() $E_W$ is given by
$E_W$ is given by
where ![]() $x,y,z,w$ are the coordinates inherited from
$x,y,z,w$ are the coordinates inherited from ![]() $W$. Thus, we can see that
$W$. Thus, we can see that ![]() $E$ is a quadratic cone.
$E$ is a quadratic cone.
For a cycle ![]() $\Gamma$ on
$\Gamma$ on ![]() $X$, we denote by
$X$, we denote by ![]() $\operatorname {mult}_{\mathsf {p}} \Gamma$ the multiplicity of
$\operatorname {mult}_{\mathsf {p}} \Gamma$ the multiplicity of ![]() $\Gamma$, viewed as a cycle on
$\Gamma$, viewed as a cycle on ![]() $W$, at the smooth point
$W$, at the smooth point ![]() $\mathsf {p} \in W$.
$\mathsf {p} \in W$.
Definition 3.5 Under the above setting, let ![]() $Z$ be a
$Z$ be a ![]() $1$-cycle supported on
$1$-cycle supported on ![]() $E_W$. By the degree of
$E_W$. By the degree of ![]() $Z$ which is denoted by
$Z$ which is denoted by ![]() $\deg _{E_W} Z$, we mean the degree of
$\deg _{E_W} Z$, we mean the degree of ![]() $Z$ viewed as a
$Z$ viewed as a ![]() $1$-cycle on
$1$-cycle on ![]() $E_W \cong \mathbb {P}^3$. By a slight abuse of notation, we use the notation
$E_W \cong \mathbb {P}^3$. By a slight abuse of notation, we use the notation ![]() $\deg _E Z = \deg _{E_W} Z$ when
$\deg _E Z = \deg _{E_W} Z$ when ![]() $Z$ is supported on
$Z$ is supported on ![]() $E$.
$E$.
Lemma 3.6 Let ![]() $\mathsf {p} \in X$ be a germ of an isolated
$\mathsf {p} \in X$ be a germ of an isolated ![]() $cA_1$-singularity. Let
$cA_1$-singularity. Let ![]() $\mathcal {M}$ be a mobile linear system of Cartier divisors on
$\mathcal {M}$ be a mobile linear system of Cartier divisors on ![]() $X$, let
$X$, let ![]() $D_1, D_2$ be general members of
$D_1, D_2$ be general members of ![]() $\mathcal {M}$, and use the notation
$\mathcal {M}$, and use the notation ![]() $\nu (\mathcal {M}) = \operatorname {ord}_E \varphi ^* \mathcal {M}$. Let
$\nu (\mathcal {M}) = \operatorname {ord}_E \varphi ^* \mathcal {M}$. Let ![]() $\Gamma = D_1 \cdot D_2$ and use the notation
$\Gamma = D_1 \cdot D_2$ and use the notation ![]() $m = \operatorname {mult}_{\mathsf {p}} \Gamma$. Then, for the
$m = \operatorname {mult}_{\mathsf {p}} \Gamma$. Then, for the ![]() $1$-cycle
$1$-cycle
which is supported on ![]() $E$, we have
$E$, we have
Proof. Let ![]() $i \colon X \to W$ and
$i \colon X \to W$ and ![]() $\tilde {i} \colon \tilde {X} \to \tilde {W}$ be the embeddings agreeing with the maps
$\tilde {i} \colon \tilde {X} \to \tilde {W}$ be the embeddings agreeing with the maps ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi _W$. Let
$\varphi _W$. Let ![]() $e \in A_1 (E_W)$ be the class of a line. Then in
$e \in A_1 (E_W)$ be the class of a line. Then in ![]() $A_1 (\tilde {W})$, we have
$A_1 (\tilde {W})$, we have
Since ![]() $D_i$ is a Cartier divisor on
$D_i$ is a Cartier divisor on ![]() $X$, it is defined by a single element in the residue ring
$X$, it is defined by a single element in the residue ring ![]() $\mathcal {O}_{X, \mathsf {p}} = \mathcal {O}_{W, \mathsf {p}}/(x y + z^2 + w^M)$, hence we can take a Cartier divisor
$\mathcal {O}_{X, \mathsf {p}} = \mathcal {O}_{W, \mathsf {p}}/(x y + z^2 + w^M)$, hence we can take a Cartier divisor ![]() $G_i$ on
$G_i$ on ![]() $W$ such that
$W$ such that ![]() $G_i|_X = D_i$. It follows that
$G_i|_X = D_i$. It follows that
 \begin{align*} \varphi_W^* i_* \Gamma &= \varphi_W^* i_* (D_1 \cdot D_2) \\ &\equiv \varphi_W^* (G_1 \cdot G_2 \cdot X) \\ &\equiv \varphi^*_W G_1 \cdot \varphi_W^*G_2 \cdot \varphi_W^* X \\ &\equiv \varphi^*_W G_1 \cdot \varphi_W^*G_2 \cdot \tilde{X} \\ &\equiv \tilde{i}_* \bigl( \varphi^*D_1 \cdot \varphi^*D_2 \bigr), \end{align*}
\begin{align*} \varphi_W^* i_* \Gamma &= \varphi_W^* i_* (D_1 \cdot D_2) \\ &\equiv \varphi_W^* (G_1 \cdot G_2 \cdot X) \\ &\equiv \varphi^*_W G_1 \cdot \varphi_W^*G_2 \cdot \varphi_W^* X \\ &\equiv \varphi^*_W G_1 \cdot \varphi_W^*G_2 \cdot \tilde{X} \\ &\equiv \tilde{i}_* \bigl( \varphi^*D_1 \cdot \varphi^*D_2 \bigr), \end{align*}
and thus
 \begin{align} \tilde{i}_* (\varphi_*^{-1} D_1 \cdot \varphi_*^{-1} D_2) &\equiv \tilde{i}_* \bigl( (\varphi^* D_1 - \nu(\mathcal{M}) E) \cdot (\varphi^* D_2 - \nu(\mathcal{M}) E) \bigr)\nonumber\\ &\equiv \tilde{i}_* \bigl( \varphi^*D_1 \cdot \varphi^* D_2 \bigr) + \tilde{i}_* (\nu(\mathcal{M})^2 E^2 )\nonumber\\ &\equiv \varphi_W^* i_* \Gamma - 2 \nu(\mathcal{M})^2 e, \end{align}
\begin{align} \tilde{i}_* (\varphi_*^{-1} D_1 \cdot \varphi_*^{-1} D_2) &\equiv \tilde{i}_* \bigl( (\varphi^* D_1 - \nu(\mathcal{M}) E) \cdot (\varphi^* D_2 - \nu(\mathcal{M}) E) \bigr)\nonumber\\ &\equiv \tilde{i}_* \bigl( \varphi^*D_1 \cdot \varphi^* D_2 \bigr) + \tilde{i}_* (\nu(\mathcal{M})^2 E^2 )\nonumber\\ &\equiv \varphi_W^* i_* \Gamma - 2 \nu(\mathcal{M})^2 e, \end{align}
where the last equivalence follows from (3.1). By (3.2), the ![]() $1$-cycle
$1$-cycle ![]() $Z$ is rationally equivalent to
$Z$ is rationally equivalent to ![]() $(m-2 \nu (\mathcal {M})^2) e$ and the claim follows.
$(m-2 \nu (\mathcal {M})^2) e$ and the claim follows.
3.3 Tower of blow-ups associated to a divisorial valuation
We set up notation for proving ![]() $2 n^2$-type inequalities.
$2 n^2$-type inequalities.
Let ![]() $\mathsf {p} \in X$ be the germ of a terminal singular point of type
$\mathsf {p} \in X$ be the germ of a terminal singular point of type ![]() $cA_1$. Let
$cA_1$. Let ![]() $\nu$ be a divisorial valuation of
$\nu$ be a divisorial valuation of ![]() $\mathbb {C} (X)$ realized by a prime divisor
$\mathbb {C} (X)$ realized by a prime divisor ![]() $E_{\infty }$ over
$E_{\infty }$ over ![]() $\mathsf {p} \in X$. Consider the tower of blow-ups realizing
$\mathsf {p} \in X$. Consider the tower of blow-ups realizing ![]() $\nu$:
$\nu$:
where ![]() $\varphi _i \colon X_i \to X_{i-1}$ is the blow-up of
$\varphi _i \colon X_i \to X_{i-1}$ is the blow-up of ![]() $X_{i-1}$ along the center
$X_{i-1}$ along the center ![]() $B_{i-1}\subset E_{i-1}$ of
$B_{i-1}\subset E_{i-1}$ of ![]() $\nu$ on
$\nu$ on ![]() $X_{i-1}$,
$X_{i-1}$, ![]() $E_i \subset X_i$ is the
$E_i \subset X_i$ is the ![]() $\varphi _i$-exceptional divisor dominating
$\varphi _i$-exceptional divisor dominating ![]() $B_{i-1}$, and
$B_{i-1}$, and ![]() $E_N$ realizes the valuation
$E_N$ realizes the valuation ![]() $\nu$, i.e.
$\nu$, i.e. ![]() $\nu = \nu _{E_N}$. For
$\nu = \nu _{E_N}$. For ![]() $j > i$, the composite
$j > i$, the composite ![]() $X_j \to X_{j-1} \to \cdots \to X_i$ is denoted by
$X_j \to X_{j-1} \to \cdots \to X_i$ is denoted by ![]() $\varphi _{j, i} = \varphi _{i+1} \circ \cdots \varphi _j$.
$\varphi _{j, i} = \varphi _{i+1} \circ \cdots \varphi _j$.
For a cycle ![]() $\Gamma$ on
$\Gamma$ on ![]() $X_i$ and
$X_i$ and ![]() $j > i$, we denote by
$j > i$, we denote by ![]() $\Gamma ^{(j)}$ its proper transform on
$\Gamma ^{(j)}$ its proper transform on ![]() $X_j$ via
$X_j$ via ![]() $\varphi _{j, i} \colon X_j \to X_i$ if no component of
$\varphi _{j, i} \colon X_j \to X_i$ if no component of ![]() $\Gamma$ is supported on
$\Gamma$ is supported on ![]() $B_i$. More generally for any object
$B_i$. More generally for any object ![]() $(\cdot )$ (cycle, divisor, linear system) on
$(\cdot )$ (cycle, divisor, linear system) on ![]() $X_i$ and any
$X_i$ and any ![]() $j > i$ we denote by
$j > i$ we denote by ![]() $(\cdot )^{(j)}$ the proper transform of
$(\cdot )^{(j)}$ the proper transform of ![]() $(\cdot )$ on
$(\cdot )$ on ![]() $X_j$.
$X_j$.
We introduce an oriented graph structure as follows: the vertices ![]() $E_j$ and
$E_j$ and ![]() $E_i$ are joined by an oriented edge, which is denoted by
$E_i$ are joined by an oriented edge, which is denoted by ![]() $j \to i$, if
$j \to i$, if ![]() $j > i$ and
$j > i$ and ![]() $B_{j-1} \subset E_i^{(j-1)}$. For
$B_{j-1} \subset E_i^{(j-1)}$. For ![]() $1 \le i < j \le N-1$, we define
$1 \le i < j \le N-1$, we define ![]() $P_{j,i}$ to be the number of paths from
$P_{j,i}$ to be the number of paths from ![]() $E_j$ to
$E_j$ to ![]() $E_i$ in the oriented graph, we set
$E_i$ in the oriented graph, we set ![]() $P_{i,i} = 1$ and we set
$P_{i,i} = 1$ and we set ![]() $P_{j,i} = 0$ for
$P_{j,i} = 0$ for ![]() $j < i$ we define
$j < i$ we define ![]() $p_i = P_{N,i}$. We define
$p_i = P_{N,i}$. We define
 \begin{align*} K &= \max \{\, i \mid B_{i-1}\text{ is a }cA_1\text{ point} \}, \\ L &= \max \{\, i \mid B_{i-1}\text{ is a point} \}, \\ \Sigma_0 &= \sum_{i=1}^K p_i, \quad \Sigma_1 = \sum_{i=K+1}^L p_i, \quad \Sigma_2 = \sum_{i=L+1}^N p_i. \end{align*}
\begin{align*} K &= \max \{\, i \mid B_{i-1}\text{ is a }cA_1\text{ point} \}, \\ L &= \max \{\, i \mid B_{i-1}\text{ is a point} \}, \\ \Sigma_0 &= \sum_{i=1}^K p_i, \quad \Sigma_1 = \sum_{i=K+1}^L p_i, \quad \Sigma_2 = \sum_{i=L+1}^N p_i. \end{align*}
Note that ![]() $B_0 = \mathsf {p}$ and we have
$B_0 = \mathsf {p}$ and we have ![]() $1 \le K \le L \le N$. The numbers
$1 \le K \le L \le N$. The numbers ![]() $P_{i,j}, p_i, K, L$ are useful for computing discrepancies and tracking multiplicities for the tower of blow-ups.
$P_{i,j}, p_i, K, L$ are useful for computing discrepancies and tracking multiplicities for the tower of blow-ups.
Lemma 3.7 The discrepancies of ![]() $E_i$ are given by the following
$E_i$ are given by the following
 \[ a(X,E_i) = \sum_{j=1}^{\min \{i,K\}} P_{i,j} + 2\sum_{j=K+1}^{\min \{i,L\}} P_{i,j} + \sum_{j=L+1}^i P_{i,j}, \]
\[ a(X,E_i) = \sum_{j=1}^{\min \{i,K\}} P_{i,j} + 2\sum_{j=K+1}^{\min \{i,L\}} P_{i,j} + \sum_{j=L+1}^i P_{i,j}, \]
in particular,
 \[ a(X,E_N) = \sum_{j=1}^K p_j + 2\sum_{j=K+1}^L p_j + \sum_{j=L+1}^N p_j = \Sigma_0 + 2 \Sigma_1 + \Sigma_2. \]
\[ a(X,E_N) = \sum_{j=1}^K p_j + 2\sum_{j=K+1}^L p_j + \sum_{j=L+1}^N p_j = \Sigma_0 + 2 \Sigma_1 + \Sigma_2. \]
Let ![]() $D$ be a divisor on
$D$ be a divisor on ![]() $X$ and set
$X$ and set ![]() $K_D = \max \{i \mid B_{i-1}\subset D^{(i-1)} \}$, then
$K_D = \max \{i \mid B_{i-1}\subset D^{(i-1)} \}$, then
 \[ \nu_{E_i}(D) = \sum_{j=1}^{\min \{K_D,i \}} P_{i,j} \nu_{E_j} (D^{j-1}), \]
\[ \nu_{E_i}(D) = \sum_{j=1}^{\min \{K_D,i \}} P_{i,j} \nu_{E_j} (D^{j-1}), \]
in particular,
 \[ \nu(D) = \sum_{j=1}^{K_D} p_j \nu_{E_j} (D^{j-1}). \]
\[ \nu(D) = \sum_{j=1}^{K_D} p_j \nu_{E_j} (D^{j-1}). \]
Proof. We prove the claims by induction. The statements clearly hold for ![]() $i = 1$, now suppose the statements hold for all
$i = 1$, now suppose the statements hold for all ![]() $k < i$.
$k < i$.
First, we define values ![]() $a_i = a(E_i,X_{i-1})$ for all
$a_i = a(E_i,X_{i-1})$ for all ![]() $i$, clearly
$i$, clearly
 \[ a_i = \begin{cases} 1, & i\le K,\\ 2, & K < i \le L,\\ 1, & L \le N. \end{cases} \]
\[ a_i = \begin{cases} 1, & i\le K,\\ 2, & K < i \le L,\\ 1, & L \le N. \end{cases} \]
By assumption of induction we have
 \[ K_{X^{(i-1)}} \sim \varphi_{i-1,0}^* (K_{X}\!) + \sum_{k=1}^{i-1} \biggl( \sum_{j=1}^k a_j P_{k,j} \biggr) E_k^{(i-1)}. \]
\[ K_{X^{(i-1)}} \sim \varphi_{i-1,0}^* (K_{X}\!) + \sum_{k=1}^{i-1} \biggl( \sum_{j=1}^k a_j P_{k,j} \biggr) E_k^{(i-1)}. \]
Next we compute ![]() $K_{X^{(i)}}$:
$K_{X^{(i)}}$:
 \begin{align*} K_{X^{(i)}} &\sim \varphi_i^* (K_{X^{(i-1)}}) + a_i E_i \sim \varphi_{i,0}^* (K_{X}\!) + \sum_{k=1}^{i-1} \biggl( \sum_{j=1}^k a_j P_{k,j} \biggr) \varphi_i^* E_k^{(i-1)} + a_i E_i\\ & \sim \varphi_{i,0}^* (K_{X}\!) + \sum_{k=1}^{i-1} \biggl( \sum_{j=1}^k a_j P_{k,j} \biggr) E_k^{(i)} + \Biggl( a_i P_{i,i} + \sum_{k \mid i\to k} \biggl( \sum_{j=1}^k a_j P_{k,j} \biggr) \Biggr)E_i. \end{align*}
\begin{align*} K_{X^{(i)}} &\sim \varphi_i^* (K_{X^{(i-1)}}) + a_i E_i \sim \varphi_{i,0}^* (K_{X}\!) + \sum_{k=1}^{i-1} \biggl( \sum_{j=1}^k a_j P_{k,j} \biggr) \varphi_i^* E_k^{(i-1)} + a_i E_i\\ & \sim \varphi_{i,0}^* (K_{X}\!) + \sum_{k=1}^{i-1} \biggl( \sum_{j=1}^k a_j P_{k,j} \biggr) E_k^{(i)} + \Biggl( a_i P_{i,i} + \sum_{k \mid i\to k} \biggl( \sum_{j=1}^k a_j P_{k,j} \biggr) \Biggr)E_i. \end{align*}
It remains to compute the coefficient at ![]() $E_i$,
$E_i$,
 \begin{align*} a(E_i,X) &= a_i P_{i,i} + \sum_{k\mid i\to k} \sum_{j=1}^k a_j P_{k,j} = a_i P_{i,i} + \sum_{k\mid i\to k} \sum_{j=1}^{i-1} a_j P_{k,j}\\ &= a_i P_{i,i} + \sum_{j=1}^{i-1} a_j \sum_{k\mid i\to k} P_{k,j} = \sum_{j=1}^i a_j P_{i,j}, \end{align*}
\begin{align*} a(E_i,X) &= a_i P_{i,i} + \sum_{k\mid i\to k} \sum_{j=1}^k a_j P_{k,j} = a_i P_{i,i} + \sum_{k\mid i\to k} \sum_{j=1}^{i-1} a_j P_{k,j}\\ &= a_i P_{i,i} + \sum_{j=1}^{i-1} a_j \sum_{k\mid i\to k} P_{k,j} = \sum_{j=1}^i a_j P_{i,j}, \end{align*}
where the second equality follows from ![]() $P_{k,j} = 0$ for
$P_{k,j} = 0$ for ![]() $j > k$ and the last equality follows from
$j > k$ and the last equality follows from
This proves the first assertion and its special case. The proof of the second assertion is analogous.
Example 3.8 Suppose in 3.3 we have ![]() $B_{i} \not \subset E_{k}^{(i)}$ for all
$B_{i} \not \subset E_{k}^{(i)}$ for all ![]() $k < i$. Then the oriented graph is the following simple chain.
$k < i$. Then the oriented graph is the following simple chain.

Clearly, in this case we have ![]() $p_1 = p_2 = \cdots = p_N = 1$ and
$p_1 = p_2 = \cdots = p_N = 1$ and
Example 3.9 Suppose ![]() $N = 4$,
$N = 4$, ![]() $B_2,B_3$ are points,
$B_2,B_3$ are points, ![]() $B_2\in E_1^{(2)} \cap E_2$, and
$B_2\in E_1^{(2)} \cap E_2$, and ![]() $B_3 = E_1^{(3)}\cap E_2^{(3)} \cap E_3$, then the graph is as follows.
$B_3 = E_1^{(3)}\cap E_2^{(3)} \cap E_3$, then the graph is as follows.

Thus, we can see that ![]() $p_1 = p_2 = 1$,
$p_1 = p_2 = 1$, ![]() $p_3 = 2$, and
$p_3 = 2$, and ![]() $p_4 = 4$.
$p_4 = 4$.
Let ![]() $\mathcal {M}$ be a mobile linear system of Cartier divisors on
$\mathcal {M}$ be a mobile linear system of Cartier divisors on ![]() $X = X_0$. Let
$X = X_0$. Let ![]() $Z_0 = D_1 \cdot D_2$ for general members
$Z_0 = D_1 \cdot D_2$ for general members ![]() $D_1, D_2 \in \mathcal {M}$. Recall that we want to prove a lower bound for
$D_1, D_2 \in \mathcal {M}$. Recall that we want to prove a lower bound for ![]() $\operatorname {mult}_{B_0} Z_0$.
$\operatorname {mult}_{B_0} Z_0$.
Example 3.10 Suppose ![]() $N=1$, that is
$N=1$, that is ![]() $\nu$ is realized by a single blow-up. Consider the intersection of the proper transforms
$\nu$ is realized by a single blow-up. Consider the intersection of the proper transforms ![]() $D_1^{(1)}, D_2^{(2)}$ on
$D_1^{(1)}, D_2^{(2)}$ on ![]() $X_1$. By Lemma 3.6 it takes the form
$X_1$. By Lemma 3.6 it takes the form
where
Note that ![]() $a(E_1,X,({1}/{n})\mathcal {M}) = (1 - ({\nu }/{n}))<0$ if and only if
$a(E_1,X,({1}/{n})\mathcal {M}) = (1 - ({\nu }/{n}))<0$ if and only if ![]() $\nu (\mathcal {M}) > n$. Thus, non-canonicity at divisor
$\nu (\mathcal {M}) > n$. Thus, non-canonicity at divisor ![]() $E_1$ implies
$E_1$ implies
Example 3.11 Suppose ![]() $N = 2$ and suppose that
$N = 2$ and suppose that ![]() $B_1$ is a point such that
$B_1$ is a point such that ![]() $X_1$ is smooth at
$X_1$ is smooth at ![]() $B_1$. As before, by Lemma 3.6 intersection on
$B_1$. As before, by Lemma 3.6 intersection on ![]() $X_1$ takes the form
$X_1$ takes the form
where
Using Lemma 3.2 we compute similar intersection on ![]() $X_2$:
$X_2$:
where
Since ![]() $\deg _{E_2} Z_2$ is non-negative we have
$\deg _{E_2} Z_2$ is non-negative we have
 \begin{align*} 0 \le
\operatorname{mult}_{B_1} (Z_0^{(1)} + Z_1) - 4
\nu_{E_2}(\mathcal{M}^{(1)})^2 &\le
\operatorname{mult}_{B_0} Z_0 + \deg_{E_1} Z_1 - 4
\nu_{E_2}(\mathcal{M}^{(1)})^2\\ & = 2
\operatorname{mult}_{B_0} Z_0 - 2 \nu_{E_1}(\mathcal{M})^2
- 4 \nu_{E_2}(\mathcal{M}^{(1)})^2,
\end{align*}
\begin{align*} 0 \le
\operatorname{mult}_{B_1} (Z_0^{(1)} + Z_1) - 4
\nu_{E_2}(\mathcal{M}^{(1)})^2 &\le
\operatorname{mult}_{B_0} Z_0 + \deg_{E_1} Z_1 - 4
\nu_{E_2}(\mathcal{M}^{(1)})^2\\ & = 2
\operatorname{mult}_{B_0} Z_0 - 2 \nu_{E_1}(\mathcal{M})^2
- 4 \nu_{E_2}(\mathcal{M}^{(1)})^2,
\end{align*}
or
It remains to use non-canonicity to find the lower bound on the right-hand side of this inequality.
In general, we proceed similarly to the examples. We define ![]() $\nu _i = \nu _{E_i} (\mathcal {M}^{(i-1)})$. For general members
$\nu _i = \nu _{E_i} (\mathcal {M}^{(i-1)})$. For general members ![]() $D_1, D_2 \in \mathcal {M}$, we define a sequence of
$D_1, D_2 \in \mathcal {M}$, we define a sequence of ![]() $1$-cycles
$1$-cycles ![]() $Z_i$ on
$Z_i$ on ![]() $X_i$ by
$X_i$ by
 \begin{equation} \begin{aligned} D_1 \cdot D_2 & = Z_0, \\ D_1^{(1)} \cdot D_2^{(1)} & = Z_0^{(1)} + Z_1, \\ & \cdots, \\ D_1^{(i)} \cdot D_2^{(i)} & = (D_1^{(i-1)} \cdot D_2^{(i-1)})^{(i)} + Z_i, \\ & \cdots, \\ D_1^{(L)} \cdot D_2^{(L)} & = (D_1^{(L-1)} \cdot D_2^{(L-1)})^{(L)} + Z_L. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} D_1 \cdot D_2 & = Z_0, \\ D_1^{(1)} \cdot D_2^{(1)} & = Z_0^{(1)} + Z_1, \\ & \cdots, \\ D_1^{(i)} \cdot D_2^{(i)} & = (D_1^{(i-1)} \cdot D_2^{(i-1)})^{(i)} + Z_i, \\ & \cdots, \\ D_1^{(L)} \cdot D_2^{(L)} & = (D_1^{(L-1)} \cdot D_2^{(L-1)})^{(L)} + Z_L. \end{aligned} \end{equation}
Note that ![]() $\operatorname {Supp} Z_i \subset E_i$ and for any
$\operatorname {Supp} Z_i \subset E_i$ and for any ![]() $i \le L$ we get
$i \le L$ we get
For any ![]() $i, j$ with
$i, j$ with ![]() $L \ge j > i$, we set
$L \ge j > i$, we set
Then there is a lower bound on multiplicities of ![]() $Z = Z_0$ at
$Z = Z_0$ at ![]() $B_i$ in terms of
$B_i$ in terms of ![]() $\nu _i$.
$\nu _i$.
Proposition 3.12 Suppose ![]() $\mathsf {p} \in X$ is a terminal singularity of type
$\mathsf {p} \in X$ is a terminal singularity of type ![]() $cA_1$, and let
$cA_1$, and let ![]() $\nu$ be a divisorial valuation of
$\nu$ be a divisorial valuation of ![]() $\mathbb {C} (X)$ centered at
$\mathbb {C} (X)$ centered at ![]() $\mathsf {p}$. Let
$\mathsf {p}$. Let ![]() $\mathcal {M}$ be a mobile linear system of Cartier divisors on
$\mathcal {M}$ be a mobile linear system of Cartier divisors on ![]() $X$ and let
$X$ and let ![]() $Z_0 = D_1 \cdot D_2$ be the intersection
$Z_0 = D_1 \cdot D_2$ be the intersection ![]() $1$-cycle of general members
$1$-cycle of general members ![]() $D_1, D_2$ in
$D_1, D_2$ in ![]() $\mathcal {M}$. Then, for
$\mathcal {M}$. Then, for ![]() $p_i, \nu _i$ and
$p_i, \nu _i$ and ![]() $m_{i, j}$ defined as above, the following inequality holds:
$m_{i, j}$ defined as above, the following inequality holds:
 \begin{equation} 2 \sum_{i=1}^K p_i \nu_i^2 + \sum_{i=K+1}^N p_i \nu_i^2 \le \sum_{i = 1}^L p_i m_{0,i}. \end{equation}
\begin{equation} 2 \sum_{i=1}^K p_i \nu_i^2 + \sum_{i=K+1}^N p_i \nu_i^2 \le \sum_{i = 1}^L p_i m_{0,i}. \end{equation}Proof. Set ![]() $d_i = \deg _{E_i} Z_i$. By Lemmas 3.2 and 3.6, we obtain a system of equalities corresponding to the sequence of cycles (3.4):
$d_i = \deg _{E_i} Z_i$. By Lemmas 3.2 and 3.6, we obtain a system of equalities corresponding to the sequence of cycles (3.4):
 \begin{equation} \begin{aligned} 2 \nu_1^2 + d_1 & = m_{0,1}, \\ 2 \nu_2^2 + d_2 & = m_{0, 2} + m_{1, 2}, \\ & \cdots, \\ 2 \nu_K^2 + d_K & = m_{0, K} + \cdots + m_{K-1. K}, \\ \nu_{K+1}^2 + d_{K+1} & = m_{0, K+1} + \cdots + m_{K, K+1}, \\ & \cdots, \\ \nu_L^2 + d_L & = m_{0, L} + \cdots + m_{L-1, L}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} 2 \nu_1^2 + d_1 & = m_{0,1}, \\ 2 \nu_2^2 + d_2 & = m_{0, 2} + m_{1, 2}, \\ & \cdots, \\ 2 \nu_K^2 + d_K & = m_{0, K} + \cdots + m_{K-1. K}, \\ \nu_{K+1}^2 + d_{K+1} & = m_{0, K+1} + \cdots + m_{K, K+1}, \\ & \cdots, \\ \nu_L^2 + d_L & = m_{0, L} + \cdots + m_{L-1, L}. \end{aligned} \end{equation}
We multiply the ![]() $i$th equality in (3.6) by
$i$th equality in (3.6) by ![]() $p_i$ and sum them up:
$p_i$ and sum them up:
 \begin{equation} 2 \sum_{i=1}^K p_i \nu_i^2 + \sum_{i=K+1}^L p_i \nu_i^2 + \sum_{i=1}^L p_i d_i = \sum_{j=1}^L p_j m_{0, j} + \sum_{i = 1}^{L-1} \sum_{j = i+1}^L p_j m_{i, j}. \end{equation}
\begin{equation} 2 \sum_{i=1}^K p_i \nu_i^2 + \sum_{i=K+1}^L p_i \nu_i^2 + \sum_{i=1}^L p_i d_i = \sum_{j=1}^L p_j m_{0, j} + \sum_{i = 1}^{L-1} \sum_{j = i+1}^L p_j m_{i, j}. \end{equation} For each ![]() $i$ with
$i$ with ![]() $0 \le i \le L-1$, we consider the expression
$0 \le i \le L-1$, we consider the expression
 \[ \sum_{j = i+1}^L p_j m_{i, j} \]
\[ \sum_{j = i+1}^L p_j m_{i, j} \]
which appears in the right-hand side of the summation (3.7). We have ![]() $m_{i, j} \le d_i$ for any
$m_{i, j} \le d_i$ for any ![]() $i, j$ with
$i, j$ with ![]() $L \ge j > i \ge 1$ by [Reference PukhlikovPuk13, Lemma 2.4].Footnote 1 Note that, for
$L \ge j > i \ge 1$ by [Reference PukhlikovPuk13, Lemma 2.4].Footnote 1 Note that, for ![]() $i \ge 1$, we have
$i \ge 1$, we have ![]() $p_i \ge \sum _{j \to i} p_j$, and if
$p_i \ge \sum _{j \to i} p_j$, and if ![]() $m_{i, j} \neq 0$, then
$m_{i, j} \neq 0$, then ![]() $j \to i$. It follows that, for
$j \to i$. It follows that, for ![]() $i = 1, \ldots, L-1$, we have
$i = 1, \ldots, L-1$, we have
 \[ \sum_{j = i + 1}^L p_j m_{i, j} = \sum_{\substack{i + 1 \le j \le L \\ m_{i,j} \ne 0}} p_j m_{i,j} \le d_i \sum_{\substack{i + 1 \le j \le L \\ j \to i}} p_j \le p_i d_i. \]
\[ \sum_{j = i + 1}^L p_j m_{i, j} = \sum_{\substack{i + 1 \le j \le L \\ m_{i,j} \ne 0}} p_j m_{i,j} \le d_i \sum_{\substack{i + 1 \le j \le L \\ j \to i}} p_j \le p_i d_i. \]
Thus, for ![]() $i = 1, \ldots, L-1$, we can remove all
$i = 1, \ldots, L-1$, we can remove all ![]() $m_{i, *}$ and
$m_{i, *}$ and ![]() $p_i d_i$ from the summation (3.7) if we replace
$p_i d_i$ from the summation (3.7) if we replace ![]() $=$ with
$=$ with ![]() $\le$, and obtain
$\le$, and obtain
 \begin{equation} 2 \sum_{i=1}^K p_i \nu_i^2 + \sum_{i = K+1}^L p_i \nu_i^2 + p_L d_L \le \sum_{i=1}^L p_i m_{0,i}. \end{equation}
\begin{equation} 2 \sum_{i=1}^K p_i \nu_i^2 + \sum_{i = K+1}^L p_i \nu_i^2 + p_L d_L \le \sum_{i=1}^L p_i m_{0,i}. \end{equation} It remains to give a lower bound for ![]() $d_L$ in terms of
$d_L$ in terms of ![]() $\nu _i$. First, we decompose
$\nu _i$. First, we decompose
where ![]() $\operatorname {Supp} \Gamma _L$ does not contain
$\operatorname {Supp} \Gamma _L$ does not contain ![]() $B_L$ and
$B_L$ and ![]() $\alpha _L \ge 0$. Thus, we may decompose
$\alpha _L \ge 0$. Thus, we may decompose
where ![]() $\operatorname {Supp} Z_{L+1} \subset E_{L+1}$. We apply Lemma 3.2(2) to
$\operatorname {Supp} Z_{L+1} \subset E_{L+1}$. We apply Lemma 3.2(2) to ![]() $\varphi _{L+1}$:
$\varphi _{L+1}$:
Thus, we have ![]() $\alpha _L = \nu _{L+1}^2 + \deg _{E_{L+1}} Z_{L+1}$ and
$\alpha _L = \nu _{L+1}^2 + \deg _{E_{L+1}} Z_{L+1}$ and
Iterating the application of Lemma 3.2(2) for ![]() $\varphi _i$ with
$\varphi _i$ with ![]() $i = L + 2, \ldots, N$, we obtain
$i = L + 2, \ldots, N$, we obtain
 \[ d_L \ge \sum_{i = L + 1}^N \nu_i^2 \deg_{E_L} (\varphi_{i-1, L})_* B_{i-1} \ge \sum_{i= L + 1}^N \nu_i^2. \]
\[ d_L \ge \sum_{i = L + 1}^N \nu_i^2 \deg_{E_L} (\varphi_{i-1, L})_* B_{i-1} \ge \sum_{i= L + 1}^N \nu_i^2. \]
Combining this inequality with (3.8), we obtain the inequality (3.5).
Corollary 3.13 Let the notation and assumption be as in Proposition 3.12. Then the following inequality holds:
 \[ \sum_{i = 1}^L p_i m_{0, i} \ge \frac{2 \nu (\mathcal{M})^2}{\sum_{i=1}^K p_i + 2 \sum _{i=K+1}^N p_i}. \]
\[ \sum_{i = 1}^L p_i m_{0, i} \ge \frac{2 \nu (\mathcal{M})^2}{\sum_{i=1}^K p_i + 2 \sum _{i=K+1}^N p_i}. \]
Proof. The minimum of the left-hand side of (3.5), viewed as a quadratic form in ![]() $\nu _i$, under the constraint
$\nu _i$, under the constraint
 \[ \sum_{i=1}^N p_i \nu_i = \nu (\mathcal{M}), \]
\[ \sum_{i=1}^N p_i \nu_i = \nu (\mathcal{M}), \]
is attained at
 \[ 2 \nu_1 = \cdots = 2 \nu_K = \nu_{K+1} = \cdots = \nu_N = \frac{2 \nu (\mathcal{M})}{\sum_{i=1}^K p_i + 2 \sum_{i = K+1}^L p_i}. \]
\[ 2 \nu_1 = \cdots = 2 \nu_K = \nu_{K+1} = \cdots = \nu_N = \frac{2 \nu (\mathcal{M})}{\sum_{i=1}^K p_i + 2 \sum_{i = K+1}^L p_i}. \]
Calculating the minimum, we get the required inequality.
3.4  $2 n^2$-inequalities for
$2 n^2$-inequalities for  $cA_1$ points
$cA_1$ points
We keep the notation as in § 3.3. Recall that
 \begin{equation} \Sigma_0 = \sum_{i=1}^K p_i, \quad \Sigma_1 = \sum_{i = K+1}^L p_i, \quad \Sigma_2 = \sum_{i=L+1}^N p_i. \end{equation}
\begin{equation} \Sigma_0 = \sum_{i=1}^K p_i, \quad \Sigma_1 = \sum_{i = K+1}^L p_i, \quad \Sigma_2 = \sum_{i=L+1}^N p_i. \end{equation}Theorem 3.14 ( $2 n^2$-inequality for
$2 n^2$-inequality for  $cA_1$ points)
$cA_1$ points)
Let ![]() $\mathsf {p} \in X$ be a terminal singularity of type
$\mathsf {p} \in X$ be a terminal singularity of type ![]() $cA_1$,
$cA_1$, ![]() $\mathcal {M}$ be a mobile linear system of Cartier divisors on
$\mathcal {M}$ be a mobile linear system of Cartier divisors on ![]() $X$, and let
$X$, and let ![]() $n$ be a positive rational number. If
$n$ be a positive rational number. If ![]() $\mathsf {p}$ is a center of non-canonical singularities of the pair
$\mathsf {p}$ is a center of non-canonical singularities of the pair ![]() $(X, ({1}/{n}) \mathcal {M})$, then for general members
$(X, ({1}/{n}) \mathcal {M})$, then for general members ![]() $D_1, D_2$ in
$D_1, D_2$ in ![]() $\mathcal {M}$ we have
$\mathcal {M}$ we have
Proof. By the assumption, there exists a divisorial valuation ![]() $\nu$ of
$\nu$ of ![]() $\mathbb {C} (X)$ centered at
$\mathbb {C} (X)$ centered at ![]() $\mathsf {p}$ such that
$\mathsf {p}$ such that ![]() $(X, ({1}/{n}) \mathcal {M})$ is not canonical at
$(X, ({1}/{n}) \mathcal {M})$ is not canonical at ![]() $\nu$, that is, the inequality
$\nu$, that is, the inequality ![]() $\nu (\mathcal {M}) > n a(\nu,X)$ holds for
$\nu (\mathcal {M}) > n a(\nu,X)$ holds for ![]() $\nu$. Thus, by Lemma 3.7 we have
$\nu$. Thus, by Lemma 3.7 we have
Note that
for any ![]() $1 \le i \le L$. By (3.10), (3.11) and Corollary 3.13, we obtain
$1 \le i \le L$. By (3.10), (3.11) and Corollary 3.13, we obtain
It is then easy to get the required inequality.
Theorem 3.15 ( $2 n^2$-type inequality for Kawakita blow-ups)
$2 n^2$-type inequality for Kawakita blow-ups)
Let ![]() $\mathsf {p} \in X$ be a terminal singularity of type
$\mathsf {p} \in X$ be a terminal singularity of type ![]() $cA_1$, analytically equivalent to
$cA_1$, analytically equivalent to ![]() $o \in (f=0) \subset \mathbb {A}^4$, where
$o \in (f=0) \subset \mathbb {A}^4$, where
for some ![]() $M \geq 2$. Let
$M \geq 2$. Let ![]() $n$ be a positive rational number, and
$n$ be a positive rational number, and ![]() $\mathcal {M}$ be a mobile linear system of Cartier divisors on
$\mathcal {M}$ be a mobile linear system of Cartier divisors on ![]() $X$. Let
$X$. Let ![]() $E$ be the exceptional divisor of
$E$ be the exceptional divisor of ![]() $(s, 2 t - s, t, 1)$-blow-up of
$(s, 2 t - s, t, 1)$-blow-up of ![]() $\mathsf {p} \in X$, where
$\mathsf {p} \in X$, where ![]() $s, t$ are coprime integers such that
$s, t$ are coprime integers such that ![]() $0 < s \le t \le M/2$. If the pair
$0 < s \le t \le M/2$. If the pair ![]() $(X, ({1}/{n}) \mathcal {M})$ is not canonical at
$(X, ({1}/{n}) \mathcal {M})$ is not canonical at ![]() $E$, then, for general members
$E$, then, for general members ![]() $D_1, D_2$ in
$D_1, D_2$ in ![]() $\mathcal {M}$, we have
$\mathcal {M}$, we have
Proof. Consider a fan corresponding to ![]() $\mathbb {A}^4$ with the following description
$\mathbb {A}^4$ with the following description
 \begin{align*} v_x &= (1,0,0,0),\\ v_y &= (0,1,0,0),\\ v_z &= (0,0,1,0),\\ v_w &= (0,0,0,1). \end{align*}
\begin{align*} v_x &= (1,0,0,0),\\ v_y &= (0,1,0,0),\\ v_z &= (0,0,1,0),\\ v_w &= (0,0,0,1). \end{align*}
Then the toric morphism corresponding to adding the ray ![]() $\rho = (s, 2t-s, t, 1)$ to the fan is the
$\rho = (s, 2t-s, t, 1)$ to the fan is the ![]() $(s, 2t-s, t, 1)$-weighted blow-up of
$(s, 2t-s, t, 1)$-weighted blow-up of ![]() $\mathbb {A}^4$. We can also add the ray
$\mathbb {A}^4$. We can also add the ray ![]() $\rho$ by performing a sequence of regular blow-ups at points, curves, and surfaces corresponding to adding the following rays to the fan:
$\rho$ by performing a sequence of regular blow-ups at points, curves, and surfaces corresponding to adding the following rays to the fan:
 \begin{align*} u_1 &= (1,1,1,1),\\ u_2 &= (2,2,2,1),\\ &\cdots\\ u_s &= (s,s,s,1),\\ u_{s+1} &= (s,s+1,s+1,1),\\ &\cdots \\ u_{t} &= (s,t,t,1),\\ u_{t+1} &= (s,t+1,t,1),\\ &\cdots\\ u_{2t-s} &= (s,2t-s,t,1).\\ \end{align*}
\begin{align*} u_1 &= (1,1,1,1),\\ u_2 &= (2,2,2,1),\\ &\cdots\\ u_s &= (s,s,s,1),\\ u_{s+1} &= (s,s+1,s+1,1),\\ &\cdots \\ u_{t} &= (s,t,t,1),\\ u_{t+1} &= (s,t+1,t,1),\\ &\cdots\\ u_{2t-s} &= (s,2t-s,t,1).\\ \end{align*}
From this description we can see that the first ![]() $s$ morphisms are the blow-ups at a points, first at
$s$ morphisms are the blow-ups at a points, first at ![]() $(x=y=z=w=0)$, then at
$(x=y=z=w=0)$, then at ![]() $(x=y=z=u_{i}=0)$, the next
$(x=y=z=u_{i}=0)$, the next ![]() $t-s$ morphisms are blow-ups at curves
$t-s$ morphisms are blow-ups at curves ![]() $(y=z=u_i=0)$, and the last
$(y=z=u_i=0)$, and the last ![]() $t-s$ morphisms are blow-ups at surface
$t-s$ morphisms are blow-ups at surface ![]() $(y=u_i=0)$. The restriction of the morphisms to the proper transforms
$(y=u_i=0)$. The restriction of the morphisms to the proper transforms ![]() $X_i$ of
$X_i$ of ![]() $X$ gives us the
$X$ gives us the ![]() $s$ blow-ups at singular points of
$s$ blow-ups at singular points of ![]() $X$ followed by
$X$ followed by ![]() $t-s$ blow-ups at a curve and
$t-s$ blow-ups at a curve and ![]() $t-s$ blow-ups at a divisor as can be seen from the local equations of
$t-s$ blow-ups at a divisor as can be seen from the local equations of ![]() $X_i$:
$X_i$:
 \begin{align*} X_0:& \quad xy + z^2 + w^M = 0,\\ X_1:& \quad xy + z^2 + u_1^{M-2} w^M = 0,\\ &\cdots \\ X_s:& \quad xy + z^2 + u_s^{M-2s} w^M = 0,\\ X_{s+1}:& \quad xy + u_{s+1} z^2 + u_{s+1}^{M-2s-1} w^M = 0,\\ & \cdots\\ X_{t}:& \quad xy + u_{t}^{t-s} z^2 + u_{t}^{M-s-t} w^M= 0,\\ X_{t+1}:& \quad xy + u_{t+1}^{t-s-1} z^2 + u_{t+1}^{M-s-t-1} w^M =2,\\ & \cdots \\ X_{2t-s}:& \quad xy + z^2 + u_{2t-s}^{M-2t} w^M = 0. \end{align*}
\begin{align*} X_0:& \quad xy + z^2 + w^M = 0,\\ X_1:& \quad xy + z^2 + u_1^{M-2} w^M = 0,\\ &\cdots \\ X_s:& \quad xy + z^2 + u_s^{M-2s} w^M = 0,\\ X_{s+1}:& \quad xy + u_{s+1} z^2 + u_{s+1}^{M-2s-1} w^M = 0,\\ & \cdots\\ X_{t}:& \quad xy + u_{t}^{t-s} z^2 + u_{t}^{M-s-t} w^M= 0,\\ X_{t+1}:& \quad xy + u_{t+1}^{t-s-1} z^2 + u_{t+1}^{M-s-t-1} w^M =2,\\ & \cdots \\ X_{2t-s}:& \quad xy + z^2 + u_{2t-s}^{M-2t} w^M = 0. \end{align*}
We can see from the toric description that for every blow-up we have ![]() $B_i \subset E_i\setminus E_{i-1}^{(i)}$, so we can drop
$B_i \subset E_i\setminus E_{i-1}^{(i)}$, so we can drop ![]() $u_j$ in the local equation of
$u_j$ in the local equation of ![]() $X_i$ for
$X_i$ for ![]() $j< i$. This fact also implies that the graph corresponding to the tower of blow-ups is a simple chain and we have
$j< i$. This fact also implies that the graph corresponding to the tower of blow-ups is a simple chain and we have ![]() $p_i = 1$ for all
$p_i = 1$ for all ![]() $i$. Thus, we have
$i$. Thus, we have ![]() $N = t$,
$N = t$, ![]() $\Sigma _0 = K = L = s$,
$\Sigma _0 = K = L = s$, ![]() $\Sigma _1 = 0$, and
$\Sigma _1 = 0$, and ![]() $\Sigma _2 = t - s$. The required inequality is obtained by substituting these values into the inequality (3.12).
$\Sigma _2 = t - s$. The required inequality is obtained by substituting these values into the inequality (3.12).
Remark 3.16 In Theorem 3.14, compared with the ![]() $4n^2$-inequality (Theorem 1.1), we keep the dimension three but we make the germ of a point worse by introducing singularities. As a result, we weaken the original inequality.
$4n^2$-inequality (Theorem 1.1), we keep the dimension three but we make the germ of a point worse by introducing singularities. As a result, we weaken the original inequality.
On the other hand, one can increase the dimension and see what kind of singularities still satisfy the ![]() $4n^2$-inequality; see, for example, [Reference PukhlikovPuk17]. This approach has been applied to prove birational rigidity of many families of high-dimensional varieties: hypersurfaces, cyclic covers, and complete intersections [Reference PukhlikovPuk19a, Reference PukhlikovPuk19b, Reference Eckl and PukhlikovEP18, Reference Evans and PukhlikovEP19].
$4n^2$-inequality; see, for example, [Reference PukhlikovPuk17]. This approach has been applied to prove birational rigidity of many families of high-dimensional varieties: hypersurfaces, cyclic covers, and complete intersections [Reference PukhlikovPuk19a, Reference PukhlikovPuk19b, Reference Eckl and PukhlikovEP18, Reference Evans and PukhlikovEP19].
3.5 Corti inequality for  $cA_1$ points
$cA_1$ points
We keep the notation as in § 3.3 and let ![]() $\Sigma _0, \Sigma _1, \Sigma _2$ be as in (3.9). The following is a version of Corti inequality [Reference CortiCor00, Theorem 3.12] for
$\Sigma _0, \Sigma _1, \Sigma _2$ be as in (3.9). The following is a version of Corti inequality [Reference CortiCor00, Theorem 3.12] for ![]() $cA_1$ points.
$cA_1$ points.
Theorem 3.17 (Corti inequality for  $cA_1$ points)
$cA_1$ points)
Let ![]() $\mathsf {p} \in X$ be a terminal singularity of type
$\mathsf {p} \in X$ be a terminal singularity of type ![]() $cA_1$, and let
$cA_1$, and let ![]() $\mathcal {M}$ be a mobile linear system of Cartier divisors on
$\mathcal {M}$ be a mobile linear system of Cartier divisors on ![]() $X$. Let
$X$. Let ![]() $F_1, \ldots, F_l \subset X$ be irreducible surfaces containing
$F_1, \ldots, F_l \subset X$ be irreducible surfaces containing ![]() $\mathsf {p}$. For the intersection
$\mathsf {p}$. For the intersection ![]() $1$-cycle
$1$-cycle ![]() $Z = D_1 \cdot D_2$ of general members
$Z = D_1 \cdot D_2$ of general members ![]() $D_1, D_2$ in
$D_1, D_2$ in ![]() $\mathcal {M}$, we write
$\mathcal {M}$, we write
 \[ Z = Z_h + \sum_{j=1}^l Z_j, \]
\[ Z = Z_h + \sum_{j=1}^l Z_j, \]
where ![]() $\operatorname {Supp} Z_j \subset F_j$, and
$\operatorname {Supp} Z_j \subset F_j$, and ![]() $Z_h$ intersects
$Z_h$ intersects ![]() $\sum _{i=1}^l F_i$ properly. Let
$\sum _{i=1}^l F_i$ properly. Let ![]() $n$ and
$n$ and ![]() $\gamma _j$ be positive rational numbers such that
$\gamma _j$ be positive rational numbers such that ![]() $\mathsf {p}$ is a center of non-canonical singularities of the pair
$\mathsf {p}$ is a center of non-canonical singularities of the pair
 \begin{equation} \biggl( X, \frac{1}{n} \mathcal{M} - \sum_{j=1}^l \gamma_j F_j \biggr). \end{equation}
\begin{equation} \biggl( X, \frac{1}{n} \mathcal{M} - \sum_{j=1}^l \gamma_j F_j \biggr). \end{equation}
Then there are rational numbers ![]() $0 < t_j \le 1$ such that
$0 < t_j \le 1$ such that
 \[ \operatorname{mult}_{\mathsf{p}} Z_h + \sum_{j=1}^l t_j \operatorname{mult}_{\mathsf{p}} Z_j > 2 n^2 + 4 n^2 \sum_{j=1}^l \gamma_j t_j. \]
\[ \operatorname{mult}_{\mathsf{p}} Z_h + \sum_{j=1}^l t_j \operatorname{mult}_{\mathsf{p}} Z_j > 2 n^2 + 4 n^2 \sum_{j=1}^l \gamma_j t_j. \]
Proof. We first note that by Lemma 3.7
where we recall that ![]() $E_{\infty } = E_N$ is the prime exceptional divisor realizing
$E_{\infty } = E_N$ is the prime exceptional divisor realizing ![]() $\nu$. By the assumption that the pair (3.13) is not canonical at
$\nu$. By the assumption that the pair (3.13) is not canonical at ![]() $\nu$, we have
$\nu$, we have
 \begin{equation} \nu (\mathcal{M}) > n \biggl( \Sigma_0 + 2 \Sigma_1 + \Sigma_2 + \sum_{j = 1}^k \gamma_j \nu (F_j) \biggr). \end{equation}
\begin{equation} \nu (\mathcal{M}) > n \biggl( \Sigma_0 + 2 \Sigma_1 + \Sigma_2 + \sum_{j = 1}^k \gamma_j \nu (F_j) \biggr). \end{equation}
For ![]() $j = 1, \ldots, l$, we set
$j = 1, \ldots, l$, we set
 \[ K_j = \begin{cases} 0, & \text{if }\mathsf{p} \in F_j, \\ \max \bigl\{i \le L \mid B_{i-1} \notin F_j^{(i-1)} \bigr\}, & \text{otherwise}, \end{cases} \]
\[ K_j = \begin{cases} 0, & \text{if }\mathsf{p} \in F_j, \\ \max \bigl\{i \le L \mid B_{i-1} \notin F_j^{(i-1)} \bigr\}, & \text{otherwise}, \end{cases} \]
and then set
 \[ \Xi_j = \sum_{i=1}^{K_j} p_i. \]
\[ \Xi_j = \sum_{i=1}^{K_j} p_i. \]
Then by Lemma 3.7 we have
 \[ \nu (F_j) = \sum_{i = 1}^{K_j} p_i \operatorname{mult}_{B_{i-1}} F_j^{(i-1)} \ge \sum_{i = 1}^{K_j} p_i = \Xi_j. \]
\[ \nu (F_j) = \sum_{i = 1}^{K_j} p_i \operatorname{mult}_{B_{i-1}} F_j^{(i-1)} \ge \sum_{i = 1}^{K_j} p_i = \Xi_j. \]
Observe that
 \[ m_{i,0} = \operatorname{mult}_{B_{i-1}} Z_0^{(i-1)} = \operatorname{mult}_{B_{i-1}} Z_h^{(i-1)} + \sum_{j=1}^l \operatorname{mult}_{B_{i-1}} Z_j^{(i-1)}, \]
\[ m_{i,0} = \operatorname{mult}_{B_{i-1}} Z_0^{(i-1)} = \operatorname{mult}_{B_{i-1}} Z_h^{(i-1)} + \sum_{j=1}^l \operatorname{mult}_{B_{i-1}} Z_j^{(i-1)}, \]
and that if ![]() $i > K_j$, then
$i > K_j$, then ![]() $\operatorname {mult}_{B_{i-1}} Z_j^{(i-1)} = 0$. This decomposition implies that
$\operatorname {mult}_{B_{i-1}} Z_j^{(i-1)} = 0$. This decomposition implies that
 \begin{align} \sum_{i = 1}^L p_i m_{0, i} &= \sum_{i = 1}^L p_i \operatorname{mult}_{B_{i-1}} (Z_h^{(i-1)}) + \sum_{j = 1}^l \sum_{i=1}^{K_j} p_i \operatorname{mult}_{B_{i-1}} (Z_j^{(i-1)})\nonumber\\ &\le (\Sigma_0 + \Sigma_1) \operatorname{mult}_{\mathsf{p}} Z_h + \sum_{j=1}^l \Xi_j \operatorname{mult}_{\mathsf{p}} Z_j, \end{align}
\begin{align} \sum_{i = 1}^L p_i m_{0, i} &= \sum_{i = 1}^L p_i \operatorname{mult}_{B_{i-1}} (Z_h^{(i-1)}) + \sum_{j = 1}^l \sum_{i=1}^{K_j} p_i \operatorname{mult}_{B_{i-1}} (Z_j^{(i-1)})\nonumber\\ &\le (\Sigma_0 + \Sigma_1) \operatorname{mult}_{\mathsf{p}} Z_h + \sum_{j=1}^l \Xi_j \operatorname{mult}_{\mathsf{p}} Z_j, \end{align}
since ![]() $\operatorname {mult}_{B_{i-1}} (Z_h^{(i-1)}) \le \operatorname {mult}_{\mathsf {p}} Z_h$ and
$\operatorname {mult}_{B_{i-1}} (Z_h^{(i-1)}) \le \operatorname {mult}_{\mathsf {p}} Z_h$ and ![]() $\operatorname {mult}_{B_{i-1}} (Z_j^{(i-1)} )\le \operatorname {mult}_{\mathsf {p}} Z_j$ for every
$\operatorname {mult}_{B_{i-1}} (Z_j^{(i-1)} )\le \operatorname {mult}_{\mathsf {p}} Z_j$ for every ![]() $1 \le i \le L$.
$1 \le i \le L$.
By the inequality in Corollary 3.13 combined with two inequalities (3.14) and (3.15), we get the inequality
 \begin{align} & (\Sigma_0 + \Sigma_1) \operatorname{mult}_{\mathsf{p}} Z_h + \sum_{j = 1}^l \Xi_j \operatorname{mult}_{\mathsf{p}} Z_j \nonumber\\ &\qquad \ge \sum_{i=1}^L p_i m_{0,i} \nonumber\\ &\qquad > 2 n^2 \Sigma_0 + 4 n^2 \Sigma_1 + 4 n^2 \sum_{j = 1}^l \gamma_j \nu (F_j) + 2 n^2 \frac{(\Sigma_2 - \sum_{j=1}^l \gamma_j \nu (F_j))^2}{\Sigma_0 + 2 \Sigma_1 + 2 \Sigma_2}\nonumber\\ &\qquad \ge 2 n^2 (\Sigma_0 + \Sigma_1) + 4 n^2 \sum_{j=1}^l \gamma_j \Xi_j, \end{align}
\begin{align} & (\Sigma_0 + \Sigma_1) \operatorname{mult}_{\mathsf{p}} Z_h + \sum_{j = 1}^l \Xi_j \operatorname{mult}_{\mathsf{p}} Z_j \nonumber\\ &\qquad \ge \sum_{i=1}^L p_i m_{0,i} \nonumber\\ &\qquad > 2 n^2 \Sigma_0 + 4 n^2 \Sigma_1 + 4 n^2 \sum_{j = 1}^l \gamma_j \nu (F_j) + 2 n^2 \frac{(\Sigma_2 - \sum_{j=1}^l \gamma_j \nu (F_j))^2}{\Sigma_0 + 2 \Sigma_1 + 2 \Sigma_2}\nonumber\\ &\qquad \ge 2 n^2 (\Sigma_0 + \Sigma_1) + 4 n^2 \sum_{j=1}^l \gamma_j \Xi_j, \end{align}
where the last inequality follows from the inequality ![]() $\nu (F_j) \ge \Xi _j$.
$\nu (F_j) \ge \Xi _j$.
Dividing (3.16) by ![]() $\Sigma _0 + \Sigma _1$ and setting
$\Sigma _0 + \Sigma _1$ and setting
we get the required inequality.
4. Sextic double solids
Recall that a sextic double solid is a normal projective ![]() $3$-fold
$3$-fold ![]() $X$ which is a double cover of
$X$ which is a double cover of ![]() $\mathbb {P}^3$ branched along a sextic surface. A sextic double solid can be expressed as a weighted hypersurface in
$\mathbb {P}^3$ branched along a sextic surface. A sextic double solid can be expressed as a weighted hypersurface in ![]() $\mathbb {P} (1, 1, 1, 1, 3)$ with homogeneous coordinates
$\mathbb {P} (1, 1, 1, 1, 3)$ with homogeneous coordinates ![]() $x, y, z, t, w$ of weights
$x, y, z, t, w$ of weights ![]() $1, 1, 1, 1, 3$, respectively, defined by an equation of the form
$1, 1, 1, 1, 3$, respectively, defined by an equation of the form
where ![]() $g_6 \in \mathbb {C} [x, y, z, t]$ is a homogeneous polynomial of degree
$g_6 \in \mathbb {C} [x, y, z, t]$ is a homogeneous polynomial of degree ![]() $6$.
$6$.
The aim of this section is to prove the following.
Theorem 4.1 Let ![]() $X$ be a factorial sextic double solid with at worst terminal singularities of type
$X$ be a factorial sextic double solid with at worst terminal singularities of type ![]() $cA_1$. Then
$cA_1$. Then ![]() $X$ is birationally superrigid.
$X$ is birationally superrigid.
In the rest of this section, ![]() $X$ is a sextic double solid and we assume that
$X$ is a sextic double solid and we assume that ![]() $X$ is factorial and has only terminal Gorenstein singularities. We do not impose any other condition on the singularities unless otherwise specified. We denote by
$X$ is factorial and has only terminal Gorenstein singularities. We do not impose any other condition on the singularities unless otherwise specified. We denote by ![]() $\pi \colon X \to \mathbb {P}^3$ the double cover and by
$\pi \colon X \to \mathbb {P}^3$ the double cover and by ![]() $B \subset \mathbb {P}^3$ the branch divisor which is a sextic surface.
$B \subset \mathbb {P}^3$ the branch divisor which is a sextic surface.
Remark 4.2 Under the assumption that a sextic double solid ![]() $X$ has only Gorenstein terminal singularities,
$X$ has only Gorenstein terminal singularities, ![]() $\mathbb {Q}$-factoriality of
$\mathbb {Q}$-factoriality of ![]() $X$ is equivalent to factoriality of
$X$ is equivalent to factoriality of ![]() $X$, that is,
$X$, that is, ![]() $\operatorname {Pic} (X) = \operatorname {Cl} (X) = \mathbb {Z} [-K_X]$ (see [Reference KawamataKaw88, Lemma 5.1]).
$\operatorname {Pic} (X) = \operatorname {Cl} (X) = \mathbb {Z} [-K_X]$ (see [Reference KawamataKaw88, Lemma 5.1]).
4.1 Exclusion of smooth points
The exclusion of smooth points as a maximal center is done as follows.
Proposition 4.3 [Reference Cheltsov and ParkCP10, Lemma 3.1]
No smooth point of ![]() $X$ is a maximal center.
$X$ is a maximal center.
4.2 Exclusion of curves
Lemma 4.4 A curve on ![]() $X$ is not a maximal center except possibly for a curve of degree
$X$ is not a maximal center except possibly for a curve of degree ![]() $1$ which passes through a singular point of
$1$ which passes through a singular point of ![]() $X$ and whose image via
$X$ and whose image via ![]() $\pi$ is not contained in the sextic surface
$\pi$ is not contained in the sextic surface ![]() $B$.
$B$.
Proof. Let ![]() $\Gamma$ be a curve on
$\Gamma$ be a curve on ![]() $X$. Suppose that
$X$. Suppose that ![]() $\Gamma$ is a maximal center. Then
$\Gamma$ is a maximal center. Then ![]() $(- K_X \cdot \Gamma ) < (-K_X)^3 = 2$ by Lemma 2.7. It follows that
$(- K_X \cdot \Gamma ) < (-K_X)^3 = 2$ by Lemma 2.7. It follows that ![]() $\Gamma$ is a curve of degree
$\Gamma$ is a curve of degree ![]() $1$ on
$1$ on ![]() $X$. By the assumption, there exists a movable linear system
$X$. By the assumption, there exists a movable linear system ![]() $\mathcal {M} \sim - n K_X$ on
$\mathcal {M} \sim - n K_X$ on ![]() $X$ such that the pair
$X$ such that the pair ![]() $(X, ({1}/{n}) \mathcal {M})$ is not canonical along
$(X, ({1}/{n}) \mathcal {M})$ is not canonical along ![]() $\Gamma$. In particular, we have
$\Gamma$. In particular, we have ![]() $\operatorname {mult}_{\Gamma } \mathcal {M} > n$.
$\operatorname {mult}_{\Gamma } \mathcal {M} > n$.
In the following, we merely repeat the arguments in the proof of [Reference Cheltsov and ParkCP10, Lemma 3.8] for readers’ convenience. Suppose that ![]() $\pi (\Gamma )$ is contained in the sextic surface
$\pi (\Gamma )$ is contained in the sextic surface ![]() $B \subset \mathbb {P}^3$. We choose and fix a smooth point
$B \subset \mathbb {P}^3$. We choose and fix a smooth point ![]() $\mathsf {p} \in \Gamma$ which is contained in the smooth locus of
$\mathsf {p} \in \Gamma$ which is contained in the smooth locus of ![]() $X$ and which is not contained in any curve in
$X$ and which is not contained in any curve in ![]() $\operatorname {Bs} \mathcal {M}$ other than
$\operatorname {Bs} \mathcal {M}$ other than ![]() $\Gamma$. Let
$\Gamma$. Let ![]() $L \subset \mathbb {P}^3$ be a general line tangent to
$L \subset \mathbb {P}^3$ be a general line tangent to ![]() $B$ at
$B$ at ![]() $\pi (\mathsf {p})$ and let
$\pi (\mathsf {p})$ and let ![]() $\Delta$ be the inverse image of
$\Delta$ be the inverse image of ![]() $L$ by
$L$ by ![]() $\pi$. We see that
$\pi$. We see that ![]() $\Delta$ is a curve of degree
$\Delta$ is a curve of degree ![]() $2$ which is singular at
$2$ which is singular at ![]() $\mathsf {p}$. Moreover, by our choice of
$\mathsf {p}$. Moreover, by our choice of ![]() $\mathsf {p}$,
$\mathsf {p}$, ![]() $\Delta$ is not contained in the base locus of
$\Delta$ is not contained in the base locus of ![]() $\mathcal {M}$. Then we obtain
$\mathcal {M}$. Then we obtain
This is a contradiction.
In the following, let ![]() $\Gamma$ be a curve of degree
$\Gamma$ be a curve of degree ![]() $1$ such that
$1$ such that ![]() $\Gamma \cap \operatorname {Sing} X \ne \emptyset$ and
$\Gamma \cap \operatorname {Sing} X \ne \emptyset$ and ![]() $\pi (\Gamma ) \not \subset B$. The image
$\pi (\Gamma ) \not \subset B$. The image ![]() $\pi (\Gamma ) \subset \mathbb {P}^3$ is a line and we can write
$\pi (\Gamma ) \subset \mathbb {P}^3$ is a line and we can write
where ![]() $\ell _1, \ell _2 \in \mathbb {C} [x, y, z, t]$ are linear forms and
$\ell _1, \ell _2 \in \mathbb {C} [x, y, z, t]$ are linear forms and ![]() $g_3 \in \mathbb {C} [x, y, z, t]$ is a cubic form. We define
$g_3 \in \mathbb {C} [x, y, z, t]$ is a cubic form. We define ![]() $\mathcal {P}$ to be the linear subsystem of
$\mathcal {P}$ to be the linear subsystem of ![]() $| -K_X|$ consisting of members containing
$| -K_X|$ consisting of members containing ![]() $\Gamma$, which is the pencil generated by
$\Gamma$, which is the pencil generated by ![]() $\ell _1$ and
$\ell _1$ and ![]() $\ell _2$, and let
$\ell _2$, and let ![]() $S, T$ be distinct general members of
$S, T$ be distinct general members of ![]() $\mathcal {P}$. We have
$\mathcal {P}$. We have ![]() $T|_S = \Gamma + \Delta$, where
$T|_S = \Gamma + \Delta$, where
By the assumption that ![]() $\pi (\Gamma ) \not \subset B$, we have
$\pi (\Gamma ) \not \subset B$, we have ![]() $g_3 \ne 0$, in other words,
$g_3 \ne 0$, in other words, ![]() $\Delta \ne \Gamma$. Consider the scheme-theoretic intersection
$\Delta \ne \Gamma$. Consider the scheme-theoretic intersection
which consists of ![]() $3$ points counting with multiplicity.
$3$ points counting with multiplicity.
Remark 4.5 We have ![]() $\Gamma \cap \Delta = \pi ^{-1} (\pi (\Gamma ) \cap B)$ set-theoretically. A singular point
$\Gamma \cap \Delta = \pi ^{-1} (\pi (\Gamma ) \cap B)$ set-theoretically. A singular point ![]() $\mathsf {p} \in X$ necessary satisfies
$\mathsf {p} \in X$ necessary satisfies ![]() $\pi (\mathsf {p}) \in B$, so that a point
$\pi (\mathsf {p}) \in B$, so that a point ![]() $\mathsf {p} \in \Gamma \cap \operatorname {Sing} X$ is contained in
$\mathsf {p} \in \Gamma \cap \operatorname {Sing} X$ is contained in ![]() $\Gamma \cap \Delta$.
$\Gamma \cap \Delta$.
We choose and fix a point ![]() $\mathsf {p} \in \Gamma$ which is a
$\mathsf {p} \in \Gamma$ which is a ![]() $cA_k$ point of
$cA_k$ point of ![]() $X$, where
$X$, where ![]() $k = 1, 2$. We choose homogeneous coordinates
$k = 1, 2$. We choose homogeneous coordinates ![]() $x, y, z, t, w$ of
$x, y, z, t, w$ of ![]() $\mathbb {P} (1, 1, 1, 1, 3)$ so that
$\mathbb {P} (1, 1, 1, 1, 3)$ so that ![]() $X$ is defined by
$X$ is defined by
where ![]() $f_i = f_i (y, z, t)$ is a homogeneous polynomial of degree
$f_i = f_i (y, z, t)$ is a homogeneous polynomial of degree ![]() $i$, and
$i$, and ![]() $\mathsf {p} = (1:0:0:0:0)$. This choice of coordinates is possible by [Reference PaemurruPae21, Theorem A]. Replacing coordinates
$\mathsf {p} = (1:0:0:0:0)$. This choice of coordinates is possible by [Reference PaemurruPae21, Theorem A]. Replacing coordinates ![]() $y, z, t$ (while fixing the point
$y, z, t$ (while fixing the point ![]() $\mathsf {p} = (1:0:0:0:0)$), we may assume
$\mathsf {p} = (1:0:0:0:0)$), we may assume ![]() $\pi (\Gamma ) = (z = t = 0) \subset \mathbb {P}^3$, that is,
$\pi (\Gamma ) = (z = t = 0) \subset \mathbb {P}^3$, that is, ![]() $\ell _1 = z$ and
$\ell _1 = z$ and ![]() $\ell _2 = t$. Then we can write
$\ell _2 = t$. Then we can write
for some ![]() $\lambda, \mu, \nu \in \mathbb {C}$. Note that at least one of
$\lambda, \mu, \nu \in \mathbb {C}$. Note that at least one of ![]() $\lambda, \mu, \nu$ is non-zero since
$\lambda, \mu, \nu$ is non-zero since ![]() $\pi (\Gamma ) \not \subset B$. Note also that
$\pi (\Gamma ) \not \subset B$. Note also that
since ![]() $\Gamma \subset X$. With this choice of coordinates, the pencil
$\Gamma \subset X$. With this choice of coordinates, the pencil ![]() $\mathcal {P}$ is generated by
$\mathcal {P}$ is generated by ![]() $z$ and
$z$ and ![]() $t$. The point
$t$. The point ![]() $\mathsf {p}$ is a multiplicity
$\mathsf {p}$ is a multiplicity ![]() $1$ (respectively,
$1$ (respectively, ![]() $2$, respectively,
$2$, respectively, ![]() $3$) point of
$3$) point of ![]() $\Gamma \cap \Delta$ if and only if
$\Gamma \cap \Delta$ if and only if ![]() $\lambda \ne 0$ (respectively,
$\lambda \ne 0$ (respectively, ![]() $\lambda = 0$ and
$\lambda = 0$ and ![]() $\mu \ne 0$, respectively,
$\mu \ne 0$, respectively, ![]() $\lambda = \mu = 0$ and
$\lambda = \mu = 0$ and ![]() $\nu \ne 0$). Let
$\nu \ne 0$). Let ![]() $S$ be a general member of
$S$ be a general member of ![]() $\mathcal {P}$. We analyze the type of
$\mathcal {P}$. We analyze the type of ![]() $G (S, \mathsf {p}, \Gamma )$.
$G (S, \mathsf {p}, \Gamma )$.
Lemma 4.6 Under the notation and assumption as above, let ![]() $\mathsf {p} \in \Gamma$ be a
$\mathsf {p} \in \Gamma$ be a ![]() $cA_1$ point of
$cA_1$ point of ![]() $X$. Then the following assertions hold.
$X$. Then the following assertions hold.
(1) If
 $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 1$, then
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 1$, then  $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type  $A_{1, 1}$.
$A_{1, 1}$.(2) If
 $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 2$, then
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 2$, then  $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type  $A_{1, 1}$ or
$A_{1, 1}$ or  $A_{3, 2}$.
$A_{3, 2}$.(3) If
 $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 3$, then
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 3$, then  $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type  $A_{1, 1}$,
$A_{1, 1}$,  $A_{3, 2}$ or
$A_{3, 2}$ or  $A_{5, 3}$.
$A_{5, 3}$.
Proof. We choose homogeneous coordinates of ![]() $\mathbb {P} := \mathbb {P} (1, 1, 1, 1, 3)$ as above, that is,
$\mathbb {P} := \mathbb {P} (1, 1, 1, 1, 3)$ as above, that is, ![]() $\mathsf {p} = (1:0:0:0:0)$,
$\mathsf {p} = (1:0:0:0:0)$, ![]() $X$ is defined by the (4.3), and
$X$ is defined by the (4.3), and ![]() $\Gamma$ is as given in (4.4). In the following, we assume that a general member
$\Gamma$ is as given in (4.4). In the following, we assume that a general member ![]() $S \in \mathcal {P}$ is cut out by the equation
$S \in \mathcal {P}$ is cut out by the equation ![]() $t = \theta z$ for a general
$t = \theta z$ for a general ![]() $\theta \in \mathbb {C}$. We set
$\theta \in \mathbb {C}$. We set ![]() $U_x := \mathbb {P} (1, 1, 1, 1, 3) \setminus (x = 0)$ and, by a slight abuse of notation, we identify
$U_x := \mathbb {P} (1, 1, 1, 1, 3) \setminus (x = 0)$ and, by a slight abuse of notation, we identify ![]() $U_x$ with the affine space
$U_x$ with the affine space ![]() $\mathbb {A}^4$ with affine coordinates
$\mathbb {A}^4$ with affine coordinates ![]() $y, z, t, w$.
$y, z, t, w$.
We first prove assertion (1). Suppose ![]() $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 1$, that is,
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 1$, that is, ![]() $\lambda \ne 0$. In view of the (4.5), we can write
$\lambda \ne 0$. In view of the (4.5), we can write
where ![]() $\ell (z, t)$ and
$\ell (z, t)$ and ![]() $q (z, t)$ are linear and quadratic forms, respectively. Note that at least one of
$q (z, t)$ are linear and quadratic forms, respectively. Note that at least one of ![]() $\ell (z, t)$ and
$\ell (z, t)$ and ![]() $q (z, t)$ is non-zero since
$q (z, t)$ is non-zero since ![]() $\mathsf {p} \in X$ is of type
$\mathsf {p} \in X$ is of type ![]() $cA_1$. By eliminating the variable
$cA_1$. By eliminating the variable ![]() $t = \theta z$,
$t = \theta z$, ![]() $S$ is defined in
$S$ is defined in ![]() $\mathbb {P} (1, 1, 1, 1, 3)$ by the equation
$\mathbb {P} (1, 1, 1, 1, 3)$ by the equation
where ![]() $\zeta, \eta \in \mathbb {C}$ satisfy
$\zeta, \eta \in \mathbb {C}$ satisfy ![]() $(\zeta, \eta ) \ne (0,0)$. By setting
$(\zeta, \eta ) \ne (0,0)$. By setting ![]() $x = 1$,
$x = 1$, ![]() $S \cap U_x$ is isomorphic to the hypersurface in
$S \cap U_x$ is isomorphic to the hypersurface in ![]() $\mathbb {A}^3_{y, z, w}$ defined by
$\mathbb {A}^3_{y, z, w}$ defined by
where ![]() $h_{\ge 3} (y, z)$ is a polynomial of order at least
$h_{\ge 3} (y, z)$ is a polynomial of order at least ![]() $3$. The point
$3$. The point ![]() $\mathsf {p} = (1:0:0:0:0)$ corresponds to the origin and the curve
$\mathsf {p} = (1:0:0:0:0)$ corresponds to the origin and the curve ![]() $\Gamma$ is defined in
$\Gamma$ is defined in ![]() $\mathbb {A}^3$ by the equations
$\mathbb {A}^3$ by the equations
It is easy to see that ![]() $\mathsf {p} \in S$ is of type
$\mathsf {p} \in S$ is of type ![]() $A_1$ and the proper transform via the blow-up of
$A_1$ and the proper transform via the blow-up of ![]() $\mathsf {p} \in S$ of
$\mathsf {p} \in S$ of ![]() $\Gamma$ intersects the exceptional divisor transversally at one point. It follows that
$\Gamma$ intersects the exceptional divisor transversally at one point. It follows that ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{1, 1}$.
$A_{1, 1}$.
We prove assertion (2). Suppose ![]() $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 2$, that is,
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 2$, that is, ![]() $\lambda = 0$ and
$\lambda = 0$ and ![]() $\mu \ne 0$. We can write
$\mu \ne 0$. We can write
where ![]() $\ell (z, t)$ and
$\ell (z, t)$ and ![]() $q (z, t)$ are linear and quadratic forms, respectively. Let
$q (z, t)$ are linear and quadratic forms, respectively. Let ![]() $\zeta, \eta \in \mathbb {C}$ be such that
$\zeta, \eta \in \mathbb {C}$ be such that ![]() $\ell (z, \theta z) = \zeta z$ and
$\ell (z, \theta z) = \zeta z$ and ![]() $q (z, \theta z) = \eta z^2$. Then, by eliminating
$q (z, \theta z) = \eta z^2$. Then, by eliminating ![]() $t$ and setting
$t$ and setting ![]() $x = 1$,
$x = 1$, ![]() $S \cap U_x$ is isomorphic to the hypersurface in
$S \cap U_x$ is isomorphic to the hypersurface in ![]() $\mathbb {A}^3_{y, z, w}$ defined by the equation
$\mathbb {A}^3_{y, z, w}$ defined by the equation
where ![]() $h_2, h_3 \in \mathbb {C} [y, z]$ are homogeneous polynomials of degree
$h_2, h_3 \in \mathbb {C} [y, z]$ are homogeneous polynomials of degree ![]() $2, 3$, respectively, and
$2, 3$, respectively, and ![]() $h_{\ge 5} \in \mathbb {C} [y, z]$ is a polynomial of order at least
$h_{\ge 5} \in \mathbb {C} [y, z]$ is a polynomial of order at least ![]() $5$. The curve
$5$. The curve ![]() $\Gamma$ is defined in
$\Gamma$ is defined in ![]() $\mathbb {A}^3$ by the equations
$\mathbb {A}^3$ by the equations
Suppose that ![]() $\ell (z, t) \ne 0$. Then
$\ell (z, t) \ne 0$. Then ![]() $\zeta \ne 0$, and it is easy to see that
$\zeta \ne 0$, and it is easy to see that ![]() $\mathsf {p} \in S$ is of type
$\mathsf {p} \in S$ is of type ![]() $A_1$ and
$A_1$ and ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{1, 1}$.
$A_{1, 1}$.
Suppose that ![]() $\ell (z, t) = 0$. Then
$\ell (z, t) = 0$. Then ![]() $\zeta = 0$ and
$\zeta = 0$ and ![]() $\eta \ne 0$. The exceptional divisor
$\eta \ne 0$. The exceptional divisor ![]() $E$ of the blow-up
$E$ of the blow-up ![]() $\tilde {S} \to S$ of
$\tilde {S} \to S$ of ![]() $S$ at
$S$ at ![]() $\mathsf {p}$ is isomorphic to the hypersurface
$\mathsf {p}$ is isomorphic to the hypersurface
where the polynomial ![]() $-w^2 + \eta z^2$ is the least degree part of (4.7). It follows that
$-w^2 + \eta z^2$ is the least degree part of (4.7). It follows that ![]() $E = E_+ + E_-$, where
$E = E_+ + E_-$, where ![]() $E_{\pm } = (w \pm \sqrt {\eta } z = 0)$ are smooth rational curves which meet only at
$E_{\pm } = (w \pm \sqrt {\eta } z = 0)$ are smooth rational curves which meet only at ![]() $\mathsf {q} := (1:0:0) \in \tilde {\mathbb {P}}^2$. By (4.8), the proper transform
$\mathsf {q} := (1:0:0) \in \tilde {\mathbb {P}}^2$. By (4.8), the proper transform ![]() $\tilde {\Gamma } \subset \tilde {S}$ of
$\tilde {\Gamma } \subset \tilde {S}$ of ![]() $\Gamma$ intersect
$\Gamma$ intersect ![]() $E$ only at
$E$ only at ![]() $\mathsf {q}$. The point
$\mathsf {q}$. The point ![]() $\tilde {\mathsf {p}}$ is in the
$\tilde {\mathsf {p}}$ is in the ![]() $y$-chart, denoted by
$y$-chart, denoted by ![]() $\tilde {S}_y$, of the blow-up
$\tilde {S}_y$, of the blow-up ![]() $\tilde {S} \to S$, and
$\tilde {S} \to S$, and ![]() $\tilde {S}_y$ is the hypersurface in
$\tilde {S}_y$ is the hypersurface in ![]() $\tilde {\mathbb {A}}^3 := \mathbb {A}^3_{y, z, w}$ defined by
$\tilde {\mathbb {A}}^3 := \mathbb {A}^3_{y, z, w}$ defined by
Note that ![]() $\tilde {\mathsf {p}}$ corresponds to the origin, and it is an ordinary double point of
$\tilde {\mathsf {p}}$ corresponds to the origin, and it is an ordinary double point of ![]() $\tilde {S}$. Moreover, on
$\tilde {S}$. Moreover, on ![]() $\tilde {S}_y$, we have
$\tilde {S}_y$, we have
 \begin{align*} \tilde{\Gamma} &= (z = w - \mu y - \nu y^2 = 0) \subset \tilde{\mathbb{A}}^3, \\ E_{\pm} &= (y = w - \sqrt{\eta} z = 0) \subset \tilde{\mathbb{A}}^3. \end{align*}
\begin{align*} \tilde{\Gamma} &= (z = w - \mu y - \nu y^2 = 0) \subset \tilde{\mathbb{A}}^3, \\ E_{\pm} &= (y = w - \sqrt{\eta} z = 0) \subset \tilde{\mathbb{A}}^3. \end{align*}
Let ![]() $\hat {S} \to \tilde {S}$ be the blow-up of
$\hat {S} \to \tilde {S}$ be the blow-up of ![]() $\tilde {S}$ at
$\tilde {S}$ at ![]() $\tilde {\mathsf {p}}$ with exceptional curve
$\tilde {\mathsf {p}}$ with exceptional curve ![]() $F$. Then
$F$. Then ![]() $\hat {S}$ is smooth along
$\hat {S}$ is smooth along ![]() $F$,
$F$,
is a smooth rational curve, and ![]() $\hat {\Gamma } \cap F = \{(1:0:\mu )\}$,
$\hat {\Gamma } \cap F = \{(1:0:\mu )\}$, ![]() $F \cap \hat {E}_{\pm } = \{(0:1: \pm \sqrt {\eta })\}$,
$F \cap \hat {E}_{\pm } = \{(0:1: \pm \sqrt {\eta })\}$, ![]() $\hat {\Gamma } \cap \hat {E}_{\pm } = \emptyset$. This shows that
$\hat {\Gamma } \cap \hat {E}_{\pm } = \emptyset$. This shows that ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{3, 2}$.
$A_{3, 2}$.
We prove assertion (3). Suppose ![]() $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 3$, that is,
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 3$, that is, ![]() $\lambda = \mu = 0$ and
$\lambda = \mu = 0$ and ![]() $\nu \ne 0$. We can write
$\nu \ne 0$. We can write
as before. If ![]() $\ell (z, t) \ne 0$, then
$\ell (z, t) \ne 0$, then ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{1, 1}$ as in the previous case. We assume
$A_{1, 1}$ as in the previous case. We assume ![]() $\ell (z, t) = 0$. Then
$\ell (z, t) = 0$. Then ![]() $q (z, t) \ne 0$, and by eliminating
$q (z, t) \ne 0$, and by eliminating ![]() $t$ and setting
$t$ and setting ![]() $x = 1$,
$x = 1$, ![]() $S \cap U_x$ is isomorphic to the hypersurface in
$S \cap U_x$ is isomorphic to the hypersurface in ![]() $\mathbb {A}^3_{y, z, w}$ defined by the equation
$\mathbb {A}^3_{y, z, w}$ defined by the equation
where ![]() $\eta \in \mathbb {C}$ is non-zero and
$\eta \in \mathbb {C}$ is non-zero and ![]() $h (y, z)$ is a polynomial consisting of monomials of degree
$h (y, z)$ is a polynomial consisting of monomials of degree ![]() $2, 3, 4, 5$. The curve
$2, 3, 4, 5$. The curve ![]() $\Gamma$ is defined in
$\Gamma$ is defined in ![]() $\mathbb {A}^3$ by the equations
$\mathbb {A}^3$ by the equations
We write
where ![]() $\alpha _i \in \mathbb {C}$. Let
$\alpha _i \in \mathbb {C}$. Let ![]() $\tilde {S} \to S$ be the blow-up of
$\tilde {S} \to S$ be the blow-up of ![]() $S$ at
$S$ at ![]() $\mathsf {p}$ with exceptional divisor
$\mathsf {p}$ with exceptional divisor ![]() $E$. We see that
$E$. We see that ![]() $E = E_+ + E_-$, where
$E = E_+ + E_-$, where
are smooth rational curves which meet only at ![]() $\tilde {\mathsf {p}} := (1:0:0) \in \tilde {\mathbb {P}}^2$. Moreover the proper transform
$\tilde {\mathsf {p}} := (1:0:0) \in \tilde {\mathbb {P}}^2$. Moreover the proper transform ![]() $\tilde {\Gamma } \subset \tilde {S}$ of
$\tilde {\Gamma } \subset \tilde {S}$ of ![]() $\Gamma$ meet
$\Gamma$ meet ![]() $E_{\pm }$ only at
$E_{\pm }$ only at ![]() $\tilde {\mathsf {p}}$. The
$\tilde {\mathsf {p}}$. The ![]() $y$-chart
$y$-chart ![]() $\tilde {S}_y$ of the blow-up
$\tilde {S}_y$ of the blow-up ![]() $\tilde {S} \to S$ is the hypersurface in
$\tilde {S} \to S$ is the hypersurface in ![]() $\tilde {\mathbb {A}}^3 := \mathbb {A}^3_{y, z, w}$ defined by
$\tilde {\mathbb {A}}^3 := \mathbb {A}^3_{y, z, w}$ defined by
where the omitted terms consist of monomials divisible by ![]() $z$. The point
$z$. The point ![]() $\tilde {\mathsf {p}}$ corresponds to the origin of
$\tilde {\mathsf {p}}$ corresponds to the origin of ![]() $\tilde {\mathbb {A}}^3$. On this chart
$\tilde {\mathbb {A}}^3$. On this chart ![]() $\tilde {S}_y$, we have
$\tilde {S}_y$, we have
 \begin{align*} \tilde{\Gamma} &= (z = w - \nu y^2 = 0) \subset \tilde{\mathbb{A}}^3, \\ E_{\pm} &= (y = w \pm \sqrt{\eta} z = 0) \subset \tilde{\mathbb{A}}^3. \end{align*}
\begin{align*} \tilde{\Gamma} &= (z = w - \nu y^2 = 0) \subset \tilde{\mathbb{A}}^3, \\ E_{\pm} &= (y = w \pm \sqrt{\eta} z = 0) \subset \tilde{\mathbb{A}}^3. \end{align*}
Now let ![]() $\hat {S} \to \tilde {S}$ be the blow-up of
$\hat {S} \to \tilde {S}$ be the blow-up of ![]() $\tilde {S}$ at
$\tilde {S}$ at ![]() $\tilde {\mathsf {p}}$ with exceptional divisor
$\tilde {\mathsf {p}}$ with exceptional divisor
The proper transform ![]() $\hat {\Gamma } \subset \hat {S}$ of
$\hat {\Gamma } \subset \hat {S}$ of ![]() $\Gamma$ intersects
$\Gamma$ intersects ![]() $F$ only at the point
$F$ only at the point ![]() $\hat {\mathsf {p}} := (1:0:0) \in \hat {\mathbb {P}}^2$. We denote by
$\hat {\mathsf {p}} := (1:0:0) \in \hat {\mathbb {P}}^2$. We denote by ![]() $\hat {S}_y$ the
$\hat {S}_y$ the ![]() $y$-chart of the blow-up
$y$-chart of the blow-up ![]() $\hat {S} \to \tilde {S}$ at
$\hat {S} \to \tilde {S}$ at ![]() $\tilde {\mathsf {p}}$, which is the hypersurface in
$\tilde {\mathsf {p}}$, which is the hypersurface in ![]() $\hat {\mathbb {A}}^3$ defined by
$\hat {\mathbb {A}}^3$ defined by
The point ![]() $\hat {\mathsf {p}}$ corresponds to the origin of
$\hat {\mathsf {p}}$ corresponds to the origin of ![]() $\hat {\mathbb {A}}^3$, and
$\hat {\mathbb {A}}^3$, and ![]() $\hat {S}$ has an ordinary double point at
$\hat {S}$ has an ordinary double point at ![]() $\hat {\mathsf {p}}$. Note that the proper transforms
$\hat {\mathsf {p}}$. Note that the proper transforms ![]() $\hat {E}_{\pm } \subset \hat {S}$ of
$\hat {E}_{\pm } \subset \hat {S}$ of ![]() $E_{\pm }$ are both disjoint from the
$E_{\pm }$ are both disjoint from the ![]() $y$-chart
$y$-chart ![]() $\hat {S}_y$.
$\hat {S}_y$.
Suppose that ![]() $\alpha _2 \ne 0$. In this case
$\alpha _2 \ne 0$. In this case ![]() $\tilde {S}$ has an ordinary double point at
$\tilde {S}$ has an ordinary double point at ![]() $\tilde {\mathsf {p}}$. We see that
$\tilde {\mathsf {p}}$. We see that ![]() $\hat {\Gamma }$ intersects
$\hat {\Gamma }$ intersects ![]() $F$ transversally at
$F$ transversally at ![]() $\hat {\mathsf {p}}$,
$\hat {\mathsf {p}}$, ![]() $F \cap \hat {E}_{\pm } = \{(0:1:\pm \sqrt {\eta })\}$, and
$F \cap \hat {E}_{\pm } = \{(0:1:\pm \sqrt {\eta })\}$, and ![]() $\hat {E}_{\pm } \cap \hat {\Gamma } = \emptyset$. This shows that
$\hat {E}_{\pm } \cap \hat {\Gamma } = \emptyset$. This shows that ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{3, 2}$.
$A_{3, 2}$.
Suppose that ![]() $\alpha _2 = 0$. In this case we have
$\alpha _2 = 0$. In this case we have ![]() $F = F_+ + F_-$, where
$F = F_+ + F_-$, where
and we have ![]() $F_+ \cap F_- \cap \hat {\Gamma } = \{\hat {\mathsf {p}}\}$. On the
$F_+ \cap F_- \cap \hat {\Gamma } = \{\hat {\mathsf {p}}\}$. On the ![]() $y$-chart
$y$-chart ![]() $\hat {S}_y$, we have
$\hat {S}_y$, we have
 \begin{align*} \hat{\Gamma} &= (z = w - \nu y = 0) \subset \hat{\mathbb{A}}^3, \\ F_{\pm} &= (y = w \pm \sqrt{\eta} z = 0) \subset \hat{\mathbb{A}}^3. \end{align*}
\begin{align*} \hat{\Gamma} &= (z = w - \nu y = 0) \subset \hat{\mathbb{A}}^3, \\ F_{\pm} &= (y = w \pm \sqrt{\eta} z = 0) \subset \hat{\mathbb{A}}^3. \end{align*}
Let ![]() $\breve {S} \to \hat {S}$ be the blow-up of
$\breve {S} \to \hat {S}$ be the blow-up of ![]() $\hat {S}$ at
$\hat {S}$ at ![]() $\hat {\mathsf {p}}$ with exceptional divisor
$\hat {\mathsf {p}}$ with exceptional divisor ![]() $G$. We have an isomorphism
$G$. We have an isomorphism
and, hence, ![]() $G$ is a smooth rational curve. Let
$G$ is a smooth rational curve. Let ![]() $\breve {\Gamma }$,
$\breve {\Gamma }$, ![]() $\breve {E}_{\pm }$, and
$\breve {E}_{\pm }$, and ![]() $\breve {F}_{\pm }$ be proper transforms of
$\breve {F}_{\pm }$ be proper transforms of ![]() $\Gamma$,
$\Gamma$, ![]() $E_{\pm }$, and
$E_{\pm }$, and ![]() $F_{\pm }$ on
$F_{\pm }$ on ![]() $\breve {S}$, respectively. We have
$\breve {S}$, respectively. We have ![]() $G \cap \breve {\Gamma } = \{(1:0:\nu )\}$ and
$G \cap \breve {\Gamma } = \{(1:0:\nu )\}$ and ![]() $G \cap \breve {F}_{\pm } = \{(0:1:\pm \sqrt {\eta })\}$. This shows that
$G \cap \breve {F}_{\pm } = \{(0:1:\pm \sqrt {\eta })\}$. This shows that ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{5, 3}$. This completes the proof.
$A_{5, 3}$. This completes the proof.
Lemma 4.7 Under the notation and assumption as above, let ![]() $\mathsf {p} \in \Gamma$ be a
$\mathsf {p} \in \Gamma$ be a ![]() $cA_2$-point of
$cA_2$-point of ![]() $X$. Then the following assertions hold.
$X$. Then the following assertions hold.
(1) If
 $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 1$, then
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 1$, then  $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type  $A_{2, 1}$.
$A_{2, 1}$.(2) If
 $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 2$, then
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 2$, then  $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type  $A_{3, 2}$.
$A_{3, 2}$.(3) If
 $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 3$, then
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 3$, then  $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type  $A_{3, 2}$ or
$A_{3, 2}$ or  $A_{5, 3}$.
$A_{5, 3}$.
Proof. We use the same notation as in the previous proof.
We prove assertion (1). Suppose ![]() $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 1$, that is,
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 1$, that is, ![]() $\lambda \ne 0$. Since
$\lambda \ne 0$. Since ![]() $\mathsf {p} \in X$ is of type
$\mathsf {p} \in X$ is of type ![]() $cA_2$, we have
$cA_2$, we have ![]() $f_2 = \lambda ^2 y^2$ and
$f_2 = \lambda ^2 y^2$ and ![]() $f_3 (0, z, t) \ne 0$ as a polynomial. Then, by eliminating
$f_3 (0, z, t) \ne 0$ as a polynomial. Then, by eliminating ![]() $t$ and setting
$t$ and setting ![]() $x = 1$,
$x = 1$, ![]() $S \cap U_x$ is isomorphic to the hypersurface in
$S \cap U_x$ is isomorphic to the hypersurface in ![]() $\mathbb {A}^3_{y, z, w}$ defined by the equation
$\mathbb {A}^3_{y, z, w}$ defined by the equation
where ![]() $\alpha, \beta, \zeta \in \mathbb {C}$ with
$\alpha, \beta, \zeta \in \mathbb {C}$ with ![]() $\zeta \ne 0$ and
$\zeta \ne 0$ and ![]() $h_{\ge 4} (y, z)$ is a polynomial of order at least
$h_{\ge 4} (y, z)$ is a polynomial of order at least ![]() $4$. The point
$4$. The point ![]() $\mathsf {p} = (1:0:0:0:0)$ corresponds to the origin and the curve
$\mathsf {p} = (1:0:0:0:0)$ corresponds to the origin and the curve ![]() $\Gamma$ is defined in
$\Gamma$ is defined in ![]() $\mathbb {A}^3$ by the (4.6). Let
$\mathbb {A}^3$ by the (4.6). Let ![]() $\tilde {S} \to S$ be the blow-up of
$\tilde {S} \to S$ be the blow-up of ![]() $S$ at
$S$ at ![]() $\mathsf {p}$ with exceptional divisor
$\mathsf {p}$ with exceptional divisor ![]() $E$. Then
$E$. Then ![]() $E = E_+ + E_-$, where
$E = E_+ + E_-$, where
The surface ![]() $\tilde {S}$ is smooth outside the singular locus of
$\tilde {S}$ is smooth outside the singular locus of ![]() $E$. The singular locus of
$E$. The singular locus of ![]() $E$ is the intersection point
$E$ is the intersection point ![]() $\mathsf {q}$ of
$\mathsf {q}$ of ![]() $E_+$ and
$E_+$ and ![]() $E_-$, where
$E_-$, where ![]() $\mathsf {q} = (0:1:0) \in \tilde {\mathbb {P}}^2$. The point
$\mathsf {q} = (0:1:0) \in \tilde {\mathbb {P}}^2$. The point ![]() $\mathsf {q}$ corresponds to the origin of the
$\mathsf {q}$ corresponds to the origin of the ![]() $z$-chart
$z$-chart ![]() $\tilde {S}_z$ which is the hypersurface in
$\tilde {S}_z$ which is the hypersurface in ![]() $\tilde {\mathbb {A}}^3 := \mathbb {A}^3_{y, z, w}$ defined by
$\tilde {\mathbb {A}}^3 := \mathbb {A}^3_{y, z, w}$ defined by
It follows that ![]() $\tilde {S}$ is smooth at
$\tilde {S}$ is smooth at ![]() $\tilde {\mathsf {p}}$. Then, since
$\tilde {\mathsf {p}}$. Then, since ![]() $\Gamma$ is defined by the (4.6), we have
$\Gamma$ is defined by the (4.6), we have ![]() $\tilde {\Gamma } \cap E = \{\mathsf {q}'\}$, where
$\tilde {\Gamma } \cap E = \{\mathsf {q}'\}$, where ![]() $\mathsf {q}' := (1:0:\lambda ) \in \tilde {\mathbb {P}}^2$. We have
$\mathsf {q}' := (1:0:\lambda ) \in \tilde {\mathbb {P}}^2$. We have ![]() $\mathsf {q}' \in E_-$ and
$\mathsf {q}' \in E_-$ and ![]() $\mathsf {q}' \notin E_+$. This shows that
$\mathsf {q}' \notin E_+$. This shows that ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{2,1}$.
$A_{2,1}$.
We prove assertion (2). Suppose ![]() $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 2$, that is,
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 2$, that is, ![]() $\lambda = 0$ and
$\lambda = 0$ and ![]() $\nu \ne 0$. We see that
$\nu \ne 0$. We see that ![]() $f_2$ is a square of a linear form in
$f_2$ is a square of a linear form in ![]() $z$ and
$z$ and ![]() $t$. We may assume
$t$. We may assume ![]() $f_2 = z^2$ by replacing
$f_2 = z^2$ by replacing ![]() $z$ and
$z$ and ![]() $t$. By eliminating
$t$. By eliminating ![]() $t$ and setting
$t$ and setting ![]() $x = 1$,
$x = 1$, ![]() $S \cap U_x$ is isomorphic to the hypersurface in
$S \cap U_x$ is isomorphic to the hypersurface in ![]() $\mathbb {A}^3_{y, z, w}$ defined by the equation
$\mathbb {A}^3_{y, z, w}$ defined by the equation
where ![]() $h_2 (y, z)$ is a homogeneous polynomial of degree
$h_2 (y, z)$ is a homogeneous polynomial of degree ![]() $2$ and
$2$ and ![]() $h_{\ge 5} (y, z)$ is a polynomial of order at least
$h_{\ge 5} (y, z)$ is a polynomial of order at least ![]() $5$. The curve
$5$. The curve ![]() $\Gamma$ is defined in
$\Gamma$ is defined in ![]() $\mathbb {A}^3$ by the (4.8). By repeating similar computations as in assertion (2) of Lemma 4.6, we see that
$\mathbb {A}^3$ by the (4.8). By repeating similar computations as in assertion (2) of Lemma 4.6, we see that ![]() $\mathsf {p} \in S$ is of type
$\mathsf {p} \in S$ is of type ![]() $A_3$ and
$A_3$ and ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{3, 2}$.
$A_{3, 2}$.
Table 1. Types of ![]() $G (S, \mathsf {p}, \Gamma )$.
$G (S, \mathsf {p}, \Gamma )$.

We prove assertion (3). Suppose ![]() $\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 3$, that is,
$\operatorname {mult}_{\mathsf {p}} \Gamma \cap \Delta = 3$, that is, ![]() $\lambda = \mu = 0$ and
$\lambda = \mu = 0$ and ![]() $\nu \ne 0$. As in previous arguments,
$\nu \ne 0$. As in previous arguments, ![]() $S \cap U_x$ is isomorphic to the hypersurface in
$S \cap U_x$ is isomorphic to the hypersurface in ![]() $\mathbb {A}^3_{y, z, w}$ defined by the equation
$\mathbb {A}^3_{y, z, w}$ defined by the equation
where ![]() $h (y, z)$ is a polynomial consisting of monomials of degree
$h (y, z)$ is a polynomial consisting of monomials of degree ![]() $2, 3, 4, 5$. The curve
$2, 3, 4, 5$. The curve ![]() $\Gamma$ is defined in
$\Gamma$ is defined in ![]() $\mathbb {A}^3$ by the (4.9). By the same argument as in the proof of Lemma 4.6(3), we conclude that
$\mathbb {A}^3$ by the (4.9). By the same argument as in the proof of Lemma 4.6(3), we conclude that ![]() $G (S, \mathsf {p}, \Gamma )$ is of type
$G (S, \mathsf {p}, \Gamma )$ is of type ![]() $A_{3, 2}$ or
$A_{3, 2}$ or ![]() $A_{5, 3}$.
$A_{5, 3}$.
The results obtained by Lemmas 4.6 and 4.7 are summarized in Table 1, where the correction term given in the right-most column is the number ![]() $k (n-k+1)/(n+1)$ (corresponding to the extended graph of type
$k (n-k+1)/(n+1)$ (corresponding to the extended graph of type ![]() $A_{n, k}$) appearing in Lemma 2.11.
$A_{n, k}$) appearing in Lemma 2.11.
Proposition 4.8 Let ![]() $X$ be a factorial sextic double solid with at worst terminal singularities of type
$X$ be a factorial sextic double solid with at worst terminal singularities of type ![]() $cA_1$ and
$cA_1$ and ![]() $cA_2$. Then no curve on
$cA_2$. Then no curve on ![]() $X$ is a maximal center.
$X$ is a maximal center.
Proof. By Lemma 4.4, it remains to consider a curve ![]() $\Gamma$ of degree
$\Gamma$ of degree ![]() $1$ such that
$1$ such that ![]() $\Gamma \cap \operatorname {Sing} X \ne \emptyset$ and
$\Gamma \cap \operatorname {Sing} X \ne \emptyset$ and ![]() $\pi (\Gamma ) \not \subset B$.
$\pi (\Gamma ) \not \subset B$.
Let ![]() $\mathcal {P} \subset | - K_X |$ be the pencil as above, and let
$\mathcal {P} \subset | - K_X |$ be the pencil as above, and let ![]() $S, T \in \mathcal {P}$ be general members. By [Reference OkadaOka20b, Lemma 10.4],
$S, T \in \mathcal {P}$ be general members. By [Reference OkadaOka20b, Lemma 10.4], ![]() $S$ and
$S$ and ![]() $T$ are smooth outside
$T$ are smooth outside ![]() $\Gamma \cap \operatorname {Sing} X$. We have
$\Gamma \cap \operatorname {Sing} X$. We have ![]() $T|_S = \Gamma + \Delta$, where
$T|_S = \Gamma + \Delta$, where ![]() $\Delta \ne \Gamma$ is also a curve of degree
$\Delta \ne \Gamma$ is also a curve of degree ![]() $1$. By (4.2), we see that
$1$. By (4.2), we see that ![]() $\Gamma \cap \Delta$ consists of
$\Gamma \cap \Delta$ consists of ![]() $3$ points counting with multiplicity.
$3$ points counting with multiplicity.
We compute the self-intersection number ![]() $(\Gamma ^2)_S$. Let
$(\Gamma ^2)_S$. Let ![]() $\mathsf {p}_1, \ldots, \mathsf {p}_l$ be the points in
$\mathsf {p}_1, \ldots, \mathsf {p}_l$ be the points in ![]() $\Gamma \cap \operatorname {Sing} (X)$. By Remark 4.5, these points are contained in
$\Gamma \cap \operatorname {Sing} (X)$. By Remark 4.5, these points are contained in ![]() $\Gamma \cap \Delta$. We set
$\Gamma \cap \Delta$. We set ![]() $m_i = \operatorname {mult}_{\mathsf {p}_i} \Gamma \cap \Delta$. Then
$m_i = \operatorname {mult}_{\mathsf {p}_i} \Gamma \cap \Delta$. Then ![]() $l \le \sum m_i \le 3$. Let
$l \le \sum m_i \le 3$. Let ![]() $A_{n_i, k_i}$ be the type of
$A_{n_i, k_i}$ be the type of ![]() $G (S, \mathsf {p}_i, \Gamma )$ which is described in Lemmas 4.6 and 4.7 (see also Table 1). Since
$G (S, \mathsf {p}_i, \Gamma )$ which is described in Lemmas 4.6 and 4.7 (see also Table 1). Since ![]() $K_S = 0$ and
$K_S = 0$ and ![]() $\Gamma \cong \mathbb {P}^1$, we have
$\Gamma \cong \mathbb {P}^1$, we have
 \[ (\Gamma^2)_S = - 2 + \sum_{i = 1}^l \frac{k_i (n_i - k_i + 1)}{n_i + 1} \]
\[ (\Gamma^2)_S = - 2 + \sum_{i = 1}^l \frac{k_i (n_i - k_i + 1)}{n_i + 1} \]
by Lemma 2.11. By considering all the possible combinations of singular points ![]() $\mathsf {p}_1, \ldots, \mathsf {p}_l$ satisfying
$\mathsf {p}_1, \ldots, \mathsf {p}_l$ satisfying ![]() ${\sum } m_i \le 3$, we have the upper bound
${\sum } m_i \le 3$, we have the upper bound
where this maximum (of the correction term corresponding to singular points) is attained when ![]() $\Gamma \cap \Delta$ consists of
$\Gamma \cap \Delta$ consists of ![]() $3$ multiplicity
$3$ multiplicity ![]() $1$ points of
$1$ points of ![]() $\Gamma \cap \Delta$ which are
$\Gamma \cap \Delta$ which are ![]() $cA_2$ singular points of
$cA_2$ singular points of ![]() $X$. Since
$X$. Since ![]() $T|_S = \Gamma + \Delta$, we have
$T|_S = \Gamma + \Delta$, we have
Thus, by Lemma 2.8, the curve ![]() $\Gamma$ is not a maximal center.
$\Gamma$ is not a maximal center.
4.3 Exclusion of  $cA_1$ points and proof of Theorem 4.1
$cA_1$ points and proof of Theorem 4.1
Proposition 4.9 Let ![]() $X$ be a factorial sextic double solid with at worst terminal singularities of type
$X$ be a factorial sextic double solid with at worst terminal singularities of type ![]() $cA_1$. Then no singular point on
$cA_1$. Then no singular point on ![]() $X$ is a maximal center.
$X$ is a maximal center.
Proof. Let ![]() $\mathsf {p} \in X$ be a
$\mathsf {p} \in X$ be a ![]() $cA_1$ point. Suppose that
$cA_1$ point. Suppose that ![]() $\mathsf {p}$ is a maximal center. Then, by Theorem 3.14, there exists a mobile linear system
$\mathsf {p}$ is a maximal center. Then, by Theorem 3.14, there exists a mobile linear system ![]() $\mathcal {M} \subset |\mathcal {O}_X (n)|$ on
$\mathcal {M} \subset |\mathcal {O}_X (n)|$ on ![]() $X$ such that
$X$ such that
where ![]() $D_1, D_2$ are general members in
$D_1, D_2$ are general members in ![]() $\mathcal {M}$. Let
$\mathcal {M}$. Let ![]() $\mathcal {H}$ be the linear subsystem of
$\mathcal {H}$ be the linear subsystem of ![]() $|\mathcal {O}_X (1)|$ consisting of divisors vanishing at
$|\mathcal {O}_X (1)|$ consisting of divisors vanishing at ![]() $\mathsf {p}$. Then the base locus of
$\mathsf {p}$. Then the base locus of ![]() $\mathcal {H}$ consists of at most
$\mathcal {H}$ consists of at most ![]() $2$ points (including
$2$ points (including ![]() $\mathsf {p}$) and, hence, we can take a divisor
$\mathsf {p}$) and, hence, we can take a divisor ![]() $S$ in
$S$ in ![]() $\mathcal {H}$ which does not contain any component of the effective
$\mathcal {H}$ which does not contain any component of the effective ![]() $1$-cycle
$1$-cycle ![]() $D_1 \cdot D_2$. Then, we have
$D_1 \cdot D_2$. Then, we have
This is a contradiction and ![]() $\mathsf {p}$ is not a maximal center.
$\mathsf {p}$ is not a maximal center.
4.4 Sarkisov links centered at  $cA_3$ singular points
$cA_3$ singular points
Let ![]() $X$ be a factorial sextic double solid with only terminal Gorenstein singularities and suppose that
$X$ be a factorial sextic double solid with only terminal Gorenstein singularities and suppose that ![]() $X$ admits a
$X$ admits a ![]() $cA_3$ point
$cA_3$ point ![]() $\mathsf {p} \in X$. Then
$\mathsf {p} \in X$. Then ![]() $X$ is a hypersurface of degree
$X$ is a hypersurface of degree ![]() $6$ in
$6$ in ![]() $\mathbb {P} (1, 1, 1, 1, 3)$ with homogeneous coordinates
$\mathbb {P} (1, 1, 1, 1, 3)$ with homogeneous coordinates ![]() $x, y, z, t, w$ of weights
$x, y, z, t, w$ of weights ![]() $1, 1, 1, 1, 3$, respectively, and by [Reference PaemurruPae21, Theorem A] the defining polynomial can be written as
$1, 1, 1, 1, 3$, respectively, and by [Reference PaemurruPae21, Theorem A] the defining polynomial can be written as
where ![]() $f_i \in \mathbb {C} [y, z, t]$ is a homogeneous polynomial of degree
$f_i \in \mathbb {C} [y, z, t]$ is a homogeneous polynomial of degree ![]() $i$. Moreover, the
$i$. Moreover, the ![]() $cA_3$ point
$cA_3$ point ![]() $\mathsf {p}$ is
$\mathsf {p}$ is ![]() $(1:0:0:0:0) \in X$. We set
$(1:0:0:0:0) \in X$. We set ![]() $g_4 = f_4 - \tfrac {1}{4} f_2^2$ and then
$g_4 = f_4 - \tfrac {1}{4} f_2^2$ and then
Let ![]() $X_{\pm } \subset \mathbb {P} (1, 1, 1, 1, 3)$ be the hypersurface defined by
$X_{\pm } \subset \mathbb {P} (1, 1, 1, 1, 3)$ be the hypersurface defined by ![]() $f_{\pm } = 0$. We see that
$f_{\pm } = 0$. We see that ![]() $X$ is isomorphic to
$X$ is isomorphic to ![]() $X_{\pm }$ by the coordinate change
$X_{\pm }$ by the coordinate change ![]() $w \mapsto w \pm (x^2 t + \tfrac {1}{2} x f_2)$.
$w \mapsto w \pm (x^2 t + \tfrac {1}{2} x f_2)$.
We set ![]() $U = X \setminus (x = 0) \cap X$ and
$U = X \setminus (x = 0) \cap X$ and ![]() $U_{\pm } = X_{\pm } \setminus (x = 0) \cap {X_{\pm }}$ which are affine open subsets of
$U_{\pm } = X_{\pm } \setminus (x = 0) \cap {X_{\pm }}$ which are affine open subsets of ![]() $X$ and
$X$ and ![]() $X_{\pm }$, respectively, and we have
$X_{\pm }$, respectively, and we have
 \begin{align*} U &= (- w^2 + t^2 + t f_2 + f_4 + f_5 + f_6 = 0) \subset \mathbb{A}^4_{y, z, t, w}, \\ U_{\pm} &= (- w (w \pm (t + f_2)) + g_4 + f_5 + f_6 = 0) \subset \mathbb{A}^4_{y, z, t, w}. \end{align*}
\begin{align*} U &= (- w^2 + t^2 + t f_2 + f_4 + f_5 + f_6 = 0) \subset \mathbb{A}^4_{y, z, t, w}, \\ U_{\pm} &= (- w (w \pm (t + f_2)) + g_4 + f_5 + f_6 = 0) \subset \mathbb{A}^4_{y, z, t, w}. \end{align*}
Let ![]() $\varphi \colon Y \to X$ and
$\varphi \colon Y \to X$ and ![]() $\varphi _{\pm } \colon Y_{\pm } \to X_{\pm }$ be the birational morphisms obtained as the weighted blow-up of
$\varphi _{\pm } \colon Y_{\pm } \to X_{\pm }$ be the birational morphisms obtained as the weighted blow-up of ![]() $U$ and
$U$ and ![]() $U_{\pm }$ at the origin with weights
$U_{\pm }$ at the origin with weights ![]() $\operatorname {wt} (y, z, t, w) = (1, 1, 2, 2)$ and
$\operatorname {wt} (y, z, t, w) = (1, 1, 2, 2)$ and ![]() $\operatorname {wt} (y, z, t, w) = (1, 1, 1, 3)$, respectively. According to the classification of divisorial contractions to
$\operatorname {wt} (y, z, t, w) = (1, 1, 1, 3)$, respectively. According to the classification of divisorial contractions to ![]() $cA$ points [Reference KawakitaKaw03, Theorem 1.13],
$cA$ points [Reference KawakitaKaw03, Theorem 1.13], ![]() $\varphi, \varphi _{\pm }$ are all the divisorial contractions of
$\varphi, \varphi _{\pm }$ are all the divisorial contractions of ![]() $\mathsf {p} \in X$ with discrepancy
$\mathsf {p} \in X$ with discrepancy ![]() $1$. We sometimes identify
$1$. We sometimes identify ![]() $\varphi _{\pm }$ with the composite
$\varphi _{\pm }$ with the composite ![]() $Y_{\pm } \xrightarrow {\varphi _{\pm }} X_{\pm } \cong X$. We call
$Y_{\pm } \xrightarrow {\varphi _{\pm }} X_{\pm } \cong X$. We call ![]() $\varphi _+$,
$\varphi _+$, ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi _-$ the
$\varphi _-$ the ![]() $(3, 1, 1, 1)$-,
$(3, 1, 1, 1)$-, ![]() $(2, 2, 1, 1)$-and
$(2, 2, 1, 1)$-and ![]() $(1, 3, 1, 1)$-Kawakita blow-ups of
$(1, 3, 1, 1)$-Kawakita blow-ups of ![]() $\mathsf {p} \in X$, respectively.
$\mathsf {p} \in X$, respectively.
4.4.1  $(3, 1, 1, 1)$- and
$(3, 1, 1, 1)$- and  $(1, 3, 1, 1)$-Kawakita blow-ups
$(1, 3, 1, 1)$-Kawakita blow-ups
We consider the ![]() $(3, 1, 1, 1)$- and
$(3, 1, 1, 1)$- and ![]() $(1, 3, 1, 1)$-Kawakita blow-ups
$(1, 3, 1, 1)$-Kawakita blow-ups ![]() $\varphi _{\pm }$ of
$\varphi _{\pm }$ of ![]() $\mathsf {p} \in X$, and show that there is a Sarkisov self-link initiated by
$\mathsf {p} \in X$, and show that there is a Sarkisov self-link initiated by ![]() $\varphi _{\pm }$ if
$\varphi _{\pm }$ if ![]() $\varphi _{\pm }$ is a maximal extraction.
$\varphi _{\pm }$ is a maximal extraction.
Let ![]() $\pi _{X_{\pm }} \colon X_{\pm } \dashrightarrow \mathbb {P} (1, 1, 1, 3)$ be the projection to the coordinates
$\pi _{X_{\pm }} \colon X_{\pm } \dashrightarrow \mathbb {P} (1, 1, 1, 3)$ be the projection to the coordinates ![]() $y, z, t, w$, which is defined outside the point
$y, z, t, w$, which is defined outside the point ![]() $\mathsf {p} = (1:0:0:0:0) \in X_{\pm }$. The sections
$\mathsf {p} = (1:0:0:0:0) \in X_{\pm }$. The sections ![]() $y, z, t \in \mathrm {H}^0 (X_{\pm }, -K_{X_{\pm }})$ lift to sections
$y, z, t \in \mathrm {H}^0 (X_{\pm }, -K_{X_{\pm }})$ lift to sections ![]() $\tilde {y}, \tilde {z}, \tilde {t}$ in
$\tilde {y}, \tilde {z}, \tilde {t}$ in ![]() $\mathrm {H}^0 (Y_{\pm }, -K_{Y_{\pm }})$, and
$\mathrm {H}^0 (Y_{\pm }, -K_{Y_{\pm }})$, and ![]() $w \in \mathrm {H}^0 (X_{\pm }, - 3 K_{X_{\pm }})$ lifts to a section
$w \in \mathrm {H}^0 (X_{\pm }, - 3 K_{X_{\pm }})$ lifts to a section ![]() $\tilde {w}$ in
$\tilde {w}$ in ![]() $\mathrm {H}^0 (Y_{\pm }, - 3 K_{Y_{\pm }})$. These sections
$\mathrm {H}^0 (Y_{\pm }, - 3 K_{Y_{\pm }})$. These sections ![]() $\tilde {y}, \tilde {z}, \tilde {z}$ and
$\tilde {y}, \tilde {z}, \tilde {z}$ and ![]() $\tilde {w}$ define the composite
$\tilde {w}$ define the composite ![]() $\pi _{Y_{\pm }} := \pi _{X_{\pm }} \circ \varphi _{\pm } \colon Y_{\pm } \dashrightarrow \mathbb {P} (1, 1, 1, 3)$, and their common zero locus (on
$\pi _{Y_{\pm }} := \pi _{X_{\pm }} \circ \varphi _{\pm } \colon Y_{\pm } \dashrightarrow \mathbb {P} (1, 1, 1, 3)$, and their common zero locus (on ![]() $Y_{\pm }$) is empty. This is verified in the following way. For the
$Y_{\pm }$) is empty. This is verified in the following way. For the ![]() $\varphi _{\pm }$-exceptional divisor
$\varphi _{\pm }$-exceptional divisor ![]() $E_{\pm }$, we have the natural isomorphism
$E_{\pm }$, we have the natural isomorphism
and the restriction of the sections ![]() $\tilde {y}, \tilde {z}, \tilde {t}, \tilde {w}$ on
$\tilde {y}, \tilde {z}, \tilde {t}, \tilde {w}$ on ![]() $E_{\pm }$ are
$E_{\pm }$ are ![]() $y, z, t, w$, respectively. Thus, their common zero loci on
$y, z, t, w$, respectively. Thus, their common zero loci on ![]() $E_{\pm }$ and, hence, on
$E_{\pm }$ and, hence, on ![]() $Y_{\pm }$, are empty. It follows that
$Y_{\pm }$, are empty. It follows that ![]() $\pi _{Y_{\pm }} \colon Y_{\pm } \to \mathbb {P} (1, 1, 1, 3)$ is a morphism. The defining polynomial
$\pi _{Y_{\pm }} \colon Y_{\pm } \to \mathbb {P} (1, 1, 1, 3)$ is a morphism. The defining polynomial ![]() $f_{\pm }$ given in (4.11) is quadratic with respect to
$f_{\pm }$ given in (4.11) is quadratic with respect to ![]() $x$:
$x$:
We set
and denote by ![]() $\tilde {D}_i$ the proper transform of
$\tilde {D}_i$ the proper transform of ![]() $D_i$ on
$D_i$ on ![]() $Y_{\pm }$. We see that
$Y_{\pm }$. We see that ![]() $\pi _{Y_{\pm }}$ is a generically finite morphism of degree
$\pi _{Y_{\pm }}$ is a generically finite morphism of degree ![]() $2$ which contracts the subset
$2$ which contracts the subset ![]() $\Xi := \tilde {D}_4 \cap \tilde {D}_5 \cap \tilde {D}_6$ onto its image
$\Xi := \tilde {D}_4 \cap \tilde {D}_5 \cap \tilde {D}_6$ onto its image
Let ![]() $Y_{\pm } \xrightarrow {\psi _{\pm }} Z_{\pm } \xrightarrow {\pi _{Z_{\pm }}} \mathbb {P} (1, 1, 1, 3)$ be the Stein factorization of
$Y_{\pm } \xrightarrow {\psi _{\pm }} Z_{\pm } \xrightarrow {\pi _{Z_{\pm }}} \mathbb {P} (1, 1, 1, 3)$ be the Stein factorization of ![]() $\pi _{Y_{\pm }}$. Then
$\pi _{Y_{\pm }}$. Then ![]() $\psi _{\pm }$ is the birational morphism defined by
$\psi _{\pm }$ is the birational morphism defined by ![]() $|- r K_{Y_{\pm }} |$ for sufficiently large
$|- r K_{Y_{\pm }} |$ for sufficiently large ![]() $r > 0$ and
$r > 0$ and ![]() $\pi _{Z_{\pm }}$ is a double cover. Note that
$\pi _{Z_{\pm }}$ is a double cover. Note that ![]() $-K_{Y_{\pm }}$ is nef and big but not ample. Let
$-K_{Y_{\pm }}$ is nef and big but not ample. Let ![]() $\iota _{\pm } \colon Z_{\pm } \to Z_{\pm }$ be the biregular involution interchanging two points in fibers of the double cover
$\iota _{\pm } \colon Z_{\pm } \to Z_{\pm }$ be the biregular involution interchanging two points in fibers of the double cover ![]() $\pi _{Z_{\pm }}$, and consider the diagram
$\pi _{Z_{\pm }}$, and consider the diagram

where ![]() $\tau _{\pm } := \psi ^{-1}_{\pm } \circ \iota _{\pm } \circ \psi _{\pm }$.
$\tau _{\pm } := \psi ^{-1}_{\pm } \circ \iota _{\pm } \circ \psi _{\pm }$.
Proposition 4.10 Let ![]() $X$ be a factorial sextic double solid
$X$ be a factorial sextic double solid ![]() $X$ with only terminal Gorenstein singularities and let
$X$ with only terminal Gorenstein singularities and let ![]() $\mathsf {p} \in X$ be a
$\mathsf {p} \in X$ be a ![]() $cA_3$ point. Let
$cA_3$ point. Let ![]() $\varphi _{\pm } \colon Y_{\pm } \to X$ be the
$\varphi _{\pm } \colon Y_{\pm } \to X$ be the ![]() $(3, 1, 1, 1)$- and
$(3, 1, 1, 1)$- and ![]() $(1, 3, 1, 1)$-Kawakita blow-ups with center
$(1, 3, 1, 1)$-Kawakita blow-ups with center ![]() $\mathsf {p}$. Then one of the following holds.
$\mathsf {p}$. Then one of the following holds.
(1) We have
 $\psi _{\pm }$ is divisorial. In this case
$\psi _{\pm }$ is divisorial. In this case  $\varphi _{\pm }$ is not a maximal extraction.
$\varphi _{\pm }$ is not a maximal extraction.(2) We have
 $\psi _{\pm }$ is small. In this case
$\psi _{\pm }$ is small. In this case  $\tau _{\pm }$ is the flop of
$\tau _{\pm }$ is the flop of  $\psi _{\pm }$ and the diagram (4.12) gives a Sarkisov self-link
$\psi _{\pm }$ and the diagram (4.12) gives a Sarkisov self-link  $\sigma _{\pm } \colon X \dashrightarrow X$ initiated by
$\sigma _{\pm } \colon X \dashrightarrow X$ initiated by  $\varphi _{\pm }$.
$\varphi _{\pm }$.
Proof. This follows from the above arguments and [Reference OkadaOka18, Lemma 3.2].
4.4.2  $(2, 2, 1, 1)$-Kawakita blow-up
$(2, 2, 1, 1)$-Kawakita blow-up
We consider the ![]() $(2, 2, 1, 1)$-Kawakita blow-up
$(2, 2, 1, 1)$-Kawakita blow-up ![]() $\varphi \colon Y \to X$ of
$\varphi \colon Y \to X$ of ![]() $\mathsf {p} \in X$, and show that
$\mathsf {p} \in X$, and show that ![]() $\varphi$ is not a maximal extraction.
$\varphi$ is not a maximal extraction.
Proposition 4.11 Let ![]() $X$ be a factorial sextic double solid
$X$ be a factorial sextic double solid ![]() $X$ with only terminal Gorenstein singularities and let
$X$ with only terminal Gorenstein singularities and let ![]() $\mathsf {p} \in X$ be a
$\mathsf {p} \in X$ be a ![]() $cA_3$ point. Let
$cA_3$ point. Let ![]() $\varphi \colon Y \to X$ be the
$\varphi \colon Y \to X$ be the ![]() $(2, 2, 1, 1)$-Kawakita blow-up. Then
$(2, 2, 1, 1)$-Kawakita blow-up. Then ![]() $\varphi$ is not a maximal extraction.
$\varphi$ is not a maximal extraction.
Proof. Let ![]() $\pi \colon X \dashrightarrow \mathbb {P} (1, 1, 1, 2, 4)$ be the map defined by
$\pi \colon X \dashrightarrow \mathbb {P} (1, 1, 1, 2, 4)$ be the map defined by
Let ![]() $y, z, t, \alpha, \beta$ be the homogeneous coordinates of
$y, z, t, \alpha, \beta$ be the homogeneous coordinates of ![]() $\mathbb {P} (1, 1, 1, 2, 4)$ of weights
$\mathbb {P} (1, 1, 1, 2, 4)$ of weights ![]() $1, 1, 1, 2, 4$, respectively. Then the image of
$1, 1, 1, 2, 4$, respectively. Then the image of ![]() $\pi$, denoted by
$\pi$, denoted by ![]() $Z$, is the hypersurface in
$Z$, is the hypersurface in ![]() $\mathbb {P} (1, 1, 1, 2, 4)$ defined by
$\mathbb {P} (1, 1, 1, 2, 4)$ defined by
where ![]() $h$ is obtained by replacing
$h$ is obtained by replacing ![]() $x t$ by
$x t$ by ![]() $\alpha$ and
$\alpha$ and ![]() $w t$ by
$w t$ by ![]() $\beta$ in
$\beta$ in ![]() $t^2 f$. The sections
$t^2 f$. The sections ![]() $y, z, t, x t, w t$ lift to pluri-anticanonical sections on
$y, z, t, x t, w t$ lift to pluri-anticanonical sections on ![]() $Y$ and their common zero locus (on
$Y$ and their common zero locus (on ![]() $Y$) is empty. It follows that the induced map
$Y$) is empty. It follows that the induced map ![]() $\psi = \pi \circ \varphi \colon Y \dashrightarrow Z$ is a morphism, and we have the following commutative diagram.
$\psi = \pi \circ \varphi \colon Y \dashrightarrow Z$ is a morphism, and we have the following commutative diagram.

Note that ![]() $\psi$ is a birational morphism and it contracts the proper transform of the divisor
$\psi$ is a birational morphism and it contracts the proper transform of the divisor ![]() $(t = 0)_X$ to the curve
$(t = 0)_X$ to the curve
Moreover, ![]() $\psi$ is defined by
$\psi$ is defined by ![]() $| - r K_Y |$ for a sufficiently large
$| - r K_Y |$ for a sufficiently large ![]() $r > 0$ and, thus, any curve contracted by
$r > 0$ and, thus, any curve contracted by ![]() $\psi$ is
$\psi$ is ![]() $K_Y$-trivial. It follows that there are infinitely many curves on
$K_Y$-trivial. It follows that there are infinitely many curves on ![]() $Y$ which intersect
$Y$ which intersect ![]() $-K_Y$ non-positively and the
$-K_Y$ non-positively and the ![]() $\psi$-exceptional divisor
$\psi$-exceptional divisor ![]() $E$ positively. By [Reference OkadaOka18, Lemma 2.20],
$E$ positively. By [Reference OkadaOka18, Lemma 2.20], ![]() $\varphi$ is not a maximal extraction.
$\varphi$ is not a maximal extraction.
Remark 4.12 Let ![]() $X$ be a factorial sextic double solid with only terminal
$X$ be a factorial sextic double solid with only terminal ![]() $cA_1, cA_2, cA_3$ points. We can exclude smooth points and
$cA_1, cA_2, cA_3$ points. We can exclude smooth points and ![]() $cA_1$ points as a maximal center by Propositions 4.3 and 4.9. Moreover, by the argument of Proposition 4.8, we can exclude curves on
$cA_1$ points as a maximal center by Propositions 4.3 and 4.9. Moreover, by the argument of Proposition 4.8, we can exclude curves on ![]() $X$ except possibly for curves of degree
$X$ except possibly for curves of degree ![]() $1$ passing through a
$1$ passing through a ![]() $cA_3$ point. Therefore, for the proof of birational rigidity of
$cA_3$ point. Therefore, for the proof of birational rigidity of ![]() $X$, it remains to show the following.
$X$, it remains to show the following.
• Any curve of degree
 $1$ passing through a
$1$ passing through a  $cA_3$ point is not a maximal center.
$cA_3$ point is not a maximal center.• Any
 $cA_2$ point is not a maximal center.
$cA_2$ point is not a maximal center.• Any divisorial contraction to a
 $cA_3$ point with discrepancy at least
$cA_3$ point with discrepancy at least  $2$ (if it exists) is not a maximal extraction.
$2$ (if it exists) is not a maximal extraction.
4.5 Factorial sextic double solids
In this section, we provide a criterion for ![]() $\mathbb {Q}$-factoriality of sextic double solids with terminal
$\mathbb {Q}$-factoriality of sextic double solids with terminal ![]() $cA_1$ singularities. If a
$cA_1$ singularities. If a ![]() $3$-fold
$3$-fold ![]() $X$ with only terminal
$X$ with only terminal ![]() $cA_1$ singularities is a Fano, a hypersurface of
$cA_1$ singularities is a Fano, a hypersurface of ![]() $\mathbb {P}^4$, or a cyclic cover of
$\mathbb {P}^4$, or a cyclic cover of ![]() $\mathbb {P}^3$, the Picard group is isomorphic to the second integral cohomology because
$\mathbb {P}^3$, the Picard group is isomorphic to the second integral cohomology because ![]() $\mathrm {H}^1 (X, \mathcal {O}_X\!) = \mathrm {H}^2 (X, \mathcal {O}_X\!) = 0$. In this case,
$\mathrm {H}^1 (X, \mathcal {O}_X\!) = \mathrm {H}^2 (X, \mathcal {O}_X\!) = 0$. In this case, ![]() $\mathbb {Q}$-factoriality of
$\mathbb {Q}$-factoriality of ![]() $X$ can be determined by the following global topological property.
$X$ can be determined by the following global topological property.
Proposition 4.13 Let ![]() $X$ be a
$X$ be a ![]() $3$-fold with only terminal
$3$-fold with only terminal ![]() $cA_1$ singularities. Suppose that
$cA_1$ singularities. Suppose that ![]() $\mathrm {H}^1 (X, \mathcal {O}_X) = \mathrm {H}^2 (X, \mathcal {O}_X) = 0$. Then
$\mathrm {H}^1 (X, \mathcal {O}_X) = \mathrm {H}^2 (X, \mathcal {O}_X) = 0$. Then ![]() $X$ is
$X$ is ![]() $\mathbb {Q}$-factorial if and only if
$\mathbb {Q}$-factorial if and only if
Proof. It is enough to show that (4.13) holds if and only if
where ![]() $\mathrm {Cl}$ denotes the divisor class group and
$\mathrm {Cl}$ denotes the divisor class group and ![]() $\mathrm {Pic}$ denotes the Picard group. It follows from
$\mathrm {Pic}$ denotes the Picard group. It follows from ![]() $\mathrm {H}^1 (X, \mathcal {O}_X\!) = \mathrm {H}^2 (X, \mathcal {O}_X\!) = 0$ that
$\mathrm {H}^1 (X, \mathcal {O}_X\!) = \mathrm {H}^2 (X, \mathcal {O}_X\!) = 0$ that ![]() $\mathrm {H}^2 (X, \mathbb {Q}) \cong \mathrm {Pic}(X)\otimes \mathbb {Q}$. Therefore, it is enough to show that
$\mathrm {H}^2 (X, \mathbb {Q}) \cong \mathrm {Pic}(X)\otimes \mathbb {Q}$. Therefore, it is enough to show that ![]() $\mathrm {H}_4 (X, \mathbb {Q}) \cong \mathrm {Cl}(X)\otimes \mathbb {Q}$.
$\mathrm {H}_4 (X, \mathbb {Q}) \cong \mathrm {Cl}(X)\otimes \mathbb {Q}$.
Let ![]() $\pi :\widetilde {X}\to X$ be a resolution of singularities and let
$\pi :\widetilde {X}\to X$ be a resolution of singularities and let ![]() $E_i$,
$E_i$, ![]() $i=1,\ldots, r$, be its exceptional prime divisors. We denote by
$i=1,\ldots, r$, be its exceptional prime divisors. We denote by ![]() $E$ the exceptional locus of
$E$ the exceptional locus of ![]() $\pi$, i.e.
$\pi$, i.e. ![]() $E=\bigcup E_i$. Then, we can obtain the commutative diagram
$E=\bigcup E_i$. Then, we can obtain the commutative diagram

from the natural transformation in [Reference FultonFul75, § 5]. Note that
and the homomorphism ![]() $\pi ^C_*: \mathrm {Cl}(\widetilde {X})\otimes \mathbb {Q}\to \mathrm {Cl}(X)\otimes \mathbb {Q}$ given by the resolution morphism is surjective with the kernel generated by the exceptional divisors. Since
$\pi ^C_*: \mathrm {Cl}(\widetilde {X})\otimes \mathbb {Q}\to \mathrm {Cl}(X)\otimes \mathbb {Q}$ given by the resolution morphism is surjective with the kernel generated by the exceptional divisors. Since ![]() $\widetilde {X}$ is a smooth projective
$\widetilde {X}$ is a smooth projective ![]() $3$-fold,
$3$-fold,
where the last isomorphism follows from the Poincaré duality. There is an exact sequence
where ![]() $\widetilde {X}/E$ is the quotient topological space of
$\widetilde {X}/E$ is the quotient topological space of ![]() $\widetilde {X}$ by the subspace
$\widetilde {X}$ by the subspace ![]() $E$ and it is topologically equivalent to
$E$ and it is topologically equivalent to ![]() $X$. The exact sequence shows that the kernel of the homomorphism
$X$. The exact sequence shows that the kernel of the homomorphism ![]() $\pi _*^H:\mathrm {H}_4 (\widetilde {X}, \mathbb {Q})\to \mathrm {H}_4 (X, \mathbb {Q})$ is
$\pi _*^H:\mathrm {H}_4 (\widetilde {X}, \mathbb {Q})\to \mathrm {H}_4 (X, \mathbb {Q})$ is ![]() $\oplus _{i=1}^{r} \mathbb {Q} E_i$. This implies that the bottom horizontal homomorphism in (
$\oplus _{i=1}^{r} \mathbb {Q} E_i$. This implies that the bottom horizontal homomorphism in (
) is injective.
Since the singularities of ![]() $X$ are only terminal
$X$ are only terminal ![]() $cA_1$, we may assume that each
$cA_1$, we may assume that each ![]() $E_i$ is a smooth rational surface. This implies that
$E_i$ is a smooth rational surface. This implies that ![]() $\mathrm {H}_3(E_i, \mathbb {Q})=\mathrm {H}^1(E_i, \mathbb {Q})=0$. It then follows from a Mayer–Vietoris sequence that
$\mathrm {H}_3(E_i, \mathbb {Q})=\mathrm {H}^1(E_i, \mathbb {Q})=0$. It then follows from a Mayer–Vietoris sequence that ![]() $\mathrm {H}_3(E, \mathbb {Q})=0$. This vanishing shows that the homomorphism
$\mathrm {H}_3(E, \mathbb {Q})=0$. This vanishing shows that the homomorphism ![]() $\pi _*^H$ is surjective. Consequently, the bottom horizontal homomorphism in (4.14) is surjective and, hence, it is an isomorphism.
$\pi _*^H$ is surjective. Consequently, the bottom horizontal homomorphism in (4.14) is surjective and, hence, it is an isomorphism.
The duality (4.13) fails on singular varieties in general (for instance, see Examples 4.18 and 4.21). The failure of the duality can be measured by the difference of their dimensions, so called, the defect of ![]() $X$
$X$
With this notion, one may say that ![]() $X$ is
$X$ is ![]() $\mathbb {Q}$-factorial if and only if
$\mathbb {Q}$-factorial if and only if ![]() $\delta _X = 0$.
$\delta _X = 0$.
We consider a double cover ![]() $X$ of
$X$ of ![]() $\mathbb {P}^3$ branched along a surface
$\mathbb {P}^3$ branched along a surface ![]() $B \subset \mathbb {P}^3$ of degree
$B \subset \mathbb {P}^3$ of degree ![]() $2 r$ with only Du Val singularities. We can regard
$2 r$ with only Du Val singularities. We can regard ![]() $X$ as a hypersurface of degree
$X$ as a hypersurface of degree ![]() $2 r$ in the weighted projective space
$2 r$ in the weighted projective space ![]() $\mathbb {P} = \mathbb {P} (1, 1, 1, 1, r)$. In general, the singular points on
$\mathbb {P} = \mathbb {P} (1, 1, 1, 1, r)$. In general, the singular points on ![]() $X$ may have an effect on the integral (co)homology groups of
$X$ may have an effect on the integral (co)homology groups of ![]() $X$ (see [Reference ClemensCle83, Reference CynkCyn02, Reference DimcaDim90]). However, it follows from a Lefschetz-type theorem [Reference MavlyutovMav99, Proposition 1.4] that
$X$ (see [Reference ClemensCle83, Reference CynkCyn02, Reference DimcaDim90]). However, it follows from a Lefschetz-type theorem [Reference MavlyutovMav99, Proposition 1.4] that ![]() $\operatorname {Pic} (X) \cong \operatorname {Pic} (\mathbb {P})$, in particular,
$\operatorname {Pic} (X) \cong \operatorname {Pic} (\mathbb {P})$, in particular, ![]() $\operatorname {rank} (\operatorname {Pic} (X)) = 1$.
$\operatorname {rank} (\operatorname {Pic} (X)) = 1$.
Meanwhile, as mentioned previously, it follows from [Reference KawamataKaw88, Lemma 5.1] that on Gorenstein terminal ![]() $3$-folds, factoriality is equivalent to
$3$-folds, factoriality is equivalent to ![]() $\mathbb {Q}$-factoriality. Therefore, in our case, the double solid
$\mathbb {Q}$-factoriality. Therefore, in our case, the double solid ![]() $X$ is
$X$ is ![]() $\mathbb {Q}$-factorial if and only if it is factorial.
$\mathbb {Q}$-factorial if and only if it is factorial.
It is not simple to compute the defect. Fortunately, a method to compute some Hodge numbers for resolutions of double solids branched along surfaces with only Du Val singularities has been introduced by Rams [Reference RamsRam08] which has evolved from the paper of Clemens [Reference ClemensCle83]. Rams [Reference RamsRam08] formulated the difference between the Hodge numbers of the big resolution ![]() $Y$ and the Hodge numbers of
$Y$ and the Hodge numbers of ![]() $\mathbb {P}$. Here the big resolution
$\mathbb {P}$. Here the big resolution ![]() $\rho \colon Y \to X$ is defined by the composition of blow-ups:
$\rho \colon Y \to X$ is defined by the composition of blow-ups:
where ![]() $\rho _i \colon Y_i \to Y_{i-1}$ for
$\rho _i \colon Y_i \to Y_{i-1}$ for ![]() $i = 1, \ldots, k$, is the blow-up with center
$i = 1, \ldots, k$, is the blow-up with center ![]() $\operatorname {Sing} (Y_{i-1}) \ne \emptyset$ and
$\operatorname {Sing} (Y_{i-1}) \ne \emptyset$ and ![]() $Y_{k} = Y$ is smooth. Note that all singularities and infinitely near singularities of
$Y_{k} = Y$ is smooth. Note that all singularities and infinitely near singularities of ![]() $X$ are isolated double points, in particular, each
$X$ are isolated double points, in particular, each ![]() $\rho _i$ is a blow-up centered at closed points. The Hodge numbers of
$\rho _i$ is a blow-up centered at closed points. The Hodge numbers of ![]() $\mathbb {P}$ are considered with the Zariski sheaf of germs of
$\mathbb {P}$ are considered with the Zariski sheaf of germs of ![]() $1$-forms
$1$-forms ![]() $\overline {\Omega }^1_{\mathbb {P}} := \iota _* (\Omega ^1_{\operatorname {reg} (\mathbb {P})})$, where
$\overline {\Omega }^1_{\mathbb {P}} := \iota _* (\Omega ^1_{\operatorname {reg} (\mathbb {P})})$, where ![]() $\iota \colon \operatorname {reg} (\mathbb {P}) \to \mathbb {P}$ is the inclusion.
$\iota \colon \operatorname {reg} (\mathbb {P}) \to \mathbb {P}$ is the inclusion.
The defect of ![]() $X$ appears in a Hodge number of the big resolution
$X$ appears in a Hodge number of the big resolution ![]() $Y$ of
$Y$ of ![]() $X$, i.e.
$X$, i.e.
where ![]() $\mu _X$ is the number of components of the exceptional locus of the big resolution
$\mu _X$ is the number of components of the exceptional locus of the big resolution ![]() $\rho$ (see [Reference RamsRam08, Theorem 4.1]). Note that
$\rho$ (see [Reference RamsRam08, Theorem 4.1]). Note that ![]() $h^1 (\mathbb {P}, \overline {\Omega }^1_{\mathbb {P}}) = \operatorname {rank} (\operatorname {Pic} (\mathbb {P})) = 1$.
$h^1 (\mathbb {P}, \overline {\Omega }^1_{\mathbb {P}}) = \operatorname {rank} (\operatorname {Pic} (\mathbb {P})) = 1$.
If the double solid ![]() $X$ has only terminal
$X$ has only terminal ![]() $cA_1$ singularities, then the surface
$cA_1$ singularities, then the surface ![]() $B$ has only
$B$ has only ![]() $A_n$ singularities. Conversely, the double solid branched along a surface with only
$A_n$ singularities. Conversely, the double solid branched along a surface with only ![]() $A_n$ singularities has only terminal
$A_n$ singularities has only terminal ![]() $cA_1$ singularities. Meanwhile, a non-cyclic Du Val singular point of
$cA_1$ singularities. Meanwhile, a non-cyclic Du Val singular point of ![]() $B$ yields a terminal
$B$ yields a terminal ![]() $cA_2$ singular point on
$cA_2$ singular point on ![]() $X$.
$X$.
From now on, for our purpose we suppose that the double solid ![]() $X$ has only terminal
$X$ has only terminal ![]() $cA_1$ singularities unless otherwise mentioned.
$cA_1$ singularities unless otherwise mentioned.
We adopt the method given by [Reference RamsRam08, Theorem 4.1] to compute the defect ![]() $\delta _X$. To do so, we put
$\delta _X$. To do so, we put
where the condition ![]() $(\mathbf {A})$ is as follows.
$(\mathbf {A})$ is as follows.
For each singular point ![]() $p \in \operatorname {Sing} (B)$, suppose the surface
$p \in \operatorname {Sing} (B)$, suppose the surface ![]() $B$ is given by
$B$ is given by
for some positive integer ![]() $m$ locally around
$m$ locally around ![]() $p$, where the
$p$, where the ![]() $x_{i,p}$ are analytic coordinates centered at the point
$x_{i,p}$ are analytic coordinates centered at the point ![]() $p$ and
$p$ and ![]() $f (x_{1,p}, x_{2,p}, x_{3,p})$ is a polynomial of order strictly greater than
$f (x_{1,p}, x_{2,p}, x_{3,p})$ is a polynomial of order strictly greater than ![]() $1$ with respect to the weights
$1$ with respect to the weights ![]() $\operatorname {wt} (x_{1,p}) = {1}/({m+1})$,
$\operatorname {wt} (x_{1,p}) = {1}/({m+1})$, ![]() $\operatorname {wt} (x_{2,p}) = \operatorname {wt} (x_{3,p}) = \tfrac {1}{2}$. For the singular point
$\operatorname {wt} (x_{2,p}) = \operatorname {wt} (x_{3,p}) = \tfrac {1}{2}$. For the singular point ![]() $p$, impose the following conditions:
$p$, impose the following conditions:
 \begin{align*}
(\mathrm{C}_{p,0}):&\quad H (p) = 0; \\ (\mathrm{C}_{p,j}): &\quad {\frac{\partial^j
H}{\partial x_{1,p}^j} (p) = 0\text{ for } 1 \le j \le
\biggl \lceil \frac{m}{2} \biggr \rceil -1}.
\end{align*}
\begin{align*}
(\mathrm{C}_{p,0}):&\quad H (p) = 0; \\ (\mathrm{C}_{p,j}): &\quad {\frac{\partial^j
H}{\partial x_{1,p}^j} (p) = 0\text{ for } 1 \le j \le
\biggl \lceil \frac{m}{2} \biggr \rceil -1}.
\end{align*}
Theorem 4.14 The defect of the double solid ![]() $X$ with only terminal
$X$ with only terminal ![]() $cA_1$ singularities is given by
$cA_1$ singularities is given by
Proof. The following have been verified in [Reference DolgachevDol82, Theorem in § 1.4 and Theorem in § 2.3]:
 \[ \begin{array}{ll} \mathrm{H}^i (\mathbb{P}, \mathcal{O}_{\mathbb{P}} (-2 r)) = 0, & \text{for }i \le 3; \\ \mathrm{H}^i (\mathbb{P}, \mathcal{O}_{\mathbb{P}} (-4 r)) = 0, & \text{for }i \le 3; \\ \mathrm{H}^2 (\mathbb{P}, \overline{\Omega}^1_{\mathbb{P}}) = 0; & \\ \mathrm{H}^i (\mathbb{P}, \overline{\Omega}^1_{\mathbb{P}} \otimes \mathcal{O}_{\mathbb{P}} (-2 r)) = 0, & \text{for }i = 1, 2, 3. \end{array} \]
\[ \begin{array}{ll} \mathrm{H}^i (\mathbb{P}, \mathcal{O}_{\mathbb{P}} (-2 r)) = 0, & \text{for }i \le 3; \\ \mathrm{H}^i (\mathbb{P}, \mathcal{O}_{\mathbb{P}} (-4 r)) = 0, & \text{for }i \le 3; \\ \mathrm{H}^2 (\mathbb{P}, \overline{\Omega}^1_{\mathbb{P}}) = 0; & \\ \mathrm{H}^i (\mathbb{P}, \overline{\Omega}^1_{\mathbb{P}} \otimes \mathcal{O}_{\mathbb{P}} (-2 r)) = 0, & \text{for }i = 1, 2, 3. \end{array} \]
Then [Reference RamsRam08, Theorem 4.1] yields
As shown in the proof of Proposition 4.13, ![]() $\dim _{\mathbb {Q}} (\mathrm {H}_4 (X, \mathbb {Q})) =\mathrm {rank}(\mathrm {Cl}(X))$. Moreover,
$\dim _{\mathbb {Q}} (\mathrm {H}_4 (X, \mathbb {Q})) =\mathrm {rank}(\mathrm {Cl}(X))$. Moreover, ![]() $\dim _{\mathbb {Q}} (\mathrm {H}^2 (X, \mathbb {Q})) =\mathrm {rank}(\mathrm {Pic}(X))=1$. Therefore,
$\dim _{\mathbb {Q}} (\mathrm {H}^2 (X, \mathbb {Q})) =\mathrm {rank}(\mathrm {Pic}(X))=1$. Therefore,
 \begin{align*} \delta_X&=\dim_{\mathbb{Q}} (\mathrm{H}_4 (X, \mathbb{Q})) - \dim_{\mathbb{Q}} (\mathrm{H}^2 (X, \mathbb{Q}))\\ &=\mathrm{rank}(\mathrm{Cl}(X)) -1\\ &=\mathrm{rank}(\mathrm{Cl}(Y)) -\mu_X-1\\ &=\mathrm{rank}(\mathrm{Pic}(Y)) -\mu_X-1\\ &=\dim_{\mathbb{Q}} (\mathrm{H}^2 (Y, \mathbb{Q})) -\mu_X-1\\ &=\dim (\mathcal{H}_X\!) - (h^0 (\mathbb{P}^3, \mathcal{O}_{\mathbb{P}^3} (3 r - 4)) - \mu_X\!). \end{align*}
\begin{align*} \delta_X&=\dim_{\mathbb{Q}} (\mathrm{H}_4 (X, \mathbb{Q})) - \dim_{\mathbb{Q}} (\mathrm{H}^2 (X, \mathbb{Q}))\\ &=\mathrm{rank}(\mathrm{Cl}(X)) -1\\ &=\mathrm{rank}(\mathrm{Cl}(Y)) -\mu_X-1\\ &=\mathrm{rank}(\mathrm{Pic}(Y)) -\mu_X-1\\ &=\dim_{\mathbb{Q}} (\mathrm{H}^2 (Y, \mathbb{Q})) -\mu_X-1\\ &=\dim (\mathcal{H}_X\!) - (h^0 (\mathbb{P}^3, \mathcal{O}_{\mathbb{P}^3} (3 r - 4)) - \mu_X\!). \end{align*}
Theorem 4.14 reduces the topological problem to a relatively simpler problem concerning the linear system ![]() $|\mathcal {O}_{\mathbb {P}^3} (3 r - 4)|$ and
$|\mathcal {O}_{\mathbb {P}^3} (3 r - 4)|$ and ![]() $0$-dimensional subschemes in
$0$-dimensional subschemes in ![]() $\mathbb {P}^3$.
$\mathbb {P}^3$.
Corollary 4.15 The double solid ![]() $X$ is factorial if and only if the condition
$X$ is factorial if and only if the condition ![]() $(\mathbf {A})$ imposes linearly independent
$(\mathbf {A})$ imposes linearly independent ![]() $\mu _X$ conditions on
$\mu _X$ conditions on ![]() $\mathrm {H}^0 (\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3} (3 r - 4))$.
$\mathrm {H}^0 (\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3} (3 r - 4))$.
Corollary 4.16 Suppose that the surface ![]() $B$ has singularities
$B$ has singularities
where ![]() $a_i$ is the number of singular points of type
$a_i$ is the number of singular points of type ![]() $A_i$ on
$A_i$ on ![]() $B$. If the double solid
$B$. If the double solid ![]() $X$ is
$X$ is ![]() $\mathbb {Q}$-factorial, then
$\mathbb {Q}$-factorial, then
 \[ \sum_{n=1}^m a_n \biggl \lceil \frac{n}{2} \biggr \rceil \le h^0 (\mathbb{P}^3, \mathcal{O}_{\mathbb{P}^3} (3 r - 4)) = \frac{1}{2} (3 r - 1)(3 r - 2)(r - 1). \]
\[ \sum_{n=1}^m a_n \biggl \lceil \frac{n}{2} \biggr \rceil \le h^0 (\mathbb{P}^3, \mathcal{O}_{\mathbb{P}^3} (3 r - 4)) = \frac{1}{2} (3 r - 1)(3 r - 2)(r - 1). \]
Proof. A singular point ![]() $p$ of type
$p$ of type ![]() $A_n$ yields
$A_n$ yields ![]() $\lceil {n}/{2} \rceil$ conditions
$\lceil {n}/{2} \rceil$ conditions ![]() $(\mathrm {C}_{p,j})$,
$(\mathrm {C}_{p,j})$, ![]() $0 \le j \le \lceil {m}/{2} \rceil -1$, on
$0 \le j \le \lceil {m}/{2} \rceil -1$, on ![]() $\mathrm {H}^0 (\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3} (3 r - 4))$. Therefore, the statement follows from Corollary 4.15.
$\mathrm {H}^0 (\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3} (3 r - 4))$. Therefore, the statement follows from Corollary 4.15.
Following the argument based on a Lefschetz-type theorem as in [Reference Cheltsov and ParkCP10, Example 1.5], we can construct an example of a non-![]() $\mathbb {Q}$-factorial double solid
$\mathbb {Q}$-factorial double solid ![]() $X$ branched along a surface
$X$ branched along a surface ![]() $B$ with only terminal
$B$ with only terminal ![]() $cA_k$ singularities.
$cA_k$ singularities.
Example 4.17 Let ![]() $B$ be the surface of degree
$B$ be the surface of degree ![]() $2 r$, where
$2 r$, where ![]() $r \ge 2$, defined by
$r \ge 2$, defined by
where ![]() $f_{2 r - 1}\in \mathbb {C}[x,y,z]$ is a general homogeneous polynomial of degree
$f_{2 r - 1}\in \mathbb {C}[x,y,z]$ is a general homogeneous polynomial of degree ![]() $2 r - 1$. Then the surface
$2 r - 1$. Then the surface ![]() $B$ has
$B$ has ![]() $2 r - 3$ singular points of type
$2 r - 3$ singular points of type ![]() $A_1$,
$A_1$, ![]() $2 r -1$ singular points of type
$2 r -1$ singular points of type ![]() $A_{2 r - 3}$, and one singular point of type
$A_{2 r - 3}$, and one singular point of type ![]() $D_4$. The double solid
$D_4$. The double solid ![]() $X$ branched along the surface
$X$ branched along the surface ![]() $B$ has
$B$ has ![]() $4 r - 4$ terminal singular points of type
$4 r - 4$ terminal singular points of type ![]() $cA_1$ and one terminal singular point of type
$cA_1$ and one terminal singular point of type ![]() $cA_2$. Furthermore, it can be defined by the weighted homogeneous equation
$cA_2$. Furthermore, it can be defined by the weighted homogeneous equation
The hyperplane section defined by ![]() $x = 0$ splits into two divisors given by the equation
$x = 0$ splits into two divisors given by the equation
each of which is a non-![]() $\mathbb {Q}$-Cartier divisor.
$\mathbb {Q}$-Cartier divisor.
We can construct the following non-![]() $\mathbb {Q}$-factorial double solid with only terminal
$\mathbb {Q}$-factorial double solid with only terminal ![]() $cA_1$ singularities based on the fact that a variety with a small resolution is not
$cA_1$ singularities based on the fact that a variety with a small resolution is not ![]() $\mathbb {Q}$-factorial. In this example, Theorem 4.14 confirms that its defect is positive, with the aid of the Cayley–Bacharach theorem.
$\mathbb {Q}$-factorial. In this example, Theorem 4.14 confirms that its defect is positive, with the aid of the Cayley–Bacharach theorem.
Example 4.18 Let ![]() $V$ be the smooth
$V$ be the smooth ![]() $3$-fold of bidegree
$3$-fold of bidegree ![]() $(2, r)$,
$(2, r)$, ![]() $r\geq 2$, in
$r\geq 2$, in ![]() $\mathbb {P}^1 \times \mathbb {P}^3$ defined by the bihomogeneous equation
$\mathbb {P}^1 \times \mathbb {P}^3$ defined by the bihomogeneous equation
where ![]() $f_r$ and
$f_r$ and ![]() $h_r$ are general homogeneous polynomials of degree
$h_r$ are general homogeneous polynomials of degree ![]() $r$ in
$r$ in ![]() $\mathbb {C}[x, y,z]$. In addition, we denote the natural projection of
$\mathbb {C}[x, y,z]$. In addition, we denote the natural projection of ![]() $V$ to
$V$ to ![]() $\mathbb {P}^3$ by
$\mathbb {P}^3$ by ![]() $\pi \colon V \to \mathbb {P}^3$. The system of equations
$\pi \colon V \to \mathbb {P}^3$. The system of equations
defines exactly ![]() $r^2$ points in
$r^2$ points in ![]() $\mathbb {P}^3$. The
$\mathbb {P}^3$. The ![]() $3$-fold
$3$-fold ![]() $V$ then has exactly
$V$ then has exactly ![]() $r^2$ curves
$r^2$ curves ![]() $C_i$,
$C_i$, ![]() $i = 1, \ldots, r^2$, such that
$i = 1, \ldots, r^2$, such that ![]() $H \cdot C_i = 0$, where
$H \cdot C_i = 0$, where ![]() $H$ is a divisor cut by a hypersurface of bidegree
$H$ is a divisor cut by a hypersurface of bidegree ![]() $(0, 1)$ in
$(0, 1)$ in ![]() $\mathbb {P}^1 \times \mathbb {P}^3$. The projection
$\mathbb {P}^1 \times \mathbb {P}^3$. The projection ![]() $\pi$ has degree
$\pi$ has degree ![]() $2$ outside the points
$2$ outside the points ![]() $\pi (C_i)$. The model
$\pi (C_i)$. The model
 \[ \operatorname{Proj} \biggl( \bigoplus_{n \ge 0} \mathrm{H}^0 (V, \mathcal{O}_V (n H)) \biggr) \]
\[ \operatorname{Proj} \biggl( \bigoplus_{n \ge 0} \mathrm{H}^0 (V, \mathcal{O}_V (n H)) \biggr) \]
of ![]() $V$ is the double cover
$V$ is the double cover ![]() $X$ of
$X$ of ![]() $\mathbb {P}^3$ branched along the surface
$\mathbb {P}^3$ branched along the surface ![]() $B$ defined by
$B$ defined by
It has ![]() $r^2$ terminal singular points of type
$r^2$ terminal singular points of type ![]() $cA_1$ each of which comes from each curve
$cA_1$ each of which comes from each curve ![]() $C_i$. The morphism
$C_i$. The morphism ![]() $\phi _{|m H|} \colon V \to X$ given by the complete linear system of bidegree
$\phi _{|m H|} \colon V \to X$ given by the complete linear system of bidegree ![]() $(0, m)$ on
$(0, m)$ on ![]() $V$ with sufficiently large
$V$ with sufficiently large ![]() $m$ contracts these
$m$ contracts these ![]() $r^2$ curves to
$r^2$ curves to ![]() $cA_1$ points of
$cA_1$ points of ![]() $X$. Therefore, it is a small morphism of
$X$. Therefore, it is a small morphism of ![]() $V$ onto
$V$ onto ![]() $X$ and, hence, the double cover
$X$ and, hence, the double cover ![]() $X$ cannot be
$X$ cannot be ![]() $\mathbb {Q}$-factorial.
$\mathbb {Q}$-factorial.
Meanwhile, we can also verify that ![]() $X$ cannot be
$X$ cannot be ![]() $\mathbb {Q}$-factorial from the view point of Theorem 4.14. The surface
$\mathbb {Q}$-factorial from the view point of Theorem 4.14. The surface ![]() $B$ has
$B$ has ![]() $r^2$ singular points of type
$r^2$ singular points of type ![]() $A_{2r-1}$ on the plane
$A_{2r-1}$ on the plane ![]() $\Pi$ defined by
$\Pi$ defined by ![]() $t=0$. These singular points
$t=0$. These singular points ![]() $p_i$,
$p_i$, ![]() $i=1,\ldots, r^2$, on
$i=1,\ldots, r^2$, on ![]() $B$ impose conditions (
$B$ impose conditions (![]() $\mathrm {C}_{p_i,r-1}$)
$\mathrm {C}_{p_i,r-1}$)
on ![]() $\mathrm {H}^0(\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3}(3r-4))$. These conditions can also be regarded as vanishing conditions at
$\mathrm {H}^0(\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3}(3r-4))$. These conditions can also be regarded as vanishing conditions at ![]() $p_i$ for
$p_i$ for ![]() $\mathrm {H}^0(\Pi, \mathcal {O}_\Pi (2r-3))$ since
$\mathrm {H}^0(\Pi, \mathcal {O}_\Pi (2r-3))$ since
 \[ \mathrm{H}^0(\mathbb{P}^3, \mathcal{O}_{\mathbb{P}^3}(3r-4))=\bigoplus_{k=0}^{3r-4}t^{3r-4-k}\mathbb{C}[x,y,z]_{k}, \]
\[ \mathrm{H}^0(\mathbb{P}^3, \mathcal{O}_{\mathbb{P}^3}(3r-4))=\bigoplus_{k=0}^{3r-4}t^{3r-4-k}\mathbb{C}[x,y,z]_{k}, \]
where ![]() $\mathbb {C}[x,y,z]_{k}$ is the space of homogenous polynomials of degree
$\mathbb {C}[x,y,z]_{k}$ is the space of homogenous polynomials of degree ![]() $k$ in variables
$k$ in variables ![]() $x, y, z$. The points
$x, y, z$. The points ![]() $p_i$'s are the intersection points of the two plane curves of degree
$p_i$'s are the intersection points of the two plane curves of degree ![]() $r$ defined by
$r$ defined by ![]() $f_r(x, y, z)=0$ and
$f_r(x, y, z)=0$ and ![]() $g_r(x,y,z)=0$ on
$g_r(x,y,z)=0$ on ![]() $\Pi$. It therefore follows from the Cayley-Bacharach theorem ([Reference Eisenbud, Green and HarrisEGH96, Theorem CB4]) that the vanishing conditions at
$\Pi$. It therefore follows from the Cayley-Bacharach theorem ([Reference Eisenbud, Green and HarrisEGH96, Theorem CB4]) that the vanishing conditions at ![]() $p_i$'s on
$p_i$'s on ![]() $\mathrm {H}^0(\Pi, \mathcal {O}_\Pi (2r-3))$ are linearly dependent. Therefore, the conditions
$\mathrm {H}^0(\Pi, \mathcal {O}_\Pi (2r-3))$ are linearly dependent. Therefore, the conditions
are linearly dependent on ![]() $\mathrm {H}^0(\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3}(3r-4))$. It then follows from Corollary 4.15 that
$\mathrm {H}^0(\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3}(3r-4))$. It then follows from Corollary 4.15 that ![]() $X$ is not
$X$ is not ![]() $\mathbb {Q}$-factorial, i.e.
$\mathbb {Q}$-factorial, i.e. ![]() $\delta _X>0$.
$\delta _X>0$.
Example 4.19 Let ![]() $B$ be the surface of degree
$B$ be the surface of degree ![]() $2 r$, where
$2 r$, where ![]() $r \ge 2$, defined by
$r \ge 2$, defined by
where ![]() $L_1 (x, y, z), \ldots, L_{2 r} (x, y, z)$ are general linear forms.
$L_1 (x, y, z), \ldots, L_{2 r} (x, y, z)$ are general linear forms.
Then the surface ![]() $B$ has exactly
$B$ has exactly ![]() $r (2 r - 1)$ singular points and they are
$r (2 r - 1)$ singular points and they are ![]() $A_{2 r - 2}$ singularities. These singular points correspond to the intersection points
$A_{2 r - 2}$ singularities. These singular points correspond to the intersection points ![]() $p_{n m}$ of the lines
$p_{n m}$ of the lines ![]() $L_n (x, y, z)$ and
$L_n (x, y, z)$ and ![]() $L_m (x, y, z)$ on the plane
$L_m (x, y, z)$ on the plane ![]() $t = 0$,
$t = 0$, ![]() $1 \le n< m \le 2 r$. The double solid
$1 \le n< m \le 2 r$. The double solid ![]() $X$ branched along the surface
$X$ branched along the surface ![]() $B$ also has
$B$ also has ![]() $r (2 r -1)$ terminal singular points of type
$r (2 r -1)$ terminal singular points of type ![]() $cA_1$.
$cA_1$.
Let ![]() $F_{l} (x, y, z)$ be a general from of degree
$F_{l} (x, y, z)$ be a general from of degree ![]() $l$ in
$l$ in ![]() $x, y, z$. For
$x, y, z$. For ![]() $0 \le j \le r-2$ and
$0 \le j \le r-2$ and ![]() $1 \le n< m \le 2 r$, put
$1 \le n< m \le 2 r$, put
It is a form of degree ![]() $3 r - 4$. Observe that for fixed
$3 r - 4$. Observe that for fixed ![]() $n, m, j$,
$n, m, j$,
 \[ \begin{array}{ll} \dfrac{\partial^j H_{n, m, j}}{\partial t^j} (p_{n m}) \ne 0; & \\ \dfrac{\partial^k H_{n, m, j}}{\partial t^k} (p_{n m}) = 0, & \text{if }k \ne j; \\ \dfrac{\partial^k H_{n, m, j}}{\partial t^k} (p_{n' m'}) = 0, & \text{if }(n', m') \ne (n, m). \end{array} \]
\[ \begin{array}{ll} \dfrac{\partial^j H_{n, m, j}}{\partial t^j} (p_{n m}) \ne 0; & \\ \dfrac{\partial^k H_{n, m, j}}{\partial t^k} (p_{n m}) = 0, & \text{if }k \ne j; \\ \dfrac{\partial^k H_{n, m, j}}{\partial t^k} (p_{n' m'}) = 0, & \text{if }(n', m') \ne (n, m). \end{array} \]
This implies that the ![]() $r (2 r - 1)(r -1)$ conditions
$r (2 r - 1)(r -1)$ conditions ![]() $\{(\mathrm {C}_{p_{n m}, j})\}$ impose linearly independent conditions on
$\{(\mathrm {C}_{p_{n m}, j})\}$ impose linearly independent conditions on ![]() $\mathrm {H}^0 (\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3} (3 r - 4))$. Therefore, Corollary 4.15 implies that the double solid
$\mathrm {H}^0 (\mathbb {P}^3, \mathcal {O}_{\mathbb {P}^3} (3 r - 4))$. Therefore, Corollary 4.15 implies that the double solid ![]() $X$ is factorial.
$X$ is factorial.
The ![]() $\mathbb {Q}$-factoriality of nodal double solids has been studied extensively in [Reference Cheltsov and ParkCP10, Reference CheltsovChe09, Reference Hong and ParkHP07, Reference KloostermanKlo22]. Their results are mainly based on the result of [Reference ClemensCle83]. As mentioned previously, in this section, we use the result of [Reference RamsRam08] that is applicable to the cases with wider range of singularities. Before we proceed, let us mention that some results in [Reference Cheltsov and ParkCP10, Reference CheltsovChe09, Reference Hong and ParkHP07, Reference KloostermanKlo22] remain true if we allow only singularities slightly worse than nodes.
$\mathbb {Q}$-factoriality of nodal double solids has been studied extensively in [Reference Cheltsov and ParkCP10, Reference CheltsovChe09, Reference Hong and ParkHP07, Reference KloostermanKlo22]. Their results are mainly based on the result of [Reference ClemensCle83]. As mentioned previously, in this section, we use the result of [Reference RamsRam08] that is applicable to the cases with wider range of singularities. Before we proceed, let us mention that some results in [Reference Cheltsov and ParkCP10, Reference CheltsovChe09, Reference Hong and ParkHP07, Reference KloostermanKlo22] remain true if we allow only singularities slightly worse than nodes.
Theorem 4.20 Let ![]() $X$ be the double solid branched along a surface
$X$ be the double solid branched along a surface ![]() $B$ of degree
$B$ of degree ![]() $2r$. Suppose that
$2r$. Suppose that ![]() $B$ has at worst
$B$ has at worst ![]() $A_1$ and
$A_1$ and ![]() $A_2$ singularities.
$A_2$ singularities.
(1) If the number of singular points of
 $X$ is less than
$X$ is less than  $r (2 r -1)$, then
$r (2 r -1)$, then  $X$ is factorial.
$X$ is factorial.(2) If the number of singular points of
 $X$ is
$X$ is  $r (2 r -1)$ and
$r (2 r -1)$ and  $X$ is not
$X$ is not  $\mathbb {Q}$-factorial, then the surface
$\mathbb {Q}$-factorial, then the surface  $B$ is defined by an equation of the form
where
$B$ is defined by an equation of the form
where \[ f_r (x, y, z, t)^2 + f_1 (x, y, z, t) f_{2 r - 1} (x, y, z, t) = 0, \]
\[ f_r (x, y, z, t)^2 + f_1 (x, y, z, t) f_{2 r - 1} (x, y, z, t) = 0, \]
 $f_i (x, y, z, t)\in \mathbb {C}[x,y,z,t]$ is a homogeneous polynomial of degree
$f_i (x, y, z, t)\in \mathbb {C}[x,y,z,t]$ is a homogeneous polynomial of degree  $i$.
$i$.
Proof. The statements have been verified under the condition that ![]() $B$ has only
$B$ has only ![]() $A_1$ singularities in [Reference Cheltsov and ParkCP10, Theorem B], [Reference CheltsovChe09, Theorem 3], [Reference Hong and ParkHP07, Theorems 4.3 and 5.3], and [Reference KloostermanKlo22, Theorem 4.6]. However, as
$A_1$ singularities in [Reference Cheltsov and ParkCP10, Theorem B], [Reference CheltsovChe09, Theorem 3], [Reference Hong and ParkHP07, Theorems 4.3 and 5.3], and [Reference KloostermanKlo22, Theorem 4.6]. However, as ![]() $A_1$ singularities, singular points of type
$A_1$ singularities, singular points of type ![]() $A_2$ on
$A_2$ on ![]() $B$ produce only one condition
$B$ produce only one condition ![]() $(\mathrm {C}_{p,0})$ in the condition
$(\mathrm {C}_{p,0})$ in the condition ![]() $(\mathbf {A})$. From the view point of factoriality, we do not have to distinguish between
$(\mathbf {A})$. From the view point of factoriality, we do not have to distinguish between ![]() $A_1$ and
$A_1$ and ![]() $A_2$. Therefore, the proofs of [Reference CheltsovChe09, Theorem 3] and [Reference KloostermanKlo22, Theorem 4.6] work verbatim for the case when
$A_2$. Therefore, the proofs of [Reference CheltsovChe09, Theorem 3] and [Reference KloostermanKlo22, Theorem 4.6] work verbatim for the case when ![]() $B$ allows
$B$ allows ![]() $A_2$ singularities also.
$A_2$ singularities also.
Example 4.21 Let ![]() $B$ be the surface of degree
$B$ be the surface of degree ![]() $2 r$, where
$2 r$, where ![]() $r \ge 2$, defined by
$r \ge 2$, defined by
where ![]() $h_{2 r - 1}$ is a general homogeneous polynomial of degree
$h_{2 r - 1}$ is a general homogeneous polynomial of degree ![]() $2 r - 1$. Then the surface
$2 r - 1$. Then the surface ![]() $B$ has exactly
$B$ has exactly ![]() $2 r - 1$ singular points which are of type
$2 r - 1$ singular points which are of type ![]() $A_{2 r - 1}$. The double solid
$A_{2 r - 1}$. The double solid ![]() $X$ branched along the surface
$X$ branched along the surface ![]() $B$ also has
$B$ also has ![]() $2 r - 1$ terminal singular points of type
$2 r - 1$ terminal singular points of type ![]() $cA_1$. As before, this can be defined by the weighted homogeneous equation
$cA_1$. As before, this can be defined by the weighted homogeneous equation
The hyperplane section defined by ![]() $x = 0$ splits into two divisors given by the equation
$x = 0$ splits into two divisors given by the equation
each of which is a non-![]() $\mathbb {Q}$-Cartier divisor.
$\mathbb {Q}$-Cartier divisor.
Example 4.21 leads to the following conjecture.
Conjecture 4.22 Let ![]() $X$ be the double solid branched along a sextic surface with at worst
$X$ be the double solid branched along a sextic surface with at worst ![]() $A_m$ singularities. If the number of singular points on
$A_m$ singularities. If the number of singular points on ![]() $X$ is at most four, then
$X$ is at most four, then ![]() $X$ is factorial.
$X$ is factorial.
However, due to our limited understanding of Du Val singularities of sextic surfaces, we can currently confirm it only under a specific additional condition.
Theorem 4.23 Conjecture 4.22 holds good under the assumption that ![]() $B$ allows at most four and at worst
$B$ allows at most four and at worst ![]() $A_4$ singularities.
$A_4$ singularities.
Proof. We assume that ![]() $B$ has four singular points denoted by
$B$ has four singular points denoted by ![]() $p_1, \ldots, p_4$. The proof for the case of a smaller number of singular points is nearly identical.
$p_1, \ldots, p_4$. The proof for the case of a smaller number of singular points is nearly identical.
For each index ![]() $i$, the singular point
$i$, the singular point ![]() $p_i$ is of type
$p_i$ is of type ![]() $A_{m_i}$ with
$A_{m_i}$ with ![]() $m_i \leq 4$. Each point imposes linear conditions given by
$m_i \leq 4$. Each point imposes linear conditions given by
 \begin{align*} (\mathrm{C}_{i,0}):&\quad H (p_i) = 0; \\ (\mathrm{C}_{i,1}):&\quad \frac{\partial H}{\partial x_{1, p_i}} (p_i) = 0 \text{ if } m_i=3 \text{ or } 4 \end{align*}
\begin{align*} (\mathrm{C}_{i,0}):&\quad H (p_i) = 0; \\ (\mathrm{C}_{i,1}):&\quad \frac{\partial H}{\partial x_{1, p_i}} (p_i) = 0 \text{ if } m_i=3 \text{ or } 4 \end{align*}
on the linear system of quintic hypersurfaces ![]() $H$ in
$H$ in ![]() $\mathbb {P}^3$. To establish our claim, it suffices to demonstrate that for any given condition
$\mathbb {P}^3$. To establish our claim, it suffices to demonstrate that for any given condition ![]() $(\mathrm {C}_{i,j})$, there exists a quintic hypersurface
$(\mathrm {C}_{i,j})$, there exists a quintic hypersurface ![]() $H$ that violates the condition
$H$ that violates the condition ![]() $(\mathrm {C}_{i,j})$ while simultaneously satisfying the remaining conditions.
$(\mathrm {C}_{i,j})$ while simultaneously satisfying the remaining conditions.
We employ homogeneous coordinates ![]() $(x:y:z: t)$ for
$(x:y:z: t)$ for ![]() $\mathbb {P}^3$. Consider a fixed condition
$\mathbb {P}^3$. Consider a fixed condition ![]() $(\mathrm {C}_{i,j})$. Without loss of generality, we assume that
$(\mathrm {C}_{i,j})$. Without loss of generality, we assume that ![]() $p_i = (1:0:0:0)$ for convenience, and set
$p_i = (1:0:0:0)$ for convenience, and set ![]() $i = 4$.
$i = 4$.
In the case when ![]() $m_4 \ge 2$, assume that the Zariski tangent planes at
$m_4 \ge 2$, assume that the Zariski tangent planes at ![]() $p_4$ are defined by
$p_4$ are defined by ![]() $y = 0$ and
$y = 0$ and ![]() $z = 0$, respectively. We may regard
$z = 0$, respectively. We may regard ![]() $x_{1, p_4}$ as
$x_{1, p_4}$ as ![]() $t$.
$t$.
Case 1: the four singular points are not collinear. Select a line passing through ![]() $p_4$ that includes the maximum number of singular points
$p_4$ that includes the maximum number of singular points ![]() $p_1, p_2, p_3$. Such a line accommodates at least two and at most three singular points since the four singular points are not collinear. We may therefore assume that
$p_1, p_2, p_3$. Such a line accommodates at least two and at most three singular points since the four singular points are not collinear. We may therefore assume that ![]() $p_3$ lies outside the line. For
$p_3$ lies outside the line. For ![]() $k=1, 2$, let
$k=1, 2$, let ![]() $H_{k3}$ be a general hyperplane that contains
$H_{k3}$ be a general hyperplane that contains ![]() $p_k$ and
$p_k$ and ![]() $p_3$. Note that
$p_3$. Note that ![]() $H_{k3}$ does not vanish at
$H_{k3}$ does not vanish at ![]() $p_4$.
$p_4$.
Set
Then,
 \[ \det \begin{pmatrix} P_1 & P_2 \\
\dfrac{\partial P_1}{\partial t} & \dfrac{\partial
P_2}{\partial t} \end{pmatrix} (p_4)
=(H_{13}^4H_{23}^5)(p_4) \ne 0. \]
\[ \det \begin{pmatrix} P_1 & P_2 \\
\dfrac{\partial P_1}{\partial t} & \dfrac{\partial
P_2}{\partial t} \end{pmatrix} (p_4)
=(H_{13}^4H_{23}^5)(p_4) \ne 0. \]
Therefore, for the given condition ![]() $(\mathrm {C}_{4,j})$, there exists a point
$(\mathrm {C}_{4,j})$, there exists a point ![]() $(\mu _1:\mu _2) \in \mathbb {P}^1$ such that between two values
$(\mu _1:\mu _2) \in \mathbb {P}^1$ such that between two values
 \begin{align*} (0)&\quad (\mu_1 P_1 + \mu_2 P_2)(p_4), \\ (1)&\quad \frac{\partial}{\partial t} (\mu_1 P_1+ \mu_2 P_2)(p_4), \end{align*}
\begin{align*} (0)&\quad (\mu_1 P_1 + \mu_2 P_2)(p_4), \\ (1)&\quad \frac{\partial}{\partial t} (\mu_1 P_1+ \mu_2 P_2)(p_4), \end{align*}
the value ![]() $(j)$ is non-zero whereas the other is zero. Then the quintic
$(j)$ is non-zero whereas the other is zero. Then the quintic
violates the condition ![]() $(\mathrm {C}_{4,j})$ but satisfies all the other conditions.
$(\mathrm {C}_{4,j})$ but satisfies all the other conditions.
Case 2: the four singular points are collinear. In this case, if ![]() $m_k, m_\ell \geq 2$, then the intersection line of Zariski tangent planes at
$m_k, m_\ell \geq 2$, then the intersection line of Zariski tangent planes at ![]() $p_k$ must be distinct from that of Zariski tangent planes at
$p_k$ must be distinct from that of Zariski tangent planes at ![]() $p_\ell$. Otherwise, the surface
$p_\ell$. Otherwise, the surface ![]() $B$ would be singular along the intersection line.
$B$ would be singular along the intersection line.
Subcase 1-1: ![]() $m_4\leq 2$. Suppose
$m_4\leq 2$. Suppose ![]() $m_k\leq 2$ for some
$m_k\leq 2$ for some ![]() $k\leq 3$, say
$k\leq 3$, say ![]() $k=3$. Take a general hyperplane
$k=3$. Take a general hyperplane ![]() $H_i$ passing through
$H_i$ passing through ![]() $p_i$. Then the quintic
$p_i$. Then the quintic ![]() $H_1^2H_2^2H_3$ violates the condition
$H_1^2H_2^2H_3$ violates the condition ![]() $(\mathrm {C}_{4,0})$ but satisfies all other conditions. Therefore, we may assume that
$(\mathrm {C}_{4,0})$ but satisfies all other conditions. Therefore, we may assume that ![]() $m_1, m_2, m_3\geq 3$. Given that the intersection lines of Zariski tangent planes at
$m_1, m_2, m_3\geq 3$. Given that the intersection lines of Zariski tangent planes at ![]() $p_1$,
$p_1$, ![]() $p_2$,
$p_2$, ![]() $p_3$ are all different, there exists a hyperplane
$p_3$ are all different, there exists a hyperplane ![]() $H_k$ for some
$H_k$ for some ![]() $k\in \{1,2,3\}$ such that
$k\in \{1,2,3\}$ such that ![]() $H_k(p_4)\ne 0$,
$H_k(p_4)\ne 0$, ![]() $H_k(p_k)=0$, and
$H_k(p_k)=0$, and ![]() $({\partial H_k}/{\partial x_{1, p_k}}) (p_k) = 0$. Assume, for instance, that
$({\partial H_k}/{\partial x_{1, p_k}}) (p_k) = 0$. Assume, for instance, that ![]() $k=3$. Then the quintic
$k=3$. Then the quintic ![]() $H_1^2H_2^2H_3$ fails the condition
$H_1^2H_2^2H_3$ fails the condition ![]() $(\mathrm {C}_{4,0})$ but satisfies all other conditions.
$(\mathrm {C}_{4,0})$ but satisfies all other conditions.
Subcase 1-2: ![]() $m_4\geq 3$. Among the three points
$m_4\geq 3$. Among the three points ![]() $p_1$,
$p_1$, ![]() $p_2$, and
$p_2$, and ![]() $p_3$, we either have
$p_3$, we either have ![]() $m_k, m_\ell \leq 2$ or
$m_k, m_\ell \leq 2$ or ![]() ${m_k, m_\ell \geq 3}$. For both cases, we may assume that
${m_k, m_\ell \geq 3}$. For both cases, we may assume that ![]() $k=2$ and
$k=2$ and ![]() $\ell =3$.
$\ell =3$.
Let ![]() $H_1$ be a general hyperplane passing through
$H_1$ be a general hyperplane passing through ![]() $p_1$.
$p_1$.
If ![]() $m_2$,
$m_2$, ![]() $m_3 \leq 2$, then for each
$m_3 \leq 2$, then for each ![]() $i=2,3$, we consider a general hyperplane
$i=2,3$, we consider a general hyperplane ![]() $H_i$ passing through
$H_i$ passing through ![]() $p_i$.
$p_i$.
If ![]() $m_2$,
$m_2$, ![]() $m_3 \geq 3$, then there exists a hyperplane
$m_3 \geq 3$, then there exists a hyperplane ![]() $H_i$ for
$H_i$ for ![]() $i=2, 3$, such that
$i=2, 3$, such that ![]() ${H_i(p_4) \neq 0}$,
${H_i(p_4) \neq 0}$, ![]() $H_i(p_i) = 0$, and
$H_i(p_i) = 0$, and ![]() $({\partial H_k}/{\partial x_{1, p_i}})(p_i) = 0$. We select such a general hyperplane
$({\partial H_k}/{\partial x_{1, p_i}})(p_i) = 0$. We select such a general hyperplane ![]() $H_i$.
$H_i$.
We set
Then,
 \[ \det \begin{pmatrix} P_1 & P_2 \\ \dfrac{\partial P_1}{\partial t} & \dfrac{\partial P_2}{\partial t} \end{pmatrix} (p_4) =(H_1^4H_2^3H_3^2)(p_4) \ne 0. \]
\[ \det \begin{pmatrix} P_1 & P_2 \\ \dfrac{\partial P_1}{\partial t} & \dfrac{\partial P_2}{\partial t} \end{pmatrix} (p_4) =(H_1^4H_2^3H_3^2)(p_4) \ne 0. \]
As in Case 1, for the given condition ![]() $(\mathrm {C}_{4,j})$, there is a point
$(\mathrm {C}_{4,j})$, there is a point ![]() $(\mu _1:\mu _2) \in \mathbb {P}^1$ such that the quintic
$(\mu _1:\mu _2) \in \mathbb {P}^1$ such that the quintic
violates the condition ![]() $(\mathrm {C}_{4,j})$ but satisfies all the other conditions.
$(\mathrm {C}_{4,j})$ but satisfies all the other conditions.
5. Prime Fano  $3$-fold weighted complete intersections
$3$-fold weighted complete intersections
We consider some prime Fano ![]() $3$-fold weighted complete intersections with only
$3$-fold weighted complete intersections with only ![]() $cA_1$ points together with terminal quotient singular points, and prove their birational rigidity. We make the setting precise.
$cA_1$ points together with terminal quotient singular points, and prove their birational rigidity. We make the setting precise.
Setting 5.1 Let ![]() $X$ be a prime Fano
$X$ be a prime Fano ![]() $3$-fold which is either a weighted hypersurface of index
$3$-fold which is either a weighted hypersurface of index ![]() $1$ in one of the families listed in Table 2, or a weighted complete intersection of codimension
$1$ in one of the families listed in Table 2, or a weighted complete intersection of codimension ![]() $2$ and index
$2$ and index ![]() $1$ in one of the families listed in Table 3. Let
$1$ in one of the families listed in Table 3. Let ![]() $\mathbb {P}$ be the ambient weighted projective space of
$\mathbb {P}$ be the ambient weighted projective space of ![]() $X$. We assume that
$X$. We assume that ![]() $X$ is quasi-smooth along the singular locus
$X$ is quasi-smooth along the singular locus ![]() $\operatorname {Sing} (\mathbb {P})$ of
$\operatorname {Sing} (\mathbb {P})$ of ![]() $\mathbb {P}$.
$\mathbb {P}$.
Table 2. Fano ![]() $3$-fold weighted hypersurfaces of index
$3$-fold weighted hypersurfaces of index ![]() $1$.
$1$.
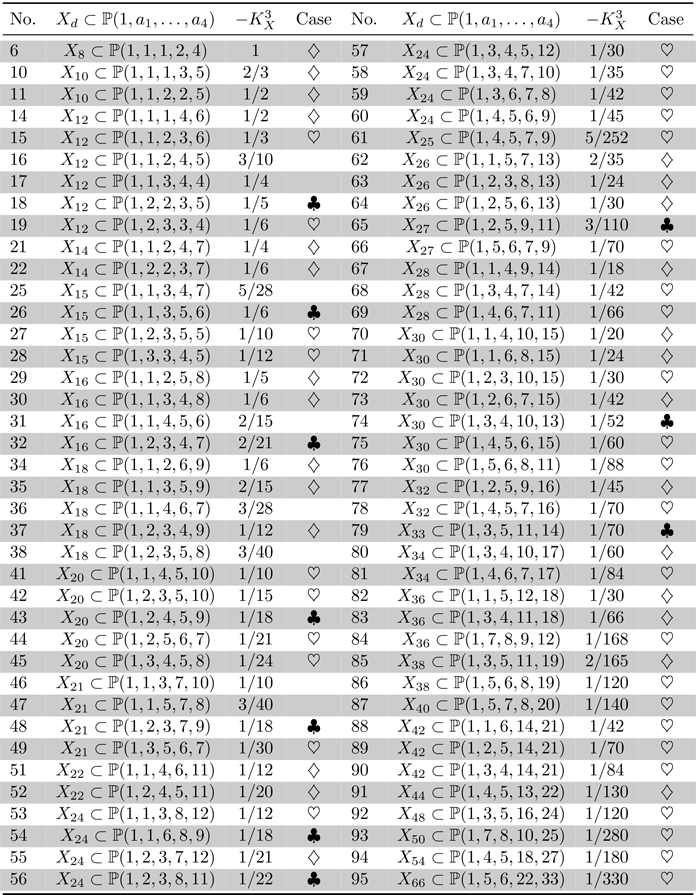
Theorem 5.2 Let ![]() $X$ be as in Setting 5.1 and suppose that
$X$ be as in Setting 5.1 and suppose that ![]() $X$ has at worst
$X$ has at worst ![]() $cA_1$ points in addition to terminal quotient singular points. Then
$cA_1$ points in addition to terminal quotient singular points. Then ![]() $X$ is birationally rigid.
$X$ is birationally rigid.
Remark 5.3 Let ![]() $X \subset \mathbb {P}$ be as in Setting 5.1. Then the subset
$X \subset \mathbb {P}$ be as in Setting 5.1. Then the subset ![]() $X \cap \operatorname {Sing} (\mathbb {P})$ consists of the terminal cyclic quotient singular points of
$X \cap \operatorname {Sing} (\mathbb {P})$ consists of the terminal cyclic quotient singular points of ![]() $X$ coming from the ambient space since
$X$ coming from the ambient space since ![]() $X$ is quasi-smooth along
$X$ is quasi-smooth along ![]() $\operatorname {Sing} (\mathbb {P})$. Any other singular point of
$\operatorname {Sing} (\mathbb {P})$. Any other singular point of ![]() $X$, if it exists, is contained in a smooth locus of
$X$, if it exists, is contained in a smooth locus of ![]() $\mathbb {P}$ so that it is a hypersurface, hence Gorenstein, singular point of
$\mathbb {P}$ so that it is a hypersurface, hence Gorenstein, singular point of ![]() $X$. In Theorem 5.2, these hypersurface singular points are assumed to be
$X$. In Theorem 5.2, these hypersurface singular points are assumed to be ![]() $cA_1$ points.
$cA_1$ points.
Table 3. Fano ![]() $3$-fold weighted complete intersections of codimension
$3$-fold weighted complete intersections of codimension ![]() $2$ and index
$2$ and index ![]() $1$.
$1$.
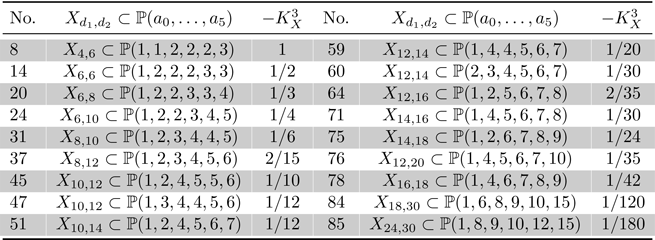
We fix some notation. Let ![]() $\mathbb {P} = \mathbb {P} (a_0, \ldots, a_n)$ be a weighted projective space with homogeneous coordinates
$\mathbb {P} = \mathbb {P} (a_0, \ldots, a_n)$ be a weighted projective space with homogeneous coordinates ![]() $x_0, \ldots, x_n$ of weights
$x_0, \ldots, x_n$ of weights ![]() $a_0, \ldots, a_n$, respectively. For homogeneous polynomials
$a_0, \ldots, a_n$, respectively. For homogeneous polynomials ![]() $g_1, \ldots, g_N$ in variables
$g_1, \ldots, g_N$ in variables ![]() $x_0, \ldots, x_n$, we denote by
$x_0, \ldots, x_n$, we denote by
the closed subscheme defined by the homogeneous ideal ![]() $(g_1, \ldots, g_N)$.
$(g_1, \ldots, g_N)$.
Definition 5.4 Under the above notation, let ![]() $V = (f_1 = \cdots = f_m = 0) \subset \mathbb {P}$ be a closed subscheme, where
$V = (f_1 = \cdots = f_m = 0) \subset \mathbb {P}$ be a closed subscheme, where ![]() $f_1, \ldots, f_m$ are homogeneous polynomials in variables
$f_1, \ldots, f_m$ are homogeneous polynomials in variables ![]() $x_0, \ldots, x_n$. The quasi-smooth locus
$x_0, \ldots, x_n$. The quasi-smooth locus ![]() $\operatorname {Qsm} (V)$ of
$\operatorname {Qsm} (V)$ of ![]() $V$ is defined to be the image of the smooth locus of
$V$ is defined to be the image of the smooth locus of ![]() $C^*_V := C_V \setminus \{o\}$ under the natural map
$C^*_V := C_V \setminus \{o\}$ under the natural map ![]() $\mathbb {A}^{n+1} \setminus \{o\} \to \mathbb {P}$, where
$\mathbb {A}^{n+1} \setminus \{o\} \to \mathbb {P}$, where
is the affine cone of ![]() $V$ and
$V$ and ![]() $o$ is the origin of
$o$ is the origin of ![]() $\mathbb {A}^{n+1}$. For a subset
$\mathbb {A}^{n+1}$. For a subset ![]() $S \subset V$, we say that
$S \subset V$, we say that ![]() $V$ is quasi-smooth along
$V$ is quasi-smooth along ![]() $S$ if
$S$ if ![]() $S \subset \operatorname {Qsm} (V)$. We say that
$S \subset \operatorname {Qsm} (V)$. We say that ![]() $V$ is quasi-smooth if it is quasi-smooth along
$V$ is quasi-smooth if it is quasi-smooth along ![]() $V$, that is,
$V$, that is, ![]() $V = \operatorname {Qsm} (V)$.
$V = \operatorname {Qsm} (V)$.
For ![]() $X \subset \mathbb {P}$ as in Setting 5.1 and
$X \subset \mathbb {P}$ as in Setting 5.1 and ![]() $s \in \{x, y, z, t, w\}$, we set
$s \in \{x, y, z, t, w\}$, we set
5.1 Exclusion of curves
Proposition 5.5 Let ![]() $X$ be as in Setting 5.1. Then no curve on
$X$ be as in Setting 5.1. Then no curve on ![]() $X$ is a maximal center.
$X$ is a maximal center.
Proof. Suppose that there is a curve ![]() $\Gamma \subset X$ which is a maximal center. By [Reference KawamataKaw96], there exists no divisorial contraction centered along a curve through a terminal quotient singular point. Hence,
$\Gamma \subset X$ which is a maximal center. By [Reference KawamataKaw96], there exists no divisorial contraction centered along a curve through a terminal quotient singular point. Hence, ![]() $\Gamma$ does not pass through a terminal quotient singular point. In particular, we have
$\Gamma$ does not pass through a terminal quotient singular point. In particular, we have ![]() $(-K_X \cdot \Gamma ) \ge 1$ since
$(-K_X \cdot \Gamma ) \ge 1$ since ![]() $-K_X$ is a Cartier divisor on an open subset containing
$-K_X$ is a Cartier divisor on an open subset containing ![]() $\Gamma$ and, thus,
$\Gamma$ and, thus, ![]() $(-K_X \cdot \Gamma )$ is a positive integer. On the other hand we have
$(-K_X \cdot \Gamma )$ is a positive integer. On the other hand we have ![]() $(-K_X)^3 \le 1$. By Lemma 2.7,
$(-K_X)^3 \le 1$. By Lemma 2.7, ![]() $\Gamma$ cannot be a maximal center. This is a contradiction and the proof is complete.
$\Gamma$ cannot be a maximal center. This is a contradiction and the proof is complete.
5.2 Exclusion of smooth points
The aim of this section is to show that no smooth point on ![]() $X$ is a maximal center for
$X$ is a maximal center for ![]() $X$ as in Setting 5.1. It may be possible to say that this follows from the same arguments as in [Reference Cheltsov and ParkCP17, § 2.1] and [Reference OkadaOka14, § 7]. However, we reproduce the proofs in a general setting mainly because these arguments will also be useful in the exclusion of
$X$ as in Setting 5.1. It may be possible to say that this follows from the same arguments as in [Reference Cheltsov and ParkCP17, § 2.1] and [Reference OkadaOka14, § 7]. However, we reproduce the proofs in a general setting mainly because these arguments will also be useful in the exclusion of ![]() $cA_1$ points as a maximal center (see § 5.3).
$cA_1$ points as a maximal center (see § 5.3).
Definition 5.6 Let ![]() $V$ be a closed subscheme of a weighted projective space
$V$ be a closed subscheme of a weighted projective space ![]() $\mathbb {P} (a_0, \ldots, a_n)$ with homogeneous coordinates
$\mathbb {P} (a_0, \ldots, a_n)$ with homogeneous coordinates ![]() $x_0, \ldots, x_n$ of weights
$x_0, \ldots, x_n$ of weights ![]() $a_0, \ldots, a_n$, respectively, and let
$a_0, \ldots, a_n$, respectively, and let ![]() $\mathsf {p} \in V$ be a point. We say that homogeneous polynomials
$\mathsf {p} \in V$ be a point. We say that homogeneous polynomials ![]() $g_1, \ldots, g_N$ in variables
$g_1, \ldots, g_N$ in variables ![]() $x_0, \ldots, x_n$ (respectively, effective Weil divisors
$x_0, \ldots, x_n$ (respectively, effective Weil divisors ![]() $D_1, \ldots, D_N$ on
$D_1, \ldots, D_N$ on ![]() $V$) isolate
$V$) isolate ![]() $\mathsf {p}$ or they are
$\mathsf {p}$ or they are ![]() $\mathsf {p}$-isolating polynomials (respectively,
$\mathsf {p}$-isolating polynomials (respectively, ![]() $\mathsf {p}$-isolating divisors) if the set
$\mathsf {p}$-isolating divisors) if the set
is a finite set of points including ![]() $\mathsf {p}$. For a positive integer
$\mathsf {p}$. For a positive integer ![]() $e$, we also say that
$e$, we also say that ![]() $g_1, \ldots, g_N$ (respectively,
$g_1, \ldots, g_N$ (respectively, ![]() $D_1, \ldots, D_N$) are
$D_1, \ldots, D_N$) are ![]() $\mathsf {p}$-isolating polynomials of degree at most
$\mathsf {p}$-isolating polynomials of degree at most ![]() $e$ (respectively,
$e$ (respectively, ![]() $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most ![]() $e$) if
$e$) if ![]() $\max \{ \deg g_1, \ldots, \deg g_N \} \le e$ (respectively,
$\max \{ \deg g_1, \ldots, \deg g_N \} \le e$ (respectively, ![]() $D_i \in |\mathcal {O}_V (e_i)|$ for
$D_i \in |\mathcal {O}_V (e_i)|$ for ![]() $i = 1, \ldots, N$ and
$i = 1, \ldots, N$ and ![]() $\max \{e_1, \ldots, e_N\} \le e$).
$\max \{e_1, \ldots, e_N\} \le e$).
Remark 5.7 Let ![]() $V$ be as in Definition 5.6 and let
$V$ be as in Definition 5.6 and let ![]() $\mathsf {p} \in V$ be a point. Suppose that there are
$\mathsf {p} \in V$ be a point. Suppose that there are ![]() $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most ![]() $e$. Let
$e$. Let ![]() $\Gamma \subset V$ be a closed subset such that
$\Gamma \subset V$ be a closed subset such that ![]() $\mathsf {p} \in \Gamma$ and any component of
$\mathsf {p} \in \Gamma$ and any component of ![]() $\Gamma$ is of positive dimension. Then we can take a divisor
$\Gamma$ is of positive dimension. Then we can take a divisor ![]() $D \in |\mathcal {O}_V (e')|$ for some
$D \in |\mathcal {O}_V (e')|$ for some ![]() $e' \le e$ such that
$e' \le e$ such that ![]() $\mathsf {p} \in \operatorname {Supp} D$ and no component of
$\mathsf {p} \in \operatorname {Supp} D$ and no component of ![]() $\Gamma$ is contained in
$\Gamma$ is contained in ![]() $\operatorname {Supp} D$.
$\operatorname {Supp} D$.
Lemma 5.8 Let ![]() $V$ be a complete intersection of codimension
$V$ be a complete intersection of codimension ![]() $c \in \{1, 2\}$ in a weighted projective space
$c \in \{1, 2\}$ in a weighted projective space ![]() $\mathbb {P} (a_0, \ldots, a_n)$ with homogeneous coordinates
$\mathbb {P} (a_0, \ldots, a_n)$ with homogeneous coordinates ![]() $x_0, \ldots, x_n$ of weights
$x_0, \ldots, x_n$ of weights ![]() $a_0, \ldots, a_n$, respectively.
$a_0, \ldots, a_n$, respectively.
(1) Let
 $\mathsf {p} \in V$ be a point.
$\mathsf {p} \in V$ be a point.
(a) There exist
 $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most
 \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, \ldots, n\} \}. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, \ldots, n\} \}. \]
(b) If there is
 $k$ such that
$k$ such that  $\mathsf {p} \notin \cap _{j \ne k} (x_j = 0) \cap V$, then there exist
$\mathsf {p} \notin \cap _{j \ne k} (x_j = 0) \cap V$, then there exist  $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most
 \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, \ldots, n\} \setminus \{k\} \}. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, \ldots, n\} \setminus \{k\} \}. \]
(c) If
 $c = 2$ and there are
$c = 2$ and there are  $k_1, k_2$ such that
$k_1, k_2$ such that  $\mathsf {p} \notin \cap _{j \ne k_1, k_2} (x_j = 0)$, then there exist
$\mathsf {p} \notin \cap _{j \ne k_1, k_2} (x_j = 0)$, then there exist  $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most
 \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, \ldots, \} \setminus \{k_1, k_2\} \}. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, \ldots, \} \setminus \{k_1, k_2\} \}. \]
(2) Let
 $\mathsf {p} \in U_{x_i} = (x_i \ne 0) \cap V$ be a point.
$\mathsf {p} \in U_{x_i} = (x_i \ne 0) \cap V$ be a point.
(a) There exist
 $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most
 \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid j \in \{0, 1, \ldots, n\} \}. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid j \in \{0, 1, \ldots, n\} \}. \]
(b) If there is
 $k \ne i$ such that
$k \ne i$ such that  $\mathsf {p} \notin \cap _{j \ne k} (x_j = 0) \cap V$, then there exists
$\mathsf {p} \notin \cap _{j \ne k} (x_j = 0) \cap V$, then there exists  $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most
 \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid j \in \{0, 1, \ldots, n\} \setminus \{k\} \}. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid j \in \{0, 1, \ldots, n\} \setminus \{k\} \}. \]
(c) If
 $c = 2$ and there are
$c = 2$ and there are  $k_1, k_2 \ne i$ such that
$k_1, k_2 \ne i$ such that  $\mathsf {p} \notin \cap _{j \ne k_1, k_2} (x_j = 0) \cap V$, then there exists
$\mathsf {p} \notin \cap _{j \ne k_1, k_2} (x_j = 0) \cap V$, then there exists  $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most
 \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid j \in \{0, 1, \ldots, n\} \setminus \{k_1, k_2\} \}. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid j \in \{0, 1, \ldots, n\} \setminus \{k_1, k_2\} \}. \]
Proof. We set ![]() $U_{x_j} = (x_j \ne 0) \cap V$. Part (1) follows from part (2) since
$U_{x_j} = (x_j \ne 0) \cap V$. Part (1) follows from part (2) since ![]() $V$ is covered by the
$V$ is covered by the ![]() $U_{x_j}$.
$U_{x_j}$.
We prove part (2). We can write ![]() $\mathsf {p} = (\alpha _0:\cdots :\alpha _n)$, with
$\mathsf {p} = (\alpha _0:\cdots :\alpha _n)$, with ![]() $\alpha _i \ne 0$. We set
$\alpha _i \ne 0$. We set ![]() $m_j = \operatorname {lcm} (a_i, a_j)$. Then the polynomials in the set
$m_j = \operatorname {lcm} (a_i, a_j)$. Then the polynomials in the set
isolate ![]() $\mathsf {p}$, and the first assertion follows by considering the divisors
$\mathsf {p}$, and the first assertion follows by considering the divisors ![]() $(g_j = 0) \cap V$.
$(g_j = 0) \cap V$.
Suppose that ![]() $\mathsf {p} \notin \cap _{j \ne k} (x_j = 0) \cap V$, where
$\mathsf {p} \notin \cap _{j \ne k} (x_j = 0) \cap V$, where ![]() $k \ne i$. Then the natural projection
$k \ne i$. Then the natural projection
is a finite morphism in a neighborhood of ![]() $\mathsf {p} \in V$. The polynomials in the set
$\mathsf {p} \in V$. The polynomials in the set
isolate ![]() $\tau (\mathsf {p}) \in \mathbb {P}'$, that is, the common zero locus of the polynomials in the above set is a finite set of points on
$\tau (\mathsf {p}) \in \mathbb {P}'$, that is, the common zero locus of the polynomials in the above set is a finite set of points on ![]() $\mathbb {P}'$. It follows that the common zero locus of the polynomials in the same set, considered as a subset of
$\mathbb {P}'$. It follows that the common zero locus of the polynomials in the same set, considered as a subset of ![]() $\mathbb {P} (a_0, \ldots, a_n)$, is again a finite set of points since
$\mathbb {P} (a_0, \ldots, a_n)$, is again a finite set of points since ![]() $\tau$ is a finite morphism. This shows that the above set isolates
$\tau$ is a finite morphism. This shows that the above set isolates ![]() $\mathsf {p}$ and the second assertion is proved.
$\mathsf {p}$ and the second assertion is proved.
Suppose that ![]() $c = 2$ and
$c = 2$ and ![]() $\mathsf {p} \notin \cap _{j \ne k_1, k_2} (x_j = 0) \cap V$, where
$\mathsf {p} \notin \cap _{j \ne k_1, k_2} (x_j = 0) \cap V$, where ![]() $k_1, k_2 \ne i$. Then the natural projection
$k_1, k_2 \ne i$. Then the natural projection
is a finite morphism in a neighborhood of ![]() $\mathsf {p} \in V$. By the similar argument as above considering the set
$\mathsf {p} \in V$. By the similar argument as above considering the set
we obtain the third assertion.
Lemma 5.9 Let ![]() $X$ be a prime Fano
$X$ be a prime Fano ![]() $3$-fold weighted hypersurface of index
$3$-fold weighted hypersurface of index ![]() $1$ which belongs to one of the families listed in Table 2. Let
$1$ which belongs to one of the families listed in Table 2. Let ![]() $\mathsf {p} \in X$ be a point contained in the smooth locus of the ambient weighted projective space. Then the following assertions hold.
$\mathsf {p} \in X$ be a point contained in the smooth locus of the ambient weighted projective space. Then the following assertions hold.
(1) There exist
 $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most  $4/(-K_X\!)^3$ except when the family number of
$4/(-K_X\!)^3$ except when the family number of  $X$ is
$X$ is  $25$ and
$25$ and  $\mathsf {p} \in (x = y = z = 0) \cap X$.
$\mathsf {p} \in (x = y = z = 0) \cap X$.(2) If
 $X$ belongs to a family which is given one of
$X$ belongs to a family which is given one of  $\heartsuit, \diamondsuit, \clubsuit$ in the ‘Case’ column of Table 2, then there exist
$\heartsuit, \diamondsuit, \clubsuit$ in the ‘Case’ column of Table 2, then there exist  $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most  $2/(-K_X^3\!)$.
$2/(-K_X^3\!)$.
Proof. Let ![]() $X = X_d \subset \mathbb {P} (a_0, a_1, \ldots, a_4) =: \mathbb {P}$ with
$X = X_d \subset \mathbb {P} (a_0, a_1, \ldots, a_4) =: \mathbb {P}$ with ![]() $1 = a_0 \le a_1 \le \cdots \le a_4$, where
$1 = a_0 \le a_1 \le \cdots \le a_4$, where ![]() $d = a_1 + \cdots + a_4$. Let
$d = a_1 + \cdots + a_4$. Let ![]() $x, y, z, t, w$ be homogeneous coordinates of weights
$x, y, z, t, w$ be homogeneous coordinates of weights ![]() $a_0, a_1, a_2, a_3, a_4$, respectively.
$a_0, a_1, a_2, a_3, a_4$, respectively.
We prove assertion (2). We consider ![]() $X$ belonging to a family which is given one of
$X$ belonging to a family which is given one of ![]() $\heartsuit, \diamondsuit, \clubsuit$ in the ‘Case’ column of Table 2. Then the assertions follow from the following observations.
$\heartsuit, \diamondsuit, \clubsuit$ in the ‘Case’ column of Table 2. Then the assertions follow from the following observations.
• Case:
 $X$ belongs to a family with
$X$ belongs to a family with  $\heartsuit$. We have
and the assertion follows from Lemma 5.8(1)(a).
$\heartsuit$. We have
and the assertion follows from Lemma 5.8(1)(a). \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 3, 4\} \} \le 2/(-K_X\!)^3, \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 3, 4\} \} \le 2/(-K_X\!)^3, \]
• Case:
 $X$ belongs to a family with
$X$ belongs to a family with  $\diamondsuit$. We have
$\diamondsuit$. We have  $a_3 < a_4$,
$a_3 < a_4$,  $a_4 \mid d$, and
It follows from
$a_4 \mid d$, and
It follows from \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 3\} \} \le 2/(-K_X\!)^3. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 3\} \} \le 2/(-K_X\!)^3. \]
 $a_3 < a_4$ and
$a_3 < a_4$ and  $a_4 \mid d$ that the monomial
$a_4 \mid d$ that the monomial  $w^{d/a_4}$ appears in the defining polynomial of
$w^{d/a_4}$ appears in the defining polynomial of  $X$ with non-zero coefficient and, thus,
$X$ with non-zero coefficient and, thus,  $(x = y = z = t = 0) \cap X = \emptyset$. The assertion now follows from Lemma 5.8(1)(b).
$(x = y = z = t = 0) \cap X = \emptyset$. The assertion now follows from Lemma 5.8(1)(b).• Case:
 $X$ belongs to a family with
$X$ belongs to a family with  $\clubsuit$. We have
$\clubsuit$. We have  $a_2 < a_3 < a_4$,
$a_2 < a_3 < a_4$,  $a_3 \mid d$ and
It follows from
$a_3 \mid d$ and
It follows from \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 4\} \} \le 2/(-K_X\!)^3. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 4\} \} \le 2/(-K_X\!)^3. \]
 $a_2 < a_3 < a_4$ and
$a_2 < a_3 < a_4$ and  $a_3 \mid d$ that the monomial
$a_3 \mid d$ that the monomial  $t^{d/a_3}$ appears in the defining polynomial of
$t^{d/a_3}$ appears in the defining polynomial of  $X$ with non-zero coefficient and, thus,
$X$ with non-zero coefficient and, thus,  $(x = y = z = w = 0) \cap X = \emptyset$. The assertion now follows from Lemma 5.8(1)(b).
$(x = y = z = w = 0) \cap X = \emptyset$. The assertion now follows from Lemma 5.8(1)(b).
We prove assertion (1). It is enough to consider ![]() $X$ whose family number
$X$ whose family number ![]() $\mathsf {i}$ belongs to
$\mathsf {i}$ belongs to
• Case:
 $\mathsf {i} \in \{17, 31, 38\}$. We have
and the assertion follows from Lemma 5.8(1)(a).
$\mathsf {i} \in \{17, 31, 38\}$. We have
and the assertion follows from Lemma 5.8(1)(a). \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 3, 4\} \} \le 4/(-K_X)^3, \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 3, 4\} \} \le 4/(-K_X)^3, \]
• Case:
 $\mathsf {i} \in \{16, 36, 46, 47\}$. In this case
$\mathsf {i} \in \{16, 36, 46, 47\}$. In this case  $a_3 \mid d$ and
$a_3 \mid d$ and  $w^{d/a_3}$ appears in the defining polynomial of
$w^{d/a_3}$ appears in the defining polynomial of  $X$. Hence
$X$. Hence  $(x = y = z = w = 0) \cap X = \emptyset$. We have
and the assertion follows from Lemma 5.8(1)(b).
$(x = y = z = w = 0) \cap X = \emptyset$. We have
and the assertion follows from Lemma 5.8(1)(b). \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 4\} \} \le 4/(-K_X\!)^3, \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid i, j \in \{0, 1, 2, 4\} \} \le 4/(-K_X\!)^3, \]
• Case:
 $\mathsf {i} = 25$. By the assumption, we have
$\mathsf {i} = 25$. By the assumption, we have  $\mathsf {p} \in U_x \cup U_y \cup U_z$. For
$\mathsf {p} \in U_x \cup U_y \cup U_z$. For  $i = 0, 1, 2$, it is straightforward to check
Thus, the assertion follows from Lemma 5.8(2)(a).
$i = 0, 1, 2$, it is straightforward to check
Thus, the assertion follows from Lemma 5.8(2)(a). \[ \max \{ \operatorname{lcm} (a_i, a_j) \mid j \in \{0, 1, 2, 3, 4\} \} \le 4/(-K_X)^3. \]
\[ \max \{ \operatorname{lcm} (a_i, a_j) \mid j \in \{0, 1, 2, 3, 4\} \} \le 4/(-K_X)^3. \]
The proof is now complete.
Lemma 5.10 Let ![]() $X$ be a prime Fano
$X$ be a prime Fano ![]() $3$-fold weighted complete intersection of codimension
$3$-fold weighted complete intersection of codimension ![]() $2$ and index
$2$ and index ![]() $1$ which belongs to one of the families listed in Table 3. Let
$1$ which belongs to one of the families listed in Table 3. Let ![]() $\mathsf {p} \in X$ be a point which is contained in the smooth locus of the ambient weighted projective space. Then there exist
$\mathsf {p} \in X$ be a point which is contained in the smooth locus of the ambient weighted projective space. Then there exist ![]() $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most ![]() $2/(-K_X)^3$.
$2/(-K_X)^3$.
Proof. Let ![]() $X = X_{d_1, d_2} \subset \mathbb {P} (a_0, \ldots, a_5)$ with
$X = X_{d_1, d_2} \subset \mathbb {P} (a_0, \ldots, a_5)$ with ![]() $a_0 \le \cdots \le a_5$ and
$a_0 \le \cdots \le a_5$ and ![]() $d_1 < d_2$. Let
$d_1 < d_2$. Let ![]() $x, y, z, t, v, w$ be homogeneous coordinates of weights
$x, y, z, t, v, w$ be homogeneous coordinates of weights ![]() $a_0, a_1, a_2, a_3, a_4, a_5$, respectively, and let
$a_0, a_1, a_2, a_3, a_4, a_5$, respectively, and let ![]() $f_1, f_2 \in \mathbb {C} [x, y, z, t, v, w]$ be the defining polynomials of
$f_1, f_2 \in \mathbb {C} [x, y, z, t, v, w]$ be the defining polynomials of ![]() $X$ of degree
$X$ of degree ![]() $d_1, d_2$, respectively. We denote by
$d_1, d_2$, respectively. We denote by ![]() $\mathsf {i}$ the family number of
$\mathsf {i}$ the family number of ![]() $X$.
$X$.
We consider the case ![]() $\mathsf {i} = 60, 71, 76, 78, 84, 85$. We have
$\mathsf {i} = 60, 71, 76, 78, 84, 85$. We have
and, thus, the assertion follows from Lemma 5.8(1)(a).
Case: ![]() $\mathsf {i} = 8, 20, 31, 45, 47, 59$. In this case
$\mathsf {i} = 8, 20, 31, 45, 47, 59$. In this case ![]() $a_4 < a_5$,
$a_4 < a_5$, ![]() $a_5 \mid d_2$ and
$a_5 \mid d_2$ and
Then ![]() $w^{d_2/a_5} \in f_2$ since
$w^{d_2/a_5} \in f_2$ since ![]() $a_4 < a_5$ and
$a_4 < a_5$ and ![]() $a_5 \mid d_2$ and, thus,
$a_5 \mid d_2$ and, thus, ![]() $(x = y = z = t = v = 0) \cap X = \emptyset$. The assertion follows from Lemma 5.8(1)(b).
$(x = y = z = t = v = 0) \cap X = \emptyset$. The assertion follows from Lemma 5.8(1)(b).
We consider the case ![]() $\mathsf {i} = 24, 37, 51, 64, 75$. In this case
$\mathsf {i} = 24, 37, 51, 64, 75$. In this case ![]() $a_2 < a_3 < a_4 < a_5$,
$a_2 < a_3 < a_4 < a_5$, ![]() $d_1 < a_3 + a_5$,
$d_1 < a_3 + a_5$, ![]() $a_3 \mid d_1$,
$a_3 \mid d_1$, ![]() $a_5 \mid d_2$, and
$a_5 \mid d_2$, and
Then
for some non-zero ![]() $\alpha, \beta \in \mathbb {C}$. It follows that
$\alpha, \beta \in \mathbb {C}$. It follows that ![]() $(x = y = z = v = 0) \cap X = \emptyset$ and, thus, the assertion follows from Lemma 5.8(1)(c).
$(x = y = z = v = 0) \cap X = \emptyset$ and, thus, the assertion follows from Lemma 5.8(1)(c).
We consider the case ![]() $\mathsf {i} = 14$. In this case, we have
$\mathsf {i} = 14$. In this case, we have ![]() $(x = y z = t = 0) \cap X = \emptyset$ and
$(x = y z = t = 0) \cap X = \emptyset$ and
Thus, the assertion follows from Lemma 5.8(1)(c), and the proof is complete.
Remark 5.11 In Lemmas 5.9 and 5.10, we do not assume that ![]() $\mathsf {p}$ is a smooth point of
$\mathsf {p}$ is a smooth point of ![]() $X$, and the case where
$X$, and the case where ![]() $\mathsf {p}$ is a Gorenstein singular point of
$\mathsf {p}$ is a Gorenstein singular point of ![]() $X$ is covered. This is utilized in the proof of Lemma 5.13.
$X$ is covered. This is utilized in the proof of Lemma 5.13.
Proposition 5.12 Let ![]() $X$ be as in Setting 5.1. Then no smooth point on
$X$ be as in Setting 5.1. Then no smooth point on ![]() $X$ is a maximal center.
$X$ is a maximal center.
Proof. Let ![]() $\mathsf {p} \in X$ be a smooth point. If
$\mathsf {p} \in X$ be a smooth point. If ![]() $X$ is a weighted hypersurface and its family number is
$X$ is a weighted hypersurface and its family number is ![]() $25$, and
$25$, and ![]() $\mathsf {p}$ is contained in
$\mathsf {p}$ is contained in ![]() $(x = y = z = 0) \cap X$, then we can repeat the argument of the proof of [Reference Cheltsov and ParkCP17, Lemma 2.1.5] without any change and conclude that
$(x = y = z = 0) \cap X$, then we can repeat the argument of the proof of [Reference Cheltsov and ParkCP17, Lemma 2.1.5] without any change and conclude that ![]() $\mathsf {p}$ is not a maximal center. In what follows, we assume that
$\mathsf {p}$ is not a maximal center. In what follows, we assume that ![]() $\mathsf {p} \notin (x = y = z = 0) \cap X$ when
$\mathsf {p} \notin (x = y = z = 0) \cap X$ when ![]() $X$ is a weighted hypersurface and its family number is
$X$ is a weighted hypersurface and its family number is ![]() $25$.
$25$.
Suppose that ![]() $X$ admits a smooth point
$X$ admits a smooth point ![]() $\mathsf {p} \in X$ which is a maximal center. Then there exists a movable linear system
$\mathsf {p} \in X$ which is a maximal center. Then there exists a movable linear system ![]() $\mathcal {M} \subset | - n K_X |$ such that
$\mathcal {M} \subset | - n K_X |$ such that ![]() $\mathsf {p}$ is a center of non-canonical singularities of
$\mathsf {p}$ is a center of non-canonical singularities of ![]() $(X, ({1}/{n}) \mathcal {M})$. Let
$(X, ({1}/{n}) \mathcal {M})$. Let ![]() $D_1, D_2 \in \mathcal {M}$ be general members of
$D_1, D_2 \in \mathcal {M}$ be general members of ![]() $\mathcal {M}$. By Lemmas 5.9 and 5.10, we can take a divisor
$\mathcal {M}$. By Lemmas 5.9 and 5.10, we can take a divisor ![]() $T \in | - l K_X |$ for some positive integer
$T \in | - l K_X |$ for some positive integer ![]() $l \le 4/(-K_X^3)$ such that
$l \le 4/(-K_X^3)$ such that ![]() $\operatorname {Supp} T$ passes through
$\operatorname {Supp} T$ passes through ![]() $\mathsf {p}$ and does not contain any component of
$\mathsf {p}$ and does not contain any component of ![]() $D_1 \cap D_2$. Thus, we have
$D_1 \cap D_2$. Thus, we have
where the last inequality follows from the ![]() $4 n^2$-inequality for smooth points (see Theorem 1.1). This is a contradiction.
$4 n^2$-inequality for smooth points (see Theorem 1.1). This is a contradiction.
5.3 Exclusion of  $cA_1$ points
$cA_1$ points
The aim of this section is to exclude singularities of type ![]() $cA_1$ on
$cA_1$ on ![]() $X$ as a maximal singularity for
$X$ as a maximal singularity for ![]() $X$ as in Setting 5.1.
$X$ as in Setting 5.1.
Lemma 5.13 Let ![]() $X$ be as in Setting 5.1 and let
$X$ be as in Setting 5.1 and let ![]() $\mathsf {p} \in X$ be a singular point contained in the smooth locus of the ambient weighted projective space. Then there exist
$\mathsf {p} \in X$ be a singular point contained in the smooth locus of the ambient weighted projective space. Then there exist ![]() $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most ![]() $2/(-K_X^3\!)$.
$2/(-K_X^3\!)$.
Proof. By Lemmas 5.9 and 5.10, it remains to consider the case where ![]() $X$ is a weighted hypersurface whose family number
$X$ is a weighted hypersurface whose family number ![]() $\mathsf {i}$ belongs to
$\mathsf {i}$ belongs to
We consider the case ![]() $\mathsf {i} = 38$. In this case
$\mathsf {i} = 38$. In this case ![]() $X = X_{18} \subset \mathbb {P} (1, 2, 3, 5, 8)$. We claim that the set
$X = X_{18} \subset \mathbb {P} (1, 2, 3, 5, 8)$. We claim that the set ![]() $\Delta := (x = y = z = 0) \cap X$ is contained in
$\Delta := (x = y = z = 0) \cap X$ is contained in ![]() $\operatorname {Qsm} (X)$. Let
$\operatorname {Qsm} (X)$. Let ![]() $f = f (x, y, z, t, w)$ be the defining polynomial of
$f = f (x, y, z, t, w)$ be the defining polynomial of ![]() $X$. We have
$X$. We have ![]() $f = \alpha t^2 w + \beta y w^2 + \gamma z t^3 + G$, where
$f = \alpha t^2 w + \beta y w^2 + \gamma z t^3 + G$, where ![]() $\alpha, \beta, \gamma \in \mathbb {C}$ and
$\alpha, \beta, \gamma \in \mathbb {C}$ and ![]() $G = G (x, y, z, t, w) \in (x, y, z)^2$. We have
$G = G (x, y, z, t, w) \in (x, y, z)^2$. We have ![]() $(\alpha, \gamma ) \ne (0, 0)$ and
$(\alpha, \gamma ) \ne (0, 0)$ and ![]() $\beta \ne 0$. If
$\beta \ne 0$. If ![]() $\alpha \ne 0$, then
$\alpha \ne 0$, then ![]() $\Delta$ consists of
$\Delta$ consists of ![]() $2$ points which are the
$2$ points which are the ![]() $\tfrac {1}{5} (1, 2, 3)$ point and the
$\tfrac {1}{5} (1, 2, 3)$ point and the ![]() $\frac {1}{8} (1, 3, 5)$ point and, hence,
$\frac {1}{8} (1, 3, 5)$ point and, hence, ![]() $X$ is quasi-smooth along
$X$ is quasi-smooth along ![]() $\Delta$. Suppose that
$\Delta$. Suppose that ![]() $\alpha = 0$. In this case
$\alpha = 0$. In this case ![]() $\Gamma = (x = y = z = 0)$ is a curve and it is straightforward to check that
$\Gamma = (x = y = z = 0)$ is a curve and it is straightforward to check that ![]() $X$ is quasi-smooth along
$X$ is quasi-smooth along ![]() $\Gamma$ since
$\Gamma$ since ![]() $\beta \ne 0$ and
$\beta \ne 0$ and ![]() $\gamma \ne 0$. The claim is proved. It follows that
$\gamma \ne 0$. The claim is proved. It follows that ![]() $\mathsf {p} \in U_x \cup U_y \cup U_z$ and there exist
$\mathsf {p} \in U_x \cup U_y \cup U_z$ and there exist ![]() $\mathsf {p}$-isolating divisors of degree at most
$\mathsf {p}$-isolating divisors of degree at most ![]() $3 a_4$ by Lemma 5.8(2)(a), and we have
$3 a_4$ by Lemma 5.8(2)(a), and we have ![]() $3 a_4 = 24 \le 2/(-K_X\!)^3 = 80/3$.
$3 a_4 = 24 \le 2/(-K_X\!)^3 = 80/3$.
Table 4. Descriptions of ![]() $f (0, 0, z, t, w)$.
$f (0, 0, z, t, w)$.
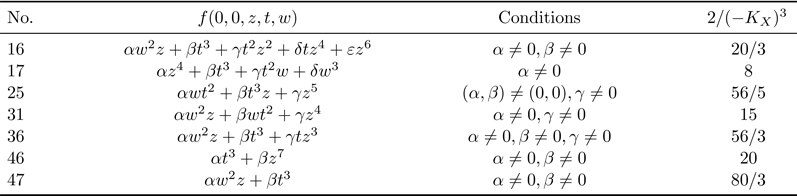
Finally, we consider the case ![]() $\mathsf {i} \in \{16, 17, 25, 31, 36, 46, 47\}$. In this case
$\mathsf {i} \in \{16, 17, 25, 31, 36, 46, 47\}$. In this case ![]() $X = X_d \subset \mathbb {P} (1, 1, a_2, a_3, a_4)$ with
$X = X_d \subset \mathbb {P} (1, 1, a_2, a_3, a_4)$ with ![]() $d = 1 + a_2 + a_3 + a_4$ and
$d = 1 + a_2 + a_3 + a_4$ and ![]() $a_2 \ge 2$. We claim that
$a_2 \ge 2$. We claim that ![]() $\mathsf {p} \in U_x \cup U_y$. Assume to the contrary that
$\mathsf {p} \in U_x \cup U_y$. Assume to the contrary that ![]() $\mathsf {p} \in (x = y = 0) \cap X$. Recall that
$\mathsf {p} \in (x = y = 0) \cap X$. Recall that ![]() $\mathsf {p}$ is a singular point of
$\mathsf {p}$ is a singular point of ![]() $X$, hence it is either a hypersurface singular point or a cyclic quotient terminal singular point (see Remark 5.3). In the latter case
$X$, hence it is either a hypersurface singular point or a cyclic quotient terminal singular point (see Remark 5.3). In the latter case ![]() $\mathsf {p}$ is contained in the singular locus of the ambient weighted projective space. Hence,
$\mathsf {p}$ is contained in the singular locus of the ambient weighted projective space. Hence, ![]() $\mathsf {p} \in X$ is a hypersurface singularity and, in particular,
$\mathsf {p} \in X$ is a hypersurface singularity and, in particular, ![]() $X$ is not quasi-smooth at
$X$ is not quasi-smooth at ![]() $\mathsf {p}$. Thus, we have
$\mathsf {p}$. Thus, we have
An explicit description of ![]() $f (0, 0, z, t, w)$ is given in the second column of Table 4, where the coefficients
$f (0, 0, z, t, w)$ is given in the second column of Table 4, where the coefficients ![]() $\alpha, \beta, \ldots$ satisfy the conditions given in the third column. It is then straightforward to see that either the equations in (5.1) have only trivial solution or they imply that
$\alpha, \beta, \ldots$ satisfy the conditions given in the third column. It is then straightforward to see that either the equations in (5.1) have only trivial solution or they imply that ![]() $\mathsf {p} \in \{\mathsf {p}_z, \mathsf {p}_t, \mathsf {p}_w\}$. We have a contradiction in the former case, and the latter case is impossible since any point in
$\mathsf {p} \in \{\mathsf {p}_z, \mathsf {p}_t, \mathsf {p}_w\}$. We have a contradiction in the former case, and the latter case is impossible since any point in ![]() $\{\mathsf {p}_z, \mathsf {p}_t, \mathsf {p}_w\} \cap X$ is a quotient singular point of
$\{\mathsf {p}_z, \mathsf {p}_t, \mathsf {p}_w\} \cap X$ is a quotient singular point of ![]() $X$. Thus, the claim is proved, and we have
$X$. Thus, the claim is proved, and we have ![]() $\mathsf {p} \in U_x \cup U_y$. By Lemma 5.8 (2-a), there exist
$\mathsf {p} \in U_x \cup U_y$. By Lemma 5.8 (2-a), there exist ![]() $\mathsf {p}$-isolating divisors of degree most
$\mathsf {p}$-isolating divisors of degree most ![]() $a_4$. It is easy to check
$a_4$. It is easy to check ![]() $a_4 \le 2/(-K_X)^3$ (see the fourth column of Table 4) and the proof is complete.
$a_4 \le 2/(-K_X)^3$ (see the fourth column of Table 4) and the proof is complete.
Proposition 5.14 Let ![]() $X$ be as in Setting 5.1, and let
$X$ be as in Setting 5.1, and let ![]() $\mathsf {p} \in X$ be a singular point of type
$\mathsf {p} \in X$ be a singular point of type ![]() $cA_1$. Then
$cA_1$. Then ![]() $\mathsf {p}$ is not a maximal center.
$\mathsf {p}$ is not a maximal center.
Proof. Suppose that ![]() $\mathsf {p} \in X$ is a maximal center. Then there exists a movable linear system
$\mathsf {p} \in X$ is a maximal center. Then there exists a movable linear system ![]() $\mathcal {M} \sim - n K_X$ such that
$\mathcal {M} \sim - n K_X$ such that ![]() $\mathsf {p}$ is the center of a non-canonical singularities of the pair
$\mathsf {p}$ is the center of a non-canonical singularities of the pair ![]() $(X, ({1}/{n}) \mathcal {M})$. Let
$(X, ({1}/{n}) \mathcal {M})$. Let ![]() $D_1, D_2 \in \mathcal {M}$ be general members. Then by Lemma 5.13, we can take a divisor
$D_1, D_2 \in \mathcal {M}$ be general members. Then by Lemma 5.13, we can take a divisor ![]() $T \in |- l K_X |$ for some positive integer
$T \in |- l K_X |$ for some positive integer ![]() $l \le 2/(-K_X\!)^3$ such that
$l \le 2/(-K_X\!)^3$ such that ![]() $\operatorname {Supp} T$ passes through
$\operatorname {Supp} T$ passes through ![]() $\mathsf {p}$ and does not contain any component of
$\mathsf {p}$ and does not contain any component of ![]() $D_1 \cap D_2$. Thus, we have
$D_1 \cap D_2$. Thus, we have
where the last inequality follows from Theorem 3.14. This is a contradiction.
5.4 Links centered at quotient points and proof of Theorem 5.2
Proposition 5.15 Let ![]() $X$ be as in Setting 5.1 and let
$X$ be as in Setting 5.1 and let ![]() $\mathsf {p} \in X$ be a terminal quotient singular point. If the point
$\mathsf {p} \in X$ be a terminal quotient singular point. If the point ![]() $\mathsf {p}$ is a maximal center, then there exists an elementary self-link
$\mathsf {p}$ is a maximal center, then there exists an elementary self-link ![]() $X \dashrightarrow X$ of type II initiated by the Kawamata blow-up at
$X \dashrightarrow X$ of type II initiated by the Kawamata blow-up at ![]() $\mathsf {p}$.
$\mathsf {p}$.
Proof. Suppose that ![]() $X$ is a weighted hypersurface. Then the same arguments as in [Reference Cheltsov and ParkCP17, Chapter 5] prove the assertion. To be more precise, although
$X$ is a weighted hypersurface. Then the same arguments as in [Reference Cheltsov and ParkCP17, Chapter 5] prove the assertion. To be more precise, although ![]() $X$ is assumed to be quasi-smooth in [Reference Cheltsov and ParkCP17], the arguments in [Reference Cheltsov and ParkCP17, Chapter 5] in fact relies only on the quasi-smoothness of
$X$ is assumed to be quasi-smooth in [Reference Cheltsov and ParkCP17], the arguments in [Reference Cheltsov and ParkCP17, Chapter 5] in fact relies only on the quasi-smoothness of ![]() $X$ along
$X$ along ![]() $X \cap \operatorname {Sing} (\mathbb {P})$, where
$X \cap \operatorname {Sing} (\mathbb {P})$, where ![]() $\mathbb {P}$ is the ambient weighted projective
$\mathbb {P}$ is the ambient weighted projective ![]() $4$-space, in addition to the basic assumption that
$4$-space, in addition to the basic assumption that ![]() $X$ is a prime Fano
$X$ is a prime Fano ![]() $3$-fold.
$3$-fold.
Similarly, for weighted complete intersections of codimension 2, the same arguments as in [Reference OkadaOka14, § 7] and [Reference Ahmadinezhad and ZucconiAZ16, § 4] prove the assertion.
Remark 5.16 It should be mentioned that, for some weighted hypersurface ![]() $X$ of index
$X$ of index ![]() $1$ which is not listed Table 2, the arguments in [Reference Cheltsov and ParkCP17, Chapter 5] do rely on the entire quasi-smoothness of
$1$ which is not listed Table 2, the arguments in [Reference Cheltsov and ParkCP17, Chapter 5] do rely on the entire quasi-smoothness of ![]() $X$. For example, the singular point of type
$X$. For example, the singular point of type ![]() $\tfrac {1}{3} (1, 1, 2)$ on a quasi-smooth member
$\tfrac {1}{3} (1, 1, 2)$ on a quasi-smooth member ![]() $X_{17} \subset \mathbb {P} (1, 2, 3, 5, 7) =: \mathbb {P}$ of family No.
$X_{17} \subset \mathbb {P} (1, 2, 3, 5, 7) =: \mathbb {P}$ of family No. ![]() $33$ is excluded as a maximal center in [Reference Cheltsov and ParkCP17, Chapter 5] and the proof of this fact does rely on the quasi-smoothness of
$33$ is excluded as a maximal center in [Reference Cheltsov and ParkCP17, Chapter 5] and the proof of this fact does rely on the quasi-smoothness of ![]() $X$ (not only on the quasi-smoothness along
$X$ (not only on the quasi-smoothness along ![]() $X \cap \operatorname {Sing} \mathbb {P}$).
$X \cap \operatorname {Sing} \mathbb {P}$).
6. Del Pezzo fibrations of degree  $1$
$1$
The aim of this section is to prove the following by the method of maximal singularities developed in [Reference PukhlikovPuk98] and [Reference OkadaOka20a] combined with Corti's inequality for smooth points and ![]() $cA_1$ points.
$cA_1$ points.
Theorem 6.1 Let ![]() $\pi \colon X \to \mathbb {P}^1$ be a del Pezzo fibration of degree
$\pi \colon X \to \mathbb {P}^1$ be a del Pezzo fibration of degree ![]() $1$ with only
$1$ with only ![]() $cA_1$ points. If
$cA_1$ points. If ![]() $X/\mathbb {P}^1$ satisfies the
$X/\mathbb {P}^1$ satisfies the ![]() $K^2$-condition (1.1), then it is birationally superrigid.
$K^2$-condition (1.1), then it is birationally superrigid.
The rest of this section is devoted to the proof of Theorem 6.1. In what follows, let ![]() $\pi \colon X \to \mathbb {P}^1$ be a del Pezzo fibration of degree
$\pi \colon X \to \mathbb {P}^1$ be a del Pezzo fibration of degree ![]() $1$ with only
$1$ with only ![]() $cA_1$ singularities and assume that
$cA_1$ singularities and assume that ![]() $X$ satisfies the
$X$ satisfies the ![]() $K^2$-condition (1.1). We denote by
$K^2$-condition (1.1). We denote by ![]() $F \in \operatorname {Pic} (X)$ the fiber class.
$F \in \operatorname {Pic} (X)$ the fiber class.
We recall that by [Reference PukhlikovPuk98, p. 117] the variety ![]() $X$ can be embedded in a toric
$X$ can be embedded in a toric ![]() $\mathbb {P} (1, 1, 2, 3)$-bundle
$\mathbb {P} (1, 1, 2, 3)$-bundle ![]() $P \to \mathbb {P}^1$ in such a way that the morphism
$P \to \mathbb {P}^1$ in such a way that the morphism ![]() $\pi$ coincides with the restriction of
$\pi$ coincides with the restriction of ![]() $P \to \mathbb {P}^1$. A fiber of
$P \to \mathbb {P}^1$. A fiber of ![]() $\pi$ is a Gorenstein del Pezzo surface (which can be non-normal), and it is an irreducible and reduced hypersurface of degree
$\pi$ is a Gorenstein del Pezzo surface (which can be non-normal), and it is an irreducible and reduced hypersurface of degree ![]() $6$ in
$6$ in ![]() $\mathbb {P} (1, 1, 2, 3)$.
$\mathbb {P} (1, 1, 2, 3)$.
Proposition 6.2 [Reference PukhlikovPuk98, § 3]
Under the above setting, no curve on ![]() $X$ is a center of non-canonical singularities of the pair
$X$ is a center of non-canonical singularities of the pair ![]() $(X, ({1}/{n}) \mathcal {M})$ for any movable linear system
$(X, ({1}/{n}) \mathcal {M})$ for any movable linear system ![]() $\mathcal {M} \subset | - n K_X + m F |$ on
$\mathcal {M} \subset | - n K_X + m F |$ on ![]() $X$.
$X$.
Proof. In [Reference PukhlikovPuk98, § 3] this statement is proven under the assumption that ![]() $X$ is smooth, but the same proof works in Gorenstein case.
$X$ is smooth, but the same proof works in Gorenstein case.
We say that an irreducible curve ![]() $C \subset X$ is horizontal if
$C \subset X$ is horizontal if ![]() $\pi (C) = \mathbb {P}^1$ and that it is vertical if
$\pi (C) = \mathbb {P}^1$ and that it is vertical if ![]() $\pi (C)$ is a point. A
$\pi (C)$ is a point. A ![]() $1$-cycle
$1$-cycle ![]() $C$ is horizontal (respectively, vertical) if every irreducible curve in
$C$ is horizontal (respectively, vertical) if every irreducible curve in ![]() $\operatorname {Supp} C$ is horizontal (respectively, vertical).
$\operatorname {Supp} C$ is horizontal (respectively, vertical).
Proof of Theorem 6.1 Suppose that ![]() $X/\mathbb {P}^1$ is not birationally superrigid. Then there exists a Mori fiber space
$X/\mathbb {P}^1$ is not birationally superrigid. Then there exists a Mori fiber space ![]() $Y/T$ and a birational map
$Y/T$ and a birational map ![]() $\sigma \colon X \dashrightarrow Y$ which is not square. Let
$\sigma \colon X \dashrightarrow Y$ which is not square. Let ![]() $\mathcal {M} \subset | - n K_X + m F |$ be the proper transform on
$\mathcal {M} \subset | - n K_X + m F |$ be the proper transform on ![]() $X$ of a very ample complete linear system on
$X$ of a very ample complete linear system on ![]() $Y$. The
$Y$. The ![]() $K^2$-condition (1.1) implies that
$K^2$-condition (1.1) implies that ![]() $-K_X$ is not in the movable cone of
$-K_X$ is not in the movable cone of ![]() $X$ and, thus,
$X$ and, thus, ![]() $m \ge 0$. By Proposition 6.2 and [Reference OkadaOka20a, Proposition 2.7], there are points
$m \ge 0$. By Proposition 6.2 and [Reference OkadaOka20a, Proposition 2.7], there are points ![]() $\mathsf {p}_1, \ldots, \mathsf {p}_k \in X$ in distinct
$\mathsf {p}_1, \ldots, \mathsf {p}_k \in X$ in distinct ![]() $\pi$-fibers and positive rational numbers
$\pi$-fibers and positive rational numbers ![]() $\lambda _1, \ldots, \lambda _k$ such that
$\lambda _1, \ldots, \lambda _k$ such that ![]() $\mathsf {p}_1, \ldots, \mathsf {p}_k$ are centers of non-canonical singularities of the pair
$\mathsf {p}_1, \ldots, \mathsf {p}_k$ are centers of non-canonical singularities of the pair ![]() $(X, ({1}/{n}) \mathcal {M} - \sum \lambda _i F_i)$ and
$(X, ({1}/{n}) \mathcal {M} - \sum \lambda _i F_i)$ and ![]() $\sum \lambda _i > m/n$, where
$\sum \lambda _i > m/n$, where ![]() $F_i$ is the
$F_i$ is the ![]() $\pi$-fiber containing
$\pi$-fiber containing ![]() $\mathsf {p}_i$.
$\mathsf {p}_i$.
Let ![]() $D_1, D_2$ be general members of
$D_1, D_2$ be general members of ![]() $\mathcal {M}$ and let
$\mathcal {M}$ and let ![]() $Z := D_1 \cdot D_2$. We decompose
$Z := D_1 \cdot D_2$. We decompose ![]() $Z$ into the vertical and the horizontal components,
$Z$ into the vertical and the horizontal components, ![]() $Z = Z^v + Z^h$, and write
$Z = Z^v + Z^h$, and write
where the support of ![]() $Z_i^v$ is in a
$Z_i^v$ is in a ![]() $\pi$-fiber and
$\pi$-fiber and ![]() $Z^h$ is horizontal. By Corti's inequality Theorem 3.17, there are numbers
$Z^h$ is horizontal. By Corti's inequality Theorem 3.17, there are numbers ![]() $t_i$,
$t_i$, ![]() $i = 1, \ldots, k$, with
$i = 1, \ldots, k$, with ![]() $0 < t_i \le 1$ such that
$0 < t_i \le 1$ such that
We have
and, thus,
Note that ![]() $F_i$ is isomorphic to an irreducible and reduced weighted hypersurface of degree
$F_i$ is isomorphic to an irreducible and reduced weighted hypersurface of degree ![]() $6$ in
$6$ in ![]() $\mathbb {P} (1, 1, 2, 3)$. By [Reference OkadaOka20a, Lemma 2.10], we can take a curve
$\mathbb {P} (1, 1, 2, 3)$. By [Reference OkadaOka20a, Lemma 2.10], we can take a curve ![]() $C_i \in |\mathcal {O}_{F_i} (2)|$ which passes through
$C_i \in |\mathcal {O}_{F_i} (2)|$ which passes through ![]() $\mathsf {p}_i$ and which does not contain any component of
$\mathsf {p}_i$ and which does not contain any component of ![]() $\operatorname {Supp} (Z_i^v)$. Then we can take a divisor
$\operatorname {Supp} (Z_i^v)$. Then we can take a divisor ![]() $H_i \in |- 2 K_X + r_i F |$, where
$H_i \in |- 2 K_X + r_i F |$, where ![]() $r_i$ is a sufficiently large integer, such that
$r_i$ is a sufficiently large integer, such that ![]() $H_i|_{F_i} = C_i$. We have
$H_i|_{F_i} = C_i$. We have
and, by the inequality ![]() $\sum \lambda _i > m/n$, we have
$\sum \lambda _i > m/n$, we have
 \begin{equation} (-K_X \cdot Z^v) = \sum_{i=1}^k (-K_X \cdot Z^v_i) > \frac{k}{2} n^2 + 2 n^2 \sum_{i=1}^k \lambda_i > \frac{1}{2} n^2 + 2 m n. \end{equation}
\begin{equation} (-K_X \cdot Z^v) = \sum_{i=1}^k (-K_X \cdot Z^v_i) > \frac{k}{2} n^2 + 2 n^2 \sum_{i=1}^k \lambda_i > \frac{1}{2} n^2 + 2 m n. \end{equation} We define ![]() $\ell := -K_X \cdot F \in \operatorname {\overline {NE}} (X)$ so that
$\ell := -K_X \cdot F \in \operatorname {\overline {NE}} (X)$ so that ![]() $\mathbb {R}_{\ge 0} \cdot \ell \subset \operatorname {\overline {NE}} (X)$ is the extremal ray corresponding to
$\mathbb {R}_{\ge 0} \cdot \ell \subset \operatorname {\overline {NE}} (X)$ is the extremal ray corresponding to ![]() $\pi$. Denote by
$\pi$. Denote by ![]() $[Z^h] \in \operatorname {\overline {NE}} (X)$ the class of
$[Z^h] \in \operatorname {\overline {NE}} (X)$ the class of ![]() $Z^h$. We can write
$Z^h$. We can write ![]() $[Z^h] = \alpha (-K_X\!)^2 + \beta \ell$ for some numbers
$[Z^h] = \alpha (-K_X\!)^2 + \beta \ell$ for some numbers ![]() $\alpha, \beta$. We have
$\alpha, \beta$. We have ![]() $\alpha = (F \cdot Z^h) = n^2$, and the
$\alpha = (F \cdot Z^h) = n^2$, and the ![]() $K^2$-condition (1.1) implies that
$K^2$-condition (1.1) implies that ![]() $\beta \ge 0$. It follows that
$\beta \ge 0$. It follows that
Combining this with
we obtain the inequality
Two inequalities (6.1) and (6.2) are impossible, and this shows that ![]() $X/\mathbb {P}^1$ is birationally superrigid.
$X/\mathbb {P}^1$ is birationally superrigid.
Acknowledgements
The authors would like to express their gratitude to Byung Hee An for his assistance with Proposition 4.13. The authors would also like to thank the referee for the careful reading and suggestions. The first author was supported by KIAS Individual Grant no. MG069802 and IBS-R003-D1. The second author is partially supported by JSPS KAKENHI Grant Numbers JP18K03216 and JP22H01118. The third author was supported by the Simons Investigator Award HMS, National Science Fund of Bulgaria, National Scientific Program ‘Excellent Research and People for the Development of European Science’ (VIHREN), Project No. KP-06-DV-7. The fourth author has been supported by IBS-R003-D1, Institute for Basic Science in Korea.
Conflicts of Interest
None.