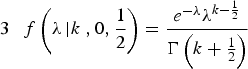1. INTRODUCTION
The Global Navigation Satellite System (GNSS) failure rate is a key parameter in the design of safety, liability or mission critical applications. At present, only the Global Positioning System (GPS) publishes a Performance Standard (PS) for civilian use which includes service commitments relating to this probability (GPS, 2008). The commitment of 10−5 per hour per satellite, translates to about 3 per year over the entire constellation (GPS, 2001). This value is based on a blend of experience obtained from past failure events (Van Dyke et al., Reference Van Dyke, Kovach, Kraemer, Lavrakas, Fernow, Reese, Attallah and Baevitz2003; Reference Van Dyke, Kovach, Lavrakas and Carroll2004) and reliability analysis undertaken for the constellation and ground segment.
The use of GNSS within the safety critical domain of civil aviation has led to many integrity monitoring developments. Placing trust within the service commitments provided by GNSS Service Providers (GSPs) represents an external risk to aviation certification authorities whose primary role is to maintain the safety of passengers and crews within its airspace. To meet aviation's strict requirements, a number of approaches have been undertaken to lessen the external risk of the certification authority.
These solutions or augmentations are the Satellite-Based Augmentation System (SBAS), the Ground-Based Augmentation System (GBAS) and the Aircraft-Based Augmentation System (ABAS) (ICAO, 2010). The latter includes the class of consistency checking algorithms known as Receiver Autonomous Integrity Monitoring (RAIM). SBAS is built on dense regional networks of stations incorporating fault monitors which place very little trust in the core GNSS. GBAS utilises local reference stations with monitors whose performance is based on equally conservative prior probabilities of fault occurrence. In fact, the US GBAS implementation known as LAAS (Local Area Augmentation System) assumes 10−4 per hour per satellite, ten times that of the service commitment (Pullen et al., Reference Lee, Pullen and Enge2006).
Integrity Monitoring techniques are often founded on equating the integrity risk for a failure to the product of the probability of occurrence of the failure, often expressed in the range domain, and the probability of missed detection, expressed in the position domain. It is defined as the event of the positioning error e exceeding the alert limit AL and the monitoring test statistic T not exceeding the threshold T h (Lee and Van Dyke, Reference Lee and Van Dyke2002).
The total integrity risk is then predicated on summing mutually exclusive failure cases. The RAIM methodology employed in ABAS (Lee and Van Dyke, Reference Lee and Van Dyke2002; RTCA, 2004), is inherently founded on a satellite fault probability of 10−5 per hour (Pullen et al., Reference Lee, Pullen and Enge2006; Lee and Van Dyke, Reference Lee and Van Dyke2002).
Future architectures are being assessed within the aviation community which aim to provide the relative autonomy and low costs of RAIM without the need to place significant trust in the core GNSS (FAA, 2010; Blanch et al., Reference Blanch, Walter, Enge, Wallner, Amarillo-Fernandez, Dellago, Ioannides, Hernandez-Fernandez, Belabbas, Spletter and Rippl2013). One such architecture, Advanced RAIM (ARAIM), is the subject of the Working Group C ARAIM Technical subgroup (ARAIM SG) (Blanch et al., Reference Blanch, Walter, Enge, Wallner, Amarillo-Fernandez, Dellago, Ioannides, Hernandez-Fernandez, Belabbas, Spletter and Rippl2013; WG-C, 2012). Discussion within the ARAIM SG has focused on the question of how much trust can be placed in the core GNSS? This paper proposes a solution to the associated question of how we quantify the trust we place in the core GNSS?
The methodology presented is applicable to any safety, liability or mission critical GNSS application that places trust in the core GNSS. The alternative is to assume that all GNSS fault modes occur with a probability of unity as taken for the ionosphere threat to CAT II/III GBAS (Murphy et al., Reference Murphy, Harris, Pullen, Pervan, Saito and Brenner2010).
This paper is organised as follows. Section 2 presents the available methodologies. Section 3 presents the failure types and partitions them for the appropriate analysis of Sections 6 and 8. Section 4 introduces the failure rate model. Section 5 presents the Bayesian inference methodology. Section 6 applies Bayesian inference to the observed continuous time fault history. Section 7 presents the application to new satellite blocks. Section 8 addresses discrete time failures. Section 9 presents the combined failure model including an algorithmic framework outlining the role of the preceding sections before Section 10 concludes.
2. FOUNDATIONS
This paper determines the probability of failure onset without accounting for the transition from a fault mode to the fault-free mode following control segment intervention (GPS, 2008; Blanch, Reference Blanch2012). A number of different approaches may be taken as outlined below.
2.1. Acceptance of the Performance Standard
A first approach could be to accept the standards provided by the core GNSS such as in the GPS Standard Positioning Service (SPS) Performance Standard (PS) (GPS, 2008) and the associated external risk. The GPS SPS PS defines a Major Service Failure (MSF) as having occurred when the Instantaneous User Ranging Error (IURE) exceeds 4·42 times the satellite's broadcast User Ranging Accuracy (URA). The standard then states that an MSF will not occur with a probability greater than 10−5 per hour per satellite which equates to approximately three failures per year over the constellation. The URA is broadcast for each satellite and varies with time, as does the true distribution of the IURE, whereas from the user perspective, a ranging failure, which may lead to a positioning failure, depends upon the time-varying user-satellite geometry. Furthermore, the MSF magnitude could potentially be larger than the failures that must be addressed, to support, say LPV-200 (Localizer performance with Vertical Guidance) operations with ARAIM (ICAO, 2010; FAA, 2010; WG-C, 2012).
2.2. Fault Tree Analysis
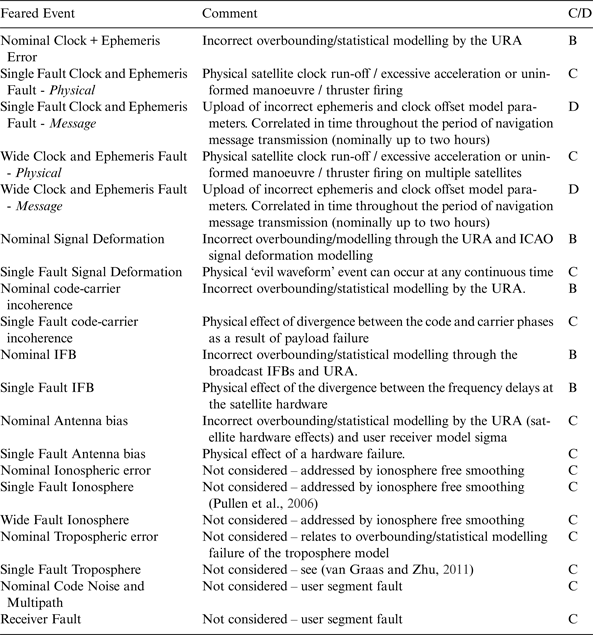
Alternatively, fault tree analysis could be applied within a risk assessment of the core GNSS space and ground segments. A Failure Modes and Effects Analysis (FMEA) is performed, capturing the faults with the potential to cause a positioning failure (Van Dyke et al., Reference Van Dyke, Kovach, Kraemer, Lavrakas, Fernow, Reese, Attallah and Baevitz2003; Van Dyke et al., Reference Van Dyke, Kovach, Lavrakas and Carroll2004). Table 1 presents the list of feared events considered for ARAIM (WG-C, 2012). The advantage of this approach is setting very low probabilities to rare faults with sufficient justification. However, there is a tendency to conservatively but arbitrarily inflate the prior probabilities of other failure events, thus negating the gains.
Table 1. Feared Events.

2.3. Empirical Approach
The approach taken in this paper is to estimate the failure rate for the ensemble of feared events using the fault history. It is a methodology readily available to the navigation community given the extensive data stored globally and thus enables the use of data mining activities to capture the occurrence of failure events (Heng et al., Reference Heng, Gao, Walter and Enge2010). Previous fault analyses employed within the augmentation system definitions have assumed failure rates for different feared events based on an analytical expert opinion, to which conservative factors are then applied (Shively, Reference Shively1999).
3. FAILURES AND FEARED EVENTS
The approach taken in this paper is based on the true unknown time-varying satellite failure rate λ. In order to fully understand its properties, the following failure definitions are considered:
• Ranging/Positioning Failure: the event that the instantaneous error (range or position domain) exceeds a predefined threshold (Figures 1 and 2) (GPS, 2008).
• Integrity Failure: the event that the probability of an instantaneous position error exceeding a predefined threshold without timely detection, exceeds a predefined probability limit (Figure 3) (ICAO, 2006).
• Overbounding Failure: the frequency density which lies outside the assumed model (Figure 4) (DeCleene, Reference DeCleene2000).
• Statistical Failure: a change in the underlying error distribution to a ‘failure’ state defined by statistical parameters (i.e. mean and sigma) (Figure 5) (Lee et al., Reference Lee, Pullen and Enge2006).

Figure 1. Range Error Failure.

Figure 2. Positioning Failure.

Figure 3. Integrity Failure.

Figure 4. Overbounding Failure.

Figure 5. Statistical Modelling Failure.
These definitions may be applied in the range domain, position domain or test statistic domain (Sturza, Reference Sturza1989). While the performance commitments are naturally in the range domain (GPS, 2008), the position domain is used for the application requirements (ICAO, 2010).
Navigation system requirements are expressed in terms of either positioning failures or integrity failures (ICAO, 2010), yet implicit assumptions are made that the mathematical techniques employed and the physical assumptions taken are valid. This provides the link between the natural definitions of Figures 2 and 3 with those of Figures 4 and 5. The MSF event (GPS, 2008) is a function of URA. However, when the IURE remains below the 4·42 × URA value, a change in the underlying error distribution, such as an increased mean or inflated standard deviation can also represent a failure condition. This is the case if the zero-mean Gaussian model parameterised by URA no longer overbounds the true distribution.
In this paper, the range failure of Figure 1 is taken as the baseline. While such events may be understood to occur at the onset of the defined failure windows shown in Figures 1, 2 and 3, it is not immediately obvious how a rate can be applied to the failure interpretations expressed by Figure 4 and 5.
Table 1 lists the most commonly considered feared events (WG-C, 2012). Column three codifies whether the fault occurs at a punctual continuous (and random) point in time (C) or during a discrete sample with correlation throughout the sample period (typically two hours) (D). These cases are handled separately in Sections 5–6 and 8 respectively. Nominal events consisting of both types are denoted (B).
A failure (condition) as defined by Figures 1 to 5 is distinguished from a fault being the physical event (payload functioning in an abnormal state). The table of feared events presents both faults and other events that may occur nominally and lead to a failure condition. In that regard a feared event is a type of fault.
The rate λ does not include failures due to the signal environment or user segment equipment. The probability of space and control segment failures depends upon the satellite's hardware (clock age, payload, block design) or the ground control segment (network, software, operational status). This variability of the failure rate λ as a function of time is addressed in the following section.
4. FAILURE RATE MODEL
This paper presents a Bayesian approach to determining the true failure rate (O'Hagan and Forster, Reference O'Hagan and Forster2003). It is assumed that the physical process's true failure rate exists and may be estimated using Bayesian analysis as opposed to a classical approach (Neyman, Reference Neyman1937). While a confidence distribution may be constructed by extending the classical notion of the confidence interval, such an approach has not been extensively formalised (Fraser, Reference Fraser2011). The advantages of a Bayesian approach are that it allows a more natural means to express the posterior distribution for the estimated random parameter. Furthermore, understanding this parameter to be time-varying and random allows an easier interpretation of the conditions in which the approach is valid (as expressed in hypotheses 1–3). Finally, while this paper ultimately selects a non-informative prior, the Bayesian approach maintains the possibility of combining the technique with prior information from an FMEA.
Following this Bayesian approach, initially the mathematical formulation is restricted to punctual, continuous time events. If the true instantaneous failure rate is known to be constant then the number of failures observed over a given duration would follow a Poisson process (Cox and Isham, Reference Cox and Isham1980). Due to changes in the control segment, the active satellite clock and aging of payload components, the true instantaneous failure rate varies with time. The Non-Homogeneous Poisson Process (NHPP) with variable failure rate λ(t) models this real system (Pham, Reference Pham2006). Under the NHPP the true expected number of failure events up to time T is:
The probability of k failures having occurred over the period [0, T] is then known to follow the standard Poisson relation:
To utilise this result in the future, the following two hypotheses are assumed:
H1. Short term variations in λ(t) are not observable
H2.
 $$\forall T\; \exists S \gt T\; s.t\; \displaystyle{{m\left( T \right)} \over T} \ge \displaystyle{{\mathop \smallint \int_0^S \lambda \left( t \right)dt\;} \over S}\hfill$$
$$\forall T\; \exists S \gt T\; s.t\; \displaystyle{{m\left( T \right)} \over T} \ge \displaystyle{{\mathop \smallint \int_0^S \lambda \left( t \right)dt\;} \over S}\hfill$$
Hypothesis 1 states that while the system changes from ground operational actions, satellite aging and other factors, the impact on the instantaneous probability of failure cannot be determined from data. It is a hidden variables statement that supposes all that is indeterminable may be considered random. What is of interest is the likelihood that the number of failure events exceeds the number that is predicted.
Aircraft perform approach and landing operations using monitoring algorithms predicated on a particular failure probability. If the true failure probability exceeds this value during an approach but this value is not determinable as the fluctuations from causal relations are too complex to determine, it is then appropriate to assert that the system meets the integrity requirements based on the best available knowledge. The alternative is to estimate the impact of satellite aging and all other factors upon the failure rate. However, the authors’ view is that this is too complex to model appropriately.
Hypothesis 2 goes further by relating the expected failure rate at time T to future expectations of the failure rate. It states that a future time S exists where the true expected failure rate will be no greater than the current expected rate. It may be understood that the total system reliability does not degrade over the long term. Note this hypothesis applies to the total system rather than a particular satellite. It asserts that a future time S may be found, and not that the condition holds for all S.
The service commitment may then be understood as implementing sound processes, by maintaining the same rigour in satellite and ground system design, mitigating observed problems in the control segment operations and maintaining satellites as they age. The variable λ is then used as the true mean failure rate λ = m(t)/T which for the purposes of notational simplicity is scaled to be the rate per T (to be rescaled when expressing the results per hour as in Table 4) and the model reduces to the Poisson Process (Cox and Isham, Reference Cox and Isham1980).
5. BAYESIAN INFERENCE
Inference may be made using past failure data to estimate the posterior distribution of λ. Bayes theorem for a continuous variable λ with discrete events k is as follows (Box and Tiao, Reference Box and Tiao1973):
where P(k|λ) is the probability of k failure events occuring over T given λ, f(λ) is the continuous prior PDF for λ and f(λ|k) is the continuous posterior PDF for λ.
The quantity of interest is the continuous posterior distribution for the failure rate f(λ|k). Over a given period with a given definition of failure, k may be determined. The Poisson model determines the values the function P(k|λ) takes while the prior probability f(λ) may be formed using two approaches (Box and Tiao, Reference Box and Tiao1973; Jeffreys, Reference Jeffreys1946):
A. Non-informative reference priors giving the data maximum weight over prior information
B. Priors expressed using standard conjugates based on ‘expert opinion’
For completeness, both approaches are used to check whether the choice of prior has a strong impact on the results. The form of the conjugate prior distribution does not influence the inference output significantly; what is critical are the Cumulative Distribution Function (CDF) percentiles.
Firstly, the conjugate distribution to the Poisson distribution which may be used for the prior f(λ), the gamma distribution, is introduced (Raiffa and Schlaifer, Reference Raiffa and Schlaifer1961):
with shape parameter ν, scale parameter 1/α, and the gamma function Γ(·)
Three reference priors are employed (Box and Tiao, Reference Box and Tiao1973; Jeffreys, Reference Jeffreys1946):
Bayes Uniform Prior: (ν = 1 & α = 0)
Albert's Prior: (ν = 0 & α = 0)
Jeffrey's Prior (ν = 1/2 & α = 0):
Although there is no single standard reference prior, Jeffrey's prior is the most commonly employed.
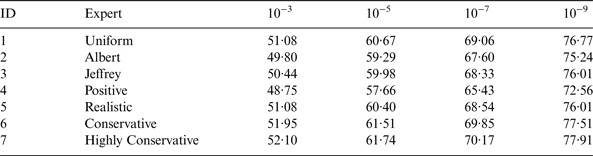
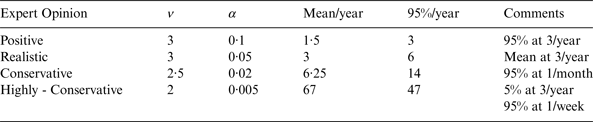
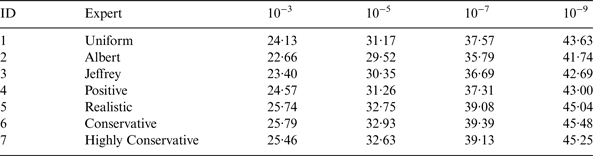
In addition, hypothetical expert opinions are considered, expressed in terms of the conjugate prior. The gamma distribution parameters and percentiles are given in Table 2, selected with respect to the GPS constellation.
Table 2. Expert Opinion Conjugate Priors.

The positive expert in the first row of Table 2 is the expert opinion of following the recent trend. The realistic expert view follows GPS SPS PS (GPS, 2008) while the conservative view holds a 95% confidence that a fault per month is to be expected and the highly conservative a 95% confidence of a fault per week. Table 3 presents the respective Gamma distribution parameters.
Table 3. Prior Distribution Parameters.

Employing the parameters given in Table 3 gives the following posterior distributions:
 $${\hskip-20pc{1}}\hskip0.6pc f\left( {\lambda \left \vert k \right.,0,1\;} \right) = \displaystyle{{e^{ - \lambda} \lambda ^k} \over {{\it \Gamma} \left( {k + 1} \right)}}$$
$${\hskip-20pc{1}}\hskip0.6pc f\left( {\lambda \left \vert k \right.,0,1\;} \right) = \displaystyle{{e^{ - \lambda} \lambda ^k} \over {{\it \Gamma} \left( {k + 1} \right)}}$$ $${\hskip-20.5pc{2}}\hskip0.6pc f\left( {\lambda \left \vert k \right.,0,0} \right) = {{e^{ - \lambda} \lambda ^{k - 1}} \over {{\it \Gamma} \left( k \right)}}$$
$${\hskip-20.5pc{2}}\hskip0.6pc f\left( {\lambda \left \vert k \right.,0,0} \right) = {{e^{ - \lambda} \lambda ^{k - 1}} \over {{\it \Gamma} \left( k \right)}}$$ $${\hskip-19.7pc{3}}\hskip0.6pc f\left( {\lambda \left \vert k \right.,0,{1 \over 2}} \right) = {{e^{ - \lambda} \lambda ^{k - {1 \over 2}}} \over {{\it \Gamma} \left( {k + {1 \over 2}} \right)}}$$
$${\hskip-19.7pc{3}}\hskip0.6pc f\left( {\lambda \left \vert k \right.,0,{1 \over 2}} \right) = {{e^{ - \lambda} \lambda ^{k - {1 \over 2}}} \over {{\it \Gamma} \left( {k + {1 \over 2}} \right)}}$$ $${\hskip-13pc{4-7}}\hskip0.6pcf\left( {\lambda \left \vert k \right.,\alpha, \nu} \right) = \displaystyle{{e^{ - \left( {1 + \alpha} \right)\lambda} \lambda ^{k + \nu - 1} \left( {1 + \alpha} \right)^{k + \nu}} \over {{\it \Gamma} \left( {k + \nu} \right)}}\; $$
$${\hskip-13pc{4-7}}\hskip0.6pcf\left( {\lambda \left \vert k \right.,\alpha, \nu} \right) = \displaystyle{{e^{ - \left( {1 + \alpha} \right)\lambda} \lambda ^{k + \nu - 1} \left( {1 + \alpha} \right)^{k + \nu}} \over {{\it \Gamma} \left( {k + \nu} \right)}}\; $$
Integrating the posterior distributions with a k value taken from the fault history determines the true failure rate with a given level of confidence. Example results are given in the Appendix for various k values and show only minor differences. The exception is for a low k value (Table A1) as a result of choosing the conjugate distribution parameters to best fit the tail. For full constellations with a long service history, the differences are much smaller (Table 9) and the prior distribution has little impact on the posterior distribution. In the case of low k value it may be more appropriately argued that the “no prior information” rule should be applied. Therefore, Jeffrey's prior is employed for the remainder of the paper.
6. FAULT HISTORY
Consider the fault history of the existing constellations, GPS and GLONASS. A data mining approach presented by Heng et al. (Reference Heng, Gao, Walter and Enge2010) and Heng (Reference Heng2012) found a total of 28 potential GPS anomalies over the period 2004 to mid-2012. Here an anomaly is defined with respect to the service commitments, when the instantaneous user ranging error exceeds 4.42 times the URA (GPS, 2008). The anomalies are potential as they have not been fully verified in an independent manner and any faults lasting less than 15 minutes may not be included. Of the 28 potential anomalies, 21 were clock faults and fit the continuous definition.
Using the posterior distribution given by Jeffrey's prior:
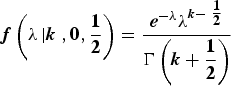 $${\bi f}\left( {{\bi \lambda} \left \vert {\bi k} \right.,{\bf 0},\displaystyle{{\bf 1 \over \bf 2}}} \right) = \displaystyle{{{\bi e}^{ - {\bi \lambda}} {\bi \lambda} ^{{\bi k} - \textstyle{{\bf 1 \over \bf 2}}}} \over {{\bi \Gamma} \left( {{\bi k} + \displaystyle{{\bf 1 \over \bf 2}}} \right)}}$$
$${\bi f}\left( {{\bi \lambda} \left \vert {\bi k} \right.,{\bf 0},\displaystyle{{\bf 1 \over \bf 2}}} \right) = \displaystyle{{{\bi e}^{ - {\bi \lambda}} {\bi \lambda} ^{{\bi k} - \textstyle{{\bf 1 \over \bf 2}}}} \over {{\bi \Gamma} \left( {{\bi k} + \displaystyle{{\bf 1 \over \bf 2}}} \right)}}$$and the fault history obtained by Heng et al. (Reference Heng2012) gives the confidences for the true past mean failure probability shown in Table 4. Note that a constellation of 30 satellites is assumed for the purposes of transforming to a per satellite basis. This gives a total number of hourly periods of 2235330 over the 8½ year period.
Table 4. GPS Failure Rate Confidence.

Table 4 shows that while values greater than the service commitments are obtained for all confidence levels larger than 95%, the inflation of 10−5 is not excessive. The relationship between confidence percentile and failure rate is approximately log-linear. Confidence bounds up to 10−9 are presented as this presents the lower bound on risks that must be mitigated, known to have potentially catastrophic consequences in civil aviation (EASA, 2012). A confidence level is considered rather than fault rate but this provides some justification to the range of percentiles.
The highest confidence percentile of 10−9 requires a reasonable inflation factor of only 2·8 over the GPS service commitments. However, note that the discrete time faults addressed in Section 8 must also be included.
Heng (Reference Heng2012) also analyses the GLONASS fault history. Using an arbitrary fault threshold of the IURE of 50 m (no public service commitments exist for GLONASS) a total of 192 potential anomalies were identified from 2009 to August 2012. Using this result, Table 5 presents the equivalent confidence levels of the GLONASS failure rate based on the assumption of a 24 satellite constellation. This gives a total number of hourly periods of 777888 over the assessment period in Heng (Reference Heng2012).
Table 5. GLONASS Failure Rate Confidence.

Using the data from (Heng, Reference Heng2012), the GLONASS failure rates are an order of magnitude greater than those of GPS. The log-linear relationship is preserved and a high confidence leads to only a reasonable inflation over the best estimate.
This section has presented the results of the methodology using the best available fault history data from Heng (Reference Heng2012), but the approach could be re-applied using different failure thresholds to obtain appropriate results. This is particularly relevant for GLONASS in regard to which Heng (Reference Heng2012) utilised a threshold of 50 m, which is large with respect to some applications.
7. NEW CONSTELLATIONS
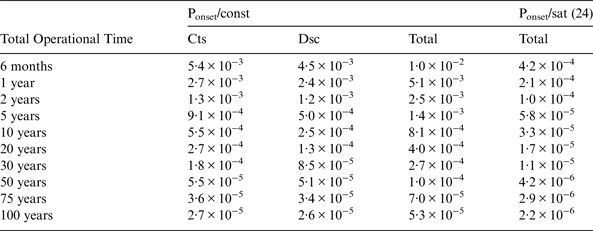
In Section 6, the inference methodology was applied to fault history data of the existing constellations. In this section, the failure rates are derived for new constellations, such as Galileo or BeiDou, or new blocks of satellites that may require a reset of the fault history.
Consider the failure rates with given confidences as a function of the observation window T, starting at an initial operating capability. It is assumed for the analysis that no faults are observed over this period but to maintain conservatism, a value of k = 1 is used, thereby extending the applicability of the derived values in the immediate period following a failure.
Table 6 shows the total (fault-free) operational time of a constellation of 24 satellites and the corresponding derived probability of failure with a confidence of 1–10−9.
Table 6. Derived Failure Probabilities vs. Constellation Operational Time.

8. DISCRETE TIME EVENTS
In the previous sections the NHPP was used to model the failure rate for punctual continuous time fault events. Consider discrete time failures that occur over a sample period such as incorrect ephemeris parameters. A temporal correlation exists between the presence of a fault at neighbouring times. This may be over the standard navigation message period of applicability (2 hours for GPS) or up to a maximum of the data period used for orbit determination (48 hours).
For discrete events, the appropriate model is an inhomogenous Binomial process, but no simplification to the standard Binomial process through taking the mean over time exists. Instead the real process is considered to be a sequence of events with probability of failure s = {p 1, p 2, p 3 …} and the following assumption is imposed:
H3. The sequence S is non-increasing (p k ≥ p k + 1)
This is a stronger condition than hypotheses H1 and H2 applied in the continuous time case. It only applies to the navigation message type faults that depend on the ground network and may be understood as the ground network does not degrade over time. Under this assumption the standard Binomial process model is used to conservatively infer the posterior distribution for the current p based on past fault data.
where: ![]() $\left( {\matrix{ n \cr k \cr}} \right) = \displaystyle{{n!} \over {k!\left( {n - k} \right)!}}$, k is the number of failure events, n is the number of independent samples and p i the true probability of fault during a single independent sample indexed by i.
$\left( {\matrix{ n \cr k \cr}} \right) = \displaystyle{{n!} \over {k!\left( {n - k} \right)!}}$, k is the number of failure events, n is the number of independent samples and p i the true probability of fault during a single independent sample indexed by i.
The conjugate prior distribution to the binomial is the beta distribution (Johnson et al., Reference Johnson, Kotz and Balakrishnan1995).
The Jeffrey's prior parameter values to minimise the impact of prior information for the beta distribution are: ![]() $\alpha = \displaystyle{{1}\ over {2}} \& \beta = \displaystyle{{1} \over {2}}$ which give the following posterior distribution.
$\alpha = \displaystyle{{1}\ over {2}} \& \beta = \displaystyle{{1} \over {2}}$ which give the following posterior distribution.
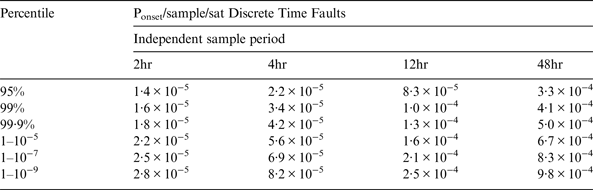
The percentiles are determined by integrating up to the fault probability. While the true time between independent navigation messages remains open to debate, values of 2 hours (nominal navigation message validity, 4 hours (nominal curve fit period), 12 hours (approximate orbital period) and 48 hours (data period used for orbit modelling) are used. These correlation times lead to numbers of samples of 898272, 449136, 149712 and 37428 on the basis of a 24 satellite constellation operating from 1 Jan 2004 to 16 July 2012, being the period employed in Heng (Reference Heng2012). Table 7 shows the probability of failure per sample following the integration of the posterior distribution, while Table 8 converts these values to per hour figures and show higher confidence is obtained without an extreme increase in the failure rate reflecting the continuous case. Although the larger correlation time decreases the number of samples, due to the factoring by the period, Table 8 shows only a minor sensitivity to this assumption. Note however, that the longer correlation time faults could be subject to longer exposure times if there are no guarantees of detection by the control segment. Alternatively, a more complex model could be employed to reflect this (Blanch, Reference Blanch2012).
Table 7. GPS Discrete Failure Rate Confidence.

Table 8. GPS Discrete Failure Rate Confidence per hour.

Considering the discrete model for new systems or constellations gives confidence levels on the probability of failure as shown in Table 9.
Table 9. Derived Failure Probabilities vs. Constellation Operational Time.

9. ALL EVENTS MODEL
In order to summarise the steps required to arrive at the bounds of the total failure rate as given in Table 10, Figure 6 presents the process in full.

Figure 6. Failure Rate Bounding Process.
Table 10. GPS Total Failure Rate Confidence.

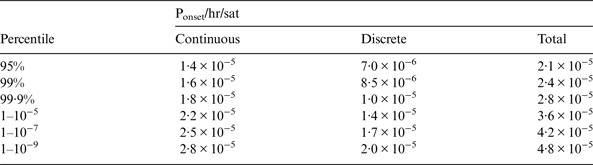
The results provided in Sections 6 and 8 are used to complete a table of the total probability of failure per hour and per satellite using the more conservative 48 hour sample period.
Table 10 shows that in order to have a high confidence, factors of the order of 2 to 5 are required based on the fault history provided in Heng (Reference Heng2012). Table 11 presents the equivalent total failure model for the case of new satellite constellations or blocks and the associated operational time.
Table 11. Operational Time.

10. CONCLUSIONS
This work has presented a novel approach to the setting of failure probability assumptions for GNSS safety, liability and mission critical applications - a methodology has been defined while carefully stating the assumptions needed to infer a future reliability statistics approach based on past data. Results have been presented for two intrinsic fault types, continuous faults which are punctual events occurring at any continuous point in time and discrete faults whose occurrence is tied to an independent single sample. This dichotomy is crucial so as not to model certain fault types using an inappropriate model.
Confidence bounds have been determined for the failure probability of continuous faults in the range 1–3 times larger than the service commitment of 10−5 per hour per satellite with extremely high confidence. This suggests that the analysis matches well the service commitments but could enable a quantified layer of conservatism to be applied. Similarly, for the discrete time events, conservative factors of 1–2 are determined. Therefore, for the total fault probability factors up to 5 are obtained. Application of the methodology to new blocks of satellites has shown how quickly confidence could be gained from a new constellation or modernisation programs in the absence of failures.
The natural objection to this analysis is whether making inferences on past data is applicable to future failure probability predictions. However, such inductive argument is intrinsic to the service commitment statements and any other statements relating to future performance.
The step forward taken by this paper is in introducing a quantifiable conservative bound avoiding the need for arbitrary assumptions. The probability of failure is considered a random time varying parameter whose distribution is estimated rather than deriving a more simplistic point estimate. Secondly, justification is given to using inference on past data for future operations. From the point of view of a fastidious system designer, this paper gives confidence to the existing GPS performance commitments with some small conservative factors applied to provide the confidence margins preferred. The paper also shows the approach applied to new constellations with limited fault histories (e.g. Galileo). In future, informative priors could be included to take account of an FMEA undertaken within the constellation design, testing and validation.
DISCLAIMER
The views and conclusions expressed in this paper are those of the authors only and do not reflect official standpoints of any organisation or working group.
APPENDIX
This appendix presents tables giving the confidence bounds for different failure number cases and for each of the priors considered in the paper.
Table A1. k = 1 confidence bounds.

Table A2. k = 2 confidence bounds.

Table A3. k = 10 confidence bounds.

Table A4. k = 30 confidence bounds.