Introduction
Accurate topographic maps of the polar ice sheets are an invaluable input into, and test of, models of their dynamic behaviour (Reference HuybrechtsHuybrechts 1990). They provide useful information on the morphology of the ice sheet and can be used to delineate drainage basins and flowlines, (Reference DrewryDrewry 1983). This information can, in turn, provide information about the ice rheology.
Due to its size and remoteness, however, Antarctica has relatively poor coverage by ground-based surveys. Consequently, large areas, especially the East Antarctic ice sheet, have a paucity of terrestrial elevation measurements (Reference DrewryDrewry 1983). Where there are data, they are mostly barometric estimates from pressure altimetry either from radio-echo sounding (RES) flights or oversnow traverses. Such measurements are prone to signif-icant errors which, in general, become larger the farther inland they are made. This is because they are usually referenced to mean sea level (m.s.1.) at the coast (Reference SteedSteed 1980).
The use of satellite radar-altimeter data to derive surface heights over ice sheets is now well established, Reference Brooks, Campbell, Ramseier, Stanley and Zwally(e.g. Brooks and others 1978); (Reference Zwally, Bindschadler, Brenner, Martin and ThomasZwally and others 1983). However, until the launch of ERS-l in July 1991, the coverage has been limited to a latitude of 72° S. This has allowed accurate topographic mapping of a number of marginal ice shelves (Reference Partington, Cudlip, McIntyre and King-Helee.g. Partington and others 1987); (Reference Ridley, Cudlip, McIntyre and RapleyRidley and others 1989) and part of Terre Addie (Remy and others, (Reference Remy, Mazzega, Houry, Brossier and MinsterRemy and others 1989). The two largest ice shelves- the Filchner-Ronne and Ross Ice Shelves- and much of the interior of the ice sheet, however, remained uncharted by satellite altimetry. The coverage of ERS-l extends to 81.50 S and therefore provides useful height data over much of the East Antarctic ice sheet and the West Antarctic ice shelves. This paper presents some of the first results of topographic mapping of the ice sheet and compares these with previous estimates of surface elevation from terrestrial measurements. A comparison with recent levelling surveys provides confirmation of the accuracy of the altimeter data.
Data analysis and reduction
Altimeter data
ERS-I altimeter data are distributed in two forms. The first, distributed as wave-form data, comprises a comprehensive data set with corrections, quality flags and wave forms at the full sampling rate of 20 Hz (335m alongtrack). At present, however, only limited amounts of these data are available. The second are known as the fastdelivery (FD) data and are a summary product, with a reduced spatial resolution of 6.7km (1 Hz) along-track. No wave forms are included and a relatively limited range of other parameters is provided.
In this study, four 35 d repeats of FD data were used (cycles 83, 85, 87 and 89), comprising approximately 1000 000 measurements of surface elevation over the Antarctic continent. These data were improved with the use of ESA precise orbits, which are available approximately 3-6 months after acquisition (ESA, 1992).
In the absence of wave forms, it is necessary to carry out careful filtering to remove erroneous data. Several criteria were used, based on ancillary parameters included in the data. One of these is the "pulsepeakiness" parameter, which can be used to determine whether a leading edge is present within the range window of the altimeter. Only data with peakiness values between 1.0 and 2.5 were accepted. These values were chosen after a detailed analysis of the performance of the ERS-I altimeter using wave-form data (Reference ScottScott and others 1992). A standard deviation of range is also included in the product, derived from the 20 samples that comprise the I Hz averaged data. Large values of this parameter indicate poor tracking and/or complex surface returns. Data with a standard deviation range of greater than 25m were also discarded. These two filters removed almost 40% of the data. A larger proportion was removed from the marginal areas where the slopes are higher and the tracking performance of the altimeter is, consequently, worse
Analysis of cross-over data (discussed later) indicated, however, that a small percentage of erroneous elevations was still being included and a further stage of filtering was required. The data were gridded into a DEM by calculating the mean value of elevation from all data within a radius of 10km from the grid point. If no data were present, then bilinear interpolation, using neighbouring grid points, was used up to a maximum radius of 50km to estimate the height at the grid point. Finally, the grid was smoothed using quadratic interpolation. From the gridding procedure, it was possible to derive standard deviations (σ) for each grid point based on the difference in elevation of the grid value and the altimeter measurements used in calculating it. Data with elevations greater than 30-from their respective grid-point value (after taking into account any displacement from the grid, by bilinear interpolation) were discarded. Although this is not, strictly, a test for erroneous data, this approach was found to remove gross outliers, which had not been identified in the previous filtering steps.
A rcpeat-track analysis was also used to remove outliers. A repeat track is the identical revolution in a particular cycle of orbits. In this case, four cycles of 35 drepeat data were available, providing four repeat tracks for every revolution. The mean and standard deviation were calculated from the sum of the four values for each point, using linear interpolation to account for offsets in the along-track positions of the points. Where less than four points were available, no standard deviation was estimated. These two additional steps in data filtering removed a further I% of erroneous points.
The data coverage, after filtering, for one of the 35 d repeats is shown in Figure 1. It is similar for the other repeats. One of the most obvious features of Figure 1. is the excellent coverage of the ice shelves and the relatively poor covcrage of the marginal areas with higher slopes. For example, there are relatively few data over the Antarctic Peninsula, as is the case for the Transantarctic Mountains and other mountainous regions such as Prince Charles Range and Fimbulheimem. A comparison with a plot of surface slopes (calculated from the DEM) indicates a high degree of correlation between areas with poor data coverage and slope. with the use of wave-form data (allowing more precise data filtering) and a more robust tracking facility of the ERS-l altimeter known as "ice mode"(which is available only for wave-form data), many of the areas with few data will have improved coverage (Reference ScottScott and others 1992).
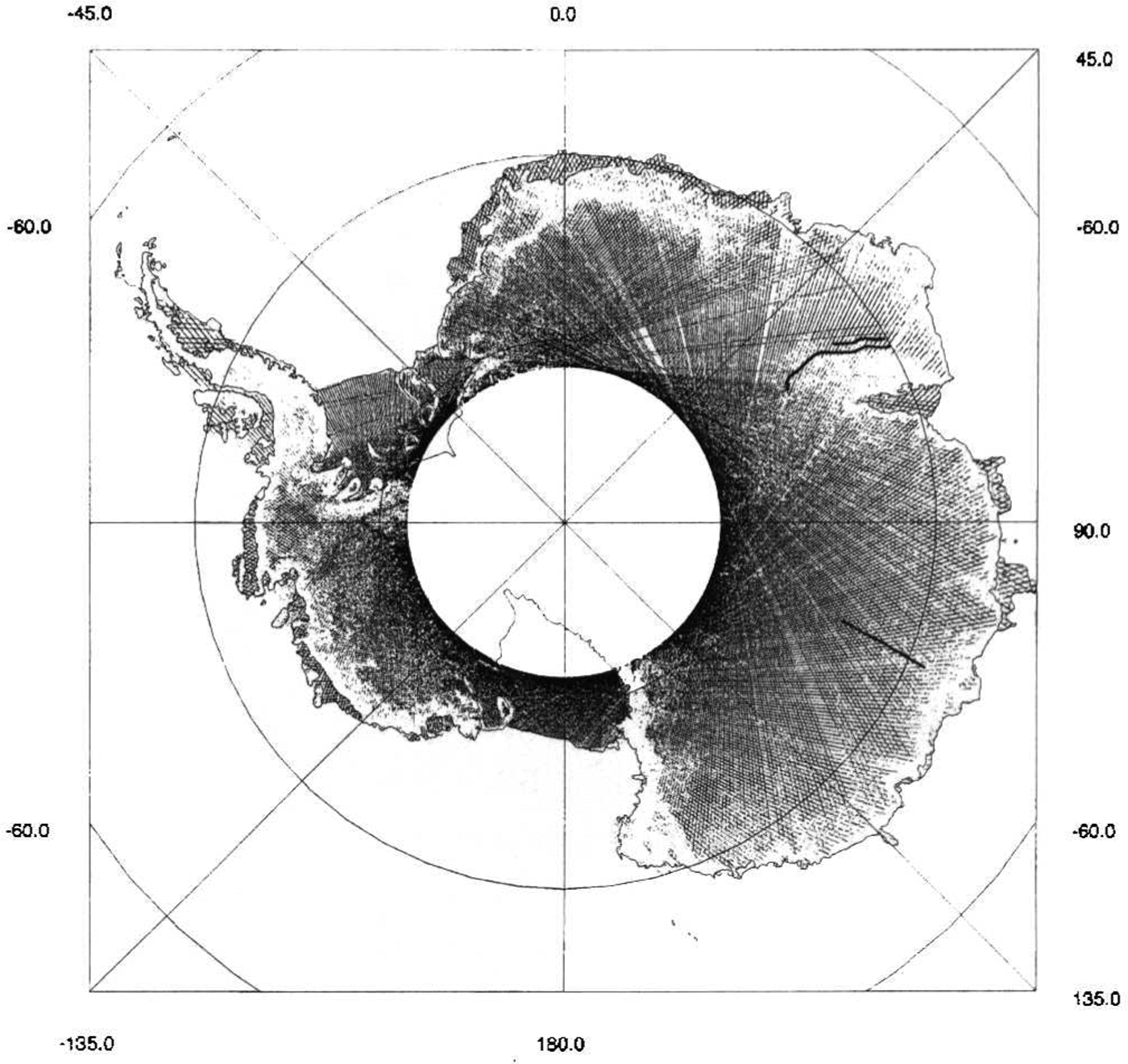
Fig. 1. Radar-altimeter coverage, after filtering, for one 35 d repeat. Also shown as heavy lines are the locations of the levelling surveys discussed in the text.
A slope-induced error correction was applied by the relocation method (Reference Brenner, Bindschadler, Thomas and ZwallyBrenner and others 1983), using a procedure described elsewhere (Reference BamberBamber 1994). The method takes into account Earth curvature and uses all the data to produce a data base of slope cells. The DEM was recalculated after the final filtering and slope correction and the OSU91-A geopotential model (Reference Rapp, Wang and PavlisRapp and others 1991) was used to convert the elevations into values relative to the gcoid. A polar stereographic projection, with origin at the South Pole, and standard parallel of 710 S was used to translate from polar to Cartesian coordinates. The grid spacing was 20 km. This is identical to the format of a digitized version of the SPRIfolio map (Reference Budd, Jenssen and SmithBudd and others 1984) and, consequently, allows for a quantitative comparison between the two. Gridding at a higher resolution provides more detailed information for studies of specific areas (Reference Bamber and Bentleye.g.Bamber and Bentley 1994), although the differences would not be seen on a map of the whole ice sheet as the elevation range is too, great
Error sources
The errors in the satellite-altimeter estimate of elevation comprise two components: E = Erandom + Ebias
Random errors
The orbit and atmospheric errors associated with the FD data amount to about 60 cm and have been discussed elsewhere (Reference Bamber and BentleyBamber and Bentley 1994). There is a random and systematic error due to not recalculating the range estimate, a process known as retraeking (Reference Martin, Zwally, Brenner and erMartin and others 1983), which can only be carried out on wave forms. The magnitudes of these errors were assessed by calculating the mean and standard deviation of the retraeking correction obtained from a small data set of wave forms over Antarctica. A threshold retraeking technique (Bamber, 199'1) was used and the mean correction was found to be -0.44 ± 0.91 m, at the 95% confidence limit, for 150000 wave forms.
The combined random errors can be determined from a comparison of crossing points of descending and ascending orbits. The standard deviation of 43864 crossovers was 6.8m. If this is the random component of the height error on two measurements, then combining four repeat tracks red uces the error on a single elevation estimate to 2.4m. The cross-over differences were contoured to indicate the regional distribution of the random height error. Areas with no cross-overs, or high values, were found in regions of high relief such as around the margins and along the Transantarctic Mountains and indicate poor tracking and, consequently, higher height errors.
Biases
The geographically correlated orbit error and uncertainties in the geoid amount to about 2m and have been discussed, in detail, elsewhere (Reference Bamber and BentleyBamber and Bentley 1994). There is a 0.41m bias due to not applying a ret racking correction (discussed earlier) and this is also likely to be geographically correlated as the bias is a function, primarily, of surface slope (Bamber, 1991.
Slope-correction errors
The slope-correction procedure groups the data into rectangular cells (Reference BamberBamber 1994). The data in each cell are then fitted to a plane by a least-squares method. Due to the relatively coarse spatial resolution of the FD data :6.7km), it was necessary to make the cell size 25km by 35km. Undulations within each cell will, therefore, be smoothed out to a mean value for the whole cell. To assess the errors in slope correction, the standard deviation of the fit parameters in each cell was determined using a singular value decomposition algorithm (Reference Press, Flannery, Teukolsky and VetterlingPress and others 1986). It was not possihle to do this for every cell due to the volume of data required, so a sub-set of cells was selected along four longitude lines 4j" apart from each other. For the 306 cells selected in this manner, the standard deviation was 0.11 m for a mean correction of 4m.
In regions where there is poor data coverage (Fig. 1), the error on slope correction is larger than the value quoted above. Furthermore, for slopes greater than 0.65° (the half-power beam width of the altimeter antenna), the elevation estimates are not reliable for two primary reasons. First, the data coverage in these areas is poor. This, in turn, leads to a poor estimate of the local slope and, hence, a large error in slope correction. Secondly, the antenna pattern drops off rapidly beyond 0.65° and the returned power is, therefore, much lower than for flatter areas. Regions with slopes greater than 0.65" represent, however. only 8.7% of the ice-sheet area covered.
In regions where there is poor data coverage Fig. 1, the error on slope correction is larger than the value quoted above. Furthermore, for slopes greater than 0.65° (the half-power beam width of the altimeter antenna), the elevation estimates are not reliable for two primary reasons. First, the data coverage in these areas is poor. This, in turn, leads to a poor estimate of the local slope and, hence, a large error in slope correction. Secondly, the antenna pattern drops off rapidly beyond 0.65° and the returned power is, therefore, much lower than for flatter areas. Regions with slopes greater than 0.65" represent, however. only 8.7% of the ice-sheet area covered.
Errors in the terrestrial data set
The SPRI folio surface-elevation map was derived from a number of data sources, primarily pressure altimetry from RES flights. Changes in surface pressure due to weather systems can produce errors of up to 150m in elevation over distances of a few hundred kilometres (Reference SteedSteed 1980). Lsing a random-walk procedure, however, it has been estimated that the RES surface elevations are accurate to better than 50 m, with positional errors of «5 kmReference Drewry, Jordan and Jankowski(Drewry and others 1982). The free-floating constantdensity balloons (TWERLE data; (Reference Levanon, Julian and SuomiLevanon and others 1977) that were used in the folio map are believed to be accurate to 60 m in elevation.
Much of the terrestrial data were referenced to m.s.l. This is not always the same as the elevation of the geoid which, for Antarctica is assumed to be roughly 1.5 m above m.s.1. (personal communication from R. H. (Reference Rapp, Wang and PavlisRapp 1993).Furthermore, there are short time-scale fluctuations in m.s.1. due to eddies and tides which can amount to several metres in shallow continental shelf water.
A DEM of the SPRI folio elevations was produced by digitizing the 1: 6000000 scale map (Reference Budd, Jenssen and SmithBudd and others 1984). A I nun error in the digitization point introduces a 600 m error in position or a 7m error in elevation (for the maximum surtace slope considered here of 0.65°). This is insignificant with respect to the data errors. However, the original map used had folds in it, which produce small distortions when flattened, and it is not known what quality control was used when digitizing. From the digitized contours, the data were gridded into a DEM by an unknown procedure. To determine the eflect of these various processes, values from the DEM were compared with the original folio map for two transects running east-west and along the zero meridian through the South Pole. Differences of up to 90 m were found and for the 33 points sampled the mean diflerence was 10.7 ± 44 m. A signif-icant element of the error in this data set is due, therefore, to the digitization and/or gridding process. Furthermore, these errors are not randomly distributed and tend to be larger in areas of higher slope.
Results
To provide the maximum visual definition, the altimeterderived DEM is displayed as a shaded isometric plot. Figure 2 is a view from the south with thc Ross Icc Shelf in the foreground. Roosevelt Island and the southern tip of Siple Dome are visible, as is the subglacial lake at Vostok Station (the crescent-shaped shadow on the central part of the plateau).
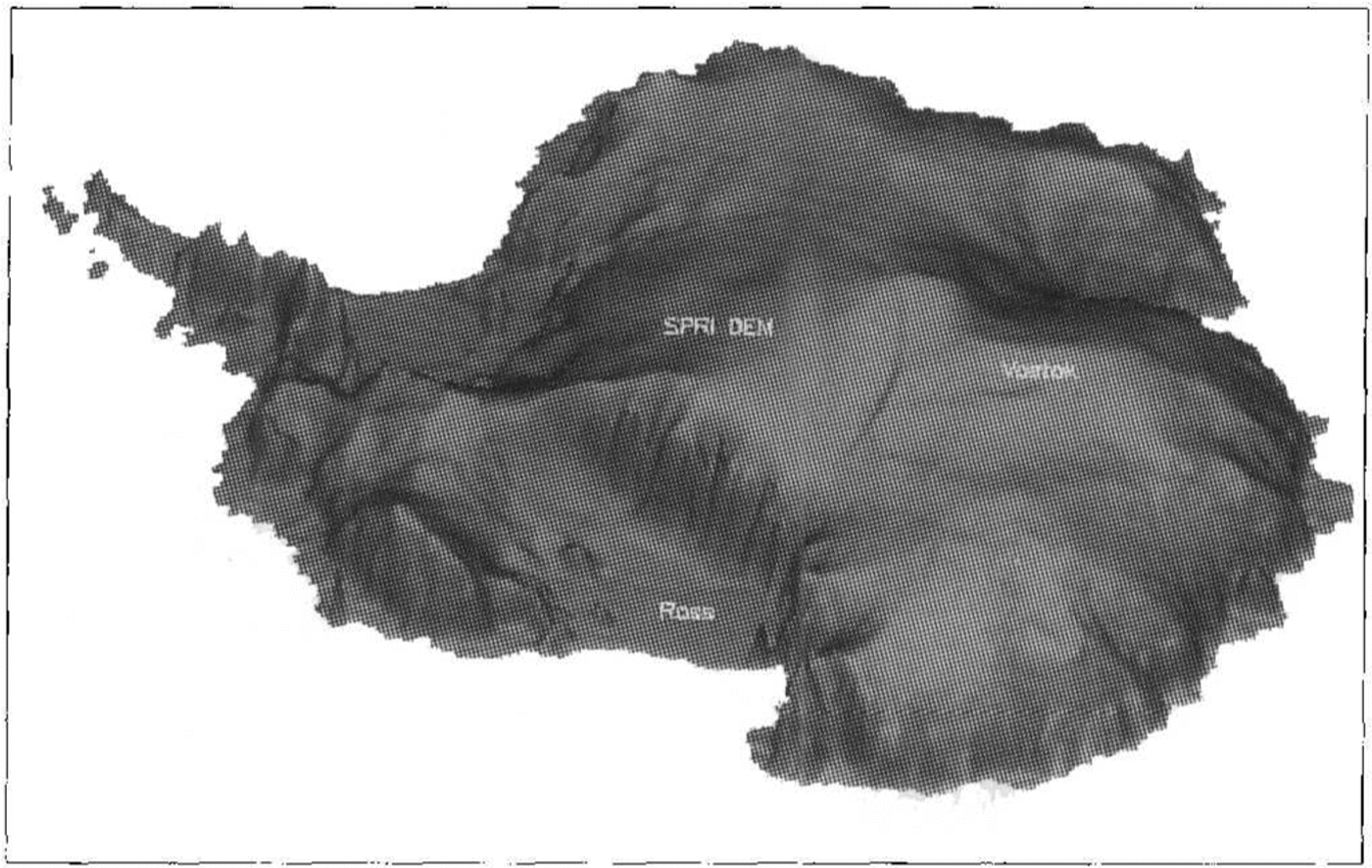
Fig. 2. Shaded isometric view from the south with the Ross Ice Shelf in the foreground. The area south of 81.5° has been filled in with the SPRI folio DEAl. The surface expression of the subglacial lake is visible as a cresentshaped shadow on the central part of the plateau.
South of 81.5°, the SPRT DEM was used to fill in the missing data. There are two attributes of this data set that are immediately obvious. First, there is a step in elevation between the altimetric heights and the folio values (discussed later). Secondly, it is evident that the level of detail in the altimeter data is much greater-the surface of the folio DEM is smoothly varying in comparisondespite being gridded with the same spacing. A finer grid spacing in the altimetry, used on smaller areas, has revealed even greater detail about the morphology of the ice sheet and ice shelves .(Reference Bamber and Bentleye.g Bamber and Bentley 1994). The altimeter DEM is also displayed in a planimetric view in Figure 3. In this perspective, the ice divides stand out very clearly. Ridge B appears to flatten out before reaching Dome Argus, which itsclfseems to be flat. Again, the subglacial lake at Vostok is iden tifiable. There appears to be good agrcement bctwecn the two DEMs for the location of the ridge from Hercules Dome on to the West Antarctic ice sheet but the discrepancy in elevations in the east is clearly visible.
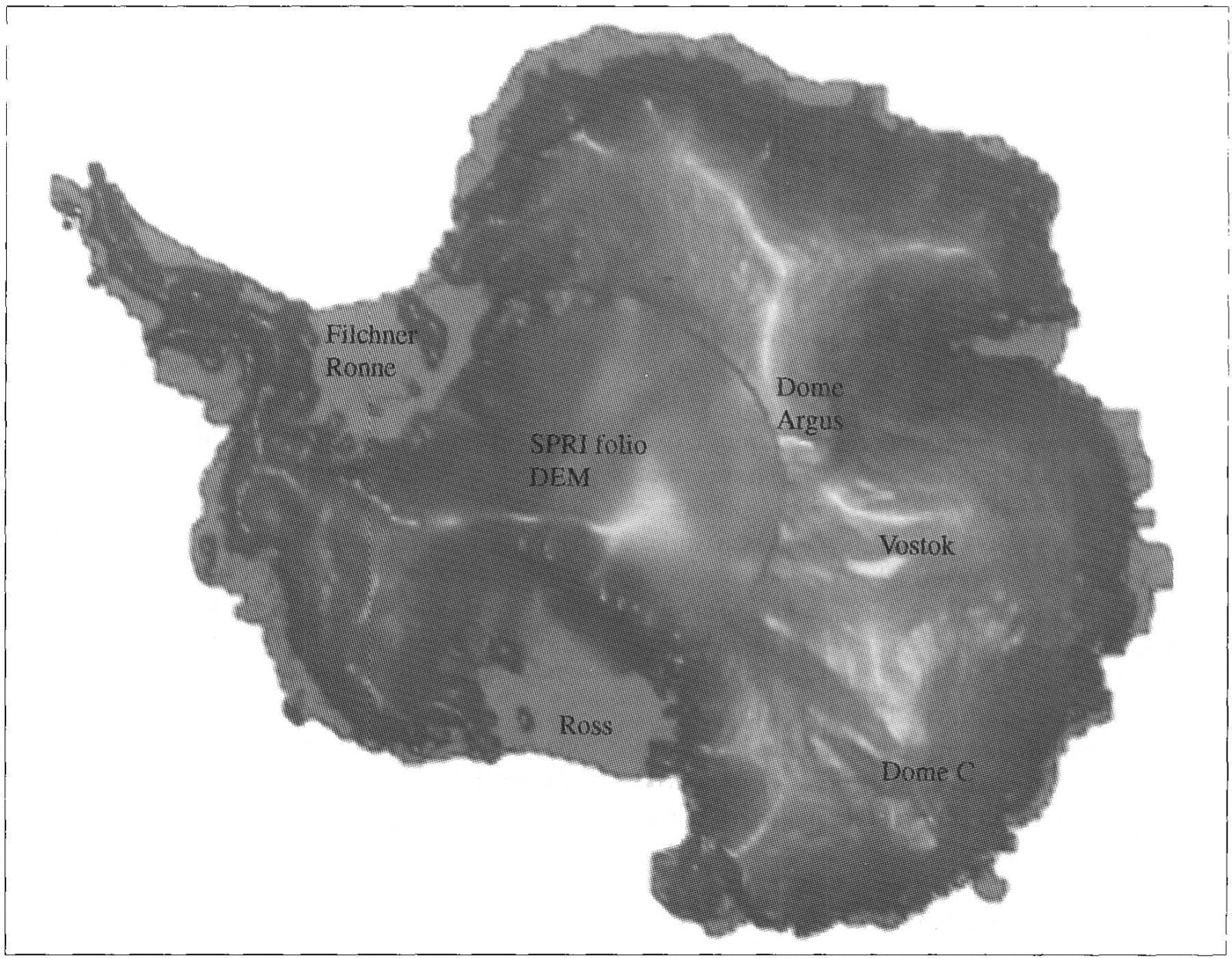
Fig. 3. Planimetric, shaded view of the Antarctic ice sheet.fiom ERS-l radar altimetry. South of 81.5°, the SPRI folio DEM has been used.
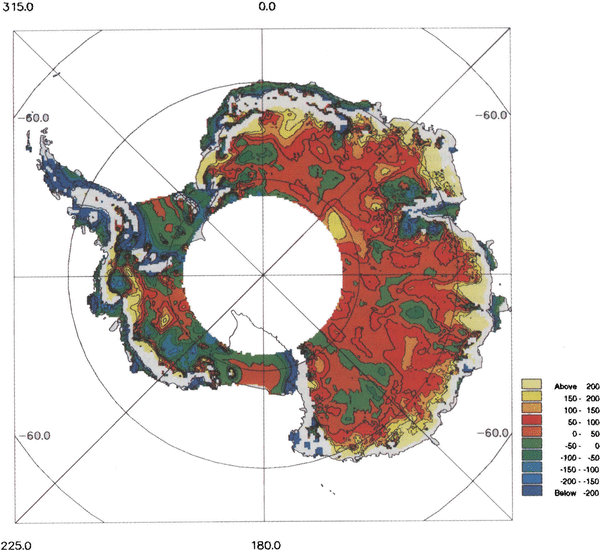
To obtain a quantitative estimate of the degree of agreement between the two data sets, a difference plot was produced by subtracting tbe SPRI folio DEM from the radar-altimeter DEM Fig. 4. Where the local slopes (on a 40km scale length) were >0.65°, no value was estimated and appears in white in the figure. Differences in excess of 200111 are evident. This is approximately four times the combined rms measurement error of the data (͌50m). Regions which lie within the rms errors represent only 37% of the arca covered by the satellite and a significant proportion of this is due to the two major ice shelves, the Filchner-Ronne and Ross Ice Shelves. The other main area where agreement is better than 50m is in the vicinity of Dome C and south of George V Land, again where there is a good RES coverage. There are two bands oflow differences which start about 300 km south of Casey and Mirnyy Stations and seem to coincide with the location of a satellite Doppler-positioning traverse and a geodetic levelling traverse, respectively. The other area of agreement «50 m difference) is to be found in southern Dronning Maud Land. This is surprising given the relative dearth of terrestrial data - a sparse distribution of geodetic levelling data and no RES flight lines.
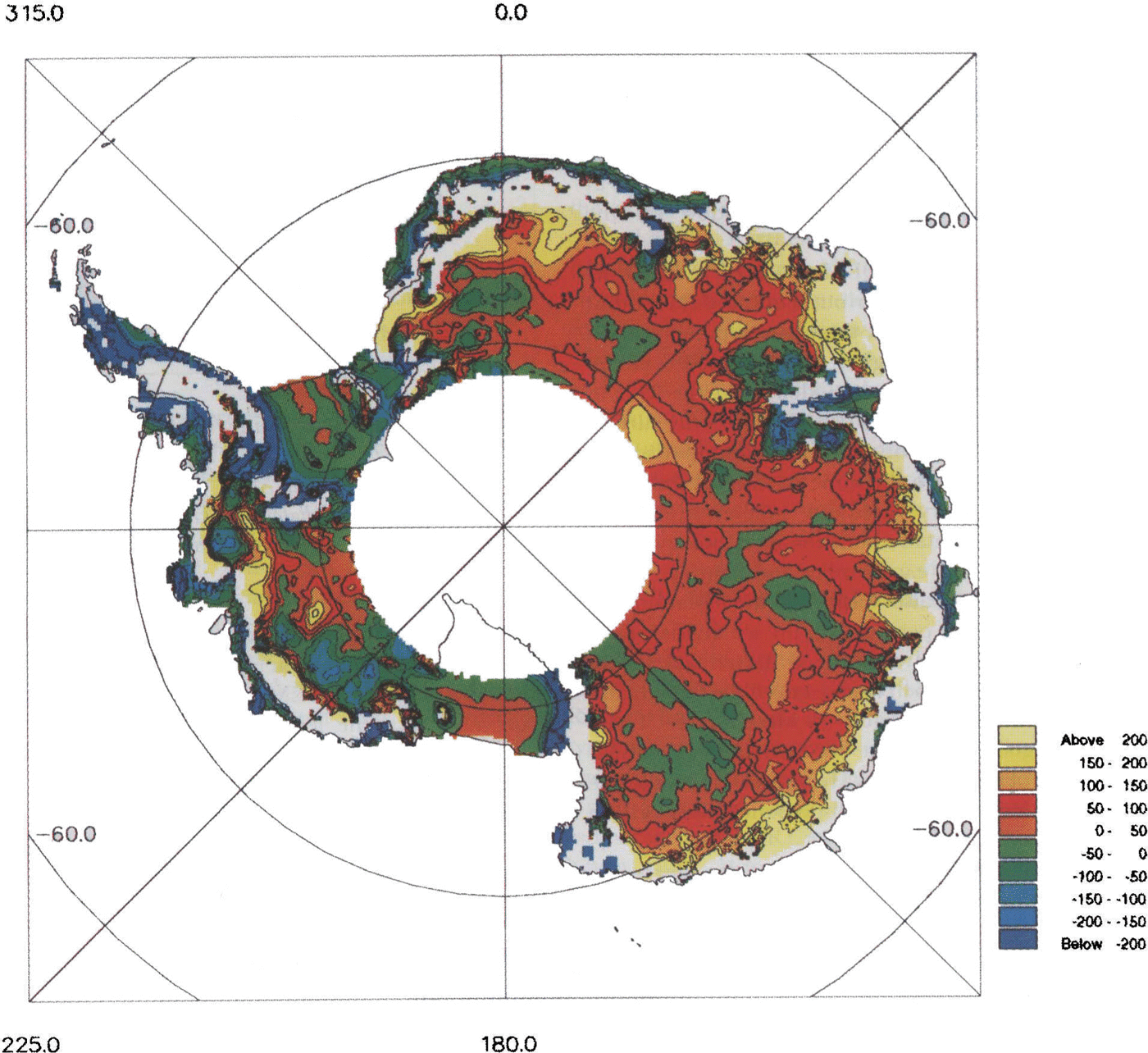
Fig. 4. Alap of altimeter-SPRI folio DEM differences for areas with a slope <0.65°.The contour interval is 50m.
The worst agreement (differences of >IOOm) tends to exist in regions where there is poor coverage of terrestrial data and/or in coastal regions. These areas include much of the Antarctic Peninsula, Dronning Maud Land, the region around Valkyrjedomen and a large part of Wilkes Land west of about 110° E. Differences of 100m are found in the rdatively flat area south of the Amery Ice Shelf in the vicinity of Dome Argus Fig. 4, most probably due to the large distance from the coast (͌1OOOkm)and the paucity of ground data. Along the East Antarctic coast there are some differences in excess of 200m. Examination of the coverage of terrestrial data indicates that from Casey (R͌lll°E) to Mawson Station (͌64°E) there are only a handful of measurements across the coastline, and up the steepest part of the ice sheet. All the way round to Coats Land (30°W), the distribution of coastal points is sporadic. However, in these areas, the altimeter and digitization errors are larger and it is, consequently, not so clear what the dominant error is. Even where there is good coverage of terrestrial data, such as in Enderby Land or Terre Adélie, the differences are still large, suggesting that the altimeter DEM may be in error in these regions. However, in a previous study using Seasat wave-form data, differences in excess of 100m have been reported between the satdli te altimetry and terrestrial data in Terre Adelie (Reference Brooks and NorcrossBrooks and Norcross 1982); (Reference Remy, Mazzega, Houry, Brossier and MinsterRemy and others 1989).
Differences in excess of 200m can be seen in a small region centred at about 78° S, 112°W. Such an increase in surface elevation would be, presumably, reflected by an equivalent increase in bedrock elevation, which is bclow sea level (b.s.l.) in this region. It is possible, therefore, that the area of ice grounded b.s.l. might be reduced with the use of accurate surface-elevation data.
Comparison with ground-truth data
The observed differences are significantly larger than expected, given the estimated errors for the two data sets. Some of this can be attributed to the digitization of the folio map. Given the magnitude of the differences, however, it was considered desirable to “validate” the models against an accurate and independent (i.e. data not used in the generation of either DEM) ground traverse in an area where the differences were significant (>50 m). Three geodetic levelling data sets were obtained. Their locations are shown in Figure 1. The first two (which will be referred to as the Lambert traverses) lie to the south and east of the Amery Ice Shelf and were collected during the austral summers of 1991-92 and 1992-93. The height estimates were obtained from GPS measurements every 30km, with barometric elevations every 8-15m in between. At control stations, the accuracy is 1-2 m, rising to 5m at the midpoint between controls (personal commmunication from M. Higham, 1993).
DEM elevations at the traverse points were calculated using a bilinear interpolation procedure. A plot of the longer of the two Lambert traverses is shown in Figure 5a. No ground-traverse data were available between 470 and 550 km along-track, and this is the reason for the break in the plot. Good agreement is obtained between the altimeter DEM and the traverse. The meai' difference (altimeter-ground traverse) is -1.3m with a standard deviation of 14m. As can be seen from the plot, the magnitude of the standard deviation is partly due to the short wavelength <20 km) und ula tions in the traverse data, which have been smoothed out in the DEM. The mean difference lies well within the combined measurement errors. A very similar result is obtained for the Wilkes Land traverse (mean difference 3 m, standard deviation 15m) and this is shown in Figure 5b. This confirms the error estimates made for the altimeter elevations for slopes <0.65°.
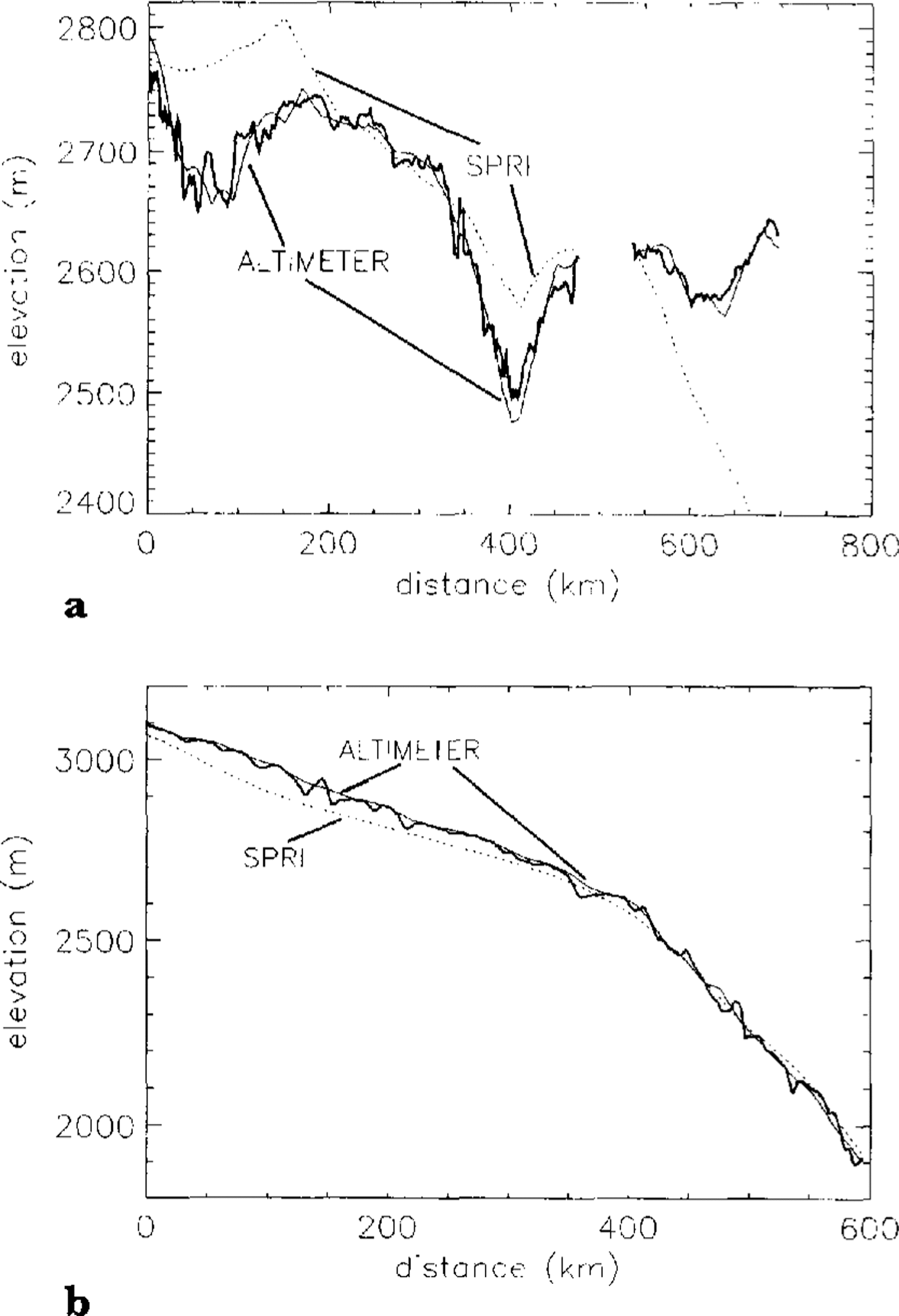
Fig. 5a. A comparison between the altimeter and folio DEM (dotted line) elevations and the longer if the two levelling traverses (thick line) in the Lambert Glacier basin region. There is a break in the ground-traverse data at about 470 km along-track. b. A comparison between the altimeter and folio DEAf (dotted line) elevations and the levelling traverse (thick line) in Wilkes Land.
It can be seen that the SPRI folio DEM deviates from the traverse data by as much as 250 m. To determine whether these differences were due to the digitization process, the elevations were recalculated from the original SPRI map at the locations of maximum deviation from the traverse data. Depending on the location, the difIerences were due solely to digitization, errors in the original map or a combination of the two.
It is hoped that most of the digitization errors will have been removed in a more recent compilation of terrestrial elevation data known as the Antarctic Digital Database, (Reference Cooper, Thomson and EdwardsCooper and others 1993). This data base has been compiled with the most recent maps of the coastline and should provide a considerably improved DEM in the marginal areas compared with the SPRI folio. In the interior, however, the data are primarily derived from the folio. The data base was, unfortunately, not available for this study.
Summary
A DEM up to a latitudinal limit of 81.5°S has been produced providing unparalleled accuracy for surface elevations south of 72°. Comparison with levelling surveys indicates that the mean error is on the order of a few metres for the interior of the ice sheet. It is believed that this DEM provides a considerable improvement on previous topographic maps of surface elevation. To allow comparison with the SPRI folio DEM, the altimeter data were gridded with a 20km spacing. However, the data have also been gridded with a 10km spacing to allow better definition of topographic features. This data set is available for scientific applications.
The differences seen between the DEM derived from terrestrial data and the satellite altimetry have been attributed to several causes, including the paucity of terrestrial measurements for large areas of the ice sheet. The cause of the large differences (>200m) along the East - Antarctic margins cannot be uniquely identified due to the relatively poor coverage by the satellite data in this region. The use of wave-form and ice-mode data, however, combined with better atmospheric corrections, will provide a substantial improvement in accuracy and coverage, especially in the margins. The inclusion of these data in the production of an improved DEM is currently under way.
Detailed investigations of specific areas are also under way using wave-field migration techniques, removing the need for slope correction and retracking. Furthermore, this work offers the potential of resolving undulations on a much shorter wavelength than is possible by more conventional approaches (Reference Wingham, Rapley and MorleyWingham and others 1993).
Acknowledgements
The author would like to thank colleagues at MSSL for useful discussions and assistance, J. Morley for help with the slope-correction software, M. Higham, M. Reynolds and R. Kiernan for providing the Lambert traverse data, and N. Young for providing the Wilkes Land traverse elata. Funding for J.L.B. was through a U.K. NERC grant GR3/7836.