Introduction
Recently, we have assembled a very large fraction of the published information on the mass balance of small glaciers into a single dataset. (By convention, “small glaciers” are regarded as all glaciers other than the Antarctic and Greenland ice sheets.) Mass balance is the difference between gains and losses of glacier mass. Glaciers gain mass mainly from snowfall and the permanent refreezing of meltwater, and lose mass mainly by run-off of meltwater; loss by ice now into the sea may also be important. Accurate measurement of all the terms in the balance is a challenge which is rarely met. The measurements are time-consuming and expensive. Therefore, they are sparsely distributed and, in attempting to diagnose the mass balance of the cryosphere as a whole, it is essential to make the most of what is available. Our purposes here are:
To estimate balance “normals” (i.e. averages) and trends for as many glaciers as possible, and for the entire small-glacier component of the cryosphere, over an appropriate reference period, 1961–90;
To evaluate the uncertainties attached to these estimates, and in particular (i) to judge the validity of some of the statistical assumptions which must be made in the effort to extract the maximum of reliable information from the observations, and (ii) to consider the possibility of biases in the pool of measurements;
To describe the evolution of mass balance and to assess its consistency with what else is known of climatic change over the period 1940–95;
To assess the bearing of these mass-balance estimates on global climatic change and sea-level rise.
We find that during the reference period, taking probable biases into account, small glaciers were probably in equilibrium or had very slightly negative mass balance. Mass balance was least negative during the 1960s and has probably decreased since then but, when biases are corrected, it is found that the contribution of small glaciers to sea-level rise must be less than previously estimated and may be nil.
The Mass-Balance Measurement Ensemble
Compilation
We have compiled all the measurements of small-glacier mass balance which we were able to locate. Measurements were accepted if they were from small land-based expanses of ice with consistent, well-defined kinematics. That is, now-lines, from divide to terminus, had to be either included or excluded in their entirety. For example, measurements relating to only one sector of an ice cap were deemed acceptable when it was clear that there was no now across any boundary of the sector. Some published balance estimates leave out parts of an accumulation zone or ablation zone or both; such estimates were excluded. The reporting of “measurements” which are in fact cartographical or statistical estimates is an insidious problem. This applies, for example, to Sonnblickkees (Reference Haeberli and MüllerHaeberli and Müller, 1988; Reference Haeberli and HoelzleHaeberli and Hoelzle, 1993), for which balance estimates for 1981–88 are based on indirect calculations explained by Reference SlupetzkySlupetzky (1991). We are moderately confident that there are no such estimates in our dataset but acknowledge that further inquiry is needed.
The quantity of information available in support of mass-balance measurements varies greatly. For certain glaciers, e.g. McCall Glacier (Reference Trabant and BensonTrabant and Benson, 1986) and the north Cascade Range glaciers studied by Reference PeltoPelto (1988, Reference Pelto1996, Reference Pelto1997; see also the criticisms of Reference Meier, Armstrong and DyurgerovMeier and others, 1997), a great amount of detail has been published not only about the measurements but also about errors. At the other extreme are glaciers for which only a bare minimum of information has been published. For example, data for Neh Nar Glacier are known only from a graph in Reference KulkarniKulkarni (1992), with location and other details gleaned from Reference Nijampurkar, Bhandari and VohraNijampurkar and others (1982), while Reference FristrupFristrup (1952) gave only the slenderest indications about methodology for Christian Erichsen Ice Cap. We accepted measurements when it was reasonably clear that they satisfied our criteria. We have begun an attempt to improve the documentation of measurements systematically but this will be a substantial endeavour.
The period 1940–95 excludes only one measured glacier, Fourteenth of July Glacier on West Spitsbergen, for which Reference AhlmannAhlmann (1935) measured a balance of –460 mm a−1 (including about –60 mm a−1 due to calving) in 1934. In addition, the early measurements on Rhonegletscher, Switzerland, are excluded; these measurements (Reference Chen and FunkChen and Funk, 1990) yield an average balance of –130 mm a−1 for 1885–09. (The units appropriate for mass balance are kg m−2 a−1, or more simply mm a−1 of water equivalent.) Potentially acceptable measurements have been made, but not fully processed and/or not published, for a small number of glaciers. These include “Drambuie” Glacier, Ellesmere Island (Reference Koerner, Jania and HagenKoerner, 1995); Mitdluagkat Gletscher, southeast Greenland (Reference HumlumHumlum, 1992); and a number of glaciers in the Indian Himalaya (Reference Nijampurkar, Bhandari and VohraNijampurkar and others, 1982).
After our compilation was substantially completed we became aware of the work of Reference DyurgerovDyurgerov (1994) and Reference Dyurgerov and MeierDyurgerov and Meier (1997a, Reference Dyurgerov and Meierb). Our aims being almost identical, there was very substantial overlap between the two datasets but each contained information not to be found in the other. We have made progress in reconciling the two measurement ensembles but more remains to be done. Our dataset is available electronically from ftp://ftp.trentu.ca/pub/gghydro.
Basic information
The measurements considered here come from 251 glaciers. There are 2555 annual measurements of mass balance covering 2602 years. We thought that it would be useful to focus on a reference or normal period during which the number of glaciers was comparatively large and steady; we selected 1961–90, during which there are 2053 annual measurements, covering 2095 years, from 231 different glaciers. The number of measured glaciers reached 27 in 1961 and has exceeded 50 in each year since 1964, but it has never reached 100 in any year.
A major difficulty is that most balance time series are short (Fig. 1). For 1961–90, the modal series length is 1 year. Of the 231 series, 101 are longer than 5 years, 41 are longer than 20 years, and only 14 cover all 30 years. We prefer to regard every measurement, rather than every glacier, as having equal statistical promise a priori. To give due weight to estimates from glaciers with different record lengths, we try to supply appropriate estimates of uncertainty.
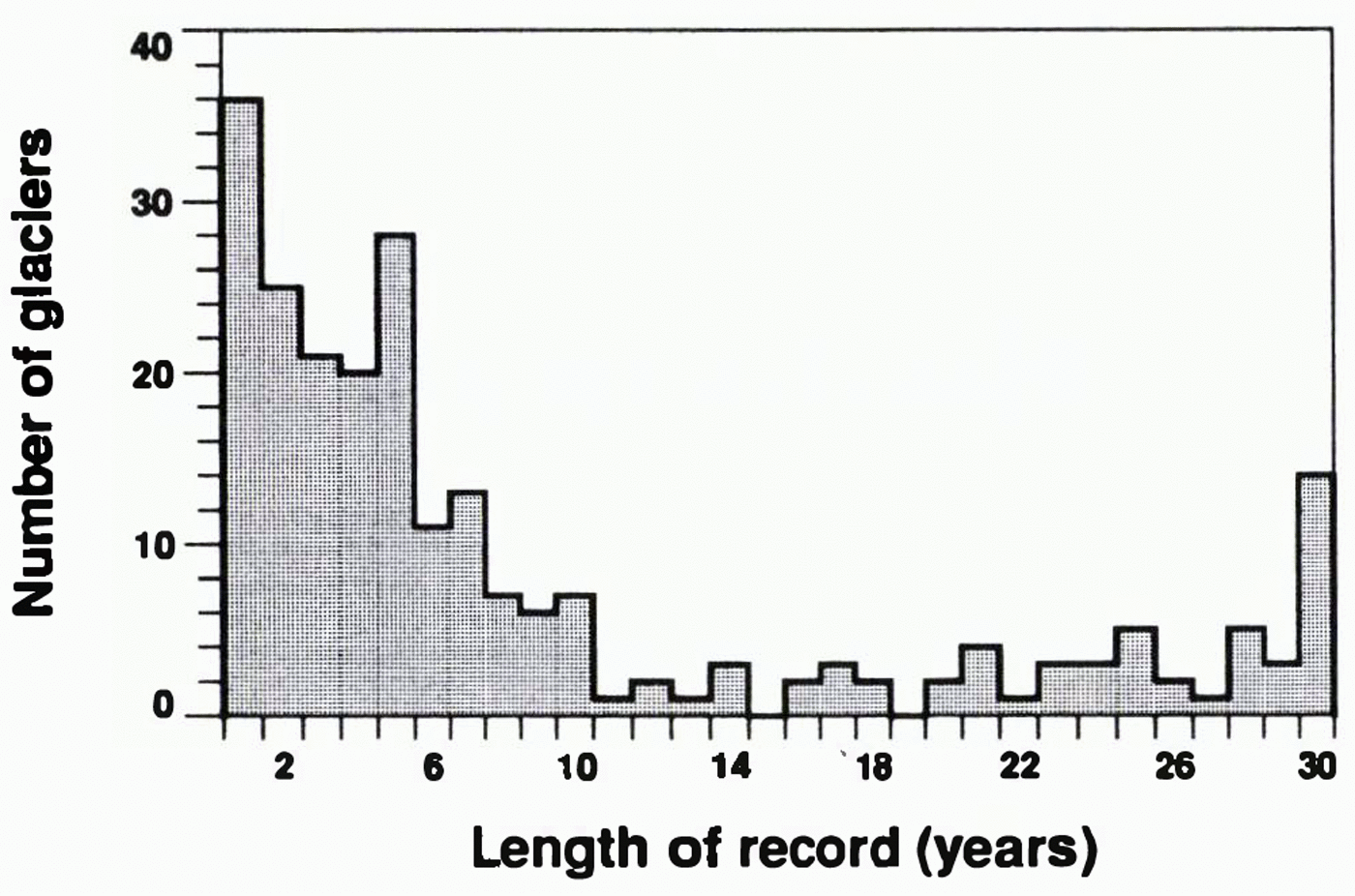
Fig. 1. Frequency distribution of lengths of mass-balance time series for the reference period 1961–90. Multi-year measurements are counted as only 1 year.
Related but lesser problems are that many series contain gaps and that some include, or consist of, multi-year measurements. Gaps complicate calculations but present no conceptual difficulty. Multi-year measurements need to be assimilated carefully into the larger set of annual measurements. We ignore them when calculating autocorrelations; when calculating correlations between series we retain them if an equivalent multi-year estimate can be computed for the second series in the pair and discard them otherwise. We assign standard errors to multi-year measurements according to a simple model, described below, for the growth in uncertainty with measurement interval.
Spatial representativeness
Glaciers with mass-balance measurements are scattered thinly and unevenly over the cryosphere. During 1961–90, there are measurements from glaciers with a total extent of 13 693 km2, to be compared with a total small-glacier area of well over 500 000 km2. Interpolating from measured to unmeasured glaciers will therefore introduce uncertainty beyond that of the measurements. Figure 2 illustrates the nature of the problem.
Half of the world’s small-glacier ice has more than ten measured glaciers within 1000 km (fig. 2a), while three-quarters has at least one mass-balance measurement within 400 km (fig. 2b). Thus, the prospects for spatial interpolation might be much worse. The more measured glaciers near to an unmeasured cell, the more likely is it that an interpolation algorithm will be able to produce useful estimates of mass balance for the unmeasured cell. For example, ten measurements (if suitably distributed) suffice for the estimation of a cubic polynomial in two horizontal coordinates; if information from as far away as 1000 km were useful in estimating the mass balance of an unmeasured glacier, we could probably make such estimates, with a cubic polynomial, for half of the worlds small glaciers. Of course, this begs the question of what to do about the other half. Further, and regrettably, it turns out that in general information from 1000 km away is not very useful for this purpose. We have attempted to develop a solution, described below, for this problem, but it is clear that more work will have to be done on it.
The zonal distribution of measured glaciers (fig. 3a) is skewed towards less remote regions. Glaciers in northern mid-latitudes are over-represented, and Scandinavian and Alaskan latitudes are well represented (although in fact measurements from southern Alaska are proportionately very few). Allowing for the minimal extent of tropical glacier ice, the tropics are not badly represented, but the Arctic and the Himalaya–Tibetan region are seriously under-represented and there are no measurements at all from Patagonia.
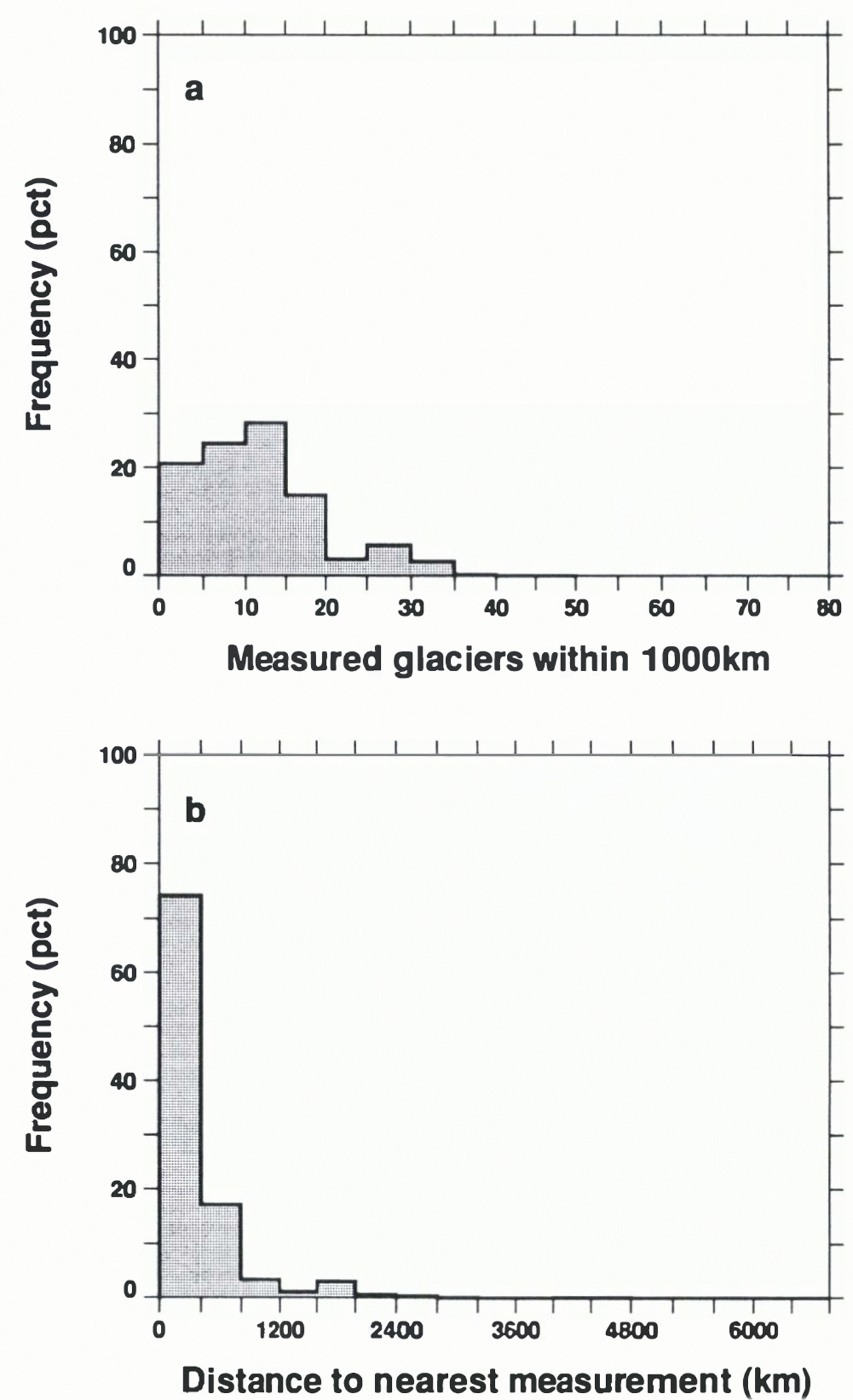
Fig. 2. (a) Frequency distribution, over all of the world’s small-glacier ice, of the number of glaciers within 1000 km having mass-balance measurements. The centre of each glacierized 1° × 1° cell was occupied in turn. For each cell not belonging to one of the ice sheets, the number of glaciers with mass-balance measurements within 1000 km was counted, weighted by the glacierized area of the cell (Reference CogleyCogley, 1998), and accumulated in the appropriate bin on the horizontal axis. (b) Distribution of distance to nearest glacier having at least one mass-balance measurement.
There is no immediately obvious latitudinal variation of mass balance (fig. 3b). A reasonable first impression is that the measurements suggest a state of highly variable but on average slightly negative balance for small glaciers considered as a whole.
Measurement Errors
Random errors
Mass-balance measurement errors are substantial, but it is rare for measurements to be published with a detailed evaluation of the attendant errors. Most of the random error arises from the non-representativeness of the sparse stake network from which the whole-glacier estimate is built up, and this sampling uncertainty would in any case be very expensive to evaluate routinely. For a glacier with which we are familiar, we have deduced (Reference Cogley, Adams, Ecclestone, Jung-Rothenhäusler and OmmanneyCogley and others, 1995, Reference Cogley, Adams, Ecclestone and Ommanney1996) random errors of ± 200 mm a−1 in any one annual mass-balance estimate, which is comparable with the magnitude deduced by Reference LliboutryLliboutry (1974) and with measurements presented by Reference Braithwaite and OlesenBraithwaite and Olesen (1989), and which we think likely to be typical. The number of published measurements accompanied by reliable error estimates is so few that we adopt ± 200 mm a−1 as a universal standard error for all single-year measurements in the ensemble.
To be precise, this error applies to single-stake measurements as estimates of the balance of narrow elevation bands and one might expect whole-glacier balance estimates, based on tens of stakes, to be somewhat less uncertain. The error of a whole-glacier estimate based on n truly random (i.e. uncorrelated) single-stake estimates should be reduced by a factor of the order of ![]() . But single-stake estimates are not random samples of the whole-glacier mass balance: Reference Cogley, Adams, Ecclestone and OmmanneyCogley and others (1996) showed that correlations between annual time series from single stakes are extremely high and remain high even when the stakes are separated by up to 1000 m in elevation. (The relevance of this finding depends on the assumption that correlations in time are measures of correlation in space.)
lated stakes, the whole-glacier balance would be no less uncertain than that of any one stake. In a real net work of very well-correlated stakes, uncertainty will indeed decrease slightly as the number of stakes increases but we neglect this reduction.
. But single-stake estimates are not random samples of the whole-glacier mass balance: Reference Cogley, Adams, Ecclestone and OmmanneyCogley and others (1996) showed that correlations between annual time series from single stakes are extremely high and remain high even when the stakes are separated by up to 1000 m in elevation. (The relevance of this finding depends on the assumption that correlations in time are measures of correlation in space.)
lated stakes, the whole-glacier balance would be no less uncertain than that of any one stake. In a real net work of very well-correlated stakes, uncertainty will indeed decrease slightly as the number of stakes increases but we neglect this reduction.
Measurements spanning more than 1 year are considered to be more uncertain than single-year measurements, because where stake networks are involved it is likely that the more time passes the more information is lost. We assume arbitrarily that the standard error grows at a rate of 10% a−1:
where m is the number of years spanned by the measurement, se1 = 200 mm a−1 as assumed above and f = 0.1. In computing the statistics for any balance series, the usual weights w = 1/se12 are replaced by w m = m/sem2. There is no physical basis for this assumption, which is in need of testing; however, it affects only 47 of the 2602 balance years in the dataset.
There is a risk, when comparing balance normals based on different record lengths, that the normals may vary systematically and spuriously with record length. We have established that this is not so. However, the sampling variance of very short records (N y ≤ ~6 years) is so large that some of them have unrealistically low standard deviations, which would give them undue weight in comparisons with other records. We impose the constraint that the standard error of balance series with N y ≤ 5 not be less than ![]() , where σ 20 = 342 mm a−1 is the average standard deviation among series with N y ≥ 20. This device is also how we incorporate series with only one measurement into the analysis; with N y = 1, their standard error becomes 342 mm a−1.
, where σ 20 = 342 mm a−1 is the average standard deviation among series with N y ≥ 20. This device is also how we incorporate series with only one measurement into the analysis; with N y = 1, their standard error becomes 342 mm a−1.
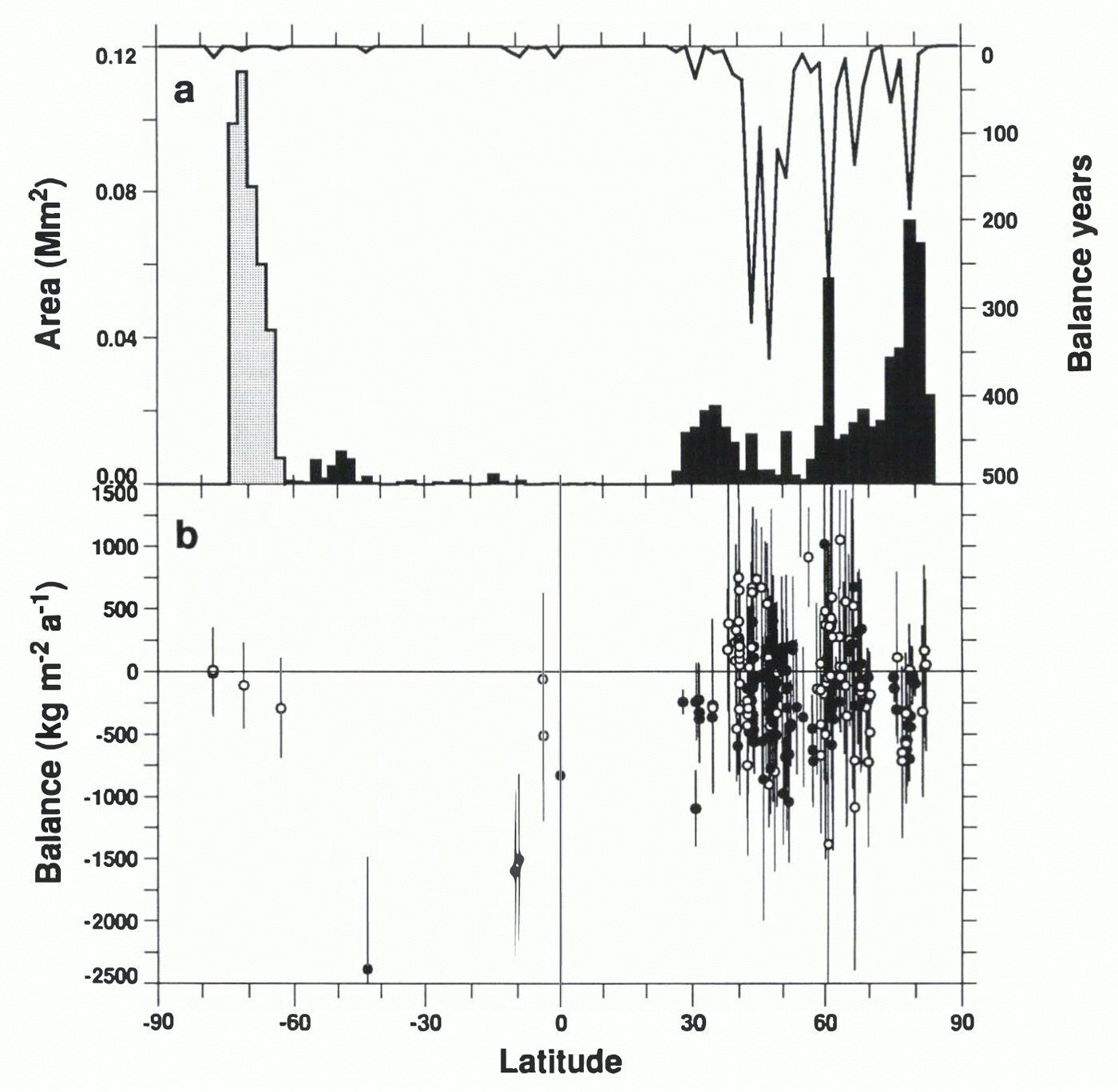
Fig. 3. (a) For 2° zones, the solid bars show the area (lefthand in calculations, the Antarctic Peninsula (stippled bars) is included as a reminder of concerns that its climatic response time may be much shorter than that of excluding 0.401 Mm 2 in the Antarctic Peninsula; this estimate agrees very well with the 0.680 Mm 2 of Reference Meier and BahrMeier and Bahr (1996) and Reference Dyurgerov and MeierDyurgerov and Meier (1997b) when their inclusion of 0.070 Mm 2 in small Antarctic ice caps is allowed for. The line shows the number of years covered by mass-balance measurements (righthand axis) during 1961–90. (b) Solid circles with two-standard-error bars represent balance normals in kg m −2 a −1 (or mm water a −1) from single glaciers with N y ≥ 5. Open circles represent single glaciers with record length N y < 5; the standard error for these glaciers was set to the average standard deviation among glaciers with N y ≥ 20, divided by the square root of Reference Haeberli, Hoelzle and SuterHaeberli and others (1996) and Reference Haeberli and HoelzleHaeberli and Hoelzle (1993), and their precursor volumes, but about 60 other sources were also used.
Systematic errors
Internal accumulation
Among possible measurement biases, the most pervasive is probably that due to neglect of internal accumulation, which is the permanent refreezing of meltwater which percolates downwards out of the current year’s accumulated snowpack. Internal accumulation is confined to, and in fact defines, the lower percolation zone (Reference Adams, Cogley and EcclestoneAdams and others, 1995), which extends from the equilibrium line upwards to the wet snow line (above which meltwater fails to percolate out of the current year’s snowpack). The only situations in which glaciers can be expected not to have a lower percolation zone are (a) where the wet snow line is below the minimum elevation of the glacier, which happens only in Antarctica, or (b) where the equilibrium line lies above the glacier, the entire surface of which then suffers net annual ablation; although not uncommon, situation (b) is not the norm. Strictly, internal accumulation is not a necessary consequence of deep percolation, for if the ice is thin and/or temperate the meltwater may escape the glacier without re-freezing. In general, however, there is no reason to suppose that internal accumulation can be neglected. Its magnitude will vary with intensity and duration of surface melting, and with the shifting relationship between the climatic and the hypsometric zonation of the glacier.
Internal accumulation is very difficult to measure reliably and very few of the measurements in the ensemble can have been corrected for it. Reference Hooke, Johnson, Brugger, Hanson and HoldsworthHooke and others (1987) measured mass balance on Barnes Ice Cap and made estimates of the density anomaly due to refrozen meltwater at depth. They found that internal accumulation was equal on average to 56 mm a−1 over five measurements for which the average corrected mass balance was –20 mm a−1. Based on careful surveys, they argued that internal accumulation was 40–80 mm a−1 for 1971–84, a period for which average annual mass balance was –175 mm a−1. Reference Trabant and BensonTrabant and Benson (1986) relied on both temperature and density measurements to estimate internal accumulation for four balance years on McCall Glacier. The averages of internal accumulation and corrected mass balance were 51 and –208 mm a−1, respectively. Reference Lliboutry and EchevinLliboutry and Echevin (1975) used the temperature anomaly to estimate internal accumulation at stakes on Glacier St. Sorlin in 1972 and 1973; it is not practical to convert these estimates to whole-glacier values but they are certainly consistent with the other estimates discussed here.
This evidence suggests that internal accumulation has a typical magnitude of tens of millimetres on glaciers whose mass-balance magnitude is a few times larger. Therefore, it ought not to be neglected but there is as yet no practical way to correct for it. For many glaciers, we do not even know yet whether a correction has been applied already. All we can do at present is to take note that most published mass balances may be too negative by up to tens of millimetres.
Glaciers with calving termini
For 1961–90 our dataset includes eight annual balance estimates from four calving glaciers. A further 13 such estimates are available from outside the reference period, three more calving glaciers being represented. Although the areal proportion of calving glaciers is not well known, these figures suggest that calving glaciers are under-represented, and if they have mass balances significantly different from those of glaciers which terminate on dry land it is probable that the dataset is biased. It is impossible at present to say anything conclusive about this bias. The four caking glaciers mentioned above have an average balance of –150 mm a−1 for 1961–90; if we add the ten measurements available from two of them for 1991–95, the average becomes –84 mm a−1. Both of these averages are close to the global averages to be presented below.
Calving is not the only way in which floating glacier tongues can lose mass. This point is addressed in our conclusion.
Errors in estimates of small-glacier extent
The extent of small-glacier ice was derived from a hydro-graphic database Reference CogleyCogley, 1998). Areas were estimated by counting, on maps of scale 1: 1000 000, the incidence of land-cover types beneath 100 intersections of a grid overlaid on each 1° × 1° cell. The extents of glacier ice can be compared to detailed tabulations prepared for the World Glacier Inventory (Reference Haeberli, Bösch, Scherler, Ostrem and WallénHaeberli and others, 1989). Glacier distributions (Reference OmmanneyOmmanney, 1969; Reference Haeberli, Bösch, Scherler, Ostrem and WallénHaeberli and others, 1989; Reference Hagen, Liestol, Roland and JorgensenHagen and others, 1993; Reference Bedford and BarryBedford and Barry, 1995) accounting for about one-third of the total extent of small glaciers were analyzed to determine the extent of glacierization in each 1° × 1° cell. Here, we use only information from fully inventoried regions, so that problems such as the omission of very small glaciers do not compromise the comparison. The root-mean-square (rms) difference between GGHYDRO estimates (Reference CogleyCogley, 1998) and World Glacier Inventory estimates (taken to have uncertainties of ± 2% or better was 24.9% (table 1) but this turns out to be due mainly to the allocation Cell size Mean difference GGHYDRO–WGI rms difference GGHYDRO–WGI Number of 1 ° × 1 ° cells%%1° × 1°–0.724.93972° × 2°–0.38.61933° × 3°–0.57.21284° × 4°–0.56.11015° × 5°–0.86.878 of a few very large glaciers to single cells in the World Glacier Inventory. To get a fairer picture, we composited the information into progressively larger cells, as shown in Table 1, and from this exercise we conclude that the uncertainty in our estimates of 1° × 1° small-glacier extent is ± 6–8%. The mean differences are systematically slightly negative, probably because the coarse counting method of GGHYDRO (100 point samples per 1° × 1° cell) tends to miss very small glaciers. Based on Table 1, we adopt a standard error of ± 8% for 1° × 1° small-glacier areas.
Table 1. Comparison of estimates of small-glacier extent. GGHYDRO is the database described by Reference CogleyCogley (1998). WGI represents glacier-inventory data from Reference Haeberli, Bösch, Scherler, Ostrem and WallénHaeberli and others (1989). Reference OmmanneyOmmanney (1969), Reference Hagen, Liestol, Roland and JorgensenHagen and others (1993) and Reference Bedford and BarryBedford and Barry (1995)

Statistical Attributes of Measurement Ensemble
The theory of the statistics of small samples provides a natural means for placing samples of variable size on an equal inferential footing, but the power of conventional statistical tests is severely limited by the shortness of the time series. The same drawback makes it almost impossible to decide, for most glaciers, whether their balance series satisfy the two most restrictive assumptions on which these tests rest, namely that the series consist of (a) independent random samples drawn (b) from a Gaussian distribution. To evade this problem, we concentrate on statistical attributes of the ensemble rather than those of individual time series.
To evaluate the independence of successive elements of mass-balance time series, we first computed lag m autocorrelations for all observed series, with m from 1 up to as large as 10 whenever possible. The observations were detrended before the autocorrelations were estimated. All of the resulting correlograms showed autoregressive behaviour, i.e. r m < r 1 for all m > 1. We therefore concentrate on estimates of the lag 1 autocorrelation r 1, choosing a lower limit of 5 years for series length. As Table 2 shows, 2.0% of the balance series have r 1 different from zero with probability 0.95 or greater. That is, 2.0% of them appear to exhibit serial dependence, which suggests that the independence of samples is a reasonable assumption on the whole. However, these results need to be placed in statistical context.
To do this, we conduct Monte Carlo tests. We create ensembles of series having the same number of series and the p(|r 1| > 0) > 0.95N y ≥ 5N y ≥ 20Number of series10044Observed2.02.3Normal, ρ 1 = 0.01.93.7Normal, ρ 1 = 0.37.118.6Normal, ρ 1 = 0.627.370.4Normal, ρ 1 = 0.939.995.1Uniform2.24.2p(normality) < 0.05N y ≥ 5N y ≥ 20 Number of series12944Observed5.44.5Normal, ρ 1 = 0.04.44.7Uniform15.632.9 same distribution of series lengths as the observed ensemble, but with the series elements drawn at random from the normal distribution using a standard autoregressive algorithm of order 1 (Reference Box, Jenkins and ReinselBox and others, 1994) with the true lag 1 autocorrelation ρ 1 prescribed. For each of several values of ρ 1, we generate 1000 ensembles; for each series in each ensemble we compute r 1 and estimate the probability that it differs from zero; and in Table 2 we list the average frequency, over the 1000 ensembles, of probabilities exceeding 0.95. For comparison, Table 2 also shows results for ensembles of series drawn from the uniform distribution.
Table 2. Statistical attributes of the ensemble of balance time series. Each row represents the results of tests on 1000 replications of an ensemble of time series mimicking the observed mass-balance ensemble

The observed frequency of significant serial dependence is almost the same as that found in independent random Gaussian samples (ρ 1 = 0.0). However, the significance test has very little power to distinguish slight or moderate dependence (ρ 1 = 0.3, say) from complete independence, at least for ensembles having the observed distribution of record lengths. Moderate serial dependence can reduce noticeably our confidence in estimates of the mean (Reference Zwiers and von StorchZwiers and von Storch, 1995). If there were a physically real difference between observed and ρ 1 = 0.0 probabilities it would be interesting, but we conclude, cautiously, that Table 2 provides justification for assuming that mass-balance series consist in fact of independent random samples.
Series in the observed ensemble were tested for normality using the Shapiro–Wilktest (Reference Stephens and StephensStephens, 1986). The ensemble includes about as many series which fail this test as does a set of 1000 comparable random Gaussian ensembles. Again, caution is warranted because of lack of power; when we sample the uniform distribution, chosen for comparison, the test performs weakly, identifying only one-third of these non-Gaussian samples even for longer series. In effect, Table 2 shows that we have found no evidence against the hypothesis that mass-balance series are normally distributed.
Thus, we accept that mass-balance samples are both independent and Gaussian. This means, for example, that the conventional t-test for differences of means and differences from zero is valid and relevant, and that the standard error of the balance normal, inversely proportional to ![]() may be taken quantitatively (but approximately) as an indicator of uncertainty.
may be taken quantitatively (but approximately) as an indicator of uncertainty.
Results
Balance normals and trends, 1961–90
The average of the 231 balance normals in the ensemble is –120 mm a−1 and the average of the 2053 measured balances (i.e. of the normals weighted by record length) is –179 mm a−1. When each of the normals is duly weighted by its standard error, their average becomes –168 ± 36 mm a−1. (All uncertainties here, quoted and plotted as error bars, are given as ± twice the standard error.) These figures confirm the impression given by figure 3b.
In Figure 4, we restrict attention to series with N y ≥ 5, seeking to avoid some of the statistical difficulties presented by the shortest series. The distribution of balance normals (fig. 4a) has a negative mode near –100 mm a−1 and three-quarters of the normals are negative. The average is –195 ± 59 mm a−1. We regard this estimate as the most reliable among these simple calculations. Its confidence region is wide enough to embrace two of the other three estimates. We shall sec, however, that there is more to be taken into account. Here, we simply note that this estimate is less negative than Meier’s much-quoted estimate (Reference MeierMeier, 1984; Reference Kuhn, Warrick, Barrow and WigleyKuhn, 1993) of –306 ± 173 mm a−1, to be discussed below.

Fig. 4. (a) Distribution of 129 balance normals, 1961–90, with Ny ≥ 5, in physical units. (b) Distribution of the balance normals of panel (a) in approximate units of statistical confidence. The abscissa is the balance normal divided by its standard error. For large, independent, random Gaussian samples, the probability that this quantity differs from zero is 67, 95, . . . % at ± 1, ± 2, . . . units on the horizontal axis. However, most balance records are short and follow Student’s distribution instead, so the histogram gives a slightly generous impression of the proportion of glaciers with non-zero mass balance. (c) Distribution of balance trends, 1961–90, divided by their standard errors.
When we invoke the statistical assumptions which were justified in the last section, and consider the distribution of balance normals in units of standard error, it emerges (fig. 4b) that 64% of observed normals are indistinguishable from zero, if we ask for 95% confidence or ± 2 standard errors; 33% have negative and 2% have positive balances.
If mass balance is to be a useful indicator of climatic change, it is necessary to be able to identify balance trends. A non-zero mass balance merely shows that the glacier is not presently at an equilibrium size and that its climatic forcing over some unknown time span has been positive or negative. It would be valuable to know this time span but, notwithstanding the kinematie insights of Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others (1989) and empirical analyses based upon them (e.g. Reference McClung and ArmstrongMcClung and Armstrong, 1993), little is known with precision about the response times of small glaciers to climatic forcing. On a (century-long) time-scale comparable to the Jóhannesson response time, Reference HaeberliHaeberli (1995) has had some success in explaining geodetically estimated mass balance as a function of change in glacier length. On short time-scales, however, trends in length (Reference WoodWood, 1988) are not reliable guides to balance trends (e.g. Reference EchelmeyerEchelmeyer and others, 1996). It is on these shorter time-scales that balance trends might convey timely information about environmental change but figure 4c shows that very few glaciers exhibit balance trends. The significant trends tend to be negative (towards more negative mass balance) but only 12 % are significantly negative (2% being significantly positive) and the average is only –0.3 standard errors. It is probable that many small glaciers are in fact at equilibrium and that, for the others, expectable trends (Reference Kuhn, Warrick, Barrow and WigleyKuhn, 1993) are too small for detection given present methods and uncertainties. Difficulties of detection aside, however, it is a paradox that mass balance should appear to be negative in the absence of trends. Reference Cogley, Adams, Ecclestone and OmmanneyCogley and others (1996) showed that a glacier not at equilibrium ought to exhibit a trend in mass balance.
Evolution of mass balance, 1940–95
Here, we depart from the reference period 1961–90 and admit all available balance measurements made since 1940, with the aim of exploring possible variations with time in the mass balance of small glaciers. We compute averages of all balances measured during each year, assigning to years which are part of a multi-year measurement the increased standard error described earlier. The histogram in figure 5a shows why 1961–90 is a reasonable reference period; measurements are much fewer in earlier years, and fewer in the most recent years because some measurements have yet to be published. The impression of stability during 1961–90 is rather misleading; the population of from 50 to 90 glaciers is in fact a shifting population, with very few glaciers contributing information throughout the 30 year span.
While trends in single-glacier records are elusive, the composite picture shown in figure 5a seems to be clearer. It suggests that over the last 50–60 years small-glacier mass balance was least negative in the middle 1960s. There is weak evidence that it was more negative in the 1940s and 1950s, and stronger evidence that it has been growing more negative from the 1960s to the 1990s. The suggestion of strongly negative balance in the 1940s is particularly suspect, because of the extremely small sample and the fact that the measurements are almost entirely confined to the Alps and Scandinavia. The solid line in figure 5b connects decadal averages of the annual averages in figure 5a. It reinforces the picture conveyed by the annual averages. The remaining information in figure 5b is discussed below.
A shortcoming of Figure 5 is that the errors shown are based on the assumption that the glaciers are independent random samples from a Gaussian distribution. We have established that the assumption of normality is a reasonable one; tests show that in only 4 years is the distribution of the available measurements inconsistent with the hypothesis of normality, in each case because of one or two outlying measurements.
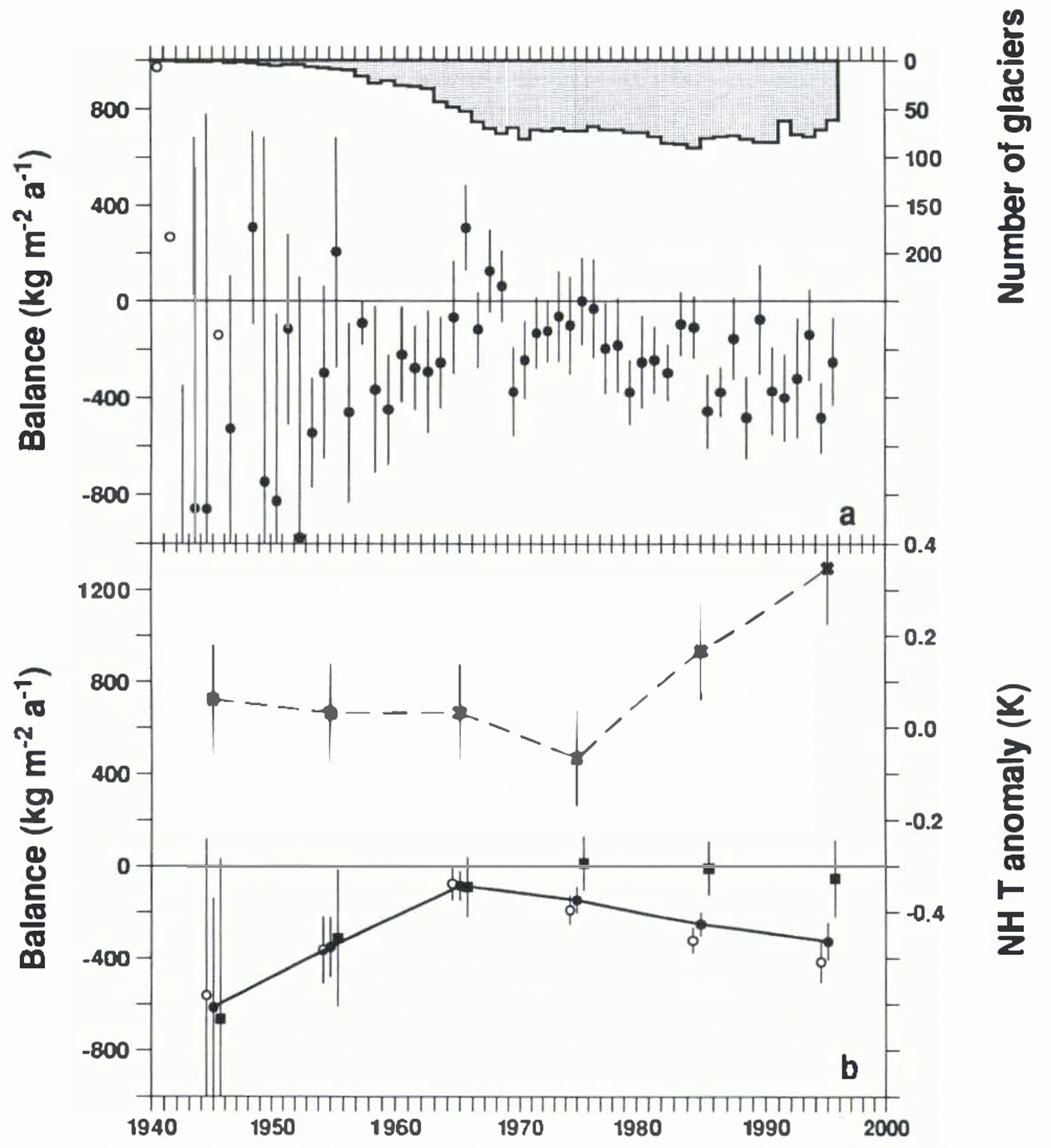
Fig. 5. (a) For 1940–95, the histogram shows the number of glaciers for which mass balance was measured in each year. Solid circles: average of all mass-balance measurements for each year; open circles represent years with only one measurement. (b) Solid circles connected by solid line: decadal averages of mass balance; open circles: decadal averages for glaciers with areas less than 16 km2; solid squares: decadal averages for glaciers with areas greater than 16 km 2; crosses connected by dashed line: decadal surface air-temperature anomaly for the Northern Hemisphere (Reference Jones, Raper, Bradley, Diaz, Kelly and WigleyJones and others, 1986, Reference Jones, Osborn and Briffa1997; Reference Jones and BriffaJones and Briffa, 1992; updated to 1995 from http://www.cru.uea.ac.uk/advance10k).
But, as we show next, the balance series are not independent of each other and, in consequence, the error bars in Figure 5 are somewhat too short.
Bias in the Measurement Ensemble
Spatial bias
Correlation structure in the spatial field of mass balance has been of considerable interest (Reference Letréguilly and ReynaudLetréguilly and Reynaud, 1990; Reference Trupin, Meier and WahrTrupin and others, 1992; Reference Dyurgerov and MeierDyurgerov and Meier, 1997b; Reference Meier, Armstrong and DyurgerovMeier and others, 1997). Here, we present what we believe to be the first global analysis of such structure at the level of individual glaciers and use it to make a preliminary estimate of spatially corrected small-glacier mass balance.
Time series from nearby glaciers are highly correlated (fig. 6a). Correlation coefficients exceed 0.8 and even 0.9 at separations of a few kilometres and decrease to zero at separations of about 1500 km. By least-squares fitting, we obtain the relationship r(s) = 0.90 exp[–s/620], shown as the curve in figure 6a; s is the separation between glaciers in kilometres. The scale length of about 600 km, which must be interpreted in the context of Figure 2, suggests that spatial interpolation should yield meaningful estimates of mass balance for at least some of the unmeasured part of the cryosphere. However, there is nothing to be gained by consulting “nearby” measurements for guidance when they are no closer than about two scale lengths to the estimation site; at such remote sites, one might as well interpolate the global average.

Fig. 6. (a) Correlation between balance series (Ny ≥ 5, 1961–90) as a function of the distance separating their glaciers. Each symbol is an average of correlations between 24 pairs of series (or more at the greater separations), from a total of 5193 pairs involving 129 different glaciers. The fitted curve is discussed in the text. (b) As in panel (a) but here the quantity plotted is the standard error of the estimate of  , the balance normal of glacier 1, from a linear relationship with glacier 2: B 1 = a 0 + a 1 × B 2, where the ai are fitted parameters and the B j are annual balance estimates for glacier j.
, the balance normal of glacier 1, from a linear relationship with glacier 2: B 1 = a 0 + a 1 × B 2, where the ai are fitted parameters and the B j are annual balance estimates for glacier j.
At separations of 2000 km and greater, there is some evidence of periodic structure in the correlogram. We conjecture that the periodicity is real and is related to long wavelength features of the meteorology of the Northern Hemisphere mid-latitudes, as documented for example by Reference Thiébaux and PedderThiébaux and Pedder (1987). It would repay effort to search more carefully for evidence of this periodicity. To do so, however, would require relaxation of the simple assumptions of isotropy (correlations independent of direction, depending only on distance) and homogeneity (correlations independent of location on which figure 6a is based. It would he difficult to incorporate directional and locational dependence, i.e. large-scale spatial trends, in a worldwide analysis of mass balance based on only ~200 data points.
After inspection of the scatter in figure 6a, we elected to fit a model for decay only to data for s ≤ 1750 km and that is the curve which appears in the figure. For each glacierized 1° × 1° cell (Reference CogleyCogley, 1998), we estimated the m ass balance by spatial interpolation in spherical geometry, using polynomials of order 3 or 4. Each observed normal was weighted by its own uncertainty (fig. 3b) and its distance from the glacierized cell. The weight for distance was taken from figure 6b, which is analogous to figure 6a but shows the standard error of estimate obtained when balance series serve as predictors of distant balance normals. The weighting scheme has the effect of making cells with many nearby measurements “good” (the uncertainty of the estimate is dominated by measurement error), while remote cells have estimates near the global average but with very large uncertainty (all the observed normals, being far away, themselves have large uncertainties).
The performance of the interpolation algorithm was checked through a cross-validation exercise, in which mass balance was estimated at the site of each of the 231 available balance normals in turn, using the normals from the other sites. This showed that the algorithm is unbiased but imprecise: the mean difference between observed and interpolated balances was –6 mm a−1 but the rms difference was 412 mm a−1. The lack of precision arises largely from the dataset containing a mixture of measurements with near neighbours, where performance was good, and without near neighbours, where performance was bad.
The global average balance estimated with spatial interpolation is –136 ± 19 mm a−1. The error is certainly too small, because it assumes naively that 1° × 1° cells have un-correlated errors. However, our concern is to assess spatial bias and to the extent that spatial interpolation can make this assessment it appears not to be large. The spatially corrected estimate differs little from the average of measurements, –195 ± 59 mm a−1. The sign of the correction, in the direction of less-negative mass balance, may or may not be significant depending on how much the estimated uncertainties underestimate the true uncertainties. We suggest that it is significant and shows that there are fewer measurements in regions where mass balance is less negative.
Bias due to glacier-size distributions
A further bias in the available observations is demonstrated by Figure 7, which clarifies results on size and number distributions obtained through a scaling analysis by Reference Meier and BahrMeier and Bahr (1996). The measurement ensemble is heavily weighted towards smaller glaciers (fig. 7a; dots): 70% of the measurements are from glaciers smaller than 16 km2. The most numerous glaciers in reality (as represented by the incomplete World Glacier Inventory; thick line) are those with areas of 0.125–0.5 km2 but the preferred size of measured glaciers is noticeably larger at 2–8 km2.
figure 7b shows that there is, very roughly, a correspondence between the glacier-size distribution in reality (thick line) and the size distribution of measured glaciers (dots). This correspondence will not, however, be reflected in the results of a conventional statistical analysis in which each measured glacier (cf. fig. 7a) is given unit weight or is weighted by its record length.
The size mismatch between measurement effort (dots in figure 7a) and actual glacier sizes (thick line in figure 7b) is serious and significant when seen in the context of figure 7c, which shows that the mass balance of small glaciers is currently negative only over a restricted range of glacier sizes. Roughly, glaciers with A < 16 km2 have significantly negative mass balance, while larger and much more extensive glaciers are at equilibrium. Glaciers smaller than 0.125 km2 also appear to be at equilibrium but their total areal extent is negligible. If we weight the size-interval estimates of figure 7c by the actual size distribution of figure 7b (thick line), the resulting global estimate of small-glacier mass balance, corrected for size bias, is only –35 ± 89 mm a−1. This is not a speculative result but it is unexpected and requires further investigation, particularly since the sample is tiny and is extremely tiny in the range of larger sizes. It points to a need for more accurate ways of modelling (Reference Oerlemans and FortuinOerlemans and Fortuin, 1992) mass balances, especially of larger, more logistically challenging glaciers. And it challenges the conventional wisdom about the state of health of small glaciers.

Fig. 7. (a) Frequency distributions if number of glaciers (thick line) and of measurements of annual balance (dots and thin line) by size of glacier. Eachglacier or balance measurement has weight 1. Glacier distributions are from Reference Haeberli, Bösch, Scherler, Ostrem and WallénHaeberli and others (1989), Reference OmmanneyOmmanney (1969), Reference Hagen, Liestol, Roland and JorgensenHagen and others (1993) and Reference Bedford and BarryBedford and Barry (1995). Balance-data distributions, from this study, represent a total of 2095 balance years and a total sampled area of 13 693 km2, in logarithmic intervals on the size axis. (b) Frequency distributions of small-glacier extent by size of glacier. Each glacier (thick line) or measured glacier (dots and thin line) is weighted by its size. (c) Average annual balance as a function of glacier size. All single annual-balance measurements from all glaciers in each size interval are lumped together.
Discussion and Conclusion
Practical considerations
With hindsight, we can see that the allocation of glaciological effort to measurements of mass balance has not been optimal. The spatial distribution of measurements is more like that of glaciologists than that of glaciers. The resources of small working units have understandably been directed towards glaciers of manageable size but, at least from the standpoint of addressing problems of global scale, it now appears desirable that the glaciological community should form larger consortia which can obtain and retain the resources needed for long-term monitoring of substantially larger glaciers and in more remote regions. A lot can still be done, even with the existing base of information, to improve understanding of the uncertainties in mass-balance measurements, but another desirable development would be for measurement net works to be designed explicitly with the estimation of errors in mind. Reduction of the magnitude of errors should also be a high priority.
Implications
The results presented above amount to circumstantial, if not stronger, evidence that the small-glacier component of the cryosphere was at equilibrium, to within estimated uncertainty, during our reference period. The negative average mass balance yielded by simple calculations is an underestimate according to several lines of argument: biases due to neglect of internal accumulation, uneven spatial coverage and uneven sampling of the spectrum of glacier sizes all lead in the same direction with varying amounts of confidence and empirical support. The general absence of trends in time series from single glaciers may also be a relevant item of evidence.
Our estimate, even without corrections for biases, is less negative than a widely quoted standard (Reference MeierMeier, 1984), which is –306 ± 173 mm a−1 and applies to 1900–61. The disparity of time may explain part of this difference, suggesting decelerating recovery from the Little Ice Age during the 20th century. Some of the disparity may be methodological; Meier relied on regionalization of less-extensive balance data, and interpolated using hydrometeorological models and scaling. Recently, Reference Meier and PeltierMeier (1993) has presented an increased estimate which includes the small glaciers of Greenland and has made an allowance for internal accumulation; the new estimate is equivalent in mass-balance terms to –225 ± 125 mm a−1. Now (Reference Dyurgerov and MeierDyurgerov and Meier, 1997b), a further increase has been suggested, to –130 ± 33 mm a−1; this estimate includes the Greenland ice caps but does not correct reported measurements for internal accumulation. It is very close to our estimate with a correction for spatial bias, –136 ±19 mm a−1, which is not entirely unexpected, because the input data to the two estimates, for 1961–90, are almost identical. Dyurgerov and Meier, however, corrected for spatial bias by computing regional averages; thus, two quite independent spatial-bias corrections yield a similar result.
The bias due to neglect of internal accumulation is very poorly quantified. We guess that, if it could be incorporated with the correction for spatial bias, the result would be a global average mass balance somewhat more positive than –100 mm a−1. The bias due to poor sampling of larger glaciers (Fig. 7), which has not been given explicit quantitative recognition before, is better quantified than the others, although it should be remembered that the World Glacier Inventory is not complete. This size bias is apparently large enough that, when it is corrected without correcting the other biases, the estimated global average mass balance becomes indistinguishable from a state of equilibrium. However, more work will be needed before all of the biases can be corrected for simultaneously. They are not necessarily additive.
Why are measured glaciers a biased set? The bias towards very small size, for reasons of manageability, may be complemented by a bias towards accessibility. This would imply that, on average, measured glaciers reach lower maximum elevations than would be representative of their regions; they would be likely to have relatively smaller accumulation areas, which would explain their relatively more negative balances. Alternatively, or in addition, there may be a physical explanation for the observed dependence of mass balance on glacier size. For example, size may be an alias for temperature; the observed dependence would be explained if larger glaciers are on average colder, for colder glaciers will tend to respond to warm forcing by heating up rather than by producing more meltwater. It may be that many of the smaller glaciers are products of the cooling of the Little Ice Age. They could have grown to typical thicknesses, of the order of 50 m, in 250 years with mass balances of +200 mm a−1, and with their contemporary balance of –200 mm a−1 they would disappear in another 250 years. This latter speculation may or may not have merit, but it is fruitful and testable because it implies that both the longevity of glaciers and their insensitivity to climatic forcing must increase with size.
There is some indication, in figure 5b, that larger glaciers may indeed be less sensitive to contemporary forcing. For example, the decrease of average mass balance from the 1970s to the 1990s can be interpreted as a trend of –9.0 mm a−2 for all glaciers but for glaciers larger and smaller than 16 km2 the trends are –3.3 and –11.3 mm a−2, respectively. figure 5b also shows that the evolution of mass balance is broadly in agreement, as it should be, with that of Northern Hemisphere temperature. The earlier decades appear anomalous but we have little trust in their balance estimates. For later decades, if we regard changes in balance as due solely to changes in temperature (in the absence of suitable large-scale measures of other controlling variables), the sensitivity dB/dT can be estimated as about –160 mm a−1 K−1 for the larger and –550 mm a−1 K−1 for the smaller glaciers.
The trends quoted above are all statistically significant. In this, figure 5b is in contrast with figure 4c, a comparison which illustrates the extent of averaging needed to extract a signal from sparse and noisy mass-balance data. We have verified that the trend of –9.0 ± 1.7 mm a−2 for all glaciers is not an artefact of changes in the average size of measured glaciers, which exhibits no trend over the relevant time span.
The finding that small glaciers are probably at equilibrium is directly relevant to the study of changes in sea level. Recent analyses summarized by Reference Warrick, Provost, Meier, Woodworth, Houghton, Filho, Callander, Harris, Kallenberg and MaskellWarrick and others (1996; cf. Reference Meier and PeltierMeier, 1993; Reference Cogley, Adams, Ecclestone, Jung-Rothenhäusler and OmmanneyCogley and others, 1995) yield contemporary rates of sea-level rise of 1.4–2.5 m m a−1, although the estimates are beset by subtle difficulties (e.g. Reference Davis and MitrovicaDavis and Mitrovica, 1996). Anthropogenic activities appear to account for about 0.10 mm a−1 of this total, with estimates ranging up to at least 0.50 mm a−1 and down to –0.40 mm a−1. Thermal expansion of ocean water may contribute about 0.60 mm a−1 (Reference De Wolde, Bintanja and OerlemansDe Wolde and others, 1995; cf. their fig. 5 for 1960–90). There is thus a substantial shortfall which can only reasonably be met by contributions from the cryosphere.
Our uncorrected mass-balance estimate for small glaciers is 0.32 ± 0.10 mm a−1, when translated into sea-level equivalents, and the estimate corrected for size bias translates to 0.06 ± 0.15 mm a−1. Obviously, these estimates, smaller than the 0.46 ± 0.26 mm a−1 of Reference MeierMeier (1984), complicate the problem of explaining the observed sea-level rise. Even the uncorrected small-glacier estimate could be accommodated entirely within the cryosphere by increased annual accumulation of only 5–10 m m a−1 over the ice sheets, if there were no cancelling losses. This is much smaller than can be resolved. Mass-balance estimates for the two ice sheets are extremely uncertain but suggest a state of equilibrium (Reference Oerlemans, Barrow and WigleyOerlemans, 1993; Reference Ohmura, Wild and BengtssonOhmura and others, 1996; Reference Warrick, Provost, Meier, Woodworth, Houghton, Filho, Callander, Harris, Kallenberg and MaskellWarrick and others, 1996).
Recent inferences of very large basal melting rates at the grounding lines of ice-sheet outlet glaciers Oacobs and others, 1992, 1996; Reference RignotRignot, 1997) may point to one of the important unidentified contributors to sea-level rise. The basal meltwater makes its contribution to sea-level rise when it flows across the grounding line as ice; the implication of these inferences is that the flux across the grounding line must be much greater, and the balance of the grounded ice upstream more negative, than previously supposed. These estimates may also apply to small glaciers with calving termini. It is too early, however, to judge their accuracy. The present net cryospheric contribution to sea-level rise is therefore most safely regarded as indeterminate.
The difficulty of predicting future sea-level rise in consequence of global warming is also exacerbated. Some geological evidence (Reference Miller and de VernalMiller and de Vernal, 1992) suggests that Northern Hemisphere ice sheets grow in response to warming, and simple thermodynamics indicates, at least for Antarctica, that ice-sheet mass balance should increase with temperature (because accumulation will increase without a corresponding increase in melting). Now, we have to recognize that sensitivities dB/dT also vary within the small-glacier category as a function of glacier size. It may be helpful to regard the cryosphere as having a self-buffering capacity in response to changes in forcing. That is, its transient response to warming may be for small glaciers to shrink and larger ones to grow, while medium-sized ones (Fig. 7c) show little or no response. The cryosphere is a substantial component of the climatic system, and its self-buffering capacity may have a role in reducing the sensitivity of the system and perhaps in explaining why it has been difficult to detect the expected onset of warming induced by greenhouse gases.
Acknowledgements
We thank M. B. Dyurgerov and M. F. Meier for helpful cooperation, and M. F. Meier and W. Haeberli for thorough and thoughtful reviews. We thank the National Hydrology Research Institute, Environment Canada, Saskatoon, and the Polar Continental Shelf Project, Energy Mines and Resources Canada, Ottawa, for support.











