1. Introduction
The internal structure and flow mechanisms of rock glaciers are poorly understood. Rock glaciers are composed of a mixture of ice and rock, where the rock debris ranges in size from silt to medium-sized boulders. They are covered with an ice-free debris mantle up to a few meters thick, which could inhibit or nearly eliminate surface ablation as a significant component of mass balance (Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllHarris and Pedersen, 1998; Reference KaufmannKonrad and Humphrey, 2000). Rock glaciers are typically thin (<50 m), and they move relatively slowly, typically on the order of 1 ma–1 or slower. While the rheology of the ice—rock mixture is likely to be different than that of clean glacier ice, we still might expect that, as with glaciers (the term glacier is used to denote ice glacier in the following text), both internal deformation and motion at the bed govern their flow.
A rare glimpse into the internal structure of a rock glacier has been made possible by the quasi-periodic calving of Fireweed rock glacier (FRG), Alaska, U.S.A. (Reference Elconin and LaChapelleElconin and LaChapelle, 1997). These authors found that the rock glacier was composed of a heterogeneous mixture of ice and rock and contained several indicators of deformation. They also discuss the origins of the ice and rock. In addition, this rock glacier has relatively high surface velocities (>3 ma–1) compared to velocities commonly observed on most other rock glaciers. Here we describe observations of surface velocities and topography, and investigate the correlation among the calving, precipitation and velocity variations. We then analyze the velocities in order to estimate the nature and magnitude of basal motion and internal deformation. From these models and the observed flow we are able to estimate the rheological parameters of the rock glacier mixture. We recognize that rock glaciers may be of either permafrost origin or glacial origin, or they may evolve from a glacier to a rock glacier (Reference HaeberliHaeberli, 1985; Reference HughesHumlum, 1988). Our analysis of the flow is valid, given present knowledge, for a deforming mixture of ice and rock derived by either process.
2. Description of Fireweed Rock Glacier
2.1. Location and overview
This rock glacier is situated in south central Alaska on the southern flank of the Wrangell Mountains (Fig. 1a). It flows down a north-facing valley on Fireweed Mountain, and is the largest of 12 rock glaciers flowing from the mountain each in their own valley. The valley that FRG occupies has a drainage area of 4.6 km2 and previously contained a glacier, as evident by the broader U-shaped valley and moraines near the terminus (Fig. 2). There are three tributaries that originate at elevations of 1400–1600 m and coalesce to form the main trunk, which terminates at 1000 m in a narrow, steep-sided valley (Fig. 3a). On the main trunk, V-shaped longitudinal furrows separate contributions from the tributaries (Fig. 1), and each tributary (and its contribution to the main trunk) is distinct in coloration due to different lithologies. We term these distinct contributions on the main trunk as a “flow” (Fig. 2). The rock glacier is >2 km long from the head of the middle tributary to the terminus. The west tributary flows for about 400 m before merging with the middle tributary at a position about 800 m up-glacier from the confluence with the east tributary. The east tributary is about 1350 m long from its head to the confluence with the main trunk, and the main trunk flows for about 470 m (Fig. 1b) from the confluence of the east and middle tributaries to the break in slope at the terminus (the “terminus break”). This valley geometry is to be compared with that of some well-studied rock glaciers in the Alps and Svalbard, such as Murtél and Grüben in Switzerland and rock glaciers in Svalbard (Reference HaeberliHaeberli, 1985; Reference HumlumKääb and others, 1997; Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllHaeberli and others, 1998; Reference Berthling, Etzelmüller, Isaksen and SollidBerthling and others, 2000). These rock glaciers are typically <1 km long and consist of a single flow extending onto a broad plain of relatively constant slope. We also note that a rock glacier is often considered a form of alpine permafrost (e.g. Reference HaeberliHaeberli, 1985; Reference HumlumKääb and others, 1997).

Fig. 1. Location (a), topography (b) and geometry (c, d) of Fireweed rock glacier. Contours are interpolated from surface profiles along the margins and center lines of each tributary and flow. Thickness measurements in (c) and (d) are from geophysical soundings (Reference Bucki, Echelmeyer and MacInnesBucki and others, 2004). Hae is height above ellipsoid. W.F., M.F. and E.F. are the west, middle, and east flows respectively of the main trunk. I and II mark the steep sections referred to in the text.

Fig. 2. Oblique air photo showing the convergence of the three tributaries into the main trunk. “A” indicates lateral moraines from previous glaciation, and “B” longitudinal ridges and furrows thought to delineate the ice-rich region of E.F. Notation as in Figure 1. (Photograph by R. Elconin.)

Fig. 3. Caved terminus photos. (a) Photograph of terminus in 1993 showing a cavern washed out by the swollen stream (photograph by R. Elconin). (b) The calved terminus in 2001. “D” is the location of the ice-rich region. Contributions of the flows to the face are marked as E.F., M.F. and W.F. The top of the photograph is ~90 m in width. Note the person near the bottom of the talus. (Photograph by L. Cox.) (c) Close-up of the ice-rich region, 2001. View across the calved face from the east margin toward the west. (Photograph by M. Truffer.)
With geophysical exploration methods, especially transient electromagnetic ones, we determined the thickness of the main trunk of the rock glacier to be about 55 m (Fig. 1). In addition to this depth-to-bedrock measurement, we observed a seismic, and to a lesser extent a resistivity, discontinuity ranging from a depth of about 15 m in the upper middle tributary to about 30 m in the main trunk (Reference Bucki, Echelmeyer and MacInnesBucki and others, 2004).
2.2. Climate and thermal regime
FRG exists entirely below the regional equilibrium-line altitude of nearby glaciers, which is ~1800 m a.s.l. as observed in late August 2000 and 2001. Semi-permanent snow-patches, resulting from avalanche debris and shading, exist in all cirques and along the margin. In the nearby town of McCarthy (460 m elevation and 9 km to the southeast), mean annual precipitation is 0.42 m and average snow depth during the winter is 0.35 m.
Using temperature data loggers we obtained continuous year-long surface temperatures (Fig. 4) from each tributary of FRG and from the moraine adjacent to the main trunk (“A” in Fig. 2). Ground surface temperatures were measured on the rock glacier at elevations of 1355–1443 m. The lowest recorded temperature was –3.2°C at 1435 m and was recorded at the end of winter. On the moraine at a lower elevation (1065 m), measured temperatures were never lower than 0°C. However, due to sensor malfunction, the record was truncated near the end of winter, which is the time period during which the lowest temperatures were observed at other locations. From the remaining record there we infer that ground surface temperatures remained near freezing or slightly below freezing until the end of winter. From these temperatures we infer that temperatures at depth within the rock glacier are likely lower than these temperatures. Typical regional snowpack is thin (<1 m) and we are careful to use these observed temperatures as an annual average temperature since the thin snowpack may not completely insulate the ground from ambient air. Additionally, heat-transfer processes in coarse blocky layers, such as a debris mantle on a rock glacier, are poorly understood. It is possible to estimate the mean annual temperature at FRG for all elevations to be in the range –4 to –7°C by using temperatures measured in McCarthy and a lapse rate of 5°C km–1.

Fig. 4. Ground surface temperature measurements. Sensors were placed along the center line of each of the tributaries at the elevation noted in parentheses. Moraine was placed on the western moraine near the main trunk, marked “A” in Figure 2. Notation as in previous figures.
2.3. Tributaries and debris mantle
The rock debris mantle is composed of two main lithologies: a fine-grained felsic igneous rock and a fine-grained mud-stone. Both occur in different states of hydrothermal alteration. On the east tributary, the debris is composed of ~65% unaltered igneous rock and ~35% mudstone. On the middle tributary, it consists of about equal parts of the two unaltered rock types. The mantle of the west tributary is composed of ~20% altered mudstone and ~80% mostly altered igneous rock; this high percentage of altered rocks gives the west tributary and flow a reddish hue.
Reference Elconin and LaChapelleElconin and LaChapelle (1997) measured the thickness of the debris mantle on the middle tributary to be 0.7–1.2 m in moulin-like and bergschrund-like features, while at the terminus they found the mantle to be 2–3 m thick. Seismic soundings 90 m up-glacier of the terminus indicate a debris mantle thickness of about 2.5 m (Reference Bucki, Echelmeyer and MacInnesBucki and others, 2004). This thickening of the debris mantle toward the terminus has been observed on other rock glaciers (Reference Barsch, Giardino, Shroder and VitekBarsch, 1987).
Rocks of 0.1–0.6 m diameter make up the visible debris mantle; their average size decreases from the head to the terminus. Soils are nearly absent on the upper tributaries, but are more common on the main trunk, where they occur as a matrix between the blocks and in the furrows between the flows. A few small shrubs and grasses occur in these areas.
2.4. Surface features
Much of the rock glacier has a convex transverse surface profile (Fig. 1c). This shape is most evident where there are no talus slopes draping onto the rock glacier’s surface. In some areas where talus overlaps onto the surface, the surface is concave. However, in other areas where talus falls toward the rock glacier, a trough 2–3 m deep separates the rock glacier and the talus slope, which does not appear to contribute to its mass balance. But, in some years of our study, a few of these troughs have been completely filled with snow, making a smooth transition from the talus slope to the rock glacier, and possibly allowing avalanched rock debris to be deposited on the surface.
Transverse ridges exist on two of the tributaries, but unlike those on many other rock glaciers (e.g. those studied by Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllKääb and others, 1998) they do not occur near the terminus. The most distinct set of these transverse ridges occurs on the upper west tributary, while ridges in the middle tributary are small. There are also crevasse-like features (“C” in Fig. 2); the extent to which they penetrate below the debris mantle cover is unknown. The “crevasses” are associated with a steep area on the middle tributary (labeled I in Figs 1 and 2). Above this steep section the crevasses are orientated similar to marginal shear crevasses on glaciers, which tend to intersect the valley walls at an angle of about 45° up-glacier. The crevasses occur where the transverse surface is convex and a large 3–6 m deep trough separates the surface of the rock glacier from the valley walls (Fig. 1). Within the steep section, crevasses are oriented perpendicular to flow, similar to those found above an icefall. Below the steep section, crevasse-like features are found along much of the middle flow, while along the west flow the crevasse patterns smooth out below the steep section. The steep section of the east tributary (II in Figs 1 and 2) is smooth and does not have crevasses or ridges. On the lower 150 m of the east flow, there is a set of longitudinal ridges and furrows (“B” in Fig. 2) associated with distinct internal structures that are exposed at the terminus during calving events. There are also steep lateral sides at the margins of the main trunk that together with the bedrock walls also create furrows. The depths of these furrows and the ones mid-channel rarely exceed 3 m.
2.5. Terminus calving events and internal structure
The terminus of this rock glacier experiences periodic calving. This unique characteristic may be the result of the constricted V-shaped valley in which the glacier terminates. A bottleneck in the valley may cause the terminus to over-steepen as the rock glacier advances or the bottleneck focuses the flow of the stream in such a way that the lower part of the glacier is washed out during heavy rain (Fig. 3a).
In 1993 the terminus calved and provided a complete transverse exposure of its internal structure (Reference Elconin and LaChapelleElconin and LaChapelle, 1997). The calving event followed a period of heavy rainfall at the end of August. When first observed (1 September) the terminus was overhanging and undercut by the proglacial stream as shown in Figure 3a. The calving and melt ablation of the exposed terminus caused a retreat of about 50 m. By September 1995, the terminus was completely draped by a steep slope of rock debris and it had advanced since the calving event.
From the exposure created during the 1993 calving event, Reference Elconin and LaChapelleElconin and LaChapelle (1997) described the internal structure as a “consolidated mixture of ice and rock”, with a bulk ice concentration greater than 50% (and up to 70%). Generally the clasts are ice-supported, but may be separated by only a few millimeters. They concluded that this mixture is formed by the accumulation of ice and talus at the bases of the cirque headwalls. The accumulation includes sedimentary (glacial) and periglacial (or permafrost) processes, although it is unknown if one process dominates. Photographs (e.g. Fig. 3) and descriptions of the terminus exposure show heterogeneous concentrations of ice and rock. An ice-rich region (~90% ice) exists at the terminus of the east flow (Fig. 3c). The longitudinal ridges and furrows on the east flow (“B” in Fig. 2) appear to be a surface expression of this ice-rich area, and anomalously large surface velocities exist there. The remainder of the east flow contains 30–50% ice. At the terminus, the middle flow is largely overrun or displaced by the east flow and, as a result, it contributes little to the exposed face. Where the middle flow outcropped, it has an ice concentration of about 30%. The west flow contains about 50% ice or greater. It should be noted that these localized percentages were difficult to estimate and are subject to considerable uncertainty, perhaps as much as 10–20% (personal communication from Reference Rabus and EchelmeyerR. F. Elconin, 2001). Reference Elconin and LaChapelleElconin and LaChapelle (1997) found thin layers of bubble-free and debris-free ice within the terminus face. They also found aligned debris clasts, foliation and elongated bubbles, all of which indicate deformation.
The terminus again calved after August 2000 and before May 2001, and we believe that it may calve regularly. This recent event may have occurred as early as September 2000, when there was a period of extreme rainfall, with more than twice as much precipitation as during the rain event prior to the 1993 calving. Rainfall in McCarthy over the 7 day period 20–26 September 2000 was almost 13 cm, whereas 5 cm of rain fell in late August 1993. The overall magnitude of the 1993 calving event was much larger than the 2001 event. However, we note that the over-steepened terminal face observed in September 2001 may cause additional calving over the following year.
Estimates based on observations made in August 2001 indicate that about 12 000 m3 of material were removed from the snout as a result of calving. A talus apron skirted the bottom third of the terminus (Fig. 3b), but its volume was estimated to be only a fraction of the estimated calved material. The remainder of the calved material was melted or washed away by the proglacial stream. The timing of the calving event coincided with changes in surface velocity on the lower main trunk, as described in the following section.
3. Surface Topography and Velocity Field
3.1. Methods
The geometry of the rock glacier was determined by topographic surveys of the surface and by geophysical soundings (Reference Bucki, Echelmeyer and MacInnesBucki and others, 2004). A longitudinal section of the main trunk is shown in Figure 1d. In 1997 we established a survey network of four benchmarks (Fig. 5) using global positioning system (GPS) methods. A theodolite and electronic distance meter were used for the surface and motion surveys. The center-line thickness of the main trunk of the rock glacier was determined as 50–60 m using geophysical soundings, and the channel shape can be approximated as a parabola (Fig. 1c).

Fig. 5. Surface velocities of FRG. Center points of the arrows mark the location of the velocity markers. (a) The entire rock glacier showing location of “survey benchmarks” denoted by diamonds. (b) Detailed diagram of the main trunk. TP is the terminus survey point referred to in the text and is located along the terminus break.
Over 300 positions on the 0.83 km2 total surface area were surveyed to define the surface topography and margins. This included longitudinal profiles of each of the tributaries with a position measured about every 50 m along flow. The uncertainties for these measurements are about 0.3 m in both the horizontal and vertical. More detailed surveys were made of the terminus break.
Velocity markers were positioned in four transverse profiles on the main trunk (profiles A–D in Fig. 5b), and throughout the tributaries. On the tributaries, many of the markers were placed along the longitudinal profile (Fig. 5). The markers were 60 cm sections of steel-reinforcement bar (“rebar”) that were set into the debris layer so that only ~3–15 cm projected above the rough surface. Stability of the markers was good, and minimal tilting occurred over the measurement period. Limited velocity surveys of these markers began in 1997, followed by more complete surveys in the summers of 1998–2001. From 1993 until 1998, velocities were monitored using a series of painted rocks positioned across the main trunk (R. F. Elconin, unpublished data); these data overlap and agree with the higher-resolution data obtained using the rebar markers. Long-term average velocities were calculated over the 2 year period July 1999–August 2001. To detect seasonal variations in flow, surveys were made in late June/early July and then again in late August/early September of both 1999 and 2000. Surveys made in 1999 and later have estimated horizontal and vertical position errors of about 0.02 and 0.04 m on the main trunk, respectively, and 0.04 and 0.07 m on the tributaries. Estimated errors for the pre-1999 surveys are about twice these values.
3.2. Topography
The elevation along each longitudinal profile shown in Figure 5 is shown in Figure 6a. The local surface slope at each of these markers was calculated from the surface elevations over a longitudinal distance of 100 m. Using the measured strain rates, we determined this distance as “appropriate” for our flow analysis according to Reference Kääb, Gudmundsson and HoelzleKamb and Echelmeyer (1986). The uncertainty of these local surface slopes is about 0.5°. Along the center lines of the main trunk and tributaries, the surface slope ranges from about 3° to 27°; the steepest sections are labeled I and II in Figures 1 and 2. (This does not include the terminus front or the margins that dip toward the valley walls, which have slopes of about 40°.) The average slope of the main trunk is about 13°; the middle tributary, inclusive of the steep section, averages about 16°, and both the east and west tributaries average 14°.

Fig. 6. (a) Center-line surface profile along the tributaries and main trunk (center-line location shown in Fig. 5a). Hae is height above ellipsoid. (b) Horizontal velocities (ma–1) along the profiles. (c) Strain rate between the velocity markers (×0.001a–1).
3.3. The terminus front and terminus break
In July 1999, a marker (TP) was set into the debris mantle on the west flow about 3 m up-glacier of the terminus break (Figs 3b and 5b). From this location, the average slope of the terminus front was measured to be about 38° in 1999 and 2000. By August 2001, calving had removed material between the marker and the old terminus break, and the average slope of the calved terminus was 40°. However, following calving the upper 20 m was nearly vertical, with a lower-angled talus apron below (Fig. 3b).
The transverse position of the terminus break was measured from 1999 to 2001 (Fig. 7). From 2000 to 2001 the break retreated by calving in the central portion and it advanced somewhat near the margins. Some material was removed from the marginal areas by calving, but there was still a net advance there. Removal of material by the calving was evident everywhere along the terminus, with exposed ice, fresh surfaces and the close-to-vertical face (Fig. 3b). The largest calving retreat was in the east flow, where Reference Elconin and LaChapelleElconin and LaChapelle (1997) described the ice-rich region.

Fig. 7. Velocity profiles A and B (location shown in Fig. 5b). (a) Asymmetric profile A; (b) more symmetric profile B.
3.4. The surface velocity field
Horizontal surface velocities (1999–2001 averages) are <0.5 ma–1 on the upper tributaries of the rock glacier and increase on the main trunk to a maximum of 3.8 ma–1 as measured 80 m above the terminus on the east flow (Figs 5 and 6). At the terminus break of the west flow, the speed was about 4 ma–1 (Fig. 7). (The error in these 2 year velocities is about 0.03 ma–1.) We analyzed air photos taken in 1957, 1970 and 1994 by comparing the change in relative location of features on the rock glacier with nearby stationary features of known dimension. This revealed that the presently observed surface velocities have persisted for several decades. These are exceptional velocities for a rock glacier; typical velocities are 2 ma–1 or less (Reference HaeberliHaeberli, 1985; Reference Barsch, Giardino, Shroder and VitekBarsch, 1987; Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllKääb and others, 1998; Reference Konrad and HumphreyKonrad and others, 1999). The steep sections of the east and middle tributaries have somewhat higher velocities than the other tributaries, but in general there appears to be no direct correlation between surface slope and surface velocity (cf. Fig. 6a and b). For example, in the steep section I, the slope is 27° and the speed is 1.5 ma–1, while just above this steep section, where the local slope is 17°, velocities are about 2.0 ma–1.
3.4.1. Surface velocity field of the main trunk
The magnitude of the velocity increases by as much as 1.5 ma–1 from profile B to profile A, a distance of 100 m (Fig. 6b). The velocity profile at A is asymmetric (Fig. 7a). The largest velocities on the rock glacier (except at marker TP) are on the east flow, where they are associated with the ice-rich region identified in the calving front. The velocity vectors in this ice-rich region are oriented about 10° more westward than the general channel direction, and the flow appears to displace (or override) the ice-poor part of the rock glacier (Figs 2 and 5b).
The transverse velocity pattern at profile B is more symmetric, but it is plug-like in shape (Fig. 7b), having high marginal shear strain rates. The velocities measured close to the margins are about 0.6 ma–1; these give effective transverse gradients in velocity of about 0.3 a–1 near the east margin and 0.1 a–1 at the west margin, assuming there is no marginal “sliding”. Similarly, the near-margin transverse velocity gradients at profile A are about 0.2 a–1. Profiles C and D show similar patterns to those found at profile B, including the nearly plug-like flow.
3.4.2. Longitudinal strain rates
Longitudinal strain rates were estimated from the measured 2 year average velocities over a longitudinal separation Δx between markers:
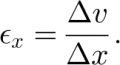
Figure 6c shows the longitudinal strain rate along the central flowlines. They are small, generally about 0.002 a–1, but increase to 0.008 a–1 near some of the steeper sections. Errors for these strain rates range from 0.0004 a–1 to 0.0008 a–1. Reference HumlumKääb and others (1997) measured similar values at Grüben rock glacier. These are about an order of magnitude less than typical strain rates on temperate valley glaciers, but are similar to those measured on McCall Glacier in arctic Alaska, where they correspond to a low mass-balance gradient and mass flux (Reference PatersonRabus and Echelmeyer, 1997).
The pattern of strain rate is unlike that expected on a glacier, where the accumulation area is generally extending, the ablation area is compressive and the rate of extension is often high where the surface slopes are high. On FRG, the strain rates increase above steep sections I and II and decrease within them. The strain rates are negative (compressive) at the base of the steep section (I) of the middle tributary, as expected, but they are positive below steep section II of the east tributary. Strain rates increase within the narrowing main trunk between profiles B and A. The largest longitudinal strain rates of about 0.015 a–1 were measured on the west flow near profile A and marker TP.
3.4.3. Seasonal variations
Motion surveys indicate that there is temporal variability in velocity at both seasonal and annual time-scales. Figure 8 shows the 2 year average annual velocity (thick line), along with velocities measured over shorter time intervals. The velocity variations are to be compared with their estimated errors over the 2000–01 interval (~0.03 ma–1) and over the shorter summer intervals (~0.15 ma–1). The velocities in summer 1999 were less than the 2 year average by 40% at profile A, 30% at profile B and 13% at profiles C and D. Velocities during the calving year July 2000–August 2001 were higher than average, especially at profile A. After calving, velocities were largest on the east flow. At profile A velocities were as much as 1.2 ma–1 above the 2 year average, and at B they were about 0.7 ma–1 above the average.

Fig. 8. Temporal velocity variations at profiles A (a) and B(b).
Strain rates also exhibit temporal variability. For example, in the lowermost 100 m of the east flow, strain rates were especially high (0.05 a–1) over the 2000–01 period, being twice those measured over the previous 3 years (0.02 a–1).
4. Analysis of Surface Velocities and Calving
4.1. Precipitation, velocity and calving
Precipitation records from 1987 to 2001 for McCarthy were obtained from the U.S. National Climate Data Center. The average annual precipitation over this interval was about 42 cm a–1, and the three years with the highest recorded precipitation were 1988, 1993 and 2000.
Although our data are limited, there appears to be a correlation between times of increased precipitation and both velocity changes on the main trunk and calving at the terminus (Fig. 9; terminus status and velocity in 1988 are unknown). The highest annual velocities measured at profile A correspond to those years having calving events, and the elevated velocities measured in the two years following the 1993 calving are likely associated with that event. It is inferred that velocities remained high while the terminus advanced into its pre-calved geometry. After calving, a longitudinal force imbalance exists at the unsupported face, providing an additional “pulling” force on the nearby portion of the rock glacier, analogous to the effect proposed by Reference Hooke, Dahlin and KauperHughes (1986). As the valley fills in and the terminus returns to its sloping, non-calved geometry (e.g. 1996–2000), longitudinal stress gradients near the terminus decrease and the near-terminus velocities decrease.

Fig. 9. Annual precipitation, calving events, and annual surface velocities on the center line at profiles A–C.
Both the calving event in 1993 and that in 2001 were associated with periods of high rainfall and an accompanying period of larger-than-normal velocities. Thus, increased precipitation, particularly large rainfall events, likely promotes calving, and this calving affects the surface velocity near the terminus. Of course, we would also expect that the terminus must build back up to some given geometry before it can again calve. This scenario is reasonable, but the limited resolution and coverage of our dataset does not preclude other possibilities.
4.2. Basal motion and deformation
The plug-like velocity profiles suggest that there are two contributions to the surface velocity, one from internal deformation (u d) and one from motion along basal and marginal interfaces (u bed). As already noted, Reference Elconin and LaChapelleElconin and LaChapelle (1997) observed features that indicate deformation of the ice—rock mixture. In addition, temporal variations in the velocities strongly suggest a basal component of flow. Assuming that sliding or basal motion is the same everywhere across the bed, and extrapolating the observed velocities at profile A to the margins, suggests that u d ≈ 2ma–1 and u bed ≈ 1ma–1. Similarly, at profile B, we estimate u d ≈ 1.2 ma–1 and u bed ≈ 0.6 ma–1. Flow models discussed next provide some further insight into these two contributions.
4.3. Channel geometry, flow models and rheology
The internal deformation of both glaciers (Reference NyePaterson, 1994) and permafrost (Reference Andersland and LadanyiAndersland and Ladanyi, 1994) is often described in terms of a power-law rheology. For simple shear in a vertical plane, with x aligned parallel to flow and y positive upward, we have
where τxy
is the shear stress,
![]() is the strain rate and A is the flow-law parameter, which can vary with temperature, debris content and impurities. The flow-law exponent typically is n ≤ 5 for ice-rich permafrost (Reference Andersland and LadanyiAndersland and Ladanyi, 1994), and n ≤ 3 is often used for clean glacier ice (Reference NyePaterson, 1994).
is the strain rate and A is the flow-law parameter, which can vary with temperature, debris content and impurities. The flow-law exponent typically is n ≤ 5 for ice-rich permafrost (Reference Andersland and LadanyiAndersland and Ladanyi, 1994), and n ≤ 3 is often used for clean glacier ice (Reference NyePaterson, 1994).
The calculation of shear stress for a rock glacier is complicated by the additional mass of the debris mantle, and by the often unknown density of the mixture. For a two-layer rock glacier with a deforming core of average thickness h and density ρ c, and an overlying debris mantle of thickness d and density ρ m, we have, at the bed,
where α is an appropriately averaged surface slope, g is the gravitational acceleration and f is a channel shape factor. Assuming the debris mantle rides passively on top of the deforming core (Reference Kamb and EchelmeyerKaufmann, 1998), Equations (2a) and (2b) lead to a center-line surface velocity of
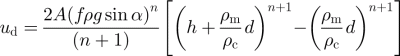
(Reference Konrad and HumphreyKonrad and others, 1999). (In Reference Konrad and HumphreyKonrad and others (1999) the last term of this formula is incorrect, but in Reference KaufmannKonrad and Humphrey (2000) it has been corrected. The shape factor is not included in either version, and it is incorrectly applied to non-center-line surface velocities in the first version.) For d ≪ h, the last term can be ignored. Here we take ρ m to be about 2200 kg m–3 by assuming the mantle is composed of rock debris having a density of about 2800 kg m–3 and about 20% air space. Likewise, we estimate ρ c to be about 1850 kg m–3, by assuming equal volumes of ice and rock debris. With Equation (2b) we calculate the basal shear stress (τxy ), for an assumed parabolic channel geometry at profile B where h = 58 m, d = 2 m (Reference Bucki, Echelmeyer and MacInnesBucki and others, 2004), α = 9° and f = 0:55 (width = 158 m), to be about 0.9 bar.
How the flow-law parameter of ice varies with debris content is poorly understood; as a result, in order to use Equation (3), we must make a priori assumptions about A within the rock glacier. First, we assume that A is constant with depth and take u bed = 0. With the assumed geometry at profile B, and Equation (3) with n = 3, we find A = 0.14 a–1bar–3. This is about the same value found for temperate ice (e.g. Reference Hoelzle, Wagner, Kääb and Vonder MühllHooke, 1981; Reference Rabus and EchelmeyerTruffer and others, 2001). However, this conclusion is based on the assumption that there is no basal or marginal motion, contrary to the observed plug flow, as discussed in section 4.2.
4.3.1. Velocity profile and channel geometries
The analysis based on Equation (3) is limited to the center-line velocity. Information on flow mechanisms can also be obtained from the shape of a transverse velocity profile. Reference Nickling and BennettNye (1965) calculated the deformational velocity profiles of a glacier in various channel shapes, and Reference DrewryEchelmeyer (1983) extended this analysis to various values of n. Here we compare the results of Reference DrewryEchelmeyer (1983), scaled to the observed center-line velocity, with the velocity at profile B (Fig. 10a). For any reasonable n (with constant A), the fit of parabolic channel flow to the observed velocities is poor as long as we assume no basal motion.

Fig. 10. Channel-flow analysis. (a) Modeled flow in a parabolic channel for various values of n. (b) Parabolic channel with sliding. (c) Rectangular channel for various channel depths. (d) Modeled flow at profile B for a shallow (~27 m) rectangular channel with sliding at 27 m and zero velocity below and n = 3, as discussed in the text.
We can include basal motion by adding u d and u bed directly, although we acknowledge that this direct addition is likely more complicated because of stress transfer and the non-linear rheology expressed by Equation (2) (Reference Rabus and EchelmeyerTruffer and others, 2001). Assuming a parabolic channel at B, with h = 58 m, and using u d = 1.2 ma–1 and u bed = 0.6 ma–1, we find a flow-law parameter of A = 0.08 a–1 bar–3. This is slightly less than that of temperate ice. However, the predicted velocity profile does not match the shape of the observed profile (Fig. 10b). Additional modeling shows that no assumed parabolic geometry with the measured center-line depth can reproduce the observed velocity pattern at profile B for any reasonable values of A, n and u bed.
Each of these models assumes that deformation occurs throughout the rock glacier mixture in a channel geometry that is approximately parabolic. However, we note that the geophysical soundings on this rock glacier indicate a seismic discontinuity at 15–30 m depth. Also, observations at Murtél and Pontresina-Schafberg rock glaciers in Switzerland indicate that all of the deformation is concentrated at (and possibly above) a shear horizon within the mixture (Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllHaeberli and others, 1998; Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllHoelzle and others, 1998). Following these observations, we consider models with localized deformation at and above a plane at some depth in a parabolic channel of center-line depth 58 m. To simplify the computations, we assume that deformation is limited to the rectangular subsection of the channel so defined, with “sliding” around its perimeter. We considered rectangular channels (Reference Nickling and BennettNye, 1965) with depths ranging from 58 to 10 m and n = 3. (Of course, a 58 m deep rectangular channel is unreasonable, given the projected shape of the valley walls.) We find that the fit for a rectangular subsection with no sliding is still poor (Fig. 10c). A reasonable fit to the observed velocity profile arises from a model which has assumed a 27 m deep rectangular subsection (f = 0:87), u bed = 0.6 ma–1 and u d = 1.2 ma–1 (Fig. 10d). However, we note that this model is not unique. For this shallow rectangular model, we calculate the driving stress with Equation (2b) to be about 0.7 bar, taking α = 9°, d = 2 m, ρ m = 2200 kg m–3, ρ c = 1850 kg m–3 and h = 27 m. The value for A required to fit the observed surface velocity is 0.26 a–1 bar–3. This is roughly twice as soft as clean temperate ice.
Thus, the geophysical observations and the observed velocity profile suggest that there is a quasi-rectangular core that deforms more easily than clean ice, and that there is a zone of localized deformation at the base and sides of this core. Again, these results are for illustration purposes only. They do fit the observed surface velocity profiles, but they are not unique.
4.3.2. Longitudinal stress gradients and the flow-law parameter
Here we investigate the possible effects of longitudinal stress gradients on the flow of the ice/rock mixture that likely exist within the rock glacier. Variations in rock glacier geometry, such as those shown in Figure 1, produce longitudinal stress gradients that influence the motion. Following Reference Kääb, Gudmundsson and HoelzleKamb and Echelmeyer (1986), we can approximately account for longitudinal stress gradients by assuming an appropriate longitudinal average of slope, thickness and shape factor. These authors show that the center-line velocity in a non-parallel-sided channel is given by an exponentially weighted average:
where
is the deformational velocity calculated for an average parallel-sided reference state and Δ denotes the difference between reference state and the actual geometry at a longitudinal position s along the glacier. L is the length of the glacier and l is the longitudinal coupling length, which is about twice the ice thickness for glaciers with longitudinal surface strain rates on the order of 0.01–0.05 a–1. Given the relatively small strain rates we observed near profile B, we use a coupling length of about 4h (Reference Kääb, Gudmundsson and HoelzleKamb and Echelmeyer, 1986; l = 230 m in this case). To determine an estimate of the flow-law parameter (A) for the rock glacier mixture, we combine Equations (3) and (4) to give
where A 0 is the flow-law parameter calculated without longitudinal averaging from Equation (3). An appropriate scaling factor of the exponential weighting function, K, is required because we cannot extend the analysis out to |s – x| = 2l, due to the limited length of our dataset.
We find that the effect of including these longitudinal stress gradients in each of the models discussed (Fig. 10a–d) is to decrease by about 10% the value of A required to match the observed center-line speed. For the rectangular subsection model, we assume that the depth of the subsection is constant along the length of the main trunk. Then we find that the stiffness of the mixture in the best-fit model (a 27 m deep rectangular subsection with 0.6 ma–1 sliding) is 0.27 bar–3 a–1. This is roughly 7 times softer than clean ice at the equivalent temperature of –2°C (Reference NyePaterson, 1994) and 2.5 times softer than clean temperate ice (A = 0:1 bar–3 a–1; Reference Hoelzle, Wagner, Kääb and Vonder MühllHooke, 1981; Reference Rabus and EchelmeyerTruffer and others, 2001*).
We note that the ice—rock mixture of this rock glacier may have been derived from permafrost processes (Reference Andersland and LadanyiAndersland and Ladanyi, 1994) or glacial processes. This mixture may behave similarly to other forms of debris, and the debris-laden ice found at the base of glaciers. The manner in which the rock debris influences the rheology of ice is poorly understood and observations regarding its rheology conflict. Laboratory studies have shown that weakening of ice occurs when debris concentrations are high (>70%), while at lower concentrations the mixture is stiffened with respect to clean ice (Reference HookeHooke and others, 1972; Reference Konrad, Humphrey, Steig, Clark, Potter and PfefferNickling and Bennett, 1984). The mechanism often suggested explaining stiffening by debris is that, for most concentrations, the debris particles collide and act as pinning points, thus strengthening the mixture.
In situ studies indicate that debris concentrations of 25–60% result in significant softening of ice—rock mixtures (Reference Echelmeyer and WangEchelmeyer and Wang, 1987; Reference CohenCohen, 2000). Also, extrapolation of in situ permafrost studies to the temperature and stress conditions within glaciers indicates softening with respect to clean ice. A mechanism for this softening has been suggested by Reference Echelmeyer and WangEchelmeyer and Wang (1987), in which interfacial water at the debris–ice contacts allows slip at each debris particle, lowering the effective viscosity. Cohen’s (2000) observations of the water content, fabric and deformation of debris-laden ice support this idea. This mechanism can also lead to shear planes in heavily debris-laden ice, as observed by Reference Echelmeyer and WangEchelmeyer and Wang (1987). Our inferred softening of rock glacier mixture at profile B is consistent with these later observations. If these increased values of A are indeed typical of rock glacier ice—rock mixtures, then we expect that rock glaciers would have higher surface velocities than glaciers of similar geometry and basal shear stress. However, we must note that the non-uniqueness of our best-fit model, with an interplay between the depth to the shear plane, u bed, ice—rock mixture density and A, limits these conclusions.
It is interesting that rock glaciers are often observed to be thinner and flow more slowly than even small glaciers that can have surface velocities of tens to hundreds of meters per year. Rock glaciers may require a lower driving stress for deformation; our shallow rectangular model has a driving stress of about 0.7 bar; this should be compared with driving stresses of glaciers, which are on the order of 1–1.5 bar. Given this lower “pseudo-yield stress” and the greater average density of rock glaciers, Equation (3) indicates that rock glaciers should be softer yet flow more slowly in general, primarily because their thickness is limited by this lower pseudo-yield stress.
4.4. Mass balance of Fireweed rock glacier
For glaciers, mass balance and longitudinal changes in channel geometry control the longitudinal strain rate and emergence velocity (Reference NyePaterson, 1994). On this rock glacier, the patterns of longitudinal strain rate along the rock glacier (Fig. 6c), and patterns of the measured emergence velocity (Reference BuckiBucki, 2002) are different than those typically observed on glaciers. Thus we might expect that the mass-balance distribution of the rock glacier is different than that of a glacier in both the sources and distribution of accumulation, and the insulating or cooling effects of the debris mantle (Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllHarris and Pedersen, 1998). On a rock glacier, accumulation may not be limited to talus cones, as surface water (meteoric and/or melt) can freeze below the debris mantle along the length of the rock glacier and add ice to the mixture. Near-surface ablation is severely limited by the debris mantle over the entire length of the rock glacier. This distribution of mass balance can support the convergent flow observed at the terminus of FRG, which should be compared to glaciers that typically exhibit divergent flow as a response to ablation.
At the terminus, calving (and calving-induced melt ablation; Reference Elconin and LaChapelleElconin and LaChapelle, 1997) is a significant mechanism of mass loss that does not exist on other rock glaciers. As a result, other rock glaciers are likely much further from a steady-state length than FRG, and are subject to continuous advance (Reference KaufmannKonrad and Humphrey, 2000). We suggest that FRG is subject to periodic calving. The time to the next calving event can be estimated using the flux through the rectangular section at profile B (~5700 m3 a–1), and assuming that the terminus geometry (and glacier length) that existed prior to September 2000 is necessary (but not sufficient) for calving to occur. This calculation indicates that by fall 2003 the glacier may be primed for calving once again. Of course, a rainfall event of sufficient magnitude is likely required some time after that as well.
The mass contribution from the talus cones may also be investigated by considering the material flux at profile Reference HumlumB. Elconin and LaChapelle (1997) discuss the possible mechanisms for the accumulation of ice and rock at the talus cones. Here we address the volume of material that originates in these areas. We assume that any accumulation from the freezing of surface water under the debris mantle is small, and that the rock glacier is not changing in time. However, we do note that rock glaciers can exhibit significant changes in surface height over the entire rock glacier as shown by Reference HumlumKääb and others (1997). From air photographs, we estimate that the area of talus cones in contact with the rock glacier surface (those with accumulation potential) is roughly 100 000 m2. Based on our ice and rock flux estimate at profile B (~5700 m3 a–1) and our assumption that ablation is very small, this indicates that the annual average accumulation over the area of the talus cones is about 0.057 ma–1. Any surface water freezing would reduce this accumulation rate, as would any thinning at profile B.
Using the flux estimate at profile B, a debris content of ~50% and the aerial extent of the rock glacier basin (4.6 km2), we estimate a basin-average erosion rate of 0.6 mma–1. We note that this estimate does not include material that is washed away by the rock glacier’s drainage system. However, the proglacial stream has most often been observed to be clear and free of silt with the exception of periods immediately following a calving event. This erosion rate is limited by the estimate of debris content and the total flux estimated at profile B and compares to erosion rates determined for glaciers (Reference DrewryDrewry, 1986).
5. Conclusions
The flow of FRG is similar to that of a glacier in many ways, yet there are distinct differences. We have observed strong evidence of temporal variability, motion along a basal interface and internal deformation. However, the shape of the transverse velocity profile indicates that most of the motion occurs on and above a shear plane. This shear plane is situated about halfway down into the rock glacier cross-section. At least one-third of the motion is contributed by slip (localized deformation) on this plane, and the remainder can be accounted for by internal deformation of the mixture. Thus, the effective channel shape is best modeled by a rectangular subsection about 27 m deep in a parabolic channel with a 58 m center-line depth. Our best-fit model, which is necessarily non-unique in both the depth of the shear plane and the rheological parameters of the mixture (but constrained by reasonable geometries), implies that the ice—rock mixture is up to 7 times softer than clean ice at a temperature of –2°C. This is consistent with the observations of Reference Echelmeyer and WangEchelmeyer and Wang (1987) and Reference CohenCohen (2000). It is noteworthy that anomalous geophysical findings described in Reference Bucki, Echelmeyer and MacInnesBucki and others (2004) are consistent with the presence of a shear plane at about 27 m depth, and that such a flow discontinuity has been observed on other rock glaciers (e.g. Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllHaeberli and others, 1998; Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllHoelzle and others, 1998).
We note, however, that this model does not explain the observed velocity patterns at profile A, where there appears to be enhanced deformation in the ice-rich region relative to adjacent ice-poor regions. A possible explanation for this behavior is that enhanced basal motion may occur below this ice-rich flow as it overrides and displaces the middle flow near the terminus. This is suggested by the anomalous flow vectors on the east half of profile A (Fig. 5), which are directed 10° more westward than expected for channel convergence.
Our analyses also show that longitudinal stress gradients, the shape of the channel (for which f < 1), the increased density of the rock glacier material, and the mass of the debris mantle all significantly affect the flow of a rock glacier. It has been suggested that changes in mixture temperature may lead to seasonal or annual velocity variations, such as those we observed, through variations in the flow-law parameter. However, such temperature variations beneath a thick debris layer are likely to be small (Reference Haeberli, Hoelzle, Kääb, Keller and Vonder MühllHarris and Pedersen, 1998) and insufficient to cause recognizable variations in stiffness of the core of this rock glacier. We conclude that hydraulic conditions, both englacial and subglacial, likely contribute to short-term temporal variations of rock glacier flow, as they do in glaciers.
There appears to be a correlation among near-terminus temporal velocity variations, calving and precipitation. Our data show that large rainfall events may lead to terminus calving if the terminus geometry is favorable. This in turn enhances flow near the terminus because of an increase in longitudinal stress gradients caused by the steep, unsupported calving face (e.g. Reference Hooke, Dahlin and KauperHughes, 1986). The subsequent flow into the constricted valley and a diminishing terminal slope reduces this longitudinal force imbalance with time. The calving of this rock glacier is also an important mechanism of mass loss that is not generally found on other rock glaciers.
Acknowledgements
This study was supported by U.S. National Science Foundation grant NSF-OPP98 06648. We would like to thank D. Rosenkrans and the National Park Service for cooperation and support. We appreciate the contributions of C. Bucki, L. Cox, P. Del Vecchio, R. Elconin, L. Goodman, W. Harrison, D. Mouldry, K. Smith and M. Truffer. Tazlina, Choly, Baxter and McKenzie provided K-9 support. We would also like to thank B. Hallet and an anonymous reviewer for their insightful comments that helped improve the manuscript.












