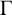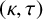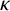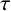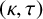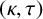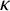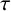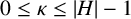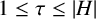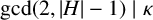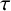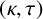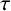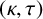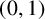1 Introduction
In the paper, all groups considered are finite groups with identity element denoted as
![]() $1$
, and all graphs considered are finite, undirected and simple. Let R be a subset of the vertex set of a graph
$1$
, and all graphs considered are finite, undirected and simple. Let R be a subset of the vertex set of a graph
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
a pair of nonnegative integers. We call R a
$\tau $
a pair of nonnegative integers. We call R a
![]() $(\kappa ,\tau )$
-regular set (or regular set for short if there is no need to emphasise the parameters
$(\kappa ,\tau )$
-regular set (or regular set for short if there is no need to emphasise the parameters
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
in the context) of
$\tau $
in the context) of
![]() $\Gamma $
if every vertex in R is adjacent to exactly
$\Gamma $
if every vertex in R is adjacent to exactly
![]() $\kappa $
vertices in R and every vertex outside R is adjacent to exactly
$\kappa $
vertices in R and every vertex outside R is adjacent to exactly
![]() $\tau $
vertices in R. In particular, we call R a perfect code of
$\tau $
vertices in R. In particular, we call R a perfect code of
![]() $\Gamma $
if
$\Gamma $
if
![]() $(\kappa ,\tau )=(0,1)$
and a total perfect code of
$(\kappa ,\tau )=(0,1)$
and a total perfect code of
![]() $\Gamma $
if
$\Gamma $
if
![]() $(\kappa ,\tau )=(1,1)$
. The concept of
$(\kappa ,\tau )=(1,1)$
. The concept of
![]() $(\kappa ,\tau )$
-regular set was introduced in [Reference Cardoso and Rama3] and further studied in [Reference Anđelić, Cardoso and Simić1, Reference Cardoso2, Reference Cardoso and Rama4, Reference Cardoso, Sciriha and Zerafa5]. Very recently, regular sets in Cayley graphs were studied in [Reference Wang, Xia and Zhou8, Reference Wang, Xia and Zhou9].
$(\kappa ,\tau )$
-regular set was introduced in [Reference Cardoso and Rama3] and further studied in [Reference Anđelić, Cardoso and Simić1, Reference Cardoso2, Reference Cardoso and Rama4, Reference Cardoso, Sciriha and Zerafa5]. Very recently, regular sets in Cayley graphs were studied in [Reference Wang, Xia and Zhou8, Reference Wang, Xia and Zhou9].
Let G be a group and X an inverse closed subset of
![]() $G\setminus \{1\}$
. The Cayley graph
$G\setminus \{1\}$
. The Cayley graph
![]() $\mathrm {Cay}(G,X)$
on G with connection set X is the graph with vertex set G and edge set
$\mathrm {Cay}(G,X)$
on G with connection set X is the graph with vertex set G and edge set
![]() $\{\{g,gx\}\mid g\in G, x\in X\}$
. A subset R of G is called a
$\{\{g,gx\}\mid g\in G, x\in X\}$
. A subset R of G is called a
![]() $(\kappa ,\tau )$
-regular set of G if there is a Cayley graph
$(\kappa ,\tau )$
-regular set of G if there is a Cayley graph
![]() $\Gamma $
on G such that R is a
$\Gamma $
on G such that R is a
![]() $(\kappa ,\tau )$
-regular set of
$(\kappa ,\tau )$
-regular set of
![]() $\Gamma $
. Regular sets of Cayley graphs are closely related to codes of groups. Let C and Y be two subsets of G and
$\Gamma $
. Regular sets of Cayley graphs are closely related to codes of groups. Let C and Y be two subsets of G and
![]() $\lambda $
a positive integer. If for every
$\lambda $
a positive integer. If for every
![]() $g\in G$
there exist precisely
$g\in G$
there exist precisely
![]() $\lambda $
pairs
$\lambda $
pairs
![]() $(c,y)\in C\times Y$
such that
$(c,y)\in C\times Y$
such that
![]() $g=cy$
, then C is called a code of G with respect to Y [Reference Green and Liebeck6]. In particular, if
$g=cy$
, then C is called a code of G with respect to Y [Reference Green and Liebeck6]. In particular, if
![]() $\lambda =1$
and Y is an inverse closed subset of G containing
$\lambda =1$
and Y is an inverse closed subset of G containing
![]() $1$
, then C is called a perfect code of G [Reference Huang, Xia and Zhou7]. Let H be a subgroup of G. It is straightforward to check that H is a
$1$
, then C is called a perfect code of G [Reference Huang, Xia and Zhou7]. Let H be a subgroup of G. It is straightforward to check that H is a
![]() $(0,\tau )$
-regular set of G if and only if H is a code of G with respect to some inverse closed subset of G. In fact, if H is a
$(0,\tau )$
-regular set of G if and only if H is a code of G with respect to some inverse closed subset of G. In fact, if H is a
![]() $(0,\tau )$
-regular set of the Cayley graph
$(0,\tau )$
-regular set of the Cayley graph
![]() $\mathrm {Cay}(G,X)$
, then H is a code of G with respect to
$\mathrm {Cay}(G,X)$
, then H is a code of G with respect to
![]() $Y:=X\cup Z$
for any inverse closed subset Z of H with cardinality
$Y:=X\cup Z$
for any inverse closed subset Z of H with cardinality
![]() $\tau $
. However, if H is a code of G with respect to Y, then H is a
$\tau $
. However, if H is a code of G with respect to Y, then H is a
![]() $(0,\tau )$
-regular set of the Cayley graph
$(0,\tau )$
-regular set of the Cayley graph
![]() $\mathrm {Cay}(G,X)$
, where
$\mathrm {Cay}(G,X)$
, where
![]() $X=Y\setminus H$
and
$X=Y\setminus H$
and
![]() $\tau ={\vert H\vert \vert Y\vert }/{|G|}$
.
$\tau ={\vert H\vert \vert Y\vert }/{|G|}$
.
It is natural to ask when a normal subgroup of a group is a regular set. This question was studied by Wang et al. in [Reference Wang, Xia and Zhou9]. They proved that, for any finite group G, if a nontrivial normal subgroup H of G is a perfect code of G, then for any pair of integers
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
with
$\tau $
with
![]() $0\leq \kappa \leq |H|-1$
,
$0\leq \kappa \leq |H|-1$
,
![]() $1\leq \tau \leq |H|$
and
$1\leq \tau \leq |H|$
and
![]() $\gcd (2,|H|-1)\mid \kappa $
, H is also a
$\gcd (2,|H|-1)\mid \kappa $
, H is also a
![]() $(\kappa ,\tau )$
-regular set of G. It was also shown in [Reference Wang, Xia and Zhou9] that there exist normal subgroups of some groups which are
$(\kappa ,\tau )$
-regular set of G. It was also shown in [Reference Wang, Xia and Zhou9] that there exist normal subgroups of some groups which are
![]() $(\kappa ,\tau )$
-regular sets for some pair of integers
$(\kappa ,\tau )$
-regular sets for some pair of integers
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
but not perfect codes of the group. In this paper, we extend the main results in [Reference Wang, Xia and Zhou9] by proving the following theorem.
$\tau $
but not perfect codes of the group. In this paper, we extend the main results in [Reference Wang, Xia and Zhou9] by proving the following theorem.
Theorem 1.1. Let G be a group and H a nontrivial normal subgroup of G. Let
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
be a pair of integers satisfying
$\tau $
be a pair of integers satisfying
![]() $0\leq \kappa \leq |H|-1$
,
$0\leq \kappa \leq |H|-1$
,
![]() $1\leq \tau \leq |H|$
and
$1\leq \tau \leq |H|$
and
![]() $\gcd (2,|H|-1)\mid \kappa $
. The following two statements hold:
$\gcd (2,|H|-1)\mid \kappa $
. The following two statements hold:
-
(i) if
 $\tau $
is even, then H is a
$\tau $
is even, then H is a
 $(\kappa ,\tau )$
-regular set of G;
$(\kappa ,\tau )$
-regular set of G; -
(ii) if
 $\tau $
is odd, then H is a
$\tau $
is odd, then H is a
 $(\kappa ,\tau )$
-regular set of G if and only if it is a perfect code of G.
$(\kappa ,\tau )$
-regular set of G if and only if it is a perfect code of G.
It was proved in [Reference Huang, Xia and Zhou7, Theorem 2.2] that a normal subgroup H of G is a perfect code of G if and only if
-
# for any
 $g\in G$
with
$g\in G$
with
 $g^{2}\in H$
, there exists
$g^{2}\in H$
, there exists
 $h\in H$
such that
$h\in H$
such that
 $(gh)^2=1$
.
$(gh)^2=1$
.
Note that condition # always holds if H is of odd order or odd index [Reference Huang, Xia and Zhou7, Corollary 2.3]. Therefore, Theorem 1.1 has the following direct corollary, which is also an immediate consequence of [Reference Huang, Xia and Zhou7, Corollary 2.3] and [Reference Wang, Xia and Zhou9, Theorem 1.2].
Corollary 1.2. Let G be a group and H a nontrivial normal subgroup of G. If either
![]() $|H|$
or
$|H|$
or
![]() $|G/H|$
is odd, then H is a
$|G/H|$
is odd, then H is a
![]() $(\kappa ,\tau )$
-regular set of G for every pair of integers
$(\kappa ,\tau )$
-regular set of G for every pair of integers
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
satisfying
$\tau $
satisfying
![]() $0\leq \kappa \leq |H|-1$
,
$0\leq \kappa \leq |H|-1$
,
![]() $1\leq \tau \leq |H|$
and
$1\leq \tau \leq |H|$
and
![]() $\gcd (2,|H|-1)\mid \kappa $
.
$\gcd (2,|H|-1)\mid \kappa $
.
Remark 1.3. It is a challenging question whether Theorem 1.1 and Corollary 1.2 can be generalised to nonnormal subgroups H of G.
Remark 1.4. Let H be a nontrivial normal subgroup of G of even order not satisfying condition #. Let
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
be a pair of integers satisfying
$\tau $
be a pair of integers satisfying
![]() $0\leq \kappa \leq |H|-1$
,
$0\leq \kappa \leq |H|-1$
,
![]() $2\leq \tau \leq |H|$
and
$2\leq \tau \leq |H|$
and
![]() $2\mid \tau $
. Then Theorem 1.1(i) and [Reference Huang, Xia and Zhou7, Theorem 2.2] imply that H is a
$2\mid \tau $
. Then Theorem 1.1(i) and [Reference Huang, Xia and Zhou7, Theorem 2.2] imply that H is a
![]() $(\kappa ,\tau )$
-regular set but not a perfect code of G.
$(\kappa ,\tau )$
-regular set but not a perfect code of G.
2 Proof of Theorem 1.1
Throughout this section, we use
![]() $\dot \bigcup _{i=1}^{n}S_{i}$
to denote the union of the pair-wise disjoint sets
$\dot \bigcup _{i=1}^{n}S_{i}$
to denote the union of the pair-wise disjoint sets
![]() $S_1,S_2,\ldots ,S_n$
. Let G be a group and H a nontrivial normal subgroup of G. Let
$S_1,S_2,\ldots ,S_n$
. Let G be a group and H a nontrivial normal subgroup of G. Let
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
be a pair of integers satisfying
$\tau $
be a pair of integers satisfying
![]() $0\leq \kappa \leq |H|-1$
,
$0\leq \kappa \leq |H|-1$
,
![]() $1\leq \tau \leq |H|$
and
$1\leq \tau \leq |H|$
and
![]() $\gcd (2,|H|-1)\mid \kappa $
. We first prove three lemmas and then complete the proof of Theorem 1.1.
$\gcd (2,|H|-1)\mid \kappa $
. We first prove three lemmas and then complete the proof of Theorem 1.1.
Lemma 2.1. If
![]() $\tau $
is even, then H is a
$\tau $
is even, then H is a
![]() $(0,\tau )$
-regular set of G.
$(0,\tau )$
-regular set of G.
Proof. Let
![]() $A:=\{1,a_{1},\ldots ,a_{s}\}$
be a left transversal of H in G. Assume that the number of involutions contained in
$A:=\{1,a_{1},\ldots ,a_{s}\}$
be a left transversal of H in G. Assume that the number of involutions contained in
![]() $a_{i}H$
is
$a_{i}H$
is
![]() $n_{i}$
for
$n_{i}$
for
![]() $1\leq i\leq s$
. Let
$1\leq i\leq s$
. Let
![]() $\sigma $
be a permutation on
$\sigma $
be a permutation on
![]() $\{1,\ldots ,s\}$
such that
$\{1,\ldots ,s\}$
such that
![]() $a_{i}^{-1}H=a_{\sigma (i)}H$
. Since H is normal in G,
$a_{i}^{-1}H=a_{\sigma (i)}H$
. Since H is normal in G,
It follows that
![]() $\sigma $
is the identity permutation or an involution. Assume that
$\sigma $
is the identity permutation or an involution. Assume that
![]() $\sigma $
fixes t integers in
$\sigma $
fixes t integers in
![]() $\{1,\ldots ,s\}$
. Then
$\{1,\ldots ,s\}$
. Then
![]() $0\leq t\leq s$
and
$0\leq t\leq s$
and
![]() $s-t$
is even. Set
$s-t$
is even. Set
![]() $\ell :={(s-t)}/{2}$
. Without loss of generality, we assume that
$\ell :={(s-t)}/{2}$
. Without loss of generality, we assume that
 $$ \begin{align*} \sigma(i)=\begin{cases} i & \text{if}~i\leq t, \\ i+\ell & \text{if}~t<i\leq t+\ell,\\ i-\ell & \text{if}~t+\ell<i\leq s.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \sigma(i)=\begin{cases} i & \text{if}~i\leq t, \\ i+\ell & \text{if}~t<i\leq t+\ell,\\ i-\ell & \text{if}~t+\ell<i\leq s.\\ \end{cases} \end{align*} $$
Then
![]() $a_iH$
is inverse closed if
$a_iH$
is inverse closed if
![]() $i\leq t$
and
$i\leq t$
and
![]() $(a_{t+j}H)^{-1}=a_{t+j+\ell }H$
for every positive integer j not greater than
$(a_{t+j}H)^{-1}=a_{t+j+\ell }H$
for every positive integer j not greater than
![]() $\ell $
. In particular,
$\ell $
. In particular,
![]() $n_{i}=0$
if
$n_{i}=0$
if
![]() $i>t$
. For every
$i>t$
. For every
![]() $i\in \{1,\ldots ,s\}$
, take a subset
$i\in \{1,\ldots ,s\}$
, take a subset
![]() $X_i$
of
$X_i$
of
![]() $a_iH$
of cardinality
$a_iH$
of cardinality
![]() $\tau $
by the following rules:
$\tau $
by the following rules:
-
• if
 $i\leq t$
and
$i\leq t$
and
 $n_i\geq \tau $
, then
$n_i\geq \tau $
, then
 $X_i$
consists of exactly
$X_i$
consists of exactly
 $\tau $
involutions;
$\tau $
involutions; -
• if
 $i\leq t$
,
$i\leq t$
,
 $n_i<\tau $
and
$n_i<\tau $
and
 $\tau -n_i$
is even, then
$\tau -n_i$
is even, then
 $X_i$
consists of
$X_i$
consists of
 $n_i$
involutions and
$n_i$
involutions and
 ${(\tau -n_i)}/{2}$
pairs of mutually inverse elements of order greater than
${(\tau -n_i)}/{2}$
pairs of mutually inverse elements of order greater than
 $2$
;
$2$
; -
• if
 $i\leq t$
,
$i\leq t$
,
 $n_i<\tau $
and
$n_i<\tau $
and
 $\tau -n_i$
is odd, then
$\tau -n_i$
is odd, then
 $X_i$
consists of
$X_i$
consists of
 $n_i-1$
involutions and
$n_i-1$
involutions and
 ${(\tau +1-n_i)}/{2}$
pairs of mutually inverse elements of order greater than
${(\tau +1-n_i)}/{2}$
pairs of mutually inverse elements of order greater than
 $2$
;
$2$
; -
• if
 $t<i\leq t+\ell $
, then
$t<i\leq t+\ell $
, then
 $X_i$
consists of exactly
$X_i$
consists of exactly
 $\tau $
elements of order greater than
$\tau $
elements of order greater than
 $2$
;
$2$
; -
• if
 $i> t+\ell $
, then set
$i> t+\ell $
, then set
 $X_i=X_{i-\ell }^{-1}$
.
$X_i=X_{i-\ell }^{-1}$
.
Note that
![]() $X_1,\ldots ,X_s$
are pair-wise disjoint. Set
$X_1,\ldots ,X_s$
are pair-wise disjoint. Set
![]() $X=\dot \bigcup _{i=1}^{s}X_{i}$
. Then X is an inverse closed subset of G satisfying
$X=\dot \bigcup _{i=1}^{s}X_{i}$
. Then X is an inverse closed subset of G satisfying
![]() $X\cap H=\emptyset $
and
$X\cap H=\emptyset $
and
![]() $\vert X\cap gH\vert =\tau $
for every
$\vert X\cap gH\vert =\tau $
for every
![]() $g\in G\setminus H$
. It follows that H is a
$g\in G\setminus H$
. It follows that H is a
![]() $(0,\tau )$
-regular set of the Cayley graph
$(0,\tau )$
-regular set of the Cayley graph
![]() $\mathrm {Cay}(G,X)$
and therefore a
$\mathrm {Cay}(G,X)$
and therefore a
![]() $(0,\tau )$
-regular set of G.
$(0,\tau )$
-regular set of G.
Lemma 2.2. If
![]() $\tau $
is odd, then H is a
$\tau $
is odd, then H is a
![]() $(0,\tau )$
-regular set of G if and only if it is a perfect code of G.
$(0,\tau )$
-regular set of G if and only if it is a perfect code of G.
Proof. The sufficiency follows from [Reference Wang, Xia and Zhou9, Theorem 1.2]. Now we prove the necessity. Let H be a
![]() $(0,\tau )$
-regular set of the Cayley graph
$(0,\tau )$
-regular set of the Cayley graph
![]() $\mathrm {Cay}(G,X)$
. Then
$\mathrm {Cay}(G,X)$
. Then
![]() $X=X^{-1}$
,
$X=X^{-1}$
,
![]() $X\cap H=\emptyset $
and
$X\cap H=\emptyset $
and
![]() $\vert X\cap gH\vert =\tau $
for every
$\vert X\cap gH\vert =\tau $
for every
![]() $g\in G\setminus H$
. Let
$g\in G\setminus H$
. Let
![]() $A:=\{1,a_{1},\ldots ,a_{s}\}$
be a left transversal of H in G and set
$A:=\{1,a_{1},\ldots ,a_{s}\}$
be a left transversal of H in G and set
![]() $X_i=X\cap a_iH$
for every
$X_i=X\cap a_iH$
for every
![]() $i\in \{1,2,\ldots ,s\}$
. Then
$i\in \{1,2,\ldots ,s\}$
. Then
![]() $X=\dot \bigcup _{i=1}^{s}X_{i}$
. If
$X=\dot \bigcup _{i=1}^{s}X_{i}$
. If
![]() $X_{i}$
contains an involution for each
$X_{i}$
contains an involution for each
![]() $i\in \{1,\ldots ,s\}$
, then H is a perfect code of G with respect to
$i\in \{1,\ldots ,s\}$
, then H is a perfect code of G with respect to
![]() $\{1,y_1,\ldots ,y_s\}$
, where
$\{1,y_1,\ldots ,y_s\}$
, where
![]() $y_i$
is an involution in
$y_i$
is an involution in
![]() $X_i$
,
$X_i$
,
![]() $i=1,\ldots ,s$
. Now we assume that there exists at least one integer
$i=1,\ldots ,s$
. Now we assume that there exists at least one integer
![]() $k\in \{1,\ldots ,s\}$
such that
$k\in \{1,\ldots ,s\}$
such that
![]() $X_{k}$
contains no involution. Then
$X_{k}$
contains no involution. Then
![]() $x^{-1}\neq x$
for every element
$x^{-1}\neq x$
for every element
![]() $x\in X_{k}$
. It follows that
$x\in X_{k}$
. It follows that
![]() $|X_{k}\cup X_{k}^{-1}|$
is even. Since
$|X_{k}\cup X_{k}^{-1}|$
is even. Since
![]() $|X_{k}|=\tau $
and
$|X_{k}|=\tau $
and
![]() $\tau $
is odd, we get
$\tau $
is odd, we get
![]() $X_k\neq X_k^{-1}$
. Since H is normal in G, we obtain
$X_k\neq X_k^{-1}$
. Since H is normal in G, we obtain
![]() $(a_kH)^{-1}=(Ha_k)^{-1}=a_k^{-1}H$
. Assume that
$(a_kH)^{-1}=(Ha_k)^{-1}=a_k^{-1}H$
. Assume that
![]() $a_k^{-1}H=a_{j}H$
for some
$a_k^{-1}H=a_{j}H$
for some
![]() $j\in \{1,\ldots ,s\}$
. Then
$j\in \{1,\ldots ,s\}$
. Then
![]() $X_{k}^{-1}\subseteq a_{j}H$
. Since
$X_{k}^{-1}\subseteq a_{j}H$
. Since
![]() $X=\dot \bigcup _{i=1}^{s}X_{i}$
and
$X=\dot \bigcup _{i=1}^{s}X_{i}$
and
![]() $X^{-1}=X$
, we conclude that
$X^{-1}=X$
, we conclude that
![]() $X_k^{-1}=X_{j}$
. Therefore, without loss of generality, we can assume that
$X_k^{-1}=X_{j}$
. Therefore, without loss of generality, we can assume that
![]() $X_i^{-1}=X_{i+\ell }$
if
$X_i^{-1}=X_{i+\ell }$
if
![]() $1\leq i\leq \ell $
and
$1\leq i\leq \ell $
and
![]() $X_i^{-1}=X_{i}$
if
$X_i^{-1}=X_{i}$
if
![]() $2\ell < i\leq s$
, where
$2\ell < i\leq s$
, where
![]() $\ell $
is a positive integer not greater than
$\ell $
is a positive integer not greater than
![]() ${s}/{2}$
. Note that
${s}/{2}$
. Note that
![]() $X_{i}$
contains at least one involution if
$X_{i}$
contains at least one involution if
![]() $X_i^{-1}=X_{i}$
(as it is of odd cardinality). For every
$X_i^{-1}=X_{i}$
(as it is of odd cardinality). For every
![]() $i\in \{1,\ldots ,s\}$
, take an element
$i\in \{1,\ldots ,s\}$
, take an element
![]() $y_i\in X_i$
by the following rules:
$y_i\in X_i$
by the following rules:
-
•
 $y_i$
is an arbitrary element in
$y_i$
is an arbitrary element in
 $X_i$
if
$X_i$
if
 $i\leq \ell $
;
$i\leq \ell $
; -
•
 $y_i=y_{i-\ell }^{-1}$
if
$y_i=y_{i-\ell }^{-1}$
if
 $\ell <i\leq 2\ell $
;
$\ell <i\leq 2\ell $
; -
•
 $y_i$
is an involution if
$y_i$
is an involution if
 $i>2\ell $
.
$i>2\ell $
.
Then H is a perfect code of G with respect to
![]() $\{1,y_1,\ldots ,y_s\}$
.
$\{1,y_1,\ldots ,y_s\}$
.
Lemma 2.3.
H is a
![]() $(\kappa ,\tau )$
-regular set of G if and only if H is a
$(\kappa ,\tau )$
-regular set of G if and only if H is a
![]() $(0,\tau )$
-regular set of G.
$(0,\tau )$
-regular set of G.
Proof. (
![]() $\Rightarrow $
) Let H be a
$\Rightarrow $
) Let H be a
![]() $(\kappa ,\tau )$
-regular set of the Cayley graph
$(\kappa ,\tau )$
-regular set of the Cayley graph
![]() $\mathrm {Cay}(G,X)$
. Then
$\mathrm {Cay}(G,X)$
. Then
![]() $|H\cap X|=\kappa $
and
$|H\cap X|=\kappa $
and
![]() $|gH\cap X|=\tau $
for every
$|gH\cap X|=\tau $
for every
![]() $g\in G\setminus H$
. Set
$g\in G\setminus H$
. Set
![]() $Y=X\setminus H$
. Then
$Y=X\setminus H$
. Then
![]() $|H\cap Y|=0$
and
$|H\cap Y|=0$
and
![]() $|gH\cap Y|=\tau $
for every
$|gH\cap Y|=\tau $
for every
![]() $g\in G\setminus H$
. Since
$g\in G\setminus H$
. Since
![]() $X^{-1}=X$
and
$X^{-1}=X$
and
![]() $H^{-1}=H$
, we get
$H^{-1}=H$
, we get
![]() $Y^{-1}=Y$
. It follows that H is a
$Y^{-1}=Y$
. It follows that H is a
![]() $(0,\tau )$
-regular set of the Cayley graph
$(0,\tau )$
-regular set of the Cayley graph
![]() $\mathrm {Cay}(G,Y)$
and therefore a
$\mathrm {Cay}(G,Y)$
and therefore a
![]() $(0,\tau )$
-regular set of G.
$(0,\tau )$
-regular set of G.
(
![]() $\Leftarrow $
) Let H be a
$\Leftarrow $
) Let H be a
![]() $(0,\tau )$
-regular set of the Cayley graph
$(0,\tau )$
-regular set of the Cayley graph
![]() $\mathrm {Cay}(G,Y)$
. Then
$\mathrm {Cay}(G,Y)$
. Then
![]() $|H\cap Y|=0$
and
$|H\cap Y|=0$
and
![]() $|gH\cap Y|=\tau $
for every
$|gH\cap Y|=\tau $
for every
![]() $g\in G\setminus H$
. Let m be the number of elements contained in H of order greater than
$g\in G\setminus H$
. Let m be the number of elements contained in H of order greater than
![]() $2$
. Then m is even and the number of involutions contained in H is
$2$
. Then m is even and the number of involutions contained in H is
![]() $|H|-1-m$
. Recall that
$|H|-1-m$
. Recall that
![]() $0\leq \kappa \leq |H|-1$
and
$0\leq \kappa \leq |H|-1$
and
![]() $\gcd (2,|H|-1)\mid \kappa $
. If
$\gcd (2,|H|-1)\mid \kappa $
. If
![]() $\kappa $
is odd, then
$\kappa $
is odd, then
![]() $|H|$
is even and therefore contains at least one involution. Take an inverse closed subset Z of H of cardinality
$|H|$
is even and therefore contains at least one involution. Take an inverse closed subset Z of H of cardinality
![]() $\kappa $
by the following rules:
$\kappa $
by the following rules:
-
• if
 $m\geq \kappa $
and
$m\geq \kappa $
and
 $\kappa $
is even, then Z consists of exactly
$\kappa $
is even, then Z consists of exactly
 ${\kappa }/{2}$
pairs of mutually inverse elements of order greater than
${\kappa }/{2}$
pairs of mutually inverse elements of order greater than
 $2$
;
$2$
; -
• if
 $m\geq \kappa $
and
$m\geq \kappa $
and
 $\kappa $
is odd, then Z consists of
$\kappa $
is odd, then Z consists of
 ${(\kappa -1)}/{2}$
pairs of mutually inverse elements of order greater than
${(\kappa -1)}/{2}$
pairs of mutually inverse elements of order greater than
 $2$
and one involution;
$2$
and one involution; -
• if
 $m<\kappa $
, then Z consists of
$m<\kappa $
, then Z consists of
 ${m}/{2}$
pairs of mutually inverse elements of order greater than
${m}/{2}$
pairs of mutually inverse elements of order greater than
 $2$
and
$2$
and
 $\kappa -m$
involutions.
$\kappa -m$
involutions.
Set
![]() $X=Y\cup Z$
. Then
$X=Y\cup Z$
. Then
![]() $|H\cap X|=\kappa $
and
$|H\cap X|=\kappa $
and
![]() $|gH\cap X|=\tau $
for every
$|gH\cap X|=\tau $
for every
![]() $g\in G\setminus H$
. Therefore, H is a
$g\in G\setminus H$
. Therefore, H is a
![]() $(\kappa ,\tau )$
-regular set of the Cayley graph
$(\kappa ,\tau )$
-regular set of the Cayley graph
![]() $\mathrm {Cay}(G,X)$
and therefore a
$\mathrm {Cay}(G,X)$
and therefore a
![]() $(\kappa ,\tau )$
-regular set of G.
$(\kappa ,\tau )$
-regular set of G.