No CrossRef data available.
Article contents
Effective bounds on differences of singular moduli that are S-units
Part of:
Abelian varieties and schemes
Arithmetic algebraic geometry
Algebraic number theory: global fields
Published online by Cambridge University Press: 22 September 2022
Abstract
Given a singular modulus
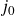$j_0$
and a set of rational primes S, we study the problem of effectively determining the set of singular moduli j such that
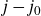$j-j_0$
is an S-unit. For every
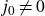$j_0 \neq 0$
, we provide an effective way of finding this set for infinitely many choices of S. The same is true if
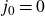$j_0=0$
and we assume the Generalised Riemann Hypothesis. Certain numerical experiments will also lead to the formulation of a “uniformity conjecture” for singular S-units.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 2 , March 2023 , pp. 415 - 450
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
References
Allombert, B., Bilu, Y. and Pizarro-Madariaga, A.. CM-points on straight lines. Analytic Number Theory (Springer, Cham, 2015), 1–18 (19).Google Scholar
Bilu, Y., Habegger, P. and Kuhne, L.. No singular modulus is a unit. Internat. Math. Res. Notices 2020 (24) (2018), 10005–10041.CrossRefGoogle Scholar
Bilu, Y., Masser, D. and Zannier, U.. An effective theorem of André for CM-points on a plane curve. Math. Proc. Camb. Phil. Soc. 154.1 (2013), 145–152.Google Scholar
Bombieri, E. and Gubler, W.. Heights in Diophantine geometry. New Mathematical Monographs, vol. 4 (Cambridge University Press, Cambridge, 2006), pp. xvi+652.Google Scholar
Bosch, S., Lutkebohmert, W. and Raynaud, M.. Néron models. Ergeb. Math. Grenzgeb. 21 (3) [Results in Mathematics and Related Areas (3)] (Springer-Verlag, Berlin, 1990), pp. x+325.Google Scholar
Cai, Y.. Bounding the difference of two singular moduli. Moscow Journal of Combinatorics and Number Theory 10.2 (2021), 95–110.Google Scholar
Campagna, F.. Arithmetic and diophantine properties of elliptic curves with complex multiplication. PhD. thesis. University of Copenhagen (2021).Google Scholar
Campagna, F.. On singular moduli that are S-units. Manuscripta Math. 166.1-2 (2021), 73–90.Google Scholar
Colmez, P.. Sur la hauteur de Faltings des variétés abéliennes à multiplication complexe. Compositio Math. 111.3 (1998), 359–368.Google Scholar
Conrad, B.. Gross-Zagier revisited. Heegner points and Rankin L-series. Math. Sci. Res. Inst. Publ. vol. 49. With an appendix by W. R. Mann (Cambridge University Press, Cambridge, 2004), pp. 67–163.Google Scholar
Cox, D. A.. Primes of the form
$x^2 + ny^2$
. Second edition. Pure and Applied Mathematics (Hoboken). Fermat, class field theory, and complex multiplication (John Wiley & Sons, Inc., Hoboken, NJ, 2013), pp. xviii+356.Google Scholar
$x^2 + ny^2$
. Second edition. Pure and Applied Mathematics (Hoboken). Fermat, class field theory, and complex multiplication (John Wiley & Sons, Inc., Hoboken, NJ, 2013), pp. xviii+356.Google ScholarDeligne, P.. Preuve des conjectures de Tate et de Shafarevitch (d’après G. Faltings). Seminar Bourbaki, Vol. 1983/84. (1985), 25–41.Google Scholar
Deuring, M.. “Die Typen der Multiplikatorenringe elliptischer Funktionenkörper”. Abhandlungen aus dem mathematischen Seminar der Universität Hamburg. Vol. 14.1 (Springer 1941), pp. 197–272.Google Scholar
Faltings, G.. “Endlichkeitssätze für abelsche Varietäten über Zahlkörpern”. Invent. Math. 73.3 (1983), 349–366.Google Scholar
Faye, B. and Riffaut, A.. Fields generated by sums and products of singular moduli. J. Number Theory 192 (2018), 37–46.Google Scholar
Frei, G.. “Heinrich Weber and the emergence of class field theory”. The History of Modern Mathematics, Vol. I (Poughkeepsie, NY, 1989) (Academic Press, Boston, MA, 1989), pp. 425–450.Google Scholar
Gaudron, É. and Remond, G.. Théorème des périodes et degrés minimaux d’isogénies. Comment. Math. Helv. 89.2 (2014), 343–403.Google Scholar
Granville, A. and Stark, H. M.. abc implies no “Siegel zeros” for L-functions of characters with negative discriminant. Invent. Math. 139.3 (2000), 509–523.Google Scholar
Gross, B. H.. Heights and the special values of L-series. Number theory (Montreal, Que., 1985). Vol. 7. CMS Conf. Proc. Amer. Math. Soc. (Providence, RI, 1987), pp. 115–187.Google Scholar
Gross, B. H.. On canonical and quasicanonical liftings. Invent. Math. 84.2 (1986), 321–326.Google Scholar
Gross, B. H. and Zagier, D. B.. On singular moduli. J. Reine Angew. Math. 355 (1985), pp. 191–220.Google Scholar
Habegger, P.. Weakly bounded height on modular curves. Acta Math. Vietnam. 35.1 (2010), 43–69.Google Scholar
Habegger, P.. Singular moduli that are algebraic units. Algebra Number Theory 9.7 (2015), 1515–1524.Google Scholar
Halter-Koch, F.. Geschlechtertheorie der Ringklassenkörper. J. Reine Angew. Math. 250 (1971), 107–108.Google Scholar
Herrero, S., Menares, R. and Rivera–Letelier, J.. p-adic distribution of CM points and Hecke orbits I: Convergence towards the Gauss point. Algebra Number Theory 14.5 (2020), 1239–1290.CrossRefGoogle Scholar
Herrero, S., Menares, R. and Rivera–Letelier, J.. p-Adic distribution of CM points and Hecke orbits. II: Linnik equidistribution on the supersingular locus. arXiv:2102.04865 (2021).CrossRefGoogle Scholar
Herrero, S., Menares, R. and Rivera–Letelier, J.. There are at most finitely many singular moduli that are S-units. arXiv:2102.05041 (2021).Google Scholar
Ihara, Y.. On the Euler-Kronecker constants of global fields and primes with small norms. Algebraic geometry and number theory.
Progr. Math. vol. 253, (Birkhauser Boston, Boston, MA, 2006), pp. 407–451.Google Scholar
Kühne, L.. An effective result of André–Oort type. Ann. of Math. (2) 176.1 (2012), 651–671.Google Scholar
Kühne, L.. An effective result of André–Oort type II. Acta Arith. 161.1 (2013), 1–19.CrossRefGoogle Scholar
Lang, S.. Elliptic functions. Second edition. Vol. 112 (Springer, New York, NY, 1987).Google Scholar
Lang, S.. Algebraic number theory. Second edition. Vol. 110. Graduate Texts in Mathematics (Springer-Verlag, New York, 1994), xiv+357.Google Scholar
Lauter, K. and Viray, B.. On singular moduli for arbitrary discriminants. Internet. Math. Res. Not. IMRN 19 (2015), 9206–9250.Google Scholar
Li, Y.. Singular units and isogenies between CM elliptic curves. Compositio. Math. 157.5 (2021), 1022–1035.Google Scholar
Mourtada, M. and Kumar Murty, V.. Omega theorems for
$(L/L^{\prime})(1, \chi_{D})$
. Int. J. Number Theory 9.3 (2013), 561–581.Google Scholar
$(L/L^{\prime})(1, \chi_{D})$
. Int. J. Number Theory 9.3 (2013), 561–581.Google ScholarNakkajima, Y. and Taguchi, Y.. A generalisation of the Chowla-Selberg formula. J. Reine Angew.
Math. 419 (1991), 119–124.Google Scholar
Neukirch, J.. Algebraic number theory. Vol. 322. Math. Wiss. [Fundamental Principles of Mathematical Sciences]. (Springer-Verlag, Berlin, 1999), pp. xviii+571.Google Scholar
Pazuki, F.. Modular invariants and isogenies. Int. J. Number Theory 15.3 (2019), 569–584.Google Scholar
The Sage Developers. SageMath, the Sage Mathematics Software System (Version 8.9) (2019).Google Scholar
Serre, J.–P. and Tate, J.. Good reduction of abelian varieties. Ann. of Math. (2) 88 (1968), 492–517.Google Scholar
Shimura, G.. Abelian varieties with complex multiplication and modular functions. Princeton Mathematical Series, vol. 46 (Princeton University Press, Princeton, NJ, 1998), pp. xvi+218.Google Scholar
Silverman, J. H.. Advanced topics in the arithmetic of elliptic curves. Graduate Texts in Mathematics, vol. 151 (Springer-Verlag, New York, 1994), pp. xiv+525.CrossRefGoogle Scholar
Silverman, J. H.. The arithmetic of elliptic curves. Second edition. Graduate Texts in Mathematics, vol. 106 (Springer, Dordrecht, 2009), pp. xx+513.Google Scholar
Voight, J.. Quaternion algebras. First edition. Graduate Texts in Mathematics, vol. 288 (Springer International Publishing, 2021), pp. XXIII, 885.Google Scholar
Weinberger, P. J.. Exponents of the class groups of complex quadratic fields. Acta Arith. 22 (1973), 117–124.Google Scholar