Introduction
A total of 411 TWERLE balloons were launched in the southern hemisphere during the second half of 1975 (TWERLE Team 1977). These superpressure balloons floated at a nominal density level of 0.25 kg m−3, which, over Antarctica, corresponds to 12.5 km. Each balloon carried three sensors: radar altimeter, ambient pressure, and temperature. A balloon and its payload are shown in Figure 1. As long as the solar panel was sufficiently illuminated, each balloon transmitted information from the three sensors once every minute. The transmissions were received by the Nimbus-5 satellite whenever the satellite was within sight of the balloon. When the satellite subtrack passed within a few degrees from the balloon (overhead pass), the satellite was within sight of the balloon for about 20 min, out of which 15 transmissions, 1 min apart, were recorded. Non-overhead passes (slanted passes) were seen for a shorter period. The shortest passes used were of 4 min duration. The radio frequency of the balloon, when received by the satellite, was shifted by the Doppler effect. The change in the Doppler shift along the pass was used to calculate the balloon's position. Two consecutive passes yielded a wind velocity. Due to the near-polar orbit of Nimbus-6, the number of passes d−1 increased from two or three for a balloon near the equator, to 13 or 14 (i.e. all the passes) near the pole. Consecutive passes were 105 min apart.

Fig.1. The TWERLE balloon.
During November 1975 to March 1976, in addition to the continuous coverage by the satellite of nearpolar balloons, two more factors contributed to the large amount of TWERLE data obtained over Antarctica. These are the 24 h d−1 illumination of the solar panels and the high concentration of balloons in the area. The average life of a balloon during TWERLE was slightly more than two months, some balloons lasting more than one year. The launching strategy and the general circulation at balloon height caused a typical daily concentration of about 40 balloons south of 45°S, during December 1975 to February 1976. Many of these balloons traversed the Antarctic continent. The extent of Antarctic coverage by TWERLE balloons was described by Reference Levanon, Julian and SuomiLevanon and others (1977). Preliminary results of ice-elevation data from TWERLE balloons were reported by Reference Levanon and BentleyLevanon and Bentley (1979). In the following discussion, the data analysis will be reviewed and final results will be given.
1. Data analysis
In order to obtain the surface elevation from the altimeter readings, it is necessary to know the altitude of the balloon above sea-level. Constant altitude could not be assumed because (1) the altitude of a constant-density level is not constant, and (2) the equilibrium density of the balloon changes, following diurnal cycles. What can be assumed constant, for several hours at least, is the altitude above sea-level of a pressure level along the balloon trajectory. This is the result of the quasi-geostrophic nature of the wind. In other words, the balloon, which follows the wind, is moving parallel to the isobars. It was concluded that the altitude of the balloon above sea-level could be calculated if the altitude of a reference pressure surface above the balloon subtrack was known once per day. 150 mbar was chosen as this reference pressure because it is the standard radiosonde level nearest to the balloon flight level.
Using TWERLE balloons and the radiosonde data, 150 mbar pressure maps were prepared daily from 16 November 1975 to 16 March 1976 (Reference Levanon and JulianLevanon and Julian 1980). TWERLE balloons which were not over the sea yielded wind data only toward the generation of these maps. Typically, the balloons near Antarctica floated 0.5 km below 150 mbar. Therefore, it was permissible to assign the wind at the balloon level to the 150 mbar level. It also justified using the temperature at the balloon level as the average temperature of the layer to 150 mbar. All the daily maps were for 1200 GMT. A 150 mbar elevation history, along the track of each balloon, was prepared from these maps. Spline interpolation was used to give continuous data between the 1200 GMT samples. Thus, the altitude of the 150 mbar surface above each balloon track was available at any point along its traverse. This information, together with readings from the three sensors, makes it possible to obtain the icesurface elevation.
The relation between the surface elevation, the altitude of the 150 mbar pressure surface, and the altimeter reading is
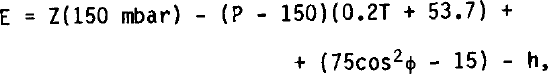
where E is the surface elevation in m a.s.l., Z(150 mbar) is the altitude of the 150 mbar surface in geopotential metres, P is the pressure sensor reading in mbar, T is the ambient temperature reading in °C, Ø is the latitude, and h is the altimeter reading in metres.
2. Sensor data examples
Two examples demonstrate typical sensor readings. Both were selected because they include some special phenomena.
Two examples demonstrate typical sensor readings. Both were selected because they include some special phenomena.
The lower half of Figure 2 gives the pressure and altimeter readings during a 19 min pass, in which balloon 1177 happened to cross the edge of the Sulzberger Ice Shelf. The upper half of Figure 2 presents the corresponding balloon track. Point A corresponds to the position of the balloon at the beginning of the satellite pass, point C to the end of the pass, and point D to the beginning of the next pass. The pressure sensor readings during the pass are very stable, indicating constant balloon altitude a.s.l. The altimeter readings, which were drawn to scale (50 m mbar"1), show a distinct step of 41 m near point B, when the balloon apparently crossed from the sea to the ice shelf. In this example, the overice altimeter readings are more stable than the overwater readings, which may be due to rough ocean surface or pack ice.

Fig.2. Data from one pass of balloon 1177, crossing from the sea to the Sulzberger Ice Shelf.
Figure 3 includes data from seven passes of balloon 77, traversing the Ronne Ice Shelf. There is a gap of two passes after the first one. The remaining six passes are consecutive. The first two passes in the figure are over-water, and the remaining five passes are over the ice shelf. The special phenomenon in this figure is the fact that during the first two over-ice passes, the altimeter locked to the bottom reflections of the ice shelf. This fact is indicated by the additional 220 m in the altimeter readings, while the pressure readings remained constant. Assuming velocity of propagation in ice of 168 m us"1, the added delay corresponds to an ice thickness of 130 m. The phenomenon of altimeter locking to the bottom reflection occurred rarely, and only near the edge of the Ronne Ice Shelf. It indicates an extremely specular bottom surface, and relatively weak ice attenuation at the altimeter frequency of 415 MHz.

Fig.3. Data from seven passes of balloon 77 over the Ronne Ice Shelf, including altimeter-locking to icebottom reflections.
3. The maps
Two ice-elevation maps of the whole Antarctic continent (excluding the peninsula) are given in Figures 4 and 5. The maps are based on TWERLE data only, except for the coast-line data, which were taken from the 1970 map published by the American Geographic Society. The maps are given in polar azimuthal equidistant projection. Contour interval is 100 m, with some of the 1 000 m intervals accentuated.

Fig.4. Elevation map of Antarctica (contouring by Duchon method). Dots represent measurement points.

Fig.5. Elevation map of Antarctica (contouring by Cressman method). 187
The two maps differ in griddlng and contouring techniques. Figure 4 is a result of a surface spline interpolation technique (Reference DuchonDuchon 1976) in which an equation is developed for each measurement. Elevation data at any grid point can be calculated from these equations. A contouring program is then used, based on linear interpolation with subdivided grid. To keep the number of equations below 200, the map is constructed from a mosaic of 24 overlapping sections. They are combined in groups of three prior to contouring. This leaves eight overlapping sections to be matched manually. The dots in Figure 4 represent the locations of measurements. Their density should help in evaluating the validity of the contour lines.
In Figure 5, the irregularly distributed measurements are first used to generate elevation data on a square net of grid points by a method used extensively in meteorology (Reference CressmanCressman 1959). The grid points are spaced at 55 km intervals, parallel to the Greenwich meridian.
In the Cressman method, the elevation data at each grid point result from averaging the elevation measurements within a given radius. Each measurement is given a weight which is the reciprocal of its distance from the grid point. This process is repeated several times with reduced radii. Contouring based on a standard fixed-grid linear interpolation Is then used for contouring each quarter, with some overlapping. The four quarters are combined manually.
The main reason for presenting the two maps is to demonstrate that, while the contouring methods differ substantially, the resulting maps are similar. This indicates that over large sections of the continent, the density of data were sufficient to dominate the contouring technique. This is true, in particular, in the plateau areas of East Antarctica and Queen Maud Land. It should be added that both contouring programs ignored mountains, and the only constraint was the coast line.
Acknowledgements
The information on which this report is based was obtained during the TWERL Experiment, supported by the US National Aeronautics and Space Administration and the National Science Foundation. The analysis was supported by a grant from the US-Israel Binational Science Foundation (BSF), Jerusalem, Israel. Special thanks are due to Mrs Yona Eyal for extensive programming work.







