1 Introduction
When a high power laser pulse interacts with a solid density target, large numbers of bound electrons are rapidly ionized by the strong laser field[Reference Huang, Kluge and Cowan1–Reference Kemp, Pfund and Meyer-ter-Vehn4]. Meanwhile, free electrons in the target are directly accelerated to mega-electronvolt (MeV) energies by the laser force[Reference Wilks, Kruer, Tabak and Langdon5–Reference Ma, Sawada, Patel, Chen, Divol, Higginson, Kemp, Key, Larson, Le Pape, Link, MacPhee, McLean, Ping, Stephens, Wilks and Beg8], and driven into the target with a current density in the order of
![]() $10^{12}~\text{A}/\text{cm}^{2}$
[Reference Huang, Kluge and Cowan1, Reference Huang, Schlenvoigt, Takabe and Cowan9]. The transport of laser-driven fast electrons continually heats and ionizes the bulk solid by collisions[Reference Huang, Kluge and Cowan1, Reference Mishra, Leblanc, Sentoku, Wei and Beg3, Reference Huang, Schlenvoigt, Takabe and Cowan9, Reference Wu, He, Yu and Fritzsche10], reaching a warm or hot dense plasma state. Simultaneously, multi-megagauss (MG) magnetic fields arise from fast electron transport both at the surface and inside the solid target[Reference Davies11–Reference Haines13]. The self-generated MG magnetic fields in turn influence the transport properties of the fast electron beam, causing beam collimation, hollowing, filamentation and so on[Reference Sentoku, Mima, Kojima and Ruhl14–Reference Leblanc and Sentoku17]. Recently, our particle-in-cell (PIC) simulations have shown that the collisional ionization potential and model are critical to determining the structure and diffusion time of the self-generated magnetic fields, while the magnetic diffusion time into a stationary plasma is inversely proportional to the plasma resistivity assuming magnetohydrodynamic condition[Reference Huang, Schlenvoigt, Takabe and Cowan9]. Thus, investigating the dynamics and structure of self-generated magnetic fields in high power laser irradiated solids is potentially important to understand the laser-produced fast electron transport, heating and ionization, bulk plasma resistivity and so on.
$10^{12}~\text{A}/\text{cm}^{2}$
[Reference Huang, Kluge and Cowan1, Reference Huang, Schlenvoigt, Takabe and Cowan9]. The transport of laser-driven fast electrons continually heats and ionizes the bulk solid by collisions[Reference Huang, Kluge and Cowan1, Reference Mishra, Leblanc, Sentoku, Wei and Beg3, Reference Huang, Schlenvoigt, Takabe and Cowan9, Reference Wu, He, Yu and Fritzsche10], reaching a warm or hot dense plasma state. Simultaneously, multi-megagauss (MG) magnetic fields arise from fast electron transport both at the surface and inside the solid target[Reference Davies11–Reference Haines13]. The self-generated MG magnetic fields in turn influence the transport properties of the fast electron beam, causing beam collimation, hollowing, filamentation and so on[Reference Sentoku, Mima, Kojima and Ruhl14–Reference Leblanc and Sentoku17]. Recently, our particle-in-cell (PIC) simulations have shown that the collisional ionization potential and model are critical to determining the structure and diffusion time of the self-generated magnetic fields, while the magnetic diffusion time into a stationary plasma is inversely proportional to the plasma resistivity assuming magnetohydrodynamic condition[Reference Huang, Schlenvoigt, Takabe and Cowan9]. Thus, investigating the dynamics and structure of self-generated magnetic fields in high power laser irradiated solids is potentially important to understand the laser-produced fast electron transport, heating and ionization, bulk plasma resistivity and so on.
Although there has been a large amount of work studying the dynamics of self-generated surface and bulk magnetic fields during high power laser–plasma interactions, both numerically and theoretically, the experimental characterization of the magnetic fields is restricted to the underdense or near critical density region of an irradiated target using conventional optical Faraday rotation probing[Reference Borghesi, MacKinnon, Bell, Gaillard and Willi18–Reference Moniruzzaman, Amit, Kamalesh, Deep, Indranuj and Kumar22]. To probe the bulk magnetic fields within overdense or solid density plasmas, the deflectometry of energetic charged particles such as electron and protons crossing the fields has recently been developed, by taking advantage of the long attenuation length of energetic charged particles in solid density plasmas[Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, Mackinnon, Patel, Smalyuk, Sangster and Knauer23, Reference Schumaker, Nakanii, McGuffey, Zulick, Chyvkov, Dollar, Habara, Kalintchenko, Maksimchuk, Tanaka, Thomas, Yanovsky and Krushelnick24]. However, this methodology is limited to a temporal resolution of several picoseconds due to the intrinsic beam pulse duration. We have recently proposed probing the bulk magnetic fields inside the solid density plasmas by X-ray polarimetry via Faraday rotation using X-ray free electron lasers (XFELs), taking advantage of simultaneous high spatial–temporal resolution and several tens of micrometers attenuation length in solid[Reference Huang, Schlenvoigt, Takabe and Cowan9]. Simulations predict that the XFEL polarization is rotated by a few hundred micro-radians after penetrating through solid density plasmas which, with improved beam parameters compared to those achieved at synchrotron light sources, are feasible to be measured with X-ray polarimetry.
In preparation for the coming experiments, we have run a series of PIC simulations to optimize the strong magnetic fields generation by systematically varying the initial laser and target parameters such as laser intensity, focal size, contrast, incident angle, target thickness, material, geometry and so on, which will be presented in this paper. The simulation results show that the strength of magnetic field has weak dependence on the solid target material, while it is sensitive to the other studied parameters. We observe that the strongest magnetic field is generated with laser incident angles and preplasma scale lengths that maximize laser absorption efficiency. The magnetic filaments driven by a Weibel-like instability seem to saturate at intensities lower than
![]() $10^{20}~\text{W}/\text{cm}^{2}$
, while the interface magnetic field between two solid layers increases as laser intensity increases from
$10^{20}~\text{W}/\text{cm}^{2}$
, while the interface magnetic field between two solid layers increases as laser intensity increases from
![]() $6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
$6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
![]() $10^{20}~\text{W}/\text{cm}^{2}$
. We also found that a strong magnetic field is generated at the interface of multilayer target due to the plasma resistivity mismatch, which is of interest to be probed via X-ray polarimetry.
$10^{20}~\text{W}/\text{cm}^{2}$
. We also found that a strong magnetic field is generated at the interface of multilayer target due to the plasma resistivity mismatch, which is of interest to be probed via X-ray polarimetry.
Figure 1 shows an example experimental setup for generating strong magnetic fields by interacting an ultra-short relativistic optical laser pulse with solid matter, and simultaneously probing it by an XFEL via Faraday rotation. Due to the high attenuation length, the XFEL is able to penetrate solid density plasmas of up to several tens of micrometer thicknesses. Assuming the entering XFEL beam is perfectly horizontally polarized, then the orientation of the polarization plane is rotated by the magnetic field component along the probe beam, weighted by the local electron density. Along the path
![]() $l$
of the probing beam through the plasma, the total rotation angle
$l$
of the probing beam through the plasma, the total rotation angle
![]() $\unicode[STIX]{x1D719}_{\text{rot}}$
of the exiting XFEL beam is given by[Reference Huang, Schlenvoigt, Takabe and Cowan9]
$\unicode[STIX]{x1D719}_{\text{rot}}$
of the exiting XFEL beam is given by[Reference Huang, Schlenvoigt, Takabe and Cowan9]
where
![]() $e$
,
$e$
,
![]() $m_{e}$
,
$m_{e}$
,
![]() $c$
,
$c$
,
![]() $\unicode[STIX]{x1D706}_{\text{XFEL}}$
,
$\unicode[STIX]{x1D706}_{\text{XFEL}}$
,
![]() $\vec{k}_{\text{XFEL}}$
,
$\vec{k}_{\text{XFEL}}$
,
![]() $\vec{B}$
and
$\vec{B}$
and
![]() $n_{e}$
are the elementary charge and rest mass of an electron, the speed of light, the wavelength and wave vector of XFEL beam, the magnetic field vector and plasma electron density, respectively. From Equation (1), we expect the polarization of an XFEL beam at photon energy of 6.457 keV to be rotated around
$n_{e}$
are the elementary charge and rest mass of an electron, the speed of light, the wavelength and wave vector of XFEL beam, the magnetic field vector and plasma electron density, respectively. From Equation (1), we expect the polarization of an XFEL beam at photon energy of 6.457 keV to be rotated around
![]() $100~\unicode[STIX]{x03BC}\text{rad}$
after propagating along
$100~\unicode[STIX]{x03BC}\text{rad}$
after propagating along
![]() $1~\unicode[STIX]{x03BC}\text{m}$
plasma within 100 MG environment magnetic field at electron density of
$1~\unicode[STIX]{x03BC}\text{m}$
plasma within 100 MG environment magnetic field at electron density of
![]() $10^{24}~\text{cm}^{-3}$
. The choice of 6.457 keV photon energy is to comply with Si channel-cut crystals as X-ray polarizers developed by Marx et al.
[Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus25, Reference Marx, Uschmann, Höfer, Lötzsch, Wehrhan, Förster, Kaluza, Stöhlker, Gies, Detlefs, Roth, Härtwig and Paulus26]. We note that, in a real experiment, the rotation angle also depends on the incident angle, polarization purity of the probing XFEL and extinction ratio of the polarizer. Beyond probing the bulk magnetic field in solid density plasmas, developing high purity X-ray polarimetry will allow future experiments to detect the vacuum birefringence[Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf27–Reference Shen, Bu, Xu, Xu, Ji, Li and Xu31], nuclear resonant forward scattering[Reference Heeg, Haber, Schumacher, Bocklage, Wille, Schulze, Loetzsch, Uschmann, Paulus, Rüffer, Röhlsberger and Evers32, Reference Heeg, Wille, Schlage, Guryeva, Schumacher, Uschmann, Schulze, Marx, Kämpfer, Paulus, Röhlsberger and Evers33], and more. In this work, we aim to optimize the chances of observing the polarization rotation by finding the laser and target parameters that maximize the magnetic field strength.
$10^{24}~\text{cm}^{-3}$
. The choice of 6.457 keV photon energy is to comply with Si channel-cut crystals as X-ray polarizers developed by Marx et al.
[Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus25, Reference Marx, Uschmann, Höfer, Lötzsch, Wehrhan, Förster, Kaluza, Stöhlker, Gies, Detlefs, Roth, Härtwig and Paulus26]. We note that, in a real experiment, the rotation angle also depends on the incident angle, polarization purity of the probing XFEL and extinction ratio of the polarizer. Beyond probing the bulk magnetic field in solid density plasmas, developing high purity X-ray polarimetry will allow future experiments to detect the vacuum birefringence[Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf27–Reference Shen, Bu, Xu, Xu, Ji, Li and Xu31], nuclear resonant forward scattering[Reference Heeg, Haber, Schumacher, Bocklage, Wille, Schulze, Loetzsch, Uschmann, Paulus, Rüffer, Röhlsberger and Evers32, Reference Heeg, Wille, Schlage, Guryeva, Schumacher, Uschmann, Schulze, Marx, Kämpfer, Paulus, Röhlsberger and Evers33], and more. In this work, we aim to optimize the chances of observing the polarization rotation by finding the laser and target parameters that maximize the magnetic field strength.

Figure 1. An illustrated experimental setup of strong magnetic field generation by interaction of an ultra-short relativistic optical laser pulse with solid matter, probed by an XFEL via Faraday rotation.
2 PIC simulation method
All simulations presented in this work have been performed using the two-dimensional in space and three-dimensional in velocity (2D3V) particle-in-cell code PICLS that includes binary collision, field and collisional ionization[Reference Sentoku and Kemp34]. Recently, the newly developed atomic interaction models including photoionization, KLL Auger ionization, K-shell vacancy decay and ionization potential depression (IPD) also have been implemented into the code which solves the X-ray radiation transport self-consistently with the nonthermal, solid density plasma dynamics[Reference Sentoku, Paraschiv, Royle, Mancini and Johzaki35, Reference Royle, Sentoku, Mancini, Paraschiv and Johzaki36]. In the whole text, the physical and numerical parameters are similar to our previous work, as listed in Table 1[Reference Huang, Schlenvoigt, Takabe and Cowan9]. Here we give a brief introduction to recall the key physical and numerical parameters and collisional ionization models. All simulations are performed with temporal resolution
![]() $\unicode[STIX]{x0394}t=13.3~\text{fs}$
and spatial resolution
$\unicode[STIX]{x0394}t=13.3~\text{fs}$
and spatial resolution
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=$
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=$
![]() $0.004~\unicode[STIX]{x03BC}\text{m}$
to resolve the plasma frequency and wavelength, respectively. The simulation box varies for different cases. In the case of Cu target with
$0.004~\unicode[STIX]{x03BC}\text{m}$
to resolve the plasma frequency and wavelength, respectively. The simulation box varies for different cases. In the case of Cu target with
![]() $20~\unicode[STIX]{x03BC}\text{m}$
thickness, the simulation box consists of
$20~\unicode[STIX]{x03BC}\text{m}$
thickness, the simulation box consists of
![]() $N_{x}\times N_{y}=6750\times 6750$
cells. The initial charge state and number of computational metallic ions in each cell are 1
$N_{x}\times N_{y}=6750\times 6750$
cells. The initial charge state and number of computational metallic ions in each cell are 1
![]() $+$
and 10, respectively, corresponding to about
$+$
and 10, respectively, corresponding to about
![]() $10Z$
computational electrons in each cell when fully ionized. Here
$10Z$
computational electrons in each cell when fully ionized. Here
![]() $Z$
is the atomic number of the metallic element. We smooth computational particle shapes by fourth-order splines and accordingly use fourth-order smoothing for the current deposition. With these parameters we achieve very good energy conservation over the complete simulation time. The p-polarized laser pulse is modeled by a Gaussian profile both in spatial and temporal dimensions with full width at half maximum (FWHM) spot size
$Z$
is the atomic number of the metallic element. We smooth computational particle shapes by fourth-order splines and accordingly use fourth-order smoothing for the current deposition. With these parameters we achieve very good energy conservation over the complete simulation time. The p-polarized laser pulse is modeled by a Gaussian profile both in spatial and temporal dimensions with full width at half maximum (FWHM) spot size
![]() $w_{\text{FWHM}}=4~\unicode[STIX]{x03BC}\text{m}$
and duration
$w_{\text{FWHM}}=4~\unicode[STIX]{x03BC}\text{m}$
and duration
![]() $t_{\text{FWHM}}=40~\text{fs}$
, respectively. Mathematically, the intensity of the laser pulse at normal incidence is written as
$t_{\text{FWHM}}=40~\text{fs}$
, respectively. Mathematically, the intensity of the laser pulse at normal incidence is written as
![]() $I(y,t)=I_{0}e^{-4\ln 2[(y-y_{0})/w_{\text{FWHM}}]^{2}}e^{-4\ln 2[(t-t_{0})/t_{\text{FWHM}}]^{2}}$
, where
$I(y,t)=I_{0}e^{-4\ln 2[(y-y_{0})/w_{\text{FWHM}}]^{2}}e^{-4\ln 2[(t-t_{0})/t_{\text{FWHM}}]^{2}}$
, where
![]() $I_{0}$
is the peak laser intensity,
$I_{0}$
is the peak laser intensity,
![]() $y_{0}$
is the transverse center position of the target, and
$y_{0}$
is the transverse center position of the target, and
![]() $t_{0}=0$
is the reference time when the peak intensity irradiates on the front surface of the target. The initial plasma ion density
$t_{0}=0$
is the reference time when the peak intensity irradiates on the front surface of the target. The initial plasma ion density
![]() $n_{i}$
is set to be realistic with a preplasma at target front surface modeled by a longitudinal exponential profile at variable scale lengths
$n_{i}$
is set to be realistic with a preplasma at target front surface modeled by a longitudinal exponential profile at variable scale lengths
![]() $0\leqslant l_{\text{ppl}}[\unicode[STIX]{x03BC}\text{m}]\leqslant 0.4$
, i.e.,
$0\leqslant l_{\text{ppl}}[\unicode[STIX]{x03BC}\text{m}]\leqslant 0.4$
, i.e.,
![]() $n_{i}=n_{i0}e^{(x-x_{0})/l_{\text{ppl}}}$
, where
$n_{i}=n_{i0}e^{(x-x_{0})/l_{\text{ppl}}}$
, where
![]() $n_{i0}$
and
$n_{i0}$
and
![]() $x_{0}=3~\unicode[STIX]{x03BC}\text{m}$
are the cutoff solid ion density and longitudinal position of laser directly irradiating solid target, respectively. To keep the plasma neutrality, the initial electron density is set to be
$x_{0}=3~\unicode[STIX]{x03BC}\text{m}$
are the cutoff solid ion density and longitudinal position of laser directly irradiating solid target, respectively. To keep the plasma neutrality, the initial electron density is set to be
![]() ${n_{e}=Z_{0}n}_{i}$
, where
${n_{e}=Z_{0}n}_{i}$
, where
![]() $Z_{0}$
is the initial ion charge state.
$Z_{0}$
is the initial ion charge state.
As we have studied previously, the collisional ionization model is crucial to determine the plasma resistivity and thus structure of the magnetic filaments[Reference Huang, Schlenvoigt, Takabe and Cowan9]. Although the Landau–Lifshitz model used to represent field ionization process is included in all simulations shown in this paper[Reference Landau and Lifshitz37], two different collisional ionization models to qualitatively indicate the effects of ionization model on the magnetic field generation are used for different PIC simulation cases. Specifically, the simulations use either Thomas–Fermi (TF) pressure ionization model[Reference More38] assuming local thermal equilibrium (LTE) condition or direct impact (DI) ionization model assuming nonlocal thermal equilibrium (NLTE) condition[Reference Kemp, Pfund and Meyer-ter-Vehn4] to represent collisional ionization process. Although intense laser-produced solid density plasmas are typically far from LTE conditions[Reference Davis and Petrov2], we could not definitely conclude that the DI model is better than the TF model in our simulations. Neither of them is precise since the detailed electronic configuration within an ion is neglected. Fully understanding the atomic ionization physics in plasmas requires a more precise treatment of ionization, excitation, photon emission and their inverse processes specially recombination in numerical simulations. The ionization physics of intense laser pulses irradiating solid targets has also been discussed in other works[Reference Braenzel, Andreev, Platonov, Klingsporn, Ehrentraut, Sandner and Schnürer39, Reference Shen, Qiao, Zhang, Kar, Zhou, Chang, Borghesi and He40]. The treatment of the TF and DI ionization models in PICLS code is introduced in our previous work[Reference Huang, Schlenvoigt, Takabe and Cowan9].
3 PIC simulation results and discussions
In this section, we will first briefly discuss the mechanisms of magnetic field generation, both on the surface and in the bulk, in high power laser–solid interactions. We then focus on systematic numerical investigation of the dependence of the bulk magnetic field generation on the initial laser and target parameters, as described above. By identifying the conditions where magnetic field generation is maximized, we pave the way to optimize near future experimental campaigns that will use XFELs to measure the bulk magnetic field inside solid density plasmas via Faraday rotation.
3.1 The mechanisms of magnetic field generation
As we know, the generation and growth of a magnetic field is governed by Faraday’s law:
![]() $\unicode[STIX]{x2202}\vec{B}/\unicode[STIX]{x2202}t=-c\unicode[STIX]{x1D6FB}\times \vec{E}$
. In high power laser–matter interactions, the quasi-stationary magnetic field caused by the hot electron transport is of great interest. Assuming magnetohydrodynamic condition, the electric field vector
$\unicode[STIX]{x2202}\vec{B}/\unicode[STIX]{x2202}t=-c\unicode[STIX]{x1D6FB}\times \vec{E}$
. In high power laser–matter interactions, the quasi-stationary magnetic field caused by the hot electron transport is of great interest. Assuming magnetohydrodynamic condition, the electric field vector
![]() $\vec{E}$
can be expressed using the generalized Ohm’s law
$\vec{E}$
can be expressed using the generalized Ohm’s law
![]() $\vec{E}\approx \unicode[STIX]{x1D702}\vec{j}+(1/en_{e})\vec{j}\times \vec{B}-(1/en_{e})\unicode[STIX]{x1D6FB}P_{e}-\vec{v}\times \vec{B}-(1/2ecn_{cr})\unicode[STIX]{x1D6FB}I_{0}$
, where
$\vec{E}\approx \unicode[STIX]{x1D702}\vec{j}+(1/en_{e})\vec{j}\times \vec{B}-(1/en_{e})\unicode[STIX]{x1D6FB}P_{e}-\vec{v}\times \vec{B}-(1/2ecn_{cr})\unicode[STIX]{x1D6FB}I_{0}$
, where
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
![]() $\vec{j}$
,
$\vec{j}$
,
![]() $P_{e}$
,
$P_{e}$
,
![]() $\vec{v}$
,
$\vec{v}$
,
![]() $n_{cr}$
and
$n_{cr}$
and
![]() $I_{0}$
are the plasma resistivity, return current, electron thermal pressure, plasma fluid velocity, critical density and laser peak intensity, respectively[Reference Haines13, Reference Mason and Tabak41]. Thus, the Faraday equation becomes
$I_{0}$
are the plasma resistivity, return current, electron thermal pressure, plasma fluid velocity, critical density and laser peak intensity, respectively[Reference Haines13, Reference Mason and Tabak41]. Thus, the Faraday equation becomes
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\vec{B}}{\unicode[STIX]{x2202}t} & = & \displaystyle -c\unicode[STIX]{x1D6FB}\times \vec{E}\nonumber\\ \displaystyle & {\approx} & \displaystyle -c\unicode[STIX]{x1D6FB}\times \left(\unicode[STIX]{x1D702}\vec{j}+\frac{1}{en_{e}}\vec{j}\times \vec{B}-\frac{1}{en_{e}}\unicode[STIX]{x1D6FB}P_{e}-\vec{v}\times \vec{B}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\frac{1}{2ecn_{cr}}\unicode[STIX]{x1D6FB}I_{0}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\vec{B}}{\unicode[STIX]{x2202}t} & = & \displaystyle -c\unicode[STIX]{x1D6FB}\times \vec{E}\nonumber\\ \displaystyle & {\approx} & \displaystyle -c\unicode[STIX]{x1D6FB}\times \left(\unicode[STIX]{x1D702}\vec{j}+\frac{1}{en_{e}}\vec{j}\times \vec{B}-\frac{1}{en_{e}}\unicode[STIX]{x1D6FB}P_{e}-\vec{v}\times \vec{B}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\frac{1}{2ecn_{cr}}\unicode[STIX]{x1D6FB}I_{0}\right).\end{eqnarray}$$
The five terms in Equation (2) come from the resistive Ohmic effect, Hall effect, Biermann battery effect, field convection and with bulk plasma flow and ponderomotive force driven direct current, respectively. From Equation (2), it is clear that a magnetic field is spontaneously generated near the front surface of a solid target irradiated by a nonuniform laser due to the Biermann battery effect, i.e.,
![]() $\unicode[STIX]{x1D6FB}T_{e}\times \unicode[STIX]{x1D6FB}n_{e}$
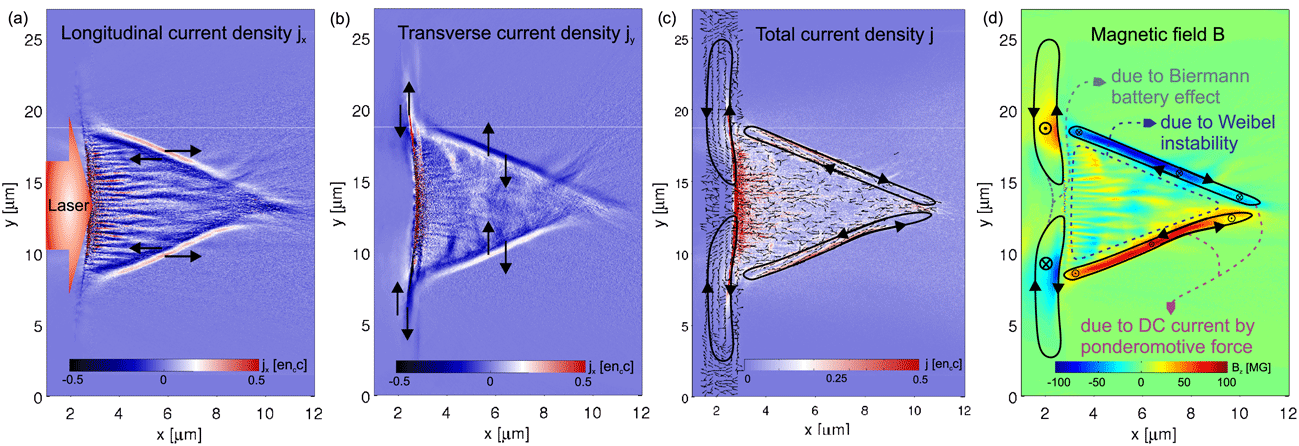
, since the electron temperature gradient is mainly along the target transverse while the density gradient is mainly along the target normal. In the absence of one-dimensional symmetry, the electrons return along a different path and thus create a current loop[Reference Haines13]. The scenario is reproduced in the PIC simulation, as shown in Figure 2. Figures 2(a)–2(c) show the spatial distributions of longitudinal current density
$\unicode[STIX]{x1D6FB}T_{e}\times \unicode[STIX]{x1D6FB}n_{e}$
, since the electron temperature gradient is mainly along the target transverse while the density gradient is mainly along the target normal. In the absence of one-dimensional symmetry, the electrons return along a different path and thus create a current loop[Reference Haines13]. The scenario is reproduced in the PIC simulation, as shown in Figure 2. Figures 2(a)–2(c) show the spatial distributions of longitudinal current density
![]() $j_{x}$
, transverse current density
$j_{x}$
, transverse current density
![]() $j_{y}$
and total current density vector
$j_{y}$
and total current density vector
![]() $\vec{j}$
, respectively. As we can see from Figure 2(c), there are two main current loops formed near the target front surface, which generate the surface magnetic field as shown in Figure 2(d). More comprehensive studies on the surface magnetic field generation due to the Biermann battery effect can be found in the literature[Reference Schoeffler, Loureiro, Fonseca and Silva42, Reference Schoeffler, Loureiro, Fonseca and Silva43].
$\vec{j}$
, respectively. As we can see from Figure 2(c), there are two main current loops formed near the target front surface, which generate the surface magnetic field as shown in Figure 2(d). More comprehensive studies on the surface magnetic field generation due to the Biermann battery effect can be found in the literature[Reference Schoeffler, Loureiro, Fonseca and Silva42, Reference Schoeffler, Loureiro, Fonseca and Silva43].

Figure 2. Two-dimensional spatial distributions of (a) longitudinal current density
![]() $j_{x}$
, (b) transverse current density
$j_{x}$
, (b) transverse current density
![]() $j_{y}$
, (c) total current density vector
$j_{y}$
, (c) total current density vector
![]() $\vec{j}$
and (d) magnetic field
$\vec{j}$
and (d) magnetic field
![]() $B$
at the time
$B$
at the time
![]() $t=24~\text{fs}$
after laser peak intensity irradiating on the target. Throughout the whole text
$t=24~\text{fs}$
after laser peak intensity irradiating on the target. Throughout the whole text
![]() $t=0~\text{fs}$
is defined to be the reference time when the laser peak intensity irradiates on the front surface of the solid target. The black arrow shows the current direction. In the whole text, the physical and numerical parameters are similar to our previous work, as listed in Table 1[Reference Huang, Schlenvoigt, Takabe and Cowan9] and briefly introduced in Section 2. The difference will be highlighted in the figure captions. For this specific simulation, we assume the laser peak intensity
$t=0~\text{fs}$
is defined to be the reference time when the laser peak intensity irradiates on the front surface of the solid target. The black arrow shows the current direction. In the whole text, the physical and numerical parameters are similar to our previous work, as listed in Table 1[Reference Huang, Schlenvoigt, Takabe and Cowan9] and briefly introduced in Section 2. The difference will be highlighted in the figure captions. For this specific simulation, we assume the laser peak intensity
![]() $10^{20}~\text{W}/\text{cm}^{2}$
and exponential preplasma with scale length of
$10^{20}~\text{W}/\text{cm}^{2}$
and exponential preplasma with scale length of
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
in front of the target. The target material is Cu with
$0.1~\unicode[STIX]{x03BC}\text{m}$
in front of the target. The target material is Cu with
![]() $20~\unicode[STIX]{x03BC}\text{m}$
thickness. This simulation uses the TF ionization model, which assumes local thermal equilibrium (LTE) condition.
$20~\unicode[STIX]{x03BC}\text{m}$
thickness. This simulation uses the TF ionization model, which assumes local thermal equilibrium (LTE) condition.
In this work, we instead focus on investigating the bulk magnetic field generation inside solid density plasmas, which is mainly due to the resistive Ohmic effect and ponderomotive force driven direct current. When the intense electron beam accelerated by a high power laser enters a solid density plasma, it carries a large current density into the target. Since the hot electron current is normally not perfectly neutralized by a bulk return current of the background plasma electrons[Reference Huang, Kluge and Cowan1], a magnetic field is generated inside the target. From the spatial distribution of total current density vector
![]() $\vec{j}$
in Figure 2(c), we can clearly see two current loops on the order of
$\vec{j}$
in Figure 2(c), we can clearly see two current loops on the order of
![]() $10^{11}~\text{A}/\text{cm}^{2}$
are originally generated in the vicinity of the laser focal spot and extend into the target bulk. This direct current (DC) is driven by the laser ponderomotive force[Reference Mason and Tabak41, Reference Gibbon44], and acts as a source generating the magnetic field which can diffuse into the bulk target. The magnitude of the ponderomotive magnetic field depends on the cross product of the density gradient and laser intensity gradient, i.e.,
$10^{11}~\text{A}/\text{cm}^{2}$
are originally generated in the vicinity of the laser focal spot and extend into the target bulk. This direct current (DC) is driven by the laser ponderomotive force[Reference Mason and Tabak41, Reference Gibbon44], and acts as a source generating the magnetic field which can diffuse into the bulk target. The magnitude of the ponderomotive magnetic field depends on the cross product of the density gradient and laser intensity gradient, i.e.,
![]() $\vec{B}\sim \unicode[STIX]{x1D6FB}n_{e}\times \unicode[STIX]{x1D6FB}I_{0}$
, and the direction is opposite to the surface magnetic field, as indicated in Figure 2(d). We notice that, this mechanism is in contrast to and possibly complemented by alternative mechanisms for magnetic generation such as return current and instabilities. Precisely understanding and distinguishing the different mechanisms require performing more carefully designed PIC simulations. At the same time, a component of the fast electron current due to the natural consequence of collective laser absorption mechanism is directed into the target. This fast electron current density is typically in the order of
$\vec{B}\sim \unicode[STIX]{x1D6FB}n_{e}\times \unicode[STIX]{x1D6FB}I_{0}$
, and the direction is opposite to the surface magnetic field, as indicated in Figure 2(d). We notice that, this mechanism is in contrast to and possibly complemented by alternative mechanisms for magnetic generation such as return current and instabilities. Precisely understanding and distinguishing the different mechanisms require performing more carefully designed PIC simulations. At the same time, a component of the fast electron current due to the natural consequence of collective laser absorption mechanism is directed into the target. This fast electron current density is typically in the order of
![]() $10^{12}~\text{A}/\text{cm}^{2}$
. The transport of such a large current into the bulk target tends to be neutralized by the counter-propagating bulk return current, and is likely to undergo Weibel-like instabilities[Reference Weibel45], resulting in generation and growth of magnetic filaments, as shown in Figure 2(d).
$10^{12}~\text{A}/\text{cm}^{2}$
. The transport of such a large current into the bulk target tends to be neutralized by the counter-propagating bulk return current, and is likely to undergo Weibel-like instabilities[Reference Weibel45], resulting in generation and growth of magnetic filaments, as shown in Figure 2(d).
In order to design experimental setups that maximize the field generated, in the following sections, we will describe the effect of different laser parameters (Section 3.2) and target parameters (Section 3.3) on the bulk magnetic field arising from the ponderomotive-driven DC current, the Weibel-like instabilities and the plasma resistivity mismatch of multilayer target, calculated from PIC simulations.
3.2 Dependence of bulk magnetic field generation on the laser parameters
In reality, high power optical laser pulses have a finite contrast with several picoseconds to nanoseconds prepulse as well as amplified spontaneous emission (ASE) prior to the main pulse[Reference Metzkes, Kluge, Zeil, Bussmann, Kraft, Cowan and Schramm46]. Due to the longtime scales, it is impractical to simulate the prepulse interactions with kinetic PIC simulations, and so instead we performed a series of runs varying the initial scale length of preplasma created by the laser prepulse, to model the effect of the imperfect laser contrast. Figure 3 shows the spatial distributions of self-generated magnetic field in laser irradiated solid Cu targets, with the scale length of preplasma ranging from 0 to
![]() $0.4~\unicode[STIX]{x03BC}\text{m}$
at
$0.4~\unicode[STIX]{x03BC}\text{m}$
at
![]() $t\approx 80~\text{fs}$
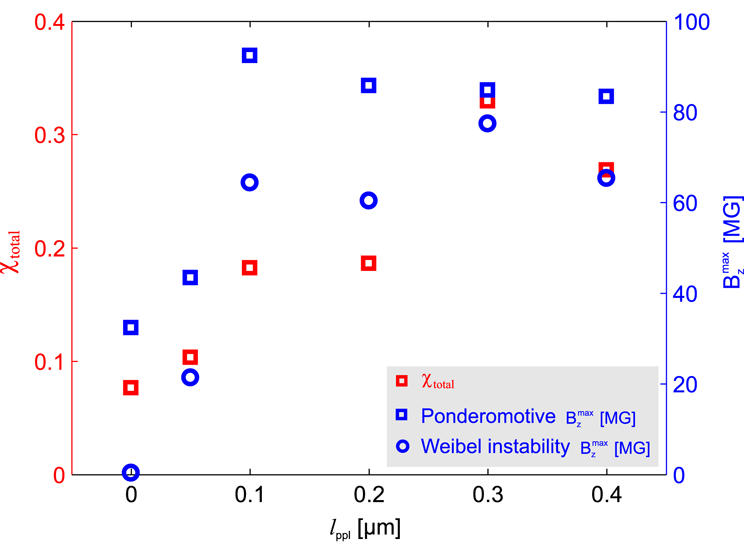
. As we can see, the maximum Weibel-like instability generated magnetic field increases with the preplasma scale length up to
$t\approx 80~\text{fs}$
. As we can see, the maximum Weibel-like instability generated magnetic field increases with the preplasma scale length up to
![]() $0.3~\unicode[STIX]{x03BC}\text{m}$
, and then it decreases at the scale length of
$0.3~\unicode[STIX]{x03BC}\text{m}$
, and then it decreases at the scale length of
![]() $0.4~\unicode[STIX]{x03BC}\text{m}$
. The trend agrees very well with the total laser absorption efficiency
$0.4~\unicode[STIX]{x03BC}\text{m}$
. The trend agrees very well with the total laser absorption efficiency
![]() $\unicode[STIX]{x1D712}_{\text{total}}$
which also maximizes at
$\unicode[STIX]{x1D712}_{\text{total}}$
which also maximizes at
![]() $l_{\text{ppl}}=0.3~\unicode[STIX]{x03BC}\text{m}$
, as shown in Figure 4. Figure 4 also shows that the maximum ponderomotive current generated magnetic field increases with the preplasma scale length up to
$l_{\text{ppl}}=0.3~\unicode[STIX]{x03BC}\text{m}$
, as shown in Figure 4. Figure 4 also shows that the maximum ponderomotive current generated magnetic field increases with the preplasma scale length up to
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
, reaching 93 MG, and then it decreases slightly at a larger scale length till
$0.1~\unicode[STIX]{x03BC}\text{m}$
, reaching 93 MG, and then it decreases slightly at a larger scale length till
![]() $0.4~\unicode[STIX]{x03BC}\text{m}$
. It is intuitive that the laser-driven current density and thus magnetic field increase with total laser absorption efficiency, since most of the laser energy converts to electron kinetic energy, and a small fraction of the laser energy then goes to the magnetic field energy. The increase in total laser absorption efficiency is in agreement with the geometric argument of increased laser–plasma interaction volume in the presence of longer preplasmas due to the longer distance of low density preplasmas[Reference Petrov, Davis and Petrova47]. The slight decrease of maximum magnetic field at larger preplasma scale is probably because more laser energy is deposited in the low density preplasma, thus reducing the total absorbed energy in the bulk target. Fully understanding the slight difference of the scaling of maximum ponderomotive current and Weibel-like instability generated magnetic fields with the preplasma scale length would require deeper theoretical modeling which is beyond the scope of this work.
$0.4~\unicode[STIX]{x03BC}\text{m}$
. It is intuitive that the laser-driven current density and thus magnetic field increase with total laser absorption efficiency, since most of the laser energy converts to electron kinetic energy, and a small fraction of the laser energy then goes to the magnetic field energy. The increase in total laser absorption efficiency is in agreement with the geometric argument of increased laser–plasma interaction volume in the presence of longer preplasmas due to the longer distance of low density preplasmas[Reference Petrov, Davis and Petrova47]. The slight decrease of maximum magnetic field at larger preplasma scale is probably because more laser energy is deposited in the low density preplasma, thus reducing the total absorbed energy in the bulk target. Fully understanding the slight difference of the scaling of maximum ponderomotive current and Weibel-like instability generated magnetic fields with the preplasma scale length would require deeper theoretical modeling which is beyond the scope of this work.

Figure 3. The spatial distributions of self-generated magnetic field in laser irradiated solid Cu target as the preplasma scale length varies from 0 to
![]() $0.4~\unicode[STIX]{x03BC}\text{m}$
at
$0.4~\unicode[STIX]{x03BC}\text{m}$
at
![]() $t\approx 80~\text{fs}$
. The thickness of the target is
$t\approx 80~\text{fs}$
. The thickness of the target is
![]() $2~\unicode[STIX]{x03BC}\text{m}$
. All other simulation parameters are the same as Figure 2.
$2~\unicode[STIX]{x03BC}\text{m}$
. All other simulation parameters are the same as Figure 2.

Figure 4. The scaling of total laser absorption efficiency
![]() $\unicode[STIX]{x1D712}_{\text{total}}$
and maximum magnetic field by ponderomotive current and Weibel-like instability with the preplasma scale length.
$\unicode[STIX]{x1D712}_{\text{total}}$
and maximum magnetic field by ponderomotive current and Weibel-like instability with the preplasma scale length.
In further simulations, we studied the effect of laser intensity, and therefore spot size, by fixing the laser energy at
![]() ${\sim}0.2~\text{J}$
and varying the intensities from
${\sim}0.2~\text{J}$
and varying the intensities from
![]() $6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
$6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
![]() $10^{20}~\text{W}/\text{cm}^{2}$
, for spot sizes of
$10^{20}~\text{W}/\text{cm}^{2}$
, for spot sizes of
![]() $8~\unicode[STIX]{x03BC}\text{m}$
to
$8~\unicode[STIX]{x03BC}\text{m}$
to
![]() $2~\unicode[STIX]{x03BC}\text{m}$
. Figure 5 shows the spatial distributions of self-generated magnetic field for three different laser intensities and spot sizes on the
$2~\unicode[STIX]{x03BC}\text{m}$
. Figure 5 shows the spatial distributions of self-generated magnetic field for three different laser intensities and spot sizes on the
![]() $\text{CH}_{2}$
–Ti two layer target, which is with an additional
$\text{CH}_{2}$
–Ti two layer target, which is with an additional
![]() $1~\unicode[STIX]{x03BC}\text{m}$
solid
$1~\unicode[STIX]{x03BC}\text{m}$
solid
![]() $\text{CH}_{2}$
layer on the front, at
$\text{CH}_{2}$
layer on the front, at
![]() $t\approx 80~\text{fs}$
. The preplasma scale length of the solid
$t\approx 80~\text{fs}$
. The preplasma scale length of the solid
![]() $\text{CH}_{2}$
layer is
$\text{CH}_{2}$
layer is
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
. The purpose to use two layers target is creating internal interface magnetic field due to the resistivity mismatch that will be discussed in Section 3.3. As we can see, the size of magnetic field seems to have a weak dependence of the laser spot size. The interface magnetic field between the
$0.1~\unicode[STIX]{x03BC}\text{m}$
. The purpose to use two layers target is creating internal interface magnetic field due to the resistivity mismatch that will be discussed in Section 3.3. As we can see, the size of magnetic field seems to have a weak dependence of the laser spot size. The interface magnetic field between the
![]() $\text{CH}_{2}$
and Ti layers increases by around a factor of 2.5 as the laser intensity increases from
$\text{CH}_{2}$
and Ti layers increases by around a factor of 2.5 as the laser intensity increases from
![]() $6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
$6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
![]() $10^{20}~\text{W}/\text{cm}^{2}$
. Since the interface magnetic field mainly comes from the source term
$10^{20}~\text{W}/\text{cm}^{2}$
. Since the interface magnetic field mainly comes from the source term
![]() $j_{y}\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
as indicated later in Equation (3), we attribute the increase to the transverse current density
$j_{y}\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
as indicated later in Equation (3), we attribute the increase to the transverse current density
![]() $j_{y}$
. The maximum magnetic field due to the Weibel-like instability increases from 18 MG to 42 MG as the laser intensity increases from
$j_{y}$
. The maximum magnetic field due to the Weibel-like instability increases from 18 MG to 42 MG as the laser intensity increases from
![]() $6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
$6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
![]() $2.5\times 10^{19}~\text{W}/\text{cm}^{2}$
but remains almost the same with the increase to
$2.5\times 10^{19}~\text{W}/\text{cm}^{2}$
but remains almost the same with the increase to
![]() $10^{20}~\text{W}/\text{cm}^{2}$
. We can therefore infer that the Weibel instability generated magnetic field saturates at laser intensity below
$10^{20}~\text{W}/\text{cm}^{2}$
. We can therefore infer that the Weibel instability generated magnetic field saturates at laser intensity below
![]() $10^{20}~\text{W}/\text{cm}^{2}$
.
$10^{20}~\text{W}/\text{cm}^{2}$
.

Figure 5. The spatial distributions of self-generated magnetic field in the cases of laser intensity and spot size at (a)
![]() $I_{0}=6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
,
$I_{0}=6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
,
![]() $R=8~\unicode[STIX]{x03BC}\text{m}$
, (b)
$R=8~\unicode[STIX]{x03BC}\text{m}$
, (b)
![]() $I_{0}=2.5\times 10^{19}~\text{W}/\text{cm}^{2}$
,
$I_{0}=2.5\times 10^{19}~\text{W}/\text{cm}^{2}$
,
![]() $R=4~\unicode[STIX]{x03BC}\text{m}$
and (c)
$R=4~\unicode[STIX]{x03BC}\text{m}$
and (c)
![]() $I_{0}=1.0\times 10^{20}~\text{W}/\text{cm}^{2}$
,
$I_{0}=1.0\times 10^{20}~\text{W}/\text{cm}^{2}$
,
![]() $R=2~\unicode[STIX]{x03BC}\text{m}$
at
$R=2~\unicode[STIX]{x03BC}\text{m}$
at
![]() $t\approx 80~\text{fs}$
, respectively. The laser energy is fixed to
$t\approx 80~\text{fs}$
, respectively. The laser energy is fixed to
![]() ${\sim}0.2~\text{J}$
. Instead of the LTE TF ionization model, the NLTE DI ionization model is used for these two specific simulations. The dependence of ionization model on magnetic field generation is investigated in our other work[Reference Huang, Schlenvoigt, Takabe and Cowan9]. The scale length of preplasma is
${\sim}0.2~\text{J}$
. Instead of the LTE TF ionization model, the NLTE DI ionization model is used for these two specific simulations. The dependence of ionization model on magnetic field generation is investigated in our other work[Reference Huang, Schlenvoigt, Takabe and Cowan9]. The scale length of preplasma is
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
for these simulations. All other simulation parameters are the same as Figure 3.
$0.1~\unicode[STIX]{x03BC}\text{m}$
for these simulations. All other simulation parameters are the same as Figure 3.
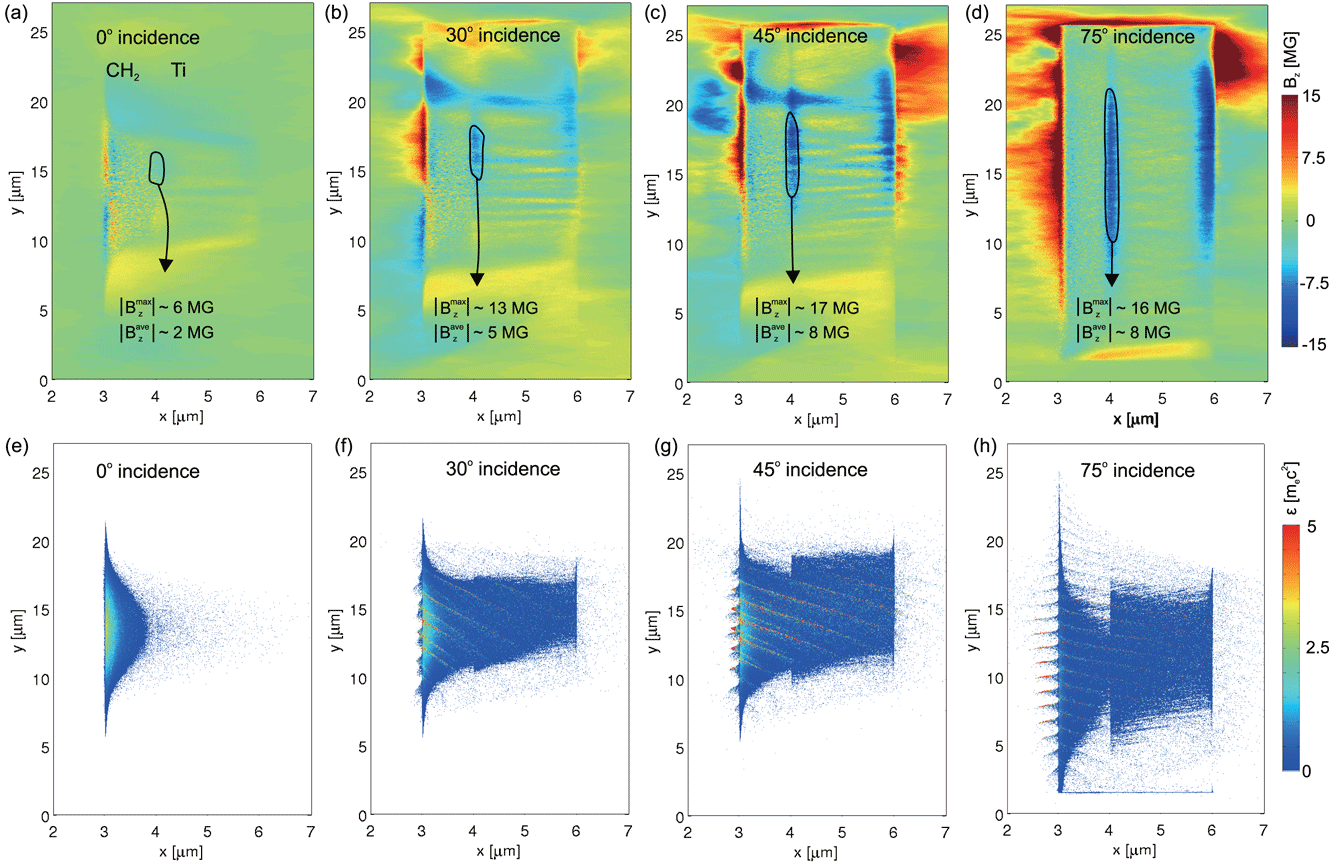
Finally in this section, we investigate the effect of laser incident angle on the self-generated interface magnetic field in a layered
![]() $\text{CH}_{2}$
–Ti target with sharp target–vacuum interfaces without preplasma irradiated by a laser pulse with peak intensity of
$\text{CH}_{2}$
–Ti target with sharp target–vacuum interfaces without preplasma irradiated by a laser pulse with peak intensity of
![]() $10^{19}~\text{W}/\text{cm}^{2}$
for
$10^{19}~\text{W}/\text{cm}^{2}$
for
![]() $\unicode[STIX]{x1D703}$
ranging from
$\unicode[STIX]{x1D703}$
ranging from
![]() $0^{\circ }$
to
$0^{\circ }$
to
![]() $75^{\circ }$
, as shown in Figures 6(a)–6(d). As we can see, both the magnitude and transverse length of the interface magnetic field increase with laser incident angle up to
$75^{\circ }$
, as shown in Figures 6(a)–6(d). As we can see, both the magnitude and transverse length of the interface magnetic field increase with laser incident angle up to
![]() $45^{\circ }$
. Compared to the normal incidence case, the maximum magnetic field at the interface increases by a factor of
$45^{\circ }$
. Compared to the normal incidence case, the maximum magnetic field at the interface increases by a factor of
![]() ${\sim}3$
for
${\sim}3$
for
![]() $45^{\circ }$
incidence. As for the prepulse scale length, the enhancement of the magnetic field with incident angle matches the total laser absorption efficiency
$45^{\circ }$
incidence. As for the prepulse scale length, the enhancement of the magnetic field with incident angle matches the total laser absorption efficiency
![]() $\unicode[STIX]{x1D712}_{\text{total}}$
. The PIC simulation results show that
$\unicode[STIX]{x1D712}_{\text{total}}$
. The PIC simulation results show that
![]() $\unicode[STIX]{x1D712}_{\text{total}}$
is 5.9%, 14.2% and 25.3% for
$\unicode[STIX]{x1D712}_{\text{total}}$
is 5.9%, 14.2% and 25.3% for
![]() $0^{\circ }$
,
$0^{\circ }$
,
![]() $30^{\circ }$
and
$30^{\circ }$
and
![]() $45^{\circ }$
incident angles, respectively. Figures 6(e)–6(h) show the spatial distribution of absorbed electron energy density for each incident angle case. It is clear that an electron bunch enters the solid target obliquely. This is mainly caused by the vacuum heating mechanism for sharp target–vacuum interfaces predicted by Brunel’s model[Reference Brunel48, Reference Gibbon, Andreev and Platonov49]. In this absorption mechanism, the laser electric field
$45^{\circ }$
incident angles, respectively. Figures 6(e)–6(h) show the spatial distribution of absorbed electron energy density for each incident angle case. It is clear that an electron bunch enters the solid target obliquely. This is mainly caused by the vacuum heating mechanism for sharp target–vacuum interfaces predicted by Brunel’s model[Reference Brunel48, Reference Gibbon, Andreev and Platonov49]. In this absorption mechanism, the laser electric field
![]() $E_{L}$
has a component
$E_{L}$
has a component
![]() $E_{d}\approx 2E_{L}\sin \unicode[STIX]{x1D703}$
normal to the target surface, which pulls bunches of electrons into the vacuum. The bunch at the surface is spatially modulated in the order of laser wavelength as seen in Figure 6. The electron bunch then returns to its initial position and continues into the solid at an angle. Thus, it is expected that the component of transverse current density
$E_{d}\approx 2E_{L}\sin \unicode[STIX]{x1D703}$
normal to the target surface, which pulls bunches of electrons into the vacuum. The bunch at the surface is spatially modulated in the order of laser wavelength as seen in Figure 6. The electron bunch then returns to its initial position and continues into the solid at an angle. Thus, it is expected that the component of transverse current density
![]() $j_{y}$
increases with the incident angle and therefore so does the source term
$j_{y}$
increases with the incident angle and therefore so does the source term
![]() $j_{y}\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
for interface magnetic field generation. As the laser pulse interacts with the target at a grazing incidence angle of
$j_{y}\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
for interface magnetic field generation. As the laser pulse interacts with the target at a grazing incidence angle of
![]() $75^{\circ }$
, the total absorption efficiency and interface magnetic field also remain almost the same as the
$75^{\circ }$
, the total absorption efficiency and interface magnetic field also remain almost the same as the
![]() $45^{\circ }$
case. Therefore we conclude that the optimization of magnetic field generation in terms of incident angle is in general consistent with the laser absorption efficiency. It is worth to notice that the growth rate of Weibel-like instability is sensitive to the density of the laser-driven hot electron beam, while the density depends on the laser intensity and preplasma[Reference Huang, Schlenvoigt, Takabe and Cowan9]. In Figure 6, the laser intensity is
$45^{\circ }$
case. Therefore we conclude that the optimization of magnetic field generation in terms of incident angle is in general consistent with the laser absorption efficiency. It is worth to notice that the growth rate of Weibel-like instability is sensitive to the density of the laser-driven hot electron beam, while the density depends on the laser intensity and preplasma[Reference Huang, Schlenvoigt, Takabe and Cowan9]. In Figure 6, the laser intensity is
![]() $10^{19}~\text{W}/\text{cm}^{2}$
and no preplasma is introduced in these simulations, which results in low hot electron density and thus weak Weibel-like instability.
$10^{19}~\text{W}/\text{cm}^{2}$
and no preplasma is introduced in these simulations, which results in low hot electron density and thus weak Weibel-like instability.

Figure 6. The spatial distributions of the self-generated interface magnetic field at
![]() $t\approx 80~\text{fs}$
(first row) and electron energy density at
$t\approx 80~\text{fs}$
(first row) and electron energy density at
![]() $t\approx -3~\text{fs}$
(second row) in layered target
$t\approx -3~\text{fs}$
(second row) in layered target
![]() $\text{CH}_{2}$
–Ti irradiated by laser pulse intensity
$\text{CH}_{2}$
–Ti irradiated by laser pulse intensity
![]() $10^{19}~\text{W}/\text{cm}^{2}$
for different incident angles ranging from
$10^{19}~\text{W}/\text{cm}^{2}$
for different incident angles ranging from
![]() $0^{\circ }$
to
$0^{\circ }$
to
![]() $75^{\circ }$
. Here we assume no preplasma in front of the target. The scale length of preplasma is
$75^{\circ }$
. Here we assume no preplasma in front of the target. The scale length of preplasma is
![]() $0~\unicode[STIX]{x03BC}\text{m}$
for these simulations. All other simulation parameters are the same as Figure 5.
$0~\unicode[STIX]{x03BC}\text{m}$
for these simulations. All other simulation parameters are the same as Figure 5.
3.3 Dependence of bulk magnetic field generation on the target parameters
Figure 7 compares the spatial distributions of free electron density and self-generated magnetic field in a laser irradiated solid Cu target in the cases of
![]() $20~\unicode[STIX]{x03BC}\text{m}$
and
$20~\unicode[STIX]{x03BC}\text{m}$
and
![]() $2~\unicode[STIX]{x03BC}\text{m}$
thicknesses with preplasma scale length of
$2~\unicode[STIX]{x03BC}\text{m}$
thicknesses with preplasma scale length of
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
at
$0.1~\unicode[STIX]{x03BC}\text{m}$
at
![]() $t=24~\text{fs}$
. Since the electron density is similar for both cases, the Faraday rotation angle mainly depends on the magnetic field. We can see in the figure that the strength of the self-generated magnetic field due to the ponderomotive DC current is quite close for both cases, i.e., the maximum magnetic field
$t=24~\text{fs}$
. Since the electron density is similar for both cases, the Faraday rotation angle mainly depends on the magnetic field. We can see in the figure that the strength of the self-generated magnetic field due to the ponderomotive DC current is quite close for both cases, i.e., the maximum magnetic field
![]() $B_{z}^{\max }$
and spatial averaged ponderomotive magnetic field
$B_{z}^{\max }$
and spatial averaged ponderomotive magnetic field
![]() $B_{z}^{\text{ave}}$
are roughly 100 MG and 60 MG, respectively. This is as expected, since the target thickness is much larger than the plasma skin layer depth (a few nanometers at this high plasma density), and therefore the hot electrons are generated under essentially the same interaction conditions. We can also see that, near the front surface of the solid target, the fields in the filament channels are also similar, i.e.,
$B_{z}^{\text{ave}}$
are roughly 100 MG and 60 MG, respectively. This is as expected, since the target thickness is much larger than the plasma skin layer depth (a few nanometers at this high plasma density), and therefore the hot electrons are generated under essentially the same interaction conditions. We can also see that, near the front surface of the solid target, the fields in the filament channels are also similar, i.e.,
![]() $B_{z}^{\max }$
and
$B_{z}^{\max }$
and
![]() $B_{z}^{\text{ave}}$
are roughly 40 MG and 30 MG, respectively. The magnetic filament near the front surface is likely caused by Weibel-like instability due to the counter-propagating hot forward-bulk return current streams, which develops in a few femtoseconds[Reference Huang, Schlenvoigt, Takabe and Cowan9].
$B_{z}^{\text{ave}}$
are roughly 40 MG and 30 MG, respectively. The magnetic filament near the front surface is likely caused by Weibel-like instability due to the counter-propagating hot forward-bulk return current streams, which develops in a few femtoseconds[Reference Huang, Schlenvoigt, Takabe and Cowan9].
At the back surface, however, the filament field strengths are very different, and in the thinner target case are similar in magnitude to the ponderomotive magnetic field. We attribute the generation of rear surface magnetic filaments to the counter-propagating hot forward-reflux current streams. In the
![]() $2~\unicode[STIX]{x03BC}\text{m}$
target, a strong hot reflux current, equal to
$2~\unicode[STIX]{x03BC}\text{m}$
target, a strong hot reflux current, equal to
![]() ${\sim}25\%$
of the hot forward current density, is reflected by the sheath electrostatic potential and re-enters the bulk target. Compared to the bulk return current, the reflux current has closer density and velocity with the hot forward current, which results in a faster growth rate of the Weibel-like instability and thus a significant enhancement of magnetic filamentation near the rear surface, as discussed in our previous paper[Reference Huang, Schlenvoigt, Takabe and Cowan9]. In contrast, the thicker target reduces the effect of the hot reflux current and therefore the magnetic filamentation near the rear surface. Consequently, we would suggest using a relatively thick target for the first of principle Faraday rotation experiments, as this reduces the strength of thin magnetic filaments. The influence of target thickness on hot electron recirculation has also been investigated in other work[Reference Mackinnon, Sentoku, Patel, Price, Hatchett, Key, Andersen, Snavely and Freeman50].
${\sim}25\%$
of the hot forward current density, is reflected by the sheath electrostatic potential and re-enters the bulk target. Compared to the bulk return current, the reflux current has closer density and velocity with the hot forward current, which results in a faster growth rate of the Weibel-like instability and thus a significant enhancement of magnetic filamentation near the rear surface, as discussed in our previous paper[Reference Huang, Schlenvoigt, Takabe and Cowan9]. In contrast, the thicker target reduces the effect of the hot reflux current and therefore the magnetic filamentation near the rear surface. Consequently, we would suggest using a relatively thick target for the first of principle Faraday rotation experiments, as this reduces the strength of thin magnetic filaments. The influence of target thickness on hot electron recirculation has also been investigated in other work[Reference Mackinnon, Sentoku, Patel, Price, Hatchett, Key, Andersen, Snavely and Freeman50].

Figure 7. The spatial distributions of free electron density and self-generated magnetic field in a laser irradiated Cu target with
![]() $20~\unicode[STIX]{x03BC}\text{m}$
and
$20~\unicode[STIX]{x03BC}\text{m}$
and
![]() $2~\unicode[STIX]{x03BC}\text{m}$
thicknesses at
$2~\unicode[STIX]{x03BC}\text{m}$
thicknesses at
![]() $t=24~\text{fs}$
.
$t=24~\text{fs}$
.
![]() $B_{z}^{\max }$
and
$B_{z}^{\max }$
and
![]() $B_{z}^{\text{ave}}$
are the maximum and spatially averaged magnetic fields in the indicated regions. The scale length of preplasma is
$B_{z}^{\text{ave}}$
are the maximum and spatially averaged magnetic fields in the indicated regions. The scale length of preplasma is
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
for these simulations. All other simulation parameters are the same as Figure 2.
$0.1~\unicode[STIX]{x03BC}\text{m}$
for these simulations. All other simulation parameters are the same as Figure 2.
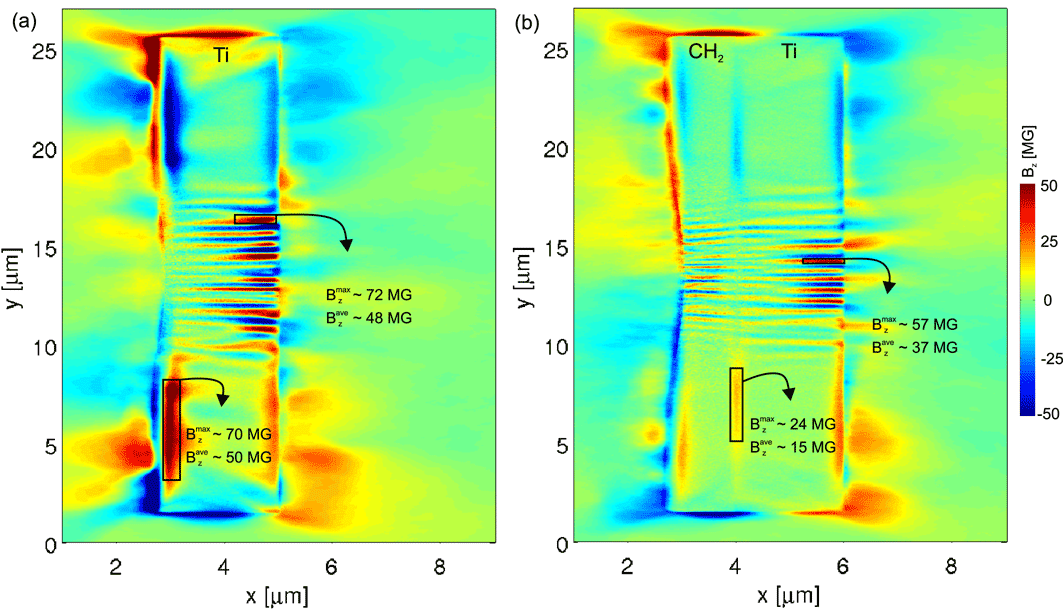
Figure 8 shows the spatial distribution of magnetic field for a
![]() $2~\unicode[STIX]{x03BC}\text{m}\;\text{Ti}$
single layer target and for the same target with an additional
$2~\unicode[STIX]{x03BC}\text{m}\;\text{Ti}$
single layer target and for the same target with an additional
![]() $1~\unicode[STIX]{x03BC}\text{m}\;\text{CH}_{2}$
layer on the front with preplasma scale length of
$1~\unicode[STIX]{x03BC}\text{m}\;\text{CH}_{2}$
layer on the front with preplasma scale length of
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
, at
$0.1~\unicode[STIX]{x03BC}\text{m}$
, at
![]() $t\approx 80~\text{fs}$
. Here we focus on studying the generation of interface magnetic fields due to the resistivity mismatch between two solid layers. If we assume the bulk magnetic field is mainly caused by the Ohmic effect, then Equation (2) can be written in a simplified scalar form:
$t\approx 80~\text{fs}$
. Here we focus on studying the generation of interface magnetic fields due to the resistivity mismatch between two solid layers. If we assume the bulk magnetic field is mainly caused by the Ohmic effect, then Equation (2) can be written in a simplified scalar form:
For the two layer targets with a density gradient
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
, the product of transverse current density and longitudinal resistivity gradient
$\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
, the product of transverse current density and longitudinal resistivity gradient
![]() $j_{\text{y}}\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
gives a source term of magnetic field generation. This scenario is reproduced in our PIC simulation, as shown in Figure 8(b). As indicated in the figure, the maximum and spatially averaged magnetic fields near the interface of the
$j_{\text{y}}\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
gives a source term of magnetic field generation. This scenario is reproduced in our PIC simulation, as shown in Figure 8(b). As indicated in the figure, the maximum and spatially averaged magnetic fields near the interface of the
![]() $\text{CH}_{2}$
and Ti layers are around 24 MG and 15 MG, respectively. Even though the magnitude is 2–3 times less than those generated by the ponderomotive current and Weibel instability, the generation and diffusion of the interface magnetic field are quite robust since it mainly depends on the material resistivity. Thus, it makes experimental measurement of the magnetic field via Faraday rotation more feasible. The interface magnetic field can be enhanced by optimizing the laser incident angle that maximizes the laser absorption efficiency and by increasing the laser intensity, as discussed in Section 3.2. The interface bulk magnetic field is also observed numerically in sandwich targets via transversely modulated resistivity profile, which is capable of collimating the transport of fast electrons[Reference Debayle, Gremillet, Honrubia and d’Humières51]. There are experimental results suggesting that interface magnetic field can be used to control and collimate laser accelerated protons[Reference Ramakrishna, Kar, Robinson, Adams, Markey, Quinn, Yuan, McKenna, Lancaster, Green, Scott, Norreys, Schreiber and Zepf52]. Therefore, we believe that the direct measurement of interface magnetic fields would allow us to deeply understand and control the properties of laser-generated electrons and accelerated ion transport.
$\text{CH}_{2}$
and Ti layers are around 24 MG and 15 MG, respectively. Even though the magnitude is 2–3 times less than those generated by the ponderomotive current and Weibel instability, the generation and diffusion of the interface magnetic field are quite robust since it mainly depends on the material resistivity. Thus, it makes experimental measurement of the magnetic field via Faraday rotation more feasible. The interface magnetic field can be enhanced by optimizing the laser incident angle that maximizes the laser absorption efficiency and by increasing the laser intensity, as discussed in Section 3.2. The interface bulk magnetic field is also observed numerically in sandwich targets via transversely modulated resistivity profile, which is capable of collimating the transport of fast electrons[Reference Debayle, Gremillet, Honrubia and d’Humières51]. There are experimental results suggesting that interface magnetic field can be used to control and collimate laser accelerated protons[Reference Ramakrishna, Kar, Robinson, Adams, Markey, Quinn, Yuan, McKenna, Lancaster, Green, Scott, Norreys, Schreiber and Zepf52]. Therefore, we believe that the direct measurement of interface magnetic fields would allow us to deeply understand and control the properties of laser-generated electrons and accelerated ion transport.

Figure 8. The spatial distribution of magnetic field for (a) a
![]() $2~\unicode[STIX]{x03BC}\text{m}$
Ti single layer target and (b) a target with an additional
$2~\unicode[STIX]{x03BC}\text{m}$
Ti single layer target and (b) a target with an additional
![]() $1~\unicode[STIX]{x03BC}\text{m}~\text{CH}_{2}$
layer in the front at
$1~\unicode[STIX]{x03BC}\text{m}~\text{CH}_{2}$
layer in the front at
![]() $t\approx 80~\text{fs}$
, respectively. NLTE DI ionization model is used here. The scale length of preplasma is
$t\approx 80~\text{fs}$
, respectively. NLTE DI ionization model is used here. The scale length of preplasma is
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
for these simulations. All other simulation parameters are the same as Figure 7.
$0.1~\unicode[STIX]{x03BC}\text{m}$
for these simulations. All other simulation parameters are the same as Figure 7.

Figure 9. The spatial distribution of magnetic field for two layers target (a)
![]() $\text{CH}_{2}$
–Al, (b)
$\text{CH}_{2}$
–Al, (b)
![]() $\text{CH}_{2}$
–Ti and (c)
$\text{CH}_{2}$
–Ti and (c)
![]() $\text{CH}_{2}$
–Au without preplasma at
$\text{CH}_{2}$
–Au without preplasma at
![]() $t\approx 80~\text{fs}$
, respectively. Here we assume the peak laser intensity
$t\approx 80~\text{fs}$
, respectively. Here we assume the peak laser intensity
![]() $10^{19}~\text{W}/\text{cm}^{2}$
and no preplasma in front of the target. All other simulation parameters are the same as Figure 8(b).
$10^{19}~\text{W}/\text{cm}^{2}$
and no preplasma in front of the target. All other simulation parameters are the same as Figure 8(b).
Finally, we investigated the effect of target material on the magnetic field generation. Figure 9 shows the spatial distribution of magnetic field for two layers targets comprising
![]() $\text{CH}_{2}$
–Al,
$\text{CH}_{2}$
–Al,
![]() $\text{CH}_{2}$
–Ti and
$\text{CH}_{2}$
–Ti and
![]() $\text{CH}_{2}$
–Au without preplasma at
$\text{CH}_{2}$
–Au without preplasma at
![]() $t\approx 80~\text{fs}$
. Here we assume the peak laser intensity is
$t\approx 80~\text{fs}$
. Here we assume the peak laser intensity is
![]() $10^{19}~\text{W}/\text{cm}^{2}$
, and that there is no preplasma in front of the target. Compared to Figure 8(b), the interface magnetic field and filament are of course much weaker, due to the reduced intensity, while the ponderomotive magnetic field is dominant. We see that the magnitude of maximum and spatially averaged magnetic fields is close for all the studied materials, which is reasonable since the ablation layer for each is the same, resulting in the same initial interaction conditions and current. In this relatively low intensity case, without preplasma, the laser-driven hot current density is much smaller, so the heating and ionization in the second layer are not as strong as in the previous case. Therefore the material of the second layer does not play a significant role in the magnetic field generation. However, as the laser intensity increases, the ionization of the second layer, which determines the resistivity, is expected to become more important in generating the interface magnetic field.
$10^{19}~\text{W}/\text{cm}^{2}$
, and that there is no preplasma in front of the target. Compared to Figure 8(b), the interface magnetic field and filament are of course much weaker, due to the reduced intensity, while the ponderomotive magnetic field is dominant. We see that the magnitude of maximum and spatially averaged magnetic fields is close for all the studied materials, which is reasonable since the ablation layer for each is the same, resulting in the same initial interaction conditions and current. In this relatively low intensity case, without preplasma, the laser-driven hot current density is much smaller, so the heating and ionization in the second layer are not as strong as in the previous case. Therefore the material of the second layer does not play a significant role in the magnetic field generation. However, as the laser intensity increases, the ionization of the second layer, which determines the resistivity, is expected to become more important in generating the interface magnetic field.
4 Conclusion and outlook
In conclusion, we have systematically investigated the bulk magnetic field generation inside a solid target irradiated by a short high power laser using numerical simulations. The effect of laser prepulse is modeled by preplasmas with an exponential density profile, with the scale length varying from 0 to
![]() $0.4~\unicode[STIX]{x03BC}\text{m}$
. The peak laser intensity and spot size range from
$0.4~\unicode[STIX]{x03BC}\text{m}$
. The peak laser intensity and spot size range from
![]() $6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
$6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
![]() $10^{20}~\text{W}/\text{cm}^{2}$
and
$10^{20}~\text{W}/\text{cm}^{2}$
and
![]() $2~\unicode[STIX]{x03BC}\text{m}$
to
$2~\unicode[STIX]{x03BC}\text{m}$
to
![]() $8~\unicode[STIX]{x03BC}\text{m}$
, and the laser incident angle to the target is scanned from
$8~\unicode[STIX]{x03BC}\text{m}$
, and the laser incident angle to the target is scanned from
![]() $0^{\circ }$
to
$0^{\circ }$
to
![]() $75^{\circ }$
. We also studied the effect of target parameters on the self-generated magnetic field by changing the target thickness, material and geometry. The simulation results suggest that the magnetic field generation is optimized with a preplasma scale length between
$75^{\circ }$
. We also studied the effect of target parameters on the self-generated magnetic field by changing the target thickness, material and geometry. The simulation results suggest that the magnetic field generation is optimized with a preplasma scale length between
![]() $0.1~\unicode[STIX]{x03BC}\text{m}$
and
$0.1~\unicode[STIX]{x03BC}\text{m}$
and
![]() $0.4~\unicode[STIX]{x03BC}\text{m}$
, and laser incident angle between
$0.4~\unicode[STIX]{x03BC}\text{m}$
, and laser incident angle between
![]() $45^{\circ }$
and
$45^{\circ }$
and
![]() $75^{\circ }$
, respectively. The simulation also implies that the bulk Weibel-like instability generated magnetic field saturates at the laser intensity lower than
$75^{\circ }$
, respectively. The simulation also implies that the bulk Weibel-like instability generated magnetic field saturates at the laser intensity lower than
![]() $10^{20}~\text{W}/\text{cm}^{2}$
, while the interface magnetic field between two solid layers increases with laser intensity ranging from
$10^{20}~\text{W}/\text{cm}^{2}$
, while the interface magnetic field between two solid layers increases with laser intensity ranging from
![]() $6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
$6.25\times 10^{18}~\text{W}/\text{cm}^{2}$
to
![]() $10^{20}~\text{W}/\text{cm}^{2}$
. It seems that the size of magnetic field has a weak dependence on the laser spot size and the material of the second solid layer does not play a significant role in interface magnetic field generation at relatively low intensity. Compared to a thin foil, a thicker target effectively reduces the hot reflux current and thus the magnetic filaments near the rear surface. For two layer solid targets, the product of transverse current density and longitudinal resistivity gradient
$10^{20}~\text{W}/\text{cm}^{2}$
. It seems that the size of magnetic field has a weak dependence on the laser spot size and the material of the second solid layer does not play a significant role in interface magnetic field generation at relatively low intensity. Compared to a thin foil, a thicker target effectively reduces the hot reflux current and thus the magnetic filaments near the rear surface. For two layer solid targets, the product of transverse current density and longitudinal resistivity gradient
![]() $j_{y}\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
gives an additional source term to generate magnetic field near the layers’ interface. This interface magnetic field generation seems quite robust, which may make its experimental measurement via Faraday rotation more feasible. With the results of this work, we are in an excellent position to maximize our chances of measuring laser-generated magnetic fields using Faraday rotation at high power laser beamlines at XFELs. One of the first examples of this will be at the European XFEL-HED endstation, in the frame of Helmholtz International Beamline for Extreme Fields at the European XFEL (HiBEF) project, where a 7.5 J/300 TW high power laser has already been installed as a permanent instrument[53] and is expected to start user operation soon. A dedicated beamtime at the European XFEL-HED endstation to investigate the performance of ultra-high purity X-ray polarimeters under the conditions of European XFEL source has already been scheduled to us in the end of May, 2019. This is expected to become the basis to probe the laser-driven ultra-strong magnetic fields inside the solid density targets, accessed via plasma Faraday rotation and imaging polarimetry.
$j_{y}\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x$
gives an additional source term to generate magnetic field near the layers’ interface. This interface magnetic field generation seems quite robust, which may make its experimental measurement via Faraday rotation more feasible. With the results of this work, we are in an excellent position to maximize our chances of measuring laser-generated magnetic fields using Faraday rotation at high power laser beamlines at XFELs. One of the first examples of this will be at the European XFEL-HED endstation, in the frame of Helmholtz International Beamline for Extreme Fields at the European XFEL (HiBEF) project, where a 7.5 J/300 TW high power laser has already been installed as a permanent instrument[53] and is expected to start user operation soon. A dedicated beamtime at the European XFEL-HED endstation to investigate the performance of ultra-high purity X-ray polarimeters under the conditions of European XFEL source has already been scheduled to us in the end of May, 2019. This is expected to become the basis to probe the laser-driven ultra-strong magnetic fields inside the solid density targets, accessed via plasma Faraday rotation and imaging polarimetry.
Acknowledgements
The authors would like to thank the HZDR HPC group for their support. The authors would also like to thank Dr. Nicholas Hartley for useful discussions.