Introduction

Mountain glaciers and ice caps are sensitive indicators of climate change. They contribute significantly to sea-level rise and will continue to do so during the decades to come (Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others, 2006; Reference MeierMeier and others, 2007). Thus, it is vitally important to understand their reaction to climate warming, which is particularly pronounced at high latitudes of the Arctic (Reference Moritz, Bitz and SteigMoritz and others, 2002). However, field monitoring of remote ice masses is resource-consuming and data are available only for a limited number of glaciers in Arctic environments (e.g. Reference DowdeswellDowdeswell and others, 1997; Reference Hagen, Melvold, Pinglot and DowdeswellHagen and others, 2003; Reference OerlemansOerlemans and others, 2005). Satellite remote sensing allows temporal and spatial changes of inaccessible glaciers and ice caps to be assessed and is frequently used in climate-change impact studies (e.g. Reference Rignot and ThomasRignot and Thomas, 2002; Reference AbdalatiAbdalati and others, 2004; Reference Paul and KääbPaul and Kääb, 2005). However, satellite remote-sensing data need to be compared to ground-truth measurements, and require a careful assessment of their limitations in order to characterize their accuracy and suitability to such applications.

Since 1959 glacier surface mass balance has been determined on several glaciers in the Canadian Arctic (Reference KoernerKoerner, 1970, Reference Koerner2005; Reference Adams, Cogley, Ecclestone and DemuthAdams and others, 1998). Reference Burgess and SharpBurgess and Sharp (2004) and Reference Mair, Burgess and SharpMair and others (2005) assessed the mass-balance and geometrical changes of Devon Ice Cap in recent decades. Reference Blatter and KappenbergerBlatter and Kappenberger (1988) determined the seasonal mass balance of ‘Laika Ice Cap’, Coburg Island, and measured englacial temperatures and surface ice velocities. Reference Greuell, Oerlemans and OerlemansGreuell and Oerlemans (1989) computed the temperature distribution in the superimposed ice zone of ‘Laika Ice Cap’.

In this study we assess the temporal and spatial changes of Laika Glacier, the largest outflow glacier of the small Laika Ice Cap, over the period 1959–2006, and make projections of future glacier extent based on climate scenarios. A methodology that combines previous field measurements, current satellite remote-sensing data and numerical modelling is presented, since none of these sources alone is complete in terms of temporal and spatial coverage. A temperature-index mass-balance model (Reference HockHock, 1999) coupled with a simple glacier-surface-evolution model is used to calculate the change in glacier extent and surface mass balance based on meteorological variables. The model is calibrated using in situ measurements and is validated using satellite remote-sensing data. The present study puts forth a methodology to assess the impacts of climate change on glaciers in areas where field measurements are scarce.

Study Site

Laika Ice Cap (unofficial name) is a small icefield with a surface area of ∼10 km² on Nirjutiqavvik (Coburg Island), Canadian Arctic Archipelago (Fig. 1). It is situated at the western edge of the North Water Polynya, a region with no sea ice during large parts of the year (Reference Barber, Hanesiak, Chan and PiwowarBarber and others, 2001). Laika Ice Cap extends from close to sea level to 530 m a.s.l. and has three outlet glaciers (Fig. 1c). Our study focuses on the main outlet glacier of the ice cap that forms a piedmont tongue on the coastal plain. In this paper, the piedmont tongue and its catchment (4.4 km²) on the ice cap are referred to as Laika Glacier (Fig. 1c).

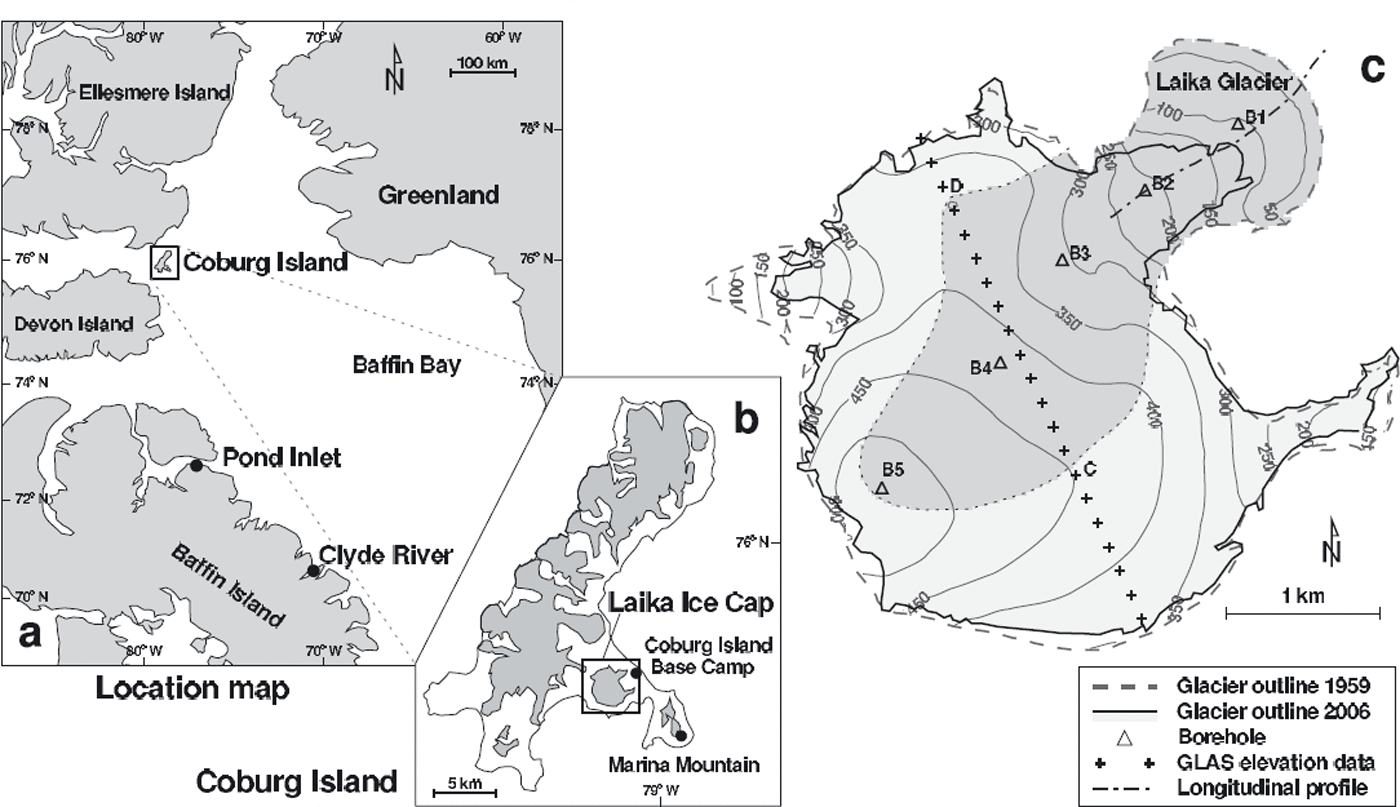
Fig. 1. (a) Location map. Coburg Island with Laika Ice Cap is enlarged in (b). The location of relevant weather stations is indicated by dots. (c) Map of Laika Ice Cap. Glacier outlines for 1959 and 2006 are obtained from aerial photographs and satellite remote-sensing data. The catchment of Laika Glacier has darker shading. Triangles indicate boreholes drilled to the bedrock in 1975 and crosses show a trace with ICESat (Ice, Cloud and land Elevation Satellite) Geoscience Laser Altimeter System (GLAS) elevation data acquired in 2006.

Superimposed ice formation and internal accumulation are significant components of the mass balance of Arctic glaciers (Reference Woodward, Sharp and ArendtWoodward and others, 1997; Reference Schneider and JanssonSchneider and Jansson, 2004). On Laika Ice Cap almost the entire net accumulation is due to superimposed ice formation, as was shown by analysis of a 20 m firn core from the top of Laika Ice Cap (Reference KappenbergerKappenberger, 1976). Meltwater over the cold and impermeable bare ice surface contributes to runoff. Thus, internal accumulation by refreezing of meltwater below the last summer surface is assumed to be of minor importance on Laika Ice Cap.

Coburg Island exhibits an Arctic maritime climate, as it is influenced by the North Water Polynya. It experiences stronger winds and higher precipitation than is usual in that latitude of the Canadian Arctic. Despite the low altitude of the mountain tops (<900 m a.s.l.), more than half of Coburg Island is glacierized (Fig. 1b). Important factors for the mass balance of Laika Ice Cap are the precipitation and the wind pattern. Precipitation increases with elevation due to orographic uplift of air masses (Reference Blatter and KappenbergerBlatter and Kappenberger, 1988). The strongest winds blow from the west and redistribute considerable amounts of snow from the windward slopes and the top of Laika Ice Cap to leeward slopes (Reference Blatter and KappenbergerBlatter and Kappenberger, 1988). This process causes an accumulation pattern which is not well correlated with elevation (Fig. 2).

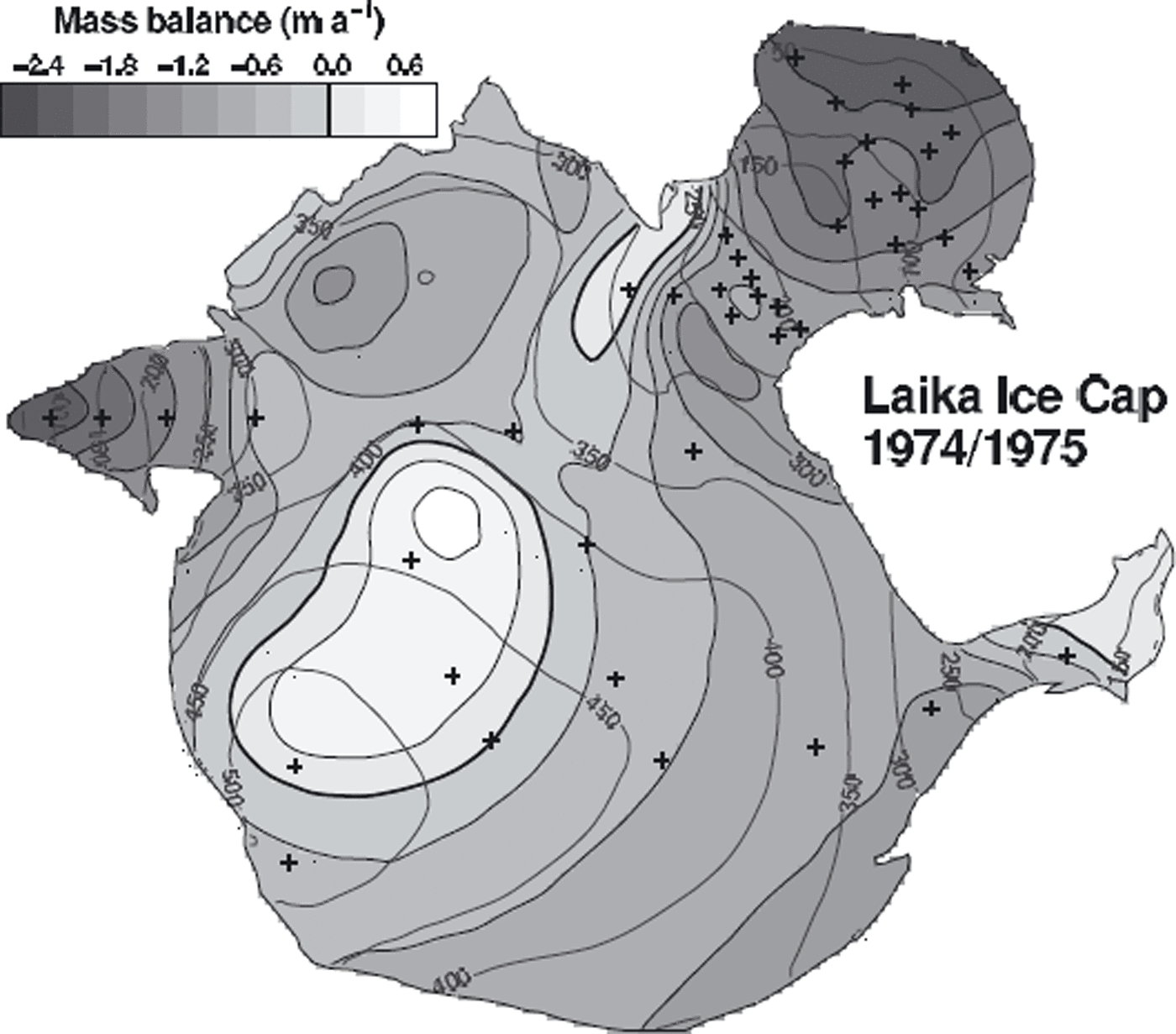
Fig. 2. Distribution of net balance as measured between 24 September 1974 and 23 August 1975. Mass-balance stakes are indicated by crosses.

Data Sources and Methods

A wide range of different data types is used in this study: (1) mass-balance measurements on Laika Ice Cap, (2) local weather observations on Coburg Island, (3) longterm meteorological time series measured at Pond Inlet and Clyde River, (4) climate re-analysis data (ERA-40, NARR) and (5) satellite observations (Landsat, ICESat, ASTER).

Meteorological time series

Homogeneous and continuous time series of daily air temperature and precipitation are required to drive the mass-balance model. However, continuous meteorological data for the Canadian Arctic are sparse and climatic variability is high. Therefore, we combine various observational series in the vicinity of the glacier and re-analysis data spanning different time periods to obtain a composite daily temperature and precipitation series (1959–2006) for Coburg Island.

Datasets

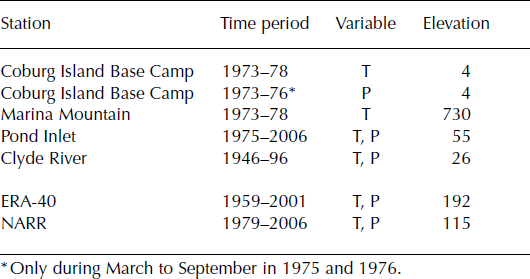
Measurements of air temperature and precipitation on Coburg Island are available for the period 1973–78. An automatic weather station (AWS) was located 1 km from the terminus of Laika Glacier at Coburg Island Base Camp. Air temperature was recorded every 3 hours using a System Lambrecht 809 Pt100 temperature sensor mounted in a Stevenson screen. The nominal accuracy of the temperature sensor is ±0.3°C at 0°C. The measurements during winter are not used because of lower data quality due to rime formation. The data of the AWS were complemented with routine manual observations (Reference Blatter and KappenbergerBlatter and Kappenberger, 1988). A Canadian standard snow and rain gauge with Nipher inverted bell wind shield was manually read every 6 hours. A significant underestimation of precipitation is likely in the case of strong winds during snowfall events. Additional measurements of daily air temperature during the summer months are available from an AWS on the top of Marina Mountain, 7 km from Coburg Island Base Camp (Fig. 1b; Table 1).

Table 1. Meteorological time series and re-analysis data (T: air temperature, P: precipitation). The elevations of the weather station and the re-analysis gridcell are given in m a.s.l.

Daily data of mean air temperature and total precipitation at Pond Inlet and Clyde River (Fig. 1a; Table 1) were downloaded from the climate archive of Environment Canada. These stations are 194 and 373 km, respectively, from Laika Ice Cap and were chosen because their topographic setting is similar to Coburg Island and their data are almost void of data gaps.

Additional information about the meteorological conditions is provided by climate re-analysis datasets. We used the European Centre for Medium-Range Weather Forecasts (ECMWF) 40 year re-analysis (ERA-40) air-temperature and precipitation time series 1959–2001 (Reference UppalaUppala and others, 2005). The ERA-40 re-analysis dataset provides continuous and consistent time series of 6 hourly air-temperature and precipitation on the N80 reduced Gaussian grid, which was resampled to a cylindrical 1° × 1° grid for this study. Daily mean values of 2 m air temperature and total precipitation (liquid and solid) of the gridpoint nearest to Laika Ice Cap were downloaded. ERA-40 precipitation is based on a daily forecast model and is not assimilated from measured station data. Daily precipitation forecasts were assembled as in Reference Schmidli, Frei and VidaleSchmidli and others (2006).

Data from the NCEP (US National Centers for Environmental Prediction) North American regional re-analysis (NARR) are available for the period 1979–2006 (Reference MesingerMesinger and others, 2006). The NARR dataset has a higher spatial resolution than ERA-40. Three-hourly temperature and precipitation data are available on a grid of ∼32 km, however, with no overlapping period with in situ weather observations at Coburg Island Base Camp. Thus, no direct comparison of measurements and re-analysis is possible.

Composite temperature and precipitation series

We now describe how meteorological information originating from different sources was combined to obtain a 50 year time series of daily temperature and precipitation for Coburg Island. The weather data of Coburg Island Base Camp are assumed to be the best representation of the local climate conditions. Daily air temperatures are highly correlated with those at Marina Mountain during June to September (r ² = 0.80), indicating that the weather conditions at the coastal station are not heavily affected by stable inversions and can be extrapolated over the entire elevation range of Laika Ice Cap.

The ERA-40 air-temperature data could not be used to extend the Coburg Island time series since correlation between ERA-40 and Coburg Island Base Camp monthly summer temperatures was absent or weak. The interannual variations are insufficiently represented.

We compared measured weather station data from Pond Inlet and Clyde River with the records of Coburg Island Base Camp. Daily air temperatures showed unsatisfactory correlations between the three sites. We resampled the time series to monthly resolution and found good correlation between both Pond Inlet and Coburg Island Base Camp, as well as Clyde River and Pond Inlet, with linear correlation coefficients of r ² = 0.85 and 0.82, respectively. This allows transfer functions for monthly mean air temperatures between these weather stations to be established. Using these linear-regression relationships, the temperatures recorded at Clyde River (1959–74) and at Pond Inlet (1975–2006) were scaled to Coburg Island. In order to obtain a daily series we down-scaled the 1959–2006 monthly air-temperature time series by applying the daily temperature deviations from the monthly mean values of the year 1977 for Coburg Island Base Camp.

We used daily average values of 2 m air temperature of the NARR gridpoint nearest to Laika Ice Cap to check the plausibility of the temperature series obtained using the regression method. Due to its higher spatial resolution the NARR dataset performs slightly better than ERA-40 in capturing the year-to-year fluctuations of temperature on Coburg Island and provides some validation of the composite temperature series.

The precipitation sums measured at Pond Inlet and Clyde River do not correlate with the time series of Coburg Island and are significantly lower. The precipitation time series of ERA-40 and NARR extracted for the gridpoints closest to Laika Glacier (∼10 km apart) were compared. In the overlapping period the annual precipitation sums of ERA-40 and NARR are well correlated (r ² = 0.64) and only differ by 1% on average. ERA-40 annual precipitation (liquid and solid) matches the data for Coburg Island Base Camp in 1973–76 within 10%. We use daily precipitation provided by the ERA-40 dataset for the period 1959–79 and NARR daily precipitation for 1980–2006. Summer temperature and annual precipitation according to the composite time series are shown in Figure 3.

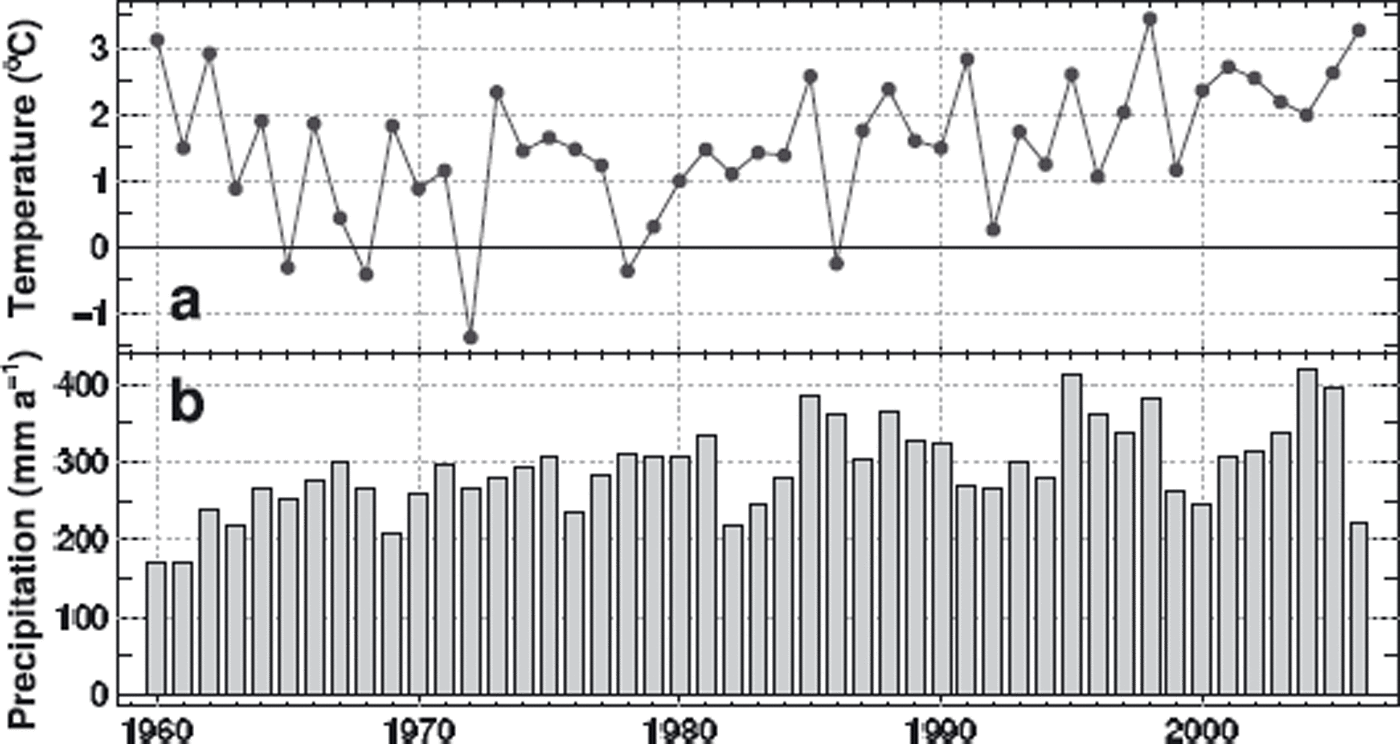
Fig. 3. (a) Mean June–September air temperature and (b) annual precipitation, according to the composite dataset for Coburg Island.

Satellite remote-sensing data

Satellite data from various sensors are used to assess the current state of Laika Glacier (Table 2). Glacier outlines were digitized from the panchromatic channel of the Landsat Enhanced Thematic Mapper (ETM) sensor for the years 2000, 2002 and 2006 at a spatial resolution of 15 m. The spatial uncertainty in the delineation of the ice margin due to shadows, limited contrast in the image and perennial snowpatches is estimated as ±100 m.

Table. 2. Satellite remote-sensing data used in this study. The estimated accuracy refers to the digitized glacier outlines (x, y) and to the elevation information (z)

One track of the Geoscience Laser Altimeter System (GLAS) on board NASA’s ICESat (Ice, Cloud and land Elevation Satellite) is available for 2006 across Laika Glacier (Fig. 1c). GLAS provides surface-elevation data with a spatial footprint of 60 m and an along-track resolution of 170 m. The accuracy of the elevation information is estimated as ±0.2 m for smooth terrain (Reference ShumanShuman and others, 2006). In rough terrain the accuracy is lower, due to the size of the laser footprint.

ASTER (Advanced Spaceborne Thermal Emission and Reflection Radiometer) is a joint effort between NASA and Japan’s Ministry of Economy, Trade and Industry (METI) and includes stereo viewing capability for DEM creation at 30 m spatial resolution. The accuracy of the altitudinal information of the DEMs is estimated as ±10 m by Reference Stearns and HamiltonStearns and Hamilton (2007). However, larger errors (±60 m) are reported in complex high-mountain topography (Reference KääbKääb and others, 2003). Retrieval of the ASTER DEM seems to be particularly unreliable over fresh snow, due to limited contrast variability and generally high reflectance values.

One good quality ASTER scene covering Coburg Island is available for June 2004 and was used to generate a DEM. We assessed the accuracy of the ASTER DEM by comparing it to GLAS ICESat elevation data in the vicinity of the ice cap over non-glacierized regions. We find a root-mean-square error rmse = 14.5 m (n = 185). Above 200 m a.s.l. the ASTER DEM underestimates surface elevation given by GLAS systematically by 9 m; at lower altitudes the elevation of the GLAS tracks is reproduced well on average. Over open sea the rmse of the ASTER DEM is 13 m. We assign an uncertainty of ±15 m to elevation information provided by ASTER. In general, the ASTER DEMs are capable of yielding information on significant spatial changes in glacier geometry. However, they are not accurate enough to allow the calculation of ice-volume changes for a small glacier. In this study, we use the ASTER DEM of 2004 as an independent spatially distributed dataset for validation of the model results.

Mass-balance and surface-evolution model

The temporal and spatial changes of Laika Glacier since 1959 are assessed using a grid-based numerical model consisting of a mass-balance model and a simple surface-evolution model.

Surface mass balance

Glacier surface mass balance is calculated using an accumulation model coupled to a distributed temperature-index melt model (Reference HockHock, 1999; Reference Huss, Bauder, Funk and HockHuss and others, 2008). In this model the degree-day factors are varied as a function of potential direct solar radiation to account for the effects of slope, aspect and shading. Temperature-index models re based on a linear relation between positive air temperature and melt rate (Reference HockHock, 2003). Several studies have shown that off-ice temperature is well suited to simulating melt using temperature-index models (e.g. Reference Lang and BraunLang and Braun, 1990).

Daily surface melt rates, M, are computed by

(1)

where F _M denotes a melt factor, r _ice/snow are radiation factors for ice and snow and I is the potential clear-sky direct radiation. Due to the empirical character of the temperature-index model the site-specific parameters, F _M and r _ice/_snow, must be calibrated using field data. Air temperature, T, at every gridcell is derived using a constant lapse rate, dT/dz. Precipitation is assumed to increase linearly with elevation (dP/dz). A correction factor, C _prec, allows the adjustment of precipitation sums, and a threshold temperature, T _thr = 1°C, distinguishes snow from rainfall. Liquid precipitation does not contribute to mass balance. Parameter values and units are shown in Table 3.

Table 3. Mass-balance model parameters, values and units

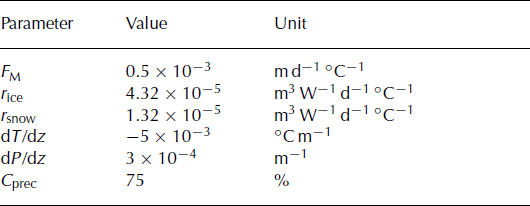
Regions with positive net balance at the end of the previous year define the firn area. Firn is treated as snow in Equation (1). The distribution of snow on Laika Ice Cap is highly influenced by wind (Fig. 2) and is relatively constant during the years with observations. In order to account for the substantial effect of snowdrift, we derived a mean distribution pattern of snow from the in situ measurements of winter mass balance. The winter-balance maps between 1974 and 1978 were normalized and averaged. This measured accumulation pattern is used to redistribute solid precipitation during each precipitation event.

The comparison of daily air temperatures measured at Coburg Island Base Camp and Marina Mountain (Fig. 1b) reveals a lapse rate of dT/dz = −5°C km⁻¹ during July and August. As these months are the most important for melt, we used this lapse rate for the modelling. The effect of refreezing meltwater in the winter snow cover is indirectly considered by tuning the parameters of the temperature-index model such that the direct seasonal mass-balance data are matched and the observed mass-balance gradients are reproduced (Fig. 4). Given the paucity of field data, additional parameters that explicitly take into account refreezing (as in, e.g., Reference ReehReeh, 1991) could not be constrained.

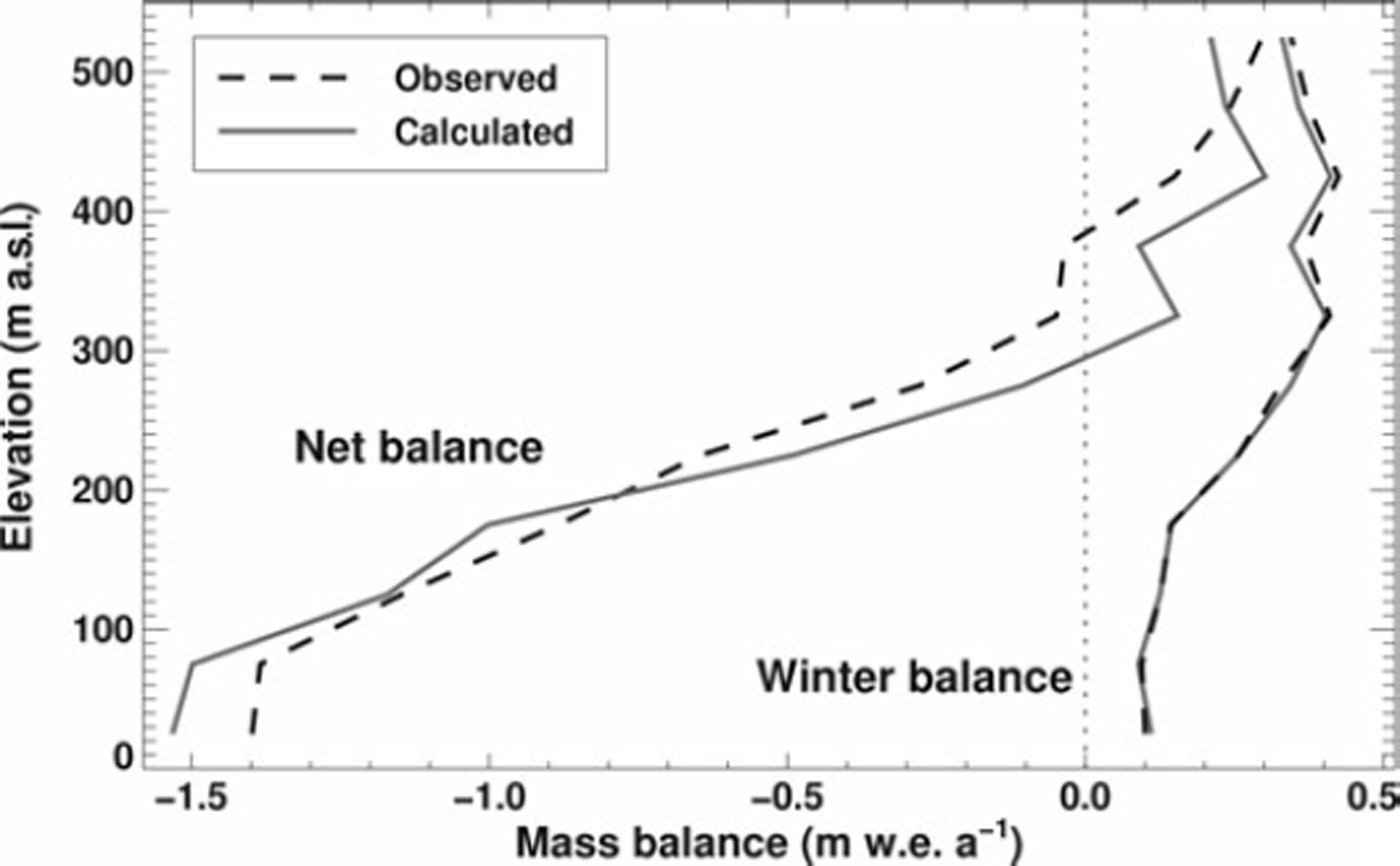
Fig. 4. Comparison of observed and calculated net balance and winter balance in 50 m elevation bands as a mean of the years 1973/74–1978/79.

We define the mean specific net balance, (in m water equivalent), as the sum of accumulation (solid precipitation) and ablation (ice- or snowmelt) over the entire glacier during the hydrological year (1 October to 30 September) divided by that year’s glacier surface area. We calculate ‘conventional’ mass balance (Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others, 2001), i.e. the glacier area is updated annually. The mean specific winter balance, , is determined during the period 1 October to 30 May and summer balance, , from 1 June to 30 September.

Glacier surface-elevation change

In order to account for the change in glacier surface elevation and ice extent over time, we use a simple model based on mass conservation. Glacier surface geometry and extent are updated annually in response to the calculated mass-balance distribution. We refrain from applying a more sophisticated ice-flow model because of the uncertain bedrock elevation (in particular in the accumulation area) and the missing in situ data for validation. Several rigorous assumptions have been made in order to simplify the ice-flow dynamics in our grid-based approach. We assume the glacier to adjust its geometry immediately to a change in surface mass balance. Considering the size and the relatively high mass-balance gradients of Laika Glacier, this approximation is reasonable. The importance of ice flux replacing mass lost by ablation in the tongue is small in periods of glacier retreat, allowing elevation-change rates in the ablation area of Laika Glacier to approach surface melt rates (Reference Blatter and KappenbergerBlatter and Kappenberger, 1988).

Our method of updating the glacier surface considers two cases of mass change: (1) (mass loss of the glacier): Regions where positive mass balances occur in the individual year are assumed to remain constant in surface elevation. The accumulated ice volume, B _acc, is equally distributed over the ablation area. For each gridcell in the ablation area the surface elevation change is given by the sum of the net balance, b _n, and the compensating effect of ice flow, b _comp, in ice equivalent. The value of b _comp is obtained with B _acc/A _abl, where _{A abl} is the area with net ablation. Consequently, near the equilibrium line b _n + b _comp may be positive. We condition the surface elevation not to increase and distribute positive residuals of b _n + b _comp further down-glacier. For ∼90% of the study period case (1) occurs. The assumptions are supported by the observation of small elevation changes in the accumulation area and rapid thinning in the ablation area during a period of glacier retreat on several Arctic ice caps (e.g. Reference AbdalatiAbdalati and others, 2004). (2) (mass gain): Elevation on the entire glacier surface increases with the calculated rate of the mean specific net balance, , in ice equivalent. This uniform thickening is assumed to occur immediately in our model, whereas in nature the spatial elevation-change patterns are more complex and are delayed by several years. However, we consider this simple parameterization to be a first-order approximation of glacier geometry change in the case of a mass gain (calculated for only 6 years of the study period). The glacier extent at the end of each year is inferred by comparing the updated glacier surface elevation with the bedrock elevation at all gridcells. The glacierized area shrinks where the ice thickness drops below zero.

The applied procedure is simple and does not require input data other than the mass-balance distribution, as well as being insensitive to uncertainties in the bedrock elevation, except for regions near the glacier terminus. In comparison to physical ice-flow modelling, our method is an alternative well suited to glaciers for which neither longterm measurements of flow speeds nor exact knowledge of the entire bedrock geometry exist.

Model calibration and validation

The glacier mass-balance and surface-evolution model is calibrated and validated in a multilayer procedure including all available data: (1) ice-volume change of the Laika Glacier tongue for 1959–71, (2) measured distribution of glacier surface net and winter mass balances for 1974–79, (3) extent of Laika Glacier known from aerial photographs in 1971 and the Landsat scenes for 2000–06, (4) GLAS ICESat elevation data for 2006 and (5) the ASTER DEM of 2004. Data types (1) and (2) are used for calibration of the mass-balance model, and (3–5) are used for validation of the combined glacier mass-balance and surface-evolution model.

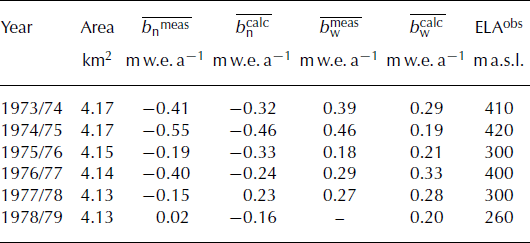
The parameters of the mass-balance model are tuned to match the measured 1959–71 ice-volume change. This is achieved by varying the melt parameters, F _M and r _ice/_snow. The accumulation parameters, C _prec and dP/dz, are calibrated simultaneously to optimize agreement between the calculated and observed seasonal mass-balance gradient (Fig. 4). Comparison of observed point mass balances interpolated on a regular 25 m grid with model results showed an rmse of 0.32 m w.e. for net balance and 0.08 m w.e. for winter balance. Measured and calculated mean specific mass balances are shown in Table 4. Some of the differences are due to varying evaluation periods; calculated mass balance is given in a fixed-date system, whereas field mass balance refers to a measurement period. This bias could only be accounted for in some years, as the dates of the field surveys were not documented systematically.

Table 4. Measured and calculated net balance, , and winter balance, , and observed equilibrium-line altitude (ELA) for Laika Glacier in all years with field data

The model is run for the period 1959–2006 and achieves good agreement with the GLAS elevation data (Fig. 5). The rmse of model and measurements is 1.7 m. Measured glacier outlines in 1971 (aerial photographs) and 2006 (Landsat) are compared to the model results, and the observed glacier extent is reproduced well (Fig. 6). The distribution of surface-elevation change of the tongue of Laika Glacier is captured by the model in 1971 (Fig. 7). The ASTER scene of 2004 provides an independent validation of the model results in the spatial domain. The differences are within the range of uncertainty (±15 m) of the satellite DEM (Fig. 7).

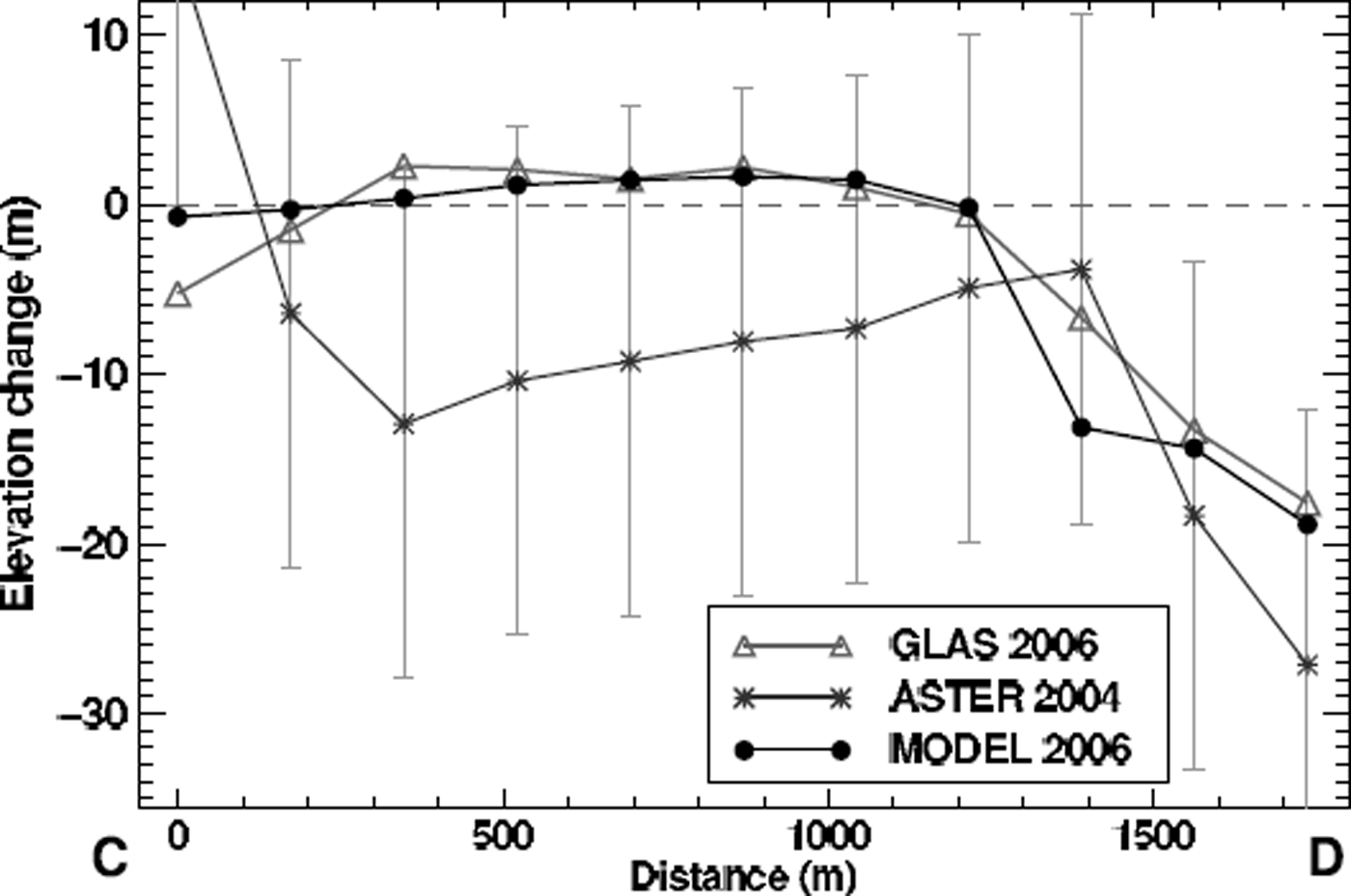
Fig. 5. Comparison of the ICESat GLAS and ASTER elevation data with model results on the glacier cross-profile C–D displayed in Figure 1c. Elevation changes are relative to the glacier surface in 1959. Error bars show the uncertainty in the ASTER DEM.

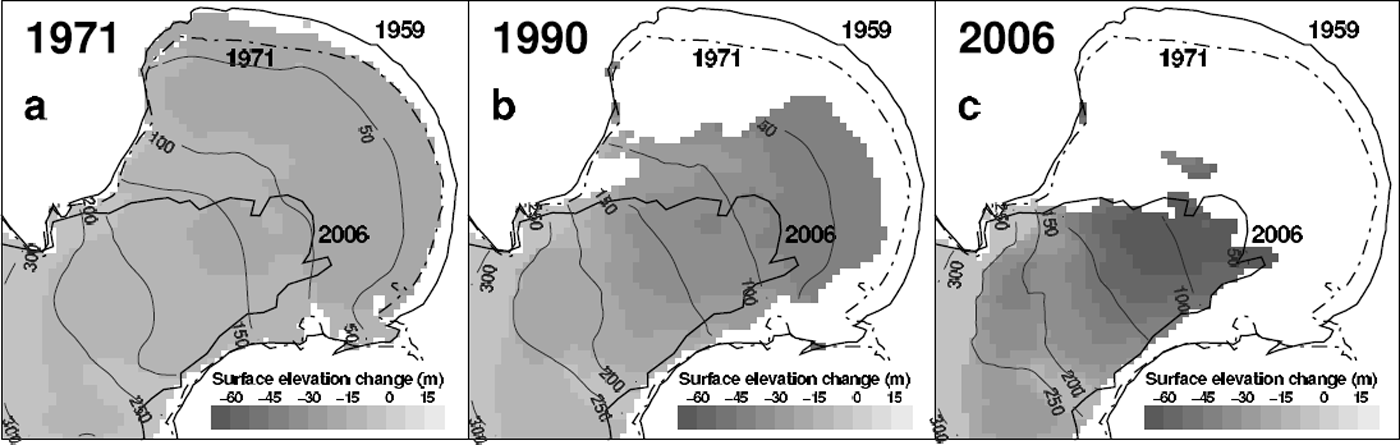
Fig. 6. Calculated extent of the piedmont tongue of Laika Glacier for snapshots in (a) 1971, (b) 1990 and (c) 2006. Observed glacier outlines in 1959, 1971 and 2006 are shown. Grey scales indicate the calculated surface-elevation change since 1959.

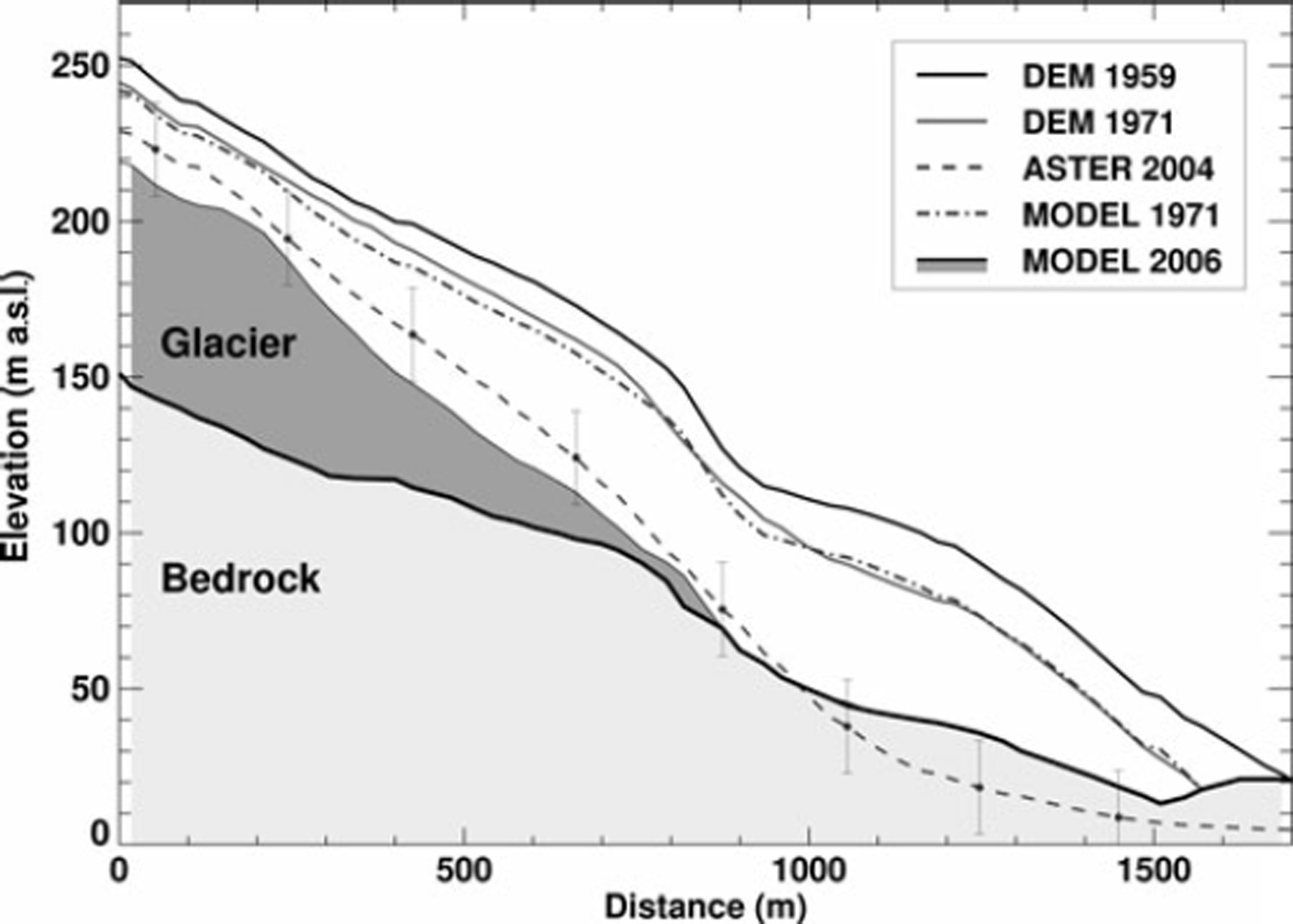
Fig. 7. Longitudinal profile of the piedmont tongue of Laika Glacier (dash-dotted line in Fig.1c). The model is capable of reproducing the surface-elevation change of the glacier tongue between 1959 and 1971 and is consistent with the ASTER DEM within its uncertainty (±15 m). Dark shading represents the glacier in 2006, light shading the bedrock.

Results and Discussion

An increase in surface elevation of ∼2 m is found in the upper reaches of the glacier by comparing the 1959 DEM and the ICESat GLAS elevation data of 2006 (Fig. 5), in spite of a substantial overall mass loss of the glacier. A similar observation was previously made in different regions of the Arctic during sub-decadal time periods (Reference KrabillKrabill and others, 2000; Reference AbdalatiAbdalati and others, 2004; Reference Bamber, Krabill, Raper and DowdeswellBamber and others, 2004). Interior thickening was attributed to an increase in precipitation by Reference AbdalatiAbdalati and others (2004). Shallow ice-coring on Devon Ice Cap, however, does not support this interpretation (Reference Colgan and SharpColgan and Sharp, 2008). Reference KoernerKoerner (2005) explains the observed thickening by a change in ice dynamics. Ice flow from the accumulation to the ablation area has decreased, leading to a rapid thinning at the glacier margin and an increase in surface elevation in the interior. Our study cannot provide a final solution to this question, but shows that a small Arctic glacier exhibits a behaviour similar to that reported for larger ice caps. Furthermore, our results indicate that the trend of peripheral thinning and interior thickening is even revealed when considering a period of five decades.

Significant lowering of the surface occurs in the lower reaches of the glacier (Figs 6 and 7). Glacier surface elevation decreased by up to 50 m near the current glacier tongue, which corresponds to mean thinning rates of >1 m a⁻¹. This has led to a substantial retreat of Laika Glacier over the past five decades. A disintegration of its piedmont tongue was initiated two decades ago. Interestingly, about one-third of the elevation changes on the piedmont tongue of Laika Glacier occurred in the period 1959–71, the first decade of the study period. Glacier retreat slowed in the 1970s and displayed increasing rates again in the 1980s and 1990s (Fig. 8). Laika Glacier decreased in area by 23% and lost 24% of its volume between 1959 and 2006.

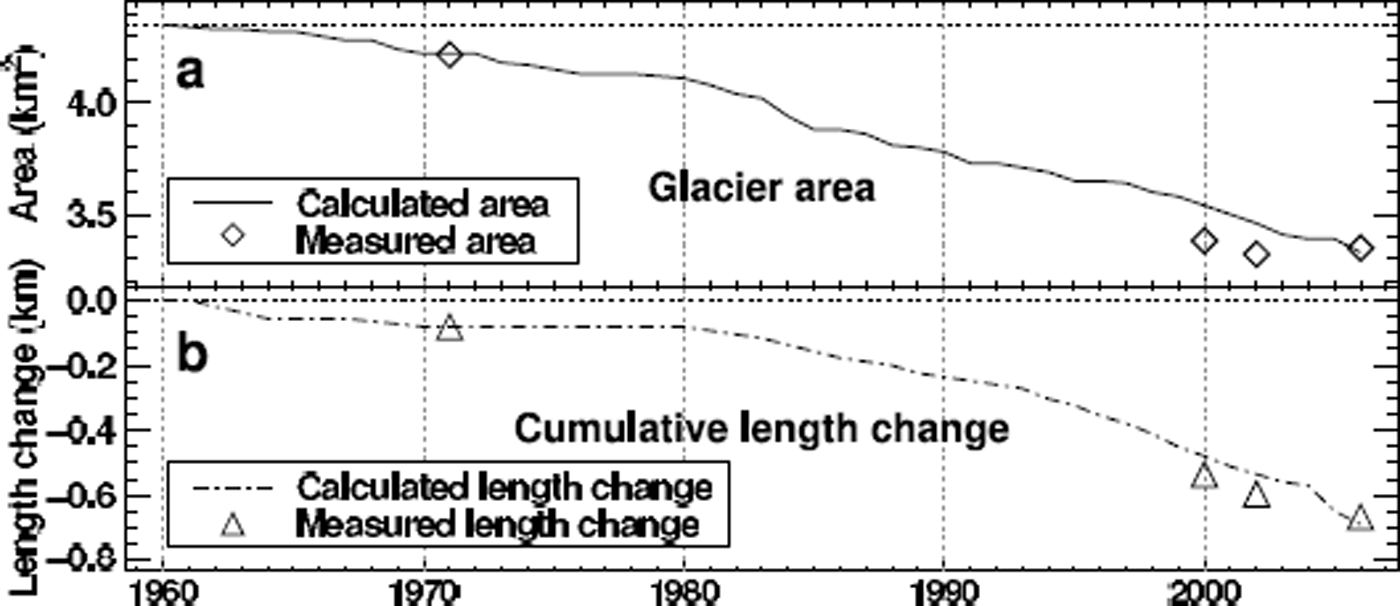
Fig. 8. Calculated time series of (a) glacier area and (b) length change of Laika Glacier in 1959–2006. Measured data points (area and length) based on photogrammetry and Landsat images are shown.

The cumulative modelled mass balance is −19.6 m w.e. (Fig. 9). The first 3 years of the study period are characterized by highly negative summer balances. The rate of mass loss shows no accelerating trend (Fig. 9). Mass loss by increased melt due to rapidly rising air temperatures (Fig. 3) is partly compensated by higher precipitation sums and the substantial decline in glacier area at low elevations (Fig. 6).

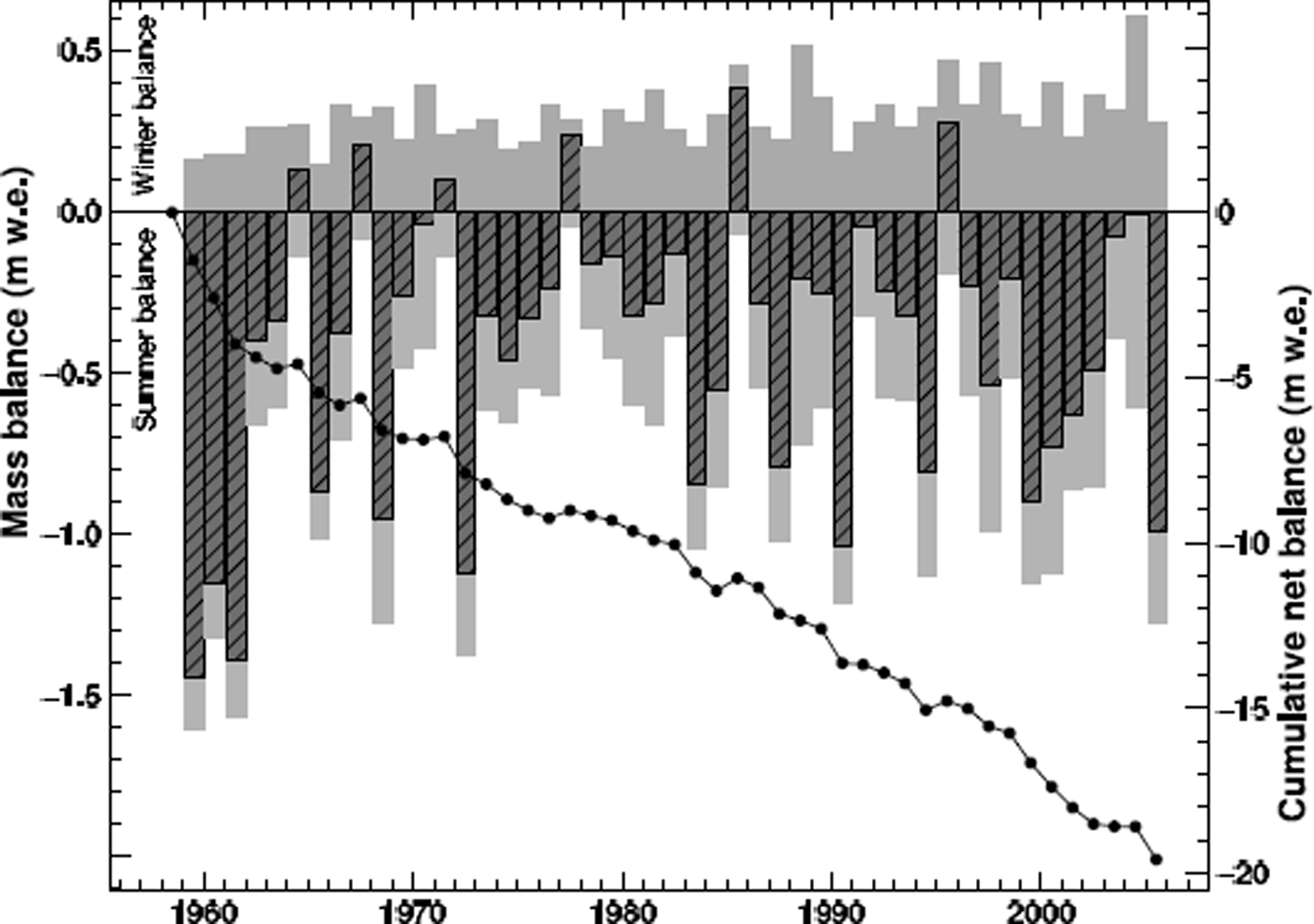
Fig. 9. Calculated mean specific mass balances shown in bars: winter balance, (positive), summer balance, (negative), net balance, (hatched), and cumulative net balance of Laika Glacier in 1959–2006.

We compare the mass-balance time series derived in this study to the data of the northwest part of Devon Ice Cap (Haeberli and others, 2000; Reference KoernerKoerner, 2005), situated ∼80 km from Coburg Island. Laika Glacier exhibits much higher cumulative mass losses and larger annual fluctuations of the mass balance (Fig. 9). The average mean specific net balance of the entire Devon Ice Cap is estimated as −0.13 m w.e. a⁻¹ for the period 1963–2000 (Reference Mair, Burgess and SharpMair and others, 2005), whereas it is −0.33 m w.e. a⁻¹ for Laika Glacier during the same period.

The mean equilibrium-line altitude is ∼350 m a.s.l. on Laika Glacier (Table 4). This is much lower than on Devon Ice Cap or on White Glacier, where the multi-decadal ELA is ∼1000 m a.s.l. (Haeberli and others, 2000). We attribute this difference to higher precipitation sums on Coburg Island due to the vicinity to the North Water Polynya. The low elevation of Laika Ice Cap makes it highly sensitive to changes in air temperature.

The model results enable us to calculate altitudinal mass-balance gradients directly derived from the gridded datasets of mass-balance distribution. The mean mass balance of Laika Glacier was evaluated in 5 year intervals in five elevation bands (Fig. 10). In the lower reaches of Laika Glacier the mass balance becomes increasingly negative, whereas there is only a minor decrease in net accumulation in the highest regions of the glacier. We find a mass-balance gradient of −0.005 a⁻¹ during the first two decades of the study period and −0.007 a⁻¹ at the beginning of the 21st century (Fig. 10). Increasing mass-balance gradients have been observed on various glaciers and indicate higher mass turnover and, thus, increased sensitivity to climate change (Reference DyurgerovDyurgerov, 2003).

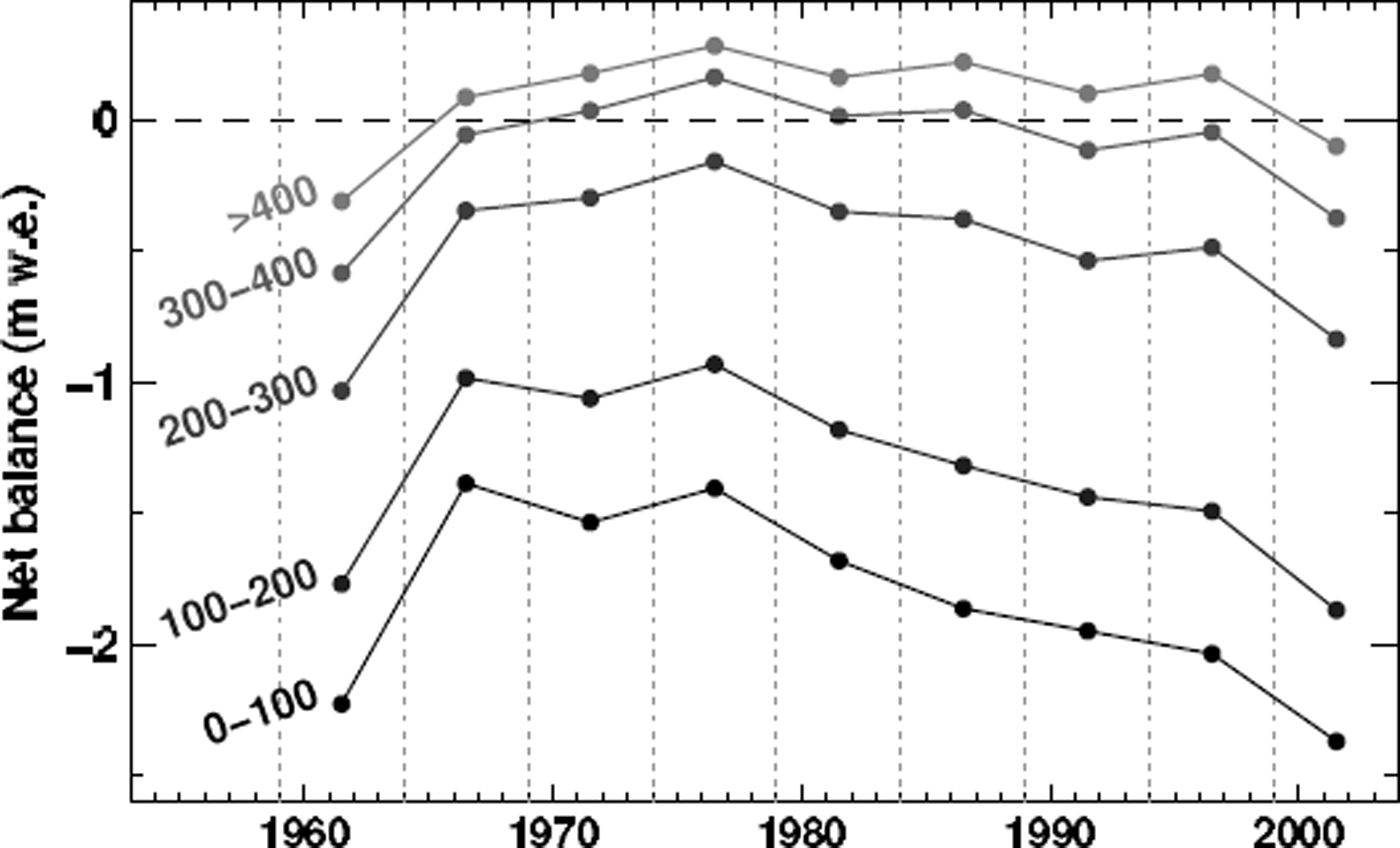
Fig. 10. Calculated mean net balances evaluated in 5 year intervals for five elevation ranges of Laika Glacier. Numbers on the left give the altitudinal extent in m a.s.l. of the elevation band considered.

The calibrated glacier mass-balance and surface-evolution model is run for the 21st century in order to estimate the stability of Laika Glacier during the next decades. We assume linear trends of air temperature and precipitation based on the SRES A1B scenario (Reference SolomonSolomon and others, 2007). In order to force the glacier model we construct a future daily meteorological time series. We randomly select years of the composite 1959–2006 series, shift their annual means to the anticipated mean values of temperature and precipitation and perform ten model runs in order to eliminate effects of intra-annual meteorological variability on the results. The means of these multiple model runs are presented. The parameters calibrated in the past are assumed to be constant in the future.

A rate of air-temperature rise of +0.05°C a⁻¹ and a change in annual precipitation of +0.2% a⁻¹ are assumed (Fig. 11a and b). The model results indicate a decrease in glacier area of 48% by 2050 compared to 1959. Laika Glacier is expected to have lost 59% of the 1959 ice volume by 2050 (Fig. 11d and e). After about 2045 the equilibrium line lies above the summit of Laika Glacier in all years, impeding net accumulation (Fig. 11c). This leads to accelerated glacier wastage and a complete disappearance of Laika Glacier before the end of the 21st century.

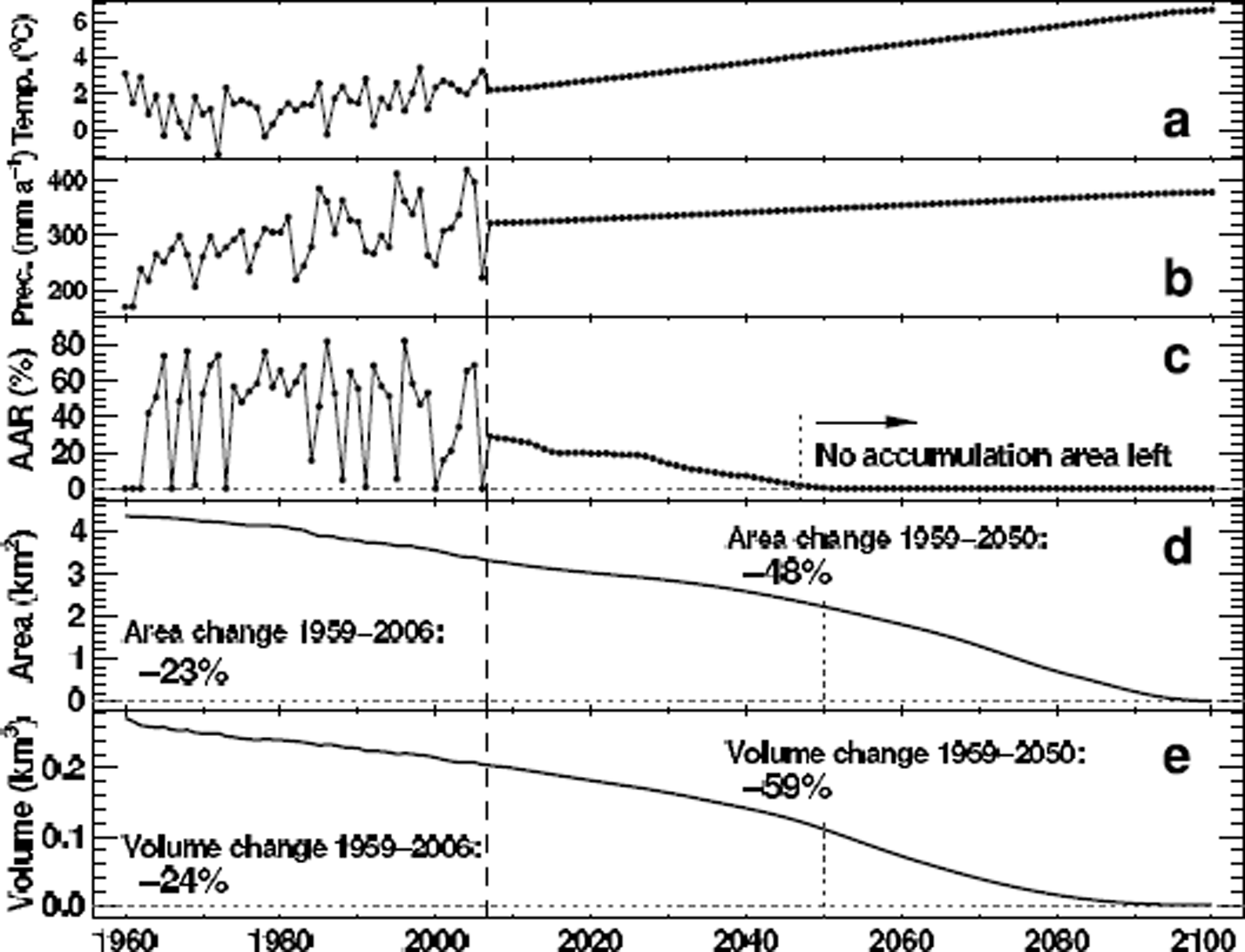
Fig. 11. Projections of future changes in Laika Glacier based on the SRES A1B scenario (Reference SolomonSolomon and others, 2007). Time series of (a) June–September air temperatures and (b) annual precipitation; (c) calculated accumulation-area ratio (AAR) of Laika Glacier and (d) changes in glacier area and (e) ice volume. Data points before 2006 are modelled using the composite meteorological series (Fig. 3).

The glacier model has several limitations. (1) By calibrating the melt parameters using the direct mass-balance measurements performed in the 1970s the percentage of meltwater refreezing in the snow cover is implicitly assumed to remain constant over time. This may not be the case in a dynamically changing climate system and could lead to errors in the projections of future ice extent. (2) The representation of the change in firn cover and the parameterization of the melt rates over firn are not well backed up with in situ measurements. (3) Altitudinal temperature gradients over glacierized surfaces display significant variations (e.g. Reference Marshall, Sharp, Burgess and AnslowMarshall and others, 2007). We assume a constant lapse rate found by comparing two weather stations on Coburg Island. Nevertheless, the glacier mass-balance and surface-evolution model is able to match various field-data types covering different time periods within their range of uncertainty. Our model approach seems to be a reasonable description of the most important processes governing the retreat of Laika Glacier.

Conclusions

The temporal and spatial changes of Laika Glacier during the past five decades were assessed using in situ measurements, observations from space and modelling. We provide homogenized long-term mass-balance time series for a small glacier in the Canadian Arctic. A substantial mass loss of Laika Glacier during the last five decades is inferred; the calculated cumulative mass balance is −19.6 m w.e., corresponding to −0.41 m w.e.a⁻¹. Laika Glacier has decreased in area and ice volume by >20% between 1959 and 2006, and its piedmont tongue is in a state of disintegration. Our results indicate a significant trend towards higher mass-balance gradients. Model runs driven by climate scenarios predict an acceleration of glacier retreat and the disappearance of Laika Glacier before the end of the 21st century. This study provides evidence for the rapid wastage of small Arctic glaciers in response to recent climatic warming.

Our methodology merges large-scale climate re-analysis datasets (ERA-40, NARR) and satellite remote-sensing data from various sensors (Landsat, ICESat, ASTER) with direct field measurements. None of these datasets is complete in terms of spatial coverage and temporal resolution. A distributed glacier mass-balance and surface-evolution model allows gaps to be closed and glacier mass changes in high temporal and spatial resolution to be derived. The combination of datasets complementing each other and modelling is of benefit and may provide comprehensive and accurate information on long-term glacier change. We emphasize that such research needs to be concurrently executed with field measurements, not only to provide a ‘reality check’, but also to maintain and further develop glacier models and satellite remote-sensing algorithms.