1 Introduction
Go (2022) is a statically typed programming language introduced by Google in 2009. It supports method overloading by allowing multiple declarations of the same method signature for different receivers. Receivers are structs, similar to structs in C. The language also supports interfaces; as in many object-oriented languages, an interface consists of a set of method signatures. But unlike in many object-oriented languages, subtyping in Go is structural not nominal.
Earlier work by Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020) introduces Featherweight Go (FG), a minimal core calculus that covers method overloading, structs, interfaces, and structural subtyping. Their work specifies static typing rules and a dynamic semantics for FG based on runtime method lookup. However, the actual Go implementation appears to employ a different dynamic semantics. Quoting Griesemer and co-workers: “ Go is designed to enable efficient implementation. Structures are laid out in memory as a sequence of fields, while an interface is a pair of a pointer to an underlying structure and a pointer to a dictionary of methods.”
In our own prior work (Sulzmann & Wehr, Reference Sulzmann and Wehr2021, Reference Sulzmann and Wehr2022), we formalize a type-directed dictionary-passing translation for FG and establish its semantic equivalence with FG’s dynamic semantics. Griesemer et al. also introduce Featherweight Generic Go (FGG), an extension of FG with generics. In this work, we show how our translation approach can be extended to deal with generics. Our focus is on the integration of generics with method overloading and structural subtyping. Hence, we consider
![]() ${\textrm{FGG}^{-}}{}$
, which is equivalent to FGG but does not support type assertions. Our contributions are as follows:
${\textrm{FGG}^{-}}{}$
, which is equivalent to FGG but does not support type assertions. Our contributions are as follows:
• We specify the translation of source
 ${\textrm{FGG}^{-}}$
programs to an untyped
${\textrm{FGG}^{-}}$
programs to an untyped
 $\lambda$
-calculus with recursive let-bindings, constructors, and pattern matching. We employ a dictionary-passing translation scheme à la type classes (Hall et al., Reference Hall, Hammond, Peyton Jones and Wadler1996) to statically resolve overloaded method calls. The translation is guided by the typing of the
$\lambda$
-calculus with recursive let-bindings, constructors, and pattern matching. We employ a dictionary-passing translation scheme à la type classes (Hall et al., Reference Hall, Hammond, Peyton Jones and Wadler1996) to statically resolve overloaded method calls. The translation is guided by the typing of the
 ${\textrm{FGG}^{-}}$
program. As the typing rules include a subsumption rule, the translation is inherently nondeterministic.
${\textrm{FGG}^{-}}$
program. As the typing rules include a subsumption rule, the translation is inherently nondeterministic.• We establish the semantic correctness of the dictionary-passing translation. The result relies on a syntactic, step-indexed logical relation (LR) to ensure well-foundedness of definitions in the presence of recursive interface types and recursive methods.
• We show that values produced by different translations of the same program are identical up to dictionaries embedded inside these values.
• We report on an implementation of the translation.
The upcoming Section 2 presents an overview of our translation by example. Section 3 gives a recap of the source language
![]() ${\textrm{FGG}^{-}}$
, whereas Section 4 defines the target language (TL) and the translation itself. Next, Section 5 establishes the formal properties of the translation, and rigorous proofs of our results can be found in the Appendix. Section 6 presents the implementation, and Section 7 covers related work. Finally, Section 8 summarizes this work and points out directions for future work.
${\textrm{FGG}^{-}}$
, whereas Section 4 defines the target language (TL) and the translation itself. Next, Section 5 establishes the formal properties of the translation, and rigorous proofs of our results can be found in the Appendix. Section 6 presents the implementation, and Section 7 covers related work. Finally, Section 8 summarizes this work and points out directions for future work.
2 Overview
This section introduces FGG (Griesemer et al., Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020) and our type-directed dictionary-passing translation through a series of examples. FGG is a tiny model of Go that includes essential typing features such as method overloading, structs, interfaces, structural subtyping, and the extension with generics. Its original formulation also includes type assertions (dynamic type casts). As we omitted this feature from our translation, we use the name
![]() ${\textrm{FGG}^{-}}{}$
to refer to the source language of our translation. Except for the omission of type assertions,
${\textrm{FGG}^{-}}{}$
to refer to the source language of our translation. Except for the omission of type assertions,
![]() ${\textrm{FGG}^{-}}{}$
and FGG are equivalent.
${\textrm{FGG}^{-}}{}$
and FGG are equivalent.
An
![]() ${\textrm{FGG}^{-}}$
program consists of declarations for structs, interfaces, methods, and a main function. Function and method bodies only contain a single return statement, and all expression are free from side effects. For the examples in this section, we extend
${\textrm{FGG}^{-}}$
program consists of declarations for structs, interfaces, methods, and a main function. Function and method bodies only contain a single return statement, and all expression are free from side effects. For the examples in this section, we extend
![]() ${\textrm{FGG}^{-}}$
with primitive types for integers and strings, with an operator + for string concatenation and a builtin function intToString, with definitions of local variables, and with function definitions.
${\textrm{FGG}^{-}}$
with primitive types for integers and strings, with an operator + for string concatenation and a builtin function intToString, with definitions of local variables, and with function definitions.
We will first consider
![]() ${\textrm{FGG}^{-}}$
without generics to highlight the idea behind our type-directed dictionary-passing translation scheme. Then, we show how the translation scheme can be adapted to deal with the addition of generics. All examples have been checked against our implementation
Footnote 1
of the translation.
${\textrm{FGG}^{-}}$
without generics to highlight the idea behind our type-directed dictionary-passing translation scheme. Then, we show how the translation scheme can be adapted to deal with the addition of generics. All examples have been checked against our implementation
Footnote 1
of the translation.
2.1 Starting without generics
The upper part of Figure 1 shows an (extended)
![]() ${\textrm{FGG}^{-}}{}$
program for formatting values as strings. The code does not use generics yet.
${\textrm{FGG}^{-}}{}$
program for formatting values as strings. The code does not use generics yet.

Fig. 1. String-formatting and its translation.
Structs in Go are similar to structs in C. A syntactic difference is the Go convention that field or variable names precede their types. Here, struct Num has a single field val of type int, so it simply acts as a wrapper for integers.
Interfaces in Go declare sets of method signatures sharing the same receiver where method names must be distinct and the receiver is left implicit. Interfaces are types and describe all receivers that implement the methods declared by the interface. In our example, interface Format declares a method format for rendering its receiver as a string. The second interface Pretty also declares format but adds a second method pretty with the intention to produce a visually more attractive output.
Methods and functions are introduced via the keyword func. A method can be distinguished from a function as the receiver argument in parenthesis precedes the method name. Methods can be overloaded on the receiver type. In lines 5 and 6, we find methods format and pretty, respectively, for receiver type Num. In the body of format, we assume a builtin function intToString for converting integers to strings. Lines 8 and 10 define two functions.
An interface only names a set of method signatures, its definition is not required for a method to be valid. For example, the methods in lines 5 and 6 could be defined without the interfaces in lines 2 and 3, or the methods could be placed before the interfaces.
However, interfaces and method definitions imply structural subtype relations. Interface Format contains a subset of the methods declared by interface Pretty. Hence, Prettys a structural subtype of Format, written (1)
![]() ${{{{{{{\texttt{Pretty} \mathrel{<:} \texttt{Format}}}}}}}}$
. Line 5 defines method format for receiver type Num, we say that Num implements method format. Hence, Num is a structural subtype of Format, written (2)
${{{{{{{\texttt{Pretty} \mathrel{<:} \texttt{Format}}}}}}}}$
. Line 5 defines method format for receiver type Num, we say that Num implements method format. Hence, Num is a structural subtype of Format, written (2)
![]() ${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
. Receiver Num also implements the pretty method, see line 6. Hence, we also find that (3)
${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
. Receiver Num also implements the pretty method, see line 6. Hence, we also find that (3)
![]() ${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Pretty}}}}}}}}$
. Structural subtype relations play a crucial role when type-checking programs.
${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Pretty}}}}}}}}$
. Structural subtype relations play a crucial role when type-checking programs.
For example, consider the function call formatSome(Num{1}) in line 11. Here, formatSome(Num{1}) is a value of the Num struct with val set to 1. From above, we find that (2)
![]() ${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
. That is, Num implements the Format interface and therefore the function call type-checks. Consider the variable declaration and assignment in line 12. Value formatSome(Num{2}) is assigned to a variable of interface type Pretty. Based on the subtype relation (3)
${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
. That is, Num implements the Format interface and therefore the function call type-checks. Consider the variable declaration and assignment in line 12. Value formatSome(Num{2}) is assigned to a variable of interface type Pretty. Based on the subtype relation (3)
![]() ${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Pretty}}}}}}}}$
the assignment type-checks. Consider the function call formatSome(pr) in line 13, where pr has type Pretty. Based on the subtype relation (1)
${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Pretty}}}}}}}}$
the assignment type-checks. Consider the function call formatSome(pr) in line 13, where pr has type Pretty. Based on the subtype relation (1)
![]() ${{{{{{{\texttt{Pretty} \mathrel{<:} \texttt{Format}}}}}}}}$
the function call type-checks.
${{{{{{{\texttt{Pretty} \mathrel{<:} \texttt{Format}}}}}}}}$
the function call type-checks.
In Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020), the dynamic behavior of programs is explained via runtime lookup of methods, where based on the receiver’s runtime type the appropriate method definition is selected. The Go (and FGG/FGG-) conditions demand that for each method name and receiver type, there can be at most one definition. This guarantees that method calls can be resolved unambiguously.
2.2 Type-directed translation
We explain the meaning of extended
![]() ${\textrm{FGG}^{-}}{}$
programs by translation into an untyped
${\textrm{FGG}^{-}}{}$
programs by translation into an untyped
![]() $\lambda$
-calculus with recursive top-level definitions, let-bindings, pattern matching, integers, strings, an operator ++ for string concatenation, and a builtin function intToString. We will use a Haskell-style notation.
$\lambda$
-calculus with recursive top-level definitions, let-bindings, pattern matching, integers, strings, an operator ++ for string concatenation, and a builtin function intToString. We will use a Haskell-style notation.
Method definitions belonging to an interface are grouped together in a dictionary of methods. Thus, method calls can be turned into primitive function calls by simply looking up the appropriate method in the dictionary. Structural subtype relations are turned into coercion functions that transform, for example, a struct value into an interface value to make sure that the appropriate dictionaries are available. Where to insert dictionaries and coercions in the program is guided by the type-checking rules. Hence, the translation is type-directed.
Our translation strategy can be summarized as follows:
Struct. An
![]() ${\textrm{FGG}^{-}}$
value at the type of a struct with n fields is represented by an n-tuple holding the values of the fields. We call such an n-tuple a struct value.
${\textrm{FGG}^{-}}$
value at the type of a struct with n fields is represented by an n-tuple holding the values of the fields. We call such an n-tuple a struct value.
Interface. An
![]() ${\textrm{FGG}^{-}}$
value at the type of an interface is represented as a pair
${\textrm{FGG}^{-}}$
value at the type of an interface is represented as a pair
![]() $(V, \mathcal{D})$
, where V is a struct value and
$(V, \mathcal{D})$
, where V is a struct value and
![]() $\mathcal D$
is a method dictionary. Such a method dictionary is a tuple holding implementations of all interface methods for V, in order of declaration in the interface. We call the pair
$\mathcal D$
is a method dictionary. Such a method dictionary is a tuple holding implementations of all interface methods for V, in order of declaration in the interface. We call the pair
![]() $(V, \mathcal{D})$
an interface value.
$(V, \mathcal{D})$
an interface value.
Coercion. A structural subtype relation
![]() $\tau \mathrel{<:} \sigma$
implies a coercion function to transform the target representation of an
$\tau \mathrel{<:} \sigma$
implies a coercion function to transform the target representation of an
![]() ${\textrm{FGG}^{-}}$
value at type
${\textrm{FGG}^{-}}$
value at type
![]() $\tau$
into a representation at type
$\tau$
into a representation at type
![]() $\sigma$
.
$\sigma$
.
The lower part of Figure 1 gives the translation of our running example. In this overview section, we identify a 1-tuple with the single value it holds.
For each field name, we assume a helper function to access the field component, see line 16. Method calls on interface values look up the respective method definition in the dictionary and apply it to the struct value embedded inside the interface value. See lines 19–21. Method definitions translate to plain functions, see lines 24–25. Recall that for each method name and receiver type, there can be at most one definition. Hence, the generated function names are all distinct.
Structural subtype relations translate to coercions, see lines 28–30. For example, (2)
![]() ${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
translates to the
${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
translates to the
![]() $\mathtt{toFormat}_{\texttt{Num}}$
coercion. Input parameter x represents a target representation of a Num value. The output
$\mathtt{toFormat}_{\texttt{Num}}$
coercion. Input parameter x represents a target representation of a Num value. The output ![]() is an interface value holding the receiver and the corresponding method definition. Coercion
is an interface value holding the receiver and the corresponding method definition. Coercion
![]() $\mathtt{toPretty}_{\texttt{Num}}$
corresponds to (3)
$\mathtt{toPretty}_{\texttt{Num}}$
corresponds to (3)
![]() ${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Pretty}}}}}}}}$
and coercion
${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Pretty}}}}}}}}$
and coercion
![]() $\mathtt{toFormat}_{{\texttt{Pretty}}}$
to (1)
$\mathtt{toFormat}_{{\texttt{Pretty}}}$
to (1)
![]() ${{{{{{{\texttt{Pretty} \mathrel{<:} \texttt{Format}}}}}}}}$
.
${{{{{{{\texttt{Pretty} \mathrel{<:} \texttt{Format}}}}}}}}$
.
The translation of the main function, starting at line 35, is guided by the type-checking of the source program. Each application of a structural subtype relation leads to the insertion of the corresponding coercion function in the target program. For example, the function call formatSome(Num{1}) translates to
![]() $\texttt{formatSome}~\texttt{(toFormat}_{{\texttt{Num}}}~\texttt{1)}$
because typing of the source requires (2)
$\texttt{formatSome}~\texttt{(toFormat}_{{\texttt{Num}}}~\texttt{1)}$
because typing of the source requires (2)
![]() ${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
. The other coercions arise for similar reasons.
${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
. The other coercions arise for similar reasons.
2.3 Adding generics
We extend our running example by including pairs, see Figure 2. The struct type Pair[T Any, U Any] is generic in the type of the pair components, T and U are type variables. When introducing type variables, we must also specify an upper type bound to constrain the set of concrete types that will replace type variables. The bounded type parameter T Any can therefore be interpreted as
![]() $\forall \texttt{T}. \texttt{T} \mathrel{<:} \texttt{Any}$
. Upper bounds are always interface types. The upper bound Any is satisfied by any type because the set of methods that need to be implemented is empty.
$\forall \texttt{T}. \texttt{T} \mathrel{<:} \texttt{Any}$
. Upper bounds are always interface types. The upper bound Any is satisfied by any type because the set of methods that need to be implemented is empty.

Fig. 2. String-formatting with generics (extending code from Figure 1).
To format pairs, we need to format the left and right component that are of generic types T and U. Hence, the method definition for format in line 4 states the type bound Format for type variables T and U. In general, bounds of type parameters for the receiver struct of a method declaration must be in a covariant subtype relation relative to the bounds in the struct declaration. This is guaranteed in our case as we find
![]() ${{{{{{{\texttt{Format} \mathrel{<:} \texttt{Any}}}}}}}}$
. Importantly, the type bounds in line 4 imply the subtype relations (4)
${{{{{{{\texttt{Format} \mathrel{<:} \texttt{Any}}}}}}}}$
. Importantly, the type bounds in line 4 imply the subtype relations (4)
![]() ${{{{{{{\texttt{T} \mathrel{<:} \texttt{Format}}}}}}}}$
and (5)
${{{{{{{\texttt{T} \mathrel{<:} \texttt{Format}}}}}}}}$
and (5)
![]() ${{{{{{{\texttt{U} \mathrel{<:} \texttt{Format}}}}}}}}$
. Thus, we can show that the method body type-checks. For example, expression this.left is of type T. Based on (4), this expression is also of type Format and therefore the method call in line 5 this.left.format() type-checks.
${{{{{{{\texttt{U} \mathrel{<:} \texttt{Format}}}}}}}}$
. Thus, we can show that the method body type-checks. For example, expression this.left is of type T. Based on (4), this expression is also of type Format and therefore the method call in line 5 this.left.format() type-checks.
We consider type-checking the main function. Instances for generic type variables must always be explicitly supplied. Hence, when constructing a pair that holds number values, see line 9, we find Pair[Num, Num].
Consider the method call p.format() in line 10. The receiver struct Pair[T Format, U Format] of the method definition in line 4 matches p’s type Pair[Num, Num] by replacing T and U by Num. The type bounds in the receiver type are satisfied as we know from above that (2)
![]() ${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
. Hence, the method call type-checks.
${{{{{{{\texttt{Num} \mathrel{<:} \texttt{Format}}}}}}}}$
. Hence, the method call type-checks.
By generalizing the above argument, we find that
That is, under the assumptions
![]() ${{{{{{{\texttt{T} \mathrel{<:} \texttt{Format}}}}}}}}$
and
${{{{{{{\texttt{T} \mathrel{<:} \texttt{Format}}}}}}}}$
and
![]() ${{{{{{{\texttt{U} \mathrel{<:} \texttt{Format}}}}}}}}$
, we can derive that
${{{{{{{\texttt{U} \mathrel{<:} \texttt{Format}}}}}}}}$
, we can derive that
![]() ${{{{{{{\texttt{Pair[T, U]} \mathrel{<:} \texttt{Format}}}}}}}}$
. In particular, we find that
${{{{{{{\texttt{Pair[T, U]} \mathrel{<:} \texttt{Format}}}}}}}}$
. In particular, we find that
![]() ${{{{{{{\texttt{Pair[Num, Num]} \mathrel{<:} \texttt{Format}}}}}}}}$
. Hence, the function call formatSome(p) in line 11 type-checks.
${{{{{{{\texttt{Pair[Num, Num]} \mathrel{<:} \texttt{Format}}}}}}}}$
. Hence, the function call formatSome(p) in line 11 type-checks.
Extending our type-directed translation scheme to deal with generics turns out to be fairly straightforward.
Bounded type parameter. A bounded type parameter T Ifce where T is a type variable and Ifce is an interface type becomes a coercion parameter toIfce
![]() $_{{\texttt{T}}}$
. At instantiation sites, coercions need to be inserted.
$_{{\texttt{T}}}$
. At instantiation sites, coercions need to be inserted.
The lower part of Figure 2 shows the translated program. Starting at line 18 we find the translation of the definition of method format for pairs. Each bounded type parameter T Format and U Format is turned into a coercion parameter ![]() . In the target, we use a curried function definition where coercion parameters are collected in a tuple.
. In the target, we use a curried function definition where coercion parameters are collected in a tuple.
A method call of format needs to supply concrete instances for these coercion parameters. See line 27 which is the translation of calling format on receiver type Pair[Num,Num]. Hence, we must pass as the first argument the tuple of coercions
![]() $\texttt{(toFormat}_{{\texttt{Num}}}$
,
$\texttt{(toFormat}_{{\texttt{Num}}}$
,
![]() $\texttt{(toFormat}_{{\texttt{Num}}}\texttt{)}$
to
$\texttt{(toFormat}_{{\texttt{Num}}}\texttt{)}$
to
![]() $\texttt{format}_{{\texttt{Pair}}}$
.
$\texttt{format}_{{\texttt{Pair}}}$
.
Subtype relation (6) implies the (parameterized) coercion ![]() in line 23. Given coercions
in line 23. Given coercions ![]() and
and ![]() , we can transform a pair p into an interface value for Format, where the method dictionary consists of the partially applied translated method definition
, we can transform a pair p into an interface value for Format, where the method dictionary consists of the partially applied translated method definition ![]() .
.
We make use of ![]() in the translation of the function call formatSome(p), see line 28. Based on the specific coercion
in the translation of the function call formatSome(p), see line 28. Based on the specific coercion ![]() , the call
, the call ![]() transforms the pair value p into the interface value
transforms the pair value p into the interface value ![]() . Then, we call formatSome on this interface value.
. Then, we call formatSome on this interface value.
2.4 Bounded type parameters of methods
There may be bounded type parameters local to methods. Consider Figure 3 where we further extend our running example. Starting at line 1 we find a definition of method formatSep for pairs. This method takes an argument s that acts as a separator when formatting pairs. Argument s is of the generic type S constrained by the type bound Format. Type parameter S is local to the method and not connected to the receiver struct. Type arguments for S must also be explicitly specified in the program text, see method calls in lines 8 and 13.

Fig. 3. Bounded type parameters of methods (extending code from Figure 2).
In the translation, bounded type parameters of methods simply become additional coercion parameters. Consider the translation of formatSep defined on pairs starting at line 21. The translated method definition first expects the coercion parameters ![]() that result from the bounded type parameters T Format and U Format of the receiver. Then, we find the receiver argument this followed by the coercion parameter
that result from the bounded type parameters T Format and U Format of the receiver. Then, we find the receiver argument this followed by the coercion parameter ![]() resulting from S Format and finally the method argument s. The translation of the method body follows the scheme we have seen so far, see lines 22–24. When calling method formatSep on a pair, we need to provide the appropriate coercions, see line 37.
resulting from S Format and finally the method argument s. The translation of the method body follows the scheme we have seen so far, see lines 22–24. When calling method formatSep on a pair, we need to provide the appropriate coercions, see line 37.
From the method definition of formatSep for pairs and from the definition of interface FormatSep, we find that the following subtype relation holds:
Subtype relation (7) implies the coercion ![]() in line 28. Thus, the function call of formatSepSome from line 14 translates to the target code starting in line 38.
in line 28. Thus, the function call of formatSepSome from line 14 translates to the target code starting in line 38.
The point to note is that a coercion parameter corresponding to a bounded type parameter of a method is not part of the dictionary; it is only supplied at the call site of the method. Consider the call x.formatSep[Format](s) in line 8. In the translation (line 33), we first partially apply the respective dictionary entry on the receiver. This is done via the target expression ![]() . Type Format is a valid instantiation for type parameter S of formatSep because
. Type Format is a valid instantiation for type parameter S of formatSep because
![]() ${{{{{{{\texttt{Format} \mathrel{<:} \texttt{Format}}}}}}}}$
in
${{{{{{{\texttt{Format} \mathrel{<:} \texttt{Format}}}}}}}}$
in
![]() ${\textrm{FGG}^{-}}$
. In the translation, this corresponds to the (identity) coercion
${\textrm{FGG}^{-}}$
. In the translation, this corresponds to the (identity) coercion ![]() . Hence, we supply the remaining arguments
. Hence, we supply the remaining arguments ![]() and s.
and s.
2.5 Bounded type parameters of structs and interfaces
Structs and interfaces may also carry bounded type parameters. In
![]() ${\textrm{FGG}^{-}}{}$
and FGG, these type parameters do not have a meaning at runtime as their purpose is only to rule out more programs statically. Hence, in our translation approach, they do not translate into additional dictionary parameters or coercions.
${\textrm{FGG}^{-}}{}$
and FGG, these type parameters do not have a meaning at runtime as their purpose is only to rule out more programs statically. Hence, in our translation approach, they do not translate into additional dictionary parameters or coercions.
Let us explain with the example in Figure 4. Struct FPair (short for “formatted pairs”) requires the type bound Format on its type parameters. The generic interface Factory defines a factory method returning formatted pairs. It requires a type bound T Format for the type FPair[T, T] in its method signature to be well formed. The need for this type bound arises because FGG’s type system does not allow to conclude from just an occurrence of FPair[T, T] that T is already a subtype of Format.

Fig. 4. Bounded type parameters of structs and interfaces (extending code from Figure 1).
Struct MyFactory defines a concrete factory implementation for FPair[Num, Num], and function doWork accepts a generic Factory[T] for arbitrary T. Again, doWork requires a type bound T Format for type Factory[T] to be well formed. The main function may then call doWork with a MyFactory value because MyFactory is a subtype of Factory[Num].
The translated code (lower part of Figure 4) demonstrates that bounded type parameters demonstrates that bounded type parameters of structs and interfaces have no representation at runtime, so the translation effectively ignores them. A struct value is still just a tuple with the fields of the struct (lines 17 and 18), and an interface value just combines a struct value with a method dictionary (e.g., line 27). Only bounded type parameters of receiver structs (Figure 2), methods (Figure 3), and functions (Figure 4) lead to additional coercion parameters.
An important point to note is that there is a difference between generic interfaces and interfaces with generic methods. Interface Factory[T] in Figure 4 is generic in T, and a subtype of Factory[U] must provide an implementation of the create method for some fixed type U. In contrast, interface FormatSep from Figure 3 is not generic but contains a method formatSep that is generic in S. A subtype of FormatSep must provide an implementation of formatSep that is also generic in S.
2.6. Outlook
Next, Section 3 formalizes
![]() ${\textrm{FGG}^{-}}$
following the description by Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020). Then, we give the details of our type-directed translation scheme in Section 4 and establish that the meaning of
${\textrm{FGG}^{-}}$
following the description by Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020). Then, we give the details of our type-directed translation scheme in Section 4 and establish that the meaning of
![]() ${\textrm{FGG}^{-}}$
programs is preserved in Section 5.
${\textrm{FGG}^{-}}$
programs is preserved in Section 5.
3 Featherweight generic Go
 $^{-}$
$^{-}$
FG (Griesemer et al., Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020) is a small subset of the full Go language (2022) golang supporting only essential features such as structs, interfaces, method overloading, and structural subtyping. In the same article, the authors add generics to FG with the goal to scale the design to full Go. The resulting calculus is called FGG. Since version 1.18, full Go includes generics as well, but with limited expressivity compared to the FGG proposal (see Section 7.1). For the translation presented in this article, we stick to the original FGG language with minor differences in presentation but excluding dynamic type assertions. We refer to this language as
![]() ${\textrm{FGG}^{-}}$
.
${\textrm{FGG}^{-}}$
.
The next two subsections introduce the syntax and the dynamic semantics of
![]() ${\textrm{FGG}^{-}}$
. We defer the definition of its static semantics until Section 4.2, where we specify it as part of the type-directed dictionary-passing translation.
${\textrm{FGG}^{-}}$
. We defer the definition of its static semantics until Section 4.2, where we specify it as part of the type-directed dictionary-passing translation.
3.1 Syntax
Figure 5 introduces the syntax of
![]() ${\textrm{FGG}^{-}}$
. We assume several countably infinite, pairwise disjoint sets for names, ranged over by
${\textrm{FGG}^{-}}$
. We assume several countably infinite, pairwise disjoint sets for names, ranged over by
![]() $\mathcal{N}$
with some subscript (upper part of the figure). Meta-variables
$\mathcal{N}$
with some subscript (upper part of the figure). Meta-variables
![]() $t_S$
and
$t_S$
and
![]() $u_S$
denote struct names,
$u_S$
denote struct names,
![]() $t_I$
and
$t_I$
and
![]() $u_I$
interface names,
$u_I$
interface names,
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
type variables, f field names, m method names, and x, y denote names for variables in expressions. Overbar notation
$\beta$
type variables, f field names, m method names, and x, y denote names for variables in expressions. Overbar notation ![]() is a shorthand for the sequence
is a shorthand for the sequence
![]() $\mathfrak s_1 \ldots \mathfrak s_n$
where
$\mathfrak s_1 \ldots \mathfrak s_n$
where
![]() $\mathfrak s$
is some syntactic construct. In some places, commas separate the sequence items. If irrelevant, we omit the n and simply write
$\mathfrak s$
is some syntactic construct. In some places, commas separate the sequence items. If irrelevant, we omit the n and simply write ![]() . Using the index variable i under an overbar marks the parts that vary from sequence item to sequence item; for example,
. Using the index variable i under an overbar marks the parts that vary from sequence item to sequence item; for example, ![]() abbreviates
abbreviates
![]() $\mathfrak s'\,\mathfrak s_1\ldots\mathfrak s'\,\mathfrak s_n$
and
$\mathfrak s'\,\mathfrak s_1\ldots\mathfrak s'\,\mathfrak s_n$
and ![]() abbreviates
abbreviates
![]() $\mathfrak s_{j1}\,\ldots\,\mathfrak s_{jq}$
.
$\mathfrak s_{j1}\,\ldots\,\mathfrak s_{jq}$
.

Fig. 5. Syntax of
![]() ${\textrm{FGG}^{-}}$
.
${\textrm{FGG}^{-}}$
.
The middle part of Figure 5 shows the syntax of types in
![]() ${\textrm{FGG}^{-}}$
. A type name t,u is either a struct or interface name. Types
${\textrm{FGG}^{-}}$
. A type name t,u is either a struct or interface name. Types
![]() $\tau$
and
$\tau$
and
![]() $\sigma$
include types variables
$\sigma$
include types variables
![]() $\alpha$
and instantiated types
$\alpha$
and instantiated types ![]() . For nongeneric structs or interfaces, we often write just t instead of t[]. Struct types
. For nongeneric structs or interfaces, we often write just t instead of t[]. Struct types
![]() $\tau_S$
,
$\tau_S$
,
![]() $\sigma_S$
and interface types
$\sigma_S$
and interface types
![]() $\tau_I$
,
$\tau_I$
,
![]() $\sigma_I$
denote syntactic subsets of the full type syntax.
$\sigma_I$
denote syntactic subsets of the full type syntax.
The lower part of Figure 5 defines the syntax of
![]() ${\textrm{FGG}^{-}}$
expressions, declarations, and programs. Expressions, ranged over by e and g, include variables x, method calls, struct literals, and field selections. A method call
${\textrm{FGG}^{-}}$
expressions, declarations, and programs. Expressions, ranged over by e and g, include variables x, method calls, struct literals, and field selections. A method call ![]() invokes method m on receiver e with type arguments
invokes method m on receiver e with type arguments ![]() and arguments
and arguments ![]() . If m does not take type arguments, we often write just
. If m does not take type arguments, we often write just ![]() . A struct literals
. A struct literals ![]() creates an instance of a struct with n fields, the arguments
creates an instance of a struct with n fields, the arguments ![]() become the values of the fields in order of appearance in the struct definition. A field selection
become the values of the fields in order of appearance in the struct definition. A field selection
![]() $e.f$
projects the value of some struct field f from expression e.
$e.f$
projects the value of some struct field f from expression e.
A method signature ![]() consists of a name m, bounded type parameters
consists of a name m, bounded type parameters
![]() $\alpha_i$
with interface type
$\alpha_i$
with interface type
![]() $\tau_{Ii}$
as upper bounds, parameters
$\tau_{Ii}$
as upper bounds, parameters
![]() $x_i$
of type
$x_i$
of type
![]() $\tau_i$
, and return type
$\tau_i$
, and return type
![]() $\tau$
. It binds
$\tau$
. It binds ![]() . The scope of a type variable
. The scope of a type variable
![]() $\alpha_i$
is
$\alpha_i$
is ![]() ,
,
![]() $\tau$
, and all upper bounds
$\tau$
, and all upper bounds ![]() , so
, so
![]() ${\textrm{FGG}^{-}}$
supports F-bounded quantification (Canning et al., Reference Canning, Cook, Hill, Olthoff and Mitchell1989). For nongeneric methods, we often write just
${\textrm{FGG}^{-}}$
supports F-bounded quantification (Canning et al., Reference Canning, Cook, Hill, Olthoff and Mitchell1989). For nongeneric methods, we often write just ![]() .
.
A declaration D comes in three forms: a struct ![]() with fields
with fields
![]() $f_i$
of type
$f_i$
of type
![]() $\tau_i$
; an interface
$\tau_i$
; an interface ![]() with method signatures
with method signatures
![]() $\overline{R}$
; or a method
$\overline{R}$
; or a method ![]() providing an implementation of method R for struct
providing an implementation of method R for struct
![]() $t_S$
. All three forms bind the type variables
$t_S$
. All three forms bind the type variables ![]() , and a method implementation additionally binds the receiver parameter x. The scope of a type variable
, and a method implementation additionally binds the receiver parameter x. The scope of a type variable
![]() $\alpha_i$
includes all upper bounds
$\alpha_i$
includes all upper bounds ![]() , the body of the declaration enclosed in
, the body of the declaration enclosed in
![]() $\{\ldots\}$
, and for method declarations also the signature R. We omit the
$\{\ldots\}$
, and for method declarations also the signature R. We omit the ![]() part completely if
part completely if ![]() is empty. Finally, a program P consists of a sequence of declarations together with a main function. Method and function bodies only contain a single expression. We follow the usual convention and identify syntactic constructs up to renaming of bound variables or type variables.
is empty. Finally, a program P consists of a sequence of declarations together with a main function. Method and function bodies only contain a single expression. We follow the usual convention and identify syntactic constructs up to renaming of bound variables or type variables.
The syntax of
![]() ${\textrm{FGG}^{-}}$
as presented here differs slightly from its original form (Griesemer et al., Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020). The original article encloses type parameters in parenthesis, and an additional
${\textrm{FGG}^{-}}$
as presented here differs slightly from its original form (Griesemer et al., Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020). The original article encloses type parameters in parenthesis, and an additional ![]() keyword starts a list of type parameters. Here, we follow the syntax of full Go and use square brackets without any keyword. Further, the original article prepends package main to each program, something we omit for succinctness. Finally, we reduce the number of syntactic meta-variables to improve readability.
keyword starts a list of type parameters. Here, we follow the syntax of full Go and use square brackets without any keyword. Further, the original article prepends package main to each program, something we omit for succinctness. Finally, we reduce the number of syntactic meta-variables to improve readability.
3.2 Dynamic semantics
Figure 6 defines a call-by-value dynamic semantics for
![]() ${\textrm{FGG}^{-}}$
using a small-step reduction semantics with evaluation contexts. The definition is largely taken from Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020).
${\textrm{FGG}^{-}}$
using a small-step reduction semantics with evaluation contexts. The definition is largely taken from Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020).

Fig. 6. Dynamic semantics of
![]() ${\textrm{FGG}^{-}}$
.
${\textrm{FGG}^{-}}$
.
We use v, u, w to denote values, where a value is a struct literal with all fields being values. A call-by-value evaluation context
![]() ${\mathcal E}$
is an expression with a hole
${\mathcal E}$
is an expression with a hole
![]() ${{\square}}$
such that the hole marks the point where the next evaluation step should happen. We write
${{\square}}$
such that the hole marks the point where the next evaluation step should happen. We write
![]() ${\mathcal E}[e]$
to denote the replacement of the hole in
${\mathcal E}[e]$
to denote the replacement of the hole in
![]() ${\mathcal E}$
with expression e. A value substitution
${\mathcal E}$
with expression e. A value substitution
![]() $\theta$
is a finite mapping
$\theta$
is a finite mapping ![]() from variables to values, whereas a type substitution
from variables to values, whereas a type substitution
![]() $\eta$
is a finite mapping
$\eta$
is a finite mapping ![]() from type variables to types. The (type) variables in the domain of a substitution must be distinct. Substitution application, written in prefix notation as
from type variables to types. The (type) variables in the domain of a substitution must be distinct. Substitution application, written in prefix notation as
![]() $\theta e$
or
$\theta e$
or
![]() $\eta e$
or
$\eta e$
or
![]() $\eta \tau$
, is defined in the usual, capture-avoiding way. When combining two sequences, we implicitly assume that both sequences have the same length. For example, combining variables
$\eta \tau$
, is defined in the usual, capture-avoiding way. When combining two sequences, we implicitly assume that both sequences have the same length. For example, combining variables ![]() and values
and values ![]() to a substitution
to a substitution ![]() implicitly assumes that there are as many variables as values.
implicitly assumes that there are as many variables as values.
The reduction relation
![]() $e \longrightarrow e'$
denotes that expression e reduces to expression e’. To avoid clutter, the sequence of declarations
$e \longrightarrow e'$
denotes that expression e reduces to expression e’. To avoid clutter, the sequence of declarations
![]() $\overline{D}$
of the underlying program is implicitly available in the rules defining this reduction relation. Rule fg-context applies a reduction step inside an expression. Rule fg-field reduces a field selection
$\overline{D}$
of the underlying program is implicitly available in the rules defining this reduction relation. Rule fg-context applies a reduction step inside an expression. Rule fg-field reduces a field selection ![]() by extracting value
by extracting value
![]() $v_i$
corresponding to field
$v_i$
corresponding to field
![]() $f_i$
from the struct literal. Rule fg-call reduces a method call
$f_i$
from the struct literal. Rule fg-call reduces a method call ![]() . It retrieves a method definition for m and
. It retrieves a method definition for m and
![]() $t_S$
and substitutes type arguments, receiver, and value arguments in the method body.
$t_S$
and substitutes type arguments, receiver, and value arguments in the method body.
Reduction in
![]() ${\textrm{FGG}^{-}}$
is deterministic (see Lemma A.1.1 in Appendix A.1 for a formal proof), assuming the following three restrictions:
${\textrm{FGG}^{-}}$
is deterministic (see Lemma A.1.1 in Appendix A.1 for a formal proof), assuming the following three restrictions:
fgg-unique-structs Each struct
![]() $t_S$
is defined at most once in the program.
$t_S$
is defined at most once in the program.
fgg-distinct-fields Each struct definition ![]() has distinct field names
has distinct field names
![]() $\overline f$
.
$\overline f$
.
fgg-unique-method-defs Each method definition ![]() is uniquely identified by struct name
is uniquely identified by struct name
![]() $t_S$
and method name m.
$t_S$
and method name m.
The first two restrictions ensure that the value for a field in rule fg-field is unambiguous. The third restriction avoids multiple matching method definitions in rule fg-call.
4 Type-directed translation
This section defines a type-directed, dictionary-passing translation from
![]() ${\textrm{FGG}^{-}}$
to an untyped
${\textrm{FGG}^{-}}$
to an untyped
![]() $\lambda$
-calculus extended with recursive let-bindings, constructors, and pattern matching. We first introduce the target language, then specify the translation itself, and last but not least give some examples. Formal properties of the translation are deferred until Section 5.
$\lambda$
-calculus extended with recursive let-bindings, constructors, and pattern matching. We first introduce the target language, then specify the translation itself, and last but not least give some examples. Formal properties of the translation are deferred until Section 5.
4.1 Target language
Figure 7 defines the syntax and the call-by-value dynamic semantics of the target language (TL). We use uppercase letters for constructs of the TL. Variables X and Y and constructors K are drawn from countably infinite, pairwise disjoint sets
![]() $\mathcal{V}_{\mathit{Var}}$
and
$\mathcal{V}_{\mathit{Var}}$
and
![]() $\mathcal{V}_{\mathit{Con}}$
, respectively. Expressions, ranged over by E and G, include variables X, constructors K, function applications
$\mathcal{V}_{\mathit{Con}}$
, respectively. Expressions, ranged over by E and G, include variables X, constructors K, function applications
![]() $E\,E'$
,
$E\,E'$
,
![]() $\lambda$
-abstractions
$\lambda$
-abstractions
![]() $\lambda X.E$
, and pattern matching via case-expressions
$\lambda X.E$
, and pattern matching via case-expressions ![]() . Patterns
. Patterns
![]() $\mathit{Pat}$
have the form
$\mathit{Pat}$
have the form ![]() , and they do not nest. We assume that all constructors in
, and they do not nest. We assume that all constructors in ![]() are distinct. To avoid some parentheses, we use the conventions that application binds to the left and that the body of a
are distinct. To avoid some parentheses, we use the conventions that application binds to the left and that the body of a
![]() $\lambda$
extends to the right as far as possible.
$\lambda$
extends to the right as far as possible.

Fig. 7. Target language (TL).
A program ![]() consists of a sequence of (mutually recursive) definitions and a (main) expression, where we assume that the variables
consists of a sequence of (mutually recursive) definitions and a (main) expression, where we assume that the variables ![]() are distinct. In the translation from
are distinct. In the translation from
![]() ${\textrm{FGG}^{-}}$
, the values
${\textrm{FGG}^{-}}$
, the values ![]() are always functions resulting as translations of
are always functions resulting as translations of
![]() ${\textrm{FGG}^{-}}$
methods. We identify expressions, pattern clauses, and programs up to renaming of bound variables. Variables are bound by
${\textrm{FGG}^{-}}$
methods. We identify expressions, pattern clauses, and programs up to renaming of bound variables. Variables are bound by
![]() $\lambda$
expressions, patterns, and let-bindings of programs.
$\lambda$
expressions, patterns, and let-bindings of programs.
Some syntactic sugar simplifies the construction of patterns, expressions, and programs. (a) We use nested patterns to abbreviate nested case-expressions. (b) We assume data constructors for tuples up to some fixed but arbitrary size. The syntax ![]() constructs an n-tuple when used as an expression, and
constructs an n-tuple when used as an expression, and ![]() deconstructs it when used in a pattern context. (c) We use patterns in
deconstructs it when used in a pattern context. (c) We use patterns in
![]() $\lambda$
-expressions; that is, the notation
$\lambda$
-expressions; that is, the notation
![]() $\lambda \mathit{Pat}. E$
stands for
$\lambda \mathit{Pat}. E$
stands for ![]() where X is fresh.
where X is fresh.
Target values V,U,W are either
![]() $\lambda$
-expressions or constructors applied to values. A constructor value
$\lambda$
-expressions or constructors applied to values. A constructor value
![]() $K\,\overline{V}^{n}$
is short for
$K\,\overline{V}^{n}$
is short for
![]() $(\ldots (K\,V_1) \ldots)\,V_n$
. A call-by-value evaluation context
$(\ldots (K\,V_1) \ldots)\,V_n$
. A call-by-value evaluation context
![]() ${\mathcal R}$
is an expression with a hole
${\mathcal R}$
is an expression with a hole
![]() ${{\square}}$
such that the hole marks the point where the next evaluation step should happen. We write
${{\square}}$
such that the hole marks the point where the next evaluation step should happen. We write
![]() ${\mathcal R}[E]$
to denote the replacement of the hole in
${\mathcal R}[E]$
to denote the replacement of the hole in
![]() ${\mathcal R}$
with expression E.
${\mathcal R}$
with expression E.
A substitution
![]() $\rho, \mu$
is a finite mapping
$\rho, \mu$
is a finite mapping ![]() from variables to values. The variables
from variables to values. The variables ![]() in the domain must be distinct. Substitution application, written in prefix notation
in the domain must be distinct. Substitution application, written in prefix notation
![]() $\rho E$
, is defined in the usual, capture-avoiding way. We use two different meta-variables
$\rho E$
, is defined in the usual, capture-avoiding way. We use two different meta-variables
![]() $\mu$
and
$\mu$
and
![]() $\rho$
for substitutions in the TL with the convention that the domain of
$\rho$
for substitutions in the TL with the convention that the domain of
![]() $\mu$
contains only top-level variables bound by
$\mu$
contains only top-level variables bound by ![]() . As top-level variables result from translating
. As top-level variables result from translating
![]() ${\textrm{FGG}^{-}}$
methods, we sometimes call
${\textrm{FGG}^{-}}$
methods, we sometimes call
![]() $\mu$
a method substitution.
$\mu$
a method substitution.
The reduction semantics for the TL is defined by two relations:
![]() $E \longrightarrow_{\mu} E'$
reduces expression E to E’ under method substitution
$E \longrightarrow_{\mu} E'$
reduces expression E to E’ under method substitution
![]() $\mu$
, and
$\mu$
, and
![]() $\mathit{Prog} \longrightarrow \mathit{Prog}'$
reduces
$\mathit{Prog} \longrightarrow \mathit{Prog}'$
reduces
![]() $\mathit{Prog}$
to
$\mathit{Prog}$
to
![]() $\mathit{Prog}'$
. The definition of the latter simply forms a method substitution
$\mathit{Prog}'$
. The definition of the latter simply forms a method substitution
![]() $\mu$
from the top-level bindings of
$\mu$
from the top-level bindings of
![]() $\mathit{Prog}$
and then reduces the main expression of
$\mathit{Prog}$
and then reduces the main expression of
![]() $\mathit{Prog}$
under
$\mathit{Prog}$
under
![]() $\mu$
(rule tl-prog. We defer the substitution of top-level-bound variables because they might be recursive.
$\mu$
(rule tl-prog. We defer the substitution of top-level-bound variables because they might be recursive.
The definition of the reduction relation for expressions extends over four rules. Rule tl-context uses evaluation context
![]() ${\mathcal R}$
to reduce inside an expression, and rule tl-lambda reduces function application in the usual way. Pattern matching in rule tl-case assumes that the scrutinee is a constructor value
${\mathcal R}$
to reduce inside an expression, and rule tl-lambda reduces function application in the usual way. Pattern matching in rule tl-case assumes that the scrutinee is a constructor value ![]() ; the lookup of a pattern clause matching K yields at most one result as we assume that clauses have distinct constructors. During a sequence of reduction steps, a variable bound by
; the lookup of a pattern clause matching K yields at most one result as we assume that clauses have distinct constructors. During a sequence of reduction steps, a variable bound by ![]() at the top-level might become a redex, as only
at the top-level might become a redex, as only
![]() $\lambda$
-bound variables are substituted right away. Thus, rule tl-method finds the value for the variable in the method substitution
$\lambda$
-bound variables are substituted right away. Thus, rule tl-method finds the value for the variable in the method substitution
![]() $\mu$
.
$\mu$
.
4.2 Translation
Before we dive into the technical details, we summarize our translation strategy.
Struct. An
![]() ${\textrm{FGG}^{-}}$
value of some struct type is represented in the TL as a struct value; that is, a tuple
${\textrm{FGG}^{-}}$
value of some struct type is represented in the TL as a struct value; that is, a tuple ![]() where n is the number of fields and
where n is the number of fields and
![]() $V_i$
represents the i-th field of the struct.
$V_i$
represents the i-th field of the struct.
Interface. An
![]() ${\textrm{FGG}^{-}}$
value of some interface type is represented in the TL as an interface value; that is a pair
${\textrm{FGG}^{-}}$
value of some interface type is represented in the TL as an interface value; that is a pair ![]() , where V is a struct value realizing the interface and
, where V is a struct value realizing the interface and
![]() $\mathcal D$
is a dictionary.
$\mathcal D$
is a dictionary.
Dictionary. A dictionary
![]() $\mathcal D$
for an interface with methods
$\mathcal D$
for an interface with methods ![]() is a tuple
is a tuple ![]() such that
such that
![]() $V_i$
is a dictionary entry for method
$V_i$
is a dictionary entry for method
![]() $R_i$
.
$R_i$
.
Dictionary entry. A dictionary entry for a method with signature ![]() is a function accepting a triple: (1) receiver, (2) tuple with coercions corresponding to the bounded type parameters
is a function accepting a triple: (1) receiver, (2) tuple with coercions corresponding to the bounded type parameters ![]() of the method, and (3) tuple for parameters
of the method, and (3) tuple for parameters ![]() .
.
Coercion. A structural subtype relation
![]() $\tau \mathrel{<:} \sigma$
implies a coercion function to transform the target representation of an
$\tau \mathrel{<:} \sigma$
implies a coercion function to transform the target representation of an
![]() ${\textrm{FGG}^{-}}$
value at type
${\textrm{FGG}^{-}}$
value at type
![]() $\tau$
into a representation at type
$\tau$
into a representation at type
![]() $\sigma$
.
$\sigma$
.
Bounded type parameter. A bounded type parameter
![]() $\alpha\,\tau_I$
becomes a coercion parameter
$\alpha\,\tau_I$
becomes a coercion parameter
![]() $X_{\alpha}$
transforming the type supplied for
$X_{\alpha}$
transforming the type supplied for
![]() $\alpha$
to its bound
$\alpha$
to its bound
![]() $\tau_I$
. At instantiation sites, coercions need to be inserted.
$\tau_I$
. At instantiation sites, coercions need to be inserted.
Method declaration. A method declaration ![]() is represented as a top-level function
is represented as a top-level function
![]() $X_{{m},{t_S}}$
accepting a quadruple: (1) tuple with coercions corresponding to the bounded type parameters
$X_{{m},{t_S}}$
accepting a quadruple: (1) tuple with coercions corresponding to the bounded type parameters ![]() of the receiver, (2) receiver x, (3) tuple with coercions corresponding to bounded type parameters
of the receiver, (2) receiver x, (3) tuple with coercions corresponding to bounded type parameters ![]() of the method, and (4) tuple for parameters
of the method, and (4) tuple for parameters ![]() .
.
In essence, the above is a more detailed description of the translation scheme motivated in Section 2. The only difference is that dictionary entries and translations of methods are now represented as uncurried functions. For example, instead of the curried representation in Figure 3

our actual translation scheme uses uncurried functions, as in the following code:

Using an uncurried representation instead of a curried representation is just a matter taste. As we have carried out the semantic equivalence proof initially based on the uncurried representation, we stick to it from now on.
4.2.1 Conventions and notations
The translation relies on three total injective functions with pairwise disjoint ranges for mapping
![]() ${\textrm{FGG}^{-}}$
names to TL variables. The first function
${\textrm{FGG}^{-}}$
names to TL variables. The first function
![]() $\mathcal{N}_{\mathit{var}} \to \mathcal{V}_{\mathit{Var}}$
translates a
$\mathcal{N}_{\mathit{var}} \to \mathcal{V}_{\mathit{Var}}$
translates a
![]() ${\textrm{FGG}^{-}}$
variable x to a TL variable X. To avoid clutter, we do not spell out the translation function explicitly but use the abbreviation that a lowercase x always translates into its uppercase counterpart X. The second function
${\textrm{FGG}^{-}}$
variable x to a TL variable X. To avoid clutter, we do not spell out the translation function explicitly but use the abbreviation that a lowercase x always translates into its uppercase counterpart X. The second function
![]() $\mathcal{N}_{\mathit{tyvar}} \to \mathcal{V}_{\mathit{Var}}$
translates an
$\mathcal{N}_{\mathit{tyvar}} \to \mathcal{V}_{\mathit{Var}}$
translates an
![]() ${\textrm{FGG}^{-}}$
type variable
${\textrm{FGG}^{-}}$
type variable
![]() $\alpha$
into a TL variable, abbreviated
$\alpha$
into a TL variable, abbreviated
![]() $X_{\alpha}$
. The third function
$X_{\alpha}$
. The third function
![]() $\mathcal{N}_{\mathit{method}} \times \mathcal{N}_{\mathit{struct}} \to \mathcal{V}_{\mathit{Var}}$
gives us the TL variable
$\mathcal{N}_{\mathit{method}} \times \mathcal{N}_{\mathit{struct}} \to \mathcal{V}_{\mathit{Var}}$
gives us the TL variable
![]() $X_{{m},{t_S}}$
representing the translation of a method m for struct
$X_{{m},{t_S}}$
representing the translation of a method m for struct
![]() $t_S$
. Here is a summary of the shorthand notations for name translation functions, where
$t_S$
. Here is a summary of the shorthand notations for name translation functions, where
![]() $\textsf{methodName}(R)$
denotes the name part of method signature R:
$\textsf{methodName}(R)$
denotes the name part of method signature R:

The notation for translating names slightly differs from the approach used in the examples of Section 2. For instance, the coercion ![]() from Figure 3 is now named
from Figure 3 is now named
![]() $X_{{\texttt{T}}}$
and method
$X_{{\texttt{T}}}$
and method ![]() becomes
becomes
![]() $X_{\texttt{formatSep},\texttt{Pair}}$
. The notation of the formal translation stresses that
$X_{\texttt{formatSep},\texttt{Pair}}$
. The notation of the formal translation stresses that
![]() $X_{{\texttt{T}}}$
and
$X_{{\texttt{T}}}$
and
![]() $X_{\texttt{formatSep},\texttt{Pair}}$
are variables of the TL.
$X_{\texttt{formatSep},\texttt{Pair}}$
are variables of the TL.
An
![]() ${\textrm{FGG}^{-}}$
type environment
${\textrm{FGG}^{-}}$
type environment
![]() $\Delta$
is a mapping
$\Delta$
is a mapping ![]() from type variables
from type variables
![]() $\alpha_i$
to their upper bounds
$\alpha_i$
to their upper bounds
![]() $\tau_{Ii}$
. An
$\tau_{Ii}$
. An
![]() ${\textrm{FGG}^{-}}$
value environment
${\textrm{FGG}^{-}}$
value environment
![]() $\Gamma$
is a mapping
$\Gamma$
is a mapping ![]() from
from
![]() ${\textrm{FGG}^{-}}$
variables
${\textrm{FGG}^{-}}$
variables
![]() $x_i$
to their types
$x_i$
to their types
![]() $\tau_i$
. An environment may contain at most one binding for a type variable or variable. We write
$\tau_i$
. An environment may contain at most one binding for a type variable or variable. We write
![]() $\emptyset$
for the empty environment,
$\emptyset$
for the empty environment,
![]() ${\textsf{dom}}(\cdot)$
for the domain of an environment, and
${\textsf{dom}}(\cdot)$
for the domain of an environment, and
![]() $\cup$
for the disjoint union of two environments. The notation
$\cup$
for the disjoint union of two environments. The notation ![]() asserts that
asserts that ![]() is a sequence of disjoint items. We let [n] denote the set
is a sequence of disjoint items. We let [n] denote the set
![]() $\{1,\ldots,n\}$
.
$\{1,\ldots,n\}$
.
In the following, we assume that the declarations
![]() $\overline{D}$
of the
$\overline{D}$
of the
![]() ${\textrm{FGG}^{-}}$
program being translated are implicitly available in all rules. This avoids the need for threading the declarations through all translation rules.
${\textrm{FGG}^{-}}$
program being translated are implicitly available in all rules. This avoids the need for threading the declarations through all translation rules.
4.2.2 Auxiliary judgments
Figure 8 defines some auxiliary judgments. The judgment ![]() , defined by rule type-inst-checked, constructs a type substitution
, defined by rule type-inst-checked, constructs a type substitution ![]() and checks that the
and checks that the ![]() conform to their upper bounds
conform to their upper bounds ![]() under type environment
under type environment
![]() $\Delta$
. In the tuple
$\Delta$
. In the tuple ![]() of
of
![]() $\lambda$
-abstractions each
$\lambda$
-abstractions each
![]() $V_i$
coerces the actual type argument to its upper bound. The relevant premise for checking upper bounds is
$V_i$
coerces the actual type argument to its upper bound. The relevant premise for checking upper bounds is ![]() , which asserts that
, which asserts that
![]() $\sigma_i$
is a structural subtype of
$\sigma_i$
is a structural subtype of
![]() $\eta \tau_{Ii}$
giving raise to a coercion function
$\eta \tau_{Ii}$
giving raise to a coercion function
![]() $V_i$
. The judgment will be defined and explained in the next subsection.
$V_i$
. The judgment will be defined and explained in the next subsection.

Fig. 8. Auxiliary judgments for the translation.
The lower part of Figure 8 defines two judgments for looking up methods defined for a struct or interface type. Judgment
![]() $\langle R,V\rangle \in {\textsf{methods}}(\Delta, \tau_S)$
states that method signature R is available for struct type
$\langle R,V\rangle \in {\textsf{methods}}(\Delta, \tau_S)$
states that method signature R is available for struct type
![]() $\tau_S$
under type environment
$\tau_S$
under type environment
![]() $\Delta$
, see rule methods-struct. The value V is a tuple of coercion functions resulting from checking the bounds of the receiver’s type parameters. Judgment
$\Delta$
, see rule methods-struct. The value V is a tuple of coercion functions resulting from checking the bounds of the receiver’s type parameters. Judgment
![]() ${\textsf{methods}}(\tau_I) = \{ \overline{R} \}$
states that the set of method signatures available for interface type
${\textsf{methods}}(\tau_I) = \{ \overline{R} \}$
states that the set of method signatures available for interface type
![]() $\tau_I$
is
$\tau_I$
is ![]() , see rule methods-iface. As stated before, this rule forms the substitution
, see rule methods-iface. As stated before, this rule forms the substitution ![]() by implicitly assuming that
by implicitly assuming that ![]() have the same length.
have the same length.
4.2.3 Translation of structural subtyping
Figure 9 defines the relation
![]() $\Delta \mathrel{\vdash_{{{\textsf{coerce}}}}} \tau \mathrel{<:} \sigma \leadsto V$
for asserting that
$\Delta \mathrel{\vdash_{{{\textsf{coerce}}}}} \tau \mathrel{<:} \sigma \leadsto V$
for asserting that
![]() $\tau$
is a structural subtype of
$\tau$
is a structural subtype of
![]() $\sigma$
, yielding a coercion function V to convert the target representations of
$\sigma$
, yielding a coercion function V to convert the target representations of
![]() $\tau$
to
$\tau$
to
![]() $\sigma$
.
$\sigma$
.

Fig. 9. Translation of structural subtyping.
Rule coerce-tyvar covers the case of a type variable
![]() $\alpha$
. The premise states that type bound
$\alpha$
. The premise states that type bound
![]() $(\alpha : \sigma_I)$
exists in the environment. By convention,
$(\alpha : \sigma_I)$
exists in the environment. By convention,
![]() $X_{\alpha}$
is the name of the corresponding coercion function. We further find that
$X_{\alpha}$
is the name of the corresponding coercion function. We further find that ![]() . Hence, we obtain the coercion function for
. Hence, we obtain the coercion function for
![]() $\alpha \mathrel{<:} \sigma$
by composition of coercion functions V and
$\alpha \mathrel{<:} \sigma$
by composition of coercion functions V and
![]() $X_{\alpha}$
.
$X_{\alpha}$
.
Rule coerce-struct-iface covers structs. The premise
![]() $\langle\eta R_i,V_i\rangle \in {\textsf{methods}}(\Delta, \tau_S)$
asserts that each method with name
$\langle\eta R_i,V_i\rangle \in {\textsf{methods}}(\Delta, \tau_S)$
asserts that each method with name
![]() $\textsf{methodName}(R_i)$
of interface
$\textsf{methodName}(R_i)$
of interface
![]() $t_I$
is defined for
$t_I$
is defined for
![]() $\tau_S$
. Value
$\tau_S$
. Value
![]() $V_i$
is a tuple with coercion parameters corresponding to the bounds of the receiver’s type parameters. Thus,
$V_i$
is a tuple with coercion parameters corresponding to the bounds of the receiver’s type parameters. Thus, ![]() is the dictionary entry for the i-th method: a function accepting receiver
is the dictionary entry for the i-th method: a function accepting receiver
![]() $Y_1$
, coercion parameters
$Y_1$
, coercion parameters
![]() $Y_2$
corresponding to bounded type parameters of the method, and the argument tuple
$Y_2$
corresponding to bounded type parameters of the method, and the argument tuple
![]() $Y_3$
. As written earlier, dictionary entries and top-level functions
$Y_3$
. As written earlier, dictionary entries and top-level functions
![]() $X_{m_i,t_S}$
are uncurried. Thus, we need to deconstruct the argument triple
$X_{m_i,t_S}$
are uncurried. Thus, we need to deconstruct the argument triple ![]() and construct a new quadruple
and construct a new quadruple ![]() for calling
for calling
![]() $X_{m_i,t_S}$
.
$X_{m_i,t_S}$
.
Rule coerce-iface-iface covers structural subtyping between interface types ![]() and
and ![]() . In this case,
. In this case,
![]() $t_I$
must declare all methods of
$t_I$
must declare all methods of
![]() $u_I$
, so we can build a dictionary for
$u_I$
, so we can build a dictionary for
![]() $u_I$
from the methods in the dictionary for
$u_I$
from the methods in the dictionary for
![]() $t_I$
. Thus, the premise of the rule requires the total function
$t_I$
. Thus, the premise of the rule requires the total function
![]() $\pi$
to be chosen in such a way that the i-th method of
$\pi$
to be chosen in such a way that the i-th method of
![]() $u_I$
has the same signature as the
$u_I$
has the same signature as the
![]() $\pi(i)$
-th method of
$\pi(i)$
-th method of
![]() $t_I$
. The translation uses pattern matching to deconstruct the dictionary of
$t_I$
. The translation uses pattern matching to deconstruct the dictionary of
![]() $t_I$
as
$t_I$
as ![]() . Then the i-th method in the dictionary of
. Then the i-th method in the dictionary of
![]() $u_I$
is
$u_I$
is
![]() $X_{\pi(i)}$
, so we construct the wanted dictionary as
$X_{\pi(i)}$
, so we construct the wanted dictionary as
![]() $\text{ (} X_{\pi(1)}\text{ ,} \ldots\text{ ,} X_{\pi(q)} \text{ )}$
.
$\text{ (} X_{\pi(1)}\text{ ,} \ldots\text{ ,} X_{\pi(q)} \text{ )}$
.
4.2.4 Translation of expressions
Figure 10 defines the typing and translation relation for expressions. The judgment
![]() $\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
states that under type environment
$\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
states that under type environment
![]() $\Delta$
and value environment
$\Delta$
and value environment
![]() $\Gamma$
, the
$\Gamma$
, the
![]() ${\textrm{FGG}^{-}}$
expression e has type
${\textrm{FGG}^{-}}$
expression e has type
![]() $\tau$
and translates to TL expression E.
$\tau$
and translates to TL expression E.

Fig. 10. Translation of expressions.
Rule var retrieves the type of
![]() ${\textrm{FGG}^{-}}$
variable x from the environment and translates x to its TL counterpart X. The context makes variable X available, see the translation of method definitions in Section 4.2.6. Rule struct type-checks and translates a struct literal
${\textrm{FGG}^{-}}$
variable x from the environment and translates x to its TL counterpart X. The context makes variable X available, see the translation of method definitions in Section 4.2.6. Rule struct type-checks and translates a struct literal ![]() . Premise
. Premise ![]() checks that type
checks that type ![]() is well formed; the definition of the judgment
is well formed; the definition of the judgment ![]() is given in Figure 11 and will be explained in the next subsection. Each argument
is given in Figure 11 and will be explained in the next subsection. Each argument
![]() $e_i$
translates to
$e_i$
translates to
![]() $E_i$
, so the result is
$E_i$
, so the result is ![]() . Rule access deals with field access
. Rule access deals with field access
![]() $e.f_i$
, where expression e must have struct type
$e.f_i$
, where expression e must have struct type ![]() such that
such that
![]() $t_S$
defines field
$t_S$
defines field
![]() $f_i$
. Thus, e translates to a tuple E, from which we extract the i-th component via pattern matching.
$f_i$
. Thus, e translates to a tuple E, from which we extract the i-th component via pattern matching.

Fig. 11. Well-formedness.
Rule call-struct handles a method call
![]() $e.m[\overline{\tau'}](\overline{e})$
, where receiver e has struct type
$e.m[\overline{\tau'}](\overline{e})$
, where receiver e has struct type
![]() $t_S[\overline{\tau}]$
and translates to E. The V in the premise corresponds to a tuple of coercion functions that result from checking the bounds of the receiver’s type parameters, whereas V’ is a tuple of coercion functions for the bounds of the type parameters of the method. Argument
$t_S[\overline{\tau}]$
and translates to E. The V in the premise corresponds to a tuple of coercion functions that result from checking the bounds of the receiver’s type parameters, whereas V’ is a tuple of coercion functions for the bounds of the type parameters of the method. Argument
![]() $e_i$
translates to
$e_i$
translates to
![]() $E_i$
. According to our translation strategy, a method declaration for m and
$E_i$
. According to our translation strategy, a method declaration for m and
![]() $t_S$
is represented as a top-level function
$t_S$
is represented as a top-level function
![]() $X_{m,t_S}$
accepting a quadruple: coercions for the receiver’s type parameters, receiver, coercions for the bounded type parameters local to the method, and method arguments. Thus, the result of the translation is
$X_{m,t_S}$
accepting a quadruple: coercions for the receiver’s type parameters, receiver, coercions for the bounded type parameters local to the method, and method arguments. Thus, the result of the translation is ![]() .
.
Rule call-iface handles a method call
![]() $e.m[\overline{\tau'}](\overline{e})$
, where receiver e has interface type
$e.m[\overline{\tau'}](\overline{e})$
, where receiver e has interface type
![]() $\tau_I$
and translates to E. Similar to call-struct, V’ is a tuple of coercion functions that result from checking the bounds of the type parameters local to the method. Expressions
$\tau_I$
and translates to E. Similar to call-struct, V’ is a tuple of coercion functions that result from checking the bounds of the type parameters local to the method. Expressions
![]() $E_i$
are the translation of the arguments
$E_i$
are the translation of the arguments
![]() $e_i$
. Following our translation strategy, receiver E is a pair where the first component is a struct value and the second component is a dictionary for the interface. Thus, we use pattern matching to extract the struct as Y and the wanted method as
$e_i$
. Following our translation strategy, receiver E is a pair where the first component is a struct value and the second component is a dictionary for the interface. Thus, we use pattern matching to extract the struct as Y and the wanted method as
![]() $X_j$
. This
$X_j$
. This
![]() $X_j$
is a function accepting a triple: receiver, coercions for bounded type parameters of the method, and method arguments. Hence, the translation result is
$X_j$
is a function accepting a triple: receiver, coercions for bounded type parameters of the method, and method arguments. Hence, the translation result is ![]() . The difference to rule call-struct is that there is no need to supply coercions for the bounded type parameters of the receiver. These coercions have already been supplied when building the dictionary, see rule coerce-struct-iface of Figure 9.
. The difference to rule call-struct is that there is no need to supply coercions for the bounded type parameters of the receiver. These coercions have already been supplied when building the dictionary, see rule coerce-struct-iface of Figure 9.
The last rule sub is a subtyping rule allowing an expression e with translation E at type
![]() $\tau$
to be assigned some (structural) supertype
$\tau$
to be assigned some (structural) supertype
![]() $\sigma$
. Premise
$\sigma$
. Premise ![]() serves two purposes: it ensures that
serves two purposes: it ensures that
![]() $\sigma$
is a supertype of
$\sigma$
is a supertype of
![]() $\tau$
and it yields a coercion function V from
$\tau$
and it yields a coercion function V from
![]() $\tau$
to
$\tau$
to
![]() $\sigma$
. The translation of e at type
$\sigma$
. The translation of e at type
![]() $\sigma$
is then
$\sigma$
is then
![]() $V\,E$
. In Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020), the subtype check is included for each form of expression. For clarity, we choose to have a separate subtyping rule as in our translation scheme each subtyping relation implies a coercion function.
$V\,E$
. In Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020), the subtype check is included for each form of expression. For clarity, we choose to have a separate subtyping rule as in our translation scheme each subtyping relation implies a coercion function.
4.2.5 Well-formedness
Figure 11 defines several well-formedness judgments. The judgments ![]() assert that a single type and multiple types, respectively, are well formed under type environment
assert that a single type and multiple types, respectively, are well formed under type environment
![]() $\Delta$
. A type variable is well formed if it is contained in
$\Delta$
. A type variable is well formed if it is contained in
![]() $\Delta$
(rule ok-tyvar). A named type
$\Delta$
(rule ok-tyvar). A named type
![]() $t[\overline{\tau}]$
is well formed if its type arguments
$t[\overline{\tau}]$
is well formed if its type arguments
![]() $\overline{\tau}$
are well formed and if they are subtypes of the upper bounds in the definition of t. The latter is checked by the premise
$\overline{\tau}$
are well formed and if they are subtypes of the upper bounds in the definition of t. The latter is checked by the premise
![]() $\Delta \mathrel{\vdash_{{{{\textsf{subst}}}}}} \overline{\alpha\,\tau_I} \mapsto \overline{\tau} : \eta \leadsto V$
of rule ok-tynamed, thereby ignoring the type substitution
$\Delta \mathrel{\vdash_{{{{\textsf{subst}}}}}} \overline{\alpha\,\tau_I} \mapsto \overline{\tau} : \eta \leadsto V$
of rule ok-tynamed, thereby ignoring the type substitution
![]() $\eta$
and the coercion functions V. We have already seen in Section 2.5 that these coercions V are not represented in the translated program because type bounds of structs and interfaces have no operational meaning.
$\eta$
and the coercion functions V. We have already seen in Section 2.5 that these coercions V are not represented in the translated program because type bounds of structs and interfaces have no operational meaning.
Judgment
![]() $\Delta \mathrel{\vdash_{{{\textsf{ok}}}}} \overline{\alpha\,\tau_I}$
asserts that bounded type parameters
$\Delta \mathrel{\vdash_{{{\textsf{ok}}}}} \overline{\alpha\,\tau_I}$
asserts that bounded type parameters
![]() $\overline{\alpha\,\tau_I}$
are well formed under type environment
$\overline{\alpha\,\tau_I}$
are well formed under type environment
![]() $\Delta$
(rule ok-bounded-typarams). Judgment
$\Delta$
(rule ok-bounded-typarams). Judgment
![]() $\Delta \mathrel{\vdash_{{{\textsf{ok}}}}} R$
ensures that a method signature is well formed (rule ok-msig). To form the combined environment
$\Delta \mathrel{\vdash_{{{\textsf{ok}}}}} R$
ensures that a method signature is well formed (rule ok-msig). To form the combined environment
![]() $\Delta \cup \{\overline{\alpha : \tau_I}\}$
in the premise requires disjointness of the type variables in
$\Delta \cup \{\overline{\alpha : \tau_I}\}$
in the premise requires disjointness of the type variables in
![]() ${\textsf{dom}}(\Delta)$
and
${\textsf{dom}}(\Delta)$
and
![]() $\overline{\alpha}$
. This can always be achieved by
$\overline{\alpha}$
. This can always be achieved by
![]() $\alpha$
-renaming the type variables bound by R.
$\alpha$
-renaming the type variables bound by R.
Judgment
![]() $\mathrel{\vdash_{{{\textsf{ok}}}}} D$
validates declaration D. A struct declaration is well formed if it is defined only once (restriction fgg-unique-structs in Section 3.2), if all field names are distinct (restriction fgg-distinct-fields), and if the field types are well formed. An interface declaration is well formed if it is defined only once, if all its method signatures are well formed, and if all methods have distinct names.
$\mathrel{\vdash_{{{\textsf{ok}}}}} D$
validates declaration D. A struct declaration is well formed if it is defined only once (restriction fgg-unique-structs in Section 3.2), if all field names are distinct (restriction fgg-distinct-fields), and if the field types are well formed. An interface declaration is well formed if it is defined only once, if all its method signatures are well formed, and if all methods have distinct names.
A method declaration for
![]() $t_S$
and m is well formed if there is no other declaration for
$t_S$
and m is well formed if there is no other declaration for
![]() $t_S$
and m (restriction fgg-unique-method-defs), if the method signature is well formed, and if each bound
$t_S$
and m (restriction fgg-unique-method-defs), if the method signature is well formed, and if each bound
![]() $\tau_{Ii}$
of the method declaration is a structural subtype of the corresponding bound
$\tau_{Ii}$
of the method declaration is a structural subtype of the corresponding bound
![]() $\tau_{Ii}'$
in the declaration of
$\tau_{Ii}'$
in the declaration of
![]() $t_S$
. In
$t_S$
. In
![]() ${\textrm{FGG}^{-}}$
, this boils down to checking that the methods of
${\textrm{FGG}^{-}}$
, this boils down to checking that the methods of
![]() $\tau_{Ii}'$
are a subset of the methods of
$\tau_{Ii}'$
are a subset of the methods of
![]() $\tau_{Ii}$
. The well-formedness conditions for method declarations do not type-check the method body. We will deal with this in the upcoming translation rule for methods.
$\tau_{Ii}$
. The well-formedness conditions for method declarations do not type-check the method body. We will deal with this in the upcoming translation rule for methods.
4.2.6 Translation of methods and programs
Figure 12 defines the translation for method declarations and programs. Rule method deals with method declarations ![]() . The translation of such a declaration is the binding
. The translation of such a declaration is the binding
![]() $X_{{m},{t_S}} = V$
. According to our translation strategy, V must be a function accepting a quadruple: coercions
$X_{{m},{t_S}} = V$
. According to our translation strategy, V must be a function accepting a quadruple: coercions
![]() $\texttt{(} \overline{X_{\alpha_i}} \texttt{)}$
for the bounded type parameters of the receiver, receiver X corresponding to x, coercions
$\texttt{(} \overline{X_{\alpha_i}} \texttt{)}$
for the bounded type parameters of the receiver, receiver X corresponding to x, coercions
![]() $\texttt{(} \overline{X_{\beta_i}} \texttt{)}$
for the bounded type parameters local to the method, and finally method arguments
$\texttt{(} \overline{X_{\beta_i}} \texttt{)}$
for the bounded type parameters local to the method, and finally method arguments
![]() $\overline{X}$
corresponding to
$\overline{X}$
corresponding to
![]() $\overline{x}$
. Binding all these variables with a
$\overline{x}$
. Binding all these variables with a
![]() $\lambda$
makes them available in the translated body E.
$\lambda$
makes them available in the translated body E.

Fig. 12. Translation of methods and programs.
Judgment
![]() $\mathrel{\vdash_{{{\textsf{prog}}}}} P \leadsto \mathit{Prog}$
denotes the translation of an
$\mathrel{\vdash_{{{\textsf{prog}}}}} P \leadsto \mathit{Prog}$
denotes the translation of an
![]() ${\textrm{FGG}^{-}}$
program P to a TL program
${\textrm{FGG}^{-}}$
program P to a TL program
![]() $\mathit{Prog}$
. Rule prog type-checks the main expression e under empty environments against some type
$\mathit{Prog}$
. Rule prog type-checks the main expression e under empty environments against some type
![]() $\tau$
to get its translation E. Next, the rule requires all struct or interface declarations to be well formed. Finally, it translates each method declaration to a binding
$\tau$
to get its translation E. Next, the rule requires all struct or interface declarations to be well formed. Finally, it translates each method declaration to a binding
![]() $X_i = V_i$
. The resulting TL program is then
$X_i = V_i$
. The resulting TL program is then ![]() .
.
4.3 Example
We now give an example of the translation. The
![]() ${\textrm{FGG}^{-}}$
code in the top part of Figure 13 defines equality for numbers
${\textrm{FGG}^{-}}$
code in the top part of Figure 13 defines equality for numbers
![]() $\mathit{Num}$
and for generic boxes
$\mathit{Num}$
and for generic boxes
![]() $\mathit{Box}[\alpha\,\mathit{Any}]$
. Interface
$\mathit{Box}[\alpha\,\mathit{Any}]$
. Interface
![]() $\mathit{Any}$
defines no methods, and it serves as an upper bound for otherwise unrestricted type variables. We take the liberty to assume a basic type
$\mathit{Any}$
defines no methods, and it serves as an upper bound for otherwise unrestricted type variables. We take the liberty to assume a basic type
![]() $\mathit{int}$
and an operator
$\mathit{int}$
and an operator
![]() $\mathtt{==}$
for equality. Interface
$\mathtt{==}$
for equality. Interface
![]() $\mathit{Eq}[\alpha]$
requires a method
$\mathit{Eq}[\alpha]$
requires a method
![]() $\mathit{eq}$
for comparing the receiver with a value of type
$\mathit{eq}$
for comparing the receiver with a value of type
![]() $\alpha$
. We provide implementations of
$\alpha$
. We provide implementations of
![]() $\mathit{eq}$
for
$\mathit{eq}$
for
![]() $\mathit{Num}$
and
$\mathit{Num}$
and
![]() $\mathit{Box}[\alpha]$
. Comparing the content of a box requires the F-bound
$\mathit{Box}[\alpha]$
. Comparing the content of a box requires the F-bound
![]() $\mathit{Eq}[\alpha]$
(Canning et al., Reference Canning, Cook, Hill, Olthoff and Mitchell1989). The main function compares two boxes for equality.
$\mathit{Eq}[\alpha]$
(Canning et al., Reference Canning, Cook, Hill, Olthoff and Mitchell1989). The main function compares two boxes for equality.

Fig. 13. Example:
![]() ${\textrm{FGG}^{-}}$
code (top) and its translation (middle) with abbreviations (bottom).
${\textrm{FGG}^{-}}$
code (top) and its translation (middle) with abbreviations (bottom).

Fig. 14. Example: translation of the method declaration for
![]() $\mathit{Box}$
and
$\mathit{Box}$
and
![]() $\mathit{eq}$
.
$\mathit{eq}$
.
The middle part of the figure shows the translation of the
![]() ${\textrm{FGG}^{-}}$
code, using abbreviations in the bottom part. Variable
${\textrm{FGG}^{-}}$
code, using abbreviations in the bottom part. Variable
![]() $X_{\mathit{eq},\mathit{Num}}$
holds the translation of the declaration of
$X_{\mathit{eq},\mathit{Num}}$
holds the translation of the declaration of
![]() $\mathit{eq}$
for
$\mathit{eq}$
for
![]() $\mathit{Num}$
; it simply compares
$\mathit{Num}$
; it simply compares
![]() $E_2$
(translation of
$E_2$
(translation of
![]() $\mathit{this}.\mathit{val}$
) with
$\mathit{this}.\mathit{val}$
) with
![]() $E_3$
(translation of
$E_3$
(translation of
![]() $\mathit{that}.\mathit{val}$
). Remember that the translation of a method declaration takes a quadruple with coercions for the bounded type parameters of the receiver, the receiver itself, coercions for the bounded type parameters of the method, and the method arguments. Here,
$\mathit{that}.\mathit{val}$
). Remember that the translation of a method declaration takes a quadruple with coercions for the bounded type parameters of the receiver, the receiver itself, coercions for the bounded type parameters of the method, and the method arguments. Here,
![]() $\texttt{(} \texttt{)}$
is a tuple of size zero, corresponding to the nonexisting type parameters, and
$\texttt{(} \texttt{)}$
is a tuple of size zero, corresponding to the nonexisting type parameters, and
![]() $\texttt{(} \mathit{That} $
) denotes a tuple of size one, corresponding to the single argument
$\texttt{(} \mathit{That} $
) denotes a tuple of size one, corresponding to the single argument
![]() $\mathit{that}$
.
$\mathit{that}$
.
The translation of
![]() $\mathit{eq}$
for
$\mathit{eq}$
for
![]() $\mathit{Box}$
is more involved. Figure 14 shows its derivation. We omit “obvious” premises and some trivial details from the derivation trees. Rule call-iface translates the body of the method. It coerces the receiver to the interface type
$\mathit{Box}$
is more involved. Figure 14 shows its derivation. We omit “obvious” premises and some trivial details from the derivation trees. Rule call-iface translates the body of the method. It coerces the receiver to the interface type
![]() $\mathit{Eq}[\alpha]$
and then extracts the method to be called via pattern matching, see
$\mathit{Eq}[\alpha]$
and then extracts the method to be called via pattern matching, see
![]() $E_1$
. The construction of the coercion is done via
$E_1$
. The construction of the coercion is done via
![]() $\Delta \mathrel{\vdash_{{{{\textsf{coerce}}}}}} \alpha \mathrel{<:} \mathit{Eq}[\alpha] \leadsto V_1$
, see subderivation
$\Delta \mathrel{\vdash_{{{{\textsf{coerce}}}}}} \alpha \mathrel{<:} \mathit{Eq}[\alpha] \leadsto V_1$
, see subderivation ![]() . Coercion
. Coercion
![]() $V_1$
is slightly more complicated then necessary because the translation does not optimize the identity coercion
$V_1$
is slightly more complicated then necessary because the translation does not optimize the identity coercion
![]() $V_2$
. Inside of
$V_2$
. Inside of
![]() $V_1$
, we use
$V_1$
, we use
![]() $X_{\alpha}$
. This variables denotes a coercion from
$X_{\alpha}$
. This variables denotes a coercion from
![]() $\alpha$
to the representation of
$\alpha$
to the representation of
![]() $\mathit{Eq}[\alpha]$
; it is bound by the
$\mathit{Eq}[\alpha]$
; it is bound by the
![]() $\lambda$
-expression in the definition of
$\lambda$
-expression in the definition of
![]() $X_{\mathit{eq},\mathit{Box}}$
.
$X_{\mathit{eq},\mathit{Box}}$
.
The translation of the main expression calls
![]() $X_{\mathit{eq},\mathit{Box}}$
with appropriate arguments, Figure 15 for the derivation. The values
$X_{\mathit{eq},\mathit{Box}}$
with appropriate arguments, Figure 15 for the derivation. The values
![]() $\texttt{((} 1\texttt{))}$
and
$\texttt{((} 1\texttt{))}$
and
![]() $\texttt{((} 2\texttt{))}$
are nested tuples of size one, representing numbers wrapped in
$\texttt{((} 2\texttt{))}$
are nested tuples of size one, representing numbers wrapped in
![]() $\mathit{Num}$
and
$\mathit{Num}$
and
![]() $\mathit{Box}$
structs. The method call of
$\mathit{Box}$
structs. The method call of
![]() $\mathit{eq}$
is translated by rule call-struct, relying on rule methods-struct to instantiate the type variable
$\mathit{eq}$
is translated by rule call-struct, relying on rule methods-struct to instantiate the type variable
![]() $\alpha$
to
$\alpha$
to
![]() $\mathit{Num}$
, as witnessed by the coercion
$\mathit{Num}$
, as witnessed by the coercion
![]() $V_3$
.
$V_3$
.

Fig. 15. Example: translation of the main function.
5 Formal properties
In this section, we establish that the type-directed translation from Section 4.2 preserves the static and dynamic semantics of
![]() ${\textrm{FGG}^{-}}$
programs. The translation as formalized is nondeterministic: for the same source program we may derive syntactically different target programs. Thus, we further show that all target programs resulting from the same source program behave equivalently. Detailed proofs for all lemmas and theorems are given in the appendix.
${\textrm{FGG}^{-}}$
programs. The translation as formalized is nondeterministic: for the same source program we may derive syntactically different target programs. Thus, we further show that all target programs resulting from the same source program behave equivalently. Detailed proofs for all lemmas and theorems are given in the appendix.
5.1 Preservation of static semantics
It is straightforward to verify that the type system originally defined for FGG is equivalent to the type system induced by the type-directed translation presented in Section 4.2, provided the FGG program does not contain type assertions. In the following, we write
![]() $\Delta \, \vdash_{\textsf{G}} \, \tau \mathrel{<:} \sigma$
for FGG’s subtyping relation,
$\Delta \, \vdash_{\textsf{G}} \, \tau \mathrel{<:} \sigma$
for FGG’s subtyping relation,
![]() $\Delta; \Gamma \, \vdash_{\textsf{G}} \, e : \tau$
for its typing relation on expressions, and
$\Delta; \Gamma \, \vdash_{\textsf{G}} \, e : \tau$
for its typing relation on expressions, and
![]() $\, \vdash_{\textsf{G}} \, P~\textsf{ok}$
for the FGG typing relation on programs. These three relations were specified by Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020). The original article on FGG also includes support for dynamic type assertions, something we do not consider for our translation. Hence, we assume that FGG expressions do not contain type assertions.
$\, \vdash_{\textsf{G}} \, P~\textsf{ok}$
for the FGG typing relation on programs. These three relations were specified by Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020). The original article on FGG also includes support for dynamic type assertions, something we do not consider for our translation. Hence, we assume that FGG expressions do not contain type assertions.
Lemma 5.1.1 (FGG typing equivalence). Typing in FGG is equivalent to the type system induced by the translation, provided there are no type assertions.
(a) If
 $\Delta \, \vdash_{\textsf{{G}}} \, \tau \mathrel{<:} \sigma$
then either
$\Delta \, \vdash_{\textsf{{G}}} \, \tau \mathrel{<:} \sigma$
then either
 $\Delta \mathrel{\vdash_{{{{\textsf{{coerce}}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
for some V or
$\Delta \mathrel{\vdash_{{{{\textsf{{coerce}}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
for some V or
 $\sigma = \tau$
and
$\sigma = \tau$
and
 $\tau$
is not an interface type.
$\tau$
is not an interface type.(b) If
 $\Delta \mathrel{\vdash_{{{{\textsf{{coerce}}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
then
$\Delta \mathrel{\vdash_{{{{\textsf{{coerce}}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
then
 $\Delta \, \vdash_{\textsf{{G}}} \, \tau \mathrel{<:} \sigma$
.
$\Delta \, \vdash_{\textsf{{G}}} \, \tau \mathrel{<:} \sigma$
.(c) If
 $\Delta; \Gamma \, \vdash_{\textsf{{G}}} \, e : \tau$
then
$\Delta; \Gamma \, \vdash_{\textsf{{G}}} \, e : \tau$
then
 $\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{\textsf{{{exp}}}}}}} e : \tau \leadsto E$
for some E.
$\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{\textsf{{{exp}}}}}}} e : \tau \leadsto E$
for some E.(d) If
 $\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{{\textsf{{exp}}}}}}} e : \tau \leadsto E$
then
$\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{{\textsf{{exp}}}}}}} e : \tau \leadsto E$
then
 $\Delta; \Gamma \, \vdash_{\textsf{{G}}} \, e : \tau'$
for some
$\Delta; \Gamma \, \vdash_{\textsf{{G}}} \, e : \tau'$
for some
 $\tau'$
and
$\tau'$
and
 $\Delta \, \vdash_{\textsf{{G}}} \, \tau' \mathrel{<:} \tau$
.
$\Delta \, \vdash_{\textsf{{G}}} \, \tau' \mathrel{<:} \tau$
.(e)
 $\, \vdash_{\textsf{{G}}} \, P~\textsf{{ok}}$
iff
$\, \vdash_{\textsf{{G}}} \, P~\textsf{{ok}}$
iff
 $\mathrel{\vdash_{\textsf{prog}}} P \leadsto \mathit{Prog}$
.
$\mathrel{\vdash_{\textsf{prog}}} P \leadsto \mathit{Prog}$
.
Claims (a) and (b) state that structural subtyping in FGG is equivalent to the relation from Figure 9, except that the latter is not reflexive for type variables and struct types. Claims (c) and (d) establish that expression typing in FGG and our expression typing from Figure 10 are equivalent modulo subtyping. The exposition in Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020) includes a subtyping check for each form of expression, whereas we choose to have a separate subtyping rule. Hence, the type computed by the original rules for FGG might be a subtype of the type deduced by our system.
FGG enjoys type soundness (see Theorems 4.3 and 4.4 of Griesemer et al. Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020). The reduction rules for FGG and
![]() ${\textrm{FGG}^{-}}{}$
are obviously equivalent. Thus, Lemma 5.1.1 gives the following type soundness result for our type system:
${\textrm{FGG}^{-}}{}$
are obviously equivalent. Thus, Lemma 5.1.1 gives the following type soundness result for our type system:
Corollary 5.1.2. Assume ![]() for some e,
for some e,
![]() $\tau$
, and E. Then either e reduces to some value of type
$\tau$
, and E. Then either e reduces to some value of type
![]() $\tau$
or e diverges.
$\tau$
or e diverges.
5.2 Preservation of dynamic semantics
This section proves that evaluating a well-typed
![]() ${\textrm{FGG}^{-}}$
program yields the same behavior as evaluating one of its translations. Thereby, we consider all possible outcomes of evaluation: reduction to a value or divergence. Further, we show that different translations of the same program have equivalent behavior.
${\textrm{FGG}^{-}}$
program yields the same behavior as evaluating one of its translations. Thereby, we consider all possible outcomes of evaluation: reduction to a value or divergence. Further, we show that different translations of the same program have equivalent behavior.
The proof of semantic equivalence is enabled by a syntactic, step-indexed logical relation that relates an
![]() ${\textrm{FGG}^{-}}$
expression and a TL expression at some
${\textrm{FGG}^{-}}$
expression and a TL expression at some
![]() ${\textrm{FGG}^{-}}$
type. We write
${\textrm{FGG}^{-}}$
type. We write
![]() $e \longrightarrow^{k} e'$
if e reduces to e’ in exactly
$e \longrightarrow^{k} e'$
if e reduces to e’ in exactly
![]() $k \in \mathbb{N}$
steps, where
$k \in \mathbb{N}$
steps, where
![]() $\mathbb{N}$
denotes the natural numbers including zero. By convention, we write
$\mathbb{N}$
denotes the natural numbers including zero. By convention, we write
![]() $e \longrightarrow^{0} e'$
to denote
$e \longrightarrow^{0} e'$
to denote
![]() $e = e'$
. The notation
$e = e'$
. The notation
![]() $e \longrightarrow^* e'$
states that
$e \longrightarrow^* e'$
states that
![]() $e \longrightarrow^{k} e'$
for some
$e \longrightarrow^{k} e'$
for some
![]() $k \in \mathbb{N}$
. We write
$k \in \mathbb{N}$
. We write
![]() $\textsf{diverge}{e}$
to denote that e does not terminate; that is, for all
$\textsf{diverge}{e}$
to denote that e does not terminate; that is, for all
![]() $k \in \mathbb{N}$
there exists some e’ with
$k \in \mathbb{N}$
there exists some e’ with
![]() $e \longrightarrow^{k} e'$
. The same definitions apply analogously to reductions in the TL.
$e \longrightarrow^{k} e'$
. The same definitions apply analogously to reductions in the TL.
5.2.1 The logical relation
The definition of the logical relation (LR) spreads over two Figures 16 and 17. In these figures, we assume that the declarations
![]() $\overline{D}$
of the
$\overline{D}$
of the
![]() ${\textrm{FGG}^{-}}$
program being translated are implicitly available in all rules. Also, we assume that an arbitrary but fixed method substitution
${\textrm{FGG}^{-}}$
program being translated are implicitly available in all rules. Also, we assume that an arbitrary but fixed method substitution
![]() $\mu$
is implicitly available to all rules. This
$\mu$
is implicitly available to all rules. This
![]() $\mu$
is used in the reduction rules of the target language to resolve let-bound variables (i.e., translations of methods). In our main theorem (Theorem 5.2.6), we will then require that
$\mu$
is used in the reduction rules of the target language to resolve let-bound variables (i.e., translations of methods). In our main theorem (Theorem 5.2.6), we will then require that
![]() $\mu$
results from translating the methods in
$\mu$
results from translating the methods in
![]() $\overline{D}$
.
$\overline{D}$
.

Fig. 16. Relating
![]() ${\textrm{FGG}^{-}}$
to TL expressions.
${\textrm{FGG}^{-}}$
to TL expressions.

Fig. 17. Relating
![]() ${\textrm{FGG}^{-}}$
to TL substitutions and declarations.
${\textrm{FGG}^{-}}$
to TL substitutions and declarations.
We now explain the LR on expressions, Figure 16. The relation
![]() $ e \approx E \in [\![\tau]\!]_{k}$
denotes that
$ e \approx E \in [\![\tau]\!]_{k}$
denotes that
![]() ${\textrm{FGG}^{-}}$
expression e and TL expression E are equivalent at type
${\textrm{FGG}^{-}}$
expression e and TL expression E are equivalent at type
![]() $\tau$
for at most k reduction steps. We call k the step index. Rule equiv-exp has two implications as its premises. The first states that if e reduces to a value v in
$\tau$
for at most k reduction steps. We call k the step index. Rule equiv-exp has two implications as its premises. The first states that if e reduces to a value v in
![]() $k' < k$
steps, then E reduces to some value V in an arbitrary number of steps and v is equivalent to V at type
$k' < k$
steps, then E reduces to some value V in an arbitrary number of steps and v is equivalent to V at type
![]() $\tau$
for the remaining
$\tau$
for the remaining
![]() $k - k'$
steps. The second premise is for diverging expressions: if e reduces in less than k steps to some expression e’ and e’ diverges, then E diverges as well.
$k - k'$
steps. The second premise is for diverging expressions: if e reduces in less than k steps to some expression e’ and e’ diverges, then E diverges as well.
The relation
![]() $v \equiv V \in [\![\tau]\!]_{k}$
defines equivalence of
$v \equiv V \in [\![\tau]\!]_{k}$
defines equivalence of
![]() ${\textrm{FGG}^{-}}$
value v and TL value V at type
${\textrm{FGG}^{-}}$
value v and TL value V at type
![]() $\tau$
with step index k. Rule equiv-struct handles the case where
$\tau$
with step index k. Rule equiv-struct handles the case where
![]() $\tau$
is a struct type. Then v must be a value of this struct type and V must be a struct value such that all field values of v and V are equivalent. Rule equiv-iface deals with the case that
$\tau$
is a struct type. Then v must be a value of this struct type and V must be a struct value such that all field values of v and V are equivalent. Rule equiv-iface deals with the case that
![]() $\tau$
is an interface type. Hence, V must be an interface value
$\tau$
is an interface type. Hence, V must be an interface value
![]() $\text{ (} U\text{ ,} \text{ (} \overline{V} \text{ )} \text{ )}$
with two requirements. First, v and U are equivalent for all step indices
$\text{ (} U\text{ ,} \text{ (} \overline{V} \text{ )} \text{ )}$
with two requirements. First, v and U are equivalent for all step indices
![]() $k_1 < k$
at some struct type
$k_1 < k$
at some struct type
![]() $\sigma_S$
. Second,
$\sigma_S$
. Second,
![]() $\text{ (} \overline{V} \text{ )}$
must be an appropriate dictionary for the methods of the interface with receiver type
$\text{ (} \overline{V} \text{ )}$
must be an appropriate dictionary for the methods of the interface with receiver type
![]() $\sigma_S$
. To check this requirement, rule method-lookup defines the auxiliary
$\sigma_S$
. To check this requirement, rule method-lookup defines the auxiliary
![]() $\textsf{methodLookup}(m_i, \sigma_S)$
to retrieve a quadruple
$\textsf{methodLookup}(m_i, \sigma_S)$
to retrieve a quadruple
![]() $\langle {x}{\sigma_S}{R}{e}\rangle$
from the declaration of
$\langle {x}{\sigma_S}{R}{e}\rangle$
from the declaration of
![]() $m_i$
for
$m_i$
for
![]() $\sigma_S$
. This quadruple has to be equivalent to dictionary entry
$\sigma_S$
. This quadruple has to be equivalent to dictionary entry
![]() $V_i$
for all step indices
$V_i$
for all step indices
![]() $k_2 < k$
at the signature of the method.
$k_2 < k$
at the signature of the method.
A dictionary entry is always a function value. We write
![]() $\langle {x}{\tau_S}{R}{e}\rangle \approx (\lambda X \texttt{.}{E}) \in [\![ R]\!]_{k}$
to denote equivalence between a quadruple for a method declaration and some dictionary entry
$\langle {x}{\tau_S}{R}{e}\rangle \approx (\lambda X \texttt{.}{E}) \in [\![ R]\!]_{k}$
to denote equivalence between a quadruple for a method declaration and some dictionary entry
![]() $\lambda X \texttt{.} E$
. Rule equiv-method-dict-entry defines this equivalence such that method body e and
$\lambda X \texttt{.} E$
. Rule equiv-method-dict-entry defines this equivalence such that method body e and
![]() $\lambda X \texttt{.}E$
take related arguments to related outputs. Thus, the premise of the rule requires for all step indices
$\lambda X \texttt{.}E$
take related arguments to related outputs. Thus, the premise of the rule requires for all step indices
![]() $k' \leq k$
, all related type parameters
$k' \leq k$
, all related type parameters
![]() $\overline{\tau}$
and W, all related receiver values v and V, and all related arguments
$\overline{\tau}$
and W, all related receiver values v and V, and all related arguments
![]() $\overline{v}$
and
$\overline{v}$
and
![]() $\overline{V}$
that e and
$\overline{V}$
that e and
![]() $\lambda X \texttt{.}E$
yield related results when applied to the respective arguments.
$\lambda X \texttt{.}E$
yield related results when applied to the respective arguments.
The judgment
![]() $ \overline{\sigma} \approx V \in [\![\overline{\alpha\,\tau_I}]\!]_{k}$
denotes equivalence between concrete type arguments
$ \overline{\sigma} \approx V \in [\![\overline{\alpha\,\tau_I}]\!]_{k}$
denotes equivalence between concrete type arguments
![]() $\overline{\sigma}$
and their TL realization V when checking the bounds of type parameters
$\overline{\sigma}$
and their TL realization V when checking the bounds of type parameters
![]() $\overline{\alpha\,\tau_I}$
. The definition in rule equiv-bounded-typarams relies on our translation strategy that bounded type parameters are represented by coercions.
$\overline{\alpha\,\tau_I}$
. The definition in rule equiv-bounded-typarams relies on our translation strategy that bounded type parameters are represented by coercions.
Having explained all judgments from Figure 16, we verify that the recursive definitions of
![]() $ e \approx E \in [\![\tau]\!]_{k}$
and
$ e \approx E \in [\![\tau]\!]_{k}$
and
![]() $v \equiv V \in [\![\tau]\!]_{k}$
are well founded. Often, LRs are defined by induction on the structure of types. In our case, this approach does not work because interface types in
$v \equiv V \in [\![\tau]\!]_{k}$
are well founded. Often, LRs are defined by induction on the structure of types. In our case, this approach does not work because interface types in
![]() ${\textrm{FGG}^{-}}$
might be recursive, see our previous work (Sulzmann & Wehr, Reference Sulzmann and Wehr2022) for an example. Thus, we use the step index as part of a decreasing measure
${\textrm{FGG}^{-}}$
might be recursive, see our previous work (Sulzmann & Wehr, Reference Sulzmann and Wehr2022) for an example. Thus, we use the step index as part of a decreasing measure
![]() $\mathcal M$
. Writing
$\mathcal M$
. Writing
![]() $|V|$
for the size of some target value V, we define
$|V|$
for the size of some target value V, we define
![]() $\mathcal M( e \approx E \in [\![\tau]\!]_{k}) = (k, 1, 0)$
and
$\mathcal M( e \approx E \in [\![\tau]\!]_{k}) = (k, 1, 0)$
and
![]() $\mathcal M(v \equiv V \in [\![\tau]\!]_{k}) = (k, 0, |V|)$
. In equiv-exp, either k decreases or stays constant but the second component of
$\mathcal M(v \equiv V \in [\![\tau]\!]_{k}) = (k, 0, |V|)$
. In equiv-exp, either k decreases or stays constant but the second component of
![]() $\mathcal M$
decreases. In equiv-struct, k and the second component stay constant but
$\mathcal M$
decreases. In equiv-struct, k and the second component stay constant but
![]() $|V|$
decreases, and in equiv-iface together with equiv-method-dict-entry and equiv-bounded-typarams step index k decreases. Note that equiv-method-dict-entry and equiv-bounded-typarams only require
$|V|$
decreases, and in equiv-iface together with equiv-method-dict-entry and equiv-bounded-typarams step index k decreases. Note that equiv-method-dict-entry and equiv-bounded-typarams only require
![]() $k' \leq k$
. This is ok because we already have
$k' \leq k$
. This is ok because we already have
![]() $k_2 < k$
in equiv-iface.
$k_2 < k$
in equiv-iface.
Figure 17 extends the LR to whole programs. Judgment
![]() $ \eta \approx \rho \in [\![\Delta]\!]_{k}$
denotes how a
$ \eta \approx \rho \in [\![\Delta]\!]_{k}$
denotes how a
![]() ${\textrm{FGG}^{-}}$
type substitution
${\textrm{FGG}^{-}}$
type substitution
![]() $\eta$
intended to substitute the type variables from
$\eta$
intended to substitute the type variables from
![]() $\Delta$
is related to a TL substitution
$\Delta$
is related to a TL substitution
![]() $\rho$
. The definition in rule equiv-ty-subst falls back to equivalence of type parameters. Judgment
$\rho$
. The definition in rule equiv-ty-subst falls back to equivalence of type parameters. Judgment
![]() $ \theta \approx \rho \in [\![\Gamma]\!]_{k}$
similarly relates a
$ \theta \approx \rho \in [\![\Gamma]\!]_{k}$
similarly relates a
![]() ${\textrm{FGG}^{-}}$
value substitution
${\textrm{FGG}^{-}}$
value substitution
![]() $\theta$
intended for value environment
$\theta$
intended for value environment
![]() $\Gamma$
with a TL substitution
$\Gamma$
with a TL substitution
![]() $\rho$
. See rule equiv-val-subst.
$\rho$
. See rule equiv-val-subst.
Judgment ![]() states equivalence of a function declaration with a TL variable X. Rule equiv-method-decl takes an approach similar as in rule equiv-method-dict-entry: method body e and variable X must yield related outputs when applied to related arguments. Thus, for all related type arguments
states equivalence of a function declaration with a TL variable X. Rule equiv-method-decl takes an approach similar as in rule equiv-method-dict-entry: method body e and variable X must yield related outputs when applied to related arguments. Thus, for all related type arguments
![]() $\overline{\tau}$
,
$\overline{\tau}$
,
![]() $\overline{\tau'}$
and
$\overline{\tau'}$
and
![]() $\text{ (} \overline{W}\text{ ,} \overline{W'} \text{ )}$
, all related receiver values v and V, and all related arguments
$\text{ (} \overline{W}\text{ ,} \overline{W'} \text{ )}$
, all related receiver values v and V, and all related arguments
![]() $\overline{v}$
and
$\overline{v}$
and
![]() $\overline{V}$
, the expression e and variable X must be related when applied to the appropriate arguments. However, different than in equiv-method-dict-entry, we only requires this to hold for all
$\overline{V}$
, the expression e and variable X must be related when applied to the appropriate arguments. However, different than in equiv-method-dict-entry, we only requires this to hold for all
![]() $k' < k$
.
$k' < k$
.
Judgment
![]() $\overline{D} \approx_{k} \mu$
defines equivalence between
$\overline{D} \approx_{k} \mu$
defines equivalence between
![]() ${\textrm{FGG}^{-}}$
declarations
${\textrm{FGG}^{-}}$
declarations
![]() $\overline{D}$
and TL method substitution
$\overline{D}$
and TL method substitution
![]() $\mu$
. The definition in rule equiv-decls is straightforward: each method declaration for some method m and struct
$\mu$
. The definition in rule equiv-decls is straightforward: each method declaration for some method m and struct
![]() $t_S$
must be equivalent to variable
$t_S$
must be equivalent to variable
![]() $X_{{m},{t_S}}$
.
$X_{{m},{t_S}}$
.
5.2.2 Equivalence between source and translation
To establish the desired result of semantic equivalence between a source program and one of its translations, we implicitly make the following assumptions about the globally available declarations
![]() $\overline{D}$
and method substitution
$\overline{D}$
and method substitution
![]() $\mu$
.
$\mu$
.
Assumption 5.2.1. We assume that the globally available declarations
![]() $\overline{D}$
are well formed; that is,
$\overline{D}$
are well formed; that is,
![]() $\mathrel{\vdash_{{{\textsf{ok}}}}} D_i$
for all
$\mathrel{\vdash_{{{\textsf{ok}}}}} D_i$
for all
![]() $D_i \in \overline{D}$
and
$D_i \in \overline{D}$
and ![]() for some
for some
![]() $X_i$
and
$X_i$
and
![]() $V_i$
and all
$V_i$
and all ![]() . Further, we assume that the globally available method substitution
. Further, we assume that the globally available method substitution
![]() $\mu$
has only variables of the form
$\mu$
has only variables of the form
![]() $X_{{m},{t_S}}$
in its domain.
$X_{{m},{t_S}}$
in its domain.
Several basic properties hold for our LR. For example, monotonicity gives us that with
![]() $ e \approx E \in [\![\tau]\!]_{k}$
and
$ e \approx E \in [\![\tau]\!]_{k}$
and
![]() $k' \leq k$
we also have
$k' \leq k$
we also have
![]() $ e \approx E \in [\![\tau]\!]_{k'}$
. Another property is how target and source reductions preserve equivalence:
$ e \approx E \in [\![\tau]\!]_{k'}$
. Another property is how target and source reductions preserve equivalence:
Lemma 5.2.2 (Target reductions preserve equivalence). If
![]() $ e \approx E \in [\![\tau]\!]_{k}$
and
$ e \approx E \in [\![\tau]\!]_{k}$
and
![]() $E_2 \longrightarrow^* E$
then
$E_2 \longrightarrow^* E$
then
![]() $ e \approx E_2 \in [\![\tau]\!]_{k}$
.
$ e \approx E_2 \in [\![\tau]\!]_{k}$
.
Lemma 5.2.3 (Source reductions preserve equivalence) If
![]() $ e \approx E \in [\![\tau]\!]_{k}$
and
$ e \approx E \in [\![\tau]\!]_{k}$
and
![]() $e_2 \longrightarrow e$
then
$e_2 \longrightarrow e$
then
![]() $ e_2 \approx E \in [\![\tau]\!]_{k+1}$
.
$ e_2 \approx E \in [\![\tau]\!]_{k+1}$
.
The lemmas for monotonicity and several other properties are stated in Appendix A.3, together with all proofs. We can then establish that an
![]() ${\textrm{FGG}^{-}}$
expression e is semantically equivalent to its translation E.
${\textrm{FGG}^{-}}$
expression e is semantically equivalent to its translation E.
Lemma 5.2.4 (Expression equivalence). Assume
![]() $\overline{D} \approx_{k} \mu$
and
$\overline{D} \approx_{k} \mu$
and
![]() $ \eta \approx \rho \in [\![\Delta]\!]_{k}$
and
$ \eta \approx \rho \in [\![\Delta]\!]_{k}$
and
![]() $ \theta \approx \rho \in [\![\eta \Gamma]\!]_{k}$
. If
$ \theta \approx \rho \in [\![\eta \Gamma]\!]_{k}$
. If
![]() $\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{\textsf{{{exp}}}}}}} e : \tau \leadsto E$
then
$\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{\textsf{{{exp}}}}}}} e : \tau \leadsto E$
then
![]() $ \theta \eta e \approx \rho E \in [\![\eta \tau]\!]_{k}$
.
$ \theta \eta e \approx \rho E \in [\![\eta \tau]\!]_{k}$
.
The proof is by induction on the derivation of
![]() $\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
, see Appendix A.3.2.1 (p. 49) for the full proof. We next establish semantic equivalence for method declarations.
$\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
, see Appendix A.3.2.1 (p. 49) for the full proof. We next establish semantic equivalence for method declarations.
Lemma 5.2.5 (Method equivalence) Let
![]() $\overline{D}$
and
$\overline{D}$
and
![]() $\mu$
such that for each
$\mu$
such that for each ![]() with
with
![]() $m = \textsf{{methodName}}(R)$
we have
$m = \textsf{{methodName}}(R)$
we have
![]() $ \mathrel{\vdash_{{{{\textsf{{meth}}}}}}} D \leadsto X_{{m},{t_S}} = V$
and
$ \mathrel{\vdash_{{{{\textsf{{meth}}}}}}} D \leadsto X_{{m},{t_S}} = V$
and
![]() $\mu(X_{{m},{t_S}}) = V$
for some V. Then
$\mu(X_{{m},{t_S}}) = V$
for some V. Then
![]() $\overline{D} \approx_{k} \mu$
for any k.
$\overline{D} \approx_{k} \mu$
for any k.
The proof of this lemma is by induction on k, see Appendix A.3.2.2 (p. 59) for the full proof. Finally, the following theorem states our desired result: semantic equivalence between an
![]() ${\textrm{FGG}^{-}}$
program and its translation.
${\textrm{FGG}^{-}}$
program and its translation.
Theorem 5.2.6 (Program equivalence). Let ![]() with e having type
with e having type
![]() $\tau$
. Let
$\tau$
. Let
![]() $\mu = \langle\overline{X_i \mapsto V_i}\rangle$
. Then both of the following holds:
$\mu = \langle\overline{X_i \mapsto V_i}\rangle$
. Then both of the following holds:
1. If
 $e \longrightarrow^* v$
for some value v then there exists a TL value V such that
$e \longrightarrow^* v$
for some value v then there exists a TL value V such that
 $E \longrightarrow^*_{\mu} V$
and
$E \longrightarrow^*_{\mu} V$
and
 $v \equiv V \in [\![\tau]\!]_{k}$
for any k.
$v \equiv V \in [\![\tau]\!]_{k}$
for any k.2. If e diverges then so does E.
The “with e having type
![]() $\tau$
” part means that the last rule in the derivation of the program translation has
$\tau$
” part means that the last rule in the derivation of the program translation has
![]() $\langle\emptyset,\emptyset\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
as a premise. Obviously,
$\langle\emptyset,\emptyset\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
as a premise. Obviously,
![]() $\overline{D}$
and
$\overline{D}$
and
![]() $\mu$
meet the requirements of Assumption 5.2.1. The theorem then follows from Lemmas 5.2.4 and 5.2.5. See Appendix A.3.2.3 (p. 60) for the full proof.
$\mu$
meet the requirements of Assumption 5.2.1. The theorem then follows from Lemmas 5.2.4 and 5.2.5. See Appendix A.3.2.3 (p. 60) for the full proof.
5.2.3 Equivalence between different translations
Our translation is nondeterministic because different translations of the same expression may contain distinct sequences of applications of the subsumption rule sub. Recall the example from Figure 1. There are (at least) two different ways to translate expression formatSome(Num{1}) at type Format.
1. Use rules coerce-struct-iface and sub to go directly from Num to supertype Format. The translation is then
 .
.2. First use coerce-struct-iface and sub to go from Num to Pretty, then use coerce-iface-iface and sub to go from Pretty to Format. The translation is then
 .
.
Each choice leads to a syntactically distinct target expression. In general, evaluating the target expressions might lead to syntactically different target values because target values might contain dictionaries (i.e., tuple of
![]() $\lambda$
-expressions), and different translations might produce syntactically different dictionaries.
$\lambda$
-expressions), and different translations might produce syntactically different dictionaries.
Another source of nondeterminism is that rule prog for typing programs is allowed to choose the type
![]() $\tau$
of the main expression. For example, instead of typing formatSome(Num{1}) at type Format, another translation might pick type Pretty or Num for the main expression. The choice for the type of the main expression might also lead to syntactically different target expressions.
$\tau$
of the main expression. For example, instead of typing formatSome(Num{1}) at type Format, another translation might pick type Pretty or Num for the main expression. The choice for the type of the main expression might also lead to syntactically different target expressions.
To summarize, different translations of the same source program might lead to syntactically different TL programs, and the syntactic differences might persist in the final values after evaluation. But a slightly weaker property holds: if we remove all dictionaries in the final values, then the results are syntactically equal.
Figure 18 defines a function
![]() $\textsf{erase}$
that removes all dictionaries from a TL value. The function comes in two variations:
$\textsf{erase}$
that removes all dictionaries from a TL value. The function comes in two variations:
•
 $\textsf{erase}(\tau, V)$
removes all dictionaries from value V when viewed at type
$\textsf{erase}(\tau, V)$
removes all dictionaries from value V when viewed at type
 $\tau$
. Its duty is to remove the topmost dictionary if
$\tau$
. Its duty is to remove the topmost dictionary if
 $\tau$
is an interface type. In this case, the function is partial but this is not an issue: a value viewed at an interface type is always a pair of values.
$\tau$
is an interface type. In this case, the function is partial but this is not an issue: a value viewed at an interface type is always a pair of values.•
 $\textsf{erase}(V)$
removes all dictionaries from V by replacing the
$\textsf{erase}(V)$
removes all dictionaries from V by replacing the
 $\lambda$
-expressions with a fixed, otherwise unused, nullary constructor
$\lambda$
-expressions with a fixed, otherwise unused, nullary constructor
 $\textbf{K}_{\lambda}$
. This definition relies on then fact that the translation only produces
$\textbf{K}_{\lambda}$
. This definition relies on then fact that the translation only produces
 $\lambda$
-expressions for dictionary entries. We replace
$\lambda$
-expressions for dictionary entries. We replace
 $\lambda$
-expressions with a dedicated constructor
$\lambda$
-expressions with a dedicated constructor
 $\textbf{K}_{\lambda}$
instead of the nullary tuple
$\textbf{K}_{\lambda}$
instead of the nullary tuple
 $\texttt {()}$
so as to avoid confusion between an erased
$\texttt {()}$
so as to avoid confusion between an erased
 $\lambda$
and a struct value without fields.
$\lambda$
and a struct value without fields.

Fig. 18. Erasure of dictionaries.
The following theorem states that evaluating the outcomes of two translations of the same source program yields values that are identical up to removal of dictionaries (or both diverge). This holds even if the two translations assign different types to the main expression of the source program. That is, there are no semantic ambiguities, and we can establish that our translation is coherent (Reynolds, Reference Reynolds1991).
Theorem 5.2.7 (Coherence). Let ![]() . Assume
. Assume ![]() with e having type
with e having type
![]() $\tau$
and
$\tau$
and ![]() with e having type
with e having type
![]() $\tau'$
. Define
$\tau'$
. Define
![]() $\mu = \langle\overline{X_i \mapsto V_i}\rangle$
and
$\mu = \langle\overline{X_i \mapsto V_i}\rangle$
and
![]() $\mu' = \langle\overline{X_i' \mapsto V_i'}\rangle$
. Then both of the following holds:
$\mu' = \langle\overline{X_i' \mapsto V_i'}\rangle$
. Then both of the following holds:
1. If
 $E \longrightarrow^*_{\mu} V$
for some V, then
$E \longrightarrow^*_{\mu} V$
for some V, then
 $E' \longrightarrow^*_{\mu'} V'$
for some V’ with
$E' \longrightarrow^*_{\mu'} V'$
for some V’ with
 $\textsf{{erase}}(\tau, V) = \textsf{{erase}}(\tau', V')$
.
$\textsf{{erase}}(\tau, V) = \textsf{{erase}}(\tau', V')$
.2. If E diverges then so does E’.
See Appendix A.3.3.1 (p. 63) for the proof.
5.3 Getting the step index right
The LR in Figures 16 and 17 requires at some places the step index in the premise to be strictly smaller than in the conclusion (
![]() $<$
), and other places require only less-than-or-equal (
$<$
), and other places require only less-than-or-equal (
![]() $\leq$
). In equiv-exp, we have
$\leq$
). In equiv-exp, we have
![]() $<$
to keep the definition of the LR well founded. The
$<$
to keep the definition of the LR well founded. The
![]() $<$
in rule equiv-method-decl is required for the inductive argument in the proof of Lemma 5.2.5. Rule equiv-iface also has
$<$
in rule equiv-method-decl is required for the inductive argument in the proof of Lemma 5.2.5. Rule equiv-iface also has
![]() $<$
, but rule equiv-method-dict-entry only requires
$<$
, but rule equiv-method-dict-entry only requires
![]() $\leq$
. For well-foundedness, it is crucial that one of these two rules decreases the step index. However, equally important is that the step index is not forced to decrease more than once, so we need
$\leq$
. For well-foundedness, it is crucial that one of these two rules decreases the step index. However, equally important is that the step index is not forced to decrease more than once, so we need
![]() $<$
in one rule and
$<$
in one rule and
![]() $\leq$
in the other. If both rules had
$\leq$
in the other. If both rules had
![]() $<$
, then the proof of Lemma 5.2.4 would not go through for case call-iface.
$<$
, then the proof of Lemma 5.2.4 would not go through for case call-iface.
Consider the following example in the context of Figure 13:

For values
![]() $w_1$
and
$w_1$
and
![]() $w_2$
, we may assume (5.1)
$w_2$
, we may assume (5.1)
![]() $w_1 \equiv W_1 \in [\![\mathit{Eq}[\mathit{Num}]]\!]_{k}$
and
$w_1 \equiv W_1 \in [\![\mathit{Eq}[\mathit{Num}]]\!]_{k}$
and
![]() $ w_2 \approx W_2 \in [\![\mathit{Num}]\!]_{k}$
for some k. To verify that the translation yields related expressions, we must show
$ w_2 \approx W_2 \in [\![\mathit{Num}]\!]_{k}$
for some k. To verify that the translation yields related expressions, we must show
From (5.1), via inversion of rule equiv-iface, we can derive
because the premise of the rule requires this to hold for all
![]() $k_2 < k$
. Let e be the body of the method declaration of
$k_2 < k$
. Let e be the body of the method declaration of
![]() $\mathit{eq}$
for
$\mathit{eq}$
for
![]() $\mathit{Num}$
. Inverting rule equiv-method-dict-entry for (5.3) yields
$\mathit{Num}$
. Inverting rule equiv-method-dict-entry for (5.3) yields
for
![]() $k' = k - 1$
because rule equiv-method-dict-entry has
$k' = k - 1$
because rule equiv-method-dict-entry has
![]() $\leq$
in its premise. Also, we have
$\leq$
in its premise. Also, we have
![]() $w_1.\mathit{eq}(w_2) \longrightarrow^{1} \langle\mathit{this} \mapsto w_1, \mathit{that} \mapsto w_2\rangle e$
and
$w_1.\mathit{eq}(w_2) \longrightarrow^{1} \langle\mathit{this} \mapsto w_1, \mathit{that} \mapsto w_2\rangle e$
and ![]() . Thus, with (5.4), Lemmas 5.2.2, and 5.2.3 we get
. Thus, with (5.4), Lemmas 5.2.2, and 5.2.3 we get
![]() $ w_1.\mathit{eq}(w_2) \approx E \in [\![\mathit{bool}]\!]_{k' + 1}$
. For
$ w_1.\mathit{eq}(w_2) \approx E \in [\![\mathit{bool}]\!]_{k' + 1}$
. For
![]() $k' = k - 1$
, this is exactly (5.2), as required. But if rule equiv-method-dict-entry required
$k' = k - 1$
, this is exactly (5.2), as required. But if rule equiv-method-dict-entry required
![]() $<$
in its premise, then (5.4) would only hold for
$<$
in its premise, then (5.4) would only hold for
![]() $k' = k - 2$
and we could not derive (5.2).
$k' = k - 2$
and we could not derive (5.2).
Whether we have
![]() $<$
in equiv-iface and
$<$
in equiv-iface and
![]() $\leq$
in equiv-method-dict-entry or vice versa is a matter of taste. In our previous work at MPC (Sulzmann & Wehr, Reference Sulzmann and Wehr2022), we established a dictionary-passing translation for FG without generics. The situation is slightly different there. With generics, we need two rules with respect to methods: equiv-method-decl for method declarations and equiv-method-dict-entry for dictionary entries where the coercions for the bounds of the receiver’s type parameters have already been supplied. Without generics, there are no type parameters, so a single rule suffices (rule red-rel-method in MPC). So in the article at MPC, we use
$\leq$
in equiv-method-dict-entry or vice versa is a matter of taste. In our previous work at MPC (Sulzmann & Wehr, Reference Sulzmann and Wehr2022), we established a dictionary-passing translation for FG without generics. The situation is slightly different there. With generics, we need two rules with respect to methods: equiv-method-decl for method declarations and equiv-method-dict-entry for dictionary entries where the coercions for the bounds of the receiver’s type parameters have already been supplied. Without generics, there are no type parameters, so a single rule suffices (rule red-rel-method in MPC). So in the article at MPC, we use
![]() $<$
for rule red-rel-method and
$<$
for rule red-rel-method and
![]() $\leq$
for rule red-rel-iface, the pendant to rule equiv-iface of the current article.
$\leq$
for rule red-rel-iface, the pendant to rule equiv-iface of the current article.
6 Implementation
We provide an implementation of the translation Footnote 2 written in Haskell (2022). All examples in this article were checked against the implementation. Competitive runtime performance of the translated code was not our goal. Hence, we took a convenient route and used Racket Racket as the TL. The implementation features all language concepts from Section 3, as well as type assertions, generic functions, and several base types (integers, characters, strings, and booleans).
Generic functions and base types are straightforward to support. Implementing the typing and translation rules from Figure 10 requires some care because the presence of subsumption rule sub renders the translation nondeterministic (see Section 5.2.3). We solved this problem by “inlining” the subsumption step when checking the arguments of a method call against the parameter types (rules call-struct and call-iface) and when checking the field values of a struct against the declared field types (rule struct). On formal grounds, this is justified as FG (2020) inlines the subsumption step in similar ways and typing in
![]() ${\textrm{FGG}^{-}}$
is equivalent the type system induced by our translation rules (Lemma 5.1.1). The realization of type assertions (dynamic type casts) uses type tags (Ohori & Ueno, Reference Ohori and Ueno2021). At runtime, a type assertion
${\textrm{FGG}^{-}}$
is equivalent the type system induced by our translation rules (Lemma 5.1.1). The realization of type assertions (dynamic type casts) uses type tags (Ohori & Ueno, Reference Ohori and Ueno2021). At runtime, a type assertion
![]() $e.(\tau)$
checks compatibility between e’s type tag and the type tag corresponding to
$e.(\tau)$
checks compatibility between e’s type tag and the type tag corresponding to
![]() $\tau$
.
$\tau$
.
Our implementation comes with a large test suite and contains in total 181 tests, covering all main features of the source language. See Figure 19 for a summary. We wrote 25 new tests and included all 148 tests and examples from the OOPSLA 2020 implementation. Footnote 3 Moreover, we also included eight examples from the OOPSLA 2022 implementation. Footnote 4 (The implementation for OOPSLA 2022 builds on the one for OOPSLA 2020, adding 12 new test cases. We ignored four test cases because they use concurrency features not supported by our implementation.) Most tests from OOPSLA 2020/2022 could be integrated in our test suite without changes, and for some we had to perform minor syntactic adjustments.

Fig. 19. Summary of the test suite for the implementation.
Each test is a source file in one of the following categories:
1. eval good, 73 tests: The test type-checks and evaluates successfully. For the test to succeed, the result of evaluation must match the expected result. We arrived at the expected result by inspecting the program and (if applicable) comparing it against the run of the OOPSLA 2020/2022 implementation.
2. eval bad, 15 tests: The test type-checks successfully but fails at runtime. For the test to succeed, the error message must match an expected string. We determined the expected string in similar way as for the eval good category.
3. type good, 60 tests: The test type-checks successfully but is not executed because it has no interesting operational behavior.
4. type bad, 33 tests: The test fails to type-check. For the test to succeed, the error message must match an expected string.
Some of the tests behave differently under our implementation when compared with the original implementations for OOPSLA 2020/2022:
• The OOPSLA 2020 implementation compiles generics by monomorphization; that is, generic code is specialized for all type arguments appearing in the program. But monomorphization cannot deal with all programs, so their type-checker rejects several programs based on some syntactic condition (see Section 7.1 for details). Our implementation type-checks these programs successfully.
• The OOPSLA 2020 implementation statically rejects type assertions
 $e.(\tau)$
where the type of e is a struct type, even though evaluation might succeed at runtime. Our implementation is more liberal and only rejects type assertions statically that are guaranteed to fail at runtime.
$e.(\tau)$
where the type of e is a struct type, even though evaluation might succeed at runtime. Our implementation is more liberal and only rejects type assertions statically that are guaranteed to fail at runtime.• The OOPSLA 2020 implementation rejects recursive definitions of structs. For simplicity, we omitted this check from our implementation.
• The OOPSLA 2020 implementation runs several tests only for a fixed number of reduction steps because these tests would diverge otherwise. Our implementation only type-checks such tests.
7 Related work
The related work section covers generics in Go, type classes in Haskell, LRs, and a summary of our own prior work. Footnote 5 At the end, we give an overview of the existing translations with source language FGG.
7.1 Generics in Go
The results of this work rest on the definition of FGG provided by Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020). FGG is a minimal core calculus modeling the essential features of the programming language Go (2022). It includes support for overloaded methods, interface types, structural subtyping, generics, and type assertions. Our formalization of FGG ignores dynamic type assertions but otherwise sticks to the original definition of FGG, apart from some minor cosmetic changes in presentation. We prove that the type system implied by our translation is equivalent to the original type system of FGG, and that translated programs behave the same way as under the original dynamic semantics.
The original dynamic semantics of FGG uses runtime method lookup, in the same way as we did in Section 3. The authors define an alternative semantics via monomorphization; that is, they specialize generic code for all type arguments appearing in the program. This alternative semantics is equivalent to the one based on runtime method lookup, but there exist type-correct FGG programs that cannot be monomorphized. For instance, polymorphic recursion leads to infinitely many type instantiations, so programs with a polymorphic–recursive method cannot be monomorphized. Footnote 6 Further, monomorphization often leads to a blowup in code size. In contrast, our translation handles all type-correct FGG programs, and instantiations of generic code with different type arguments do not increase the code size. However, we expect that monomorphized code will offer better performance than code generated by our dictionary-passing translation, because method dictionaries imply several indirections not present in monomorphized programs.
The current implementation of generics (Taylor&Griesemer, Reference Taylor and Griesemer2021) in Go versions 1.18, 1.19, and 1.20 (2022) differs significantly from the formalization in FGG. For example, full Go requires a method declaration for a generic struct to have exactly the same type bounds as the struct. In FGG, bounds of the receiver struct in a method declaration might be stricter than the bounds in the corresponding struct declaration. In Figure 2, we used this feature to implement formatting for the fully generic Pair type, provided the type parameters can be formatted as well. Go cannot express this scenario without falling back to dynamic type assertions.
Ellis et al. (Reference Ellis, Zhu, Yoshida and Song2022) formalize a dictionary-passing translation from a restricted subset of FGG to FG. The restriction for FGG is the same as previously explained for full Go: a method declaration must have the same type bounds as its receiver struct. The translation utilizes this restriction to translate an FGG struct together with all its methods into a single FG struct (dictionary). This approach would scale to full Go even with separate compilation because a struct and all its methods must be part of the same package. Further, the translation of Ellis et al. replaces all types in method signatures with the top-type Any, relying on dynamic type assertions to enable type-checking of the resulting FG program. The authors provide a working implementation and a benchmark suite to compare their translation against several other approaches, including the current implementation of generics in full Go. Our translation targets an extended
![]() $\lambda$
-calculus and does not restrict the type bounds of the receiver struct in a method declaration. We also provide an implementation but no evaluation of its performance.
$\lambda$
-calculus and does not restrict the type bounds of the receiver struct in a method declaration. We also provide an implementation but no evaluation of its performance.
Method dictionaries bear some resemblance to virtual method tables (vtables) used to implement virtual method dispatch in object-oriented languages (Driesen & Hölzle, Reference Driesen and Hölzle1996). The main difference between vtables and dictionaries is that there is a fixed connection between an object and its vtable (via the class of the object), whereas the connection between a value and a dictionary may change at runtime, depending on the type the value is used at. Dictionaries allow access to a method at a fixed offset, whereas vtables in the presence of multiple inheritance require a more sophisticated lookup algorithm (Alpern et al., Reference Alpern, Cocchi, Fink, Grove and Lieber2001).
Generics in class-based languages such as Java (Bracha et al., Reference Bracha, Odersky, Stoutamire and Wadler1998; Igarashi et al., Reference Igarashi, Pierce and Wadler2001), and C
![]() $\sharp$
(Kennedy & Syme, Reference Kennedy and Syme2001; Emir et al., Reference Emir, Kennedy, Russo and Yu2006) do not require a dictionary-passing translation because all methods are part of the virtual method table of an object. In Go, however, methods are not necessarily attached to the receiver struct, so additional evidence in form of dictionaries must be passed for such methods. Further, subtyping in Java and C
$\sharp$
(Kennedy & Syme, Reference Kennedy and Syme2001; Emir et al., Reference Emir, Kennedy, Russo and Yu2006) do not require a dictionary-passing translation because all methods are part of the virtual method table of an object. In Go, however, methods are not necessarily attached to the receiver struct, so additional evidence in form of dictionaries must be passed for such methods. Further, subtyping in Java and C
![]() $\sharp$
is nominal, whereas Go has structural subtyping.
$\sharp$
is nominal, whereas Go has structural subtyping.
A possible optimization to the dictionary-passing translation is selective code specialization (Dean et al., Reference Dean, Chambers and Grove1995). With this approach, the dictionary-passing translation generates code that runs for all type arguments. In addition, specialized code is generated for frequently used combinations of type arguments. This approach allows to trade code size against runtime performance. The GHC compiler for Haskell supports a SPECIALIZE pragma (GHC User’s Guide, 2022, Section 6.20.11.) that allows developers to specialize a polymorphic function to a particular type. The specialization also supports type class dictionaries.
7.2 Type classes in Haskell
The dictionary-passing translation is well studied in the context of Haskell type classes (Wadler & Blott, Reference Wadler and Blott1989; Hall et al., Reference Hall, Hammond, Peyton Jones and Wadler1996). A type class constraint translates to an extra function parameter, and constraint resolution provides a dictionary with the methods of the type class for this parameter. In FGG, structural subtyping relations imply coercions and bounded type parameters translate to coercion parameters. An interface value pairs a struct value with a dictionary for the methods of the interface. Thus, interface values can be viewed as representations of existential types (Mitchell & Plotkin, Reference Mitchell and Plotkin1988; Läufer, Reference Läufer1996; Thiemann & Wehr, Reference Thiemann and Wehr2008).
Another important property in the type class context is coherence. Bottu et al. (Reference Bottu, Xie, Marntirosian and Schrijvers2019) make use of LRs to state equivalence among distinct target terms resulting from the same source type class program. In the setting of FGG-, we first establish semantic equivalence among source and target programs, see Theorem 5.2.6. From this property, we can derive the coherence property (Theorem 5.2.7) almost for free. We believe it is worthwhile to establish a property similar to this theorem for type classes. We could employ a simple denotational semantics for source type class programs similar as Thatte (Reference Thatte1994) or Morris (Reference Morris2014), which would then be related to target programs obtained via the dictionary-passing translation.
Section 2.5 demonstrated that type bounds on generic structs and interfaces have no operational meaning. This situation is similar to contexts of data type definitions in Haskell 2010 (Marlow, Reference Marlow2010). A data type such as:
may require the context Eq a. However, an occurrence of type Set a does not imply that Eq a holds but always requires the constraint to be justified elsewhere. The GHC manual states that “this is widely considered a misfeature” (GHC Team, 2021, Section 6.4.2).
7.3 Logical relations
LRs have a long tradition of proving properties of typed programming languages. Such properties include termination (Tait, Reference Tait1967; Statman, Reference Statman1985), type safety (Skorstengaard, Reference Skorstengaard2019), and program equivalence (Pierce, Reference Pierce2004, Chapters 6, 7). A LR is often defined inductively, indexed by type. If its definition is based on an operational semantics, the LR is called syntactic (Pitts, Reference Pitts1998; Crary & Harper, Reference Crary and Harper2007). With recursive types, a step-index (Appel & McAllester, Reference Appel and McAllester2001; Ahmed, Reference Ahmed2006) provides a decreasing measure to keep the definition well founded. See Mitchell (Reference Mitchell1996, Chapter 8) and Skorstengaard (Reference Skorstengaard2019) for introductions to the topic.
LRs are often used to relate two terms of the same language. For our translation, the two terms are from different languages, related at a type from the source language. Benton & Hur (Reference Benton and Hur2009) prove correctness of compiler transformations. They use a step-indexed LR to relate a denotational semantics of the
![]() $\lambda$
-calculus with recursion to configurations of a SECD machine. Hur & Dreyer (Reference Hur and Dreyer2011) build on this idea to show equivalence between an expressive source language (polymorphic
$\lambda$
-calculus with recursion to configurations of a SECD machine. Hur & Dreyer (Reference Hur and Dreyer2011) build on this idea to show equivalence between an expressive source language (polymorphic
![]() $\lambda$
-calculus with references, existentials, and recursive types) and assembly language. Their biorthogonal, step-indexed Kripke LR does not directly relate the two languages but relies on abstract language specifications.
$\lambda$
-calculus with references, existentials, and recursive types) and assembly language. Their biorthogonal, step-indexed Kripke LR does not directly relate the two languages but relies on abstract language specifications.
Our setting is different in that we consider a source language with support for overloading. Besides structured data and functions, we need to cover recursive interface values. This leads to some challenges to get the step index right (Sulzmann & Wehr, Reference Sulzmann and Wehr2022).
Simulation or bisimulation (see e.g., Sumii & Pierce Reference Sumii and Pierce2007) is another common technique for showing program equivalences. In our setting, using this technique amounts to proving that reduction and translation commutes: if source term e reduces to e’ and translates to target term E, then e’ translates to E’ such that E reduces to E” (potentially in several steps) with
![]() $E' = E''$
. One challenge is that the two target terms E’ and E” are not necessarily syntactically equal but only semantically. In our setting, this might be the case if E’ and E” contain coercions for structural subtyping. Even if such coercions behave the same, their syntax might be different. With LR, we abstract away certain details of single-step reductions, as we only compare values, not intermediate results. A downside of the LR is that getting the step index right is sometimes not trivial.
$E' = E''$
. One challenge is that the two target terms E’ and E” are not necessarily syntactically equal but only semantically. In our setting, this might be the case if E’ and E” contain coercions for structural subtyping. Even if such coercions behave the same, their syntax might be different. With LR, we abstract away certain details of single-step reductions, as we only compare values, not intermediate results. A downside of the LR is that getting the step index right is sometimes not trivial.
Paraskevopoulou & Grover (Reference Paraskevopoulou and Grover2021) combine simulation and an untyped, step-indexed LR (Acar et al., Reference Acar, Ahmed and Blume2008) to relate the translation of a reduced expression (the E’ from the preceding paragraph) with the reduction result of the translated expression (the E”). They use this technique to prove correctness of CPS transformations using small-step and big-step operational semantics. Resource invariants connect the number of steps a term and its translation might take, allowing them to prove that divergence and asymptotic runtime is preserved by the transformation. Our LR does not support resource invariants but includes a case for divergence directly.
7.4 Prior work
Our own work published at APLAS (Sulzmann & Wehr, Reference Sulzmann and Wehr2021) and MPC (Sulzmann & Wehr, Reference Sulzmann and Wehr2022) laid the foundations for the dictionary-passing translation and its correctness proof of the present article. For the APLAS paper, we defined a dictionary-passing translation for FG (Griesemer et al., Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020), the nongeneric variant of FGG. That translation is similar in spirit to the translation presented here; it supports type assertions but not generics. The APLAS paper includes a proof for the semantic equivalence between the source FG program and its translation. The result is, however, somewhat limited as semantic equivalence only holds for terminating programs whose translation is also known to terminate.
In the MPC paper, we addressed the aforementioned limitation by extending the proof of semantic equivalence to all possible outcomes of an FG program: termination, panic (failure of a dynamic type assertion), and divergence. The proof uses a LR similar to the one used here, but without support for generics. We have already shown more differences in Section 5.3.
7.5 Summary of translations
The diagram in Figure 20 summarizes the existing translations by Griesemer et al. (OOPSLA 2020), by Ellis et al. (OOPSLA 2022), from our MPC 2022 paper (Sulzmann & Wehr, 2022), and from the article at hand. The three resulting TL programs
![]() $P_{\textrm{TL}}$
,
$P_{\textrm{TL}}$
,
![]() $P_{\textrm{TL}}'$
, and
$P_{\textrm{TL}}'$
, and
![]() $P_{\textrm{TL}}''$
are semantically equivalent because all translations preserve the dynamic semantics. Each translation with
$P_{\textrm{TL}}''$
are semantically equivalent because all translations preserve the dynamic semantics. Each translation with
![]() $P_{\textrm{FGG}}$
^ as its source has different restrictions. OOPSLA 2022 requires the receiver struct of some method declaration to have exactly the same type bounds as the struct declaration itself. OOPSLA 2020 requires
$P_{\textrm{FGG}}$
^ as its source has different restrictions. OOPSLA 2022 requires the receiver struct of some method declaration to have exactly the same type bounds as the struct declaration itself. OOPSLA 2020 requires
![]() $P_{\textrm{FGG}}$
to be monomorphizable, checked by a simple syntactic condition. The translation of this article does not support type assertions.
$P_{\textrm{FGG}}$
to be monomorphizable, checked by a simple syntactic condition. The translation of this article does not support type assertions.

Fig. 20. Summary of translations. Arrows represent translations, and
![]() $P_{\ell}$
is a program in language
$P_{\ell}$
is a program in language
![]() $\ell$
. Program
$\ell$
. Program
![]() $P_{\textrm{FGG}^{\star}}$
is subject to certain restrictions, depending on the translation being performed.
$P_{\textrm{FGG}^{\star}}$
is subject to certain restrictions, depending on the translation being performed.
8 Conclusion and future work
This article defined a type-directed dictionary-passing translation from FGG without type assertions to an extension of the untyped
![]() $\lambda$
-calculus. The translation represents a value at the type of an interface as a combination of a concrete struct value with a dictionary for all methods of the interface. Bounded type parameters become extra function arguments in the target. These extra arguments are coercions from the instantiation of a type variable to its upper bound.
$\lambda$
-calculus. The translation represents a value at the type of an interface as a combination of a concrete struct value with a dictionary for all methods of the interface. Bounded type parameters become extra function arguments in the target. These extra arguments are coercions from the instantiation of a type variable to its upper bound.
Every program in the image of the translation has the same dynamic semantics as its source program. Different translations of the same source program may result in syntactically different but equivalent target programs. The proof of semantic equivalence is based on a syntactic, step-indexed LR. The step index ensures a well-founded definition of the relation in the presence of recursive interface types and recursive methods. We also reported on an implementation of the translation.
In this article, we relied on FGG as defined by Griesemer et al. (Reference Griesemer, Hu, Kokke, Lange, Taylor, Toninho, Wadler and Yoshida2020), without reconsidering design decisions. But our translation raises several questions with respect to the design of generics in FGG and more generally also in Go. For example, the translation clearly shows that type bounds in structs and interfaces have no operational meaning. Should we eliminate these type bounds? Or should we give them a meaning inspired by Haskell’s type class mechanism? Further, a method declaration in full Go must reuse the type bounds of its struct and must be defined in the same package as the struct. Clearly, this limits extensibility and flexibility. Can we provide a more flexible design to solve the expression problem (Wadler, Reference Wadler1998) in Go, without resorting to unsafe type assertions? We would like to use the insights gained through this article to answer these and similar questions in future work.
A somewhat related point is performance. As explained earlier, generics in Go are compiled by monomorphization. This gives the best possible performance because the resulting code is specialized for each type argument. However, not all programs can be monomorphized and the increase in code size is often considered problematic. This raises another interesting question for future work. Could selective monomorphization or specialization offer a viable trade-off between performance, code size, and the ability to compile Go programs which are not monomorphizable?
A statically typed TL typically offers more room for compiler optimization (Harper & Morrisett, Reference Harper and Morrisett1995). Thus, another interesting direction for future work is a translation to a typed backend, for example, System F (Girard, Reference Girard1972; Reynolds, Reference Reynolds1974).
The work presented here does not include type assertions (dynamic type casts), although FGG supports them. We omitted type assertions from our theory for two reasons: firstly, type assertions are largely orthogonal to the dictionary-passing translation, so their inclusion would obscure the working of the translation. Secondly, type assertions would require some extra design choices to consider. In our implementation, we construct the check for a type assertion at the same place as in the source program, relying on dynamic type-tag-passing for gathering all information necessary. But other approaches are possible. For example, one could construct downcast coercions at call sites and pass these coercions around. The second option could make the treatment of type assertions more lightweight but would require significant research in this direction.
Acknowledgments
We would like to thank the anonymous reviewers for their valuable feedback and constructive suggestions, which greatly improved the quality of this paper. We acknowledge support by the Open Access Publication Fund of the Offenburg University of Applied Sciences, Germany.
Conflicts of interest
The authors report no conflict of interest.
Supplementary material
For supplementary material for this article, please visit https://github.com/skogsbaer/fgg-translate and http://doi.org/10.5281/zenodo.8147425.
A Proofs
A.1 Deterministic evaluation in
 ${\textrm{FGG}^{-}}$
and TL
${\textrm{FGG}^{-}}$
and TL
Lemma A.1.1 (Deterministic evaluation in ![]() ) If
) If
![]() $e \longrightarrow e'$
and
$e \longrightarrow e'$
and
![]() $e \longrightarrow e''$
then
$e \longrightarrow e''$
then
![]() $e' = e''$
. If
$e' = e''$
. If
![]() $E \longrightarrow E'$
and
$E \longrightarrow E'$
and
![]() $E \longrightarrow E''$
then
$E \longrightarrow E''$
then
![]() $E' = E''$
.
$E' = E''$
.
Proof. We first state and prove three sublemmas:
(a) If
 $e = {\mathcal E}_1[{\mathcal E}_2[e']]$
then there exists
$e = {\mathcal E}_1[{\mathcal E}_2[e']]$
then there exists
 ${\mathcal E}_3$
with
${\mathcal E}_3$
with
 $e = {\mathcal E}_3[e']$
. The proof is by induction on
$e = {\mathcal E}_3[e']$
. The proof is by induction on
 ${\mathcal E}_1$
.
${\mathcal E}_1$
.(b) If
 $e \longrightarrow e'$
then there exists a derivation of
$e \longrightarrow e'$
then there exists a derivation of
 $e \longrightarrow e'$
that ends with at most one consecutive application of rule fg-context. The proof is by induction on the derivation of
$e \longrightarrow e'$
that ends with at most one consecutive application of rule fg-context. The proof is by induction on the derivation of
 $e \longrightarrow e'$
. From the IH, we know that this derivation ends with at most two consecutive applications of rule fg-context. If there are two such consecutive applications, (a) allow us to merge the two evaluation contexts involved so that we need only one consecutive application of fg-context.
$e \longrightarrow e'$
. From the IH, we know that this derivation ends with at most two consecutive applications of rule fg-context. If there are two such consecutive applications, (a) allow us to merge the two evaluation contexts involved so that we need only one consecutive application of fg-context.(c) We call an
 ${\textrm{FGG}^{-}}$
expression directly reducible if it reduces but not by rule fg-context. If
${\textrm{FGG}^{-}}$
expression directly reducible if it reduces but not by rule fg-context. If
 $e_1$
and
$e_1$
and
 $e_2$
are now directly reducible and
$e_2$
are now directly reducible and
 ${\mathcal E}_1[e_1] = {\mathcal E}_2[e_2]$
then
${\mathcal E}_1[e_1] = {\mathcal E}_2[e_2]$
then
 ${\mathcal E}_1 = {\mathcal E}_2$
and
${\mathcal E}_1 = {\mathcal E}_2$
and
 $e_1 = e_2$
. For the proof, we first note that
$e_1 = e_2$
. For the proof, we first note that
 ${\mathcal E}_1 = {{\square}}$
iff
${\mathcal E}_1 = {{\square}}$
iff
 ${\mathcal E}_2 = {{\square}}$
. This holds because directly reducible expressions have no inner redexes. The rest of the proof is then a straightforward induction on
${\mathcal E}_2 = {{\square}}$
. This holds because directly reducible expressions have no inner redexes. The rest of the proof is then a straightforward induction on
 ${\mathcal E}_1$
.
${\mathcal E}_1$
.
Now assume
![]() $e \longrightarrow e'$
and
$e \longrightarrow e'$
and
![]() $e \longrightarrow e''$
. By (b), we may assume that both derivations ends with at most one consecutive application of rule fg-context. It is easy to see (as values do not reduce) that both derivations must end with the same rule. If this rule is fg-field, then
$e \longrightarrow e''$
. By (b), we may assume that both derivations ends with at most one consecutive application of rule fg-context. It is easy to see (as values do not reduce) that both derivations must end with the same rule. If this rule is fg-field, then
![]() $e' = e''$
by restrictions fgg-unique-structs and fgg-distinct-fields. If this rule is fg-call, then
$e' = e''$
by restrictions fgg-unique-structs and fgg-distinct-fields. If this rule is fg-call, then
![]() $e' = e''$
by fgg-unique-method-defs. If the rule is fg-context, we have the following situation with
$e' = e''$
by fgg-unique-method-defs. If the rule is fg-context, we have the following situation with ![]()

As neither
![]() $R_1$
nor
$R_1$
nor
![]() $R_2$
are fg-context, we know that
$R_2$
are fg-context, we know that
![]() $g_1$
and
$g_1$
and
![]() $g_2$
are directly reducible. Thus, with
$g_2$
are directly reducible. Thus, with
![]() ${\mathcal E}_1[g_1] = {\mathcal E}_2[g_2]$
and (c) we get
${\mathcal E}_1[g_1] = {\mathcal E}_2[g_2]$
and (c) we get
![]() ${\mathcal E}_1 = {\mathcal E}_2$
and
${\mathcal E}_1 = {\mathcal E}_2$
and
![]() $g_1 = g_2$
. With
$g_1 = g_2$
. With
![]() $R_1$
and
$R_1$
and
![]() $R_2$
not being fg-context, we have
$R_2$
not being fg-context, we have
![]() $g_1' = g_2'$
, so
$g_1' = g_2'$
, so
![]() $e' = e''$
as required.
$e' = e''$
as required.
Lemma A.1.2 (Deterministic evaluation in TL). If
![]() $E \longrightarrow_{\mu} E'$
and
$E \longrightarrow_{\mu} E'$
and
![]() $E \longrightarrow_{\mu} E''$
then
$E \longrightarrow_{\mu} E''$
then
![]() $E' = E''$
. Further, if
$E' = E''$
. Further, if
![]() $E \longrightarrow E'$
and
$E \longrightarrow E'$
and
![]() $E \longrightarrow E''$
then
$E \longrightarrow E''$
then
![]() $E' = E''$
.
$E' = E''$
.
Proof. We first prove the first implication of the lemma:
There are three sublemmas, analogously to the proof of Lemma A.1.1.
(a) If
 $E = {\mathcal R}_1[{\mathcal R}_2[E']]$
then there exists
$E = {\mathcal R}_1[{\mathcal R}_2[E']]$
then there exists
 ${\mathcal R}_3$
with
${\mathcal R}_3$
with
 $E = {\mathcal R}_3[E']$
.
$E = {\mathcal R}_3[E']$
.(b) If
 $E \longrightarrow_{\mu} E'$
then there exists a derivation of
$E \longrightarrow_{\mu} E'$
then there exists a derivation of
 $E \longrightarrow_{\mu} E'$
that ends with at most one consecutive application of rule tl-context.
$E \longrightarrow_{\mu} E'$
that ends with at most one consecutive application of rule tl-context.(c) We call a TL expression directly reducible if it reduces but not by rule tl-context. If
 $E_1$
and
$E_1$
and
 $E_2$
are now directly reducible and
$E_2$
are now directly reducible and
 ${\mathcal R}_1[E_1] = {\mathcal R}_2[E_2]$
, then
${\mathcal R}_1[E_1] = {\mathcal R}_2[E_2]$
, then
 ${\mathcal R}_1 = {\mathcal R}_2$
and
${\mathcal R}_1 = {\mathcal R}_2$
and
 $E_1 = E_2$
.
$E_1 = E_2$
.
The proofs of these lemmas are similar to the proofs of the sublemmas in Lemma A.1.1. Then (A1) follows with reasoning similar to the proof of Lemma A.1.1. If the derivations of
![]() $E \longrightarrow_{\mu} E'$
and
$E \longrightarrow_{\mu} E'$
and
![]() $E \longrightarrow_{\mu} E''$
both end with rule tl-case, then our assumption that the constructors of a case-expression are distinct ensures determinacy.
$E \longrightarrow_{\mu} E''$
both end with rule tl-case, then our assumption that the constructors of a case-expression are distinct ensures determinacy.
The second claim of the lemma (
![]() $E \longrightarrow E'$
and
$E \longrightarrow E'$
and
![]() $E \longrightarrow E''$
imply
$E \longrightarrow E''$
imply
![]() $E' = E''$
) then follows directly from (A1). Our assumption that the variables of a top-level let-binding are distinct ensures that the substitution
$E' = E''$
) then follows directly from (A1). Our assumption that the variables of a top-level let-binding are distinct ensures that the substitution
![]() $\mu$
built from the top-level let-bindings is well defined.
$\mu$
built from the top-level let-bindings is well defined.
![]() $\blacksquare$
$\blacksquare$
A.2 Preservation of static semantics
Proof of Lemma 5.1.1. We prove (a) and (b) by case distinctions on the last rule of the given derivations; (c) and (d) follow by induction on the derivations, using (a) and (b). Claim (e) then follows by examining the typing rules, using (c) and (d).
![]() $\blacksquare$
$\blacksquare$
A.3 Preservation of dynamic semantics
Convention A.3.1. We omit
![]() $\mu$
from reductions in the TL, writing
$\mu$
from reductions in the TL, writing
![]() $E \longrightarrow E'$
instead of
$E \longrightarrow E'$
instead of
![]() $E \longrightarrow_{\mu} E'$
.
$E \longrightarrow_{\mu} E'$
.
Definition A.3.2. We make use of some extra meta-variables and notations.
•
 ${\Phi}, {\Psi}$
denote formal type parameters
${\Phi}, {\Psi}$
denote formal type parameters
 $\overline{\alpha\,\tau_I}$
.
$\overline{\alpha\,\tau_I}$
.•
 $\hat{{\Phi}}$
denotes the type variables of
$\hat{{\Phi}}$
denotes the type variables of
 ${\Phi}$
; that is, if
${\Phi}$
; that is, if
 ${\Phi} = \overline{\alpha\,\tau_I}$
then
${\Phi} = \overline{\alpha\,\tau_I}$
then
 $\hat{{\Phi}} = \overline{\alpha}$
.
$\hat{{\Phi}} = \overline{\alpha}$
.•
 ${\phi}, {\psi}$
denote actual type arguments
${\phi}, {\psi}$
denote actual type arguments
 $\overline{\tau}$
.
$\overline{\tau}$
.•
 $M ::= [{\Phi}](\overline{x \ \tau}) \ \tau$
denotes the type part of a method signature R.
$M ::= [{\Phi}](\overline{x \ \tau}) \ \tau$
denotes the type part of a method signature R.• L denotes a type literal
 or
or  .
.•
 create a type substitution
create a type substitution
 $\eta$
form type parameters
$\eta$
form type parameters
 ${\Phi}$
and arguments
${\Phi}$
and arguments
 ${\phi}$
. It is defined like this:
${\phi}$
. It is defined like this:
 ${\overline{\alpha\, \tau}^{n}}\mapsto{\overline{\sigma}^{n}}{\langle\overline{\alpha_i \mapsto \sigma_i}^{n}\rangle}$
${\overline{\alpha\, \tau}^{n}}\mapsto{\overline{\sigma}^{n}}{\langle\overline{\alpha_i \mapsto \sigma_i}^{n}\rangle}$
A.3.1 The logical relation
Lemma A.3.3 (Monotonicity for expressions). Assume
![]() $k' \leq k$
. If
$k' \leq k$
. If
![]() $ e \approx E \in [\![\tau]\!]_{k}$
then
$ e \approx E \in [\![\tau]\!]_{k}$
then
![]() $ e \approx E \in [\![\tau]\!]_{k'}$
. If
$ e \approx E \in [\![\tau]\!]_{k'}$
. If
![]() $v \equiv V \in [\![\tau]\!]_{k}$
then
$v \equiv V \in [\![\tau]\!]_{k}$
then
![]() $v \equiv V \in [\![\tau]\!]_{k'}$
.
$v \equiv V \in [\![\tau]\!]_{k'}$
.
Proof. We proceed by induction on (k, s) where s is the combined size of v, V.
Case distinction on the last rule used in the two derivations
• Case rule equiv-exp We label the two implications in the premise of the rule as (a) and (b).
(a) Assume
 $k'' < k'$
and
$k'' < k'$
and
 $e \longrightarrow^{k''} u$
for some value u. From
$e \longrightarrow^{k''} u$
for some value u. From
 $ e \approx E \in [\![\tau]\!]_{k}$
(A2)If
$ e \approx E \in [\![\tau]\!]_{k}$
(A2)If
 $k = k'$
then
$k = k'$
then
 $u \equiv U \in [\![\tau]\!]_{k'-k''}$
. Otherwise,
$u \equiv U \in [\![\tau]\!]_{k'-k''}$
. Otherwise,
 $k' - k'' < k - k''$
, so the IH (induction hypothesis) applied to (A2) also yields
$k' - k'' < k - k''$
, so the IH (induction hypothesis) applied to (A2) also yields
 $u \equiv U \in [\![\tau]\!]_{k'-k''}$
. This proves implication (a).
$u \equiv U \in [\![\tau]\!]_{k'-k''}$
. This proves implication (a).(b) Assume
 $k'' < k'$
and
$k'' < k'$
and
 $e \longrightarrow^{k''} e'$
and
$e \longrightarrow^{k''} e'$
and
 $\textsf{diverge}{e'}$
. Then we get with
$\textsf{diverge}{e'}$
. Then we get with
 $ e \approx E \in [\![\tau]\!]_{k}$
and
$ e \approx E \in [\![\tau]\!]_{k}$
and
 $k' \leq k$
that
$k' \leq k$
that
 $\textsf{diverge}{E}$
.
$\textsf{diverge}{E}$
.
• Case rule equiv-struct Follows from IH.
• Case rule equiv-iface Obvious.
 $\blacksquare$
$\blacksquare$
End case distinction.
Lemma A.3.4 (Monotonicity for method dictionaries). If
![]() $ \langle x, \tau_S, R, e\rangle \approx V \in [\![ R']\!]_{k}$
and
$ \langle x, \tau_S, R, e\rangle \approx V \in [\![ R']\!]_{k}$
and
![]() $k' \leq k$
then
$k' \leq k$
then
![]() $ \langle x, \tau_S, R, e\rangle \approx V \in [\![ R']\!]_{k'}$
.
$ \langle x, \tau_S, R, e\rangle \approx V \in [\![ R']\!]_{k'}$
.
Proof. Obvious.
![]() $\blacksquare$
$\blacksquare$
Lemma A.3.5 (Monotonicity for type parameters). vIf
![]() $ {\phi} \approx V \in [\![{\Phi}]\!]_{k}$
and
$ {\phi} \approx V \in [\![{\Phi}]\!]_{k}$
and
![]() $k' \leq k$
then
$k' \leq k$
then
![]() $ {\phi} \approx V \in [\![{\Phi}]\!]_{k'}$
.
$ {\phi} \approx V \in [\![{\Phi}]\!]_{k'}$
.
Proof. Obvious.
![]() $\blacksquare$
$\blacksquare$
Lemma A.3.6 (Monotonicity for method declarations). Assume declaration ![]() and
and
![]() $k' \leq k$
. If
$k' \leq k$
. If
![]() $D \approx_{k} X$
then
$D \approx_{k} X$
then
![]() $D \approx_{k'} X$
.
$D \approx_{k'} X$
.
Proof. Obvious.
![]() $\blacksquare$
$\blacksquare$
Lemma A.3.7 (Monotonicity for programs). If
![]() $\overline{D} \approx_{k} \mu$
and
$\overline{D} \approx_{k} \mu$
and
![]() $k' \leq k$
then
$k' \leq k$
then
![]() $\overline{D} \approx_{k'} \mu$
.
$\overline{D} \approx_{k'} \mu$
.
Proof. Follows from Lemma A.3.6.
![]() $\blacksquare$
$\blacksquare$
A.3.2 Equivalence between source and translation
Proof of Lemma 5.2.2. Straightforward.
Proof of Lemma 5.2.3. We label the two implications in the premise of rule equiv-exp with (a) and (b).
(a) Assume
 $k' < k+1$
and
$k' < k+1$
and
 $e_2 \longrightarrow^{k'} v$
. Then by Lemma A.1.1
$e_2 \longrightarrow^{k'} v$
. Then by Lemma A.1.1
 $e_2 \longrightarrow e \longrightarrow^{k'-1} v$
. Noting that
$e_2 \longrightarrow e \longrightarrow^{k'-1} v$
. Noting that
 $k' -1 < k$
we get with the assumption
$k' -1 < k$
we get with the assumption
 $ e \approx E \in [\![\tau]\!]_{k}$
But this is exactly what is needed to prove implication (a) for
$ e \approx E \in [\![\tau]\!]_{k}$
But this is exactly what is needed to prove implication (a) for
 $ e_2 \approx E \in [\![\tau]\!]_{k+1}$
.
$ e_2 \approx E \in [\![\tau]\!]_{k+1}$
.(b) Assume
 $k' < k+1$
and
$k' < k+1$
and
 $e_2 \longrightarrow^{k'} e'$
and
$e_2 \longrightarrow^{k'} e'$
and
 $\textsf{diverge}{e'}$
. Then by Lemma A.1.1
$\textsf{diverge}{e'}$
. Then by Lemma A.1.1
 $e_2 \longrightarrow e \longrightarrow^{k'-1} e'$
. Noting that
$e_2 \longrightarrow e \longrightarrow^{k'-1} e'$
. Noting that
 $k' -1 < k$
we get with the assumption
$k' -1 < k$
we get with the assumption
 $ e \approx E \in [\![\tau]\!]_{k}$
that
$ e \approx E \in [\![\tau]\!]_{k}$
that
 $\textsf{diverge}{E}$
. This proves implication (b).
$\textsf{diverge}{E}$
. This proves implication (b).
 $\blacksquare$
$\blacksquare$
Lemma A.3.8 (Expression equivalence implies value equivalence). If
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $ v \approx V \in [\![\tau]\!]_{k}$
then
$ v \approx V \in [\![\tau]\!]_{k}$
then
![]() $v \equiv V \in [\![\tau]\!]_{k}$
.
$v \equiv V \in [\![\tau]\!]_{k}$
.
Proof. From the first implication of rule equiv-exp, we get for
![]() $k' = 0 < k$
and with
$k' = 0 < k$
and with
![]() $v \longrightarrow^{0} v$
that
$v \longrightarrow^{0} v$
that
![]() $\exists V' . V \longrightarrow^* V' \wedge v \equiv V' \in [\![\tau]\!]_{k}$
. But V is already a value, so
$\exists V' . V \longrightarrow^* V' \wedge v \equiv V' \in [\![\tau]\!]_{k}$
. But V is already a value, so
![]() $V' = V$
.
$V' = V$
.
![]() $\blacksquare$
$\blacksquare$
Lemma A.3.9 (Value equivalence implies expression equivalence). If
![]() $v \equiv V \in [\![\tau]\!]_{k}$
then
$v \equiv V \in [\![\tau]\!]_{k}$
then
![]() $ v \approx V \in [\![\tau]\!]_{k}$
for any k.
$ v \approx V \in [\![\tau]\!]_{k}$
for any k.
Proof. We have
![]() $v \longrightarrow^{0} v$
, so we get the first implication of rule equiv-exp by setting
$v \longrightarrow^{0} v$
, so we get the first implication of rule equiv-exp by setting
![]() $E = V$
and by assumption
$E = V$
and by assumption
![]() $v \equiv V \in [\![\tau]\!]_{k}$
. The second implication holds vacuously because values do not diverge.
$v \equiv V \in [\![\tau]\!]_{k}$
. The second implication holds vacuously because values do not diverge.
![]() $\blacksquare$
$\blacksquare$
Lemma A.3.10. Assume ![]() . Then the following holds:
. Then the following holds:

Proof. Let
![]() $M = [{\Phi}'](\overline[n]{x_i\ \tau_i})\,\tau$
and assume for any
$M = [{\Phi}'](\overline[n]{x_i\ \tau_i})\,\tau$
and assume for any
![]() $k', {\phi}, W$
$k', {\phi}, W$
Obviously
To show that
holds, we assume the left-hand side of the implication in the premise of rule equiv-method-dict-entry for some
![]() $k'', {\phi}', W', u, U, \overline[n]{v}, \overline[n]{V}$
:
$k'', {\phi}', W', u, U, \overline[n]{v}, \overline[n]{V}$
:
We then need to prove (A11) to show the overall goal:
Let
![]() ${\Phi} = \overline[p]{\alpha\,\sigma}$
,
${\Phi} = \overline[p]{\alpha\,\sigma}$
,
![]() ${\Phi}' = \overline[q]{\beta\,\sigma'}$
,
${\Phi}' = \overline[q]{\beta\,\sigma'}$
,
![]() ${\phi} = \overline[p]{\sigma''}$
,
${\phi} = \overline[p]{\sigma''}$
,
![]() ${\phi}' = \overline[q]{\sigma'''}$
. Then by (A5) and (A7)
${\phi}' = \overline[q]{\sigma'''}$
. Then by (A5) and (A7)
Define

Then
The
![]() $\overline[q]{\beta}$
are sufficiently fresh, so
$\overline[q]{\beta}$
are sufficiently fresh, so
![]() $\textsf{ftv}(\overline[p]{\sigma''}) \cap \overline[q]{\beta} = \emptyset$
. Hence by (A13), (A14), (A15)
$\textsf{ftv}(\overline[p]{\sigma''}) \cap \overline[q]{\beta} = \emptyset$
. Hence by (A13), (A14), (A15)
We have from (A4) and (A8)
We now prove
by verifying the implication in the premise of rule equiv-bounded-typarams. We consider two cases for every
![]() $\ell \leq k''$
.
$\ell \leq k''$
.
Case distinction whether i in [p] or in [q].
• Case
 $i \in [p]$
We need to prove
$i \in [p]$
We need to prove
 $\forall u, U . u \approx U \in [\![\sigma''_i]\!]_{\ell} \implies u \approx W_i\,U \in [\![\eta'' \sigma_i]\!]_{\ell}$
. From (A4) we get with
$\forall u, U . u \approx U \in [\![\sigma''_i]\!]_{\ell} \implies u \approx W_i\,U \in [\![\eta'' \sigma_i]\!]_{\ell}$
. From (A4) we get with
 $ u \approx U \in [\![\sigma''_i]\!]_{\ell}$
and
$ u \approx U \in [\![\sigma''_i]\!]_{\ell}$
and
 $\ell \leq k'' \overset{(A6)}{\leq} k'$
that
$\ell \leq k'' \overset{(A6)}{\leq} k'$
that
 $ u \approx W_i\,U \in [\![\eta \sigma_i]\!]_{\ell}$
. By assumption 5.2.1
$ u \approx W_i\,U \in [\![\eta \sigma_i]\!]_{\ell}$
. By assumption 5.2.1
 $\textsf{ftv}(\sigma_i) \subseteq \overline[p]{\alpha}$
, so
$\textsf{ftv}(\sigma_i) \subseteq \overline[p]{\alpha}$
, so
 $\eta'' \sigma_i = \eta \sigma_i$
by (A13) and (A15).
$\eta'' \sigma_i = \eta \sigma_i$
by (A13) and (A15).• Case
 $i \in [q]$
We need to prove
$i \in [q]$
We need to prove
 $\forall u, U . u \approx U \in [\![\sigma'''_i]\!]_{\ell} \implies u \approx W'_i\,U \in [\![\eta'' \sigma'_i]\!]_{\ell}$
. From (A8) we get with
$\forall u, U . u \approx U \in [\![\sigma'''_i]\!]_{\ell} \implies u \approx W'_i\,U \in [\![\eta'' \sigma'_i]\!]_{\ell}$
. From (A8) we get with
 $ u \approx U \in [\![\sigma'''_i]\!]_{\ell}$
that
$ u \approx U \in [\![\sigma'''_i]\!]_{\ell}$
that
 $ u \approx W'_i\,U \in [\![\eta'\eta \sigma'_i]\!]_{\ell}$
. Also,
$ u \approx W'_i\,U \in [\![\eta'\eta \sigma'_i]\!]_{\ell}$
. Also,
 $\eta'\eta \sigma'_i = \eta'' \sigma'_i$
by by (A17).
$\eta'\eta \sigma'_i = \eta'' \sigma'_i$
by by (A17).
End case distinction. This finishes the proof of (A20).
From (A9) and (A15), we have
From From (A10) and (A17),
From the assumption
![]() $\textbf{fun} \,\,({x}\,\,t_{S}[\Phi ]) mM\,\, \{\textbf{return}\,\,e\}\approx_{k} X$
, we can invert rule equiv-method-decl. Noting that
$\textbf{fun} \,\,({x}\,\,t_{S}[\Phi ]) mM\,\, \{\textbf{return}\,\,e\}\approx_{k} X$
, we can invert rule equiv-method-decl. Noting that
![]() $k'' \overset{(A6)}{\leq k' \overset{(A3)}{<} k}$
and that (A16), (A20), (A21), and (A22) give us the left-hand side of the implication in the premise of the rule, we get by the right-hand side of the implication:
$k'' \overset{(A6)}{\leq k' \overset{(A3)}{<} k}$
and that (A16), (A20), (A21), and (A22) give us the left-hand side of the implication in the premise of the rule, we get by the right-hand side of the implication:
With (A17), (A18), and (A19)
We have by (A12)
so
Thus, with (A23) and Lemma 5.2.2
as required to prove (A11).
![]() $\blacksquare$
$\blacksquare$
Definition A.3.11 (Domain). We write
![]() $\textsf{dom}(\cdot)$
for the domain of a substitution
$\textsf{dom}(\cdot)$
for the domain of a substitution
![]() $\eta$
,
$\eta$
,
![]() $\theta$
,
$\theta$
,
![]() $\rho$
or
$\rho$
or
![]() $\mu$
, of a type environment
$\mu$
, of a type environment
![]() $\Delta$
, of a value environment
$\Delta$
, of a value environment
![]() $\Gamma$
, or some type parameters
$\Gamma$
, or some type parameters
![]() ${\Phi}$
.
${\Phi}$
.
Definition A.3.12 (Free variables). We write
![]() $\textsf{fv}(\cdot)$
for the set of free term variables, and
$\textsf{fv}(\cdot)$
for the set of free term variables, and
![]() $\textsf{ftv}(\cdot)$
for the set of free type variables.
$\textsf{ftv}(\cdot)$
for the set of free type variables.
Lemma A.3.13 (Subtyping preserves equivalence). Let
![]() $\overline{D} \approx_{k} \mu$
. Assume
$\overline{D} \approx_{k} \mu$
. Assume
![]() $\Delta \mathrel{\vdash_{{{{\textsf{{coerce}}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
and
$\Delta \mathrel{\vdash_{{{{\textsf{{coerce}}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
and
![]() $ \eta \approx \rho \in [\![\Delta]\!]_{k}$
and
$ \eta \approx \rho \in [\![\Delta]\!]_{k}$
and
![]() $ e \approx E \in [\![\eta\tau]\!]_{k}$
. Then
$ e \approx E \in [\![\eta\tau]\!]_{k}$
. Then
![]() $ e \approx (\rho V)\,E \in [\![\eta \sigma]\!]_{k}$
.
$ e \approx (\rho V)\,E \in [\![\eta \sigma]\!]_{k}$
.
We prove Lemma A.3.13 with the following two lemmas.
Lemma A.3.14. Assume
![]() $\overline{D} \approx_{k} \mu$
and
$\overline{D} \approx_{k} \mu$
and
![]() $ \eta \approx \rho \in [\![\Delta]\!]_{k}$
. Let
$ \eta \approx \rho \in [\![\Delta]\!]_{k}$
. Let
![]() $ \langle R,V\rangle \in {\textsf{{methods}}}(\Delta, t_S[{\phi}])$
and define
$ \langle R,V\rangle \in {\textsf{{methods}}}(\Delta, t_S[{\phi}])$
and define
![]() $U = \lambda \text{ (} {Y} \text{ )} \texttt{.}{X_{{m},{t_S}}}\,\text{ (} \rho V\text{ ,} Y_1\text{ ,} Y_2\text{ ,} Y_3 \text{ )}$
. Then we have for all
$U = \lambda \text{ (} {Y} \text{ )} \texttt{.}{X_{{m},{t_S}}}\,\text{ (} \rho V\text{ ,} Y_1\text{ ,} Y_2\text{ ,} Y_3 \text{ )}$
. Then we have for all
![]() $k' < k$
that
$k' < k$
that
![]() $ \textsf{{methodLookup}}(m, \eta t_S[{\phi}]) \approx U \in [\![\eta R]\!]_{k'}$
.
$ \textsf{{methodLookup}}(m, \eta t_S[{\phi}]) \approx U \in [\![\eta R]\!]_{k'}$
.
Lemma A.3.15 (Substitution preserves equivalence). Assume
![]() $\overline{D} \approx_{k} \mu$
and
$\overline{D} \approx_{k} \mu$
and
![]() $ \eta \approx \rho \in [\![\Delta]\!]_{k}$
. If
$ \eta \approx \rho \in [\![\Delta]\!]_{k}$
. If
![]() $\Delta \mathrel{\vdash_{{{{\textsf{{subst}}}}}}} {\Phi} \mapsto {\phi} : \eta' \leadsto V$
then
$\Delta \mathrel{\vdash_{{{{\textsf{{subst}}}}}}} {\Phi} \mapsto {\phi} : \eta' \leadsto V$
then
![]() $ \eta {\phi} \approx \rho V \in [\![\eta {\Phi}]\!]_{k}$
.
$ \eta {\phi} \approx \rho V \in [\![\eta {\Phi}]\!]_{k}$
.
Proof of Lemmas A.3.13, A.3.14, and A.3.15. We show the three lemmas by induction on the combined height of the derivations for
![]() $\Delta \mathrel{\vdash_{{{{\textsf{coerce}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
and
$\Delta \mathrel{\vdash_{{{{\textsf{coerce}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
and
![]() $\langle R,V\rangle \in {\textsf{methods}}(\Delta, t_S[{\phi}])$
and
$\langle R,V\rangle \in {\textsf{methods}}(\Delta, t_S[{\phi}])$
and
![]() $\Delta \mathrel{\vdash_{{{{\textsf{subst}}}}}} {\Phi} \mapsto {\phi} : \eta' \leadsto V$
.
$\Delta \mathrel{\vdash_{{{{\textsf{subst}}}}}} {\Phi} \mapsto {\phi} : \eta' \leadsto V$
.
We start with the proof for Lemma A.3.13. We have from the assumptions:
Assume
![]() $k' < k$
and
$k' < k$
and
![]() $e \longrightarrow^{k'} e'$
. The second implication in the premise of rule equiv-exp holds obviously, because with
$e \longrightarrow^{k'} e'$
. The second implication in the premise of rule equiv-exp holds obviously, because with
![]() $\textsf{diverge}{e'}$
we get from (A24)
$\textsf{diverge}{e'}$
we get from (A24)
![]() $\textsf{diverge}{E}$
, so also
$\textsf{diverge}{E}$
, so also
![]() $\textsf{diverge}{(\rho V)\ E}$
.
$\textsf{diverge}{(\rho V)\ E}$
.
Thus, we only need to prove the first implication. Assume that
![]() $e' = v$
for some value v. Then via (A24) for some U
$e' = v$
for some value v. Then via (A24) for some U
We then need to verify that
![]() $(\rho V)\ U \longrightarrow^* U'$
for some U’ with
$(\rho V)\ U \longrightarrow^* U'$
for some U’ with
![]() $v \equiv U' \in [\![\eta \sigma]\!]_{k - k'}$
. In fact,
$v \equiv U' \in [\![\eta \sigma]\!]_{k - k'}$
. In fact,
![]() $k' < k$
, so with Lemma A.3.8 it suffices to show that
$k' < k$
, so with Lemma A.3.8 it suffices to show that
![]() $ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
.
$ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
.
Case distinction the last rule in the derivation of
![]() $\Delta \mathrel{\vdash_{{{{\textsf{coerce}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
coerce-tyvar
$\Delta \mathrel{\vdash_{{{{\textsf{coerce}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
coerce-tyvar
• Case COERCE-TYVAR:

Our goal to show is
With (A27) and the IH for Lemma A.3.13, we then get
Then, with
![]() $e \longrightarrow^{k'} v$
, we get
$e \longrightarrow^{k'} v$
, we get
![]() $(\rho V)\ U \longrightarrow (\rho W)\ ((\rho X_{\alpha})\ U) \longrightarrow^* U'$
for some U’ with
$(\rho V)\ U \longrightarrow (\rho W)\ ((\rho X_{\alpha})\ U) \longrightarrow^* U'$
for some U’ with
![]() $v \equiv U' \in [\![\eta \sigma]\!]_{k - k'}$
.
$v \equiv U' \in [\![\eta \sigma]\!]_{k - k'}$
.
We now prove (A27). From the assumption
![]() $ \eta \approx \rho \in [\![\Delta]\!]_{k}$
, we have
$ \eta \approx \rho \in [\![\Delta]\!]_{k}$
, we have

such that
![]() $\alpha = \alpha_j$
and
$\alpha = \alpha_j$
and
![]() $\tau_I = \tau_j$
for some
$\tau_I = \tau_j$
for some
![]() $j \in [n]$
. Inverting rule equiv-bounded-typarams on (A28) yields
$j \in [n]$
. Inverting rule equiv-bounded-typarams on (A28) yields
From (A26) by
![]() $\eta \tau = \sigma_j$
, then
$\eta \tau = \sigma_j$
, then
![]() $v \equiv U \in [\![\sigma_j]\!]_{k - k'}$
. Thus, with (A29) and Lemma A.3.9
$v \equiv U \in [\![\sigma_j]\!]_{k - k'}$
. Thus, with (A29) and Lemma A.3.9
With Lemma 5.2.3 and
![]() $e \longrightarrow^{k'} v$
then
$e \longrightarrow^{k'} v$
then
But
![]() $\tau_j = \tau_I$
and
$\tau_j = \tau_I$
and
![]() $V_j = \rho X_{\alpha}$
, so this proves (A27).
$V_j = \rho X_{\alpha}$
, so this proves (A27).
• Case coerce-struct-iface
Hence,
![]() $(\rho V)\ U \longrightarrow \text{ (} U\text{ ,} \rho\text{ (} \overline[n]{V'} \text{ )} \text{ )}$
and
$(\rho V)\ U \longrightarrow \text{ (} U\text{ ,} \rho\text{ (} \overline[n]{V'} \text{ )} \text{ )}$
and
![]() $U' := \text{ (} U\text{ ,} \rho\text{ (} \overline[n]{V'} \text{ )} \text{ )}$
is a value. We now want to show
$U' := \text{ (} U\text{ ,} \rho\text{ (} \overline[n]{V'} \text{ )} \text{ )}$
is a value. We now want to show
![]() $ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
via rule equiv-iface. Define the
$ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
via rule equiv-iface. Define the
![]() $\sigma_S$
in the premise of equiv-iface as
$\sigma_S$
in the premise of equiv-iface as
![]() $\eta \tau = t_S[\eta {\psi}]$
.
$\eta \tau = t_S[\eta {\psi}]$
.
The first premise of equiv-iface:
follows from (A26) and Lemma A.3.3. From (A30) and (A31), we get with
![]() $\sigma = t_I[{\phi}]$
the second premise as:
$\sigma = t_I[{\phi}]$
the second premise as:
We next prove the third premise of equiv-iface. Pick some
![]() $j \in [n]$
and
$j \in [n]$
and
![]() $k_2 < k -k'$
. With the assumptions
$k_2 < k -k'$
. With the assumptions
![]() $\overline{D} \approx_{k} \mu$
and
$\overline{D} \approx_{k} \mu$
and
![]() $ \eta \approx \rho \in [\![\Delta]\!]_{k}$
and with (A32), (A33), and the IH for Lemma A.3.14 we get
$ \eta \approx \rho \in [\![\Delta]\!]_{k}$
and with (A32), (A33), and the IH for Lemma A.3.14 we get
(A34), (A35), (A36), and the definition of U’ are the pieces required to derive
![]() $ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
via rule equiv-iface.
$ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
via rule equiv-iface.
• Case coerce-iface-iface
As
![]() $\eta \tau = \eta t_I[{\phi}_1]$
is an interface type, we get from (A26) by inverting rule equiv-iface for some
$\eta \tau = \eta t_I[{\phi}_1]$
is an interface type, we get from (A26) by inverting rule equiv-iface for some
![]() $W, \sigma_S, \overline[n]{W}$
that
$W, \sigma_S, \overline[n]{W}$
that
Our goal is to show
![]() $(\rho V)\ U \longrightarrow^* U'$
for some U’ with
$(\rho V)\ U \longrightarrow^* U'$
for some U’ with
![]() $ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
. Via (A40) and (A44)
$ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
. Via (A40) and (A44)
From From (A37), (A38), (A39), and (A42), we have
Pick
![]() $j \in [q]$
. Then via (A46)
$j \in [q]$
. Then via (A46)
Hence, with (A43) and (A46)
With (A41), (A48), (A47) methods-sigma and the definition of U’ in (A45), we then get by applying rule equiv-iface
![]() $ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
and with (A45) also
$ v \approx U' \in [\![\eta \sigma]\!]_{k - k'}$
and with (A45) also
![]() $(\rho V)\ U \longrightarrow^* U'$
.
$(\rho V)\ U \longrightarrow^* U'$
.
End case distinction on the last rule in the derivation of ![]()
This finishes the proof of Lemma A.3.13.
We next prove Lemma A.3.14. By inverting rule methods-struct for the assumption
![]() $\langle R,V\rangle \in {\textsf{methods}}(\Delta, t_S[{\phi}])$
, we get
$\langle R,V\rangle \in {\textsf{methods}}(\Delta, t_S[{\phi}])$
, we get
Inverting (A50) yields

Define ![]() . Then by rule method-lookup and (A49)
. Then by rule method-lookup and (A49)
By Assumption 5.2.1, the
![]() $\overline{\alpha}^n$
can be assumed to be fresh,
$\overline{\alpha}^n$
can be assumed to be fresh,
![]() $\textsf{ftv}({\Phi}) \subseteq \overline{\alpha}^n$
, and
$\textsf{ftv}({\Phi}) \subseteq \overline{\alpha}^n$
, and
![]() $\eta {\Phi} = {\Phi}$
. Applying the IH for Lemma A.3.15 on (A50) yields
$\eta {\Phi} = {\Phi}$
. Applying the IH for Lemma A.3.15 on (A50) yields
![]() $ \eta {\phi} \approx \rho V \in [\![\eta {\Phi}]\!]_{k}$
.
$ \eta {\phi} \approx \rho V \in [\![\eta {\Phi}]\!]_{k}$
.
From the assumption
![]() $\overline{D} \approx_{k} \mu$
, we get with (A49)
$\overline{D} \approx_{k} \mu$
, we get with (A49)
Then for any
![]() $k' < k$
by Lemma A.3.10, where (A53) and Lemma A.3.5 give the left-hand side of the implication:
$k' < k$
by Lemma A.3.10, where (A53) and Lemma A.3.5 give the left-hand side of the implication:

We have
![]() $\eta R \overset{A51}{=} \eta \eta' mM = \eta'' mM$
, where the last equality holds because
$\eta R \overset{A51}{=} \eta \eta' mM = \eta'' mM$
, where the last equality holds because
![]() $\textsf{ftv}(mM) \subseteq \overline{\alpha}^n$
and
$\textsf{ftv}(mM) \subseteq \overline{\alpha}^n$
and
![]() $\overline{\alpha}^n$
fresh by Assumption 5.2.1. Hence, (A52) and (A54) give the desired claim.
$\overline{\alpha}^n$
fresh by Assumption 5.2.1. Hence, (A52) and (A54) give the desired claim.
Finally, we prove Lemma A.3.15. By inverting rule type-inst-checked for the assumption
![]() $\Delta \mathrel{\vdash_{{{{\textsf{subst}}}}}} {\Phi} \mapsto {\phi} : \eta' \leadsto V$
, we get
$\Delta \mathrel{\vdash_{{{{\textsf{subst}}}}}} {\Phi} \mapsto {\phi} : \eta' \leadsto V$
, we get

Define
![]() $\eta'' = \langle\overline[n]{\alpha_i \mapsto \eta \sigma_i}\rangle$
. To prove
$\eta'' = \langle\overline[n]{\alpha_i \mapsto \eta \sigma_i}\rangle$
. To prove
![]() $ \eta {\phi} \approx \rho V \in [\![\eta {\Phi}]\!]_{k}$
, we need to show the implication
$ \eta {\phi} \approx \rho V \in [\![\eta {\Phi}]\!]_{k}$
, we need to show the implication
![]() $\forall j \in [n], k' \leq k . u \approx U \in [\![\eta \sigma_j]\!]_{k'} \implies u \approx (\rho V)\ U \in [\![\eta''\eta\tau_j]\!]_{k'}$
from the premise of rule equiv-bounded-typarams. Assume
$\forall j \in [n], k' \leq k . u \approx U \in [\![\eta \sigma_j]\!]_{k'} \implies u \approx (\rho V)\ U \in [\![\eta''\eta\tau_j]\!]_{k'}$
from the premise of rule equiv-bounded-typarams. Assume
![]() $j \in [n], k' \leq k$
, and
$j \in [n], k' \leq k$
, and
![]() $ u \approx U \in [\![\eta \sigma_j]\!]_{k'}$
. Applying the IH for Lemma A.3.13 on (A55) yields together with Lemmas A.3.5 and A.3.7 that
$ u \approx U \in [\![\eta \sigma_j]\!]_{k'}$
. Applying the IH for Lemma A.3.13 on (A55) yields together with Lemmas A.3.5 and A.3.7 that
As the
![]() $\overline{\alpha}$
are bound in
$\overline{\alpha}$
are bound in
![]() ${\Phi}$
, we may assume that
${\Phi}$
, we may assume that
![]() $\textsf{dom}(\eta) \cap \overline{\alpha} = \emptyset = \textsf{ftv}(\eta) \cap \overline{\alpha}$
. We now argue that
$\textsf{dom}(\eta) \cap \overline{\alpha} = \emptyset = \textsf{ftv}(\eta) \cap \overline{\alpha}$
. We now argue that
by induction on the structure of
![]() $\tau_j$
. The interesting case is were
$\tau_j$
. The interesting case is were
![]() $\tau_j$
is a type variable (otherwise the claim follows by the IH). If
$\tau_j$
is a type variable (otherwise the claim follows by the IH). If
![]() $\tau_j \in \overline{\alpha}$
, then
$\tau_j \in \overline{\alpha}$
, then
If
![]() $\tau_j \in \textsf{dom}(\eta)$
, then
$\tau_j \in \textsf{dom}(\eta)$
, then
If
![]() $\tau_j$
is some other type variable, (A57) holds obviously. With (A56) and (A57) we get
$\tau_j$
is some other type variable, (A57) holds obviously. With (A56) and (A57) we get
![]() $ u \approx (\rho V_j)\ U \in [\![\eta''\eta\tau_j]\!]_{k'}$
as required.
$ u \approx (\rho V_j)\ U \in [\![\eta''\eta\tau_j]\!]_{k'}$
as required.
![]() $\blacksquare$
$\blacksquare$
Lemma A.3.16 (Free variables of coercion values). If
![]() $\Delta \mathrel{\vdash_{{{{\textsf{{coerce}}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
then
$\Delta \mathrel{\vdash_{{{{\textsf{{coerce}}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
then
![]() $\textsf{{fv}}(V) \subseteq \{ X_{\alpha} \mid \alpha \in \textsf{{dom}}(\Delta) \} \cup \mathcal X$
where
$\textsf{{fv}}(V) \subseteq \{ X_{\alpha} \mid \alpha \in \textsf{{dom}}(\Delta) \} \cup \mathcal X$
where
![]() $\mathcal X = \{ X_{{m},{t_S}} \mid m \textrm{~method name}, t_S \textrm{~struct name}\}$
.
$\mathcal X = \{ X_{{m},{t_S}} \mid m \textrm{~method name}, t_S \textrm{~struct name}\}$
.
Proof. By straightforward induction on the derivation of
![]() $\Delta \mathrel{\vdash_{{{{\textsf{coerce}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
.
$\Delta \mathrel{\vdash_{{{{\textsf{coerce}}}}}} \tau \mathrel{<:} \sigma \leadsto V$
.
![]() $\blacksquare$
$\blacksquare$
A.3.2.1 Proof of Lemma 5.2.4. By induction on the derivation of
![]() $\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
. Case distinction on the last rule in the derivation.
$\langle\Delta,\Gamma\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
. Case distinction on the last rule in the derivation.
• Case var

with ![]() and
and ![]() . From the assumption
. From the assumption ![]() we get
we get ![]() as required.
as required.
• Case struct:
Applying the IH to (A60) yields
We now consider the two implications in the premise of rule equiv-exp
(a) Assume
 $k' < k$
and
$k' < k$
and
 $\theta\eta e \longrightarrow^{k'} v$
for some value v. The goal is to show that there exists some value V with
$\theta\eta e \longrightarrow^{k'} v$
for some value v. The goal is to show that there exists some value V with
 $\rho E \longrightarrow^* V$
and
$\rho E \longrightarrow^* V$
and
 $v \equiv V \in [\![\eta\tau]\!]_{k - k'}$
.
$v \equiv V \in [\![\eta\tau]\!]_{k - k'}$
.
With
![]() $\theta\eta e \longrightarrow^{k'} v$
there must exist values
$\theta\eta e \longrightarrow^{k'} v$
there must exist values
![]() $\overline[n]{v}$
such that
$\overline[n]{v}$
such that
Via (A62) and
![]() $k_i \leq k' < k$
then for all
$k_i \leq k' < k$
then for all
![]() $i \in [n]$
$i \in [n]$
We have
![]() $k - k' \leq k - k_i$
for all
$k - k' \leq k - k_i$
for all
![]() $i \in [n]$
by (A63). Thus, with (A66) and Lemma A.3.3
$i \in [n]$
by (A63). Thus, with (A66) and Lemma A.3.3
We also have with (A65) and the definition of E in (A61)
Assume
![]() $\hat{{\Phi}} = \overline[p]{\alpha}$
and
$\hat{{\Phi}} = \overline[p]{\alpha}$
and
![]() ${\phi} = \overline[p]{\sigma}$
. Then by (A59)
${\phi} = \overline[p]{\sigma}$
. Then by (A59)
![]() $\eta' = \langle\overline[p]{\alpha_i \mapsto \sigma_i}\rangle$
and for
$\eta' = \langle\overline[p]{\alpha_i \mapsto \sigma_i}\rangle$
and for
![]() $\eta'' = \langle\overline[p]{\alpha_i \mapsto \eta\sigma_i}\rangle$
, we have
$\eta'' = \langle\overline[p]{\alpha_i \mapsto \eta\sigma_i}\rangle$
, we have
By Assumption 5.2.1, we have
![]() $\textsf{ftv}(\overline[n]{\tau}) \subseteq \{\overline{\alpha}\}$
, so
$\textsf{ftv}(\overline[n]{\tau}) \subseteq \{\overline{\alpha}\}$
, so
With (A58), (A67), (A64), (A69), (A70), and rule equiv-struct, then
Together with (A68), this finishes subcase (a) for
![]() $V = \text{ (} \overline[n]{V} \text{ )}$
.
$V = \text{ (} \overline[n]{V} \text{ )}$
.
(b) Assume
 $k' < k$
and
$k' < k$
and
 $\theta\eta e \longrightarrow^{k'} e'$
and
$\theta\eta e \longrightarrow^{k'} e'$
and
 $\textsf{diverge}{e'}$
. Then
$\textsf{diverge}{e'}$
. Then
 $\textsf{diverge}{e_j}$
for some
$\textsf{diverge}{e_j}$
for some
 $j \in [n]$
, so with (A62) and (A63) also
$j \in [n]$
, so with (A62) and (A63) also
 $\textsf{diverge}{\rho E_j}$
. Thus, by definition of E in (A61),
$\textsf{diverge}{\rho E_j}$
. Thus, by definition of E in (A61),
 $\textsf{diverge}{\rho E}$
as required. access
$\textsf{diverge}{\rho E}$
as required. access
• Case Access:

Applying the IH to (A71) yields
We now consider the two implications in the premise of rule equiv-exp
(a) Assume
 $k' < k$
and
$k' < k$
and
 $\theta\eta e \longrightarrow^{k'} v$
for some value v. The goal is to show that there exists some value V with
$\theta\eta e \longrightarrow^{k'} v$
for some value v. The goal is to show that there exists some value V with
 $\rho E \longrightarrow^* V$
and
$\rho E \longrightarrow^* V$
and
 $v \equiv V \in [\![\eta\tau]\!]_{k - k'}$
.
$v \equiv V \in [\![\eta\tau]\!]_{k - k'}$
.
With
![]() $\theta\eta e \longrightarrow^{k'} v$
then
$\theta\eta e \longrightarrow^{k'} v$
then
![]() $\theta\eta e' \longrightarrow^{k''} v'$
for some v’ and
$\theta\eta e' \longrightarrow^{k''} v'$
for some v’ and
![]() $k'' < k'$
. With (A73) then for some V’
$k'' < k'$
. With (A73) then for some V’
Inverting rule equiv-struct on (A75) yields
where
![]() $\eta'' = \langle\overline[p]{\alpha_i \mapsto \eta\sigma_i}\rangle$
, assuming
$\eta'' = \langle\overline[p]{\alpha_i \mapsto \eta\sigma_i}\rangle$
, assuming
![]() $\hat{{\Phi}} = \overline[p]{\alpha}$
and
$\hat{{\Phi}} = \overline[p]{\alpha}$
and
![]() ${\phi} = \overline[p]{\sigma}$
. By Assumption 5.2.1 we have
${\phi} = \overline[p]{\sigma}$
. By Assumption 5.2.1 we have
![]() $\textsf{ftv}(\tau_j) \subseteq \{\overline{\alpha}\}$
. Thus,
$\textsf{ftv}(\tau_j) \subseteq \{\overline{\alpha}\}$
. Thus,
![]() $\eta''\tau_j = \eta\eta'\tau_j \overset{(A72)}{=} \eta\tau$
. Also,
$\eta''\tau_j = \eta\eta'\tau_j \overset{(A72)}{=} \eta\tau$
. Also,
![]() $k'' \leq k'$
, so
$k'' \leq k'$
, so
![]() $k - k' \leq k - k''$
. Hence, with (A77) and Lemma A.3.3
$k - k' \leq k - k''$
. Hence, with (A77) and Lemma A.3.3
With (A74) and the definition of E in (A72), we get
With
![]() $\theta\eta e \longrightarrow^{k'} v$
and
$\theta\eta e \longrightarrow^{k'} v$
and
![]() $\theta\eta e' \longrightarrow^{k''} v'$
and the form of v’ in (A76), we get
$\theta\eta e' \longrightarrow^{k''} v'$
and the form of v’ in (A76), we get
![]() $\theta\eta e \longrightarrow^{k'} v_j$
and
$\theta\eta e \longrightarrow^{k'} v_j$
and
![]() $v = v_j$
by rule fg-field. Define
$v = v_j$
by rule fg-field. Define
![]() $V = V_j$
and we are done with subcase (a) by (A78) and (A79).
$V = V_j$
and we are done with subcase (a) by (A78) and (A79).
(b) Assume
 $k' < k$
and
$k' < k$
and
 $\theta\eta e \longrightarrow^{k'} e''$
and
$\theta\eta e \longrightarrow^{k'} e''$
and
 $\textsf{diverge}{e''}$
. Then we must have that
$\textsf{diverge}{e''}$
. Then we must have that
 $\theta\eta e' \longrightarrow^{k''} e'''$
for some
$\theta\eta e' \longrightarrow^{k''} e'''$
for some
 $k'' < k'$
and some e”’. Thus,
$k'' < k'$
and some e”’. Thus,
 $\textsf{diverge}{e'''}$
by the definition of e in (A72) and the evaluation rules for FGG. With IH then
$\textsf{diverge}{e'''}$
by the definition of e in (A72) and the evaluation rules for FGG. With IH then
 $\textsf{diverge}{\rho E'}$
. By definition of E in (A72), then
$\textsf{diverge}{\rho E'}$
. By definition of E in (A72), then
 $\textsf{diverge}{\rho E}$
as required.
$\textsf{diverge}{\rho E}$
as required.
• Case CALL-STRUCT:
From the IH applied to (A80) and (A83)
Assume
![]() $\theta \eta e \longrightarrow^{k'} e'$
for some
$\theta \eta e \longrightarrow^{k'} e'$
for some
![]() $k' < k$
. We first consider the following situation for some values
$k' < k$
. We first consider the following situation for some values
![]() $u, \overline[n]{v}$
:
$u, \overline[n]{v}$
:
with
![]() $k'' + {\Sigma}{k_i} \leq k'$
. (A87), (A88), and (A89) are intermediate assumptions, which become true when we later prove the two implications of rule equiv-exp.
$k'' + {\Sigma}{k_i} \leq k'$
. (A87), (A88), and (A89) are intermediate assumptions, which become true when we later prove the two implications of rule equiv-exp.
We have from (A85), (A87), (A86), and (A88)
From (A81), we get by inverting rule methods-struct:
From the assumption
![]() $\overline{D} \approx_{k} \mu$
and (A92),
$\overline{D} \approx_{k} \mu$
and (A92),
Define
We have
![]() $k' - k'' - \Sigma{k_i} < k''' + 1$
by the following reasoning:
$k' - k'' - \Sigma{k_i} < k''' + 1$
by the following reasoning:

With (A95) and
![]() $k''' < k$
, we now want to use the implication from the premise of rule equiv-method-decl. We instantiate the universally quantified variables of the implication as follows:
$k''' < k$
, we now want to use the implication from the premise of rule equiv-method-decl. We instantiate the universally quantified variables of the implication as follows: ![]() . Next, we prove the left-hand side of the implication. But first assume (see (A93), (A82), (A94))
. Next, we prove the left-hand side of the implication. But first assume (see (A93), (A82), (A94))
and define
- We start by showing the first two conjuncts of the implication’s left-hand side:
(A101)
The left part of the conjunction follows from (A100). We then show
 $ \eta({\phi},{\psi}) \approx \rho \text{ (} \overline{W}\text{ ,} \overline{W'} \text{ )} \in [\![ {\Phi},{\Psi}' ]\!]_{ k }$
by proving the two implications required to fulfill the premise of rule equiv-bounded-typarams. The right part of the conjunction in (A101) then follows Lemma A.3.5.
$ \eta({\phi},{\psi}) \approx \rho \text{ (} \overline{W}\text{ ,} \overline{W'} \text{ )} \in [\![ {\Phi},{\Psi}' ]\!]_{ k }$
by proving the two implications required to fulfill the premise of rule equiv-bounded-typarams. The right part of the conjunction in (A101) then follows Lemma A.3.5.* First implication:
 $ u_j \approx U_j \in [\![\eta \tau_j']\!]_{k} \implies u_j \approx (\rho W_j)\,U_j \in [\![\eta_3 \tau_j]\!]_{k}$
for all
$ u_j \approx U_j \in [\![\eta \tau_j']\!]_{k} \implies u_j \approx (\rho W_j)\,U_j \in [\![\eta_3 \tau_j]\!]_{k}$
for all
 $j \in [p]$
and all
$j \in [p]$
and all
 $u_j, U_j$
.
$u_j, U_j$
.
From (A93) and Lemma A.3.15, we have
![]() $ \eta{\phi} \approx \rho W \in [\![\eta{\Phi}]\!]_{k}$
Hence, with
$ \eta{\phi} \approx \rho W \in [\![\eta{\Phi}]\!]_{k}$
Hence, with
![]() $ u_j \approx U_j \in [\![\eta \tau_j']\!]_{k}$
and the implication in the premise of rule equiv-bounded-typarams, we have
$ u_j \approx U_j \in [\![\eta \tau_j']\!]_{k}$
and the implication in the premise of rule equiv-bounded-typarams, we have
![]() $ u_j \approx (\rho W_j)\,U_j \in [\![\langle\overline{\alpha_i \mapsto \eta \tau'_i}\rangle\eta\tau_j]\!]_{k}$
. From Assumption 5.2.1, (A92), and (A98), we know that
$ u_j \approx (\rho W_j)\,U_j \in [\![\langle\overline{\alpha_i \mapsto \eta \tau'_i}\rangle\eta\tau_j]\!]_{k}$
. From Assumption 5.2.1, (A92), and (A98), we know that
![]() $\textsf{ftv}(\tau_j) \subseteq \{\overline{\alpha}\}$
and
$\textsf{ftv}(\tau_j) \subseteq \{\overline{\alpha}\}$
and
![]() $\overline{\alpha}$
fresh, so
$\overline{\alpha}$
fresh, so
![]() $\langle\overline{\alpha_i \mapsto \eta\tau'_i}\rangle\eta\tau_j = \eta_3 \tau_j$
. Thus,
$\langle\overline{\alpha_i \mapsto \eta\tau'_i}\rangle\eta\tau_j = \eta_3 \tau_j$
. Thus,
![]() $ u_j \approx (\rho W_j)\,U_j \in [\![\eta_3 \tau_j]\!]_{k}$
as required.
$ u_j \approx (\rho W_j)\,U_j \in [\![\eta_3 \tau_j]\!]_{k}$
as required.
* Second implication:
 $ u_j \approx U_j \in [\![\eta \tau_j''']\!]_{k} \implies u_j \approx (\rho W'_j)\,U_j \in [\![\eta_3 \tau''_j]\!]_{k}$
for all
$ u_j \approx U_j \in [\![\eta \tau_j''']\!]_{k} \implies u_j \approx (\rho W'_j)\,U_j \in [\![\eta_3 \tau''_j]\!]_{k}$
for all
 $i \in [q]$
and all
$i \in [q]$
and all
 $u_j, U_j$
.
$u_j, U_j$
.
From (A82) and Lemma A.3.15, we have
![]() $ \eta{\psi} \approx \rho W' \in [\![\eta{\Psi}]\!]_{k}$
. Hence, with
$ \eta{\psi} \approx \rho W' \in [\![\eta{\Psi}]\!]_{k}$
. Hence, with
![]() $ u_j \approx U_j \in [\![\eta \tau_j''']\!]_{k}$
, the implication in the premise of rule equiv-bounded-typarams, and (A94) then
$ u_j \approx U_j \in [\![\eta \tau_j''']\!]_{k}$
, the implication in the premise of rule equiv-bounded-typarams, and (A94) then
![]() $ u_j \approx (\rho W_j')\,U_j \in [\![\langle\overline{\beta_i \mapsto \eta\tau_i'''}\rangle\eta\eta_2\tau_j'']\!]_{k}$
. We have with (A93) and (A98) that
$ u_j \approx (\rho W_j')\,U_j \in [\![\langle\overline{\beta_i \mapsto \eta\tau_i'''}\rangle\eta\eta_2\tau_j'']\!]_{k}$
. We have with (A93) and (A98) that
![]() $\eta_2 = \langle\overline{\alpha_i \mapsto \tau_i'}\rangle$
. Because of Assumption 5.2.1, (A92), and (A99), we know that
$\eta_2 = \langle\overline{\alpha_i \mapsto \tau_i'}\rangle$
. Because of Assumption 5.2.1, (A92), and (A99), we know that
![]() $\textsf{ftv}(\tau_j'') \subseteq \{\overline{\alpha}, \overline{\beta}\}$
and
$\textsf{ftv}(\tau_j'') \subseteq \{\overline{\alpha}, \overline{\beta}\}$
and
![]() $\overline{\alpha}, \overline{\beta}$
fresh. Hence,
$\overline{\alpha}, \overline{\beta}$
fresh. Hence,
![]() $\langle\overline{\beta_i \mapsto \eta\tau_i'''}\rangle\eta\eta_2\tau_j'' = \langle\overline{\beta_i \mapsto \eta\tau_i'''}\rangle\langle\overline{\alpha_i \mapsto \eta\tau_i'}\rangle\tau_j'' \overset{A100}{=} \eta_3\tau_j''$
. Thus,
$\langle\overline{\beta_i \mapsto \eta\tau_i'''}\rangle\eta\eta_2\tau_j'' = \langle\overline{\beta_i \mapsto \eta\tau_i'''}\rangle\langle\overline{\alpha_i \mapsto \eta\tau_i'}\rangle\tau_j'' \overset{A100}{=} \eta_3\tau_j''$
. Thus,
![]() $ u_j \approx (\rho W_j')\,U_j \in [\![\eta_3\tau_j'']\!]_{k}$
as required.
$ u_j \approx (\rho W_j')\,U_j \in [\![\eta_3\tau_j'']\!]_{k}$
as required.
This finishes the proof of (A101).
- We next show the third conjunct of the implication’s left-hand side:
(A102)
We have
![]() $t_S[\eta_3 \overline{\alpha}] = t_S[\eta{\phi}]$
by (A100) and (A98). Hence, with (A90), Lemmas A.3.9, and A.3.3, it suffices to show that
$t_S[\eta_3 \overline{\alpha}] = t_S[\eta{\phi}]$
by (A100) and (A98). Hence, with (A90), Lemmas A.3.9, and A.3.3, it suffices to show that
![]() $k''' \leq k - k''$
. But this follows from construction of k”’ in (A96).
$k''' \leq k - k''$
. But this follows from construction of k”’ in (A96).
- Finally, we show the fourth conjunct:
- (A103)

By (A82), (A94), and (A99) we have
 $\eta_1 = \langle\overline[q]{\beta_i \mapsto \tau'''_i}\rangle$
. By (A93) and (A98), we have
$\eta_1 = \langle\overline[q]{\beta_i \mapsto \tau'''_i}\rangle$
. By (A93) and (A98), we have
 $\eta_2 = \langle\overline[p]{\alpha_i \mapsto \tau'_i}\rangle$
. Thus,
$\eta_2 = \langle\overline[p]{\alpha_i \mapsto \tau'_i}\rangle$
. Thus,

For the last equation, note that
 $\textsf{ftv}(\sigma_i') \subseteq \{\overline{\alpha}, \overline{\beta}\}$
by Assumption 5.2.1 and (A92), (A98), (A99). Hence, with (A91), Lemmas A.3.9, and A.3.3, it suffices to show that
$\textsf{ftv}(\sigma_i') \subseteq \{\overline{\alpha}, \overline{\beta}\}$
by Assumption 5.2.1 and (A92), (A98), (A99). Hence, with (A91), Lemmas A.3.9, and A.3.3, it suffices to show that
 $k''' \leq k - k_i$
. But this follows from construction of k”’ in (A96).
$k''' \leq k - k_i$
. But this follows from construction of k”’ in (A96).
Now (A101), (A102), and (A103) are the left-hand side of the implication of rule equiv-method-decl), which we get from (A95). The right-hand side of the implication then yields
From (A90), we have
![]() $u = t_S[\eta{\phi}]$
by inverting rule equiv-struct. Hence by (A92), (A100), and rule fg-call
$u = t_S[\eta{\phi}]$
by inverting rule equiv-struct. Hence by (A92), (A100), and rule fg-call
Also we have
where the last equation follows from (A82), (A94), (A99), (A93), (A98) and
![]() $\textsf{ftv}(\sigma') \subseteq \{\overline{\alpha}, \overline{\beta}\}$
with Assumption 5.2.1. Thus, with (A104), (A105), and Lemma 5.2.3
$\textsf{ftv}(\sigma') \subseteq \{\overline{\alpha}, \overline{\beta}\}$
with Assumption 5.2.1. Thus, with (A104), (A105), and Lemma 5.2.3
By definition of E in (A84) and with (A90) and (A91), we have
Also, we have by rules tl-context and tl-method
So far, we proved everything under the assumptions (A87), (A88), and (A89). We next consider the two implications of rule equiv-exp.
(a) Assume
 $e' = v$
for some value v. Our goal is to prove that there exists some value V such that
$e' = v$
for some value v. Our goal is to prove that there exists some value V such that
 $\rho E \longrightarrow^* V$
and
$\rho E \longrightarrow^* V$
and
 $v \equiv V \in [\![\eta\tau]\!]_{k-k'}$
. Noting that (A87), (A88), and (A89) hold, we have together with (A105):
$v \equiv V \in [\![\eta\tau]\!]_{k-k'}$
. Noting that (A87), (A88), and (A89) hold, we have together with (A105):
with
 $k'' + \Sigma{k_i} < k'$
. We have
$k'' + \Sigma{k_i} < k'$
. We have
 $k' - k'' - \Sigma{k_i} < k''' + 1$
by (A97). Hence with (A106) and (A109), we know that there exists some value V with
$k' - k'' - \Sigma{k_i} < k''' + 1$
by (A97). Hence with (A106) and (A109), we know that there exists some value V with
We have
 $k - k' \leq k''' + 1 - k' + k'' + \Sigma{k_i}$
by the following reasoning:
$k - k' \leq k''' + 1 - k' + k'' + \Sigma{k_i}$
by the following reasoning:

With (A111) and Lemma A.3.3. then
 $v \equiv V \in [\![\eta\tau]\!]_{k - k'}$
. And from (A107), (A108), (A110), and Lemma A.1.2, we have that
$v \equiv V \in [\![\eta\tau]\!]_{k - k'}$
. And from (A107), (A108), (A110), and Lemma A.1.2, we have that
 $\rho E \longrightarrow^* V$
.
$\rho E \longrightarrow^* V$
.(b) Assume
 $\textsf{diverge}{e'}$
. We then have to show
$\textsf{diverge}{e'}$
. We then have to show
 $\textsf{diverge}{\rho E}$
. Case distinction whether receiver, argument, or method call diverges.
$\textsf{diverge}{\rho E}$
. Case distinction whether receiver, argument, or method call diverges.- Case receiver diverges Then
 $\theta\eta g \longrightarrow^{k'} g''$
and
$\theta\eta g \longrightarrow^{k'} g''$
and
 $\textsf{diverge}{g''}$
. With (A85) and
$\textsf{diverge}{g''}$
. With (A85) and
 $k' < k$
then
$k' < k$
then
 $\textsf{diverge}{\rho G}$
, so by the definition of E in (A84) we get
$\textsf{diverge}{\rho G}$
, so by the definition of E in (A84) we get
 $\textsf{diverge}{\rho E}$
.
$\textsf{diverge}{\rho E}$
.- Case j-th argument diverges then
 $\theta\eta g \longrightarrow^{k''} u$
and
$\theta\eta g \longrightarrow^{k''} u$
and
 $\theta\eta e_i \longrightarrow^{k_i} v_i$
for all
$\theta\eta e_i \longrightarrow^{k_i} v_i$
for all
 $i < j$
and
$i < j$
and
 $\theta\eta e_j \longrightarrow^{k_j} e''$
and
$\theta\eta e_j \longrightarrow^{k_j} e''$
and
 $\textsf{diverge}{e''}$
. With (A86) and
$\textsf{diverge}{e''}$
. With (A86) and
 $k_j \leq k' < k$
we get
$k_j \leq k' < k$
we get
 $\textsf{diverge}{\rho E_j}$
. By definition of E in (A84), then diverge
$\textsf{diverge}{\rho E_j}$
. By definition of E in (A84), then diverge
 $\textsf{diverge}{\rho E}$
.
$\textsf{diverge}{\rho E}$
.- Case method call diverges Then we are in the situation that (A87), (A88), and (A89) hold. We then have
 \begin{equation} u.m[\eta {\psi}](\overline[n]{v}) \longrightarrow^{k' - k'' - \Sigma{k_i}} e' \end{equation}
\begin{equation} u.m[\eta {\psi}](\overline[n]{v}) \longrightarrow^{k' - k'' - \Sigma{k_i}} e' \end{equation}
Hence, with (A97), (A106), and the second implication in the premise of rule equiv-exp, we have that
 $\textsf{diverge}{X_{{m},{t_S}}\,\text{ (} \rho W\text{ ,} U\text{ ,} \rho W'\text{ ,} \text{ (} \overline{V} \text{ )} \text{ )}}$
. With (A107) and (A108) and Lemma A.1.2 then also
$\textsf{diverge}{X_{{m},{t_S}}\,\text{ (} \rho W\text{ ,} U\text{ ,} \rho W'\text{ ,} \text{ (} \overline{V} \text{ )} \text{ )}}$
. With (A107) and (A108) and Lemma A.1.2 then also
 $\textsf{diverge}{\rho E}$
as required.
$\textsf{diverge}{\rho E}$
as required.
End case distinction.
This finishes the proof for rule CALL-STRUCT.
This finishes the proof for rule call-struct.
• Case call-iface
With
From the IH applied to (A112) and (A116)
Assume
![]() $\theta \eta e \longrightarrow^{k'} e'$
for some
$\theta \eta e \longrightarrow^{k'} e'$
for some
![]() $k' < k$
. We first consider the following situation for some values
$k' < k$
. We first consider the following situation for some values
![]() $u, \overline[n]{v}$
:
$u, \overline[n]{v}$
:
with
![]() $k'' + {\Sigma}{k_i} \leq k'$
. (A121), (A122), and (A123) are intermediate assumptions, which become true when we later prove the two implications of rule equiv-exp.
$k'' + {\Sigma}{k_i} \leq k'$
. (A121), (A122), and (A123) are intermediate assumptions, which become true when we later prove the two implications of rule equiv-exp.
We have from (A119), (A120), (A121), and (A122)
From (A124) and (A113), we get by inverting rule equiv-iface
Hence, we have by (A126), (A129), (A114), and rule method-lookup
Then by (A129) and (A132)
Define
![]() $k''' := \min(k - k'' - 1, k - \Sigma{k_i} - 1)$
. Then
$k''' := \min(k - k'' - 1, k - \Sigma{k_i} - 1)$
. Then
The first four of these claims are straightforward to verify. The last can be shown with the following reasoning:

From (A134), we get the implication in the premise of rule equiv-method-dict-entry. We now show that the left-hand side of the implication holds. The universally quantified variables of the rule’s premise are instantiated as follows: ![]() . The variables in the conclusion are instantiated as follows:
. The variables in the conclusion are instantiated as follows:
![]() $x = x, \tau_S = t_S[{\phi}], m[{\Phi}](\overline[n]{x_i\ \tau_i})\,\tau = \eta_2 R', e = \eta_2 e''$
. The requirement
$x = x, \tau_S = t_S[{\phi}], m[{\Phi}](\overline[n]{x_i\ \tau_i})\,\tau = \eta_2 R', e = \eta_2 e''$
. The requirement
![]() $k''' \leq k - k'' - 1$
follows from (A135).
$k''' \leq k - k'' - 1$
follows from (A135).
We have from (A115) and (A133) the first conjunct:
From (A115), we get the second conjunct by Lemma A.3.15, (A136), by the assumptions
![]() $\overline{D} \approx_{k} \mu$
and
$\overline{D} \approx_{k} \mu$
and
![]() $ \eta \approx \rho \in [\![\Delta]\!]_{k}$
, and by Lemma A.3.5:
$ \eta \approx \rho \in [\![\Delta]\!]_{k}$
, and by Lemma A.3.5:
With (A137), (A128), (A126), and Lemma A.3.9, we get the third conjunct:
With (A138), (A125), Lemmas A.3.9, and A.3.3, we have
We next prove
by induction on
![]() $\sigma_i$
or
$\sigma_i$
or
![]() $\sigma$
. The interesting case is where
$\sigma$
. The interesting case is where
![]() $\sigma_i$
or
$\sigma_i$
or
![]() $\sigma$
is a type variable
$\sigma$
is a type variable
![]() $\alpha \in \textsf{dom}(\eta_1) \cup \textsf{dom}(\eta)$
. As the
$\alpha \in \textsf{dom}(\eta_1) \cup \textsf{dom}(\eta)$
. As the
![]() $\overline{\alpha} = \textsf{dom}(\eta_1) = \textsf{dom}(\eta_4)$
are bound in
$\overline{\alpha} = \textsf{dom}(\eta_1) = \textsf{dom}(\eta_4)$
are bound in
![]() ${\Psi}$
(see (A140)), we may assume that
${\Psi}$
(see (A140)), we may assume that
![]() $\overline{\alpha} \cap \textsf{dom}(\eta) = \emptyset = \overline{\alpha} \cap \textsf{ftv}(\eta)$
. If
$\overline{\alpha} \cap \textsf{dom}(\eta) = \emptyset = \overline{\alpha} \cap \textsf{ftv}(\eta)$
. If
![]() $\alpha \in \textsf{dom}(\eta_1)$
, then
$\alpha \in \textsf{dom}(\eta_1)$
, then
If
![]() $\alpha \in \textsf{dom}(\eta)$
, then
$\alpha \in \textsf{dom}(\eta)$
, then
We now get with (A133) and (A142) that
![]() $\eta\eta_1 \sigma_i = \eta_4\eta_2\sigma_i'$
. Hence with (A141) the fourth conjunct:
$\eta\eta_1 \sigma_i = \eta_4\eta_2\sigma_i'$
. Hence with (A141) the fourth conjunct:
Now the right-hand side of the implication of rule equiv-method-dict-entry yields with (A134)
Define
![]() $\eta_3$
such that
$\eta_3$
such that
Then with (A131) and (A140)
by induction on e”. The interesting case is the one for a type variable
![]() $\alpha$
. By Assumption 5.2.1 and (A130), we know that
$\alpha$
. By Assumption 5.2.1 and (A130), we know that
![]() $\alpha \in \hat{{\Phi}} \cup \hat{{\Psi}'}$
. Further we may assume that the type variables
$\alpha \in \hat{{\Phi}} \cup \hat{{\Psi}'}$
. Further we may assume that the type variables
![]() $\hat{{\Psi}'}$
are fresh, and we have
$\hat{{\Psi}'}$
are fresh, and we have
![]() $\textsf{dom}(\eta_2) = \hat{{\Phi}}$
by (A131) and
$\textsf{dom}(\eta_2) = \hat{{\Phi}}$
by (A131) and
![]() $\textsf{dom}(\eta_4) = \hat{{\Psi}'}$
by (A140). Thus, if
$\textsf{dom}(\eta_4) = \hat{{\Psi}'}$
by (A140). Thus, if
![]() $\alpha \in \hat{{\Phi}}$
then
$\alpha \in \hat{{\Phi}}$
then
![]() $\eta_4\eta_2\alpha = \eta_2\alpha$
because
$\eta_4\eta_2\alpha = \eta_2\alpha$
because
![]() $\hat{{\Psi}'}$
fresh, and
$\hat{{\Psi}'}$
fresh, and
![]() $\eta_3\alpha = \eta_2\alpha$
by (A131) and (A145). If
$\eta_3\alpha = \eta_2\alpha$
by (A131) and (A145). If
![]() $\alpha \in \hat{{\Psi}'}$
then
$\alpha \in \hat{{\Psi}'}$
then
![]() $\eta_4\eta_2\alpha = \eta_4\alpha$
because
$\eta_4\eta_2\alpha = \eta_4\alpha$
because
![]() $\hat{{\Psi}'}$
fresh, and
$\hat{{\Psi}'}$
fresh, and
![]() $\eta_3\alpha = \eta_4\alpha$
by (A145) and (A140).
$\eta_3\alpha = \eta_4\alpha$
by (A145) and (A140).
With (A143) and (A133)
![]() $\eta_4\eta_2 \sigma' = \eta\eta_1\sigma$
. Hence, we have with (A146), (A144)
$\eta_4\eta_2 \sigma' = \eta\eta_1\sigma$
. Hence, we have with (A146), (A144)
From (A126) and (A128), we get by inverting rule equiv-struct that
![]() $u = t_S[{\phi}]\{\ldots\}$
. Hence, by rule fg-call with (A130) and (A145)
$u = t_S[{\phi}]\{\ldots\}$
. Hence, by rule fg-call with (A130) and (A145)
Then with (A147) and Lemma 5.2.3
We also have

So far, we proved everything under the assumptions (A121), (A122), and (A123). We next consider the two implications of rule equiv-exp.
(a) Assume
 $e' = v$
for some value v. Then (A121), (A122), and (A123) We now need to show that there exists some W with
$e' = v$
for some value v. Then (A121), (A122), and (A123) We now need to show that there exists some W with
 $\rho E \longrightarrow^* W$
and
$\rho E \longrightarrow^* W$
and
 $v \equiv W \in [\![\eta \tau]\!]_{k - k'}$
. We have
$v \equiv W \in [\![\eta \tau]\!]_{k - k'}$
. We have
 $k' - k'' - \Sigma{k_i} < k''' + 1$
by (A139) Also, we have with (A123) that
$k' - k'' - \Sigma{k_i} < k''' + 1$
by (A139) Also, we have with (A123) that
Hence, (A148) gives us the existence of some W such that
We get
 $k - k' \leq k''' + 1 - (k' - k'' - \Sigma{k_i})$
by
$k - k' \leq k''' + 1 - (k' - k'' - \Sigma{k_i})$
by \begin{equation} \begin{array}{@{}r@{~}l@{}} & k''' + 1 - (k' - k'' - \Sigma k_i) \\ = & k - \max(k'' + 1, \Sigma{k_i} + 1) + 1 - k' + k'' + \Sigma{k_i} \\ = & k - \max(k'', \Sigma{k_i}) - k' + k'' + \Sigma{k_i} \\ \geq & k - (k'' + \Sigma{k_i}) - k' + (k'' + \Sigma{k_i}) \\ = & k - k' \end{array} \end{equation}
\begin{equation} \begin{array}{@{}r@{~}l@{}} & k''' + 1 - (k' - k'' - \Sigma k_i) \\ = & k - \max(k'' + 1, \Sigma{k_i} + 1) + 1 - k' + k'' + \Sigma{k_i} \\ = & k - \max(k'', \Sigma{k_i}) - k' + k'' + \Sigma{k_i} \\ \geq & k - (k'' + \Sigma{k_i}) - k' + (k'' + \Sigma{k_i}) \\ = & k - k' \end{array} \end{equation}
Hence, by Lemma A.3.3
 \begin{equation} v \approx W \in [\![\eta \eta_1 \sigma]\!]_{k - k'} \end{equation}
\begin{equation} v \approx W \in [\![\eta \eta_1 \sigma]\!]_{k - k'} \end{equation}
By (A117)
 $\eta_1 \sigma = \tau$
so
$\eta_1 \sigma = \tau$
so
 $ v \approx W \in [\![\eta \tau]\!]_{k - k'}$
and with (A149) and (A150)
$ v \approx W \in [\![\eta \tau]\!]_{k - k'}$
and with (A149) and (A150)
 $\rho E \longrightarrow^* W$
.
$\rho E \longrightarrow^* W$
.(b) Assume
 $\textsf{diverge}{e'}$
. We then have to show
$\textsf{diverge}{e'}$
. We then have to show
 $\textsf{diverge}{\rho E}$
.
$\textsf{diverge}{\rho E}$
.
Case distinction whether receiver, argument, or method call diverges
- Case receiver diverges: Then
 $\theta\eta g \longrightarrow^{k'} g'$
and
$\theta\eta g \longrightarrow^{k'} g'$
and
 $\textsf{diverge}{g'}$
. With (A119) and
$\textsf{diverge}{g'}$
. With (A119) and
 $k' < k$
then
$k' < k$
then
 $\textsf{diverge}{\rho G}$
, so by the definition of E in (A118) we get
$\textsf{diverge}{\rho G}$
, so by the definition of E in (A118) we get
 $\textsf{diverge}{\rho E}$
.
$\textsf{diverge}{\rho E}$
.- Case j-th argument diverges Then
 $\theta\eta g \longrightarrow^{k''} u$
. By (A119) and rule equiv-iface, we know that
$\theta\eta g \longrightarrow^{k''} u$
. By (A119) and rule equiv-iface, we know that  for some
for some  . Hence,
. Hence,- (A151)

Because the j-th argument diverges, we also have
 $\theta\eta e_i \longrightarrow^{k_i} v_i$
for all
$\theta\eta e_i \longrightarrow^{k_i} v_i$
for all
 $i < j$
and
$i < j$
and
 $\theta\eta e_j \longrightarrow^{k_j} e''$
and
$\theta\eta e_j \longrightarrow^{k_j} e''$
and
 $\textsf{diverge}{e''}$
. With (A120) we get
$\textsf{diverge}{e''}$
. With (A120) we get
 $\textsf{diverge}{\rho E_j}$
, so with (A151) also
$\textsf{diverge}{\rho E_j}$
, so with (A151) also
 $\textsf{diverge}{\rho E}$
.
$\textsf{diverge}{\rho E}$
.
- Case method call diverges Then we are in the situation that (A121), (A122), and (A123) hold. Thus, we get with (A123), (A148), and (A139)

Hence,
 $\textsf{diverge}{U_j\ \text{ (} U'\text{ ,} \rho V\text{ ,} \text{ (} \overline[n]{V} \text{ )} \text{ )}}$
by the implication in the premise of rule equiv-exp. So by (A149)
$\textsf{diverge}{U_j\ \text{ (} U'\text{ ,} \rho V\text{ ,} \text{ (} \overline[n]{V} \text{ )} \text{ )}}$
by the implication in the premise of rule equiv-exp. So by (A149)
 $\textsf{diverge}{\rho E}$
as required.
$\textsf{diverge}{\rho E}$
as required.
End case distinction.
• Case SUB:

From the IH, then
![]() $ \theta\eta e \approx \rho E' \in [\![\eta\sigma]\!]_{k}$
. From Lemma A.3.13, we get
$ \theta\eta e \approx \rho E' \in [\![\eta\sigma]\!]_{k}$
. From Lemma A.3.13, we get
![]() $ \theta\eta e \approx (\rho V)\,\rho E' \in [\![\eta\tau]\!]_{k}$
with
$ \theta\eta e \approx (\rho V)\,\rho E' \in [\![\eta\tau]\!]_{k}$
with
![]() $\rho E = (\rho V)\,(\rho E')$
as required.
$\rho E = (\rho V)\,(\rho E')$
as required.
End case distinction on the last rule in the derivation of
![]() $\blacksquare$
$\blacksquare$
A.3.2.2 Proof of Lemma 5.2.5. We proceed by induction on k. For
![]() $k = 0$
, we first note that
$k = 0$
, we first note that
![]() $ e \approx E \in [\![\tau]\!]_{0}$
holds for any
$ e \approx E \in [\![\tau]\!]_{0}$
holds for any
![]() $e, E, \tau$
because the two implications in the premise of rule equiv-exp hold trivially. Thus, we get
$e, E, \tau$
because the two implications in the premise of rule equiv-exp hold trivially. Thus, we get
![]() $D \approx_{0} X_{{m},{t_S}}$
for all
$D \approx_{0} X_{{m},{t_S}}$
for all ![]() by rule equiv-method-decl. Hence,
by rule equiv-method-decl. Hence,
![]() $\overline{D} \approx_{0} \mu$
by rule equiv-decls.
$\overline{D} \approx_{0} \mu$
by rule equiv-decls.
Now assume
![]() $\overline{D} \approx_{k} \mu$
(IH) for some k and prove
$\overline{D} \approx_{k} \mu$
(IH) for some k and prove
![]() $\overline{D} \approx_{k+1} \mu$
. By rule equiv-decls, we need to show
$\overline{D} \approx_{k+1} \mu$
. By rule equiv-decls, we need to show
![]() $D \approx_{k+1} X_{{m},{t_S}}$
for all
$D \approx_{k+1} X_{{m},{t_S}}$
for all
Thus, we assume the left-hand side of the implication in the premise of rule equiv-method-decl and then show the right-hand side of the implication. More specifically, let
and assume for arbitrary
![]() $k' < k + 1, {\phi} = \overline[p]{\sigma''}, {\phi}' = \overline[q]{\sigma'''}, \overline[p]{W}, \overline[q]{W'}, u, U, \overline[n]{v}, \overline[n]{V}$
the left-hand side of the implication:
$k' < k + 1, {\phi} = \overline[p]{\sigma''}, {\phi}' = \overline[q]{\sigma'''}, \overline[p]{W}, \overline[q]{W'}, u, U, \overline[n]{v}, \overline[n]{V}$
the left-hand side of the implication:
From this, we need to prove the following goal:
Define
Then with (A153), (A154), and rule EQUIV-VAL-SUBST
And with (A155), (A156), the definition of
![]() $\theta$
in (A157), and rule EQUIV-VAL-SUBST
$\theta$
in (A157), and rule EQUIV-VAL-SUBST
From the assumption ![]() , we get by inverting rule method
, we get by inverting rule method
With
![]() $k' < k+1$
we have
$k' < k+1$
we have
![]() $k' \leq k$
. With the IH and Lemma A.3.7 then
$k' \leq k$
. With the IH and Lemma A.3.7 then
(A163), (A159), (A160), and (A161) are the requirements of Lemma 5.2.4. The lemma then yields
We also have
where the first reduction follows from assumption
![]() $\mu(X_{{m},{t_S}}) = V$
and rule tl-method, the remaining steps by (A162) and (A158). With (A164) and Lemma 5.2.2 we then get (A157) as required.
$\mu(X_{{m},{t_S}}) = V$
and rule tl-method, the remaining steps by (A162) and (A158). With (A164) and Lemma 5.2.2 we then get (A157) as required.
![]() $\blacksquare$
$\blacksquare$
A.3.2.3 Proof of Theorem 5.2.6. We first prove that the assumptions of the theorem imply
![]() $ e \approx E \in [\![\tau]\!]_{k}$
for any k.
$ e \approx E \in [\![\tau]\!]_{k}$
for any k.
![]() $\overline{D}$
and
$\overline{D}$
and
![]() $\mu$
are the declarations and the substitution whose existence we assumed globally. Obviously, they meet the requirements of Assumption 5.2.1.
$\mu$
are the declarations and the substitution whose existence we assumed globally. Obviously, they meet the requirements of Assumption 5.2.1.
Assume
![]() $k \in \mathbb{N}$
. From Lemma 5.2.5, we get
$k \in \mathbb{N}$
. From Lemma 5.2.5, we get
![]() $\overline{D} \approx_{k} \mu$
. By the assumption
$\overline{D} \approx_{k} \mu$
. By the assumption ![]() , by inverting rule prog, and by the assumption that e has type
, by inverting rule prog, and by the assumption that e has type
![]() $\tau$
, we find
$\tau$
, we find
![]() $\langle\emptyset,\emptyset\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
. Lemma 5.2.4 then yields
$\langle\emptyset,\emptyset\rangle \mathrel{\vdash_{{{{\textsf{exp}}}}}} e : \tau \leadsto E$
. Lemma 5.2.4 then yields
![]() $ e \approx E \in [\![\tau]\!]_{k}$
as required.
$ e \approx E \in [\![\tau]\!]_{k}$
as required.
From
![]() $ e \approx E \in [\![\tau]\!]_{k}$
for any k and the two implications in the premise of rule equiv-exp, we then get the two claims needed to show.
$ e \approx E \in [\![\tau]\!]_{k}$
for any k and the two implications in the premise of rule equiv-exp, we then get the two claims needed to show.
![]() $\blacksquare$
$\blacksquare$
A.3.3. Equivalence between different translations
Lemma A.3.17. If
![]() $v \equiv \text{ (} \overline{V} \text{ )} \in [\![\tau]\!]_{k}$
then none of the
$v \equiv \text{ (} \overline{V} \text{ )} \in [\![\tau]\!]_{k}$
then none of the
![]() $V_i$
is a lambda.
$V_i$
is a lambda.
Proof.
Case distinction on the last rule in the derivation of
![]() $v \equiv \text{ (} \overline{V} \text{ )} \in [\![\tau]\!]_{k}$
$v \equiv \text{ (} \overline{V} \text{ )} \in [\![\tau]\!]_{k}$
• Case rule equiv-struct Then we know that
 $v = \tau_S\{\overline{v}\}$
and
$v = \tau_S\{\overline{v}\}$
and
 $\tau = \tau_S$
and for all i exists some
$\tau = \tau_S$
and for all i exists some
 $\sigma_i$
with
$\sigma_i$
with
 $v_i \equiv V_i \in [\![\sigma_i]\!]_{k}$
. But then obviously
$v_i \equiv V_i \in [\![\sigma_i]\!]_{k}$
. But then obviously
 $V_i$
cannot be a lambda.
$V_i$
cannot be a lambda.• Case rule equiv-iface Obvious.
End case distinction.
Lemma A.3.18. If
![]() $v \equiv \text{ (} U\text{ ,} \text{ (} \overline{W} \text{ )} \text{ )} \in [\![\tau_I]\!]_{k}$
with
$v \equiv \text{ (} U\text{ ,} \text{ (} \overline{W} \text{ )} \text{ )} \in [\![\tau_I]\!]_{k}$
with
![]() $k > 0$
, then all
$k > 0$
, then all
![]() $W_i$
are lambdas.
$W_i$
are lambdas.
Proof. The derivation of
![]() $v \equiv \text{ (} U\text{ ,} \text{ (} \overline{W} \text{ )} \text{ )} \in [\![\tau_I]\!]_{k}$
ends with rule equiv-iface. The premise of the rule gives us for each
$v \equiv \text{ (} U\text{ ,} \text{ (} \overline{W} \text{ )} \text{ )} \in [\![\tau_I]\!]_{k}$
ends with rule equiv-iface. The premise of the rule gives us for each
![]() $W_i$
$W_i$
for some method signature
![]() $R_i$
, struct type
$R_i$
, struct type
![]() $\sigma_S$
and all
$\sigma_S$
and all
![]() $k_2 < k$
. As
$k_2 < k$
. As
![]() $k > 0$
we know that (A165) holds for at least one
$k > 0$
we know that (A165) holds for at least one
![]() $k_2$
. Further, the derivation of (A165) ends with rule equiv-method-dict-entry, and this rule requires that
$k_2$
. Further, the derivation of (A165) ends with rule equiv-method-dict-entry, and this rule requires that
![]() $W_i$
is a lambda.
$W_i$
is a lambda.
![]() $\blacksquare$
$\blacksquare$
Lemma A.3.19. If
![]() $v \equiv V \in [\![ t_I[\overline{\tau}]]\!]_{k}$
for all
$v \equiv V \in [\![ t_I[\overline{\tau}]]\!]_{k}$
for all
![]() $k \in \mathbb{N}$
, then
$k \in \mathbb{N}$
, then
![]() $V = \text{ (} U\text{ ,} \text{ (} \overline[n]{W} \text{ )} \text{ )}$
where n is the number of methods defined by
$V = \text{ (} U\text{ ,} \text{ (} \overline[n]{W} \text{ )} \text{ )}$
where n is the number of methods defined by
![]() $t_I$
,
$t_I$
,
![]() $v = \tau_S\{\overline{v}\}$
, and
$v = \tau_S\{\overline{v}\}$
, and
![]() $v \equiv U \in [\![\tau_S]\!]_{k}$
for all
$v \equiv U \in [\![\tau_S]\!]_{k}$
for all
![]() $k \in \mathbb{N}$
.
$k \in \mathbb{N}$
.
Proof. The derivation of
![]() $v \equiv V \in [\![ t_I[\overline{\tau}]]\!]_{k}$
ends with rule equiv-iface for any
$v \equiv V \in [\![ t_I[\overline{\tau}]]\!]_{k}$
ends with rule equiv-iface for any
![]() $k \in \mathbb{N}$
. Also for all
$k \in \mathbb{N}$
. Also for all
![]() $k \in \mathbb{N}$
, the conclusion of this rule requires
$k \in \mathbb{N}$
, the conclusion of this rule requires
![]() $V = \text{ (} U\text{ ,} \text{ (} \overline[n]{W} \text{ )} \text{ )}$
, the premise of this rule states that interface
$V = \text{ (} U\text{ ,} \text{ (} \overline[n]{W} \text{ )} \text{ )}$
, the premise of this rule states that interface
![]() $t_I$
has n methods and further gives us
$t_I$
has n methods and further gives us
Obviously,
![]() $v \equiv U \in [\![\sigma_S]\!]_{k_1}$
ends with rule equiv-struct. Because value v must have the form
$v \equiv U \in [\![\sigma_S]\!]_{k_1}$
ends with rule equiv-struct. Because value v must have the form
![]() $v = \tau_S\{\overline{v}\}$
, we then know that the existentially quantified
$v = \tau_S\{\overline{v}\}$
, we then know that the existentially quantified
![]() $\sigma_S$
is the same as
$\sigma_S$
is the same as
![]() $\tau_S$
. Because (A166) holds for any
$\tau_S$
. Because (A166) holds for any
![]() $k \in \mathbb{N}$
, we then get
$k \in \mathbb{N}$
, we then get
![]() $v \equiv U \in [\![\tau_S]\!]_{k}$
for all
$v \equiv U \in [\![\tau_S]\!]_{k}$
for all
![]() $k \in \mathbb{N}$
as required.
$k \in \mathbb{N}$
as required.
![]() $\blacksquare$
$\blacksquare$
Lemma A.3.20. If
![]() $v \equiv V \in [\![\tau]\!]_{k}$
and
$v \equiv V \in [\![\tau]\!]_{k}$
and
![]() $v \equiv V' \in [\![\tau]\!]_{k}$
for any
$v \equiv V' \in [\![\tau]\!]_{k}$
for any
![]() $k \in \mathbb{N}$
, then
$k \in \mathbb{N}$
, then
![]() $\textsf{{erase}}(V) = \textsf{{erase}}(V')$
.
$\textsf{{erase}}(V) = \textsf{{erase}}(V')$
.
Proof. Define a measure function

and proceed by induction on
![]() $\mathcal M(v, \tau)$
. We first note that the derivations of
$\mathcal M(v, \tau)$
. We first note that the derivations of
![]() $v \equiv V \in [\![\tau]\!]_{k}$
all end with the same rule, independent from
$v \equiv V \in [\![\tau]\!]_{k}$
all end with the same rule, independent from
![]() $k \in \mathbb{N}$
.
$k \in \mathbb{N}$
.
Case distinction on the last rule in the derivations of
![]() $v \equiv V \in [\![\tau]\!]_{k}$
$v \equiv V \in [\![\tau]\!]_{k}$
• Case rule equiv-struct Then
 $\tau$
is a struct type, so the derivations of
$\tau$
is a struct type, so the derivations of
 $v \equiv V' \in [\![\tau]\!]_{k}$
also all end with equiv-struct. Thus, we have
$v \equiv V' \in [\![\tau]\!]_{k}$
also all end with equiv-struct. Thus, we have

As this holds for any
![]() $k \in \mathbb{N}$
and we have
$k \in \mathbb{N}$
and we have
![]() $\mathcal M(v_i, \eta\sigma_i) < \mathcal M(v, \tau)$
, we may apply the IH to (A167) and (A168) and get
$\mathcal M(v_i, \eta\sigma_i) < \mathcal M(v, \tau)$
, we may apply the IH to (A167) and (A168) and get
![]() $\textsf{erase}(V_i) = \textsf{erase}(V_i')$
for all
$\textsf{erase}(V_i) = \textsf{erase}(V_i')$
for all
![]() $i \in [n]$
. Then
$i \in [n]$
. Then
![]() $\textsf{erase}(V) = \textsf{erase}(V')$
follows by definition of
$\textsf{erase}(V) = \textsf{erase}(V')$
follows by definition of
![]() $\textsf{erase}$
.
$\textsf{erase}$
.
• Case rule equiv-iface Then
 $\tau$
is interface type. With Lemma A.3.19 then for some
$\tau$
is interface type. With Lemma A.3.19 then for some
 $\sigma_S$
and n
(A169)
$\sigma_S$
and n
(A169) (A170)
(A170)
Noting that
 $\mathcal M(v, \sigma_S) < \mathcal M(v, \tau)$
, we apply the IH to (A169) and (A170) and get
$\mathcal M(v, \sigma_S) < \mathcal M(v, \tau)$
, we apply the IH to (A169) and (A170) and get
 $\textsf{erase}(U) = \textsf{erase}(U')$
. With Lemma A.3.18 applied to assumptions
$\textsf{erase}(U) = \textsf{erase}(U')$
. With Lemma A.3.18 applied to assumptions
 $(\forall k \in \mathbb{N}) . v \equiv V \in [\![\tau]\!]_{k}$
and
$(\forall k \in \mathbb{N}) . v \equiv V \in [\![\tau]\!]_{k}$
and
 $(\forall k \in \mathbb{N}) . v \equiv V' \in [\![\tau]\!]_{k}$
, we know that all
$(\forall k \in \mathbb{N}) . v \equiv V' \in [\![\tau]\!]_{k}$
, we know that all
 $W_i, W_i'$
are lambdas. Thus, by definition of
$W_i, W_i'$
are lambdas. Thus, by definition of
 $\textsf{erase}$
$\textsf{erase}$

End case distinction.
Lemma A.3.21. If
![]() $v \equiv V \in [\![\tau]\!]_{k}$
and
$v \equiv V \in [\![\tau]\!]_{k}$
and
![]() $v \equiv V' \in [\![\tau']\!]_{k}$
for any
$v \equiv V' \in [\![\tau']\!]_{k}$
for any
![]() $k \in \mathbb{N}$
, then
$k \in \mathbb{N}$
, then
![]() $\textsf{{erase}}(\tau, V) = \textsf{{erase}}(\tau', V')$
.
$\textsf{{erase}}(\tau, V) = \textsf{{erase}}(\tau', V')$
.
Proof. We label the assumptions:
We then perform a case distinction on the form of
![]() $\tau$
and
$\tau$
and
![]() $\tau'$
. Note that neither of them can be a type variable; otherwise, (A171) and (A172) would not be derivable.
$\tau'$
. Note that neither of them can be a type variable; otherwise, (A171) and (A172) would not be derivable.
Case distinction on the forms of
![]() $\tau$
and
$\tau$
and
![]() $\tau'$
$\tau'$
• Case
 $\tau$
and
$\tau$
and
 $\tau'$
are both struct types Then all derivations of (A171) and (A172) end with rule equiv-struct. Hence,
$\tau'$
are both struct types Then all derivations of (A171) and (A172) end with rule equiv-struct. Hence,
 $\tau = \tau'$
. Thus,
$\tau = \tau'$
. Thus,
 $\textsf{erase}(V) = \textsf{erase}(V')$
by Lemma A.3.20. But by definition of
$\textsf{erase}(V) = \textsf{erase}(V')$
by Lemma A.3.20. But by definition of
 $\textsf{erase}$
, we also have
$\textsf{erase}$
, we also have
 $\textsf{erase}(\tau, V) = \textsf{erase}(V)$
and
$\textsf{erase}(\tau, V) = \textsf{erase}(V)$
and
 $\textsf{erase}(\tau', V') = \textsf{erase}(V)$
.
$\textsf{erase}(\tau', V') = \textsf{erase}(V)$
.• Case
 $\tau$
is a struct type and
$\tau$
is a struct type and
 $\tau'$
is an interface type Then all derivations of (A171) end with rule equiv-struct, so we know that
$\tau'$
is an interface type Then all derivations of (A171) end with rule equiv-struct, so we know that
 $v = \tau\{\overline{v}\}$
. Then we get with Lemma A.3.19 and (A172)
$v = \tau\{\overline{v}\}$
. Then we get with Lemma A.3.19 and (A172) \begin{equation} V' = \text{ (} U\text{ ,} W \text{ )}\\ (\forall k \in \mathbb{N}) . v \equiv U \in [\![\tau]\!]_{k} \end{equation}
\begin{equation} V' = \text{ (} U\text{ ,} W \text{ )}\\ (\forall k \in \mathbb{N}) . v \equiv U \in [\![\tau]\!]_{k} \end{equation}
With (A171) and Lemma A.3.20 and the definition of
 $\textsf{erase}$
then
$\textsf{erase}$
then \begin{equation} \textsf{erase}(\tau, \textsf{erase}(V)) = \textsf{erase}(V) = \textsf{erase}(U) = \textsf{erase}(\tau', V') \end{equation}
\begin{equation} \textsf{erase}(\tau, \textsf{erase}(V)) = \textsf{erase}(V) = \textsf{erase}(U) = \textsf{erase}(\tau', V') \end{equation}
• Case
 $\tau$
is an interface type and
$\tau$
is an interface type and
 $\tau'$
is a struct type Analogously to the preceding case.
$\tau'$
is a struct type Analogously to the preceding case.• Case
 $\tau$
and
$\tau$
and
 $\tau'$
are both interface types Then with Lemma A.3.19 and (A171) and (A172)
$\tau'$
are both interface types Then with Lemma A.3.19 and (A171) and (A172) \begin{equation} v = \sigma_S\{\overline{v}\}\\ V = \text{ (} U\text{ ,} W \text{ )}\\ V' = \text{ (} U'\text{ ,} W' \text{ )}\\ (\forall k \in \mathbb{N}) . v \equiv U \in [\![\sigma_S]\!]_{k} \\ (\forall k \in \mathbb{N}) . v \equiv U' \in [\![\sigma_S]\!]_{k} \end{equation}
\begin{equation} v = \sigma_S\{\overline{v}\}\\ V = \text{ (} U\text{ ,} W \text{ )}\\ V' = \text{ (} U'\text{ ,} W' \text{ )}\\ (\forall k \in \mathbb{N}) . v \equiv U \in [\![\sigma_S]\!]_{k} \\ (\forall k \in \mathbb{N}) . v \equiv U' \in [\![\sigma_S]\!]_{k} \end{equation}
Now Lemma A.3.20 and the definition of erase
 \begin{equation} \textsf{erase}(\tau, V) = \textsf{erase}(U) = \textsf{erase}(U') = \textsf{erase}(\tau', V') \end{equation}
\begin{equation} \textsf{erase}(\tau, V) = \textsf{erase}(U) = \textsf{erase}(U') = \textsf{erase}(\tau', V') \end{equation}
as required.
End case distinction.
A.3.3.1 Proof of Theorem 5.2.7. From ![]() and
and ![]() and e having type
and e having type
![]() $\tau$
and
$\tau$
and
![]() $\tau'$
, respectively, we get
$\tau'$
, respectively, we get
With Corollary 5.1.2, we get that either e reduces to some value v or diverges.
We now start with the first claim. Assume
![]() $E \longrightarrow^*_{\mu} V$
for some V. Then e must reduce to some value v because of Theorem 5.2.6. Again with Theorem 5.2.6 and with Lemma A.1.2:
$E \longrightarrow^*_{\mu} V$
for some V. Then e must reduce to some value v because of Theorem 5.2.6. Again with Theorem 5.2.6 and with Lemma A.1.2:
Applying Lemma A.3.21 yields
![]() $\textsf{erase}(\tau, V) = \textsf{erase}(\tau', V')$
as required.
$\textsf{erase}(\tau, V) = \textsf{erase}(\tau', V')$
as required.
For the second claim, we assume that E diverges. With Theorem 5.2.6, we know that e must diverge as well. Again with Theorem 5.2.6 we get that E’ also diverges.



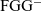
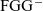
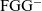
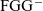




































Discussions
No Discussions have been published for this article.