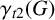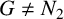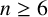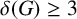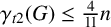1. Introduction
Domination and its variations have been extensively studied (see, for example, [Reference Chen and Xu1, Reference Dong, Shan, Kang and Li2, Reference Haynes, Hedetniemi and Slater4, Reference Henning6, Reference Henning and Yeo11]). A subset D of vertices in a graph G is a dominating set of G if every vertex of
![]() $V(G)\setminus D$
is adjacent to a vertex in D. The minimum cardinality
$V(G)\setminus D$
is adjacent to a vertex in D. The minimum cardinality
![]() $\gamma (G)$
of a dominating set is called the dominating number of G. A subset D of vertices in a graph G is a total dominating set of G if every vertex of
$\gamma (G)$
of a dominating set is called the dominating number of G. A subset D of vertices in a graph G is a total dominating set of G if every vertex of
![]() $V(G)$
is adjacent to a vertex in D. The minimum cardinality
$V(G)$
is adjacent to a vertex in D. The minimum cardinality
![]() $\gamma _{t}(G)$
of a total dominating set is called the total dominating number of G. It is worth noting that the study of total dominating sets is meaningful only on an isolate-free graph.
$\gamma _{t}(G)$
of a total dominating set is called the total dominating number of G. It is worth noting that the study of total dominating sets is meaningful only on an isolate-free graph.
Semitotal domination, introduced by Goddard et al. [Reference Goddard, Henning and McPillan3] in 2014, is a relaxed form of total domination. A subset D of vertices in an isolate-free graph G is a semitotal dominating set, abbreviated semi-TD-set, of G if it is a dominating set of G and every vertex in D is within distance 2 of another vertex of D. The semitotal domination number of G, denoted by
![]() $\gamma _{t2}(G)$
, is the minimum cardinality of a semi-TD-set in G. We refer to a minimum semi-TD-set of G as a
$\gamma _{t2}(G)$
, is the minimum cardinality of a semi-TD-set in G. We refer to a minimum semi-TD-set of G as a
![]() $\gamma _{t2}(G)$
-set. Since every total dominating set is a semi-TD-set and every semi-TD-set is a dominating set,
$\gamma _{t2}(G)$
-set. Since every total dominating set is a semi-TD-set and every semi-TD-set is a dominating set,
![]() $\gamma (G)\leqslant \gamma _{t2}(G)\leqslant \gamma _{t}(G)$
. However, the semitotal domination number is very different from the domination and total domination number. For example, the total domination number cannot be compared with the matching number, while the semitotal domination number is comparable with the matching number and cannot be greater than the matching number plus one (see [Reference Henning, Kang, Shan and Yeo7, Reference Henning and Marcon8]). That makes the study of semitotal domination interesting.
$\gamma (G)\leqslant \gamma _{t2}(G)\leqslant \gamma _{t}(G)$
. However, the semitotal domination number is very different from the domination and total domination number. For example, the total domination number cannot be compared with the matching number, while the semitotal domination number is comparable with the matching number and cannot be greater than the matching number plus one (see [Reference Henning, Kang, Shan and Yeo7, Reference Henning and Marcon8]). That makes the study of semitotal domination interesting.
There is much interest in bounds for the semitotal domination number of graphs. For example, Goddard et al. [Reference Goddard, Henning and McPillan3] proved that if G is a connected graph of order
![]() $n\geqslant 4$
, then
$n\geqslant 4$
, then
![]() $\gamma _{t2}(G)\leqslant \tfrac 12 n$
and proposed Conjecture 1.1 below. Henning and Marcon [Reference Henning and Marcon9] proved that if G is a connected claw-free cubic graph of order
$\gamma _{t2}(G)\leqslant \tfrac 12 n$
and proposed Conjecture 1.1 below. Henning and Marcon [Reference Henning and Marcon9] proved that if G is a connected claw-free cubic graph of order
![]() $n\geqslant 10$
, then
$n\geqslant 10$
, then
![]() $\gamma _{t2}(G)\leq \frac{4}{11}n$
, and conjectured that this bound can be improved to
$\gamma _{t2}(G)\leq \frac{4}{11}n$
, and conjectured that this bound can be improved to
![]() $\tfrac 13n$
if
$\tfrac 13n$
if
![]() $G\notin \{K_4,N_2\}$
, where
$G\notin \{K_4,N_2\}$
, where
![]() $N_2$
is a graph shown in Figure 1(a). This conjecture was solved by Zhu et al. [Reference Zhu, Shao and Xu13] and they proposed Conjecture 1.2 below. Zhu and Liu [Reference Zhu and Liu12] proved that Conjectures 1.1 and 1.2 hold for line graphs with minimum degree 3 and 4, respectively. In [Reference Henning5], Henning established the tight upper bounds on the upper semitotal domination number of a regular graph using edge weighting functions. For algorithmic aspects of semitotal domination in graphs, Henning and Pandey [Reference Henning and Pandey10] showed the semitotal domination problem is NP-complete for planar graphs, chordal bipartite graphs and split graphs.
$N_2$
is a graph shown in Figure 1(a). This conjecture was solved by Zhu et al. [Reference Zhu, Shao and Xu13] and they proposed Conjecture 1.2 below. Zhu and Liu [Reference Zhu and Liu12] proved that Conjectures 1.1 and 1.2 hold for line graphs with minimum degree 3 and 4, respectively. In [Reference Henning5], Henning established the tight upper bounds on the upper semitotal domination number of a regular graph using edge weighting functions. For algorithmic aspects of semitotal domination in graphs, Henning and Pandey [Reference Henning and Pandey10] showed the semitotal domination problem is NP-complete for planar graphs, chordal bipartite graphs and split graphs.

Figure 1 Two graphs:
![]() $N_2$
and
$N_2$
and
![]() $N^{\prime }_2$
, where the black vertices form a minimum semi-TD-set of their respective graphs.
$N^{\prime }_2$
, where the black vertices form a minimum semi-TD-set of their respective graphs.
Conjecture 1.1 [Reference Goddard, Henning and McPillan3]
If
![]() $G\neq K_4$
is a graph of order n with minimum degree
$G\neq K_4$
is a graph of order n with minimum degree
![]() $\delta (G)\geqslant 3$
, then
$\delta (G)\geqslant 3$
, then
![]() $\gamma _{t2}(G)\leqslant \tfrac 25n$
.
$\gamma _{t2}(G)\leqslant \tfrac 25n$
.
Conjecture 1.2 [Reference Zhu, Shao and Xu13]
If
![]() $G\neq N_2$
is a connected claw-free graph of order
$G\neq N_2$
is a connected claw-free graph of order
![]() $n\geq 6$
with minimum degree
$n\geq 6$
with minimum degree
![]() $\delta (G)\geq 3$
, then
$\delta (G)\geq 3$
, then
![]() $\gamma _{t2}(G)\leq \tfrac 13n$
.
$\gamma _{t2}(G)\leq \tfrac 13n$
.
Inspired by [Reference Henning5], using edge weighting functions, we establish the tight upper bound on the semitotal domination number of a connected claw-free graph with minimum degree at least 3. In Section 2, we give some basic definitions and a lemma as preliminaries. In Section 3, we prove that if
![]() $G\neq N_2$
is a connected claw-free graph of order
$G\neq N_2$
is a connected claw-free graph of order
![]() $n\geq 6$
with minimum degree
$n\geq 6$
with minimum degree
![]() $\delta (G)\geq 3$
, then
$\delta (G)\geq 3$
, then
![]() $\gamma _{t2}(G)\leq \frac{4}{11}n$
. Also, we construct a graph attaining this bound and thus disprove Conjecture 1.2.
$\gamma _{t2}(G)\leq \frac{4}{11}n$
. Also, we construct a graph attaining this bound and thus disprove Conjecture 1.2.
2. Preliminaries
In this section, we introduce some basic definitions and a useful lemma.
Let
![]() $G=(V(G),E(G))$
be a connected finite simple undirected graph with vertex set
$G=(V(G),E(G))$
be a connected finite simple undirected graph with vertex set
![]() $V(G)$
and edge set
$V(G)$
and edge set
![]() $E(G)$
of order
$E(G)$
of order
![]() $n=|V(G)|$
. For a vertex
$n=|V(G)|$
. For a vertex
![]() $v\in V(G)$
, we denote by
$v\in V(G)$
, we denote by
![]() $N_G(v)=\{u\in V(G) \mid uv\in E(G)\}$
the neighbourhood of v and by
$N_G(v)=\{u\in V(G) \mid uv\in E(G)\}$
the neighbourhood of v and by
![]() $N_G[v]=N_G(v)\cup \{v\}$
the closed neighbourhood of v. The degree of v is
$N_G[v]=N_G(v)\cup \{v\}$
the closed neighbourhood of v. The degree of v is
![]() $d_G(v)=|N_G(v)|$
and the number
$d_G(v)=|N_G(v)|$
and the number
![]() $\delta (G)=\min \{d_G(v)\mid v\in V(G)\}$
is the minimum degree of G. We call a path connecting vertices u and v a
$\delta (G)=\min \{d_G(v)\mid v\in V(G)\}$
is the minimum degree of G. We call a path connecting vertices u and v a
![]() $(u,v)$
-path. The distance
$(u,v)$
-path. The distance
![]() $d_G(u,v)$
between u and v is the length of a shortest
$d_G(u,v)$
between u and v is the length of a shortest
![]() $(u,v)$
-path in G. For a subset S of
$(u,v)$
-path in G. For a subset S of
![]() $V(G)$
, we denote by
$V(G)$
, we denote by
![]() $N_S(v)$
the neighbourhood of v restricted on S and by
$N_S(v)$
the neighbourhood of v restricted on S and by
![]() $G[S]$
the subgraph of G induced by S, while the graph
$G[S]$
the subgraph of G induced by S, while the graph
![]() $G-S$
is the graph obtained from G by deleting the vertices in S and all edges incident with S. A graph is claw-free if it does not contain the complete bipartite graph
$G-S$
is the graph obtained from G by deleting the vertices in S and all edges incident with S. A graph is claw-free if it does not contain the complete bipartite graph
![]() $K_{1,3}$
as an induced subgraph. If there is no confusion, then the subscript G is omitted in the notation, such as
$K_{1,3}$
as an induced subgraph. If there is no confusion, then the subscript G is omitted in the notation, such as
![]() $N(v), d(v),d(u,v)$
and so on.
$N(v), d(v),d(u,v)$
and so on.
Now consider
![]() $S_1$
and
$S_1$
and
![]() $S_2$
which are two disjoint subsets of
$S_2$
which are two disjoint subsets of
![]() $V(G)$
. Let
$V(G)$
. Let
![]() $E[S_1, S_2]=\{u_1u_2\mid u_1\in S_1$
and
$E[S_1, S_2]=\{u_1u_2\mid u_1\in S_1$
and
![]() $u_2\in S_2\}$
. For a vertex v of S, the S-external private neighbourhood of v, denoted by
$u_2\in S_2\}$
. For a vertex v of S, the S-external private neighbourhood of v, denoted by
![]() ${\textit {epn}}(v,S)$
, is the set of all vertices in
${\textit {epn}}(v,S)$
, is the set of all vertices in
![]() $V(G)\setminus S$
that are adjacent to v but to no other vertex of S. In other words, if
$V(G)\setminus S$
that are adjacent to v but to no other vertex of S. In other words, if
![]() $u\in {\textit {epn}}(v,S)$
, then
$u\in {\textit {epn}}(v,S)$
, then
![]() $u\in V(G)\setminus S$
and
$u\in V(G)\setminus S$
and
![]() $N_{G}(u)\cap S=\{v\}$
. The S-internal private
$N_{G}(u)\cap S=\{v\}$
. The S-internal private
![]() $2$
-neighbourhood of v, denoted by
$2$
-neighbourhood of v, denoted by
![]() ${\textit {ipn}}_2(v,S)$
, is the set of all vertices in
${\textit {ipn}}_2(v,S)$
, is the set of all vertices in
![]() $S\setminus \{v\}$
that are within distance 2 of v in G but at a distance greater than
$S\setminus \{v\}$
that are within distance 2 of v in G but at a distance greater than
![]() $2$
from every other vertex of S. In other words, if
$2$
from every other vertex of S. In other words, if
![]() $u\in {\textit {ipn}}_2(v,S)$
, then
$u\in {\textit {ipn}}_2(v,S)$
, then
![]() $u\in S\setminus \{v\}$
,
$u\in S\setminus \{v\}$
,
![]() $d(v,u)\leqslant 2$
and
$d(v,u)\leqslant 2$
and
![]() $d(u,w)>2$
for any vertex
$d(u,w)>2$
for any vertex
![]() $w\in S\setminus \{u,v\}$
.
$w\in S\setminus \{u,v\}$
.
A semi-TD-set in a graph G is a minimal semi-TD-set if it contains no semi-TD-set of G as a proper subset. The following result in [Reference Henning and Marcon8] provides a characterisation of minimal semi-TD-sets.
Lemma 2.1 [Reference Henning and Marcon8]
Let S be a semi-TD-set in a graph G. Then, S is a minimal semi-TD-set of G if and only if every vertex
![]() $v\in S$
satisfies at least one of the following three properties:
$v\in S$
satisfies at least one of the following three properties:
-
(a) the vertex v is isolated in
 $G[S]$
;
$G[S]$
; -
(b)
 ${\textit {ipn}}_2(v,S)\neq \emptyset $
;
${\textit {ipn}}_2(v,S)\neq \emptyset $
; -
(c)
 ${\textit {epn}}(v,S)\neq \emptyset $
.
${\textit {epn}}(v,S)\neq \emptyset $
.
3. Main result
In this section, we establish the tight upper bound on the semitotal domination number of a connected claw-free graph with minimum degree at least 3 using edge weighting functions. Before that, we define two graphs
![]() $N_2$
and
$N_2$
and
![]() $N^{\prime }_2$
as in Figure 1. Note that
$N^{\prime }_2$
as in Figure 1. Note that
![]() $N^{\prime }_2$
is a graph attaining the bound of Theorem 3.1. This shows that Conjecture 1.2 is not true.
$N^{\prime }_2$
is a graph attaining the bound of Theorem 3.1. This shows that Conjecture 1.2 is not true.
Theorem 3.1. If
![]() $G\neq N_2$
is a connected claw-free graph of order
$G\neq N_2$
is a connected claw-free graph of order
![]() $n\geq 6$
with minimum degree
$n\geq 6$
with minimum degree
![]() $\delta (G)\geq 3$
, then
$\delta (G)\geq 3$
, then
![]() $\gamma _{t2}(G)\leq \frac{4}{11}n$
, and this bound is sharp.
$\gamma _{t2}(G)\leq \frac{4}{11}n$
, and this bound is sharp.
Proof. Suppose that the theorem is false. Let G be a counterexample such that
![]() $|V(G)|$
is as small as possible. By the choice of G,
$|V(G)|$
is as small as possible. By the choice of G,
![]() $G\neq N_2$
is a connected claw-free graph of order
$G\neq N_2$
is a connected claw-free graph of order
![]() $n\geq 6$
with
$n\geq 6$
with
![]() $\delta (G)\geq 3$
such that
$\delta (G)\geq 3$
such that
![]() $\gamma _{t2}(G)> \frac{4}{11}n$
, and any connected claw-free graph
$\gamma _{t2}(G)> \frac{4}{11}n$
, and any connected claw-free graph
![]() $G'\neq N_2$
of order
$G'\neq N_2$
of order
![]() $n'<n$
with
$n'<n$
with
![]() $\delta (G')\geq 3$
has
$\delta (G')\geq 3$
has
![]() $\gamma _{t2}(G')\leq \frac{4}{11}n'$
, where
$\gamma _{t2}(G')\leq \frac{4}{11}n'$
, where
![]() $n'\geq 6$
.
$n'\geq 6$
.
For a
![]() $\gamma _{t2}(G)$
-set S, set
$\gamma _{t2}(G)$
-set S, set
![]() $\overline {S}=V(G)\setminus S$
. Define sets
$\overline {S}=V(G)\setminus S$
. Define sets
![]() $A^{S}=\{v\in S\mid {\textit {ipn}}_2(v,S)\neq \emptyset \}$
,
$A^{S}=\{v\in S\mid {\textit {ipn}}_2(v,S)\neq \emptyset \}$
,
![]() $A^S_1=\{v\in A^S \mid v\in {\textit {ipn}}_2(v',S)$
for some vertex
$A^S_1=\{v\in A^S \mid v\in {\textit {ipn}}_2(v',S)$
for some vertex
![]() $v'\in S\}$
and
$v'\in S\}$
and
![]() $A^S_2=A^S\setminus A^S_1$
. Let
$A^S_2=A^S\setminus A^S_1$
. Let
![]() $v\in A^S_1$
and
$v\in A^S_1$
and
![]() $v\in {\textit {ipn}}_2(v',S)$
. Then
$v\in {\textit {ipn}}_2(v',S)$
. Then
![]() $v'$
is the only vertex of S within distance
$v'$
is the only vertex of S within distance
![]() $2$
from v in G. Since
$2$
from v in G. Since
![]() ${\textit {ipn}}_2(v,S)\neq \emptyset $
,
${\textit {ipn}}_2(v,S)\neq \emptyset $
,
![]() $v'\in {\textit {ipn}}_2(v,S)$
and
$v'\in {\textit {ipn}}_2(v,S)$
and
![]() $v'\in A^S_1$
. Further,
$v'\in A^S_1$
. Further,
![]() ${\textit {ipn}}_2(v,S)=\{v'\}$
and
${\textit {ipn}}_2(v,S)=\{v'\}$
and
![]() ${\textit {ipn}}_2(v',S)=\{v\}$
. This implies that the vertices in
${\textit {ipn}}_2(v',S)=\{v\}$
. This implies that the vertices in
![]() $A^S_1$
are paired off. For each vertex
$A^S_1$
are paired off. For each vertex
![]() $u\in A^S_2$
, let
$u\in A^S_2$
, let
![]() $S_u={\textit {ipn}}_2(u,S)\cup \{u\}$
. If
$S_u={\textit {ipn}}_2(u,S)\cup \{u\}$
. If
![]() $u'\in {\textit {ipn}}_2(u,S)$
, then
$u'\in {\textit {ipn}}_2(u,S)$
, then
![]() $u'\notin A^S$
. Otherwise,
$u'\notin A^S$
. Otherwise,
![]() $u'\in A^S$
and
$u'\in A^S$
and
![]() $u\in {\textit {ipn}}_2(u',S)$
, for u is the only vertex of S within distance 2 from
$u\in {\textit {ipn}}_2(u',S)$
, for u is the only vertex of S within distance 2 from
![]() $u'$
in G, which contradicts the fact that
$u'$
in G, which contradicts the fact that
![]() $u\in A^S_2$
. We note that if
$u\in A^S_2$
. We note that if
![]() $u_1$
and
$u_1$
and
![]() $u_2$
are two distinct vertices in
$u_2$
are two distinct vertices in
![]() $A^S_2$
, then
$A^S_2$
, then
![]() ${\textit {ipn}}_2(u_1,S)\cap {\textit {ipn}}_2(u_2,S)=\emptyset $
. Hence,
${\textit {ipn}}_2(u_1,S)\cap {\textit {ipn}}_2(u_2,S)=\emptyset $
. Hence,
![]() $S_{u_1}\cap S_{u_2}=\emptyset $
for each pair of different vertices
$S_{u_1}\cap S_{u_2}=\emptyset $
for each pair of different vertices
![]() $u_1,u_2\in A^S_2$
. Let
$u_1,u_2\in A^S_2$
. Let
![]() $B^S=\bigcup _{u\in A^S_2}S_u$
and
$B^S=\bigcup _{u\in A^S_2}S_u$
and
![]() $C^S=S\setminus (A^S_1\cup B^S)$
. Further, we partition
$C^S=S\setminus (A^S_1\cup B^S)$
. Further, we partition
![]() $C^S$
into three subsets:
$C^S$
into three subsets:
![]() $C^S_0=\{z\mid z\in ~C^S$
and
$C^S_0=\{z\mid z\in ~C^S$
and
![]() $|{\textit {epn}}(z,S)|=0\}$
,
$|{\textit {epn}}(z,S)|=0\}$
,
![]() $C^S_1=\{z\mid z\in C^S$
and
$C^S_1=\{z\mid z\in C^S$
and
![]() $|{\textit {epn}}(z,S)|=1\}$
, and
$|{\textit {epn}}(z,S)|=1\}$
, and
![]() $C^S_2=\{z\mid z\in C^S$
and
$C^S_2=\{z\mid z\in C^S$
and
![]() $|{\textit {epn}}(z,S)|\geq 2\}$
. Then
$|{\textit {epn}}(z,S)|\geq 2\}$
. Then
![]() $S=A^S_1\cup B^S\cup C^S_0\cup C^S_1\cup C^S_2$
.
$S=A^S_1\cup B^S\cup C^S_0\cup C^S_1\cup C^S_2$
.
In particular, a vertex u of
![]() $A^S_2$
is special if
$A^S_2$
is special if
![]() $|S_u|=2$
,
$|S_u|=2$
,
![]() $d(u')=3$
and
$d(u')=3$
and
![]() $|N_{\overline {S}}(u)\setminus N_{\overline {S}}(u')|=1$
, where
$|N_{\overline {S}}(u)\setminus N_{\overline {S}}(u')|=1$
, where
![]() $\{u'\}=S_v\setminus \{u\}$
. Further, we define sets
$\{u'\}=S_v\setminus \{u\}$
. Further, we define sets
![]() $A^S_{\widetilde {2}}=\{u\mid u\in A^S_2$
and u is special
$A^S_{\widetilde {2}}=\{u\mid u\in A^S_2$
and u is special
![]() $\}$
and
$\}$
and
![]() $C^S_{\widetilde {i}}=\{z\mid z\in C^S_i$
and
$C^S_{\widetilde {i}}=\{z\mid z\in C^S_i$
and
![]() $d(z)=3\}$
for
$d(z)=3\}$
for
![]() $i\in \{0,1\}$
.
$i\in \{0,1\}$
.
A diamond in G is an induced graph of G isomorphic to
![]() $K_4-e$
. We call a diamond of G a special diamond if each of its vertices has degree 3 in G. Let
$K_4-e$
. We call a diamond of G a special diamond if each of its vertices has degree 3 in G. Let
![]() $\mathcal {D}$
be the set of vertices in a special diamond. Among all
$\mathcal {D}$
be the set of vertices in a special diamond. Among all
![]() $\gamma _{t2}(G)$
-set, we choose a
$\gamma _{t2}(G)$
-set, we choose a
![]() $\gamma _{t2}(G)$
-set S satisfying the following conditions:
$\gamma _{t2}(G)$
-set S satisfying the following conditions:
-
(1) the number of edges in
 $G[S]$
, denoted by
$G[S]$
, denoted by
 $\lambda (S)$
, is minimised;
$\lambda (S)$
, is minimised; -
(2) subject to condition (1),
 $|\mathcal {D}\cap S|$
is minimised;
$|\mathcal {D}\cap S|$
is minimised; -
(3) subject to condition (2),
 $|C^S_{\widetilde {0}}|$
is minimised;
$|C^S_{\widetilde {0}}|$
is minimised; -
(4) subject to condition (3),
 $|C^S_0|$
is minimised;
$|C^S_0|$
is minimised; -
(5) subject to condition (4),
 $|C^S_{\widetilde {1}}|$
is minimised.
$|C^S_{\widetilde {1}}|$
is minimised.
We prove the following claim about the set S.
Claim 1. S is an independent set of G.
Suppose to the contrary that there exist two adjacent vertices
![]() $v_1$
and
$v_1$
and
![]() $v_2$
in S. If
$v_2$
in S. If
![]() ${\textit {epn}}(v_1,S)\neq \emptyset $
or
${\textit {epn}}(v_1,S)\neq \emptyset $
or
![]() ${\textit {epn}}(v_2,S)\neq \emptyset $
, then without loss of generality, consider
${\textit {epn}}(v_2,S)\neq \emptyset $
, then without loss of generality, consider
![]() ${\textit {epn}}(v_1,S)\neq \emptyset $
. Let
${\textit {epn}}(v_1,S)\neq \emptyset $
. Let
![]() $x_1$
be a vertex in
$x_1$
be a vertex in
![]() ${\textit {epn}}(v_1,S)$
. Since G is claw-free, each vertex of
${\textit {epn}}(v_1,S)$
. Since G is claw-free, each vertex of
![]() $N(v_1)\setminus \{x_1,v_2\}$
is adjacent to either
$N(v_1)\setminus \{x_1,v_2\}$
is adjacent to either
![]() $x_1$
or
$x_1$
or
![]() $v_2$
. Thus,
$v_2$
. Thus,
![]() $S_1=(S\setminus \{v_1\})\cup \{x_1\}$
is a
$S_1=(S\setminus \{v_1\})\cup \{x_1\}$
is a
![]() $\gamma _{t2}(G)$
-set. However,
$\gamma _{t2}(G)$
-set. However,
![]() $\lambda (S_1)<\lambda (S)$
, for
$\lambda (S_1)<\lambda (S)$
, for
![]() $x_1$
is adjacent to no vertex of
$x_1$
is adjacent to no vertex of
![]() $S\setminus \{v_1\}$
, which contradicts the choice of S. Hence,
$S\setminus \{v_1\}$
, which contradicts the choice of S. Hence,
![]() ${\textit {epn}}(v_1,S)=\emptyset $
and
${\textit {epn}}(v_1,S)=\emptyset $
and
![]() ${\textit {epn}}(v_2,S)=\emptyset $
. By Lemma 2.1,
${\textit {epn}}(v_2,S)=\emptyset $
. By Lemma 2.1,
![]() ${\textit {ipn}}_2(v_1,S)\neq \emptyset $
and
${\textit {ipn}}_2(v_1,S)\neq \emptyset $
and
![]() ${\textit {ipn}}_2(v_2,S)\neq \emptyset $
.
${\textit {ipn}}_2(v_2,S)\neq \emptyset $
.
If
![]() ${\textit {ipn}}_2(v_1,S)\neq \{v_2\}$
, then there exists a vertex
${\textit {ipn}}_2(v_1,S)\neq \{v_2\}$
, then there exists a vertex
![]() $v_3\in {\textit {ipn}}_2(v_1,S)\setminus \{v_2\}$
. Combined with
$v_3\in {\textit {ipn}}_2(v_1,S)\setminus \{v_2\}$
. Combined with
![]() $v_1v_2\in E(G)$
,
$v_1v_2\in E(G)$
,
![]() $d(v_1,v_3)=2$
. As
$d(v_1,v_3)=2$
. As
![]() $v_3\in {\textit {ipn}}_2(v_1,S)$
, any vertex of
$v_3\in {\textit {ipn}}_2(v_1,S)$
, any vertex of
![]() $N(v_3)$
belongs to
$N(v_3)$
belongs to
![]() $\overline {S}$
and is adjacent to no vertex of
$\overline {S}$
and is adjacent to no vertex of
![]() $S\setminus \{v_1,v_3\}$
. Let
$S\setminus \{v_1,v_3\}$
. Let
![]() $x_2$
be a vertex connecting
$x_2$
be a vertex connecting
![]() $v_1$
and
$v_1$
and
![]() $v_3$
. Then
$v_3$
. Then
![]() $x_2v_2\notin E(G)$
. Since G is claw-free, each vertex of
$x_2v_2\notin E(G)$
. Since G is claw-free, each vertex of
![]() $N(v_1)\setminus \{x_2,v_2\}$
is adjacent to either
$N(v_1)\setminus \{x_2,v_2\}$
is adjacent to either
![]() $x_2$
or
$x_2$
or
![]() $v_2$
. When all vertices of
$v_2$
. When all vertices of
![]() $N(v_3)\setminus \{x_2\}$
are adjacent to
$N(v_3)\setminus \{x_2\}$
are adjacent to
![]() $x_2$
,
$x_2$
,
![]() $(S\setminus \{v_1,v_3\})\cup \{x_2\}$
is a semi-TD-set of G, which contradicts the minimality of S. However, when there exists a vertex
$(S\setminus \{v_1,v_3\})\cup \{x_2\}$
is a semi-TD-set of G, which contradicts the minimality of S. However, when there exists a vertex
![]() $x_3\in N(v_3)\setminus \{x_2\}$
such that
$x_3\in N(v_3)\setminus \{x_2\}$
such that
![]() $x_2x_3\notin E(G)$
, each vertex of
$x_2x_3\notin E(G)$
, each vertex of
![]() $N(v_3)\setminus \{x_2,x_3\}$
is adjacent to either
$N(v_3)\setminus \{x_2,x_3\}$
is adjacent to either
![]() $x_2$
or
$x_2$
or
![]() $x_3$
as G is claw-free. Then
$x_3$
as G is claw-free. Then
![]() $S_1=(S\setminus \{v_1,v_3\})\cup \{x_2,x_3\}$
is a
$S_1=(S\setminus \{v_1,v_3\})\cup \{x_2,x_3\}$
is a
![]() $\gamma _{t2}(G)$
-set. But,
$\gamma _{t2}(G)$
-set. But,
![]() $\lambda (S_1)<\lambda (S)$
, which is a contradiction.
$\lambda (S_1)<\lambda (S)$
, which is a contradiction.
Hence,
![]() ${\textit {ipn}}_2(v_1,S)= \{v_2\}$
. Similarly,
${\textit {ipn}}_2(v_1,S)= \{v_2\}$
. Similarly,
![]() ${\textit {ipn}}_2(v_2,S)= \{v_1\}$
. Further, all vertices in
${\textit {ipn}}_2(v_2,S)= \{v_1\}$
. Further, all vertices in
![]() $N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)$
are adjacent to no vertex of
$N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)$
are adjacent to no vertex of
![]() $S\setminus \{v_1,v_2\}$
. Recall that
$S\setminus \{v_1,v_2\}$
. Recall that
![]() ${\textit {epn}}(v_1,S)=\emptyset $
and
${\textit {epn}}(v_1,S)=\emptyset $
and
![]() ${\textit {epn}}(v_2,S)=\emptyset $
. Thus,
${\textit {epn}}(v_2,S)=\emptyset $
. Thus,
![]() $N_{\overline {S}}(v_1)=N_{\overline {S}}(v_2)$
. Since
$N_{\overline {S}}(v_1)=N_{\overline {S}}(v_2)$
. Since
![]() $n\geq 6$
,
$n\geq 6$
,
![]() $\gamma _{t2}(G)\geq \frac{4}{11} n>2$
. This implies that
$\gamma _{t2}(G)\geq \frac{4}{11} n>2$
. This implies that
![]() $\{v_1,v_2\}$
is not a
$\{v_1,v_2\}$
is not a
![]() $\gamma _{t2}(G)$
-set. As G is connected, there exists a vertex
$\gamma _{t2}(G)$
-set. As G is connected, there exists a vertex
![]() $x_4$
in
$x_4$
in
![]() $\overline {S}\setminus N_{\overline {S}}(v_1)$
such that
$\overline {S}\setminus N_{\overline {S}}(v_1)$
such that
![]() $x_4$
is adjacent to a vertex
$x_4$
is adjacent to a vertex
![]() $x_5$
in
$x_5$
in
![]() $N_{\overline {S}}(v_1)$
. We note that
$N_{\overline {S}}(v_1)$
. We note that
![]() $x_4$
has a neighbour in
$x_4$
has a neighbour in
![]() $S\setminus \{v_1,v_2\}$
. When all vertices of
$S\setminus \{v_1,v_2\}$
. When all vertices of
![]() $N_{\overline {S}}(v_1)$
are adjacent to
$N_{\overline {S}}(v_1)$
are adjacent to
![]() $x_5$
,
$x_5$
,
![]() $S_1=(S\setminus \{v_1,v_2\})\cup \{x_5\}$
is a semi-TD-set of G with
$S_1=(S\setminus \{v_1,v_2\})\cup \{x_5\}$
is a semi-TD-set of G with
![]() $|S_1|< |S|$
, which is a contradiction. When there exists a vertex
$|S_1|< |S|$
, which is a contradiction. When there exists a vertex
![]() $x_6\in N_{\overline {S}}(v_1)$
such that
$x_6\in N_{\overline {S}}(v_1)$
such that
![]() $x_5x_6\notin E(G)$
, each vertex of
$x_5x_6\notin E(G)$
, each vertex of
![]() $N_{\overline {S}}(v_1)\setminus \{x_5,x_6\}$
is adjacent to either
$N_{\overline {S}}(v_1)\setminus \{x_5,x_6\}$
is adjacent to either
![]() $x_5$
or
$x_5$
or
![]() $x_6$
as G is claw-free. Then
$x_6$
as G is claw-free. Then
![]() $S_1=(S\setminus \{v_1,v_2\})\cup \{x_5,x_6\}$
is a
$S_1=(S\setminus \{v_1,v_2\})\cup \{x_5,x_6\}$
is a
![]() $\gamma _{t2}(G)$
-set with
$\gamma _{t2}(G)$
-set with
![]() $\lambda (S_1)<\lambda (S)$
, which is a contradiction. This completes the proof of Claim 1.
$\lambda (S_1)<\lambda (S)$
, which is a contradiction. This completes the proof of Claim 1.
Combining Claim 1 and the claw-freeness of G, we see that x has at most two neighbours in S for any vertex x of
![]() $\overline {S}$
. We define an edge weighting function w on G:
$\overline {S}$
. We define an edge weighting function w on G:
![]() $[\overline {S},S]\rightarrow [0,1]$
. For each vertex
$[\overline {S},S]\rightarrow [0,1]$
. For each vertex
![]() $x\in \overline {S}$
, the function w assigns weight for each edge
$x\in \overline {S}$
, the function w assigns weight for each edge
![]() $e\in [\{x\},S]$
as follows.
$e\in [\{x\},S]$
as follows.
-
• If x is an S-external private neighbour, then for the unique edge
 $e\in [\{x\},S]$
,
$e\in [\{x\},S]$
,
 $w(e)=1$
.
$w(e)=1$
. -
• If x is not an S-external private neighbour and
 $N_{C^S_{\widetilde {0}}}(x)=\emptyset $
, then
$N_{C^S_{\widetilde {0}}}(x)=\emptyset $
, then
 $w(e)=\tfrac 12$
for each edge
$w(e)=\tfrac 12$
for each edge
 $e\in [\{x\},S]$
.
$e\in [\{x\},S]$
. -
• Assume that x is not an S-external private neighbour and
 $N_{C^S_{\widetilde {0}}}(x)\neq \emptyset $
. Let
$N_{C^S_{\widetilde {0}}}(x)\neq \emptyset $
. Let
 $N_{\overline {S}}(x)=\{y_1,y_2\}$
, where
$N_{\overline {S}}(x)=\{y_1,y_2\}$
, where
 $y_1\in N_{C^S_{\widetilde {0}}}(x)$
. It follows from the partition of S that
$y_1\in N_{C^S_{\widetilde {0}}}(x)$
. It follows from the partition of S that
 $y_2\in A^S_2\cup C^S_0\cup C^S_1\cup C^S_2$
.
$y_2\in A^S_2\cup C^S_0\cup C^S_1\cup C^S_2$
.-
• If
 $y_2\in A^S_{\widetilde {2}}\cup C^S_{\widetilde {0}}$
, then
$y_2\in A^S_{\widetilde {2}}\cup C^S_{\widetilde {0}}$
, then
 $w(xy_1)=w(xy_2)=\tfrac 12$
.
$w(xy_1)=w(xy_2)=\tfrac 12$
. -
• If either
 $y_2\in (A^S_2\setminus A^S_{\widetilde {2}})\cup (C^S_1\setminus C^S_{\widetilde {1}})$
, or
$y_2\in (A^S_2\setminus A^S_{\widetilde {2}})\cup (C^S_1\setminus C^S_{\widetilde {1}})$
, or
 $y_2\in C^S_{\widetilde {1}}$
and
$y_2\in C^S_{\widetilde {1}}$
and
 $|\{u\mid u\in N_{\overline {S}}(y_2) \mbox { and} N_{C^S_{\widetilde {0}}}(u)\neq \emptyset \}|=1$
, then
$|\{u\mid u\in N_{\overline {S}}(y_2) \mbox { and} N_{C^S_{\widetilde {0}}}(u)\neq \emptyset \}|=1$
, then
 $w(xy_1)=\tfrac 34$
and
$w(xy_1)=\tfrac 34$
and
 $w(xy_2)=\tfrac 14$
.
$w(xy_2)=\tfrac 14$
. -
• If either
 $y_2\in C^S_0\setminus C^S_{\widetilde {0}}$
and
$y_2\in C^S_0\setminus C^S_{\widetilde {0}}$
and
 $|\{u\mid u\in N_{\overline {S}}(y_2) \mbox { and } N_{C^S_{\widetilde {0}}}(u)\neq \emptyset \}|\leq 2$
, or
$|\{u\mid u\in N_{\overline {S}}(y_2) \mbox { and } N_{C^S_{\widetilde {0}}}(u)\neq \emptyset \}|\leq 2$
, or
 $y_2\in C^S_{\widetilde {1}}$
and
$y_2\in C^S_{\widetilde {1}}$
and
 $|\{u\mid u\in N_{\overline {S}}(y_2) \mbox { and } N_{C^S_{\widetilde {0}}}(u)\neq \emptyset \}|=2$
, then
$|\{u\mid u\in N_{\overline {S}}(y_2) \mbox { and } N_{C^S_{\widetilde {0}}}(u)\neq \emptyset \}|=2$
, then
 $w(xy_1)=\tfrac 58$
and
$w(xy_1)=\tfrac 58$
and
 $w(xy_2)=\tfrac 38$
.
$w(xy_2)=\tfrac 38$
. -
• If
 $y_2\in C^S_0\setminus C^S_{\widetilde {0}}$
and
$y_2\in C^S_0\setminus C^S_{\widetilde {0}}$
and
 $|\{u\mid u\in N_{\overline {S}}(y_2) \mbox { and } N_{C^S_{\widetilde {0}}}(u)\neq \emptyset \}|\geq 3$
, then
$|\{u\mid u\in N_{\overline {S}}(y_2) \mbox { and } N_{C^S_{\widetilde {0}}}(u)\neq \emptyset \}|\geq 3$
, then
 $w(xy_1)= \frac{9}{16}$
and
$w(xy_1)= \frac{9}{16}$
and
 $w(xy_2)= \frac{7}{16}$
.
$w(xy_2)= \frac{7}{16}$
. -
• If
 $y_2\in C^S_2$
, then
$y_2\in C^S_2$
, then
 $w(xy_1)=1$
and
$w(xy_1)=1$
and
 $w(xy_2)=0$
.
$w(xy_2)=0$
.
-
From the definition of the edge weighting functions, the sum of the weights assigned to the edges joining x to S is 1. For any subset
![]() $S_1$
of S, we define a weighting function f on
$S_1$
of S, we define a weighting function f on
![]() $S_1$
with
$S_1$
with
![]() $f(S_1)=\sum _{e\in [\overline {S},S_1]}w(e)$
. We prove the following claims.
$f(S_1)=\sum _{e\in [\overline {S},S_1]}w(e)$
. We prove the following claims.
Claim 2.
![]() $f(A^S_1)> \tfrac 74|A^S_1|$
.
$f(A^S_1)> \tfrac 74|A^S_1|$
.
Recall that the vertices in
![]() $A^S_1$
are paired off. Let
$A^S_1$
are paired off. Let
![]() $v_1$
and
$v_1$
and
![]() $v_2$
be a pair of vertices in
$v_2$
be a pair of vertices in
![]() $A^S_1$
. Then
$A^S_1$
. Then
![]() ${\textit {ipn}}_2(v_1,S)=\{v_2\}$
and
${\textit {ipn}}_2(v_1,S)=\{v_2\}$
and
![]() ${\textit {ipn}}_2(v_2,S)=\{v_1\}$
. This implies that all vertices in
${\textit {ipn}}_2(v_2,S)=\{v_1\}$
. This implies that all vertices in
![]() $N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)$
are adjacent to no vertex of
$N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)$
are adjacent to no vertex of
![]() $S\setminus \{v_1,v_2\}$
. Further, we have
$S\setminus \{v_1,v_2\}$
. Further, we have
![]() $f(\{v_1,v_2\})=|N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)|$
. Combining Claim 1 and
$f(\{v_1,v_2\})=|N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)|$
. Combining Claim 1 and
![]() $\delta (G)\geq 3$
, we have
$\delta (G)\geq 3$
, we have
![]() $|N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)|\geq 3$
. If
$|N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)|\geq 3$
. If
![]() $|N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)|= 3$
, then
$|N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)|= 3$
, then
![]() $N_{\overline {S}}(v_1)=N_{\overline {S}}(v_2)$
and
$N_{\overline {S}}(v_1)=N_{\overline {S}}(v_2)$
and
![]() $|N_{\overline {S}}(v_1)|=3$
. In this case,
$|N_{\overline {S}}(v_1)|=3$
. In this case,
![]() $n=5$
as G is claw-free and G is connected, which is a contradiction. Thus,
$n=5$
as G is claw-free and G is connected, which is a contradiction. Thus,
![]() $|N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)|\geq 4$
. Hence
$|N_{\overline {S}}(v_1)\cup N_{\overline {S}}(v_2)|\geq 4$
. Hence
![]() $f(\{v_1,v_2\})\geq 4>\tfrac 72$
and then
$f(\{v_1,v_2\})\geq 4>\tfrac 72$
and then
![]() $f(A^S_1)> \tfrac 74|A^S_1|$
.
$f(A^S_1)> \tfrac 74|A^S_1|$
.
Claim 3.
![]() $f(B^S)\geq \tfrac 74|B^S|$
.
$f(B^S)\geq \tfrac 74|B^S|$
.
Note that
![]() $B^S=\bigcup _{u\in A^S_2}S_u$
and
$B^S=\bigcup _{u\in A^S_2}S_u$
and
![]() $S_u\cap S_{u'}=\emptyset $
for any two different vertices
$S_u\cap S_{u'}=\emptyset $
for any two different vertices
![]() $u,u'\in A^S_2$
. We show that for any vertex
$u,u'\in A^S_2$
. We show that for any vertex
![]() $u_1$
of
$u_1$
of
![]() $A^S_2$
,
$A^S_2$
,
![]() $f(S_{u_1})\geq \tfrac 74|S_{u_1}|$
. Let
$f(S_{u_1})\geq \tfrac 74|S_{u_1}|$
. Let
![]() $S_{u_1}=\{u_1,\ldots ,u_{r}\}$
, where
$S_{u_1}=\{u_1,\ldots ,u_{r}\}$
, where
![]() $r=|S_{u_1}|\geq 2$
. Since
$r=|S_{u_1}|\geq 2$
. Since
![]() $\{u_2,\ldots ,\ u_{r}\}\subseteq {\textit {ipn}}_2(u_1)$
, all neighbours of
$\{u_2,\ldots ,\ u_{r}\}\subseteq {\textit {ipn}}_2(u_1)$
, all neighbours of
![]() $u_i$
in
$u_i$
in
![]() $\overline {S}$
are adjacent to no vertex of
$\overline {S}$
are adjacent to no vertex of
![]() $S\setminus \{u_1,u_i\}$
, where
$S\setminus \{u_1,u_i\}$
, where
![]() $i\in \{2,\ldots ,r\}$
. Combined with Claim 1,
$i\in \{2,\ldots ,r\}$
. Combined with Claim 1,
![]() $f(S_{u_1})\geq \sum _{i\in \{2,\ldots ,r\}}d(u_i)$
. If
$f(S_{u_1})\geq \sum _{i\in \{2,\ldots ,r\}}d(u_i)$
. If
![]() $u_1\in A^S_{\widetilde {2}}$
, then
$u_1\in A^S_{\widetilde {2}}$
, then
![]() $f(S_{u_1})=f(\{u_1,u_2\})=w(x_1u_1)+d(u_2)=w(x_1u_1)+3$
, where
$f(S_{u_1})=f(\{u_1,u_2\})=w(x_1u_1)+d(u_2)=w(x_1u_1)+3$
, where
![]() $\{x_1\}=N_{\overline {S}}(u_1)\setminus N_{\overline {S}}(u_2)$
. Since
$\{x_1\}=N_{\overline {S}}(u_1)\setminus N_{\overline {S}}(u_2)$
. Since
![]() $u_1\notin {\textit {ipn}}_2(u_2,S)$
,
$u_1\notin {\textit {ipn}}_2(u_2,S)$
,
![]() $x_1$
has a neighbour in S other than
$x_1$
has a neighbour in S other than
![]() $u_1$
. Thus,
$u_1$
. Thus,
![]() $w(x_1u_1)=\tfrac 12$
. Further,
$w(x_1u_1)=\tfrac 12$
. Further,
![]() $f(\{u_1,u_2\})=\tfrac 72$
and
$f(\{u_1,u_2\})=\tfrac 72$
and
![]() $f(S_{u_1})=\tfrac 74|S_{u_1}|$
, as desired. Thus, we may assume that
$f(S_{u_1})=\tfrac 74|S_{u_1}|$
, as desired. Thus, we may assume that
![]() $u_1\in A^S_2\setminus A^S_{\widetilde {2}}$
. Then either
$u_1\in A^S_2\setminus A^S_{\widetilde {2}}$
. Then either
![]() $r\geq 3$
, or
$r\geq 3$
, or
![]() $r=2$
and
$r=2$
and
![]() $d(u_2)\geq 4$
, or
$d(u_2)\geq 4$
, or
![]() $r=2$
and
$r=2$
and
![]() $d(u_2)=3$
and
$d(u_2)=3$
and
![]() $|N_{\overline {S}}(u_1)\setminus N_{\overline {S}}(u_2)|\geq 2$
.
$|N_{\overline {S}}(u_1)\setminus N_{\overline {S}}(u_2)|\geq 2$
.
If
![]() $r\geq 3$
, then
$r\geq 3$
, then
![]() ${3r-3}>\tfrac {7}{4}r$
. Since
${3r-3}>\tfrac {7}{4}r$
. Since
![]() $\delta (G)\geq 3$
,
$\delta (G)\geq 3$
,
![]() $f(S_{u_1})\geq \sum _{i\in \{2,\ldots ,r\}}d(u_i)\geq 3(r-1)=3r-3$
. Further,
$f(S_{u_1})\geq \sum _{i\in \{2,\ldots ,r\}}d(u_i)\geq 3(r-1)=3r-3$
. Further,
![]() $f(S_{u_1})>\tfrac 74r$
. When
$f(S_{u_1})>\tfrac 74r$
. When
![]() $r=2$
and
$r=2$
and
![]() $d(u_2)\geq 4$
,
$d(u_2)\geq 4$
,
![]() $f(S_{u_1})=f(\{u_1,u_2\})\geq d(u_2)\geq 4>\tfrac 74r$
. When
$f(S_{u_1})=f(\{u_1,u_2\})\geq d(u_2)\geq 4>\tfrac 74r$
. When
![]() $r=2$
,
$r=2$
,
![]() $d(u_2)=3$
and
$d(u_2)=3$
and
![]() $|N_{\overline {S}}(u_1)\setminus N_{\overline {S}}(u_2)|\geq 2$
, let
$|N_{\overline {S}}(u_1)\setminus N_{\overline {S}}(u_2)|\geq 2$
, let
![]() $x_1$
be a vertex in
$x_1$
be a vertex in
![]() $N_{\overline {S}}(u_1)\setminus N_{\overline {S}}(u_2)$
. From the definition of the edge weighting functions, we have
$N_{\overline {S}}(u_1)\setminus N_{\overline {S}}(u_2)$
. From the definition of the edge weighting functions, we have
![]() $w(x_1u_1)\geq \tfrac 14$
. Thus,
$w(x_1u_1)\geq \tfrac 14$
. Thus,
![]() $f(S_{u_1})=f(\{u_1,u_2\})\geq 2w(x_1u_1)+d(u_2)\geq \tfrac 12+3=\tfrac 72\geq \tfrac 74r$
. This completes the proof of Claim 3.
$f(S_{u_1})=f(\{u_1,u_2\})\geq 2w(x_1u_1)+d(u_2)\geq \tfrac 12+3=\tfrac 72\geq \tfrac 74r$
. This completes the proof of Claim 3.
Claim 4.
![]() $f(C^S_0\setminus C^S_{\widetilde {0}})\geq \tfrac 74|C^S_0\setminus C^S_{\widetilde {0}}|$
.
$f(C^S_0\setminus C^S_{\widetilde {0}})\geq \tfrac 74|C^S_0\setminus C^S_{\widetilde {0}}|$
.
Let
![]() $z_1$
be a vertex in
$z_1$
be a vertex in
![]() $C^S_0\setminus C^S_{\widetilde {0}}$
and let
$C^S_0\setminus C^S_{\widetilde {0}}$
and let
![]() $N_{\overline {S}}(z_1)=\{x_1,\ldots ,x_r\}$
, where
$N_{\overline {S}}(z_1)=\{x_1,\ldots ,x_r\}$
, where
![]() $r\geq 4$
. If we have
$r\geq 4$
. If we have
![]() $|\{x\mid x\in N_{\overline {S}}(z_1) \mbox { and } N_{C^S_{\widetilde {0}}}(x)\neq \emptyset \}|\leq 2$
, then
$|\{x\mid x\in N_{\overline {S}}(z_1) \mbox { and } N_{C^S_{\widetilde {0}}}(x)\neq \emptyset \}|\leq 2$
, then
![]() $|\{x\mid x\in N_{\overline {S}}(z_1) \mbox { and } N_{C^S_{\widetilde {0}}}(x)=\emptyset \}|\geq r-2\geq 2$
. Without loss of generality, consider
$|\{x\mid x\in N_{\overline {S}}(z_1) \mbox { and } N_{C^S_{\widetilde {0}}}(x)=\emptyset \}|\geq r-2\geq 2$
. Without loss of generality, consider
![]() $N_{C^S_{\widetilde {0}}}(x_1)=\emptyset $
and
$N_{C^S_{\widetilde {0}}}(x_1)=\emptyset $
and
![]() $N_{C^S_{\widetilde {0}}}(x_2)=\emptyset $
. By the definition of the edge weighting functions,
$N_{C^S_{\widetilde {0}}}(x_2)=\emptyset $
. By the definition of the edge weighting functions,
![]() $w(x_1z_1)= \tfrac 12$
,
$w(x_1z_1)= \tfrac 12$
,
![]() $w(x_2z_1)=\tfrac 12$
and
$w(x_2z_1)=\tfrac 12$
and
![]() $w(x_iz_1) \geq \tfrac 38$
for any
$w(x_iz_1) \geq \tfrac 38$
for any
![]() $i\in \{3,\ldots ,r\}$
. Hence,
$i\in \{3,\ldots ,r\}$
. Hence,
![]() $f(\{z_1\})\geq w(x_1z_1)+w(x_2z_1)+\sum _{i\in \{3,\ldots ,r\}}w(x_iz_1)\geq 1+\tfrac 38(r-2)\geq \tfrac 74$
. When
$f(\{z_1\})\geq w(x_1z_1)+w(x_2z_1)+\sum _{i\in \{3,\ldots ,r\}}w(x_iz_1)\geq 1+\tfrac 38(r-2)\geq \tfrac 74$
. When
![]() $|\{x\mid x\in N_{\overline {S}}(z_1) \mbox { and } N_{C^S_{\widetilde {0}}}(x)\neq \emptyset \}|\geq 3$
,
$|\{x\mid x\in N_{\overline {S}}(z_1) \mbox { and } N_{C^S_{\widetilde {0}}}(x)\neq \emptyset \}|\geq 3$
,
![]() $w(x_iz_1)\geq \frac{7}{16}$
for any
$w(x_iz_1)\geq \frac{7}{16}$
for any
![]() $i\in \{1,\ldots ,r\}$
. Then
$i\in \{1,\ldots ,r\}$
. Then
![]() $f(\{z_1\})\geq \frac{7}{16} r\geq \tfrac 74$
. In all cases, we have
$f(\{z_1\})\geq \frac{7}{16} r\geq \tfrac 74$
. In all cases, we have
![]() $f(\{z_1\})\geq \tfrac 74$
. Therefore,
$f(\{z_1\})\geq \tfrac 74$
. Therefore,
![]() $f(C^S_0\setminus C^S_{\widetilde {0}})\geq \tfrac 74|C^S_0\setminus C^S_{\widetilde {0}}|$
.
$f(C^S_0\setminus C^S_{\widetilde {0}})\geq \tfrac 74|C^S_0\setminus C^S_{\widetilde {0}}|$
.
Claim 5.
![]() $f(C^S_1)\geq \tfrac 74|C^S_1|$
.
$f(C^S_1)\geq \tfrac 74|C^S_1|$
.
Let
![]() $z_1$
be a vertex in
$z_1$
be a vertex in
![]() $C^S_1$
and
$C^S_1$
and
![]() $N_{\overline {S}}(z_1)=\{x_1,x_2,\ldots ,x_r\}$
, where
$N_{\overline {S}}(z_1)=\{x_1,x_2,\ldots ,x_r\}$
, where
![]() $\{x_1\}={\textit {epn}}(z_1,S)$
and
$\{x_1\}={\textit {epn}}(z_1,S)$
and
![]() $r\geq 3$
. According to the definition of the edge weighting functions,
$r\geq 3$
. According to the definition of the edge weighting functions,
![]() $w(x_1z_1)=1$
. When
$w(x_1z_1)=1$
. When
![]() $z_1\in C^S_1\setminus C^S_{\widetilde {1}}$
, we have
$z_1\in C^S_1\setminus C^S_{\widetilde {1}}$
, we have
![]() $r\geq 4$
and
$r\geq 4$
and
![]() $w(x_iz_1)\geq \tfrac 14$
for any
$w(x_iz_1)\geq \tfrac 14$
for any
![]() $i\in \{2,\ldots ,r\}$
. Thus,
$i\in \{2,\ldots ,r\}$
. Thus,
![]() $f(\{z_1\})=w(x_1z_1)+\sum _{i\in \{2,\ldots ,r\}}w(x_iz_1)\geq 1+\tfrac 14(r-1)\geq \tfrac 74$
. When
$f(\{z_1\})=w(x_1z_1)+\sum _{i\in \{2,\ldots ,r\}}w(x_iz_1)\geq 1+\tfrac 14(r-1)\geq \tfrac 74$
. When
![]() $z_1\in C^S_{\widetilde {1}}$
and either
$z_1\in C^S_{\widetilde {1}}$
and either
![]() $N_{C^S_{\widetilde {0}}}(x_2)=\emptyset $
or
$N_{C^S_{\widetilde {0}}}(x_2)=\emptyset $
or
![]() $N_{C^S_{\widetilde {0}}}(x_3)=\emptyset $
, without loss of generality, we can take
$N_{C^S_{\widetilde {0}}}(x_3)=\emptyset $
, without loss of generality, we can take
![]() $N_{C^S_{\widetilde {0}}}(x_2)=\emptyset $
. Then
$N_{C^S_{\widetilde {0}}}(x_2)=\emptyset $
. Then
![]() $w(x_2z_1)=\tfrac 12$
and
$w(x_2z_1)=\tfrac 12$
and
![]() $w(x_3z_1)\geq \tfrac 14$
. Further,
$w(x_3z_1)\geq \tfrac 14$
. Further,
![]() $f(z_1)=w(x_1z_1)+w(x_2z_1)+w(x_3z_1)\geq 1+\tfrac 12+\tfrac 14=\tfrac 74$
. When both
$f(z_1)=w(x_1z_1)+w(x_2z_1)+w(x_3z_1)\geq 1+\tfrac 12+\tfrac 14=\tfrac 74$
. When both
![]() $z_1\in C^S_{\widetilde {1}}$
and
$z_1\in C^S_{\widetilde {1}}$
and
![]() $N_{C^S_{\widetilde {0}}}(x_2)\neq \emptyset $
and
$N_{C^S_{\widetilde {0}}}(x_2)\neq \emptyset $
and
![]() $N_{C^S_{\widetilde {0}}}(x_3)\neq \emptyset $
, we have
$N_{C^S_{\widetilde {0}}}(x_3)\neq \emptyset $
, we have
![]() $w(x_2z_1)=w(x_3z_1)=\tfrac 38$
. Further,
$w(x_2z_1)=w(x_3z_1)=\tfrac 38$
. Further,
![]() $f(\{z_1\})=w(x_1z_1)+w(x_2z_1)+w(x_3z_1)=\tfrac 74$
. In both cases,
$f(\{z_1\})=w(x_1z_1)+w(x_2z_1)+w(x_3z_1)=\tfrac 74$
. In both cases,
![]() $f(\{z_1\})\geq \tfrac 74$
. Therefore,
$f(\{z_1\})\geq \tfrac 74$
. Therefore,
![]() $f(C^S_1)\geq \tfrac 74|C^S_1|$
.
$f(C^S_1)\geq \tfrac 74|C^S_1|$
.
Claim 6.
![]() $f(C^S_2)> \tfrac 74|C^S_2|$
.
$f(C^S_2)> \tfrac 74|C^S_2|$
.
Let
![]() $z_1$
be a vertex in
$z_1$
be a vertex in
![]() $C^S_2$
and
$C^S_2$
and
![]() $x_1,x_2$
be two vertices in
$x_1,x_2$
be two vertices in
![]() ${\textit {epn}}(z_1,S)$
. Then
${\textit {epn}}(z_1,S)$
. Then
![]() $w(x_1z_1)=w(x_2z_1)=1$
and further
$w(x_1z_1)=w(x_2z_1)=1$
and further
![]() $f(\{z_1\})\geq 2$
. Hence,
$f(\{z_1\})\geq 2$
. Hence,
![]() $f(C^S_2)\geq 2|C^S_2|> \tfrac 74|C^S_2|$
.
$f(C^S_2)\geq 2|C^S_2|> \tfrac 74|C^S_2|$
.
If
![]() $f(C^S_{\widetilde {0}})\geq \tfrac 74|C^S_{\widetilde {0}}|$
, then
$f(C^S_{\widetilde {0}})\geq \tfrac 74|C^S_{\widetilde {0}}|$
, then
![]() $f(S)\geq \tfrac 74|S|$
by Claims 2–6. From the definition of the edge weighting functions,
$f(S)\geq \tfrac 74|S|$
by Claims 2–6. From the definition of the edge weighting functions,
![]() $f(S)=n-|S|$
. It follows that
$f(S)=n-|S|$
. It follows that
![]() $|S|\leq \frac{4}{11}n$
, which is a contradiction. Thus,
$|S|\leq \frac{4}{11}n$
, which is a contradiction. Thus,
![]() $f(C^S_{\widetilde {0}})< \tfrac 74|C^S_{\widetilde {0}}|$
and there exists a vertex
$f(C^S_{\widetilde {0}})< \tfrac 74|C^S_{\widetilde {0}}|$
and there exists a vertex
![]() $y_1\in C^S_{\widetilde {0}}$
such that
$y_1\in C^S_{\widetilde {0}}$
such that
![]() $f(\{y_1\})< \tfrac 74$
. Suppose that
$f(\{y_1\})< \tfrac 74$
. Suppose that
![]() $N_{\overline {S}}(y_1)=\{x_1,x_2,x_3\}$
and
$N_{\overline {S}}(y_1)=\{x_1,x_2,x_3\}$
and
![]() $N_S(x_i)=\{y_1,y_{i+1}\}$
for any
$N_S(x_i)=\{y_1,y_{i+1}\}$
for any
![]() $i\in \{1,2,3\}$
. If
$i\in \{1,2,3\}$
. If
![]() $\{y_2,y_3,y_4\}\cap ((A^S_2\setminus A^S_{\widetilde {2}})\cup (C^S_1\setminus C^S_{\widetilde {1}})\cup C^S_2)\neq \emptyset $
, then at least one edge of
$\{y_2,y_3,y_4\}\cap ((A^S_2\setminus A^S_{\widetilde {2}})\cup (C^S_1\setminus C^S_{\widetilde {1}})\cup C^S_2)\neq \emptyset $
, then at least one edge of
![]() $\{x_1y_1,x_2y_1,x_3y_1\}$
has a weight of at least
$\{x_1y_1,x_2y_1,x_3y_1\}$
has a weight of at least
![]() $\tfrac 34$
. Further,
$\tfrac 34$
. Further,
![]() $f(\{y_1\})=w(x_1y_1)+w(x_2y_1)+w(x_3y_1)\geq \tfrac 34+\tfrac 12+\tfrac 12\geq \tfrac 74$
, which is a contradiction. Thus,
$f(\{y_1\})=w(x_1y_1)+w(x_2y_1)+w(x_3y_1)\geq \tfrac 34+\tfrac 12+\tfrac 12\geq \tfrac 74$
, which is a contradiction. Thus,
![]() $\{y_2,y_3,y_4\}\cap ((A^S_2\setminus A^S_{\widetilde {2}})\cup (C^S_1\setminus C^S_{\widetilde {1}})\cup C^S_2)=\emptyset $
. Next, we prove two claims about the set
$\{y_2,y_3,y_4\}\cap ((A^S_2\setminus A^S_{\widetilde {2}})\cup (C^S_1\setminus C^S_{\widetilde {1}})\cup C^S_2)=\emptyset $
. Next, we prove two claims about the set
![]() $\{y_2,y_3,y_4\}$
.
$\{y_2,y_3,y_4\}$
.
Claim 7.
![]() $\{y_2,y_3,y_4\}\cap A^S_{\widetilde {2}}=\emptyset $
.
$\{y_2,y_3,y_4\}\cap A^S_{\widetilde {2}}=\emptyset $
.
In contrast, we may assume that
![]() $y_2\in A^S_{\widetilde {2}}$
. Let
$y_2\in A^S_{\widetilde {2}}$
. Let
![]() $S_{y_2}=\{y_2,y_5\}$
and
$S_{y_2}=\{y_2,y_5\}$
and
![]() $N(y_5)=\{x_4,x_5,x_6\}$
, where
$N(y_5)=\{x_4,x_5,x_6\}$
, where
![]() $x_4$
is a vertex connecting
$x_4$
is a vertex connecting
![]() $y_2$
and
$y_2$
and
![]() $y_5$
. According to the definition of
$y_5$
. According to the definition of
![]() $A^S_{\widetilde {2}}$
,
$A^S_{\widetilde {2}}$
,
![]() $N(y_2)\subseteq \{x_1,x_4,x_5,x_6\}$
. Note that
$N(y_2)\subseteq \{x_1,x_4,x_5,x_6\}$
. Note that
![]() ${\textit {ipn}}_2(y_1,S)=\emptyset $
and
${\textit {ipn}}_2(y_1,S)=\emptyset $
and
![]() ${\textit {epn}}(y_1,S)=\emptyset $
. If
${\textit {epn}}(y_1,S)=\emptyset $
. If
![]() $d(x_1,y_5)\leq 2$
, then
$d(x_1,y_5)\leq 2$
, then
![]() $(S\setminus \{y_1,y_2\})\cup \{x_1\}$
is a semi-TD-set of G, which contradicts the minimality of S. Thus,
$(S\setminus \{y_1,y_2\})\cup \{x_1\}$
is a semi-TD-set of G, which contradicts the minimality of S. Thus,
![]() $d(x_1,y_5)\geq 3$
which implies that
$d(x_1,y_5)\geq 3$
which implies that
![]() $x_1x_i\notin E(G)$
for any
$x_1x_i\notin E(G)$
for any
![]() $i\in \{4,5,6\}$
. Combining
$i\in \{4,5,6\}$
. Combining
![]() $\delta (G)\geq 3$
and the claw-freeness of G, we have
$\delta (G)\geq 3$
and the claw-freeness of G, we have
![]() $x_1x_2\in E(G)$
or
$x_1x_2\in E(G)$
or
![]() $x_1x_3\in E(G)$
and
$x_1x_3\in E(G)$
and
![]() $x_4x_5\in E(G)$
or
$x_4x_5\in E(G)$
or
![]() $x_4x_6\in E(G)$
. Without loss of generality, consider
$x_4x_6\in E(G)$
. Without loss of generality, consider
![]() $x_1x_2\in E(G)$
and
$x_1x_2\in E(G)$
and
![]() $x_4x_5\in E(G)$
.
$x_4x_5\in E(G)$
.
If
![]() $x_4x_6\in E(G)$
, then
$x_4x_6\in E(G)$
, then
![]() $S_1=(S\setminus \{y_1,y_2,y_5\})\cup \{x_1,x_4\}$
is a semi-TD-set of G, which is a contradiction. Thus,
$S_1=(S\setminus \{y_1,y_2,y_5\})\cup \{x_1,x_4\}$
is a semi-TD-set of G, which is a contradiction. Thus,
![]() $x_4x_6\notin E(G)$
. Since G is claw-free,
$x_4x_6\notin E(G)$
. Since G is claw-free,
![]() $y_2x_6\notin E(G)$
. Then
$y_2x_6\notin E(G)$
. Then
![]() $y_2x_5\in E(G)$
as
$y_2x_5\in E(G)$
as
![]() $N(y_2)\subseteq \{x_1,x_4,x_5,x_6\}$
and
$N(y_2)\subseteq \{x_1,x_4,x_5,x_6\}$
and
![]() $d(y_2)\geq 3$
. Further,
$d(y_2)\geq 3$
. Further,
![]() $d(y_2)=3$
. If
$d(y_2)=3$
. If
![]() $x_5x_6\in E(G)$
, then
$x_5x_6\in E(G)$
, then
![]() $S_1=(S\setminus \{y_1,y_2,y_5\})\cup \{x_1,x_5\}$
is a semi-TD-set of G, which is a contradiction. Thus,
$S_1=(S\setminus \{y_1,y_2,y_5\})\cup \{x_1,x_5\}$
is a semi-TD-set of G, which is a contradiction. Thus,
![]() $x_5x_6\notin E(G)$
. Since G is claw-free,
$x_5x_6\notin E(G)$
. Since G is claw-free,
![]() $N(x_4)=\{y_2,y_5,x_5\}$
and
$N(x_4)=\{y_2,y_5,x_5\}$
and
![]() $N(x_5)=\{y_2,y_5,x_4\}$
. We note that
$N(x_5)=\{y_2,y_5,x_4\}$
. We note that
![]() $d(x_4)=d(x_5)=3$
and then
$d(x_4)=d(x_5)=3$
and then
![]() $G[\{y_2,y_5,x_4,x_5\}]$
is a special diamond.
$G[\{y_2,y_5,x_4,x_5\}]$
is a special diamond.
Since
![]() $y_5\in {\textit {ipn}}_2(y_2,S)$
and
$y_5\in {\textit {ipn}}_2(y_2,S)$
and
![]() $x_6y_2\notin E(G)$
,
$x_6y_2\notin E(G)$
,
![]() $x_6$
is adjacent to no vertex of
$x_6$
is adjacent to no vertex of
![]() $S\setminus \{y_5\}$
. If
$S\setminus \{y_5\}$
. If
![]() $x_6$
is not in a special diamond, then
$x_6$
is not in a special diamond, then
![]() $S_1=(S\setminus \{y_2,y_5\})\cup \{x_4,x_6\}$
is a
$S_1=(S\setminus \{y_2,y_5\})\cup \{x_4,x_6\}$
is a
![]() $\gamma _{t2}(G)$
-set with
$\gamma _{t2}(G)$
-set with
![]() $\lambda (S_1)=\lambda (S)$
but with
$\lambda (S_1)=\lambda (S)$
but with
![]() $|\mathcal {D}\cap S_1|<|\mathcal {D}\cap S|$
, which contradicts our choice of S. Thus,
$|\mathcal {D}\cap S_1|<|\mathcal {D}\cap S|$
, which contradicts our choice of S. Thus,
![]() $x_6$
is in a special diamond D. Observe that
$x_6$
is in a special diamond D. Observe that
![]() $x_6x_2\notin E(G)$
and
$x_6x_2\notin E(G)$
and
![]() $x_6x_3\notin E(G)$
. Let
$x_6x_3\notin E(G)$
. Let
![]() $V(D)=\{x_6,x_7,x_8,y_6\}$
, where
$V(D)=\{x_6,x_7,x_8,y_6\}$
, where
![]() $x_6y_6$
is the missing edge in the special diamond D. Then
$x_6y_6$
is the missing edge in the special diamond D. Then
![]() $\{x_7,x_8\}\subseteq \overline {S}$
. To dominate
$\{x_7,x_8\}\subseteq \overline {S}$
. To dominate
![]() $x_7$
and
$x_7$
and
![]() $x_8$
, we must have
$x_8$
, we must have
![]() $y_6\in S$
. If
$y_6\in S$
. If
![]() $y_6x_2\in E(G)$
, then
$y_6x_2\in E(G)$
, then
![]() $y_6\in {\textit {ipn}}_2(y_1,S)$
which contradicts
$y_6\in {\textit {ipn}}_2(y_1,S)$
which contradicts
![]() $y_1\in C^S_{\widetilde {0}}$
. Thus,
$y_1\in C^S_{\widetilde {0}}$
. Thus,
![]() $y_6x_2\notin E(G)$
. Similarly,
$y_6x_2\notin E(G)$
. Similarly,
![]() $y_6x_3\notin E(G)$
.
$y_6x_3\notin E(G)$
.
Let
![]() $N(y_6)=\{x_7,x_8,x_9\}$
. We note that
$N(y_6)=\{x_7,x_8,x_9\}$
. We note that
![]() $y_6\in {\textit {ipn}}_2(v,S)$
for some vertex
$y_6\in {\textit {ipn}}_2(v,S)$
for some vertex
![]() $v\in S$
so call
$v\in S$
so call
![]() $v = y_7$
. Then
$v = y_7$
. Then
![]() $y_7x_9\in E(G)$
. Recall that
$y_7x_9\in E(G)$
. Recall that
![]() $\{y_3,y_4\}\cap (A^S_2\setminus A^S_{\widetilde {2}})=\emptyset $
. If
$\{y_3,y_4\}\cap (A^S_2\setminus A^S_{\widetilde {2}})=\emptyset $
. If
![]() $y_7x_2\in E(G)$
or
$y_7x_2\in E(G)$
or
![]() $y_7x_3\in E(G)$
, then
$y_7x_3\in E(G)$
, then
![]() $y_7=y_3$
or
$y_7=y_3$
or
![]() $y_4$
and
$y_4$
and
![]() $y_7\in A^S_2\setminus A^S_{\widetilde {2}}$
, which is a contradiction. Thus,
$y_7\in A^S_2\setminus A^S_{\widetilde {2}}$
, which is a contradiction. Thus,
![]() $y_7x_2\notin E(G)$
and
$y_7x_2\notin E(G)$
and
![]() $y_7x_3\notin E(G)$
. If
$y_7x_3\notin E(G)$
. If
![]() $y_7\notin {\textit {ipn}}_2(y_6,S)$
, then
$y_7\notin {\textit {ipn}}_2(y_6,S)$
, then
![]() $S_1=(S\setminus \{y_1,y_2,y_6\})\cup \{x_1,x_7\}$
is a semi-TD-set of G, which is a contradiction. Hence,
$S_1=(S\setminus \{y_1,y_2,y_6\})\cup \{x_1,x_7\}$
is a semi-TD-set of G, which is a contradiction. Hence,
![]() $y_7\in {\textit {ipn}}_2(y_6,S)$
. Let
$y_7\in {\textit {ipn}}_2(y_6,S)$
. Let
![]() $S_1=(S\setminus \{y_5\})\cup \{x_6\}$
. Clearly,
$S_1=(S\setminus \{y_5\})\cup \{x_6\}$
. Clearly,
![]() $S_1$
is a
$S_1$
is a
![]() $\gamma _{t2}(G)$
-set,
$\gamma _{t2}(G)$
-set,
![]() $\lambda (S_1)=\lambda (S)$
and
$\lambda (S_1)=\lambda (S)$
and
![]() $|\mathcal {D}\cap S_1|=|\mathcal {D}\cap S|$
. We note that
$|\mathcal {D}\cap S_1|=|\mathcal {D}\cap S|$
. We note that
![]() $y_2\in {\textit {ipn}}_2(y_1,S_1)$
and
$y_2\in {\textit {ipn}}_2(y_1,S_1)$
and
![]() $\{x_6,y_7\}\subset {\textit {ipn}}_2(y_6,S_1)$
. Further,
$\{x_6,y_7\}\subset {\textit {ipn}}_2(y_6,S_1)$
. Further,
![]() $\{y_1,y_2,x_6,y_6,y_7\}\subseteq B^{S_1}$
and
$\{y_1,y_2,x_6,y_6,y_7\}\subseteq B^{S_1}$
and
![]() $|C^{S_1}_{\widetilde {0}}|<|C^S_{\widetilde {0}}|$
, which contradicts the choice of S.
$|C^{S_1}_{\widetilde {0}}|<|C^S_{\widetilde {0}}|$
, which contradicts the choice of S.
By Claim 7, each vertex of
![]() $\{y_2,y_3,y_4\}$
belongs to
$\{y_2,y_3,y_4\}$
belongs to
![]() $C^S_0\cup C^S_{\widetilde {1}}$
.
$C^S_0\cup C^S_{\widetilde {1}}$
.
Claim 8.
![]() $\{y_2,y_3,y_4\}\cap C^S_{\widetilde {1}}\neq \emptyset $
.
$\{y_2,y_3,y_4\}\cap C^S_{\widetilde {1}}\neq \emptyset $
.
Suppose to the contrary that
![]() $\{y_2,y_3,y_4\}\cap C^S_{\widetilde {1}}=\emptyset $
. Then
$\{y_2,y_3,y_4\}\cap C^S_{\widetilde {1}}=\emptyset $
. Then
![]() $\{y_2,y_3,y_4\}\subseteq C^S_0$
. Since G is claw-free, there exists an edge in
$\{y_2,y_3,y_4\}\subseteq C^S_0$
. Since G is claw-free, there exists an edge in
![]() $G[\{x_1,x_2,x_3\}]$
, say
$G[\{x_1,x_2,x_3\}]$
, say
![]() $x_1x_2$
. If
$x_1x_2$
. If
![]() $y_2\neq y_3$
, then
$y_2\neq y_3$
, then
![]() $x_3y_2\notin E(G)$
or
$x_3y_2\notin E(G)$
or
![]() $x_3y_3\notin E(G)$
, as
$x_3y_3\notin E(G)$
, as
![]() $x_3$
has only one neighbour in
$x_3$
has only one neighbour in
![]() $S\setminus \{y_1\}$
. By symmetry, consider
$S\setminus \{y_1\}$
. By symmetry, consider
![]() $y_2x_3\notin E(G)$
(that is,
$y_2x_3\notin E(G)$
(that is,
![]() $y_2\neq y_4$
). Then
$y_2\neq y_4$
). Then
![]() $S_1=(S\setminus \{y_1,y_2\})\cup \{x_1\}$
is a dominating set of G as
$S_1=(S\setminus \{y_1,y_2\})\cup \{x_1\}$
is a dominating set of G as
![]() $y_2\in C^S_0$
and
$y_2\in C^S_0$
and
![]() $y_1\in C^S_{\widetilde {0}}$
. Since
$y_1\in C^S_{\widetilde {0}}$
. Since
![]() $|S_1|<|S|$
,
$|S_1|<|S|$
,
![]() $S_1$
cannot be a semi-TD-set of G. Combined with
$S_1$
cannot be a semi-TD-set of G. Combined with
![]() $\{y_1,y_2\}\subseteq C^S_0$
,
$\{y_1,y_2\}\subseteq C^S_0$
,
![]() $y_1$
and
$y_1$
and
![]() $y_2$
are the only two vertices of S within distance 2 from
$y_2$
are the only two vertices of S within distance 2 from
![]() $y_4$
in G, and
$y_4$
in G, and
![]() $y_4\neq y_3$
. Thus, all vertices of
$y_4\neq y_3$
. Thus, all vertices of
![]() $N_{\overline {S}}(y_4)\setminus \{x_3\}$
are adjacent to
$N_{\overline {S}}(y_4)\setminus \{x_3\}$
are adjacent to
![]() $y_2$
. Further,
$y_2$
. Further,
![]() $S_1=(S\setminus \{y_1,y_3\})\cup \{x_2\}$
is a semi-TD-set of G as
$S_1=(S\setminus \{y_1,y_3\})\cup \{x_2\}$
is a semi-TD-set of G as
![]() $y_3\in C^S_0$
and
$y_3\in C^S_0$
and
![]() $y_1\in C^S_{\widetilde {0}}$
, which contradicts the minimality of S. Hence,
$y_1\in C^S_{\widetilde {0}}$
, which contradicts the minimality of S. Hence,
![]() $y_2= y_3$
.
$y_2= y_3$
.
Since
![]() $y_1\notin {\textit {ipn}}_2(y_2,S)$
,
$y_1\notin {\textit {ipn}}_2(y_2,S)$
,
![]() $y_2x_3\notin E(G)$
(that is,
$y_2x_3\notin E(G)$
(that is,
![]() $y_2\neq y_4$
). Let
$y_2\neq y_4$
). Let
![]() $S_2=(S\setminus \{y_1,y_4\})\cup \{x_3\}$
. As
$S_2=(S\setminus \{y_1,y_4\})\cup \{x_3\}$
. As
![]() $y_4\in C^S_0$
,
$y_4\in C^S_0$
,
![]() $S_2$
is a dominating set of G. If
$S_2$
is a dominating set of G. If
![]() $d(y_2,x_3)\leq 2$
, then
$d(y_2,x_3)\leq 2$
, then
![]() $S_2$
is a semi-TD-set of G, which is a contradiction. Thus,
$S_2$
is a semi-TD-set of G, which is a contradiction. Thus,
![]() $d(y_2,x_3)> 2$
. Further,
$d(y_2,x_3)> 2$
. Further,
![]() $x_1x_3\notin E(G)$
and
$x_1x_3\notin E(G)$
and
![]() $x_2x_3\notin E(G)$
. Combining
$x_2x_3\notin E(G)$
. Combining
![]() $d(x_3)\geq 3$
and the claw-freeness of G, there exists a vertex
$d(x_3)\geq 3$
and the claw-freeness of G, there exists a vertex
![]() $x_4$
such that
$x_4$
such that
![]() $x_4x_3\in E(G)$
and
$x_4x_3\in E(G)$
and
![]() $x_4y_4\in E(G)$
. By Claim 1,
$x_4y_4\in E(G)$
. By Claim 1,
![]() $x_4\in \overline {S}$
. We note that
$x_4\in \overline {S}$
. We note that
![]() $y_2x_4\notin E(G)$
as
$y_2x_4\notin E(G)$
as
![]() $d(y_2,x_3)> 2$
. Since
$d(y_2,x_3)> 2$
. Since
![]() $y_4\in C^S_0$
,
$y_4\in C^S_0$
,
![]() $x_4\notin {\textit {epn}}(y_4,S)$
and
$x_4\notin {\textit {epn}}(y_4,S)$
and
![]() $x_4$
has a neighbour
$x_4$
has a neighbour
![]() $y_5$
in S other than
$y_5$
in S other than
![]() $y_4$
. As
$y_4$
. As
![]() $S_2$
cannot be a semi-TD-set of G,
$S_2$
cannot be a semi-TD-set of G,
![]() $y_1$
and
$y_1$
and
![]() $y_4$
are the only two vertices of S within distance 2 from
$y_4$
are the only two vertices of S within distance 2 from
![]() $y_2$
in G. Thus, all vertices of
$y_2$
in G. Thus, all vertices of
![]() $N_{\overline {S}}(y_2)\setminus \{x_1,x_2\}$
are adjacent to
$N_{\overline {S}}(y_2)\setminus \{x_1,x_2\}$
are adjacent to
![]() $y_4$
.
$y_4$
.
Let
![]() $x_5$
be a vertex in
$x_5$
be a vertex in
![]() $N_{\overline {S}}(y_2)\setminus \{x_1,x_2\}$
. Then
$N_{\overline {S}}(y_2)\setminus \{x_1,x_2\}$
. Then
![]() $x_5y_4\in E(G)$
. If
$x_5y_4\in E(G)$
. If
![]() $x_1x_5\in E(G)$
, then
$x_1x_5\in E(G)$
, then
![]() $(S\setminus \{y_1,y_2\})\cup \{x_1\}$
is a semi-TD-set of G, which is a contradiction. Thus,
$(S\setminus \{y_1,y_2\})\cup \{x_1\}$
is a semi-TD-set of G, which is a contradiction. Thus,
![]() $x_1x_5\notin E(G)$
. Recall that
$x_1x_5\notin E(G)$
. Recall that
![]() $x_1x_3\notin E(G)$
. This implies that
$x_1x_3\notin E(G)$
. This implies that
![]() $d(x_1)=3$
. Similarly,
$d(x_1)=3$
. Similarly,
![]() $d(x_2)=3$
. Note that
$d(x_2)=3$
. Note that
![]() $x_5x_3\notin E(G)$
as
$x_5x_3\notin E(G)$
as
![]() $d(y_2,x_3)> 2$
. Since G is claw-free,
$d(y_2,x_3)> 2$
. Since G is claw-free,
![]() $x_5x_4\notin E(G)$
and each vertex of
$x_5x_4\notin E(G)$
and each vertex of
![]() $N(y_4)\setminus \{x_3,x_5\}$
is adjacent to either
$N(y_4)\setminus \{x_3,x_5\}$
is adjacent to either
![]() $x_3$
or
$x_3$
or
![]() $x_5$
. Let
$x_5$
. Let
![]() $S_3=(S\setminus \{y_1,y_2,y_4\})\cup \{x_1,x_3,x_5\}$
. Then
$S_3=(S\setminus \{y_1,y_2,y_4\})\cup \{x_1,x_3,x_5\}$
. Then
![]() $S_3$
is a
$S_3$
is a
![]() $\gamma _{t2}(G)$
-set and
$\gamma _{t2}(G)$
-set and
![]() $\lambda (S_3)=\lambda (S)$
. If
$\lambda (S_3)=\lambda (S)$
. If
![]() $d(y_2)=3$
, then
$d(y_2)=3$
, then
![]() $G[\{y_1,y_2,x_1,x_3\}]$
is a special diamond. Further,
$G[\{y_1,y_2,x_1,x_3\}]$
is a special diamond. Further,
![]() $|\mathcal {D}\cap S_2|<|\mathcal {D}\cap S|$
, which contradicts the choice of S. Thus,
$|\mathcal {D}\cap S_2|<|\mathcal {D}\cap S|$
, which contradicts the choice of S. Thus,
![]() $d(y_2)\geq 4$
. Let
$d(y_2)\geq 4$
. Let
![]() $x_6$
be a vertex in
$x_6$
be a vertex in
![]() $N_{\overline {S}}(y_2)\setminus \{x_1,x_2,x_5\}$
. Then
$N_{\overline {S}}(y_2)\setminus \{x_1,x_2,x_5\}$
. Then
![]() $x_6y_4\in E(G)$
. We note that
$x_6y_4\in E(G)$
. We note that
![]() $\{y_2,y_4\}\in C^S_0\setminus C^S_{\widetilde {0}}$
and
$\{y_2,y_4\}\in C^S_0\setminus C^S_{\widetilde {0}}$
and
![]() $|\{x\mid x\in N_{\overline {S}}(y_2) \mbox { and } N_{C^S_{\widetilde {0}}}(x)\neq \emptyset \}|\leq 2$
. From the definition of the edge weighting functions, we have
$|\{x\mid x\in N_{\overline {S}}(y_2) \mbox { and } N_{C^S_{\widetilde {0}}}(x)\neq \emptyset \}|\leq 2$
. From the definition of the edge weighting functions, we have
![]() $w(x_1y_1)=w(x_2y_1)=\tfrac 58$
and
$w(x_1y_1)=w(x_2y_1)=\tfrac 58$
and
![]() $w(x_3y_1)\geq \frac{9}{16}$
. Further,
$w(x_3y_1)\geq \frac{9}{16}$
. Further,
![]() $f(\{y_1\})=w(x_1y_1)+w(x_2y_1)+w(x_3y_1)>\tfrac 74$
, which contradicts the choice of
$f(\{y_1\})=w(x_1y_1)+w(x_2y_1)+w(x_3y_1)>\tfrac 74$
, which contradicts the choice of
![]() $y_1$
.
$y_1$
.
By Claim 8, we may assume that
![]() $y_2\in C^S_{\widetilde {1}}$
. Then
$y_2\in C^S_{\widetilde {1}}$
. Then
![]() $w(x_1y_1)\geq \tfrac 58$
. If
$w(x_1y_1)\geq \tfrac 58$
. If
![]() $y_3\in C^S_{\widetilde {1}}$
, then
$y_3\in C^S_{\widetilde {1}}$
, then
![]() $w(x_2y_1)\geq \tfrac 58$
and further
$w(x_2y_1)\geq \tfrac 58$
and further
![]() $f(\{y_1\})=w(x_1y_2)+w(x_2y_2)+w(x_3y_2)\geq \tfrac 58+\tfrac 58+\tfrac 12\geq \tfrac 74$
, which is a contradiction. Thus,
$f(\{y_1\})=w(x_1y_2)+w(x_2y_2)+w(x_3y_2)\geq \tfrac 58+\tfrac 58+\tfrac 12\geq \tfrac 74$
, which is a contradiction. Thus,
![]() $y_3\in C^S_0$
. Similarly,
$y_3\in C^S_0$
. Similarly,
![]() $y_4\in C^S_0$
. This implies that
$y_4\in C^S_0$
. This implies that
![]() $y_2\neq y_3$
and
$y_2\neq y_3$
and
![]() $y_2\neq y_4$
. Let
$y_2\neq y_4$
. Let
![]() $N(y_2)=\{x_1,x_4,x_5\}$
, where
$N(y_2)=\{x_1,x_4,x_5\}$
, where
![]() $\{x_4\}= {\textit {epn}}(y_2,S)$
. If
$\{x_4\}= {\textit {epn}}(y_2,S)$
. If
![]() $N_{C^S_{\widetilde {0}}}(x_5)=\emptyset $
, then by the definition of the edge weighting functions, we have
$N_{C^S_{\widetilde {0}}}(x_5)=\emptyset $
, then by the definition of the edge weighting functions, we have
![]() $w(x_1y_1)=\tfrac 34$
. Further,
$w(x_1y_1)=\tfrac 34$
. Further,
![]() $f(\{y_1\})=w(x_1y_2)+w(x_2y_2)+w(x_3y_2)\geq \tfrac 34+\tfrac 12+\tfrac 12\geq \tfrac 74$
, which is a contradiction. Hence,
$f(\{y_1\})=w(x_1y_2)+w(x_2y_2)+w(x_3y_2)\geq \tfrac 34+\tfrac 12+\tfrac 12\geq \tfrac 74$
, which is a contradiction. Hence,
![]() $N_{C^S_{\widetilde {0}}}(x_5)\neq \emptyset $
. We proceed with a series of claims that culminate in a contradiction.
$N_{C^S_{\widetilde {0}}}(x_5)\neq \emptyset $
. We proceed with a series of claims that culminate in a contradiction.
Claim 9.
![]() $|E(G[\{x_1,x_2,x_3\}])|= 1$
.
$|E(G[\{x_1,x_2,x_3\}])|= 1$
.
Since G is claw-free,
![]() $|E(G[\{x_1,x_2,x_3\}])|\geq 1$
. If
$|E(G[\{x_1,x_2,x_3\}])|\geq 1$
. If
![]() $x_2x_1\in E(G)$
and
$x_2x_1\in E(G)$
and
![]() $x_2x_3\in E(G)$
, then
$x_2x_3\in E(G)$
, then
![]() $(S\setminus \{y_1,y_3\})\cup \{x_2\}$
is a semi-TD-set of G as
$(S\setminus \{y_1,y_3\})\cup \{x_2\}$
is a semi-TD-set of G as
![]() $y_1\in C^S_{\widetilde {0}}$
and
$y_1\in C^S_{\widetilde {0}}$
and
![]() $y_3\in C^S_{0}$
, which contradicts the minimality of S. Thus,
$y_3\in C^S_{0}$
, which contradicts the minimality of S. Thus,
![]() $x_2x_1\notin E(G)$
or
$x_2x_1\notin E(G)$
or
![]() $x_2x_3\notin E(G)$
. Similarly,
$x_2x_3\notin E(G)$
. Similarly,
![]() $x_3x_1\notin E(G)$
or
$x_3x_1\notin E(G)$
or
![]() $x_3x_2\notin E(G)$
. Suppose that
$x_3x_2\notin E(G)$
. Suppose that
![]() $|E(G[\{x_1,x_2,x_3\}])|\geq 2$
. Then
$|E(G[\{x_1,x_2,x_3\}])|\geq 2$
. Then
![]() $x_1x_2\in E(G)$
,
$x_1x_2\in E(G)$
,
![]() $x_1x_3\in E(G)$
and
$x_1x_3\in E(G)$
and
![]() $x_2x_3\notin E(G)$
. This means G has a claw, which contradicts the claw-freeness of G. Hence,
$x_2x_3\notin E(G)$
. This means G has a claw, which contradicts the claw-freeness of G. Hence,
![]() $|E(G[\{x_1,x_2,x_3\}])|= 1$
.
$|E(G[\{x_1,x_2,x_3\}])|= 1$
.
Claim 10.
![]() $y_3=y_4$
.
$y_3=y_4$
.
Assume, to the contrary, that
![]() $y_3\neq y_4$
. By Claim 9, without loss of generality, we consider
$y_3\neq y_4$
. By Claim 9, without loss of generality, we consider
![]() $E(G[\{x_1,x_2,x_3\}])= \{x_1x_2\}$
or
$E(G[\{x_1,x_2,x_3\}])= \{x_1x_2\}$
or
![]() $\{x_2x_3\}$
. Let
$\{x_2x_3\}$
. Let
![]() $S_1=(S\setminus \{y_1,y_3\})\cup \{x_2\}$
. Since
$S_1=(S\setminus \{y_1,y_3\})\cup \{x_2\}$
. Since
![]() $y_3\in C^S_0$
,
$y_3\in C^S_0$
,
![]() $S_1$
is a dominating set of G. Note that
$S_1$
is a dominating set of G. Note that
![]() $S_1$
cannot be a semi-TD-set of G. Thus, there exists a vertex y such that
$S_1$
cannot be a semi-TD-set of G. Thus, there exists a vertex y such that
![]() $y_1$
and
$y_1$
and
![]() $y_3$
are the only two vertices of S within distance 2 from y in G and
$y_3$
are the only two vertices of S within distance 2 from y in G and
![]() $d(y,x_2)>2$
. If
$d(y,x_2)>2$
. If
![]() $E(G[\{x_1,x_2,x_3\}])= \{x_2x_3\}$
, then
$E(G[\{x_1,x_2,x_3\}])= \{x_2x_3\}$
, then
![]() $d(x_2,y_4)\leq 2$
and
$d(x_2,y_4)\leq 2$
and
![]() $y=y_2$
. This implies that
$y=y_2$
. This implies that
![]() $x_5y_3\in E(G)$
. However, then
$x_5y_3\in E(G)$
. However, then
![]() $(S\setminus \{y_1,y_4\})\cup \{x_3\}$
is a semi-TD-set of G as
$(S\setminus \{y_1,y_4\})\cup \{x_3\}$
is a semi-TD-set of G as
![]() $y_4\in C^S_0$
, which contradicts the minimality of S. Hence,
$y_4\in C^S_0$
, which contradicts the minimality of S. Hence,
![]() $E(G[\{x_1,x_2,x_3\}])= \{x_1x_2\}$
. In this case,
$E(G[\{x_1,x_2,x_3\}])= \{x_1x_2\}$
. In this case,
![]() $d(y_2,x_2)\leq 2$
and
$d(y_2,x_2)\leq 2$
and
![]() $y=y_4$
. Thus, all vertices of
$y=y_4$
. Thus, all vertices of
![]() $N_{\overline {S}}(y_4)\setminus \{x_3\}$
are adjacent to
$N_{\overline {S}}(y_4)\setminus \{x_3\}$
are adjacent to
![]() $y_3$
. Let x be a vertex in
$y_3$
. Let x be a vertex in
![]() $N_{\overline {S}}(y_4)\setminus \{x_3\}$
. Then
$N_{\overline {S}}(y_4)\setminus \{x_3\}$
. Then
![]() $xy_3\in E(G)$
. Recall that
$xy_3\in E(G)$
. Recall that
![]() $d(y,x_2)>2$
. Thus,
$d(y,x_2)>2$
. Thus,
![]() $d(y_4,x_2)>2$
and
$d(y_4,x_2)>2$
and
![]() $x_2x\notin E(G)$
. Since G is claw-free,
$x_2x\notin E(G)$
. Since G is claw-free,
![]() $N_{\overline {S}}(y_4)\setminus \{x_3\}$
is a clique of G. Combining
$N_{\overline {S}}(y_4)\setminus \{x_3\}$
is a clique of G. Combining
![]() $d(x_3)\geq 3$
and the claw-freeness of G, there exists a vertex
$d(x_3)\geq 3$
and the claw-freeness of G, there exists a vertex
![]() $x'$
in
$x'$
in
![]() $N_{\overline {S}}(y_4)\setminus \{x_3\}$
such that
$N_{\overline {S}}(y_4)\setminus \{x_3\}$
such that
![]() $x_3x'\in E(G)$
. Then
$x_3x'\in E(G)$
. Then
![]() $(S\setminus \{y_3,y_4\})\cup \{x'\}$
is a semi-TD-set of G as
$(S\setminus \{y_3,y_4\})\cup \{x'\}$
is a semi-TD-set of G as
![]() $y_3\in C^S_0$
, which is a contradiction.
$y_3\in C^S_0$
, which is a contradiction.
If
![]() $y_3(=y_4)\in C^S_0\setminus C^S_{\widetilde {0}}$
, then
$y_3(=y_4)\in C^S_0\setminus C^S_{\widetilde {0}}$
, then
![]() $w(x_2y_1)\geq \frac{9}{16}$
and
$w(x_2y_1)\geq \frac{9}{16}$
and
![]() $w(x_3y_1)\geq \frac{9}{16}$
. Further,
$w(x_3y_1)\geq \frac{9}{16}$
. Further,
![]() $f(\{y_1\})=w(x_1y_2)+w(x_2y_1)+w(x_3y_1)\geq \tfrac 58+ \frac{9}{16} + \frac{9}{16} \geq \tfrac 74$
, which contradicts the choice of
$f(\{y_1\})=w(x_1y_2)+w(x_2y_1)+w(x_3y_1)\geq \tfrac 58+ \frac{9}{16} + \frac{9}{16} \geq \tfrac 74$
, which contradicts the choice of
![]() $y_1$
. Thus,
$y_1$
. Thus,
![]() $y_3\in C^S_{\widetilde {0}}$
.
$y_3\in C^S_{\widetilde {0}}$
.
Claim 11.
![]() $x_2x_3\notin E(G)$
.
$x_2x_3\notin E(G)$
.
For the sake of contradiction, suppose that
![]() $x_2x_3\in E(G)$
. If
$x_2x_3\in E(G)$
. If
![]() $d(y_2,x_2)\leq 2$
, then
$d(y_2,x_2)\leq 2$
, then
![]() $(S\setminus \{y_1,y_3\})\cup \{x_2\}$
is a semi-TD-set of G as
$(S\setminus \{y_1,y_3\})\cup \{x_2\}$
is a semi-TD-set of G as
![]() $y_3\in C^S_{\widetilde {0}}$
, which contradicts the minimality of S. Thus,
$y_3\in C^S_{\widetilde {0}}$
, which contradicts the minimality of S. Thus,
![]() $d(y_2,x_2)\geq 3$
. Similarly,
$d(y_2,x_2)\geq 3$
. Similarly,
![]() $d(y_2,x_3)\geq 3$
. This implies that
$d(y_2,x_3)\geq 3$
. This implies that
![]() $E[\{x_1,x_4,x_5\}, \{x_2,x_3\}]=\emptyset $
. If
$E[\{x_1,x_4,x_5\}, \{x_2,x_3\}]=\emptyset $
. If
![]() $d(x_2)> 3$
, then there exists a vertex x in
$d(x_2)> 3$
, then there exists a vertex x in
![]() $\overline {S}$
adjacent to
$\overline {S}$
adjacent to
![]() $x_2$
. Since G is claw-free,
$x_2$
. Since G is claw-free,
![]() $xy_3\in E(G)$
. Thus, x has a neighbour in S different from
$xy_3\in E(G)$
. Thus, x has a neighbour in S different from
![]() $y_3$
as
$y_3$
as
![]() $y_3\in C^S_{\widetilde {0}}$
. Combined with
$y_3\in C^S_{\widetilde {0}}$
. Combined with
![]() $N_{C^S_{\widetilde {0}}}(x_5)\neq \emptyset $
,
$N_{C^S_{\widetilde {0}}}(x_5)\neq \emptyset $
,
![]() $(S\setminus \{y_1,y_3\})\cup \{x_2\}$
is a semi-TD-set of G, which is a contradiction. Thus,
$(S\setminus \{y_1,y_3\})\cup \{x_2\}$
is a semi-TD-set of G, which is a contradiction. Thus,
![]() $d(x_2)=3$
. Similarly,
$d(x_2)=3$
. Similarly,
![]() $d(x_3)=3$
. Observe that
$d(x_3)=3$
. Observe that
![]() $y_1$
and
$y_1$
and
![]() $y_3$
are in the same special diamond of G.
$y_3$
are in the same special diamond of G.
If
![]() $x_1x_4\in E(G)$
, then
$x_1x_4\in E(G)$
, then
![]() $S_1=(S\setminus \{y_1,y_2,y_3\})\cup \{x_1,x_2\}$
is a dominating set of G. Otherwise,
$S_1=(S\setminus \{y_1,y_2,y_3\})\cup \{x_1,x_2\}$
is a dominating set of G. Otherwise,
![]() $x_5$
is not dominated by
$x_5$
is not dominated by
![]() $S_1$
, and further
$S_1$
, and further
![]() $x_5x_1\notin E(G)$
and
$x_5x_1\notin E(G)$
and
![]() $x_5y_3\in E(G)$
as
$x_5y_3\in E(G)$
as
![]() $y_2\in C^S_{\widetilde {1}}$
and
$y_2\in C^S_{\widetilde {1}}$
and
![]() $y_3\in C^S_{\widetilde {0}}$
. Since
$y_3\in C^S_{\widetilde {0}}$
. Since
![]() $d(x_5)\geq 3$
and G is claw-free,
$d(x_5)\geq 3$
and G is claw-free,
![]() $N(x_5)=\{y_2,y_3,x_4\}$
. In this case,
$N(x_5)=\{y_2,y_3,x_4\}$
. In this case,
![]() $G=N_2$
, which is a contradiction. As
$G=N_2$
, which is a contradiction. As
![]() $N_S(x_5)\setminus \{y_2\}\subseteq C^S_{\widetilde {0}}$
and
$N_S(x_5)\setminus \{y_2\}\subseteq C^S_{\widetilde {0}}$
and
![]() $y_3\in C^S_{\widetilde {0}}$
, there does not exist a vertex in
$y_3\in C^S_{\widetilde {0}}$
, there does not exist a vertex in
![]() $S\setminus \{y_1\}$
such that
$S\setminus \{y_1\}$
such that
![]() $y_2$
and
$y_2$
and
![]() $y_3$
are the only two vertices of S within distance 2 from it in G. Thus,
$y_3$
are the only two vertices of S within distance 2 from it in G. Thus,
![]() $S_1$
is a semi-TD-set of G which contradicts the minimality of S. Hence,
$S_1$
is a semi-TD-set of G which contradicts the minimality of S. Hence,
![]() $x_1x_4\notin E(G)$
. Since
$x_1x_4\notin E(G)$
. Since
![]() $d(x_1)\geq 3$
and G is claw-free,
$d(x_1)\geq 3$
and G is claw-free,
![]() $x_1x_5\in E(G)$
. Note that
$x_1x_5\in E(G)$
. Note that
![]() $d(x_1)=3$
. If
$d(x_1)=3$
. If
![]() $x_4x_5\in E(G)$
, then G has a claw, for
$x_4x_5\in E(G)$
, then G has a claw, for
![]() $x_5$
has a neighbour in S other than
$x_5$
has a neighbour in S other than
![]() $y_2$
, which is a contradiction. Thus,
$y_2$
, which is a contradiction. Thus,
![]() $x_4x_5\notin E(G)$
. This implies that
$x_4x_5\notin E(G)$
. This implies that
![]() $x_1$
is not in a special diamond.
$x_1$
is not in a special diamond.
Let
![]() $S_2=(S\setminus \{y_1,y_2,y_3\})\cup \{x_1,x_2,x_4\}$
. Observe that
$S_2=(S\setminus \{y_1,y_2,y_3\})\cup \{x_1,x_2,x_4\}$
. Observe that
![]() $S_2$
is a
$S_2$
is a
![]() $\gamma _{t2}(G)$
-set and
$\gamma _{t2}(G)$
-set and
![]() $\lambda (S_2)=\lambda (S)$
. If
$\lambda (S_2)=\lambda (S)$
. If
![]() $x_4$
is not in a special diamond, then
$x_4$
is not in a special diamond, then
![]() $|\mathcal {D}\cap S_2|<|\mathcal {D}\cap S|$
, which contradicts the choice of S. Thus,
$|\mathcal {D}\cap S_2|<|\mathcal {D}\cap S|$
, which contradicts the choice of S. Thus,
![]() $x_4$
is in a special diamond D of G. Let
$x_4$
is in a special diamond D of G. Let
![]() $V(D)=\{x_4,x_6,x_7,y_5\}$
, where
$V(D)=\{x_4,x_6,x_7,y_5\}$
, where
![]() $x_4y_5$
is the missing edge in the special diamond D. Clearly,
$x_4y_5$
is the missing edge in the special diamond D. Clearly,
![]() $\{x_6,x_7\}\subseteq \overline {S}$
and
$\{x_6,x_7\}\subseteq \overline {S}$
and
![]() $y_5\in S$
. We note that
$y_5\in S$
. We note that
![]() $y_5$
is an S-internal private neighbour. Let
$y_5$
is an S-internal private neighbour. Let
![]() $y_5\in {\textit {ipn}}_2(y_6,S)$
and
$y_5\in {\textit {ipn}}_2(y_6,S)$
and
![]() $x_8$
be the vertex of
$x_8$
be the vertex of
![]() $\overline {S}$
connecting
$\overline {S}$
connecting
![]() $y_5$
and
$y_5$
and
![]() $y_6$
.
$y_6$
.
If
![]() ${\textit {epn}}(y_6,S)=\emptyset $
, then
${\textit {epn}}(y_6,S)=\emptyset $
, then
![]() $S_3=(S\setminus \{y_1,y_2,y_5,y_6\})\cup \{x_1,x_4,x_8\}$
is a dominating set of G. Since
$S_3=(S\setminus \{y_1,y_2,y_5,y_6\})\cup \{x_1,x_4,x_8\}$
is a dominating set of G. Since
![]() $d(x_8)\geq 3$
, there exists a vertex x adjacent to
$d(x_8)\geq 3$
, there exists a vertex x adjacent to
![]() $xx_8\in E(G)$
. Further,
$xx_8\in E(G)$
. Further,
![]() $xy_6\in E(G)$
as G is claw-free. Combined with
$xy_6\in E(G)$
as G is claw-free. Combined with
![]() ${\textit {epn}}(y_6,S)=\emptyset $
, x has a neighbour in
${\textit {epn}}(y_6,S)=\emptyset $
, x has a neighbour in
![]() $S\setminus \{y_1,y_5,y_6\}$
. Thus, there exists a vertex in
$S\setminus \{y_1,y_5,y_6\}$
. Thus, there exists a vertex in
![]() $S_3$
within distance 2 from
$S_3$
within distance 2 from
![]() $x_8$
. It follows from the minimality of S that
$x_8$
. It follows from the minimality of S that
![]() $S_3$
cannot be a semi-TD-set of G. Thus,
$S_3$
cannot be a semi-TD-set of G. Thus,
![]() $y_3$
is at a distance greater than 2 from every other vertex of
$y_3$
is at a distance greater than 2 from every other vertex of
![]() $S_3$
. This implies that
$S_3$
. This implies that
![]() $y_3x_5\notin E(G)$
,
$y_3x_5\notin E(G)$
,
![]() $x'y_6\in E(G)$
and
$x'y_6\in E(G)$
and
![]() $x'x_8\notin E(G)$
, where
$x'x_8\notin E(G)$
, where
![]() $\{x'\}=N(y_3)\setminus \{x_2,x_3\}$
. We note that neither
$\{x'\}=N(y_3)\setminus \{x_2,x_3\}$
. We note that neither
![]() $x_8$
nor
$x_8$
nor
![]() $x'$
are in a special diamond. Otherwise,
$x'$
are in a special diamond. Otherwise,
![]() ${\textit {epn}}(y_6,S)\neq \emptyset $
or G has a claw, which is a contradiction. Further,
${\textit {epn}}(y_6,S)\neq \emptyset $
or G has a claw, which is a contradiction. Further,
![]() $(S\setminus \{y_1,y_2,y_3,y_5,y_6\})\cup \{x_1,x_2,x_6,x_8,x'\}$
is a semi-TD-set of G with
$(S\setminus \{y_1,y_2,y_3,y_5,y_6\})\cup \{x_1,x_2,x_6,x_8,x'\}$
is a semi-TD-set of G with
![]() $\lambda (S_3)=\lambda (S)$
but with
$\lambda (S_3)=\lambda (S)$
but with
![]() $|\mathcal {D}\cap S_3|<|\mathcal {D}\cap S|$
, which contradicts the choice of S. Hence,
$|\mathcal {D}\cap S_3|<|\mathcal {D}\cap S|$
, which contradicts the choice of S. Hence,
![]() ${\textit {epn}}(y_6,S)\neq \emptyset $
.
${\textit {epn}}(y_6,S)\neq \emptyset $
.
Let
![]() $x_9$
be a vertex in
$x_9$
be a vertex in
![]() ${\textit {epn}}(y_6,S)$
. Then
${\textit {epn}}(y_6,S)$
. Then
![]() $|\mathcal {D}\cap S_2|=|\mathcal {D}\cap S|$
,
$|\mathcal {D}\cap S_2|=|\mathcal {D}\cap S|$
,
![]() $\{x_1,x_2\}\cap C^{S_2}_{\widetilde {0}}=\emptyset $
and
$\{x_1,x_2\}\cap C^{S_2}_{\widetilde {0}}=\emptyset $
and
![]() $y_6\notin C^{S_2}_0$
. Further,
$y_6\notin C^{S_2}_0$
. Further,
![]() $|C^{S_2}_{\widetilde {0}}|\leq |C^S_{\widetilde {0}}|$
and
$|C^{S_2}_{\widetilde {0}}|\leq |C^S_{\widetilde {0}}|$
and
![]() $|C^{S_2}_{0}|\leq |C^S_{0}|$
. If
$|C^{S_2}_{0}|\leq |C^S_{0}|$
. If
![]() $y_6\notin C^{S_2}_{\widetilde {1}}$
, then
$y_6\notin C^{S_2}_{\widetilde {1}}$
, then
![]() $|C^{S_2}_{\widetilde {1}}|<|C^S_{\widetilde {1}}|$
, which contradicts the choice of S. Thus,
$|C^{S_2}_{\widetilde {1}}|<|C^S_{\widetilde {1}}|$
, which contradicts the choice of S. Thus,
![]() $y_6\in C^{S_2}_{\widetilde {1}}$
. Let
$y_6\in C^{S_2}_{\widetilde {1}}$
. Let
![]() $N(y_6)=\{x_8,x_9,x_{10}\}$
(possibly,
$N(y_6)=\{x_8,x_9,x_{10}\}$
(possibly,
![]() $x_{10}=x_5$
). Then
$x_{10}=x_5$
). Then
![]() $x_{10}$
has a neighbour in
$x_{10}$
has a neighbour in
![]() $S_2\setminus \{y_6,y_5,x_4,x_2\}$
. Hence,
$S_2\setminus \{y_6,y_5,x_4,x_2\}$
. Hence,
![]() $x_{10}$
has a neighbour in
$x_{10}$
has a neighbour in
![]() $S\setminus \{y_5,y_6\}$
. Let
$S\setminus \{y_5,y_6\}$
. Let
![]() $S_4=(S\setminus \{y_5\})\cup \{x_6\}$
. Then
$S_4=(S\setminus \{y_5\})\cup \{x_6\}$
. Then
![]() $S_4$
is a
$S_4$
is a
![]() $\gamma _{t2}(G)$
-set. Now,
$\gamma _{t2}(G)$
-set. Now,
![]() $\lambda (S_4)=\lambda (S)$
,
$\lambda (S_4)=\lambda (S)$
,
![]() $|\mathcal {D}\cap S_4|=|\mathcal {D}\cap S|$
,
$|\mathcal {D}\cap S_4|=|\mathcal {D}\cap S|$
,
![]() $x_6\in {\textit {epn}}_2(y_2,S_4)$
and
$x_6\in {\textit {epn}}_2(y_2,S_4)$
and
![]() $y_6\in {\textit {ipn}}_2(y,S_4)$
for some vertex y of
$y_6\in {\textit {ipn}}_2(y,S_4)$
for some vertex y of
![]() $S_4$
. Thus,
$S_4$
. Thus,
![]() $|C^{S_4}_{\widetilde {0}}|\leq |C^S_{\widetilde {0}}|$
,
$|C^{S_4}_{\widetilde {0}}|\leq |C^S_{\widetilde {0}}|$
,
![]() $|C^{S_4}_0|\leq |C^S_0|$
and
$|C^{S_4}_0|\leq |C^S_0|$
and
![]() $|C^{S_4}_{\widetilde {1}}|<|C^S_{\widetilde {1}}|$
, which contradicts the choice of S.
$|C^{S_4}_{\widetilde {1}}|<|C^S_{\widetilde {1}}|$
, which contradicts the choice of S.
By Claims 9–11, we may assume that
![]() $E(G[\{x_1,x_2,x_3\}])=\{x_1x_2\}$
. If
$E(G[\{x_1,x_2,x_3\}])=\{x_1x_2\}$
. If
![]() $x_1x_4\in E(G)$
, then
$x_1x_4\in E(G)$
, then
![]() $(S\setminus \{y_1,y_2\})\cup \{x_1\}$
is a semi-TD-set of G as
$(S\setminus \{y_1,y_2\})\cup \{x_1\}$
is a semi-TD-set of G as
![]() $y_2\in C^S_{\widetilde {1}}$
, which contradicts the minimality of S. Thus,
$y_2\in C^S_{\widetilde {1}}$
, which contradicts the minimality of S. Thus,
![]() $x_1x_4\notin E(G)$
.
$x_1x_4\notin E(G)$
.
Suppose first that
![]() $x_5y_3\in E(G)$
. Since
$x_5y_3\in E(G)$
. Since
![]() $d(x_3)\geq 3$
and G is claw-free,
$d(x_3)\geq 3$
and G is claw-free,
![]() $x_5x_3\in E(G)$
. If
$x_5x_3\in E(G)$
. If
![]() $x_5x_4\in E(G)$
, then
$x_5x_4\in E(G)$
, then
![]() $(S\setminus \{y_1,y_2,y_3\})\cup \{x_1,x_5\}$
is a semi-TD-set of G, which contradicts the choice of S. Thus,
$(S\setminus \{y_1,y_2,y_3\})\cup \{x_1,x_5\}$
is a semi-TD-set of G, which contradicts the choice of S. Thus,
![]() $x_5x_4\notin E(G)$
. Combining the claw-freeness of G and
$x_5x_4\notin E(G)$
. Combining the claw-freeness of G and
![]() $x_1x_4\notin E(G)$
, we have
$x_1x_4\notin E(G)$
, we have
![]() $x_5x_1\in E(G)$
. Since G is claw-free,
$x_5x_1\in E(G)$
. Since G is claw-free,
![]() $N(x_1)=\{y_1,y_2,x_2,x_5\}$
,
$N(x_1)=\{y_1,y_2,x_2,x_5\}$
,
![]() $N(x_2)=\{y_1,y_3,x_1\}$
,
$N(x_2)=\{y_1,y_3,x_1\}$
,
![]() $N(x_3)=\{y_1,y_3,x_5\}$
,
$N(x_3)=\{y_1,y_3,x_5\}$
,
![]() $N(x_5)=\{y_2,y_3,x_1,x_3\}$
and
$N(x_5)=\{y_2,y_3,x_1,x_3\}$
and
![]() $X_1:=N(x_4)\setminus \{y_2\}$
is a clique of G. We construct
$X_1:=N(x_4)\setminus \{y_2\}$
is a clique of G. We construct
![]() $G'$
from G by removing all vertices of
$G'$
from G by removing all vertices of
![]() $\{y_1,y_3,x_1,x_2,x_3,x_5\}$
and adding the edges between
$\{y_1,y_3,x_1,x_2,x_3,x_5\}$
and adding the edges between
![]() $\{y_2\}$
and
$\{y_2\}$
and
![]() $X_1$
such that
$X_1$
such that
![]() $\{y_2\}\cup X_1$
is a clique of
$\{y_2\}\cup X_1$
is a clique of
![]() $G'$
. Since
$G'$
. Since
![]() $d(x_4)\geq 3$
, we have
$d(x_4)\geq 3$
, we have
![]() $|X_1|\geq 2$
. Thus,
$|X_1|\geq 2$
. Thus,
![]() $G'\neq N_2$
is a connected claw-free graph of order
$G'\neq N_2$
is a connected claw-free graph of order
![]() $n'=n-6$
with
$n'=n-6$
with
![]() $\delta (G')\geq 3$
. Note that
$\delta (G')\geq 3$
. Note that
![]() $X_1\subseteq \overline {S}$
as
$X_1\subseteq \overline {S}$
as
![]() $x_4\in {\textit {epn}}(y_2,S)$
. Since S is a semi-TD-set of G, there exist a vertex y of
$x_4\in {\textit {epn}}(y_2,S)$
. Since S is a semi-TD-set of G, there exist a vertex y of
![]() $S\setminus \{y_1,y_2,y_3\}$
adjacent to some vertices of
$S\setminus \{y_1,y_2,y_3\}$
adjacent to some vertices of
![]() $X_1$
and a vertex
$X_1$
and a vertex
![]() $y'$
of
$y'$
of
![]() $S\setminus \{y_1,y_2,y_3,y\}$
within distance 2 from y in S. Hence,
$S\setminus \{y_1,y_2,y_3,y\}$
within distance 2 from y in S. Hence,
![]() $n'\geq 6$
. By the minimality of G,
$n'\geq 6$
. By the minimality of G,
![]() $\gamma _{t2}(G')\leq \frac{4}{11}n'$
. Let
$\gamma _{t2}(G')\leq \frac{4}{11}n'$
. Let
![]() $S'$
be a
$S'$
be a
![]() $\gamma _{t2}(G')$
-set. When
$\gamma _{t2}(G')$
-set. When
![]() $y_2\notin S'$
,
$y_2\notin S'$
,
![]() $S'\cup \{y_1,x_5\}$
is a semi-TD-set of G. When
$S'\cup \{y_1,x_5\}$
is a semi-TD-set of G. When
![]() $y_2\in S'$
,
$y_2\in S'$
,
![]() $(S'\setminus \{y_2\})\cup \{y_1,x_5,x_4\}$
is a semi-TD-set of G. In both cases,
$(S'\setminus \{y_2\})\cup \{y_1,x_5,x_4\}$
is a semi-TD-set of G. In both cases,
![]() $\gamma _{t2}(G)\leq \frac{4}{11}n'+2= \frac{4}{11}(n-6)+2< \frac{4}{11}n$
, which contradicts the choice of G.
$\gamma _{t2}(G)\leq \frac{4}{11}n'+2= \frac{4}{11}(n-6)+2< \frac{4}{11}n$
, which contradicts the choice of G.
Suppose next that
![]() $x_5y_3\notin E(G)$
. Let
$x_5y_3\notin E(G)$
. Let
![]() $N_S(x_5)\setminus \{y_2\}=\{y_5\}$
and
$N_S(x_5)\setminus \{y_2\}=\{y_5\}$
and
![]() $N(y_3)\setminus \{x_2,x_3\}=\{x_6\}$
. Recall that
$N(y_3)\setminus \{x_2,x_3\}=\{x_6\}$
. Recall that
![]() $N_{C^S_{\widetilde {0}}}(x_5)\neq \emptyset $
. Thus,
$N_{C^S_{\widetilde {0}}}(x_5)\neq \emptyset $
. Thus,
![]() $y_5\in C^S_{\widetilde {0}}$
. Since
$y_5\in C^S_{\widetilde {0}}$
. Since
![]() $d(x_3)\geq 3$
and G is claw-free,
$d(x_3)\geq 3$
and G is claw-free,
![]() $x_3x_6\in E(G)$
. If
$x_3x_6\in E(G)$
. If
![]() $y_5x_6\in E(G)$
, then
$y_5x_6\in E(G)$
, then
![]() $(S\setminus \{y_3,y_5\})\cup \{x_6\}$
is a semi-TD-set of G, which is a contradiction. Thus,
$(S\setminus \{y_3,y_5\})\cup \{x_6\}$
is a semi-TD-set of G, which is a contradiction. Thus,
![]() $y_5x_6\notin E(G)$
. Let
$y_5x_6\notin E(G)$
. Let
![]() $N(y_5)=\{x_5,x_7,x_8\}$
and
$N(y_5)=\{x_5,x_7,x_8\}$
and
![]() $N_S(x_6)\setminus \{y_3\}=\{y_6\}$
. If
$N_S(x_6)\setminus \{y_3\}=\{y_6\}$
. If
![]() $x_5x_1\notin E(G)$
, then
$x_5x_1\notin E(G)$
, then
![]() $x_4x_5\in E(G)$
as G is claw-free and
$x_4x_5\in E(G)$
as G is claw-free and
![]() $x_1x_4\notin E(G)$
. In this case,
$x_1x_4\notin E(G)$
. In this case,
![]() $(S\setminus \{y_1,y_2,y_5\})\cup \{x_1,x_5\}$
is a semi-TD-set of G, which contradicts the minimality of S. Thus,
$(S\setminus \{y_1,y_2,y_5\})\cup \{x_1,x_5\}$
is a semi-TD-set of G, which contradicts the minimality of S. Thus,
![]() $x_5x_1\in E(G)$
. If
$x_5x_1\in E(G)$
. If
![]() $x_5x_4\in E(G)$
, then
$x_5x_4\in E(G)$
, then
![]() $(S\setminus \{y_2,y_5\})\cup \{x_5\}$
is a semi-TD-set of G, which is a contradiction. Thus,
$(S\setminus \{y_2,y_5\})\cup \{x_5\}$
is a semi-TD-set of G, which is a contradiction. Thus,
![]() $x_5x_4\notin E(G)$
. Since G is claw-free,
$x_5x_4\notin E(G)$
. Since G is claw-free,
![]() $d(x_1)=4$
,
$d(x_1)=4$
,
![]() $d(x_2)=3$
,
$d(x_2)=3$
,
![]() $d(x_3)=3$
,
$d(x_3)=3$
,
![]() $N(x_5)\subseteq \{y_2,y_5,x_1,x_7,x_8\}$
and
$N(x_5)\subseteq \{y_2,y_5,x_1,x_7,x_8\}$
and
![]() $X_2:=N(x_6)\setminus \{y_3,x_3\}$
is a clique of G. Let
$X_2:=N(x_6)\setminus \{y_3,x_3\}$
is a clique of G. Let
![]() $G'$
be the graph obtained from G by removing all vertices of
$G'$
be the graph obtained from G by removing all vertices of
![]() $\{x_1,x_2,x_3,x_6,y_1,y_3\}$
and adding the edges between
$\{x_1,x_2,x_3,x_6,y_1,y_3\}$
and adding the edges between
![]() $\{y_2,x_5\}$
and
$\{y_2,x_5\}$
and
![]() $X_2$
such that
$X_2$
such that
![]() $\{y_2,x_5\}\cup X_2$
is a clique of
$\{y_2,x_5\}\cup X_2$
is a clique of
![]() $G'$
. We observe that
$G'$
. We observe that
![]() $G'\neq N_2$
is a connected claw-free graph of order
$G'\neq N_2$
is a connected claw-free graph of order
![]() $n'=n-6\geq 6$
with
$n'=n-6\geq 6$
with
![]() $\delta (G')\geq 3$
. Then
$\delta (G')\geq 3$
. Then
![]() $G'$
has a
$G'$
has a
![]() $\gamma _{t2}(G')$
-set
$\gamma _{t2}(G')$
-set
![]() $S'$
with at most
$S'$
with at most
![]() $\frac{4}{11}n'$
vertices by the minimality of G. When
$\frac{4}{11}n'$
vertices by the minimality of G. When
![]() $X_2\cap S'\neq \emptyset $
,
$X_2\cap S'\neq \emptyset $
,
![]() $S'\cup \{x_1,y_3\}$
is a semi-TD-set of G. When
$S'\cup \{x_1,y_3\}$
is a semi-TD-set of G. When
![]() $X_2\cap S'=\emptyset $
,
$X_2\cap S'=\emptyset $
,
![]() $S'\cup \{y_1,x_6\}$
is a semi-TD-set of G. In either case,
$S'\cup \{y_1,x_6\}$
is a semi-TD-set of G. In either case,
![]() $\gamma _{t2}(G)\leq \frac{4}{11}n'+2= \frac{4}{11} (n-6)+2 < \frac{4}{11}n$
, which is a contradiction.
$\gamma _{t2}(G)\leq \frac{4}{11}n'+2= \frac{4}{11} (n-6)+2 < \frac{4}{11}n$
, which is a contradiction.
Acknowledgement
The authors thank the referees for their careful review and helpful suggestions.