Acronym list
- UAV
-
unmanned aerial vehicle
- TSKF
-
two-stage Kalman filter
- RUL
-
remaining useful life
- LQR
-
linear quadratic regulator
- PdM
-
predictive maintenance
- MPC
-
model predictive control
- LF-MPC
-
Laguerre function-based model predictive control
- SMC
-
sliding mode control
- RL
-
reinforcement learning
- GC
-
geodetic coordinate
-
probability density function
- HD
-
health degree
Nomenclature
- HD n
-
health degree from normal state to degenerate state
- HD sf
-
health degree when airframe performance does not meet the requirements
- l n
-
critical threshold from normal work to degradation
- l sf
-
degradation threshold when the airframe performance does not meet requirements
- l af
-
comprehensive degradation threshold when actuator failure
- t n
-
time when the airframe enters degradation from the normal state
- t sf
-
time when the airframe performance does not meet the requirements
- t af
-
time when the actuator fails
- ds
-
comprehensive degradation
1.0 Introduction
Quadrotor unmanned aerial vehicle (UAV) is a typical underactuated system with nonlinear and strong coupling characteristics, which is widely used in military and civilian fields [Reference Geronel, Botez and Bueno1, Reference Wang, Yu, Mu and Zhang2]. With the accumulation of flight frequency and time, degraded problems in UAV components such as the thruster, reaction wheel and gyroscope are inevitable due to aging, wear and fatigue, among which the failure probability of actuator components accounts for 44% of the total failure rate [Reference Robertson and Stoneking3]. The degradation phenomena of the actuator present a hidden degradation characteristic for the performance of UAVs. When the degradation is mild, negative feedback can compensate for its effect on airframe position and attitude. However, as the degradation of the actuator accumulates, especially during the execution of control tasks, if appropriate online autonomous maintenance is not carried out in time, the airframe performance will inevitably exceed the expected constraint range, enter a failure state and cause security issues.
In recent years, research on prognostic and health management (PHM) for quadrotor UAVs has achieved preliminary results [Reference Dai and Wang4, Reference Sierra, Orchard, Goebel and Kulkarni5], which provide strong technical support for the maintenance and support of UAVs. Various control schemes such as linear quadratic regulator (LQR) [Reference Cohen, Abdulrahim and Forbes6], model predictive control (MPC) [Reference Erdogan, Kural and Ozsoy7], sliding mode control (SMC) [Reference Yang, Liu, Coombes, Yan and Chen8], and backstepping control [Reference Belmouhoub, Medjmadj, Bouzid, Derrouaoui and Guiatni9] have been proposed to design fault-tolerant controllers to improve the security and reliability of UAVs. Although the control methods are different, the common feature is that they all belong to the ‘post-fault’ maintenance treatment scheme after the failure, none of these approaches is predictive. However, for high-safety systems such as UAVs, avoiding faults is more applicable than tolerating faults. A new paradigm that uses both control theory and reliability theory, health-aware control (HAC) [Reference Marier, Rabbath and Lechevin10–Reference Salazar, Sanjuan, Nejjari and Sarrate12], has injected new vitality into improving UAV safety. However, HAC is a method to modify control actions based on system health information to increase system running time. As the basis of PHM, remaining useful life (RUL) predictive is crucially important for determining the timing and strategy of UAV maintenance. Four machine learning algorithms, a linear sparse model, a variant of support of vector regression, a multi-layer perceptron and an advanced tree-based algorithm were used to predict the RUL of UAV battery [Reference Mansouri, Karvelis, Georgoulas and Nikolakopoulos13]. A new method for predicting the RUL of adhesive joints on composite UAV wings has been proposed [Reference Gobbato, Conte, Kosmatka and Farrar14]. However, a small amount of existing research on RUL prediction of UAVs is also focused on individual components, lacking system-level research.
With the development of information technology, predictive maintenance (PdM) [Reference Stanton, Munir, Ikram and El-Bakry15–Reference Zhang, Yang and Wang17] as a gradually emerging maintenance strategy, is undoubtedly more meaningful to reduce the failure rate of UAVs and improve their safety by analysing equipment operation data, predicting the RUL of equipment and deciding on maintenance timing and strategy. The main methods of PdM currently include LQR [Reference Langeron, Grall and Barros18], MPC [Reference Salazar, Weber, Nejjari, Sarrate and Theilliol19] and reinforcement learning(RL) [Reference Jha, Weber, Theilliol, Ponsart and Maquin20] and so on. MPC is mostly used because of its low dependence on model accuracy and strong robustness. However, in each rolling optimisation, it is necessary to predict future multi-step outputs and optimise the solving control sequence, resulting in a decrease in solving efficiency. Therefore, how to improve computational efficiency is a difficult problem in the timely and reliable autonomous maintenance of UAVs.
Secondly, the intervention time for the autonomous maintenance strategy is directly related to the working time and RUL of the UAV. According to the definition of the first arrival time of RUL by Refs [Reference Lee and Whitmore21] and [Reference Zhang, Si, Hu and Lei22], the accurate selection of the system failure threshold is crucial for predicting the RUL of UAVs. However, the most commonly used steady-state performance index [Reference Brown and Vachtsevanos23, Reference Langeron, Grall and Barros24] does not apply to UAVs with multiple performance requirements for both position and attitude. In addition, the UAV system failure threshold needs to build a comprehensive degradation state variable with multi-actuator simultaneously degraded. Therefore, selecting an appropriate performance index and constructing a comprehensive degradation quantity that can more comprehensively reflect the health status of UAV is another key issue for accurately predicting the RUL.
In practical engineering, the actuator degradation cannot avoid the influence of measurement noise and error. Although literature [Reference Zheng, Hu, Si, Zhang and Zhang25] uses augmented state Kalman filtering (ASKF) for joint estimation of states and parameters, when the dimensionality of unknown parameters is equivalent to that of states, the computational complexity of joint estimation algorithms based on augmented states increases sharply, resulting in a significant decrease in estimation speed and accuracy. Compared to ASKF, the TSKF [Reference Chen, Sun, Liu and Song26] algorithm can reduce the dimensionality of the filter, effectively avoid numerical ill-conditioning problems, and improve the stability and computational efficiency of the algorithm. Undoubtedly, it is helpful to estimate the actual degradation accurately and reliably.
In summary, the purpose of this paper is to consider the relationship between multi-actuator degradation and quadrotor UAV performance degradation, and to adopt a more computationally efficient LF-MPC method for autonomous predictive maintenance. The innovative research work carried out mainly includes three aspects:
-
The estimation of the real-time actuator degradation rate and UAV state using TSKF, and providing a new definition of comprehensive degradation variable based on entropy weight method
-
The concept of a UAV HD was proposed by introducing Mahalanobis distance, which evaluates the UAV health status in real time and determines the failure threshold based on it
-
The LF-MPC weight matrix is modified in real time based on the HD to extend the working time limit and realise autonomous PdM for a quadrotor UAV
The rest of the work is organised as follows: Section 2 establishes a degradation model for quadrotor UAV and constructs an autonomous PdM system; Section 3 describes the hidden degradation process of actuators and predicts the RUL of UAV; Section 4 adjusts LF-MPC weight matrix based on the HD evaluation results to achieve autonomous PdM; Section 5 verifies the effectiveness of the proposed method; and Section 6 gives some conclusions.
2.0 Establishment of degradation model and autonomous PdM architecture for quadrotor UAV
An in-depth analysis of the UAV control mechanism and establishment of an accurate dynamic model is the premise and basis of carrying out the RUL prediction and autonomous PdM of a quadrotor UAV.
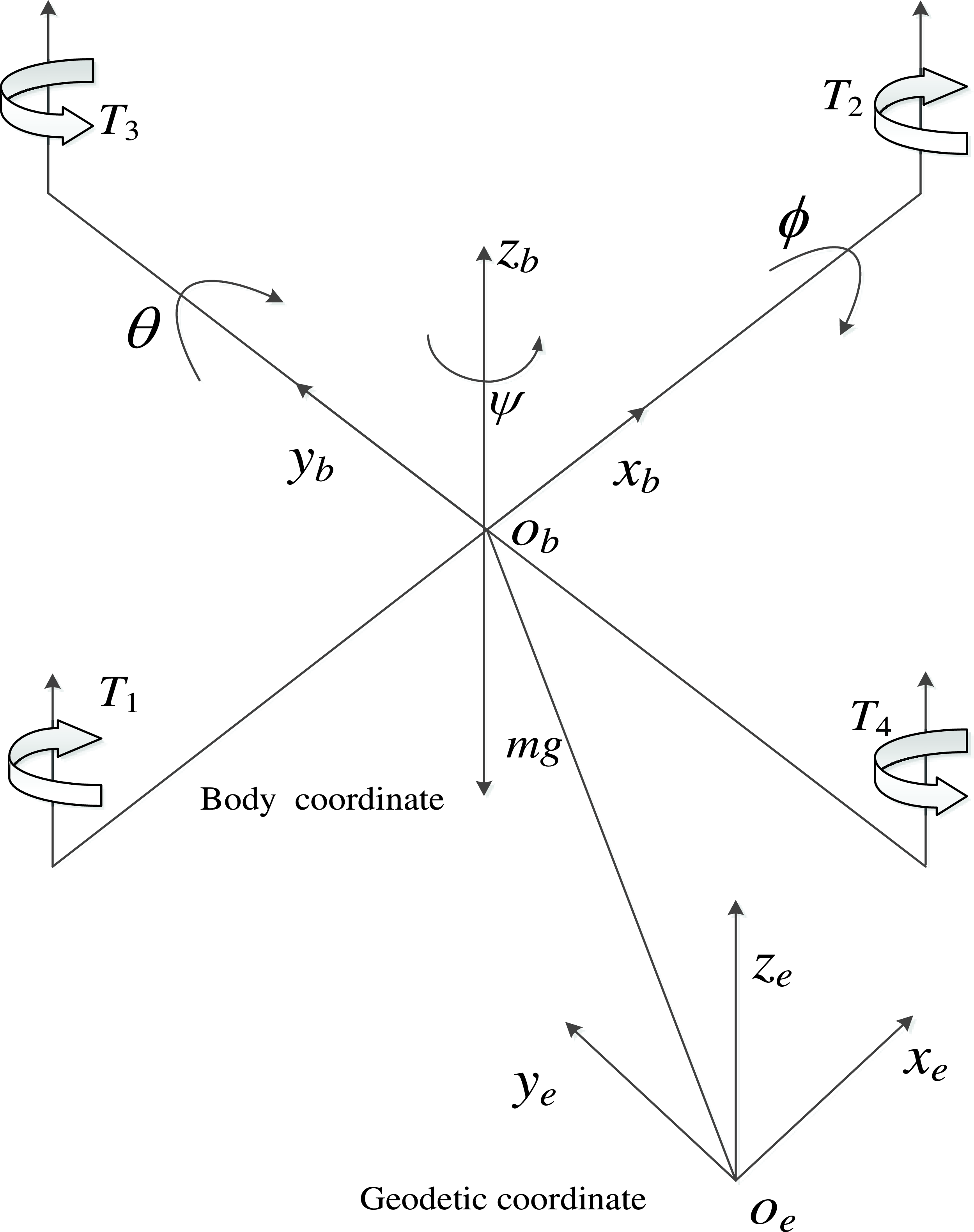
Figure 1. Structure diagram of quadrotor UAV.
2.1 Establishment of degradation model for quadrotor UAV
For a quadrotor UAV shown in Fig. 1, ignoring wind interference, the Newton-Euler formula is used to model it in a hybrid coordinate system as shown in Equation (1) [Reference Zhang, Chamseddine, Rabbath, Gordon, Su, Rakheja, Fulford, Apkarian and Gosselin27].
 \begin{align} & \ddot x = {{\left( {\cos \phi \sin \theta \cos \psi + \sin \phi \sin \psi } \right){U_z}} / m} \nonumber\\[4pt] & \ddot y = {{\left( {\cos \phi \sin \theta \sin \psi - \sin \phi \cos \psi } \right){U_z}} / m} \nonumber\\[4pt] & \ddot z = {{\left( {\cos \phi \cos \theta } \right){U_z}} / m} - g \nonumber\\[4pt] & \ddot \phi = {{\left( {\dot \theta \dot \psi \left( {{I_{yy}} - {I_{zz}}} \right) + {U_\phi }} \right)} / {{I_{xx}}}}\\[4pt] & \ddot \theta = {{\left( {\dot \phi \dot \psi \left( {{I_{zz}} - {I_{xx}}} \right) + {U_\theta }} \right)} / {{I_{yy}}}} \nonumber\\[4pt] & \ddot \psi = {{\left( {\dot \theta \dot \phi \left( {{I_{xx}} - {I_{yy}}} \right) + {U_\psi }} \right)} / } {{I_{zz}}} \nonumber \end{align}
\begin{align} & \ddot x = {{\left( {\cos \phi \sin \theta \cos \psi + \sin \phi \sin \psi } \right){U_z}} / m} \nonumber\\[4pt] & \ddot y = {{\left( {\cos \phi \sin \theta \sin \psi - \sin \phi \cos \psi } \right){U_z}} / m} \nonumber\\[4pt] & \ddot z = {{\left( {\cos \phi \cos \theta } \right){U_z}} / m} - g \nonumber\\[4pt] & \ddot \phi = {{\left( {\dot \theta \dot \psi \left( {{I_{yy}} - {I_{zz}}} \right) + {U_\phi }} \right)} / {{I_{xx}}}}\\[4pt] & \ddot \theta = {{\left( {\dot \phi \dot \psi \left( {{I_{zz}} - {I_{xx}}} \right) + {U_\theta }} \right)} / {{I_{yy}}}} \nonumber\\[4pt] & \ddot \psi = {{\left( {\dot \theta \dot \phi \left( {{I_{xx}} - {I_{yy}}} \right) + {U_\psi }} \right)} / } {{I_{zz}}} \nonumber \end{align}
where
![]() $x,y,z$
are the actual positions of the quadrotor UAV in the inertial frame with the original point at the GC,
$x,y,z$
are the actual positions of the quadrotor UAV in the inertial frame with the original point at the GC,
![]() $\phi ,\theta ,\psi $
are the roll angle, pitch angle and yaw angle, respectively. The parameters
$\phi ,\theta ,\psi $
are the roll angle, pitch angle and yaw angle, respectively. The parameters
![]() $m,{\rm{g}}$
refer to the total airframe mass and gravitational acceleration of the UAV.
$m,{\rm{g}}$
refer to the total airframe mass and gravitational acceleration of the UAV.
![]() ${I_{xx}},{I_{yy}},{I_{zz}}$
are the inertial moments about each axis.
${I_{xx}},{I_{yy}},{I_{zz}}$
are the inertial moments about each axis.
![]() ${U_z},{U_\phi },{U_\theta },{U_\psi }$
are utilised as control inputs for position regulation. Equation (2) demonstrates the correlation between UAV and motor inputs
${U_z},{U_\phi },{U_\theta },{U_\psi }$
are utilised as control inputs for position regulation. Equation (2) demonstrates the correlation between UAV and motor inputs
![]() ${u_i}$
, while
${u_i}$
, while
![]() ${U_z}$
is employed to regulate the position in
${U_z}$
is employed to regulate the position in
![]() $x,y,z$
directions. Additionally,
$x,y,z$
directions. Additionally,
![]() ${U_\phi },{U_\theta },{U_\psi }$
are implemented to govern roll, pitch and yaw respectively.
${U_\phi },{U_\theta },{U_\psi }$
are implemented to govern roll, pitch and yaw respectively.
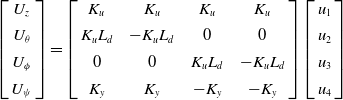 \begin{equation}\left[ {\begin{array}{*{20}{c}}{{U_z}}\\[4pt]{{U_\theta }}\\[4pt]{{U_\phi }}\\[4pt]{{U_\psi }}\end{array}} \right] = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}{{K_u}} & {{K_u}} & {{K_u}} & {{K_u}}\\[4pt]{{K_u}{L_d}} & { - {K_u}{L_d}} & 0 & 0\\[4pt]0 & 0 & {{K_u}{L_d}} & { - {K_u}{L_d}}\\[4pt]{{K_y}} & {{K_y}} & { - {K_y}} & { - {K_y}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{u_1}}\\[4pt]{{u_2}}\\[4pt]{{u_3}}\\[4pt]{{u_4}}\end{array}} \right]\end{equation}
\begin{equation}\left[ {\begin{array}{*{20}{c}}{{U_z}}\\[4pt]{{U_\theta }}\\[4pt]{{U_\phi }}\\[4pt]{{U_\psi }}\end{array}} \right] = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}{{K_u}} & {{K_u}} & {{K_u}} & {{K_u}}\\[4pt]{{K_u}{L_d}} & { - {K_u}{L_d}} & 0 & 0\\[4pt]0 & 0 & {{K_u}{L_d}} & { - {K_u}{L_d}}\\[4pt]{{K_y}} & {{K_y}} & { - {K_y}} & { - {K_y}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{u_1}}\\[4pt]{{u_2}}\\[4pt]{{u_3}}\\[4pt]{{u_4}}\end{array}} \right]\end{equation}
The variables
![]() ${u_i}(i = 1,2,3,4)$
represent the pulse-width modulation (PWM) input of the ith motor;
${u_i}(i = 1,2,3,4)$
represent the pulse-width modulation (PWM) input of the ith motor;
![]() ${L_d}$
denotes the distance from the quadrotor UAV motor to the centre of mass; and
${L_d}$
denotes the distance from the quadrotor UAV motor to the centre of mass; and
![]() ${K_u}$
is the thrust gain related to the force generated by the propeller,
${K_u}$
is the thrust gain related to the force generated by the propeller,
![]() ${K_y}$
is the torque gain related to the torque generated by the propeller.
${K_y}$
is the torque gain related to the torque generated by the propeller.
Assuming that the quadrotor UAV is hovering with no yaw (
![]() $\psi = 0$
), small roll and pitch angles, ignoring the drag term, gyroscopic and Coriolis effects, Equation (1) is simplified as:
$\psi = 0$
), small roll and pitch angles, ignoring the drag term, gyroscopic and Coriolis effects, Equation (1) is simplified as:
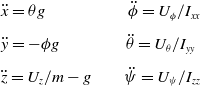 \begin{align}& \ddot x = \theta g \qquad\qquad\quad \ddot \phi = {{{U_\phi }} / {{I_{xx}}}} \nonumber\\[4pt] & \ddot y = - \phi g \qquad\qquad \ddot \theta = {{{U_\theta }} / {{I_{yy}}}}\nonumber\\[4pt] & \ddot z = {U_z} / m - g\qquad \ddot \psi = {{{U_\psi }} / {{I_{zz}}}} \end{align}
\begin{align}& \ddot x = \theta g \qquad\qquad\quad \ddot \phi = {{{U_\phi }} / {{I_{xx}}}} \nonumber\\[4pt] & \ddot y = - \phi g \qquad\qquad \ddot \theta = {{{U_\theta }} / {{I_{yy}}}}\nonumber\\[4pt] & \ddot z = {U_z} / m - g\qquad \ddot \psi = {{{U_\psi }} / {{I_{zz}}}} \end{align}
Let
![]() ${\ddot z_1} = \ddot z + g$
, define state vectors
${\ddot z_1} = \ddot z + g$
, define state vectors
![]() $x = {[x,y,{z_1},\phi ,\theta ,\psi ,\dot x,\dot y,{\dot z_1},\dot \phi ,\dot \theta ,\dot \psi ]^{\rm{T}}}$
,
$x = {[x,y,{z_1},\phi ,\theta ,\psi ,\dot x,\dot y,{\dot z_1},\dot \phi ,\dot \theta ,\dot \psi ]^{\rm{T}}}$
,
![]() $y = {[x,y,{z_1},\phi ,\theta ,\psi ]^{\rm{T}}}$
, the system inputs
$y = {[x,y,{z_1},\phi ,\theta ,\psi ]^{\rm{T}}}$
, the system inputs
![]() $u = {[{u_1},{u_2},{u_3},{u_4}]^{\rm{T}}}$
. By utilising the state vectors, the linearised model of the quadrotor UAV is obtained as shown in Equation (4).
$u = {[{u_1},{u_2},{u_3},{u_4}]^{\rm{T}}}$
. By utilising the state vectors, the linearised model of the quadrotor UAV is obtained as shown in Equation (4).
 \begin{equation}\left\{ \begin{array}{l}{\dot x(t) = Ax(t) + Bu(t)}\\[4pt]y(t) = Cx(t)\end{array} \right.\end{equation}
\begin{equation}\left\{ \begin{array}{l}{\dot x(t) = Ax(t) + Bu(t)}\\[4pt]y(t) = Cx(t)\end{array} \right.\end{equation}
where
 \begin{equation*}A = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\[4pt]0 & 0 & 0 & 0 & g & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & { - g} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}} \right]\end{equation*}
\begin{equation*}A = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\[4pt]0 & 0 & 0 & 0 & g & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & { - g} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}} \right]\end{equation*}
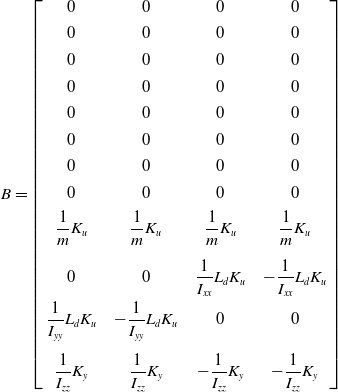 \begin{equation*}B = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]{\dfrac{1}{m}{K_u}} & {\dfrac{1}{m}{K_u}} & {\dfrac{1}{m}{K_u}} & {\dfrac{1}{m}{K_u}}\\[12pt]0 & 0 & {\dfrac{1}{{{I_{xx}}}}{L_d}{K_u}} & { - \dfrac{1}{{{I_{xx}}}}{L_d}{K_u}}\\[8pt]{\dfrac{1}{{{I_{yy}}}}{L_d}{K_u}} & { - \dfrac{1}{{{I_{yy}}}}{L_d}{K_u}} & 0 & 0\\[14pt]{\dfrac{1}{{{I_{zz}}}}{K_y}} & {\dfrac{1}{{{I_{zz}}}}{K_y}} & { - \dfrac{1}{{{I_{zz}}}}{K_y}} & { - \dfrac{1}{{{I_{zz}}}}{K_y}}\end{array}} \right]\end{equation*}
\begin{equation*}B = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0\\[4pt]{\dfrac{1}{m}{K_u}} & {\dfrac{1}{m}{K_u}} & {\dfrac{1}{m}{K_u}} & {\dfrac{1}{m}{K_u}}\\[12pt]0 & 0 & {\dfrac{1}{{{I_{xx}}}}{L_d}{K_u}} & { - \dfrac{1}{{{I_{xx}}}}{L_d}{K_u}}\\[8pt]{\dfrac{1}{{{I_{yy}}}}{L_d}{K_u}} & { - \dfrac{1}{{{I_{yy}}}}{L_d}{K_u}} & 0 & 0\\[14pt]{\dfrac{1}{{{I_{zz}}}}{K_y}} & {\dfrac{1}{{{I_{zz}}}}{K_y}} & { - \dfrac{1}{{{I_{zz}}}}{K_y}} & { - \dfrac{1}{{{I_{zz}}}}{K_y}}\end{array}} \right]\end{equation*}
 \begin{equation*}C = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\end{array}} \right]\end{equation*}
\begin{equation*}C = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\[4pt]0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\end{array}} \right]\end{equation*}
Whether the actuator can fully realise the ability of the controller to control the action
![]() $u(t)$
depends largely on its health level. Assuming that the initial execution capability of the ith actuator is
$u(t)$
depends largely on its health level. Assuming that the initial execution capability of the ith actuator is
![]() ${c_{ia0}}$
and the degradation state is
${c_{ia0}}$
and the degradation state is
![]() ${d_i}(t)$
, then the degradation rate of the actuator is
${d_i}(t)$
, then the degradation rate of the actuator is
![]() ${\lambda _i}(t) = {d_i}(t)/{c_{ia0}}$
. The loss matrix of actuator control efficiency is
${\lambda _i}(t) = {d_i}(t)/{c_{ia0}}$
. The loss matrix of actuator control efficiency is
![]() $\Gamma = diag\{ {\lambda _1}(t),{\lambda _2}(t), \cdots ,{\lambda _m}(t)\} $
,
$\Gamma = diag\{ {\lambda _1}(t),{\lambda _2}(t), \cdots ,{\lambda _m}(t)\} $
,
![]() $m$
represents the number of actuators,
$m$
represents the number of actuators,
![]() ${\lambda _i}(t) = 0$
indicating that the actuator has not degraded and
${\lambda _i}(t) = 0$
indicating that the actuator has not degraded and
![]() ${\lambda _i}(t) = 1$
indicating that the actuator has completely failed. Thus, the actual output of the actuator at time t can be expressed as
${\lambda _i}(t) = 1$
indicating that the actuator has completely failed. Thus, the actual output of the actuator at time t can be expressed as
![]() ${u_a}{\rm{(}}t) = {\rm{(}}I{\rm{ - }}\Gamma )u{\rm{(}}t)$
.
${u_a}{\rm{(}}t) = {\rm{(}}I{\rm{ - }}\Gamma )u{\rm{(}}t)$
.
The linear model of a quadrotor UAV considering actuator degradation is mathematically represented as Equation (5):
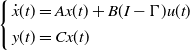 \begin{equation}\left\{ {\begin{array}{l}{\dot x(t) = Ax(t) + B(I - \Gamma )u(t)}\\[4pt]y(t) = Cx(t)\end{array}} \right.\end{equation}
\begin{equation}\left\{ {\begin{array}{l}{\dot x(t) = Ax(t) + B(I - \Gamma )u(t)}\\[4pt]y(t) = Cx(t)\end{array}} \right.\end{equation}
2.2 Construction of autonomous PdM architecture
The autonomous PdM of a UAV refers to the real-time prediction of RUL based on the airframe condition monitoring data, and the autonomous maintenance through the appropriate adjustment of the control strategy as needed. Therefore, to make a quadrotor UAV with multi-actuator degradation have PdM function should first start with the construction of an autonomous PdM architecture,as shown in Fig. 2. The system includes modules such as the airframe, actuators, LF-MPC and PdM. The core functions of the PdM module are twofold: first, TSKF is used to estimate the UAV state and actuators degradation states in real-time when they are degraded, and then determine the UAV failure threshold, predict the RUL of the airframe; the second is to determine whether the UAV needs autonomous maintenance based on RUL and provide maintenance strategies. That is, when RUL does not meet the expected working time limit, LF-MPC is used to enhance the constraints imposed on the control action on the actuator, slow down actuator degradation and extend the effective service time of the quadrotor UAV to achieve autonomous maintenance.
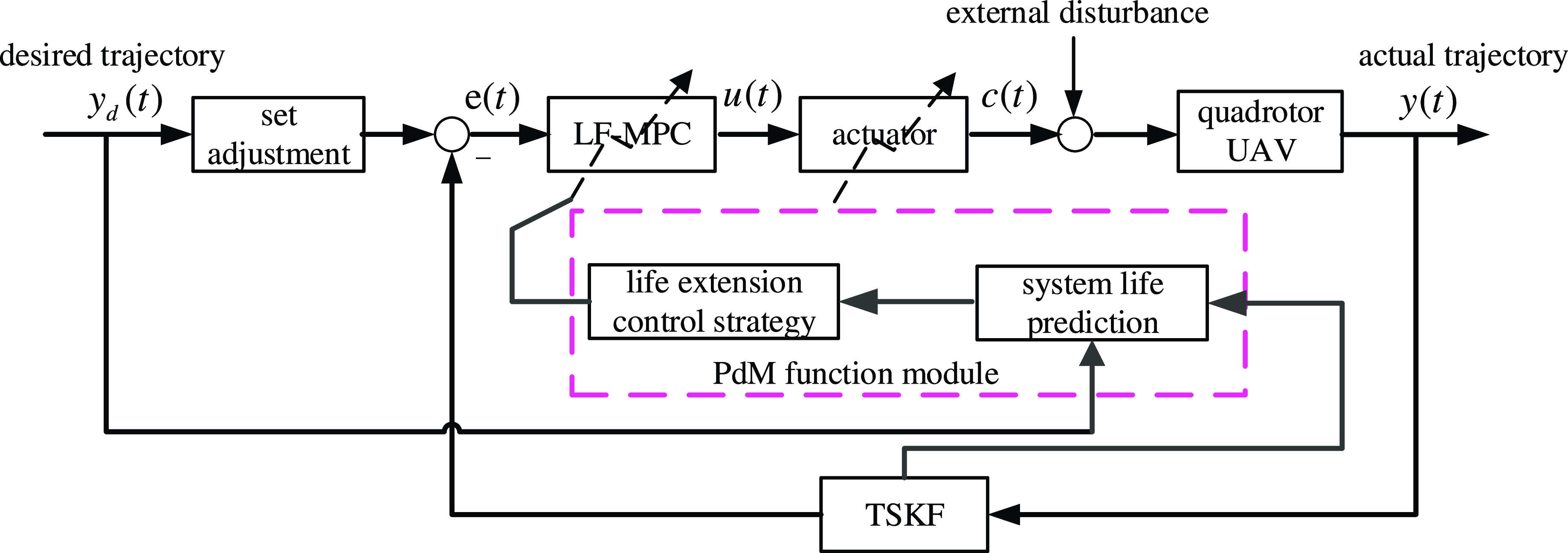
Figure 2. Structure diagram of autonomous maintenance of quadrotor UAV.
Where
![]() ${y_d}(t)$
is the expected trajectory,
${y_d}(t)$
is the expected trajectory,
![]() $y(t)$
is the actual trajectory,
$y(t)$
is the actual trajectory,
![]() $e(t)$
is the system deviation, and
$e(t)$
is the system deviation, and
![]() $u(t)$
is the control effect imposed on the actuator.
$u(t)$
is the control effect imposed on the actuator.
3.0 Hidden degradation description and RUL prediction of the actuators for a quadrotor UAV
From Fig. 2, it can be seen that actuator degradation, as a hidden degradation variable, acts on the quadrotor UAV body and affects the airframe performance. Therefore, the failure threshold of the UAV can be determined by the body performance. The airframe performance of the UAV based on the definition of UAV position and attitude can reflect its health status more comprehensively. The TSKF algorithm can obtain the optimal estimation of drone state
![]() $x$
and actuator degradation rate
$x$
and actuator degradation rate
![]() $\gamma $
while minimising mean square error.
$\gamma $
while minimising mean square error.
3.1 Description of the actuator degradation process
The brushless DC motor is the power source of the quadrotor UAV, its health status directly determines the service life of the UAV. During UAV flight, the execution force of the motor will decrease due to stator coil aging, excessive rotor shaft friction, and magnetic degradation. Considering that the above degradation processes all have nonlinear stationary degradation characteristics, the degradation of each actuator of the UAV can be modeled using the Wiener process, which is described as follows:
where
![]() $m = 1, \cdots ,4$
denotes the number of actuators. For the mth actuator,
$m = 1, \cdots ,4$
denotes the number of actuators. For the mth actuator,
![]() ${d^{(m)}}(0)$
represents the initial degradation of the actuator, without loss of generality, let
${d^{(m)}}(0)$
represents the initial degradation of the actuator, without loss of generality, let
![]() ${d^{(m)}}(0) = 0$
. represents the standard Brownian motion, while
${d^{(m)}}(0) = 0$
. represents the standard Brownian motion, while
![]() ${\mu ^{(m)}}(t;\,{\theta ^{(m)}})$
and
${\mu ^{(m)}}(t;\,{\theta ^{(m)}})$
and
![]() $\sigma _B^{(m)}$
represent the drift and diffusion coefficients of the degeneration process, respectively.
$\sigma _B^{(m)}$
represent the drift and diffusion coefficients of the degeneration process, respectively.
![]() ${\mu ^{(m)}}(t;\,{\theta ^{(m)}})$
is a nonlinear function of time, and this paper uses
${\mu ^{(m)}}(t;\,{\theta ^{(m)}})$
is a nonlinear function of time, and this paper uses
![]() ${\mu ^{(m)}}(t;\,{\theta ^{(m)}}){\rm{ = }}{\alpha ^{(m)}}{\beta ^{(m)}}{t^{{\beta ^{(m)}} - 1}}$
to characterise the nonlinear characteristics of the model.
${\mu ^{(m)}}(t;\,{\theta ^{(m)}}){\rm{ = }}{\alpha ^{(m)}}{\beta ^{(m)}}{t^{{\beta ^{(m)}} - 1}}$
to characterise the nonlinear characteristics of the model.
It is a prerequisite and foundation for autonomous PdM to obtain online observation data to estimate the hidden state and predict the RUL. Taking actuator degradation as a type of unknown bias in the system, TSKF can be used to estimate the system state and degradation rate while minimising the impact of measurement noise, thereby achieving more reliable estimation performance.
Discretise Equation (5) to obtain
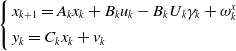 \begin{equation}\left\{ \begin{array}{l}{{x_{k + 1}} = {A_k}{x_k} + {B_k}u{}_k - {B_k}U{}_k{\gamma _k} + \omega _k^x}\\[4pt]{{y_k} = {C_k}{x_k} + {v_k}}\end{array} \right.\end{equation}
\begin{equation}\left\{ \begin{array}{l}{{x_{k + 1}} = {A_k}{x_k} + {B_k}u{}_k - {B_k}U{}_k{\gamma _k} + \omega _k^x}\\[4pt]{{y_k} = {C_k}{x_k} + {v_k}}\end{array} \right.\end{equation}
Here, the system noise
![]() $\omega _k^x$
and measurement noise
$\omega _k^x$
and measurement noise
![]() ${v_k}$
are uncorrelated Gaussian white noise with zero mean,
${v_k}$
are uncorrelated Gaussian white noise with zero mean,
![]() $Q_k^x$
and
$Q_k^x$
and
![]() ${R_k}$
are the variance matrices of the two, respectively.
${R_k}$
are the variance matrices of the two, respectively.
 \begin{equation*}{\gamma _k} = \left[ {\begin{array}{*{20}{c}}{\lambda _k^{(1)}}\\[4pt]{\lambda _k^{(2)}}\\[4pt] \vdots \\[4pt]{\lambda _k^{(m)}}\end{array}} \right],0 \lt \lambda _k^{(m)} \lt 1;\,m = 1,2, \cdots ,4,\,{U_k} = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}{u_k^{(1)}} & 0 & \cdots & 0\\[4pt]0 & {u_k^{(2)}} & {} & \vdots \\[4pt] \vdots & {} & \ddots & 0\\[4pt]0 & \cdots & 0 & {u_k^{(m)}}\end{array}} \right],\,{\gamma _{k + 1}} = {\gamma _k} + \omega _k^\gamma \end{equation*}
\begin{equation*}{\gamma _k} = \left[ {\begin{array}{*{20}{c}}{\lambda _k^{(1)}}\\[4pt]{\lambda _k^{(2)}}\\[4pt] \vdots \\[4pt]{\lambda _k^{(m)}}\end{array}} \right],0 \lt \lambda _k^{(m)} \lt 1;\,m = 1,2, \cdots ,4,\,{U_k} = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}{u_k^{(1)}} & 0 & \cdots & 0\\[4pt]0 & {u_k^{(2)}} & {} & \vdots \\[4pt] \vdots & {} & \ddots & 0\\[4pt]0 & \cdots & 0 & {u_k^{(m)}}\end{array}} \right],\,{\gamma _{k + 1}} = {\gamma _k} + \omega _k^\gamma \end{equation*}
The bias process propagation noise
![]() $\omega _k^\gamma $
is an uncorrelated Gaussian white noise with zero means, and its covariance matrix is represented by
$\omega _k^\gamma $
is an uncorrelated Gaussian white noise with zero means, and its covariance matrix is represented by
![]() $Q_k^\gamma $
.
$Q_k^\gamma $
.
The augmented discrete linear time-varying state space model with bias is formulated as
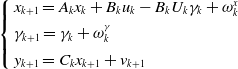 \begin{equation}\left\{ \begin{array}{l}{x_{k + 1}} = {A_k}{x_k} + {B_k}u{}_k - {B_k}U{}_k{\gamma _k} + \omega _k^x\\[4pt]{\gamma _{k + 1}} = {\gamma _k} + \omega _k^\gamma \\[4pt]{{y_{k + 1}} = {C_k}{x_{k + 1}} + {v_{k + 1}}}\end{array} \right.\end{equation}
\begin{equation}\left\{ \begin{array}{l}{x_{k + 1}} = {A_k}{x_k} + {B_k}u{}_k - {B_k}U{}_k{\gamma _k} + \omega _k^x\\[4pt]{\gamma _{k + 1}} = {\gamma _k} + \omega _k^\gamma \\[4pt]{{y_{k + 1}} = {C_k}{x_{k + 1}} + {v_{k + 1}}}\end{array} \right.\end{equation}
The minimum variance solution for estimating actuator degradation rate and state truth using TSKF is as follows:
Bias estimation
Unbiased state estimation
Filter residual and its covariance matrix
Coupled equations
The state optimal estimate and its estimation error covariance matrix are denoted by
The real degradation information
![]() $d_k^{(m)}$
of each actuator can be accurately obtained based on the actuator degradation rate
$d_k^{(m)}$
of each actuator can be accurately obtained based on the actuator degradation rate
![]() ${\hat \gamma _k}$
estimated by TSKF, which serves as a fundamental basis for the precise prediction of the RUL for a UAV. According to the definition of degradation rate,
${\hat \gamma _k}$
estimated by TSKF, which serves as a fundamental basis for the precise prediction of the RUL for a UAV. According to the definition of degradation rate,
![]() $d_k^{(m)}$
can be obtained as shown in Equation (27).
$d_k^{(m)}$
can be obtained as shown in Equation (27).
According to the estimated hidden degradation of the actuator, a more accurate distribution of the RUL for a UAV can be obtained by real-time updating.
3.2 Analysis of the degradation process of quadrotor UAV under actuator hidden degradation
Usually, the motors with the same parameters are installed on each rotor of the quadrotor UAV. During flight, degradation occurs due to factors such as coil aging and magnetic degradation or other factors. At the same time, due to various uncertain factors such as air interference and foreign matter, there are individual differences in the degradation process and the coupled superposition effect of common degradation. There are significant differences between multi-actuator degradation and single-actuator degradation on the performance of quadrotor UAVs, resulting in the uncertainty of
![]() ${t_n}$
,
${t_n}$
,
![]() ${t_{sf}}$
and
${t_{sf}}$
and
![]() ${t_{af}}$
. Where
${t_{af}}$
. Where
![]() ${t_n}$
,
${t_n}$
,
![]() ${t_{sf}}$
and
${t_{sf}}$
and
![]() ${t_{af}}$
represent the time when the airframe enters degradation from the normal state, the time when the airframe performance does not meet the requirements and the time when the actuator fails.
${t_{af}}$
represent the time when the airframe enters degradation from the normal state, the time when the airframe performance does not meet the requirements and the time when the actuator fails.
For the quadrotor UAV, failure means that the airframe performance no longer meets the requirements, and the actuator has not reached its failure threshold at this time. As an important performance index to measure the health status of equipment or system, a HD can reflect the health status of equipment or system more comprehensively. Therefore, the health state of the quadrotor UAV is quantified as a real-time HD to measure the health of the quadrotor UAV at each monitoring time, also the system failure threshold can be defined according to the HD.
Assuming that the desired state of the hovering quadrotor UAV is represented by the sample mean
![]() $\mu = {x_d} = {({x_{1d}},{x_{2d}}, \cdots ,{x_{12d}})^T}$
and the actual state estimated by the kth monitoring point is denoted as
$\mu = {x_d} = {({x_{1d}},{x_{2d}}, \cdots ,{x_{12d}})^T}$
and the actual state estimated by the kth monitoring point is denoted as
![]() $\tilde x = {({\tilde x_1},{\tilde x_2}, \cdots ,{\tilde x_{12}})^T}$
, then the Mahalanobis distance can be calculated.
$\tilde x = {({\tilde x_1},{\tilde x_2}, \cdots ,{\tilde x_{12}})^T}$
, then the Mahalanobis distance can be calculated.
where
![]() $\Sigma $
is the covariance matrix.
$\Sigma $
is the covariance matrix.
The Mahalanobis distance reflects the degree to which the current state deviates from the desired state. A negative function is used to establish the relationship between Mahalanobis distance
![]() $MD(\tilde x)$
and health degree
$MD(\tilde x)$
and health degree
![]() $HD(\tilde x)$
$HD(\tilde x)$
where b represents the shape parameter, with b>0.
Let
![]() $H{D_n}$
,
$H{D_n}$
,
![]() $H{D_{sf}}$
denote the health degree of the UAV from the normal working state to the degraded state and the HD when the airframe performance does not meet the requirements, respectively. Considering the full life cycle, it is assumed that multiple actuators have different degradation processes, and curves 1, 2, 3 and 4 in Fig. 3 give one of the degradation combinations. In Fig. 3,
$H{D_{sf}}$
denote the health degree of the UAV from the normal working state to the degraded state and the HD when the airframe performance does not meet the requirements, respectively. Considering the full life cycle, it is assumed that multiple actuators have different degradation processes, and curves 1, 2, 3 and 4 in Fig. 3 give one of the degradation combinations. In Fig. 3,
![]() ${l_n}$
,
${l_n}$
,
![]() ${l_{sf}}$
, and
${l_{sf}}$
, and
![]() ${l_{af}}$
represent the critical threshold when the quadrotor UAV from normal work to degradation, the degradation threshold when the airframe performance does not meet the requirements, and the comprehensive degradation threshold when actuator failure, respectively. For each actuator, the degree of degradation is different, resulting in
${l_{af}}$
represent the critical threshold when the quadrotor UAV from normal work to degradation, the degradation threshold when the airframe performance does not meet the requirements, and the comprehensive degradation threshold when actuator failure, respectively. For each actuator, the degree of degradation is different, resulting in
![]() ${t_n}$
,
${t_n}$
,
![]() ${t_{sf}}$
and
${t_{sf}}$
and
![]() ${t_{af}}$
are different. Therefore, to judge the influence of the degradation degree of each actuator on the airframe performance more conveniently, the comprehensive degradation quantity
${t_{af}}$
are different. Therefore, to judge the influence of the degradation degree of each actuator on the airframe performance more conveniently, the comprehensive degradation quantity
![]() $ds(t)$
(shown in the red curve in Fig. 3) can be constructed by fusing the degradation state of each actuator. In the case of multi-actuator degradation, it becomes more direct to predict the RUL of the airframe with the
$ds(t)$
(shown in the red curve in Fig. 3) can be constructed by fusing the degradation state of each actuator. In the case of multi-actuator degradation, it becomes more direct to predict the RUL of the airframe with the
![]() $HD$
as a constraint.
$HD$
as a constraint.
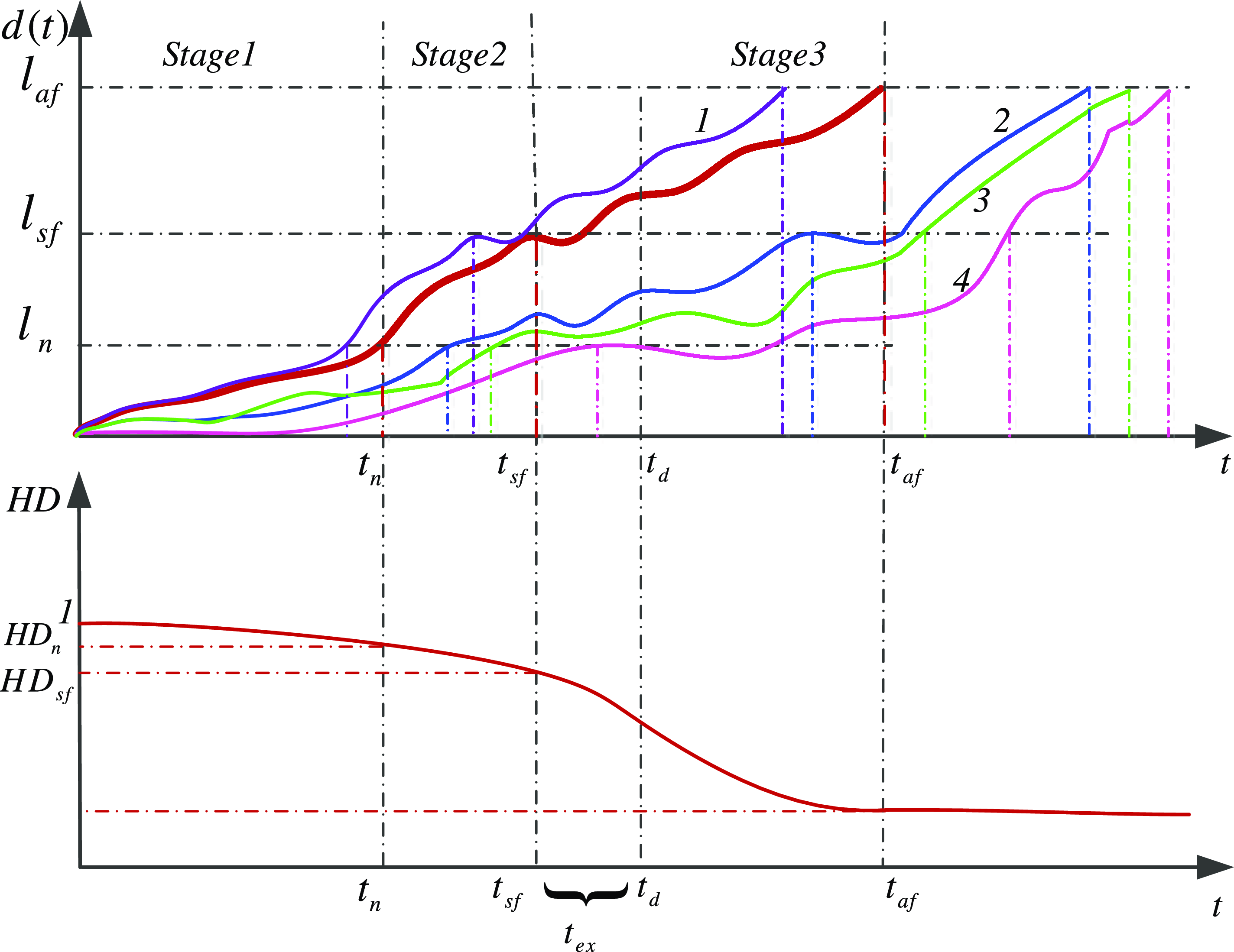
Figure 3. Schematic diagram of the actuator degradation process based on HD.
The comprehensive degradation of actuators based on the definition of airframe HD can be specifically expressed as follows:
Stage 1,
![]() $HD \in (H{D_n},1]$
, the UAV meets the work performance requirements, the integrated degradation
$HD \in (H{D_n},1]$
, the UAV meets the work performance requirements, the integrated degradation
![]() $ds(t) \lt {l_n}$
, and the degradation of each actuator has little impact on the overall performance of the UAV.
$ds(t) \lt {l_n}$
, and the degradation of each actuator has little impact on the overall performance of the UAV.
Stage 2,
![]() $HD \in [H{D_{sf}},H{D_n}]$
, the performance of the UAV decreases, and the comprehensive degradation
$HD \in [H{D_{sf}},H{D_n}]$
, the performance of the UAV decreases, and the comprehensive degradation
![]() $ds(t) \in [{l_{sf}},{l_n}]$
, indicating that the degradation degree of the actuator is gradually aggravated, which leads to the degradation of the UAV performance, and the RUL may not meet the working deadline requirements.
$ds(t) \in [{l_{sf}},{l_n}]$
, indicating that the degradation degree of the actuator is gradually aggravated, which leads to the degradation of the UAV performance, and the RUL may not meet the working deadline requirements.
Stage 3,
![]() $HD \in [0,H{D_{{\rm{s}}f}})$
, the performance of the UAV does not meet the requirements, and the comprehensive degradation
$HD \in [0,H{D_{{\rm{s}}f}})$
, the performance of the UAV does not meet the requirements, and the comprehensive degradation
![]() $ds(t) \gt {l_{sf}}$
, even if each actuator does not fail, but the HD of the quadrotor UAV is less than
$ds(t) \gt {l_{sf}}$
, even if each actuator does not fail, but the HD of the quadrotor UAV is less than
![]() $H{D_{sf}}$
, and the system fails at this time.
$H{D_{sf}}$
, and the system fails at this time.
3.3 RUL prediction of quadrotor UAV under hidden degradation of actuators
The comprehensive degradation variable, which combines the degradation state of each actuator, is undoubtedly a healthy indicator of the airframe performance. According to the expected airframe performance index, the system failure threshold of unsatisfactory performance is obtained, and then the RUL of a UAV with multi-actuator degradation can be predicted.
Since the degradation degree of each actuator has different effects on the airframe performance, each degradation quantity should not be treated the same when calculating the comprehensive degradation quantity, and different weights should be given according to the degradation process. The basic idea of the entropy weight method is to determine the objective weight according to the degradation degree of each degradation variable [Reference Xia, Yang, Lin, Xie and Zhang28]. In general, if the information entropy of a certain actuator degradation is smaller, it indicates that the degree of actuator degradation is greater, the more information it provides, the greater role it can play in the comprehensive evaluation, and the greater its weight. And vice versa, the steps for calculating the comprehensive degradation quantity using the entropy weight method are as follows.
-
(1) Data standardisation
Let
 $dat{a_{kj}} = ({d^{(m)}})^{\prime},(k = 1, \cdots ,n;\,j = 1, \cdots ,m)$
denote m actuators and n samples, and the min-max normalisation method is used to normalise the degradation data of each actuator(30)
$dat{a_{kj}} = ({d^{(m)}})^{\prime},(k = 1, \cdots ,n;\,j = 1, \cdots ,m)$
denote m actuators and n samples, and the min-max normalisation method is used to normalise the degradation data of each actuator(30) \begin{equation}{\rho _{kj}} = \frac{{dat{a_{kj}} - {\rm{min}}(dat{a_k})}}{{{\rm{max}}(dat{a_k}) - {\rm{min}}(dat{a_k})}}\end{equation}
\begin{equation}{\rho _{kj}} = \frac{{dat{a_{kj}} - {\rm{min}}(dat{a_k})}}{{{\rm{max}}(dat{a_k}) - {\rm{min}}(dat{a_k})}}\end{equation}
-
(2) Information entropy of degradation quantity
(31)where, \begin{equation}{E_j} = - ln{(n)^{ - 1}}\sum\limits_{k = 1}^n {{P_{kj}}} ln{P_{kj}}\end{equation}
\begin{equation}{E_j} = - ln{(n)^{ - 1}}\sum\limits_{k = 1}^n {{P_{kj}}} ln{P_{kj}}\end{equation}
 ${P_{kj}} = {\rho _{kj}}/\sum\limits_{k = 1}^n {{\rho _{kj}}} $
,
${P_{kj}} = {\rho _{kj}}/\sum\limits_{k = 1}^n {{\rho _{kj}}} $
,
 ${\rho _{kj}}$
represent the jth actuator degradation of the kth sample; if
${\rho _{kj}}$
represent the jth actuator degradation of the kth sample; if
 ${P_{kj}} = 0$
, then
${P_{kj}} = 0$
, then
 $\mathop {\lim }\limits_{{P_{kj}} \to \infty } {P_{kj}}{\rm{ln}}{P_{kj}} = 0$
is defined.
$\mathop {\lim }\limits_{{P_{kj}} \to \infty } {P_{kj}}{\rm{ln}}{P_{kj}} = 0$
is defined.
-
(3) Degradation quantity weight
The weight of each degradation is calculated using the information entropy.
(32) \begin{equation}{W_j} = {{1 - {E_j}} \over {m - \sum\limits_{j = 1}^m {{E_j}} }}{\rm{,}}\,\,\,\,{\rm{j}} = 1,2, \cdots {\rm{4}}\end{equation}
\begin{equation}{W_j} = {{1 - {E_j}} \over {m - \sum\limits_{j = 1}^m {{E_j}} }}{\rm{,}}\,\,\,\,{\rm{j}} = 1,2, \cdots {\rm{4}}\end{equation}
-
(4) Comprehensive degradation
(33) \begin{equation}d{s_k} = \sum\limits_{j = 1}^m {{W_j}{\rm{dat}}{{\rm{a}}_{kj}}} \end{equation}
\begin{equation}d{s_k} = \sum\limits_{j = 1}^m {{W_j}{\rm{dat}}{{\rm{a}}_{kj}}} \end{equation}
The original degradation of the BLDC motor is random, so the comprehensive degradation quantity obtained based on the entropy weight method can be modeled by the Wiener process in (6). The increment
![]() $\Delta d{s_k} = d{s_{k + 1}} - d{s_k}$
of the amount of degradation between two consecutive detection instants follows a normal distribution,
$\Delta d{s_k} = d{s_{k + 1}} - d{s_k}$
of the amount of degradation between two consecutive detection instants follows a normal distribution,
![]() $\Delta d{s_k}\sim N(\alpha (t_{k + 1}^\beta - t_k^\beta ),\sigma _B^2\Delta {t_k})$
. Let
$\Delta d{s_k}\sim N(\alpha (t_{k + 1}^\beta - t_k^\beta ),\sigma _B^2\Delta {t_k})$
. Let
![]() $DS({t_k}) = d{s_k}$
denote the integrated degradation quantity at the current time
$DS({t_k}) = d{s_k}$
denote the integrated degradation quantity at the current time
![]() ${t_k}$
, and the integrated degradation state vector
${t_k}$
, and the integrated degradation state vector
![]() $D{S_{1:k}} = (d{s_1},d{s_2}, \cdots ,d{s_k})$
.
$D{S_{1:k}} = (d{s_1},d{s_2}, \cdots ,d{s_k})$
.
Thus, for the unknown parameter
![]() $\theta = (\alpha ,\beta ,{\sigma _B})$
of the model, the likelihood function of the unknown parameter
$\theta = (\alpha ,\beta ,{\sigma _B})$
of the model, the likelihood function of the unknown parameter
![]() $\theta $
in the degraded data
$\theta $
in the degraded data
![]() $D{S_{1:k}}$
is given by.
$D{S_{1:k}}$
is given by.
 \begin{equation}L({\rm{\theta }}|\Delta d{s_i}) = \prod\nolimits_{i = 1}^k {\frac{1}{{\sqrt {2\pi (\sigma _B^2\Delta {t_i})} }}exp\left[ { - \frac{{{{(\Delta d{s_{\mathop{\rm i}\nolimits} } - \alpha (t_{i + 1}^\beta - t_i^\beta ))}^2}}}{{2(\sigma _B^2\Delta {t_i})}}} \right]} \end{equation}
\begin{equation}L({\rm{\theta }}|\Delta d{s_i}) = \prod\nolimits_{i = 1}^k {\frac{1}{{\sqrt {2\pi (\sigma _B^2\Delta {t_i})} }}exp\left[ { - \frac{{{{(\Delta d{s_{\mathop{\rm i}\nolimits} } - \alpha (t_{i + 1}^\beta - t_i^\beta ))}^2}}}{{2(\sigma _B^2\Delta {t_i})}}} \right]} \end{equation}
Taking the logarithm of both sides of Equation (34) yields:
The logarithmic likelihood function (35) was maximised using the ‘fminsearch’ function in MATLAB simulation software, resulting in obtaining the maximum likelihood estimate
![]() $\hat \theta $
for the unknown parameter
$\hat \theta $
for the unknown parameter
![]() $\theta = (\alpha ,\beta ,{\sigma _B})$
.
$\theta = (\alpha ,\beta ,{\sigma _B})$
.
Assuming that the comprehensive failure threshold of multi-actuator degradation is
![]() ${l_{af}}$
, and according to the definition of the first reach threshold, its corresponding life distribution is as follows [Reference Si, Hu, Zhang, He and Zhou29]:
${l_{af}}$
, and according to the definition of the first reach threshold, its corresponding life distribution is as follows [Reference Si, Hu, Zhang, He and Zhou29]:
 \begin{equation}{{\mathop{f}\nolimits} _T}{\rm{(}}t|\hat \theta ) \approx \frac{{{l_{af}} - \hat \alpha {t^{\hat \beta }}{\rm{(}}1 - \hat \beta )}}{{{{\hat \sigma }_B}\sqrt {2\pi {t^3}} }}\exp \left\{ {\frac{{ - {{{\rm{(}}{l_{af}} - \hat \alpha {t^{\hat \beta }})}^2}}}{{2\hat \sigma _B^2t}}} \right\}\end{equation}
\begin{equation}{{\mathop{f}\nolimits} _T}{\rm{(}}t|\hat \theta ) \approx \frac{{{l_{af}} - \hat \alpha {t^{\hat \beta }}{\rm{(}}1 - \hat \beta )}}{{{{\hat \sigma }_B}\sqrt {2\pi {t^3}} }}\exp \left\{ {\frac{{ - {{{\rm{(}}{l_{af}} - \hat \alpha {t^{\hat \beta }})}^2}}}{{2\hat \sigma _B^2t}}} \right\}\end{equation}
![]() $H{D_{sf}}$
is selected as the index to determine the failure threshold of the quadrotor UAV, and the failure threshold
$H{D_{sf}}$
is selected as the index to determine the failure threshold of the quadrotor UAV, and the failure threshold
![]() ${l_{sf}}$
is defined as the corresponding multi-actuator comprehensive degradation when the health degree
${l_{sf}}$
is defined as the corresponding multi-actuator comprehensive degradation when the health degree
![]() $HD(\tilde x)$
is less than
$HD(\tilde x)$
is less than
![]() $H{D_{sf}}$
, then:
$H{D_{sf}}$
, then:
The life of the quadrotor UAV with hidden degradation of multi-actuators refers to the life of the airframe when it works normally to the minimum HD requirement, so the life of the UAV can be defined as
where inf is the infimum operator.
The RUL of the system is expressed as follows.
Let the comprehensive degradation variable be
![]() $d{s_k}$
and
$d{s_k}$
and
![]() ${l_k}$
be the RUL of the UAV predicted at the current time
${l_k}$
be the RUL of the UAV predicted at the current time
![]() ${t_k}$
. Referring to the literature [Reference Si, Hu, Zhang, He and Zhou29] and combining with the comprehensive degradation threshold determined by Equation (37), the PDF of the RUL for a quadrotor UAV is:
${t_k}$
. Referring to the literature [Reference Si, Hu, Zhang, He and Zhou29] and combining with the comprehensive degradation threshold determined by Equation (37), the PDF of the RUL for a quadrotor UAV is:
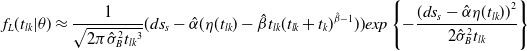 \begin{equation}{f_L}{\rm{(}}{t_{lk}}|\theta ) \approx \frac{1}{{\sqrt {2\pi \hat \sigma _B^2{t_{lk}}^3} }}{\rm{(}}d{s_s} - \hat \alpha {\rm{(}}\eta ({t_{lk}}) - \hat \beta {t_{lk}}{({t_{lk}} + {t_k})^{\hat \beta - 1}}{\rm{))}}exp\left\{ { - \frac{{{{{\rm{(}}d{s_s} - \hat \alpha \eta ({t_{lk}}))}^2}}}{{2\hat \sigma _B^2{t_{lk}}}}} \right\}\end{equation}
\begin{equation}{f_L}{\rm{(}}{t_{lk}}|\theta ) \approx \frac{1}{{\sqrt {2\pi \hat \sigma _B^2{t_{lk}}^3} }}{\rm{(}}d{s_s} - \hat \alpha {\rm{(}}\eta ({t_{lk}}) - \hat \beta {t_{lk}}{({t_{lk}} + {t_k})^{\hat \beta - 1}}{\rm{))}}exp\left\{ { - \frac{{{{{\rm{(}}d{s_s} - \hat \alpha \eta ({t_{lk}}))}^2}}}{{2\hat \sigma _B^2{t_{lk}}}}} \right\}\end{equation}
where
![]() $\eta ({t_{lk}}){\rm{ = }}{({t_k} + {t_{lk}})^{\hat \beta }} - t_k^{\hat \beta }$
,
$\eta ({t_{lk}}){\rm{ = }}{({t_k} + {t_{lk}})^{\hat \beta }} - t_k^{\hat \beta }$
,
![]() $d{s_s} = {l_{sf}} - d{s_k}$
.
$d{s_s} = {l_{sf}} - d{s_k}$
.
According to the analytical expression, the real-time prediction of the RUL of a quadrotor UAV can be quickly obtained.
4.0 MPC adaptive life extension strategy based on quadrotor UAV HD evaluation
The purpose of autonomous maintenance for quadrotor UAV is to slow down the degradation process of actuators, extend the continuous service life of the airframe, and shorten the interval between shutdowns and maintenance by sacrificing the health of the airframe to a small extent and quickly reconstructing the control law when the UAV does not meet the time constraints and the minimum HD requirements. How to design an appropriate life extension control strategy based on the RUL prediction results and the comprehensive degradation
![]() $ds(t)$
of the actuator, combined with the LF-MPC operation mechanism, is the key to extending the system life.
$ds(t)$
of the actuator, combined with the LF-MPC operation mechanism, is the key to extending the system life.
4.1 Life extension mechanism based on LF-MPC
To implement extended life control using MPC, the first step is to discretise model (4) based on the basic steps of MPC model prediction, feedback correction and rolling optimisation
 \begin{equation}\left\{ {\begin{array}{l}{{x_m}(k + 1) = {A_m}{x_m}(k) + {B_m}u(k)}\\[4pt]{y_m}(k) = {C_m}{x_m}(k)\end{array}} \right.\end{equation}
\begin{equation}\left\{ {\begin{array}{l}{{x_m}(k + 1) = {A_m}{x_m}(k) + {B_m}u(k)}\\[4pt]{y_m}(k) = {C_m}{x_m}(k)\end{array}} \right.\end{equation}
where
![]() $A_m = A^{\ast} \Delta t + I, B_m = B^{\ast} \Delta t$
.
$A_m = A^{\ast} \Delta t + I, B_m = B^{\ast} \Delta t$
.
The original state space model (41) is augmented to obtain
![]() $\Delta u$
as a manipulated variable for the future system output so that the feedback correction and rolling optimisation can be performed simultaneously.
$\Delta u$
as a manipulated variable for the future system output so that the feedback correction and rolling optimisation can be performed simultaneously.
Let
![]() $\Delta {x_m}(k) = {x_m}(k) - {x_m}(k - 1)$
,
$\Delta {x_m}(k) = {x_m}(k) - {x_m}(k - 1)$
,
![]() $\Delta u(k) = u(k) - u(k - 1)$
.
$\Delta u(k) = u(k) - u(k - 1)$
.
 \begin{equation}\left[ {\begin{array}{c}{\Delta {x_m}(k + 1)}\\[4pt]{{y_m}(k + 1)}\end{array}} \right] = \left[ {\begin{array}{c@{\quad}c}{{A_m}} & {{0_{12 \times 6}}}\\[4pt]{{C_m}{A_m}} & {{I_{6 \times 6}}}\end{array}} \right]\left[ {\begin{array}{c}{\Delta {x_m}(k)}\\[4pt]{{y_m}(k)}\end{array}} \right] + \left[ {\begin{array}{c}{{B_m}}\\[4pt]{{C_m}{B_m}}\end{array}} \right]\Delta u(k)\end{equation}
\begin{equation}\left[ {\begin{array}{c}{\Delta {x_m}(k + 1)}\\[4pt]{{y_m}(k + 1)}\end{array}} \right] = \left[ {\begin{array}{c@{\quad}c}{{A_m}} & {{0_{12 \times 6}}}\\[4pt]{{C_m}{A_m}} & {{I_{6 \times 6}}}\end{array}} \right]\left[ {\begin{array}{c}{\Delta {x_m}(k)}\\[4pt]{{y_m}(k)}\end{array}} \right] + \left[ {\begin{array}{c}{{B_m}}\\[4pt]{{C_m}{B_m}}\end{array}} \right]\Delta u(k)\end{equation}
Make
![]() ${x_u}(k) = {[\Delta {x_m}{(k)^T},{y_m}{(k)^T}]^T}$
, Equation (41) be expressed as
${x_u}(k) = {[\Delta {x_m}{(k)^T},{y_m}{(k)^T}]^T}$
, Equation (41) be expressed as
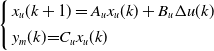 \begin{equation}\left\{ {\begin{array}{l}{{x_u}(k + 1) = {A_u}{x_u}(k) + {B_u}\Delta u(k)}\\[4pt]{{y_m}(k){\rm{ = }}{C_u}{x_u}(k)}\end{array}} \right.\end{equation}
\begin{equation}\left\{ {\begin{array}{l}{{x_u}(k + 1) = {A_u}{x_u}(k) + {B_u}\Delta u(k)}\\[4pt]{{y_m}(k){\rm{ = }}{C_u}{x_u}(k)}\end{array}} \right.\end{equation}
where
 ${A_u} = \left[ {\begin{array}{c@{\quad}c}{{A_m}} & {{0_{12 \times 6}}}\\[4pt]{{C_m}{A_m}} & {{I_{6 \times 6}}}\end{array}} \right]$
,
${A_u} = \left[ {\begin{array}{c@{\quad}c}{{A_m}} & {{0_{12 \times 6}}}\\[4pt]{{C_m}{A_m}} & {{I_{6 \times 6}}}\end{array}} \right]$
,
 ${B_u} = \left[ {\begin{array}{*{20}{c}}{{B_m}}\\[4pt]{{C_m}{B_m}}\end{array}} \right]$
,
${B_u} = \left[ {\begin{array}{*{20}{c}}{{B_m}}\\[4pt]{{C_m}{B_m}}\end{array}} \right]$
,
![]() ${C_u} = \left[{0_{6 \times 12}}{\begin{array}{*{20}{c}}{} I\end{array}_{6 \times 6}}\right]$
.
${C_u} = \left[{0_{6 \times 12}}{\begin{array}{*{20}{c}}{} I\end{array}_{6 \times 6}}\right]$
.
Assuming that the current time is
![]() $k$
,
$k$
,
![]() ${N_c}$
is the control step and
${N_c}$
is the control step and
![]() ${N_p}$
is the prediction step, a recursive Equation (44) can be obtained.
${N_p}$
is the prediction step, a recursive Equation (44) can be obtained.
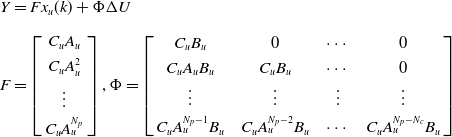 \begin{align}Y & = F{x_u}(k) + \Phi \Delta U\\[5pt]F & = \left[\begin{array}{c}C_u A_u\\[3pt]C_u A_u^2\\[3pt]\vdots\\[3pt]C_u A_u^{N_p}\end{array}\right], \Phi = \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}C_u B_u & 0 & \cdots & 0\\[3pt]C_u A_u B_u & C_u B_u & \cdots & 0\\[1pt]\vdots & \vdots & \vdots &\vdots\\[3pt]C_u A_u ^{N_p -1}B_u & C_u A_u ^{N_p -2}B_u & \cdots & C_u A_u ^{N_p- N_c}B_u\end{array}\right]\nonumber\end{align}
\begin{align}Y & = F{x_u}(k) + \Phi \Delta U\\[5pt]F & = \left[\begin{array}{c}C_u A_u\\[3pt]C_u A_u^2\\[3pt]\vdots\\[3pt]C_u A_u^{N_p}\end{array}\right], \Phi = \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}C_u B_u & 0 & \cdots & 0\\[3pt]C_u A_u B_u & C_u B_u & \cdots & 0\\[1pt]\vdots & \vdots & \vdots &\vdots\\[3pt]C_u A_u ^{N_p -1}B_u & C_u A_u ^{N_p -2}B_u & \cdots & C_u A_u ^{N_p- N_c}B_u\end{array}\right]\nonumber\end{align}
Define the prediction output
![]() $Y = [{y_m}(k + 1),{y_m}(k + 2), \cdots ,{y_m}(k + {N_p})]$
, control increment
$Y = [{y_m}(k + 1),{y_m}(k + 2), \cdots ,{y_m}(k + {N_p})]$
, control increment
![]() $\Delta U(k) = {[\Delta u(k){\rm{,}}\Delta u(k + 1){\rm{ ,}} \cdots {\rm{ ,}}\Delta u(k + {N_c} - 1)]^T}$
.
$\Delta U(k) = {[\Delta u(k){\rm{,}}\Delta u(k + 1){\rm{ ,}} \cdots {\rm{ ,}}\Delta u(k + {N_c} - 1)]^T}$
.
Set
![]() ${Y_d} = [{y_d}(k + 1),{y_d}(k + 2), \cdots ,{y_d}(k + {N_p})]$
be the system reference input at time
${Y_d} = [{y_d}(k + 1),{y_d}(k + 2), \cdots ,{y_d}(k + {N_p})]$
be the system reference input at time
![]() $k$
. To make the system output as close as possible to the input, for MPC control, the cost function is defined as follows.
$k$
. To make the system output as close as possible to the input, for MPC control, the cost function is defined as follows.
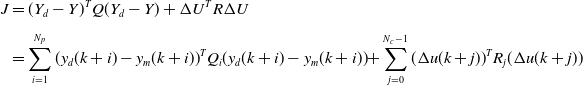 \begin{align}J & = ({Y_d} - Y{)^T}Q({Y_d} - Y) + \Delta {U^T}R\Delta U\nonumber\\[4pt]& = \sum\limits_{i = 1}^{{N_p}} {{{({y_d}(k + i) - {y_m}(k + i))}^T}{Q_i}({y_d}(k + i) - {y_m}(k + i))} {\rm{ + }}\sum\limits_{j = 0}^{{N_c} - 1} {{{(\Delta u(k + j))}^T}{R_j}(\Delta u(k + j))} \end{align}
\begin{align}J & = ({Y_d} - Y{)^T}Q({Y_d} - Y) + \Delta {U^T}R\Delta U\nonumber\\[4pt]& = \sum\limits_{i = 1}^{{N_p}} {{{({y_d}(k + i) - {y_m}(k + i))}^T}{Q_i}({y_d}(k + i) - {y_m}(k + i))} {\rm{ + }}\sum\limits_{j = 0}^{{N_c} - 1} {{{(\Delta u(k + j))}^T}{R_j}(\Delta u(k + j))} \end{align}
In the above equation, the first term reflects the ability of the UAV to follow the reference trajectory, and the second term reflects the requirement for the smooth change of the control quantities.
![]() $Q$
and
$Q$
and
![]() $R$
are the block diagonal matrices of
$R$
are the block diagonal matrices of
![]() ${Q_i}$
and
${Q_i}$
and
![]() ${R_i}$
, respectively; where,
${R_i}$
, respectively; where,
![]() ${Q_i} = diag{\{ {q_0}, \cdots ,{q_0}\} _{n \times n}}$
and
${Q_i} = diag{\{ {q_0}, \cdots ,{q_0}\} _{n \times n}}$
and
![]() ${R_i} = diag{\{ {r_0}, \cdots ,{r_0}\} _{m \times m}}$
are the error weight and control quantity weight,
${R_i} = diag{\{ {r_0}, \cdots ,{r_0}\} _{m \times m}}$
are the error weight and control quantity weight,
![]() ${q_0},{r_0}$
are the initial values of MPC. To adjust the parameters conveniently, the diagonal elements of matrices
${q_0},{r_0}$
are the initial values of MPC. To adjust the parameters conveniently, the diagonal elements of matrices
![]() $Q$
and
$Q$
and
![]() $R$
are selected as the same values here.
$R$
are selected as the same values here.
By seeking the extreme value of Equation (43), the optimal control increment at the current moment can be obtained.
Based on the idea of rolling optimisation, taking the first element of the sequence as the current control, then
In MPC, there are many parameters in each optimisation prediction window of the control sequence, which reduces the solution efficiency. The multi-objective control algorithm based on LF reduces the calculation amount by approaching the finite time domain control trajectory with fewer optimisation parameters, which can save more time for the implementation of autonomous PdM on a UAV.
At time k, the elements within the control trajectory
![]() $\Delta U$
are represented in the following impulse response form using discrete
$\Delta U$
are represented in the following impulse response form using discrete
![]() $\delta $
-functions combined with
$\delta $
-functions combined with
![]() $\Delta U$
.
$\Delta U$
.
where
 \begin{equation*}\left\{\begin{array}{l}\delta(i) = diag([\delta_1(i)\, \delta_2(i) \cdots \delta_m(i)] = diag \underbrace{([1\,\,1\cdots 1])}_m), i = 0\\[6pt]\delta(i) = diag \underbrace{([1\,\,1\cdots 1])}_m), i \neq 0\end{array}\right.\end{equation*}
\begin{equation*}\left\{\begin{array}{l}\delta(i) = diag([\delta_1(i)\, \delta_2(i) \cdots \delta_m(i)] = diag \underbrace{([1\,\,1\cdots 1])}_m), i = 0\\[6pt]\delta(i) = diag \underbrace{([1\,\,1\cdots 1])}_m), i \neq 0\end{array}\right.\end{equation*}
According to the definition of the LF,
![]() $\Delta u(k + i)$
in Equation (48) is denoted by
$\Delta u(k + i)$
in Equation (48) is denoted by
![]() ${L^T}(i)\eta $
${L^T}(i)\eta $
where
![]() $\eta = [{\eta _1}\quad {\eta _2}\quad \cdots\quad {\eta _m}]{}^T$
is the Laguerre coefficient and
$\eta = [{\eta _1}\quad {\eta _2}\quad \cdots\quad {\eta _m}]{}^T$
is the Laguerre coefficient and
![]() $L^T(i) = diag(L_1(i)^T,$
$L^T(i) = diag(L_1(i)^T,$
![]() $L_2(i)^T,\quad \cdots ,\quad L_m(i)^T),\quad i \in [1,{N_c}]$
denotes the Laguerre function.
$L_2(i)^T,\quad \cdots ,\quad L_m(i)^T),\quad i \in [1,{N_c}]$
denotes the Laguerre function.
Let
![]() ${L_q}(i) = {[{l_{1q}}(i)\quad {l_{2q}}(i)\quad \cdots\quad {l_{Nq}}(i)]^T}(q \in [1,m])$
, where
${L_q}(i) = {[{l_{1q}}(i)\quad {l_{2q}}(i)\quad \cdots\quad {l_{Nq}}(i)]^T}(q \in [1,m])$
, where
![]() $Nq$
is the number of approximation factors of the qth actuator. The relationship of LF at adjacent times is obtained by the iterative operation as follows.
$Nq$
is the number of approximation factors of the qth actuator. The relationship of LF at adjacent times is obtained by the iterative operation as follows.
where matrix
![]() ${A_{ql}}$
is a function of parameters
${A_{ql}}$
is a function of parameters
![]() ${\alpha _q}$
and
${\alpha _q}$
and
![]() ${\beta _q} = 1 - {\alpha _q}$
, and the initial condition is
${\beta _q} = 1 - {\alpha _q}$
, and the initial condition is
 \begin{equation}{A_{ql}} = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}{{\alpha _q}}& 0& 0& \cdots& 0\\[4pt]{{\beta _q}}& {{\alpha _q}}& 0& \cdots& 0\\[4pt]{ - {\alpha _q}{\beta _q}}& {{\beta _q}} &{{\alpha _q}} & \cdots &0\\[4pt] \vdots & \vdots & \vdots & \ddots & \vdots \\[4pt]{{\rm{ - }}{\alpha _q}^{{N_q} - 2}{\beta _q}}& {{\rm{ - }}{\alpha _q}^{{N_q} - 3}{\beta _q}}& {{\rm{ - }}{\alpha _q}^{{N_q} - 4}{\beta _q}} & \cdots &{{\alpha _q}}\end{array}} \right]\end{equation}
\begin{equation}{A_{ql}} = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}{{\alpha _q}}& 0& 0& \cdots& 0\\[4pt]{{\beta _q}}& {{\alpha _q}}& 0& \cdots& 0\\[4pt]{ - {\alpha _q}{\beta _q}}& {{\beta _q}} &{{\alpha _q}} & \cdots &0\\[4pt] \vdots & \vdots & \vdots & \ddots & \vdots \\[4pt]{{\rm{ - }}{\alpha _q}^{{N_q} - 2}{\beta _q}}& {{\rm{ - }}{\alpha _q}^{{N_q} - 3}{\beta _q}}& {{\rm{ - }}{\alpha _q}^{{N_q} - 4}{\beta _q}} & \cdots &{{\alpha _q}}\end{array}} \right]\end{equation}
Substituting (49) into (43) gives the state variables and output variables of the system at time i after time k as follows
 \begin{equation}\left\{ {\begin{array}{l}{{x_u}(k + i|k) = {A_u}^i{x_u}(k) + \sum\limits_{p = 0}^{i - 1} {{A_u}^{i - p - 1}} {B_u}L{{(p)}^T}\eta = {A_u}^i{x_u}(k) + \phi {{(i)}^T}\eta }\\[9pt]{{y_m}(k + i|k){\rm{ = }}{C_u}{x_u}(k + i|k){\rm{ = }}{C_u}{A_u}^i{x_u}(k) + {C_u}\phi {{(i)}^T}\eta }\end{array}} \right.\end{equation}
\begin{equation}\left\{ {\begin{array}{l}{{x_u}(k + i|k) = {A_u}^i{x_u}(k) + \sum\limits_{p = 0}^{i - 1} {{A_u}^{i - p - 1}} {B_u}L{{(p)}^T}\eta = {A_u}^i{x_u}(k) + \phi {{(i)}^T}\eta }\\[9pt]{{y_m}(k + i|k){\rm{ = }}{C_u}{x_u}(k + i|k){\rm{ = }}{C_u}{A_u}^i{x_u}(k) + {C_u}\phi {{(i)}^T}\eta }\end{array}} \right.\end{equation}
where
![]() $\phi {(i)^T} = \sum\limits_{p = 0}^{i - 1} {{A_u}^{i - p - 1}} {B_u}L{(p)^T}{\rm{, }}(i \in [1,{N_p}])$
.
$\phi {(i)^T} = \sum\limits_{p = 0}^{i - 1} {{A_u}^{i - p - 1}} {B_u}L{(p)^T}{\rm{, }}(i \in [1,{N_p}])$
.
By replacing
![]() $\Delta u(k + i)$
with
$\Delta u(k + i)$
with
![]() ${L^T}(i)\eta $
, the parameter
${L^T}(i)\eta $
, the parameter
![]() $\eta $
becomes the only optimised parameter vector to replace
$\eta $
becomes the only optimised parameter vector to replace
![]() $\Delta U$
. Due to the smaller dimension of parameter
$\Delta U$
. Due to the smaller dimension of parameter
![]() $\eta $
than
$\eta $
than
![]() $\Delta U$
, the calculation amount is reduced and the speed is improved, which is the advantage of LF-MPC over traditional MPC in life extension.
$\Delta U$
, the calculation amount is reduced and the speed is improved, which is the advantage of LF-MPC over traditional MPC in life extension.
According to the LF definition, substituting (49) into (45) yields.
Substituting Equation (53) into (54), retaining only the terms associated with
![]() $\eta $
, and obtain
$\eta $
, and obtain
 \begin{equation}J(k) = {\eta ^T}\left(\sum\limits_{i = 1}^{{N_p}} \phi (i)\Omega \phi (i) + R\right)\eta + 2{\eta ^T}\left(\sum\limits_{i = 1}^{{N_p}} {\phi (i)\Omega {A_u}^i{x_u}(k)} \right){\rm{ - }}2{\eta ^T}\left(\sum\limits_{i = 1}^{{N_p}} {\phi (i){C_u}^T{Q_i}{y_d}(k + i|k)} \right)\end{equation}
\begin{equation}J(k) = {\eta ^T}\left(\sum\limits_{i = 1}^{{N_p}} \phi (i)\Omega \phi (i) + R\right)\eta + 2{\eta ^T}\left(\sum\limits_{i = 1}^{{N_p}} {\phi (i)\Omega {A_u}^i{x_u}(k)} \right){\rm{ - }}2{\eta ^T}\left(\sum\limits_{i = 1}^{{N_p}} {\phi (i){C_u}^T{Q_i}{y_d}(k + i|k)} \right)\end{equation}
Let
![]() $\frac{{\partial J}}{{\partial \eta }}{\rm{ = }}0$
, then the parameter vector
$\frac{{\partial J}}{{\partial \eta }}{\rm{ = }}0$
, then the parameter vector
![]() $\eta $
that optimises the performance index can be obtained as
$\eta $
that optimises the performance index can be obtained as
 \begin{equation}{\eta ^ * } = \left(\sum\limits_{i = 1}^{{N_p}} \phi (i)\Omega \phi {{(i)}^T} + R\right)^{ - 1} \times \left(\sum\limits_{i = 1}^{{N_p}} \phi (i)\Xi ({y_d}(k + i) - {C_u}{A_u}^i{x_u}(k))\right) \end{equation}
\begin{equation}{\eta ^ * } = \left(\sum\limits_{i = 1}^{{N_p}} \phi (i)\Omega \phi {{(i)}^T} + R\right)^{ - 1} \times \left(\sum\limits_{i = 1}^{{N_p}} \phi (i)\Xi ({y_d}(k + i) - {C_u}{A_u}^i{x_u}(k))\right) \end{equation}
where
![]() $\Omega = {C_u}^T{Q_i}{C_u}$
,
$\Omega = {C_u}^T{Q_i}{C_u}$
,
![]() $\Xi = {C_u}^T{Q_i}$
.
$\Xi = {C_u}^T{Q_i}$
.
According to the life extension mechanism, by decreasing the element value of
![]() $Q$
and increasing the element value of
$Q$
and increasing the element value of
![]() $R$
, it is possible to relax the constraint of error performance indicators, reduce actuator execution pressure, and delay degradation, thereby achieving the goal of prolonging the RUL for the quadrotor UAV.
$R$
, it is possible to relax the constraint of error performance indicators, reduce actuator execution pressure, and delay degradation, thereby achieving the goal of prolonging the RUL for the quadrotor UAV.
Assuming that the expected safe working time of a quadrotor UAV is
![]() ${t_d}$
, in order to achieve the expected working time limit
${t_d}$
, in order to achieve the expected working time limit
![]() ${t_d}$
, the shortest expected life extension time
${t_d}$
, the shortest expected life extension time
![]() ${t_{ex}}$
should be calculated based on the RUL prediction result
${t_{ex}}$
should be calculated based on the RUL prediction result
![]() ${t_{lk}}$
at time
${t_{lk}}$
at time
![]() ${t_k}$
. When
${t_k}$
. When
![]() ${t_{ex}} \gt 0$
, the system needs to be maintained autonomously.
${t_{ex}} \gt 0$
, the system needs to be maintained autonomously.
4.2 Adaptive autonomous PdM strategy of LF-MPC based on HD
From the above analysis, it can be seen that there is a close relationship between actuator degradation and system performance. When the degradation is small, due to the effect of feedback control, the degradation has a relatively small impact on system performance, while when the degradation increases, the system performance will deteriorate. Due to the definition of the Mahalanobis distance HD, which comprehensively considers the impact of actuator degradation on various states of the system, can provide a more comprehensive evaluation of the impact of actuator degradation on the system. Therefore, when the quadrotor UAV does not meet the requirements of a working time limit, autonomous maintenance can adjust the weight matrices
![]() ${Q_i}$
and
${Q_i}$
and
![]() $R$
in real-time based on HD, to achieve a balance between steady-state performance and control capability of the UAV.
$R$
in real-time based on HD, to achieve a balance between steady-state performance and control capability of the UAV.
The UAV initially has no degradation, with
![]() $HD = 1$
. As the hidden degradation of the actuator increases, the airframe state deviates from the expected value, and the health level decreases. The more severe the degradation, the smaller the health level. Combining the HD evaluation results with maintenance requirements, degradation has a relatively small impact on the UAV during
$HD = 1$
. As the hidden degradation of the actuator increases, the airframe state deviates from the expected value, and the health level decreases. The more severe the degradation, the smaller the health level. Combining the HD evaluation results with maintenance requirements, degradation has a relatively small impact on the UAV during
![]() $HD \gt H{D_n}$
and does not require correction; when
$HD \gt H{D_n}$
and does not require correction; when
![]() $H{D_{sf}} \le HD \le H{D_{\rm{n}}}$
does not meet the working time limit
$H{D_{sf}} \le HD \le H{D_{\rm{n}}}$
does not meet the working time limit
![]() ${t_d}$
requirements, adjust the weight matrix. The greater the change in
${t_d}$
requirements, adjust the weight matrix. The greater the change in
![]() $HD$
, the greater the maintenance requirement. Increase the
$HD$
, the greater the maintenance requirement. Increase the
![]() ${Q_i}$
and
${Q_i}$
and
![]() $R$
adjustment scale, and the smaller the change in
$R$
adjustment scale, and the smaller the change in
![]() $HD$
, the smaller the maintenance requirement, and fine-tune
$HD$
, the smaller the maintenance requirement, and fine-tune
![]() ${Q_i}$
and
${Q_i}$
and
![]() $R$
; however, when
$R$
; however, when
![]() $HD \lt H{D_{sf}}$
, the correction of the weight matrices of
$HD \lt H{D_{sf}}$
, the correction of the weight matrices of
![]() ${Q_i}$
and
${Q_i}$
and
![]() $R$
should be stopped. In summary, the adjustment trend of the weight matrix integrating HD and maintenance demand in Fig. 4 can be obtained.
$R$
should be stopped. In summary, the adjustment trend of the weight matrix integrating HD and maintenance demand in Fig. 4 can be obtained.

Figure 4. Schematic diagram of weight matrix
![]() $\Delta q$
and
$\Delta q$
and
![]() $\Delta r$
adjustment based on HD.
$\Delta r$
adjustment based on HD.
It can be seen that the changes of
![]() $\Delta q$
and
$\Delta q$
and
![]() $\Delta r$
with
$\Delta r$
with
![]() $HD$
roughly follow an exponential law. Therefore, the matrices
$HD$
roughly follow an exponential law. Therefore, the matrices
![]() ${Q_i}$
and
${Q_i}$
and
![]() $R$
, and correction quantities
$R$
, and correction quantities
![]() $\Delta q$
and
$\Delta q$
and
![]() $\Delta r$
based on HD can be expressed as:
$\Delta r$
based on HD can be expressed as:
 \begin{equation}\left\{ {\begin{array}{l}{q(k + 1) = q(k) - \Delta q,\Delta q = \dfrac{1}{{{K_1} + {e^{HD}}}}}\\[10pt]{r(k + 1) = r(k) + \Delta r,\Delta r = \dfrac{1}{{{K_2} + {e^{HD}}}}}\end{array}} \right.\end{equation}
\begin{equation}\left\{ {\begin{array}{l}{q(k + 1) = q(k) - \Delta q,\Delta q = \dfrac{1}{{{K_1} + {e^{HD}}}}}\\[10pt]{r(k + 1) = r(k) + \Delta r,\Delta r = \dfrac{1}{{{K_2} + {e^{HD}}}}}\end{array}} \right.\end{equation}
where,
![]() $q(t) \geqslant {q_{min}}$
,
$q(t) \geqslant {q_{min}}$
,
![]() $r(t) \le {r_{max}}$
, the parameters can change the range of adjustment parameters
$r(t) \le {r_{max}}$
, the parameters can change the range of adjustment parameters
![]() $\Delta q$
and
$\Delta q$
and
![]() $\Delta r$
.
$\Delta r$
.
4.3 Autonomous PdM process of quadrotor UAV based on HD
For the quadrotor UAV with multi-actuator degradation, the TSKF method is used to estimate the degradation of each actuator and the UAV state in real-time, the entropy weight method is used to obtain the comprehensive variables and the system HD is calculated in real-time. Considering the system performance and deadline constraints, the online autonomous maintenance strategy of a quadrotor UAV is implemented as in Fig. 5.
5.0 Simulation experiment and result analysis
5.1 Experimental description
To verify the effectiveness of the proposed approach in the article, the object parameters were selected for simulation experiments as shown in Table 1. The LF-MPC control parameters are taken as follows:
![]() ${N_c} = 30$
,
${N_c} = 30$
,
![]() ${N_p} = 5$
. The Laguerre polynomial parameter is taken as
${N_p} = 5$
. The Laguerre polynomial parameter is taken as
![]() $\alpha = [0.7,0.7,0.7,0.7]$
,
$\alpha = [0.7,0.7,0.7,0.7]$
,
![]() ${N_q} = [7,7,7,7]$
. The initial values of the error weight and control quantity weight matrix are taken as
${N_q} = [7,7,7,7]$
. The initial values of the error weight and control quantity weight matrix are taken as
![]() ${q_0} = 2$
and
${q_0} = 2$
and
![]() ${r_0} = 0.01$
, respectively, and the constraints
${r_0} = 0.01$
, respectively, and the constraints
![]() ${q_{min}} = 1.5$
and
${q_{min}} = 1.5$
and
![]() ${r_{max}} = 1.0$
are satisfied, and the sampling period is
${r_{max}} = 1.0$
are satisfied, and the sampling period is
![]() $\Delta t = 0.1$
.
$\Delta t = 0.1$
.
Table 1. Physical parameters of quadrotor UAV

Assuming that the HDs of the quadrotor UAV is
![]() $H{D_n} = 0.9$
and
$H{D_n} = 0.9$
and
![]() $H{D_{sf}} = 0.7$
respectively when the airframe performance starts to degrade and does not meet the requirements, and the expected working time limit is
$H{D_{sf}} = 0.7$
respectively when the airframe performance starts to degrade and does not meet the requirements, and the expected working time limit is
![]() ${t_d} = 500min$
.
${t_d} = 500min$
.
5.2 RUL prediction of a quadrotor UAV
Set the initial value of the filter to
 \begin{align*}Q_{}^x = \left[ {\begin{array}{c@{\quad}c}{{{10}^{{\rm{ - }}10}} \times {I_{6 \times 6}}} & {{0_{6 \times 6}}}\\[4pt]{{0_{6 \times 6}}} &{{{10}^{{\rm{ - }}12}} \times {I_{6 \times 6}}}\end{array}} \right],\,\,{Q^v} = \left[ {\begin{array}{c@{\quad}c}{{{10}^{{\rm{ - }}12}} \times {I_{6 \times 6}}} & {{0_{6 \times 6}}}\\[4pt]{{0_{6 \times 6}}} &{{{10}^{{\rm{ - }}14}} \times {I_{6 \times 6}}}\end{array}} \right]\end{align*}
\begin{align*}Q_{}^x = \left[ {\begin{array}{c@{\quad}c}{{{10}^{{\rm{ - }}10}} \times {I_{6 \times 6}}} & {{0_{6 \times 6}}}\\[4pt]{{0_{6 \times 6}}} &{{{10}^{{\rm{ - }}12}} \times {I_{6 \times 6}}}\end{array}} \right],\,\,{Q^v} = \left[ {\begin{array}{c@{\quad}c}{{{10}^{{\rm{ - }}12}} \times {I_{6 \times 6}}} & {{0_{6 \times 6}}}\\[4pt]{{0_{6 \times 6}}} &{{{10}^{{\rm{ - }}14}} \times {I_{6 \times 6}}}\end{array}} \right]\end{align*}
Considering that the four actuators of the quadrotor UAV undergo varying degrees of degradation, the TSKF algorithm is applied to obtain the estimated value of the degradation process shown in Fig. 6. It can be seen that TSKF can effectively estimate the true values and reflect the actual degradation process.

Figure 5. Flow chart of autonomous PdM algorithm for quadrotor UAV based on HD.
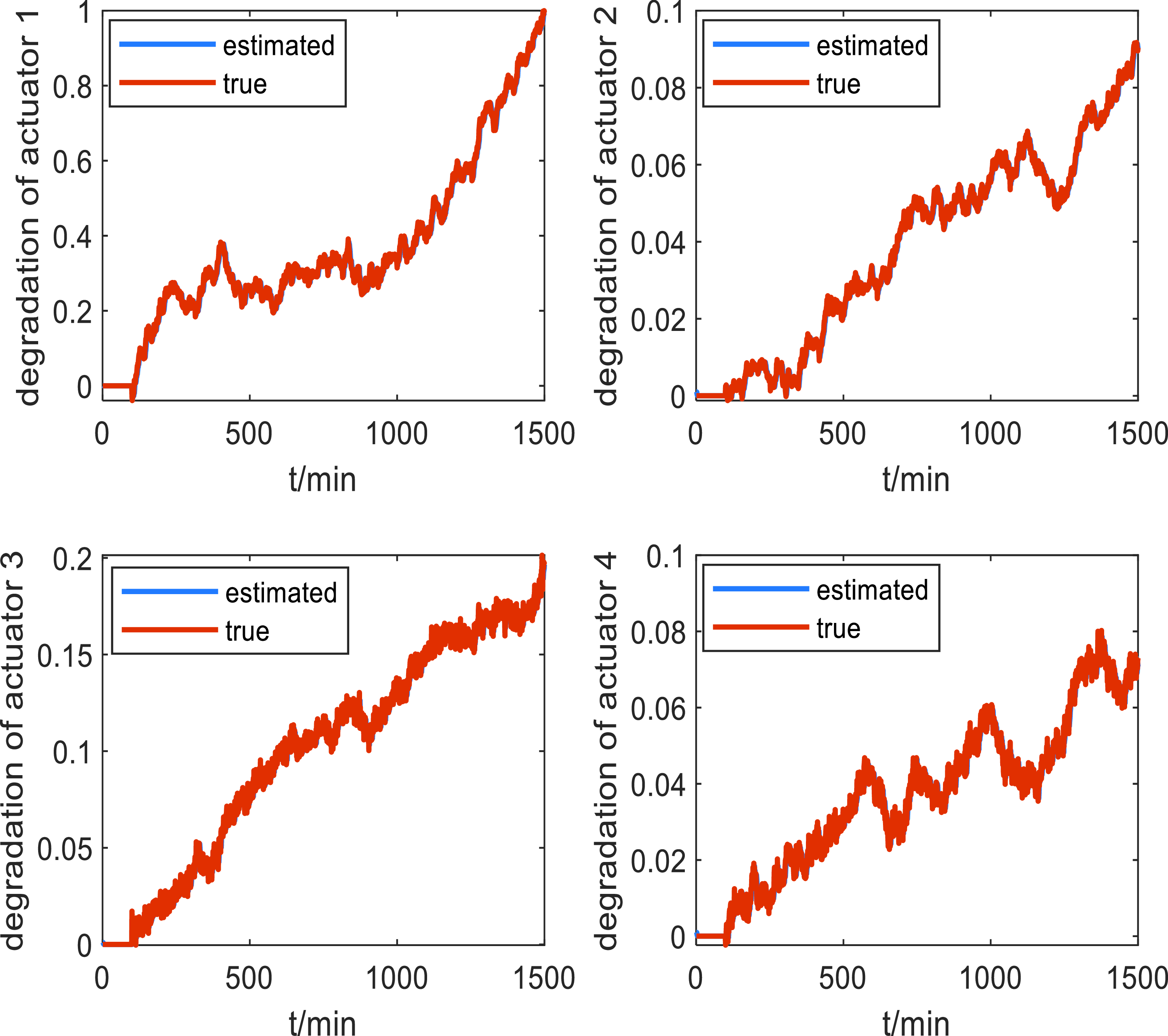
Figure 6. True value and estimated value of actuator degradation.
The curve of the comprehensive degradation quantity obtained by using the aforementioned entropy weight method is shown in Fig. 7. From the graph, it can be seen that the comprehensive degradation
![]() $ds(t)$
has a high consistency with the degradation trend of the severely degraded actuator 1, so the comprehensive degradation also follows the Wiener process, and the parameter estimation uses the ‘fminsearch’ function, which is obtained
$ds(t)$
has a high consistency with the degradation trend of the severely degraded actuator 1, so the comprehensive degradation also follows the Wiener process, and the parameter estimation uses the ‘fminsearch’ function, which is obtained
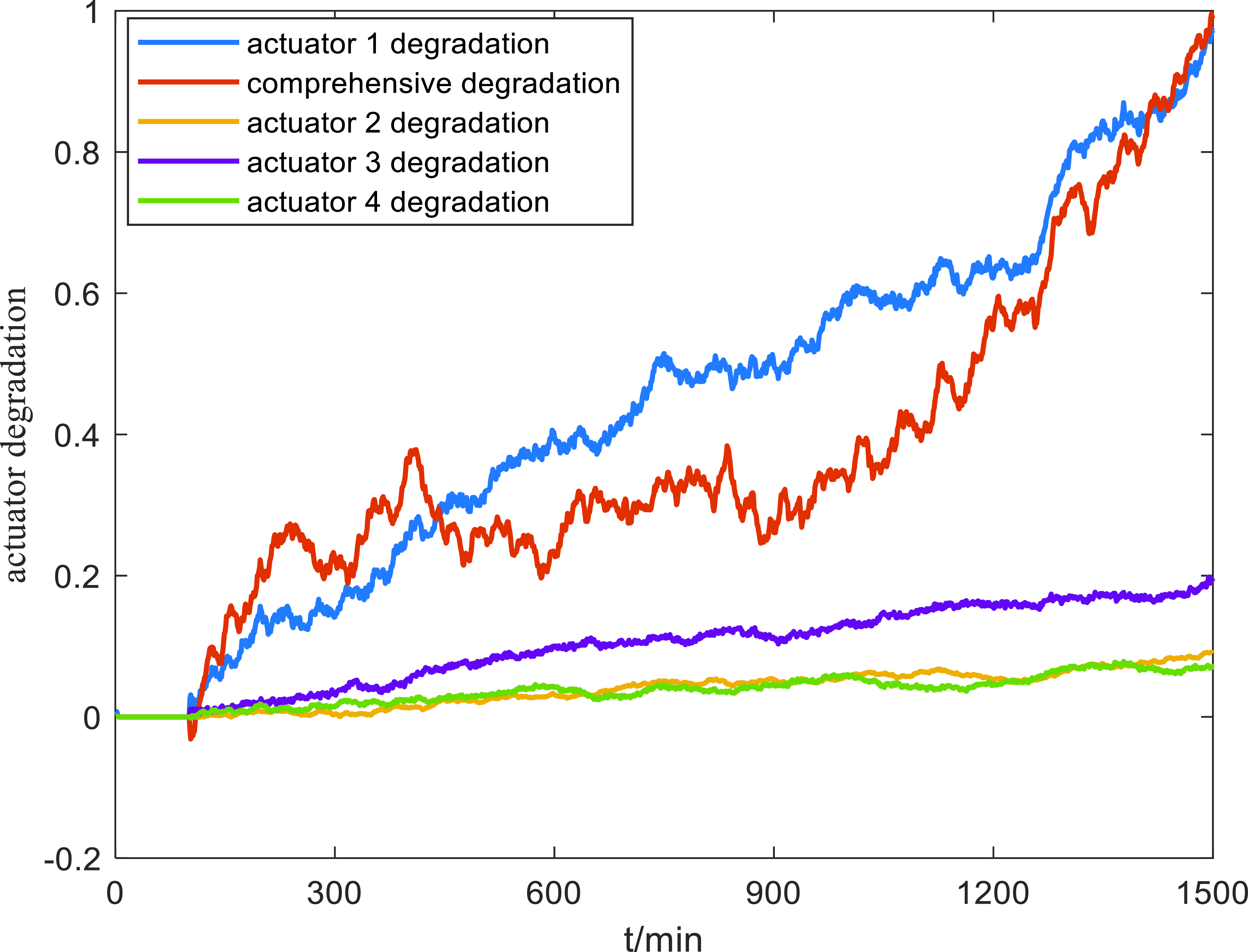
Figure 7. Degradation curves for both comprehensive and individual actuator.
![]() $\hat \alpha {\rm{ = }}0.0021,\,\hat \beta {\rm{ = }}1.3373,\,\,{\hat \sigma _{\rm{B}}}{\rm{ = }}0.0098.$
$\hat \alpha {\rm{ = }}0.0021,\,\hat \beta {\rm{ = }}1.3373,\,\,{\hat \sigma _{\rm{B}}}{\rm{ = }}0.0098.$
The red line in Fig. 8 shows the position and attitude changes of the quadrotor UAV during the degradation process of the four actuators before implementing the maintenance strategy. As an important indicator of autonomous maintenance, an airframe HD is an important basis for determining maintenance timing and maintenance of a quadrotor UAV.
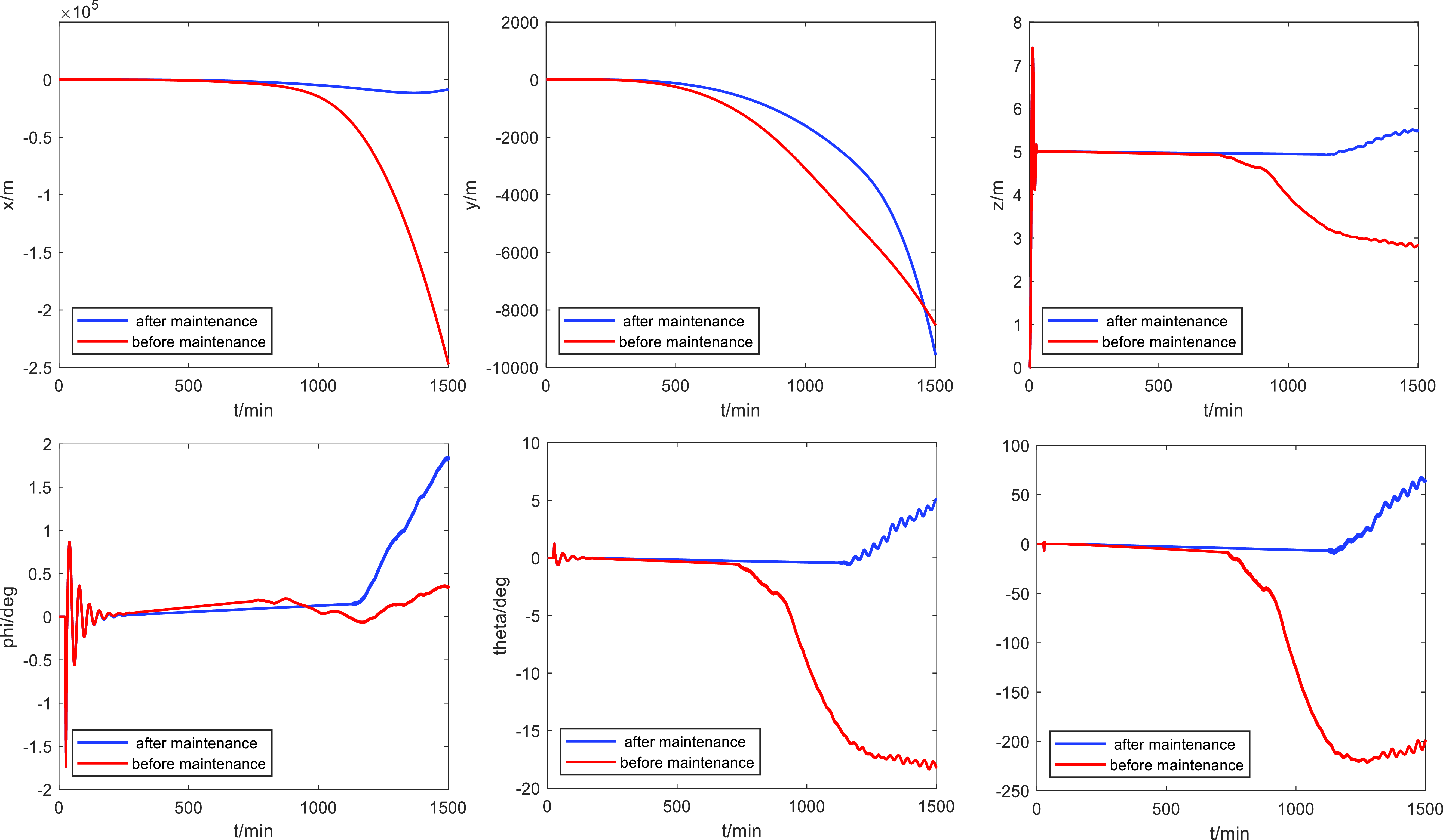
Figure 8. Response curve of quadrotor UAV with actuator degradation.
The red line in Fig. 9 shows the change curve of airframe HD before maintenance.
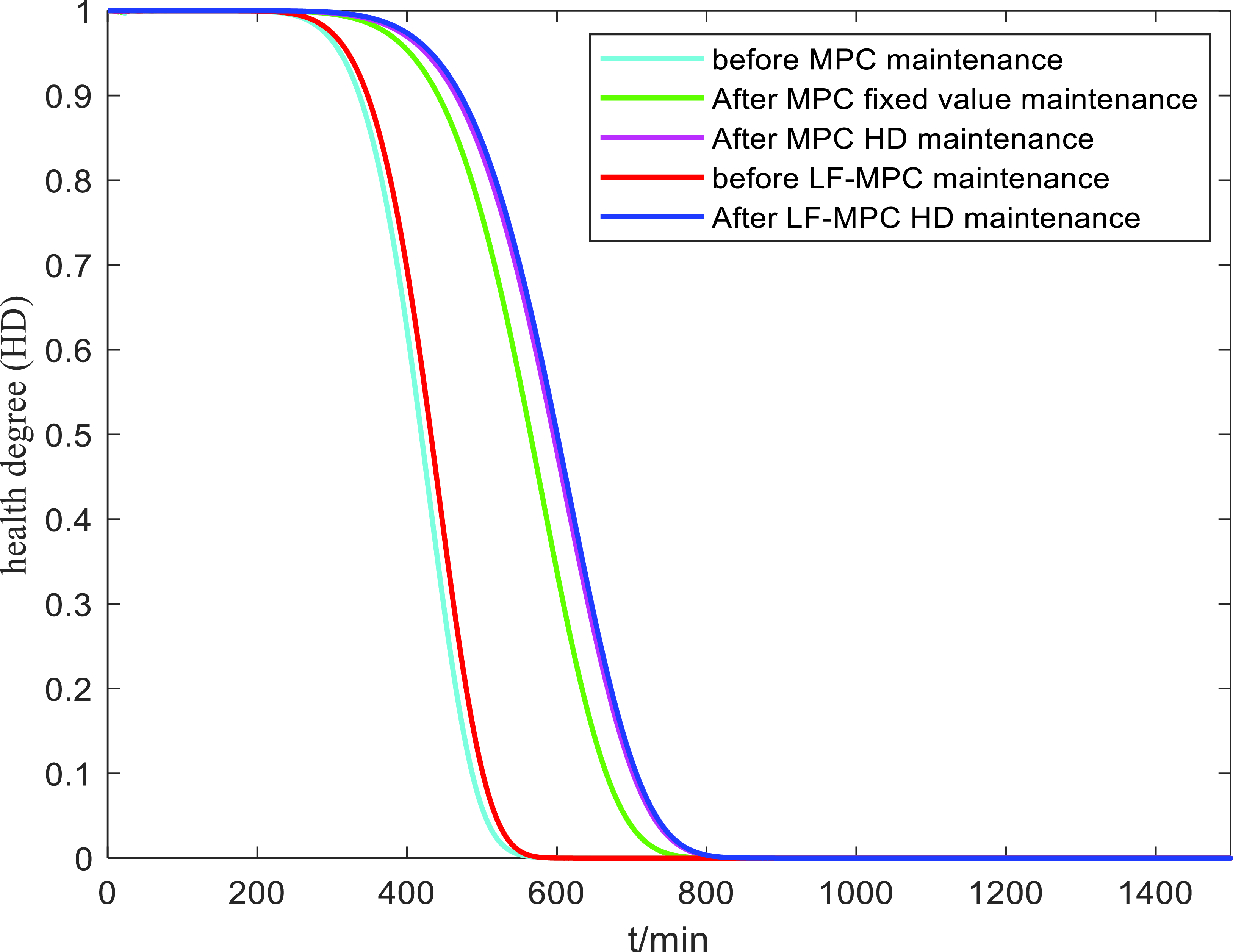
Figure 9. Change curve of HDs.
For the health failure threshold
![]() $H{D_{sf}} = 0.7$
, according to (37), the comprehensive failure threshold
$H{D_{sf}} = 0.7$
, according to (37), the comprehensive failure threshold
![]() ${l_{sf}} = 0.3587$
is obtained, and the RUL distribution of the quadrotor UAV is calculated using (40). Then the RUL distribution is shown in Fig. 10. When the quadrotor UAV exceeds the desired HD constraint, the life of the UAV is
${l_{sf}} = 0.3587$
is obtained, and the RUL distribution of the quadrotor UAV is calculated using (40). Then the RUL distribution is shown in Fig. 10. When the quadrotor UAV exceeds the desired HD constraint, the life of the UAV is
![]() ${t_{sf}} = 399\,min$
, which does not meet the desired working time requirements. It can be seen that the airframe performance is constrained based on the HD and the comprehensive degradation perception quantity is combined to make the airframe RUL prediction more direct, convenient and accurate.
${t_{sf}} = 399\,min$
, which does not meet the desired working time requirements. It can be seen that the airframe performance is constrained based on the HD and the comprehensive degradation perception quantity is combined to make the airframe RUL prediction more direct, convenient and accurate.
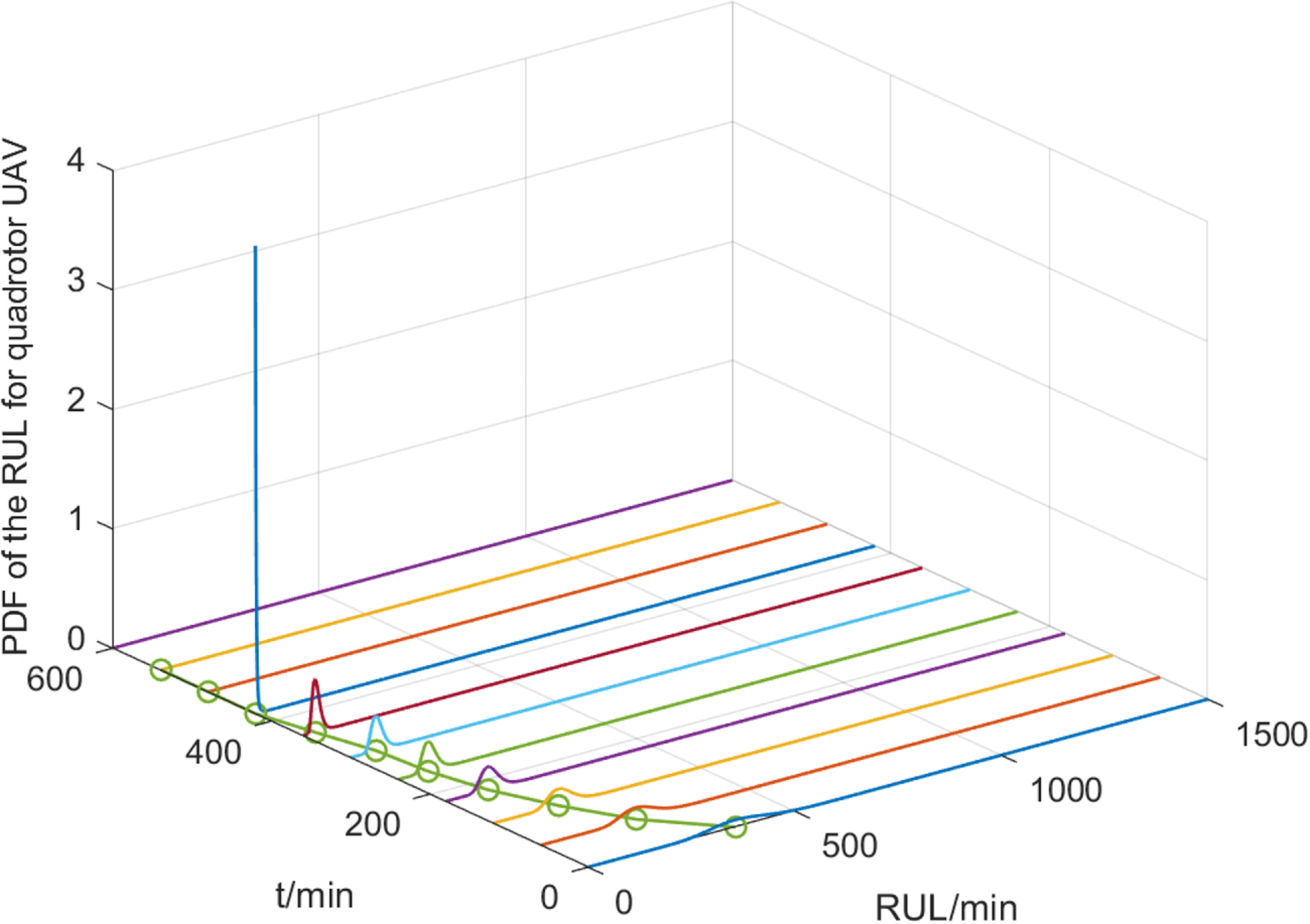
Figure 10. Distribution of RUL of quadrotor UAV.
5.3 Autonomous PdM effect of quadrotor UAV
According to the above autonomous maintenance strategy of the quadrotor UAV, when
![]() $H{D_n} = 0.9$
, the UAV enters a degraded state. If the minimum expected life extension time
$H{D_n} = 0.9$
, the UAV enters a degraded state. If the minimum expected life extension time
![]() ${t_{{\rm{ex}}}} \gt 0$
, it is considered to adaptively adjust
${t_{{\rm{ex}}}} \gt 0$
, it is considered to adaptively adjust
![]() $\Delta q$
and
$\Delta q$
and
![]() $\Delta r$
based on (58), and carry out autonomous maintenance by reducing the
$\Delta r$
based on (58), and carry out autonomous maintenance by reducing the
![]() $Q$
matrix and increasing the weight value of each diagonal element in the
$Q$
matrix and increasing the weight value of each diagonal element in the
![]() $R$
matrix.
$R$
matrix.
Therefore, maintenance begins after the airframe enters a degraded state. Take
![]() ${K_1} = 120$
and
${K_1} = 120$
and
![]() ${K_2} = 100$
to obtain the matrix
${K_2} = 100$
to obtain the matrix
![]() $Q$
and
$Q$
and
![]() $R$
correction values
$R$
correction values
![]() $\Delta q$
and
$\Delta q$
and
![]() $\Delta r$
adjustment curves in Fig. 11, as well as the weight matrix
$\Delta r$
adjustment curves in Fig. 11, as well as the weight matrix
![]() $Q$
and
$Q$
and
![]() $R$
change curves after adjustment in Fig. 12.
$R$
change curves after adjustment in Fig. 12.
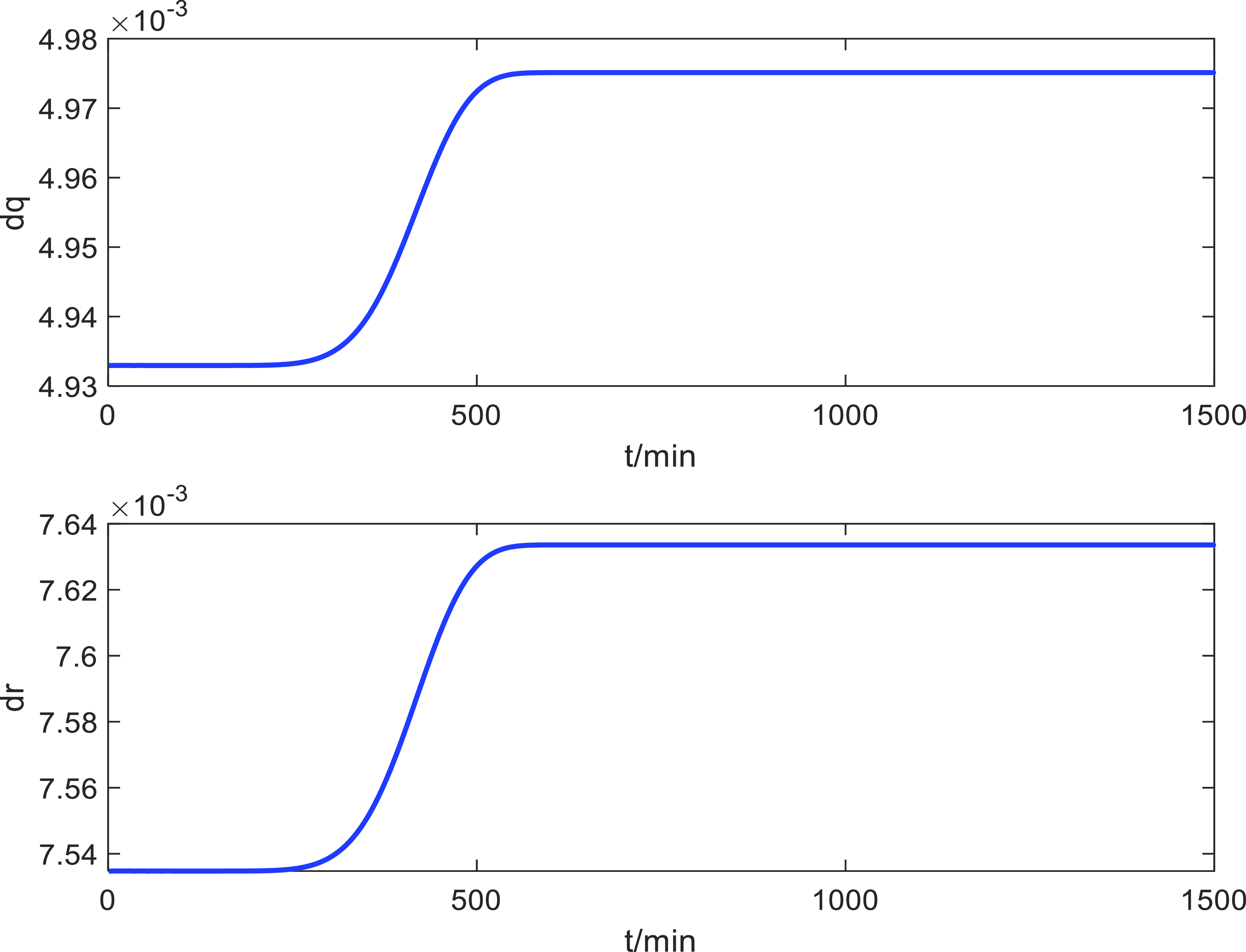
Figure 11. Adjustment curve of
![]() $\Delta q$
and
$\Delta q$
and
![]() $\Delta r$
.
$\Delta r$
.

Figure 12. Adjustment curve of Q and R for life extension control.
Based on this maintenance strategy, the position, attitude and HD changes of the UAV after maintenance are obtained as shown in Figs 8 and 9 with blue curves.
Figure 13 shows the variation curve of the control voltage u of the actuator before and after autonomous maintenance. It can be seen that the output pressure of the actuator is effectively relieved, the degradation process is delayed, and the HD of the UAV is also improved after maintenance, which can provide more time for the normal work of the UAV.

Figure 13. Control quantity curve before and after actuator maintenance.
After adopting the autonomous PdM method proposed in this paper, the RUL distribution of the UAV is shown in Fig. 14, and the airframe life is extended to
![]() ${t_{sf}} = 551\,min$
, which meets the requirement of the HD and working time of the UAV at the same time. This further verifies the effectiveness of the method of adaptively adjusting the weight matrix based on the HD for the autonomous maintenance of the UAV.
${t_{sf}} = 551\,min$
, which meets the requirement of the HD and working time of the UAV at the same time. This further verifies the effectiveness of the method of adaptively adjusting the weight matrix based on the HD for the autonomous maintenance of the UAV.
To verify the superiority of the adaptive maintenance strategy based on HD in this paper, it is compared with the fixed factor weight correction method and the MPC HD maintenance method. The adjustment factors of
![]() $Q$
and
$Q$
and
![]() $R$
are
$R$
are
![]() ${\delta _1} = 0.008$
and
${\delta _1} = 0.008$
and
![]() ${\delta _2} = 0.009$
. Figure 9 shows the change curves of the HD of the three methods, and the advantages of the proposed method can be seen.
${\delta _2} = 0.009$
. Figure 9 shows the change curves of the HD of the three methods, and the advantages of the proposed method can be seen.
Table 2 shows the failure thresholds and airframe life after no maintenance and different maintenance strategies. It can be seen that there are two advantages to using the LF-MPC method. Firstly, compared to MPC control, under the same control time domain conditions, the LF-MPC calculation efficiency is improved and the control speed is increased. Therefore, the airframe life before the extension of life is increased by 12 min compared to MPC, which improves the control effect; secondly, from the perspective of maintenance strategy, MPC HD maintenance is better than fixed value maintenance, and LF-MPC HD maintenance is better than MPC health maintenance. The reason is also that the adaptive maintenance strategy based on LF-MPC HD is far less than the control time domain after the adoption of LF, resulting in a relatively reduced amount of computation in the solution of quadratic programming, improved real-time performance and more targeted maintenance.
Table 2. Failure threshold and airframe life under different maintenance strategies


Figure 14. Distribution of the RUL of the quadrotor UAV after maintenance.
6.0 Conclusion
This paper focuses on the research of life prediction and autonomous maintenance methods for a hovering quadrotor UAV, considering the hidden degradation of multi-actuators. The TSKF method is used to estimate the system state and the degradation rate of each actuator in real time, and the actuator degradation is fused into a comprehensive degradation by the entropy weight method. The first failure threshold is determined based on the definition of system HD, and the analytical solution of the RUL of the quadrotor UAV is obtained. Considering the HD and working time constraints, the LF-MPC weight matrix was adjusted according to the health index to achieve the goal of autonomous maintenance.
In practice, the working state of a UAV includes hovering, pitch, yaw, roll and other attitudes. This paper considers the basic hovering state from UAV modeling to subsequent methods, and the subsequent research will be further extended to other states. Considering the HD and working time constraints, the LF-MPC weight matrix was adjusted according to the health index to achieve the goal of autonomous maintenance.
Author contributions
Conceptualisation, F.S. and W.L.; methodology, F.S.; software, F.S.; validation, F.S. and D.J.; formal analysis, F.S.; investigation, F.S.; resources, W.L.; data curation, D.J.; writing—original draft preparation, F.S.; writing—review and editing, F.S. and W.L.; visualisation, F.S. and H. M.; supervision, W.L.; funding acquisition, D.J. and H. M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grants no. 62063017, 62263020).
Data availability statement
Not applicable.
Competing interests
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
























