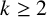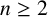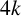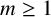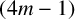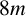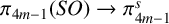1 Introduction
Let q be a positive integer and let
![]() $W_g := \#_g (S^{q} \times S^{q})$
be the g-fold connected sum of the manifold
$W_g := \#_g (S^{q} \times S^{q})$
be the g-fold connected sum of the manifold
![]() $S^{q} \times S^{q}$
with itself. Two compact, connected smooth
$S^{q} \times S^{q}$
with itself. Two compact, connected smooth
![]() $2q$
-manifolds
$2q$
-manifolds
![]() $M_0$
and
$M_0$
and
![]() $M_1$
with the same Euler characteristic are stably diffeomorphic, written
$M_1$
with the same Euler characteristic are stably diffeomorphic, written
![]() $M_0 \cong _{\text {st}} M_1$
, if there exists a nonnegative integer g and a diffeomorphism
$M_0 \cong _{\text {st}} M_1$
, if there exists a nonnegative integer g and a diffeomorphism
Note that
![]() $S^{q} \times S^{q}$
admits an orientation-reversing diffeomorphism. Hence, the same is true of
$S^{q} \times S^{q}$
admits an orientation-reversing diffeomorphism. Hence, the same is true of
![]() $W_g$
and it follows that when the
$W_g$
and it follows that when the
![]() $M_i$
are orientable the diffeomorphism type of the connected sum does not depend on orientations.
$M_i$
are orientable the diffeomorphism type of the connected sum does not depend on orientations.
A paradigm of modified surgery, as developed by Kreck [Reference KreckKre99], is that one first seeks to classify
![]() $2q$
-manifolds up to stable diffeomorphism, and then for each
$2q$
-manifolds up to stable diffeomorphism, and then for each
![]() $M_0$
, one tries to understand its stable class:
$M_0$
, one tries to understand its stable class:
The efficacy of this method was first demonstrated by Hambleton and Kreck, who applied it to
![]() $4$
-manifolds with finite fundamental group in a series of papers [Reference Hambleton and KreckHK88a, Reference Hambleton and KreckHK88b, Reference Hambleton and KreckHK93a, Reference Hambleton and KreckHK93b].
$4$
-manifolds with finite fundamental group in a series of papers [Reference Hambleton and KreckHK88a, Reference Hambleton and KreckHK88b, Reference Hambleton and KreckHK93a, Reference Hambleton and KreckHK93b].
However, the Browder–Novikov–Sullivan–Wall surgery exact sequence [Reference WallWal99] aims instead to classify manifolds within a fixed homotopy class. In general, there is no obvious relationship between homotopy equivalence and stable diffeomorphism, although in some cases, there are implications, for example, [Reference Davis, Boden, Hambleton, Nicas and ParkDav05]. To enable a comparison between the two approaches, we define the homotopy stable class of
![]() $M_0$
to be
$M_0$
to be
Our aim is to investigate the cardinality of
![]() $\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_0)$
, and, in particular, we provide new examples of simply connected manifolds with arbitrarily large homotopy stable class.
$\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_0)$
, and, in particular, we provide new examples of simply connected manifolds with arbitrarily large homotopy stable class.
Throughout this article, we consider closed, connected, simply connected, smooth manifolds. To define the intersection form and related invariants, we orient all manifolds. When necessary, to achieve unoriented results, we later factor out the effect of the choice of orientation.
When the dimension is
![]() $4k{+}2$
, Kreck showed that the stable class of such manifolds is trivial [Reference KreckKre99, Theorem D]. We therefore focus on dimensions
$4k{+}2$
, Kreck showed that the stable class of such manifolds is trivial [Reference KreckKre99, Theorem D]. We therefore focus on dimensions
![]() $4k$
with
$4k$
with
![]() $k>1$
(dimension four is discussed separately below). Kreck also showed that for every such simply connected manifold
$k>1$
(dimension four is discussed separately below). Kreck also showed that for every such simply connected manifold
![]() $M^{4k}$
, the stable class of
$M^{4k}$
, the stable class of
![]() $M^{4k} \# W_1$
is trivial. However, as pointed out by Kreck and Schafer [Reference Kreck and SchaferKS84, I], for
$M^{4k} \# W_1$
is trivial. However, as pointed out by Kreck and Schafer [Reference Kreck and SchaferKS84, I], for
![]() $k \!> \! 1$
, examples of closed, simply connected
$k \!> \! 1$
, examples of closed, simply connected
![]() $(2k-1)$
-connected
$(2k-1)$
-connected
![]() $4k$
-manifolds M with arbitrarily large homotopy stable class have been implicit in the literature since Wall’s classification of these manifolds up to the action of the group of homotopy spheres [Reference WallWal62]. These examples are distinguished by their intersection form
$4k$
-manifolds M with arbitrarily large homotopy stable class have been implicit in the literature since Wall’s classification of these manifolds up to the action of the group of homotopy spheres [Reference WallWal62]. These examples are distinguished by their intersection form
which must be definite (to have inequivalent forms); moreover, to realise the forms by closed, almost-parallelisable manifolds, they must have signature divisible by
![]() $8 |bP_{4k}|$
, where
$8 |bP_{4k}|$
, where
![]() $|bP_{4k}|$
is the order of the group of homotopy
$|bP_{4k}|$
is the order of the group of homotopy
![]() $(4k{-}1)$
-spheres that bound parallelisable manifolds [Reference Milnor and KervaireMK60, Corollary on page 457].
$(4k{-}1)$
-spheres that bound parallelisable manifolds [Reference Milnor and KervaireMK60, Corollary on page 457].
In this paper, we consider examples where the intersection form is isomorphic to the standard hyperbolic form
 $$ \begin{align*} H^+(\mathbb{Z}) = \left(\mathbb{Z}^2, \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) \right) \end{align*} $$
$$ \begin{align*} H^+(\mathbb{Z}) = \left(\mathbb{Z}^2, \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) \right) \end{align*} $$
and where there is an additional invariant, a homomorphism
![]() $f : \mathbb {Z}^2 \to \mathbb {Z}$
. The pair
$f : \mathbb {Z}^2 \to \mathbb {Z}$
. The pair
![]() $(H^+(\mathbb {Z}),f)$
is an example of an extended symmetric form; see Definition 3.5. The isometries of the rank two hyperbolic form are highly restricted: they are generated by switching the two basis vectors and multiplying both basis vectors by
$(H^+(\mathbb {Z}),f)$
is an example of an extended symmetric form; see Definition 3.5. The isometries of the rank two hyperbolic form are highly restricted: they are generated by switching the two basis vectors and multiplying both basis vectors by
![]() $-1$
. As such, the unordered pair
$-1$
. As such, the unordered pair
considered up to multiplication of both integers by
![]() $-1$
, gives an invariant of the isometry class of the extended symmetric form
$-1$
, gives an invariant of the isometry class of the extended symmetric form
![]() $(H^+(\mathbb {Z}),f)$
. However, in the Witt class, or stable equivalence class, only the divisibility
$(H^+(\mathbb {Z}),f)$
. However, in the Witt class, or stable equivalence class, only the divisibility
![]() $d:= \gcd (a,b)$
and the product
$d:= \gcd (a,b)$
and the product
![]() $A=ab$
are invariants. Since a fixed number A can often be factorised in many ways as a product of coprime integers
$A=ab$
are invariants. Since a fixed number A can often be factorised in many ways as a product of coprime integers
![]() $a,b$
, if we can define a suitable f, this simple algebra has the chance to detect large stable classes. In the proof of our first main theorem, we define such an f using the cohomology ring of the manifolds we construct.
$a,b$
, if we can define a suitable f, this simple algebra has the chance to detect large stable classes. In the proof of our first main theorem, we define such an f using the cohomology ring of the manifolds we construct.
Theorem 1.1. Fix positive integers n and
![]() $k \geq 2$
. There are infinitely many stable diffeomorphism classes of closed, smooth, simply connected
$k \geq 2$
. There are infinitely many stable diffeomorphism classes of closed, smooth, simply connected
![]() $4k$
-manifolds
$4k$
-manifolds
![]() $\{[M_i]_{\mathrm {st}} \}_{i=1}^{\infty }$
, such that
$\{[M_i]_{\mathrm {st}} \}_{i=1}^{\infty }$
, such that
![]() $|\mathcal {S}^{\mathrm {st}}_h(M_i)| \geq n$
. Moreover,
$|\mathcal {S}^{\mathrm {st}}_h(M_i)| \geq n$
. Moreover,
![]() $\mathcal {S}^{\mathrm {st}}_h(M_i)$
contains a subset
$\mathcal {S}^{\mathrm {st}}_h(M_i)$
contains a subset
![]() $\{M^j_i\}_{j=1}^n$
of cardinality n, where
$\{M^j_i\}_{j=1}^n$
of cardinality n, where
![]() $M^1_i = M_i$
, and each
$M^1_i = M_i$
, and each
![]() $M^j_i$
is stably parallelisable and has hyperbolic intersection form.
$M^j_i$
is stably parallelisable and has hyperbolic intersection form.
Here, stably parallelisable means that the tangent bundle becomes trivial after taking the Whitney sum with a trivial bundle of sufficiently high rank. More than one notion of stabilisation appears in this article, one for manifolds and one for vector bundles.
Kreck and Schafer [Reference Kreck and SchaferKS84] constructed examples of
![]() $4k$
-manifolds M with nontrivial finite fundamental groups, such that the homotopy stable class of M contains distinct elements with hyperbolic intersection forms. However, as far as we know, our construction gives the first simply connected examples and the first for which the homotopy stable class has been shown to have arbitrary cardinality. In a companion paper [Reference Conway, Crowley, Powell and SixtCCPS21], we investigate the homotopy stable class in more detail, also for manifolds with nontrivial fundamental group, and we relate the homotopy stable class to computations of the
$4k$
-manifolds M with nontrivial finite fundamental groups, such that the homotopy stable class of M contains distinct elements with hyperbolic intersection forms. However, as far as we know, our construction gives the first simply connected examples and the first for which the homotopy stable class has been shown to have arbitrary cardinality. In a companion paper [Reference Conway, Crowley, Powell and SixtCCPS21], we investigate the homotopy stable class in more detail, also for manifolds with nontrivial fundamental group, and we relate the homotopy stable class to computations of the
![]() $\ell $
-monoid from [Reference Crowley and SixtCS11].
$\ell $
-monoid from [Reference Crowley and SixtCS11].
The manifolds we construct to prove Theorem 1.1 are shown to be homotopically inequivalent using their cohomology rings. An alternative construction to obtain nontrivial homotopy stable class instead uses Pontryagin classes to define the homomorphism f in an extended symmetric form. This was alluded to in [Reference Kreck and SchaferKS84], but not carried through. Section 3 proves a theorem which implies the following result.
Theorem 1.2. For every
![]() $m \geq 1$
, there exists a pair of closed, smooth,
$m \geq 1$
, there exists a pair of closed, smooth,
![]() $(4m{-}1)$
- connected
$(4m{-}1)$
- connected
![]() $8m$
-manifolds
$8m$
-manifolds
![]() $M_1$
and
$M_1$
and
![]() $M_2$
with hyperbolic intersection forms that are stably diffeomorphic but not homotopy equivalent.
$M_2$
with hyperbolic intersection forms that are stably diffeomorphic but not homotopy equivalent.
Compared with the manifolds from Theorem 1.1 (for even k), the manifolds
![]() $M_1$
and
$M_1$
and
![]() $M_2$
from Theorem 1.2 are not stably parallelisable; however, since they are
$M_2$
from Theorem 1.2 are not stably parallelisable; however, since they are
![]() $(4m{-}1)$
-connected and have the same intersection pairing, their cohomology rings are isomorphic. In particular, once again, the intersection form does not help.
$(4m{-}1)$
-connected and have the same intersection pairing, their cohomology rings are isomorphic. In particular, once again, the intersection form does not help.
To show that the manifolds in Theorem 1.2 are not homotopy equivalent, we use Wall’s homotopy classification of
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds [Reference WallWal62, Lemma 8], which makes use of an extended symmetric form
$8m$
-manifolds [Reference WallWal62, Lemma 8], which makes use of an extended symmetric form
![]() $(H^+(\mathbb {Z}),f : \mathbb {Z}^2 \to \mathbb {Z}/j_m)$
, where
$(H^+(\mathbb {Z}),f : \mathbb {Z}^2 \to \mathbb {Z}/j_m)$
, where
![]() $j_m$
is the order of the image of the stable J-homomorphism
$j_m$
is the order of the image of the stable J-homomorphism
![]() $J : \pi _{4m-1}(SO) \to \pi ^s_{4m-1}$
; see Section 3.
$J : \pi _{4m-1}(SO) \to \pi ^s_{4m-1}$
; see Section 3.
Remark 1.3. The limiting factor preventing us from exhibiting arbitrarily large homotopy stable classes in Theorem 1.2 is that our lower bound on the cardinality of
![]() $\mathcal{S}_{\mathrm{h}}^{\mathrm{st}}(M_1)$
depends only on the number of primes dividing
$\mathcal{S}_{\mathrm{h}}^{\mathrm{st}}(M_1)$
depends only on the number of primes dividing
![]() $j_m$
. This grows with m, but in a fixed dimension, cannot be made arbitrarily large. However, if we instead count diffeomorphism classes, then we show in Theorem 3.3(2) that the stable class can be arbitrarily large for
$j_m$
. This grows with m, but in a fixed dimension, cannot be made arbitrarily large. However, if we instead count diffeomorphism classes, then we show in Theorem 3.3(2) that the stable class can be arbitrarily large for
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds with hyperbolic intersection forms.
$8m$
-manifolds with hyperbolic intersection forms.
1.1 Dimension four
Dimension four was absent from the above discussion. This is because closed, smooth, simply connected 4-manifolds M and N are stably diffeomorphic if and only if they are homotopy equivalent. Here is an outline of why this holds. First, two such 4-manifolds are stably diffeomorphic if and only if there are orientations such that they have the same signatures, Euler characteristics, and
![]() $w_2$
-types, that is,
$w_2$
-types, that is,
![]() $\sigma (M)=\sigma (N)$
,
$\sigma (M)=\sigma (N)$
,
![]() $\chi (M)=\chi (N)$
, and their intersection forms have the same parity (even or odd). Thus homotopy equivalence implies stable diffeomorphism. For the other direction,
$\chi (M)=\chi (N)$
, and their intersection forms have the same parity (even or odd). Thus homotopy equivalence implies stable diffeomorphism. For the other direction,
![]() $\sigma (M)=\sigma (N)$
and
$\sigma (M)=\sigma (N)$
and
![]() $\chi (M)=\chi (N)$
implies that the intersection forms are either both definite or both indefinite. In the definite case, the intersection forms must be diagonal by Donaldson’s theorem [Reference DonaldsonDon83], and so the intersection forms are isometric and therefore the manifolds are homotopy equivalent [Reference MilnorMil58a, Reference WhiteheadWhi49]. In the indefinite case, the intersection form is determined up to isometry by its rank, parity and signature, and so again M and N are homotopy equivalent. Thus, the assumption that
$\chi (M)=\chi (N)$
implies that the intersection forms are either both definite or both indefinite. In the definite case, the intersection forms must be diagonal by Donaldson’s theorem [Reference DonaldsonDon83], and so the intersection forms are isometric and therefore the manifolds are homotopy equivalent [Reference MilnorMil58a, Reference WhiteheadWhi49]. In the indefinite case, the intersection form is determined up to isometry by its rank, parity and signature, and so again M and N are homotopy equivalent. Thus, the assumption that
![]() $k \geq 2$
was essential in Theorem 1.1.
$k \geq 2$
was essential in Theorem 1.1.
One way in which an analogous phenomenon does occur in dimension four is by considering spin
![]() $^{c}$
structures. Seiberg–Witten invariants of 4-manifolds and Heegaard–Floer cobordism maps are indexed by spin
$^{c}$
structures. Seiberg–Witten invariants of 4-manifolds and Heegaard–Floer cobordism maps are indexed by spin
![]() $^{c}$
structures. The first Chern class
$^{c}$
structures. The first Chern class
![]() $c_1$
of the spin
$c_1$
of the spin
![]() $^{c}$
structure then defines the map f in the extended symmetric forms. We illustrate this in Section 4, using the 4-manifold
$^{c}$
structure then defines the map f in the extended symmetric forms. We illustrate this in Section 4, using the 4-manifold
![]() $S^2 \times S^2$
.
$S^2 \times S^2$
.
Theorem 1.4. Let
![]() $C \in \mathbb {Z}$
with
$C \in \mathbb {Z}$
with
![]() $|C| \geq 16$
and
$|C| \geq 16$
and
![]() $8 \mid C$
. Define
$8 \mid C$
. Define
![]() $P(C)$
to be the number of distinct primes dividing
$P(C)$
to be the number of distinct primes dividing
![]() $C/8$
. There are
$C/8$
. There are
![]() $n := 2^{P(C)-1}$
stably equivalent spin
$n := 2^{P(C)-1}$
stably equivalent spin
![]() $^{c}$
structures
$^{c}$
structures
![]() $\mathfrak {s}_1,\ldots ,\mathfrak {s}_n$
on
$\mathfrak {s}_1,\ldots ,\mathfrak {s}_n$
on
![]() $S^2 \times S^2$
with
$S^2 \times S^2$
with
![]() $c_1(\mathfrak {s}_i)^2 = C \in H^4(S^2 \times S^2) \cong \mathbb {Z}$
that are all pairwise inequivalent.
$c_1(\mathfrak {s}_i)^2 = C \in H^4(S^2 \times S^2) \cong \mathbb {Z}$
that are all pairwise inequivalent.
1.2 Organisation
Section 2 proves Theorem 1.1, Section 3 proves Theorem 1.2 and Section 4 proves Theorem 1.4.
1.3 Conventions
Throughout this paper, all manifolds are compact, simply connected and smooth. As mentioned above, we also equip our manifolds with an orientation. For the remainder of this paper, all (co)homology groups have integral coefficients. We write
![]() $\mathbb {N}_0 := \mathbb {N} \cup \{0\}$
.
$\mathbb {N}_0 := \mathbb {N} \cup \{0\}$
.
2 Simply connected
 $4k$
-manifolds with arbitrarily large stable class
$4k$
-manifolds with arbitrarily large stable class
We prove Theorem 1.1 by stating and proving Proposition 2.2 below. In the proposition, we construct a collection of
![]() $4k$
-manifolds
$4k$
-manifolds
![]() $N_{a,b}$
for each unordered pair of positive integers
$N_{a,b}$
for each unordered pair of positive integers
![]() $\{a, b\}$
such that
$\{a, b\}$
such that
![]() $(2k)!$
divides
$(2k)!$
divides
![]() $2ab$
. If
$2ab$
. If
![]() $\{a,b\} \neq \{a',b'\}$
, then
$\{a,b\} \neq \{a',b'\}$
, then
![]() $N_{a,b}$
and
$N_{a,b}$
and
![]() $N_{a',b'}$
are not homotopy equivalent. However,
$N_{a',b'}$
are not homotopy equivalent. However,
![]() $ab = a'b'$
if and only if
$ab = a'b'$
if and only if
![]() $N_{a,b}$
and
$N_{a,b}$
and
![]() $N_{a',b'}$
are stably diffeomorphic. Moreover, every manifold
$N_{a',b'}$
are stably diffeomorphic. Moreover, every manifold
![]() $N_{a,b}$
is closed, simply connected, has hyperbolic intersection form and is stably parallelisable. Thus, the proposition immediately implies Theorem 1.1.
$N_{a,b}$
is closed, simply connected, has hyperbolic intersection form and is stably parallelisable. Thus, the proposition immediately implies Theorem 1.1.
First we have a lemma. To rule out orientation-reversing homotopy equivalences, we appeal to the following observation.
Lemma 2.1. Let N and
![]() $N'$
be closed, oriented
$N'$
be closed, oriented
![]() $4k$
-manifolds. Suppose that a class z freely generates
$4k$
-manifolds. Suppose that a class z freely generates
![]() $H^2(N)$
and satisfies that
$H^2(N)$
and satisfies that
![]() $z^{2k}=n$
for some nonzero
$z^{2k}=n$
for some nonzero
![]() $n\in \mathbb {Z} = H^{4k}(N)$
, and similarly for
$n\in \mathbb {Z} = H^{4k}(N)$
, and similarly for
![]() $(N',z')$
. Then any homotopy equivalence
$(N',z')$
. Then any homotopy equivalence
![]() $f : N \to N'$
must be orientation preserving.
$f : N \to N'$
must be orientation preserving.
Proof. Assume that f is of degree
![]() $\varepsilon =\pm 1$
. Since f is a homotopy equivalence, N and
$\varepsilon =\pm 1$
. Since f is a homotopy equivalence, N and
![]() $N'$
have isomorphic cohomology rings. In particular,
$N'$
have isomorphic cohomology rings. In particular,
![]() $H^2(N')\cong \mathbb {Z}$
is generated by
$H^2(N')\cong \mathbb {Z}$
is generated by
![]() $z'= \pm (f^{*})^{-1}(z)$
. Since
$z'= \pm (f^{*})^{-1}(z)$
. Since
![]() ${z'}^{2k}=n$
in
${z'}^{2k}=n$
in
![]() $H^{4k}(N') \cong \mathbb {Z}$
and
$H^{4k}(N') \cong \mathbb {Z}$
and
![]() $f^*({z'}^{2k})=z^{2k}$
, properties of the cap and cup products show that
$f^*({z'}^{2k})=z^{2k}$
, properties of the cap and cup products show that
Since
![]() $n\neq 0$
, this implies that f must be orientation preserving.
$n\neq 0$
, this implies that f must be orientation preserving.
Now we proceed with the construction of the promised manifolds.
Proposition 2.2. Fix
![]() $k>1$
. Given an unordered pair
$k>1$
. Given an unordered pair
![]() $\{a, b\}$
of positive coprime integers such that
$\{a, b\}$
of positive coprime integers such that
![]() $(2k)!$
divides
$(2k)!$
divides
![]() $2ab$
, there exists a closed, oriented,
$2ab$
, there exists a closed, oriented,
![]() $4k$
-manifold
$4k$
-manifold
![]() $N^{4k}_{a,b}$
with the following properties.
$N^{4k}_{a,b}$
with the following properties.
-
(i) The manifold
 $N_{a, b}$
is simply connected and stably parallelisable.
$N_{a, b}$
is simply connected and stably parallelisable. -
(ii) The ring
 $H^*(N_{a,b})$
has generators
$H^*(N_{a,b})$
has generators
 $w, x, y, z$
and
$w, x, y, z$
and
 $1$
of degrees
$1$
of degrees
 $2k{+}2$
,
$2k{+}2$
,
 $2k$
,
$2k$
,
 $2k$
,
$2k$
,
 $2$
and
$2$
and
 $0$
, respectively, with
$0$
, respectively, with
 $z^k = ax + by, x^2 = 0 = y^2,2abw=z^{k+1}, xz = bw, yz = aw$
and
$z^k = ax + by, x^2 = 0 = y^2,2abw=z^{k+1}, xz = bw, yz = aw$
and
 $xy$
generates
$xy$
generates
 $H^{4k}(N_{a, b})$
.
$H^{4k}(N_{a, b})$
.
In particular, the intersection form of
![]() $N_{a, b}$
is hyperbolic and
$N_{a, b}$
is hyperbolic and
![]() $z^{2k} = 2ab xy$
is
$z^{2k} = 2ab xy$
is
![]() $2ab$
times a fundamental class of
$2ab$
times a fundamental class of
![]() $N_{a, b}$
. If
$N_{a, b}$
. If
![]() $\{a, b\} \neq \{a', b'\}$
, then
$\{a, b\} \neq \{a', b'\}$
, then
![]() $N_{a, b}$
and
$N_{a, b}$
and
![]() $N_{a', b'}$
have nonisomorphic integral cohomology rings and so are not homotopy equivalent. Moreover,
$N_{a', b'}$
have nonisomorphic integral cohomology rings and so are not homotopy equivalent. Moreover,
![]() $ab = a'b'$
if and only if
$ab = a'b'$
if and only if
![]() $N_{a,b}$
and
$N_{a,b}$
and
![]() $N_{a',b'}$
are stably diffeomorphic.
$N_{a',b'}$
are stably diffeomorphic.
Proof. Note that if we have a manifold
![]() $N_{a,b}$
and if we choose a stable normal framing on
$N_{a,b}$
and if we choose a stable normal framing on
![]() $N_{a, b}$
, then the pair
$N_{a, b}$
, then the pair
![]() $(N_{a, b}, z)$
corresponds to a (normally) framed manifold over
$(N_{a, b}, z)$
corresponds to a (normally) framed manifold over
![]() $\mathbb {C} P^{\infty }$
using the identification
$\mathbb {C} P^{\infty }$
using the identification
![]() $H^2(N_{a,b}) \cong [N_{a,b},\mathbb {C} P^{\infty }]$
. This motivates the method we use, constructing
$H^2(N_{a,b}) \cong [N_{a,b},\mathbb {C} P^{\infty }]$
. This motivates the method we use, constructing
![]() $N_{a, b}$
by framed surgery on stably normally framed manifolds over
$N_{a, b}$
by framed surgery on stably normally framed manifolds over
![]() $\mathbb {C} P^{\infty }$
. It then follows automatically that the manifolds we obtain are stably parallelisable, since a manifold with trivial stable normal bundle has trivial stable tangent bundle too.
$\mathbb {C} P^{\infty }$
. It then follows automatically that the manifolds we obtain are stably parallelisable, since a manifold with trivial stable normal bundle has trivial stable tangent bundle too.
We start with
![]() $S^2$
together with the unique framing of its stable normal bundle corresponding to a choice of orientation, and consider the corresponding dual orientation class
$S^2$
together with the unique framing of its stable normal bundle corresponding to a choice of orientation, and consider the corresponding dual orientation class
![]() $\alpha \in H^2(S^2)$
. Take the
$\alpha \in H^2(S^2)$
. Take the
![]() $2k$
-fold product of
$2k$
-fold product of
![]() $S^2$
with itself,
$S^2$
with itself,
and define
![]() $\beta _0 \in H^2(X_{0})$
to be the class that restricts to
$\beta _0 \in H^2(X_{0})$
to be the class that restricts to
![]() $\alpha $
in each
$\alpha $
in each
![]() $S^2$
factor. This means that under the inclusion
$S^2$
factor. This means that under the inclusion
in the j th factor,
![]() $\iota _j^*(\,\beta _0) = \alpha $
. Equivalently, let
$\iota _j^*(\,\beta _0) = \alpha $
. Equivalently, let
![]() $p_i : S^2 \times \cdots \times S^2 \to S^2$
be the i th projection. Then
$p_i : S^2 \times \cdots \times S^2 \to S^2$
be the i th projection. Then
![]() $\beta _0 = \sum _{i=1}^{2k} p_i^*(\alpha )$
. An elementary calculation shows that
$\beta _0 = \sum _{i=1}^{2k} p_i^*(\alpha )$
. An elementary calculation shows that
Here we write
![]() $[X_0]^* \in H^{4k}(X_0)$
for the dual of the fundamental class
$[X_0]^* \in H^{4k}(X_0)$
for the dual of the fundamental class
![]() $[X_0] \in H_{4k}(X_0)$
. To make this calculation, use
$[X_0] \in H_{4k}(X_0)$
. To make this calculation, use
![]() $\beta _0 = \sum _{i=1}^{2k} p_i^*(\alpha )$
and note that:
$\beta _0 = \sum _{i=1}^{2k} p_i^*(\alpha )$
and note that:
-
(i)
 $p_i^*(\alpha ) \cup p_j^*(\alpha ) = p_j^*(\alpha ) \cup p_i^*(\alpha )$
for
$p_i^*(\alpha ) \cup p_j^*(\alpha ) = p_j^*(\alpha ) \cup p_i^*(\alpha )$
for
 $i \neq j$
;
$i \neq j$
; -
(ii)
 $p_i^*(\alpha ) \cup p_i^*(\alpha ) = p_i^*(\alpha \cup \alpha ) = p_i^*(0) =0$
and
$p_i^*(\alpha ) \cup p_i^*(\alpha ) = p_i^*(\alpha \cup \alpha ) = p_i^*(0) =0$
and -
(iii)
 $p_1^*(\alpha ) \cup \cdots \cup p_{2k}^*(\alpha ) = [X_0]^*$
.
$p_1^*(\alpha ) \cup \cdots \cup p_{2k}^*(\alpha ) = [X_0]^*$
.
By assumption, there is a positive integer j such that
![]() $2ab = j(2k)!$
. Take
$2ab = j(2k)!$
. Take
![]() $X_1 := \#^j X_0$
to be the framed j-fold connected sum of
$X_1 := \#^j X_0$
to be the framed j-fold connected sum of
![]() $X_0$
and
$X_0$
and
![]() $\beta _1 \in H^2(X_1)$
to be the class that restricts to
$\beta _1 \in H^2(X_1)$
to be the class that restricts to
![]() $\beta _0$
in each summand. That is,
$\beta _0$
in each summand. That is,
![]() $H^2(X_1) \cong \bigoplus ^{j} H^2(X_0)$
and
$H^2(X_1) \cong \bigoplus ^{j} H^2(X_0)$
and
![]() $\beta _1 = (\,\beta _0,\ldots ,\beta _0)$
. Then,
$\beta _1 = (\,\beta _0,\ldots ,\beta _0)$
. Then,
The element
![]() $\beta _1 \in H^2(X_1)$
and the normal framing on
$\beta _1 \in H^2(X_1)$
and the normal framing on
![]() $X_1$
define a normal map
$X_1$
define a normal map
where we take the trivial bundle over
![]() $\mathbb {C} P^{\infty }$
. By surgery below the middle dimension, the normal map
$\mathbb {C} P^{\infty }$
. By surgery below the middle dimension, the normal map
![]() $(\,\beta _1, \overline {\beta }_1)$
is normally bordant to a
$(\,\beta _1, \overline {\beta }_1)$
is normally bordant to a
![]() $2k$
-connected map
$2k$
-connected map
![]() $(\,\beta _2, \overline {\beta }_2) : X_2 \to \mathbb {C} P^{\infty }$
. Since
$(\,\beta _2, \overline {\beta }_2) : X_2 \to \mathbb {C} P^{\infty }$
. Since
![]() $X_0$
has signature zero, the same holds for
$X_0$
has signature zero, the same holds for
![]() $X_1$
and
$X_1$
and
![]() $X_2$
. Since the stable normal bundle of
$X_2$
. Since the stable normal bundle of
![]() $X_2$
is framed, so is the stable tangent bundle. Therefore, the stable tangent bundle has the trivial
$X_2$
is framed, so is the stable tangent bundle. Therefore, the stable tangent bundle has the trivial
![]() $2k$
th Wu class vanishing and so the intersection form on
$2k$
th Wu class vanishing and so the intersection form on
![]() $X_2$
is even. Let
$X_2$
is even. Let
![]() $z_{\infty } \in H^2(\mathbb {C} P^{\infty })$
be the generator restricting to
$z_{\infty } \in H^2(\mathbb {C} P^{\infty })$
be the generator restricting to
![]() $\alpha \in H^2(\mathbb {C} P^1) = H^2(S^2)$
via the inclusion
$\alpha \in H^2(\mathbb {C} P^1) = H^2(S^2)$
via the inclusion
![]() $\mathbb {C} P^1 \to \mathbb {C} P^{\infty }$
, and consider the Poincaré dual of
$\mathbb {C} P^1 \to \mathbb {C} P^{\infty }$
, and consider the Poincaré dual of
![]() $\beta _2^*(z_{\infty }^k)$
,
$\beta _2^*(z_{\infty }^k)$
,
Since
![]() $\beta _2 : X_2 \to \mathbb {C} P^{\infty }$
is
$\beta _2 : X_2 \to \mathbb {C} P^{\infty }$
is
![]() $2k$
-connected,
$2k$
-connected,
![]() $H_{2k}(X_2) \to H_{2k}(\mathbb {C} P^{\infty }) \cong \mathbb {Z}$
is onto and therefore splits since
$H_{2k}(X_2) \to H_{2k}(\mathbb {C} P^{\infty }) \cong \mathbb {Z}$
is onto and therefore splits since
![]() $\mathbb {Z}$
is free. Since all homology groups are torsion-free, the dual map can be identified with the map
$\mathbb {Z}$
is free. Since all homology groups are torsion-free, the dual map can be identified with the map
![]() $\beta _2^* : H^{2k}(\mathbb {C} P^{\infty }) \to H^{2k}(X_2)$
on cohomology. The splitting for
$\beta _2^* : H^{2k}(\mathbb {C} P^{\infty }) \to H^{2k}(X_2)$
on cohomology. The splitting for
![]() $\beta _2$
dualises to a splitting for
$\beta _2$
dualises to a splitting for
![]() $\beta _2^*$
, so the image of a generator
$\beta _2^*$
, so the image of a generator
![]() $\beta _2^*(z^k_{\infty })$
generates a summand. Applying Poincaré duality, we see that
$\beta _2^*(z^k_{\infty })$
generates a summand. Applying Poincaré duality, we see that
![]() $u \in H_{2k}(X_2)$
is a primitive element; that is, u generates a summand of
$u \in H_{2k}(X_2)$
is a primitive element; that is, u generates a summand of
![]() $H_{2k}(X_2)$
.
$H_{2k}(X_2)$
.
We take the connected sum with an additional copy of
![]() $S^{2k} \times S^{2k}$
with null-bordant framing and trivial map to
$S^{2k} \times S^{2k}$
with null-bordant framing and trivial map to
![]() $\mathbb {C} P^{\infty }$
to obtain
$\mathbb {C} P^{\infty }$
to obtain
and a normal map
![]() $(\,\beta _3, \overline {\beta }_3) : X_3 \to \mathbb {C} P^{\infty }$
. Note that up until this point, we have only used the product
$(\,\beta _3, \overline {\beta }_3) : X_3 \to \mathbb {C} P^{\infty }$
. Note that up until this point, we have only used the product
![]() $ab$
, rather than the data of the pair
$ab$
, rather than the data of the pair
![]() $\{a,b\}$
. This changes for the upcoming construction of
$\{a,b\}$
. This changes for the upcoming construction of
![]() $X_4 = N_{a,b}$
.
$X_4 = N_{a,b}$
.
The intersection form
![]() $\lambda _{X_3}$
of
$\lambda _{X_3}$
of
![]() $X_3$
has an orthogonal decomposition corresponding to the connected sum decomposition of
$X_3$
has an orthogonal decomposition corresponding to the connected sum decomposition of
![]() $X_3$
:
$X_3$
:
where
![]() $H^+(\mathbb {Z})$
is the standard symmetric hyperbolic form. Note that since
$H^+(\mathbb {Z})$
is the standard symmetric hyperbolic form. Note that since
![]() $\lambda _{X_2}$
is even, so is
$\lambda _{X_2}$
is even, so is
![]() $\lambda _{X_3}$
. Let
$\lambda _{X_3}$
. Let
![]() $\{e, f\}$
be a standard basis for
$\{e, f\}$
be a standard basis for
![]() $H^+(\mathbb {Z})$
. Since a and b are coprime, we may and shall choose integers
$H^+(\mathbb {Z})$
. Since a and b are coprime, we may and shall choose integers
![]() $c, d$
such that
$c, d$
such that
![]() $ad-bc = 1$
. We also write
$ad-bc = 1$
. We also write
![]() $u = \mathrm {PD}(\,\beta _3^*(z_{\infty }^k))$
. Here note that u is essentially the same element as the element
$u = \mathrm {PD}(\,\beta _3^*(z_{\infty }^k))$
. Here note that u is essentially the same element as the element
![]() $u \in H_2(X_2)$
that we defined above thinking of
$u \in H_2(X_2)$
that we defined above thinking of
![]() $H_2(X_2)$
as a subgroup of
$H_2(X_2)$
as a subgroup of
![]() $H_2(X_3)$
. Keeping this in mind, we have that
$H_2(X_3)$
. Keeping this in mind, we have that
since
![]() $z_{\infty }^{2k}$
generates
$z_{\infty }^{2k}$
generates
![]() $H^{4k}(\mathbb {C} P^{\infty })$
and since
$H^{4k}(\mathbb {C} P^{\infty })$
and since
![]() $(\,\beta _3)_*$
sends
$(\,\beta _3)_*$
sends
![]() $[X_3]$
to the same multiple of the generator of
$[X_3]$
to the same multiple of the generator of
![]() $H_{4k}(\mathbb {C} P^{\infty })$
as that to which
$H_{4k}(\mathbb {C} P^{\infty })$
as that to which
![]() $(\,\beta _1)_*$
sends
$(\,\beta _1)_*$
sends
![]() $[X_1]$
. Since
$[X_1]$
. Since
![]() $u \in H_{2k}(X_2) \subseteq H_{2k}(X_3)$
is primitive and since
$u \in H_{2k}(X_2) \subseteq H_{2k}(X_3)$
is primitive and since
![]() $\lambda _{X_2}$
is nonsingular, there is an element
$\lambda _{X_2}$
is nonsingular, there is an element
![]() $v'' \in H_{2k}(X_2) \subseteq H_{2k}(X_3)$
such that
$v'' \in H_{2k}(X_2) \subseteq H_{2k}(X_3)$
such that
Now set
![]() $v' := (ad + bc)v''$
as well as
$v' := (ad + bc)v''$
as well as
Here, we use that the form
![]() $\lambda _{X_3}$
is even. Since
$\lambda _{X_3}$
is even. Since
![]() $u \in H_2(X_2)$
and
$u \in H_2(X_2)$
and
![]() $e,f \in H^+(\mathbb {Z})$
, we observe that
$e,f \in H^+(\mathbb {Z})$
, we observe that
![]() $\lambda _{X_3}(u, e) = \lambda _{X_3}(u, f) = 0$
. As a consequence, the elements
$\lambda _{X_3}(u, e) = \lambda _{X_3}(u, f) = 0$
. As a consequence, the elements
![]() $u, v$
span a subspace
$u, v$
span a subspace
![]() $H_{u, v} \subseteq H_{2k}(X_3)$
, where
$H_{u, v} \subseteq H_{2k}(X_3)$
, where
![]() $\lambda _{X_3}$
restricted to
$\lambda _{X_3}$
restricted to
![]() $H_{u, v}$
has matrix
$H_{u, v}$
has matrix
 $$ \begin{align*} A= \left( \begin{array}{cc} 2ab & ad + bc \\ ad+bc & 2cd \end{array} \right), \end{align*} $$
$$ \begin{align*} A= \left( \begin{array}{cc} 2ab & ad + bc \\ ad+bc & 2cd \end{array} \right), \end{align*} $$
which has determinant
![]() $4abcd - (ad+bc)^2 = -(ad-bc)^2 = -1$
. Hence,
$4abcd - (ad+bc)^2 = -(ad-bc)^2 = -1$
. Hence,
![]() $H_{u, v}$
is an orthogonal summand of
$H_{u, v}$
is an orthogonal summand of
![]() $(H_{2k}(X_3), \lambda _{X_3})$
and a calculation shows that
$(H_{2k}(X_3), \lambda _{X_3})$
and a calculation shows that
![]() $H_{u, v}$
is hyperbolic with standard basis
$H_{u, v}$
is hyperbolic with standard basis
![]() $\{e_1, f_1\}$
, where
$\{e_1, f_1\}$
, where
![]() $u = ae_1 + bf_1$
and
$u = ae_1 + bf_1$
and
![]() $v=ce:1 +d f_1$
. To see this, let
$v=ce:1 +d f_1$
. To see this, let
![]() $P:= (\begin {smallmatrix} a&b \\ c&d \end {smallmatrix})$
and note that
$P:= (\begin {smallmatrix} a&b \\ c&d \end {smallmatrix})$
and note that
![]() $P (\begin {smallmatrix} 0&1 \\ 1&0 \end {smallmatrix}) P^T =A$
.
$P (\begin {smallmatrix} 0&1 \\ 1&0 \end {smallmatrix}) P^T =A$
.
The orthogonal complement of
![]() $H_{u, v}$
, namely
$H_{u, v}$
, namely
![]() $H_{u, v}^{\perp }$
, has signature equal to the signature of
$H_{u, v}^{\perp }$
, has signature equal to the signature of
![]() $X_3$
, which is zero; and hence since the intersection form is even,
$X_3$
, which is zero; and hence since the intersection form is even,
![]() $H_{u, v}^{\perp }$
is stably hyperbolic.
$H_{u, v}^{\perp }$
is stably hyperbolic.
We assert that
![]() $H_{u, v}^{\perp }$
maps trivially to
$H_{u, v}^{\perp }$
maps trivially to
![]() $H_{2k}(\mathbb {C} P^{\infty })$
under
$H_{2k}(\mathbb {C} P^{\infty })$
under
![]() $\beta _{3*}$
. To see this, first note that
$\beta _{3*}$
. To see this, first note that
![]() $H^{2k}(\mathbb {C} P^{\infty }) \cong \mathbb {Z}$
, generated by
$H^{2k}(\mathbb {C} P^{\infty }) \cong \mathbb {Z}$
, generated by
![]() $z^k_{\infty }$
. We have an isomorphism
$z^k_{\infty }$
. We have an isomorphism
Recall that now
![]() $u = \mathrm {PD}(\,\beta _3^*(z_{\infty }^k)) \in H_{u,v}$
and let
$u = \mathrm {PD}(\,\beta _3^*(z_{\infty }^k)) \in H_{u,v}$
and let
![]() $x \in H_{u, v}^{\perp }$
. Then,
$x \in H_{u, v}^{\perp }$
. Then,
Since
![]() $z^k_{\infty } \cap -$
is an isomorphism, this implies that
$z^k_{\infty } \cap -$
is an isomorphism, this implies that
![]() $(\,\beta _{3})_*(x)=0$
, which proves the assertion.
$(\,\beta _{3})_*(x)=0$
, which proves the assertion.
Now, since
![]() $\beta _3 : X_3 \to \mathbb {C} P^{\infty }$
is
$\beta _3 : X_3 \to \mathbb {C} P^{\infty }$
is
![]() $2k$
-connected and since
$2k$
-connected and since
![]() $H_{u, v}^{\perp }$
maps trivially to
$H_{u, v}^{\perp }$
maps trivially to
![]() $H_{2k}(\mathbb {C} P^{\infty })$
, the Hurewicz theorem and the linked long exact sequences
$H_{2k}(\mathbb {C} P^{\infty })$
, the Hurewicz theorem and the linked long exact sequences

show that every element of
![]() $H_{u, v}^{\perp }$
is represented by a map from a
$H_{u, v}^{\perp }$
is represented by a map from a
![]() $2k$
-sphere in
$2k$
-sphere in
![]() $\pi _{2k}(X_3)$
. Hence, standard surgery arguments allow us to perform framed surgery on
$\pi _{2k}(X_3)$
. Hence, standard surgery arguments allow us to perform framed surgery on
![]() $(\,\beta _3, \overline {\beta }_3) : X_3 \to \mathbb {C} P^{\infty }$
to kill
$(\,\beta _3, \overline {\beta }_3) : X_3 \to \mathbb {C} P^{\infty }$
to kill
![]() $H_{u, v}^{\perp }$
. We obtain a normal map
$H_{u, v}^{\perp }$
. We obtain a normal map
![]() $(\,\beta _4, \overline {\beta }_4) : X_4 \to \mathbb {C} P^{\infty }$
, with intersection form isomorphic to
$(\,\beta _4, \overline {\beta }_4) : X_4 \to \mathbb {C} P^{\infty }$
, with intersection form isomorphic to
![]() $(H_{u, v}, \lambda _{X_3}|_{H_{u, v}})$
. The manifold
$(H_{u, v}, \lambda _{X_3}|_{H_{u, v}})$
. The manifold
is the required manifold, as we verify next. We use the orientation corresponding to the fundamental class
![]() $[N_{a,b}]$
induced from tracking
$[N_{a,b}]$
induced from tracking
![]() $[X_0]$
through the construction.
$[X_0]$
through the construction.
We have already noted at the beginning of the proof that the construction via normally framed surgery implies that
![]() $N_{a,b}$
is stably parallelisable. As the map
$N_{a,b}$
is stably parallelisable. As the map
![]() $\beta _4 : N_{a,b} \to \mathbb {C} P^{\infty }$
is
$\beta _4 : N_{a,b} \to \mathbb {C} P^{\infty }$
is
![]() $2k$
-connected and since there is an isomorphism
$2k$
-connected and since there is an isomorphism
![]() ${\theta : H_{2k}(N_{a,b}) \to H_{u, v} \cong \mathbb {Z}^2}$
, the manifold
${\theta : H_{2k}(N_{a,b}) \to H_{u, v} \cong \mathbb {Z}^2}$
, the manifold
![]() $N_{a,b}$
is simply connected and has the correct integral (co)homology groups. By construction of
$N_{a,b}$
is simply connected and has the correct integral (co)homology groups. By construction of
![]() $N_{a,b}$
, we can assume that
$N_{a,b}$
, we can assume that
![]() $\theta $
is an isometry. To verify that
$\theta $
is an isometry. To verify that
![]() $N_{a,b}$
has the required cohomology ring, we set
$N_{a,b}$
has the required cohomology ring, we set
Since
![]() $u = ae_1 + b f_1$
, it follows that
$u = ae_1 + b f_1$
, it follows that
![]() $z^k = a x + by$
. Since
$z^k = a x + by$
. Since
![]() $\theta ^{-1}(e_1), \theta ^{-1}( f_1)$
form a standard hyperbolic basis for
$\theta ^{-1}(e_1), \theta ^{-1}( f_1)$
form a standard hyperbolic basis for
![]() $(H_{2k}(N_{a,b}), \lambda _{N_{a,b}})$
, it follows that
$(H_{2k}(N_{a,b}), \lambda _{N_{a,b}})$
, it follows that
![]() $xy$
generates
$xy$
generates
![]() $H^{4k}(N_{a,b})$
and
$H^{4k}(N_{a,b})$
and
![]() $z^{2k} \cap [N_{a,b}]>0$
. Finally, since
$z^{2k} \cap [N_{a,b}]>0$
. Finally, since
![]() $z^{k-1}$
generates
$z^{k-1}$
generates
![]() $H^{2k-2}(N_{a,b}) \cong \mathbb {Z}$
, there is a generator
$H^{2k-2}(N_{a,b}) \cong \mathbb {Z}$
, there is a generator
![]() $w \in H^{2k+2}(N_{a,b})$
such that
$w \in H^{2k+2}(N_{a,b})$
such that
![]() $z^{k-1}w = xy$
. The remaining properties of
$z^{k-1}w = xy$
. The remaining properties of
![]() $H^*(N_{a,b})$
follow from Poincaré duality.
$H^*(N_{a,b})$
follow from Poincaré duality.
Finally, let
![]() $\langle {z^k}\rangle \subseteq H^{2k}(N_{a,b})$
be the subgroup generated by
$\langle {z^k}\rangle \subseteq H^{2k}(N_{a,b})$
be the subgroup generated by
![]() $z^k$
and consider the isomorphism class of the pair
$z^k$
and consider the isomorphism class of the pair
![]() $(H^{2k}(N_{a,b}), \langle {z^k}\rangle )$
. This pair, modulo the action of the self-equivalences of
$(H^{2k}(N_{a,b}), \langle {z^k}\rangle )$
. This pair, modulo the action of the self-equivalences of
![]() $N_{a,b}$
on
$N_{a,b}$
on
![]() $H^{2k}(N_{a,b})$
, is a homotopy invariant of
$H^{2k}(N_{a,b})$
, is a homotopy invariant of
![]() $N_{a,b}$
. Since
$N_{a,b}$
. Since
![]() $z^{2k} \neq 0$
and since
$z^{2k} \neq 0$
and since
![]() $z^{2k} \cap [N_{a,b}]>0$
, every self-homotopy equivalence of
$z^{2k} \cap [N_{a,b}]>0$
, every self-homotopy equivalence of
![]() $N_{a,b}$
is orientation preserving by Lemma 2.1.
$N_{a,b}$
is orientation preserving by Lemma 2.1.
Thus,
![]() $\langle {z^k}\rangle $
modulo the action of
$\langle {z^k}\rangle $
modulo the action of
![]() $\mathrm {Aut}(H^+(\mathbb {Z}))$
is a homotopy invariant. We claim that the pair
$\mathrm {Aut}(H^+(\mathbb {Z}))$
is a homotopy invariant. We claim that the pair
![]() $\{a, b\}$
is an invariant of this action. To see this, from the form of the matrix A above, it is easy to see that the automorphisms of the hyperbolic form are
$\{a, b\}$
is an invariant of this action. To see this, from the form of the matrix A above, it is easy to see that the automorphisms of the hyperbolic form are
 $$ \begin{align*}\pm \operatorname{\mathrm{Id}} \text{ and } \pm \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right).\end{align*} $$
$$ \begin{align*}\pm \operatorname{\mathrm{Id}} \text{ and } \pm \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right).\end{align*} $$
So automorphisms can change the sign of both a and b simultaneously, and they can switch a and b. Then since we always take
![]() $a,b>0$
, the unordered pair of positive integers
$a,b>0$
, the unordered pair of positive integers
![]() $\{a,b\}$
is an invariant of the homotopy type. Hence, if there is a homotopy equivalence
$\{a,b\}$
is an invariant of the homotopy type. Hence, if there is a homotopy equivalence
![]() $N_{a, b} \to N_{a', b'}$
, then we have
$N_{a, b} \to N_{a', b'}$
, then we have
![]() $\{a, b\} = \{a', b'\}$
.
$\{a, b\} = \{a', b'\}$
.
Now we address the final statement of the proposition, which concerns stable diffeomorphism. Observe that
![]() $\mathbb {Z} \cong H^2(N_{a,b}) \cong H^2(N_{a,b} \# S^{2k} \times S^{2k})$
, and that the image of z, which we call
$\mathbb {Z} \cong H^2(N_{a,b}) \cong H^2(N_{a,b} \# S^{2k} \times S^{2k})$
, and that the image of z, which we call
![]() $z_{\mathrm{st}} \in H^2(N_{a,b} \# S^{2k} \times S^{2k})$
, satisfies
$z_{\mathrm{st}} \in H^2(N_{a,b} \# S^{2k} \times S^{2k})$
, satisfies
![]() $z_{\mathrm{st}}^{2k} = 2ab[N_{a,b} \# S^{2k} \times S^{2k}]$
. Since this property of
$z_{\mathrm{st}}^{2k} = 2ab[N_{a,b} \# S^{2k} \times S^{2k}]$
. Since this property of
![]() $z_{\mathrm{st}}$
and the fundamental class are preserved under diffeomorphism, it follows that if
$z_{\mathrm{st}}$
and the fundamental class are preserved under diffeomorphism, it follows that if
![]() $N_{a,b}$
and
$N_{a,b}$
and
![]() $N_{a',b'}$
are stably diffeomorphic, then
$N_{a',b'}$
are stably diffeomorphic, then
![]() ${ab = a' b'}$
.
${ab = a' b'}$
.
However, for a fixed product
![]() $ab = a'b'$
, the manifolds
$ab = a'b'$
, the manifolds
![]() $N_{a,b}$
and
$N_{a,b}$
and
![]() $N_{a',b'}$
are obtained from the
$N_{a',b'}$
are obtained from the
![]() $4k$
-manifold
$4k$
-manifold
![]() $X_3$
by performing surgery on a stably hyperbolic form
$X_3$
by performing surgery on a stably hyperbolic form
![]() $H_{u, v}^{\perp }$
. Recall that u and v depend on
$H_{u, v}^{\perp }$
. Recall that u and v depend on
![]() $a,b$
, so in particular, we may need to stabilise a different number of times for
$a,b$
, so in particular, we may need to stabilise a different number of times for
![]() $H_{u, v}^{\perp }$
versus
$H_{u, v}^{\perp }$
versus
![]() $H_{u', v'}^{\perp }$
to make them hyperbolic. Let
$H_{u', v'}^{\perp }$
to make them hyperbolic. Let
![]() $h(u,v)$
and
$h(u,v)$
and
![]() $h(u',v')$
be the number of stabilisations required and let
$h(u',v')$
be the number of stabilisations required and let
![]() $h:= \max \{h(u,v),h(u',v')\}$
. Then for some g,
$h:= \max \{h(u,v),h(u',v')\}$
. Then for some g,
as desired. So indeed,
![]() $ab=a'b'$
if and only if
$ab=a'b'$
if and only if
![]() $N_{a,b} \cong _{\text {st}} N_{a',b'}$
.
$N_{a,b} \cong _{\text {st}} N_{a',b'}$
.
3
 $\textbf{(}4m{-}1\textbf{)}$
-connected
$\textbf{(}4m{-}1\textbf{)}$
-connected
 $8m$
-manifolds with nontrivial homotopy stable class
$8m$
-manifolds with nontrivial homotopy stable class
In this section, for every
![]() $m \geq 1$
, we construct
$m \geq 1$
, we construct
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds with hyperbolic intersection form and with nontrivial homotopy stable class. Specifically, we describe certain
$8m$
-manifolds with hyperbolic intersection form and with nontrivial homotopy stable class. Specifically, we describe certain
![]() $8m$
-manifolds
$8m$
-manifolds
![]() $M_{a,b}$
, for positive integers a and b, and we give bounds from above and below on the size of the homotopy stable class of
$M_{a,b}$
, for positive integers a and b, and we give bounds from above and below on the size of the homotopy stable class of
![]() $M_{a,b}$
in terms of a, b and m. In particular, for each m, there are infinitely many choices of
$M_{a,b}$
in terms of a, b and m. In particular, for each m, there are infinitely many choices of
![]() $a,b$
such that
$a,b$
such that
![]() $|\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})|>1$
.
$|\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})|>1$
.
In contrast to the manifolds in the previous section, the homotopically inequivalent manifolds constructed here have isomorphic integral cohomology rings, but are not stably parallelisable. We detect that our manifolds are not homotopy equivalent using a refinement of the m th Pontryagin class.
This section is organised as follows. In Section 3.1, we recall some facts about exotic spheres and the J homomorphism, which we need for the statement and the proof of Theorem 3.3. We state this theorem in Section 3.2. In Section 3.3, we recall Wall’s classification of
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds up to the action of the group of homotopy
$8m$
-manifolds up to the action of the group of homotopy
![]() $8m$
-spheres, then in Section 3.4, we determine the stable classification of such manifolds, again up to the action of the homotopy spheres. Next, in Section 3.5, we construct the manifolds
$8m$
-spheres, then in Section 3.4, we determine the stable classification of such manifolds, again up to the action of the homotopy spheres. Next, in Section 3.5, we construct the manifolds
![]() $M_{a,b}$
appearing in Theorem 3.3 and we prove this theorem in Section 3.6.
$M_{a,b}$
appearing in Theorem 3.3 and we prove this theorem in Section 3.6.
3.1 Exotic spheres and the J-homomorphism
Let
![]() $\Theta _n$
denote the group of h-cobordism classes of homotopy n-spheres, that is closed, connected, oriented n-manifolds that are homotopy equivalent to
$\Theta _n$
denote the group of h-cobordism classes of homotopy n-spheres, that is closed, connected, oriented n-manifolds that are homotopy equivalent to
![]() $S^n$
, with the group operation given by connected sum. By [Reference Kervaire and MilnorKM63], these are finite abelian groups. We briefly recall some of what is known about them, focussing on dimensions
$S^n$
, with the group operation given by connected sum. By [Reference Kervaire and MilnorKM63], these are finite abelian groups. We briefly recall some of what is known about them, focussing on dimensions
![]() $n=8m$
and
$n=8m$
and
![]() $n=8m{-}1$
, for
$n=8m{-}1$
, for
![]() $m\geq 1$
.
$m\geq 1$
.
Recall that
![]() $bP_{n+1} \subseteq \Theta _n$
is the subgroup of h-cobordism classes of homotopy n-spheres that bound parallelisable
$bP_{n+1} \subseteq \Theta _n$
is the subgroup of h-cobordism classes of homotopy n-spheres that bound parallelisable
![]() $(n{+}1)$
-manifolds. Kervaire and Milnor showed that this is a finite cyclic group and, for
$(n{+}1)$
-manifolds. Kervaire and Milnor showed that this is a finite cyclic group and, for
![]() $n{+}1 = 4\ell> 4$
, the order of
$n{+}1 = 4\ell> 4$
, the order of
![]() $bP_{n+1}$
is given by a formula in terms of Bernoulli numbers and the image of the J-homomorphism [Reference Kervaire and MilnorKM63]. Following results of Adams [Reference AdamsAda66] and Quillen [Reference QuillenQui71] on the J-homomorphism, this formula led to the computation of
$bP_{n+1}$
is given by a formula in terms of Bernoulli numbers and the image of the J-homomorphism [Reference Kervaire and MilnorKM63]. Following results of Adams [Reference AdamsAda66] and Quillen [Reference QuillenQui71] on the J-homomorphism, this formula led to the computation of
![]() $|bP_{4\ell }|$
; we give more details shortly. The group
$|bP_{4\ell }|$
; we give more details shortly. The group
![]() $bP_{4\ell }$
is generated by the boundary of Milnor’s
$bP_{4\ell }$
is generated by the boundary of Milnor’s
![]() $E_8$
plumbing [Reference BrowderBro72, V], a
$E_8$
plumbing [Reference BrowderBro72, V], a
![]() $4\ell $
-manifold obtained from plumbing disc bundles according to the
$4\ell $
-manifold obtained from plumbing disc bundles according to the
![]() $E_8$
lattice.
$E_8$
lattice.
Let
be the stable J-homomorphism [Reference WhiteheadWhi42, Section 3], where
![]() $\pi ^s_{n}$
is the stable n-stem. Kervaire and Milnor [Reference Kervaire and MilnorKM63] showed that
$\pi ^s_{n}$
is the stable n-stem. Kervaire and Milnor [Reference Kervaire and MilnorKM63] showed that
![]() $\Theta _{8m} \cong \mathop{\mathrm{coker}}\nolimits J_{8m}$
and that there is a short exact sequence
$\Theta _{8m} \cong \mathop{\mathrm{coker}}\nolimits J_{8m}$
and that there is a short exact sequence
Later Brumfiel [Reference BrumfielBru68] defined a splitting
![]() $\Theta _{8m-1} \to bP_{8m}$
and so proved that
$\Theta _{8m-1} \to bP_{8m}$
and so proved that
Consider a
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifold W with boundary
$8m$
-manifold W with boundary
![]() $\partial W \in \Theta _{8m-1}$
. Extending work of Stolz [Reference StolzSto85] and Burklund et al. [Reference Burklund, Hahn and SengerBHS19], Burklund and Senger [Reference Burklund and SengerBS20, Theorem 1.2] proved that
$\partial W \in \Theta _{8m-1}$
. Extending work of Stolz [Reference StolzSto85] and Burklund et al. [Reference Burklund, Hahn and SengerBHS19], Burklund and Senger [Reference Burklund and SengerBS20, Theorem 1.2] proved that
![]() $[\partial W] \in bP_{8m}$
, except possibly when
$[\partial W] \in bP_{8m}$
, except possibly when
![]() $m=3$
, when they also showed that
$m=3$
, when they also showed that
![]() $2[\partial W] \in bP_{24}$
. For our purposes later in this section, we also assume that W has signature
$2[\partial W] \in bP_{24}$
. For our purposes later in this section, we also assume that W has signature
![]() $0$
. This ensures that
$0$
. This ensures that
![]() $\partial W$
is a multiple of the homotopy sphere denoted
$\partial W$
is a multiple of the homotopy sphere denoted
![]() $\Sigma _Q$
by Krannich and Reinhold [Reference Krannich and ReinholdKR20, Section 2]; see just below Lemma 3.9 for the definition of
$\Sigma _Q$
by Krannich and Reinhold [Reference Krannich and ReinholdKR20, Section 2]; see just below Lemma 3.9 for the definition of
![]() $\Sigma _Q$
.
$\Sigma _Q$
.
Definition 3.1. Let
![]() $\mathfrak {bp}_m$
be the order of
$\mathfrak {bp}_m$
be the order of
![]() $\Sigma _Q$
in
$\Sigma _Q$
in
![]() $\Theta _{8m-1}$
.
$\Theta _{8m-1}$
.
Remark 3.2. The precise value of
![]() $\mathfrak {bp}_m$
can be calculated, assuming knowledge of the relevant Bernoulli numbers, from [Reference Krannich and ReinholdKR20, Lemma 2.7]. In particular,
$\mathfrak {bp}_m$
can be calculated, assuming knowledge of the relevant Bernoulli numbers, from [Reference Krannich and ReinholdKR20, Lemma 2.7]. In particular,
![]() $\mathfrak {bp}_m \mid |bP_{8m}|$
. This is clear when
$\mathfrak {bp}_m \mid |bP_{8m}|$
. This is clear when
![]() $m \neq 3$
, since
$m \neq 3$
, since
![]() $\Sigma _Q \in bP_{8m}$
. It follows from a direct calculation when
$\Sigma _Q \in bP_{8m}$
. It follows from a direct calculation when
![]() $m = 3$
, given that the projection of
$m = 3$
, given that the projection of
![]() $\Sigma _Q$
to
$\Sigma _Q$
to
![]() $bP_{24}$
has order divisible by
$bP_{24}$
has order divisible by
![]() $2$
.
$2$
.
We now recall some facts about the J-homomorphism for context and later use. We start with the stable J-homomorphism
![]() $J_{4m-1} : \pi _{4m-1}(SO) \to \pi ^s_{4m-1}$
and write
$J_{4m-1} : \pi _{4m-1}(SO) \to \pi ^s_{4m-1}$
and write
For example,
Later, we use the fact that
![]() $4 \mid j_m$
, for
$4 \mid j_m$
, for
![]() $m = 1, 2$
, as we see here. Since the stable homotopy groups of spheres are finite, so is
$m = 1, 2$
, as we see here. Since the stable homotopy groups of spheres are finite, so is
![]() $j_m$
. Since
$j_m$
. Since
![]() $\pi _{4m-1}(SO) \cong \mathbb {Z}$
, in fact
$\pi _{4m-1}(SO) \cong \mathbb {Z}$
, in fact
![]() $\operatorname{\mathrm {Im}}(J_{4m-1}) \cong \mathbb {Z}/j_m$
. By [Reference AdamsAda66] (see, for example, [Reference Lück, Farrell, Göttsche and LückLüc02, Theorem 6.26]),
$\operatorname{\mathrm {Im}}(J_{4m-1}) \cong \mathbb {Z}/j_m$
. By [Reference AdamsAda66] (see, for example, [Reference Lück, Farrell, Göttsche and LückLüc02, Theorem 6.26]),
![]() $j_m$
can be computed using the denominator of the rational number
$j_m$
can be computed using the denominator of the rational number
![]() $B_m/4m$
, where
$B_m/4m$
, where
![]() $B_m \in \mathbb {Q}$
is the m th Bernoulli number, defined by the generating function
$B_m \in \mathbb {Q}$
is the m th Bernoulli number, defined by the generating function
 $$ \begin{align*}\frac{e^t}{e^t-1} = 1 - \frac{t}{2} + \sum_{n = 1}^{\infty} \frac{(-1)^{n+1} B_n}{(2n)!} t^{2n}.\end{align*} $$
$$ \begin{align*}\frac{e^t}{e^t-1} = 1 - \frac{t}{2} + \sum_{n = 1}^{\infty} \frac{(-1)^{n+1} B_n}{(2n)!} t^{2n}.\end{align*} $$
By [Reference Kervaire and MilnorKM63, Section 7],
![]() $|bP_{8m}|/(2^{4m-2} (2^{4m-1} -1))$
equals the numerator of the rational number
$|bP_{8m}|/(2^{4m-2} (2^{4m-1} -1))$
equals the numerator of the rational number
![]() $2B_{2m}/m$
, from which one can compute
$2B_{2m}/m$
, from which one can compute
![]() $|bP_{8m}|$
.
$|bP_{8m}|$
.
Next we consider the unstable J-homomorphism,
![]() $J_{4m-1, 4m} : \pi _{4m-1}(SO_{4m}) \to \pi _{8m-1}(S^{4m})$
, which, along with the stable J-homomorphism, the Euler class
$J_{4m-1, 4m} : \pi _{4m-1}(SO_{4m}) \to \pi _{8m-1}(S^{4m})$
, which, along with the stable J-homomorphism, the Euler class
![]() $\mathrm {e}$
and the Hopf-invariant H, fits into the following commutative diagram with exact rows:
$\mathrm {e}$
and the Hopf-invariant H, fits into the following commutative diagram with exact rows:

The commutativity of the left-hand square in (*) is equivalent to the classical statements that
![]() $\mathrm {e} = H \circ J_{4m-1, 4m}$
and that the J-homomorphism commutes with stabilisation [Reference James and WhiteheadJW54, 1.2 and 1.3]. That
$\mathrm {e} = H \circ J_{4m-1, 4m}$
and that the J-homomorphism commutes with stabilisation [Reference James and WhiteheadJW54, 1.2 and 1.3]. That
![]() $\mathrm {e} \oplus S$
is injective with index
$\mathrm {e} \oplus S$
is injective with index
![]() $2$
is reviewed in [Reference WallWal62, page 171]. That the same statements hold for
$2$
is reviewed in [Reference WallWal62, page 171]. That the same statements hold for
![]() $H \oplus S$
follows from Toda’s calculations in the exceptional cases
$H \oplus S$
follows from Toda’s calculations in the exceptional cases
![]() $m = 1, 2$
[Reference TodaTod62, V, (iii) and (vii)] and from Adams’ solution of the Hopf invariant
$m = 1, 2$
[Reference TodaTod62, V, (iii) and (vii)] and from Adams’ solution of the Hopf invariant
![]() $1$
problem for
$1$
problem for
![]() $m> 2$
[Reference AdamsAda60]. For
$m> 2$
[Reference AdamsAda60]. For
![]() $m> 2$
, both
$m> 2$
, both
![]() $\mathrm {e}(\pi _{4m-1}(SO_{4m})) \subseteq \mathbb {Z}$
and
$\mathrm {e}(\pi _{4m-1}(SO_{4m})) \subseteq \mathbb {Z}$
and
![]() $H(\pi _{8m-1}(S^{4m})) \subseteq \mathbb {Z}$
are index 2 subgroups and stabilisation is a split surjection, [Reference AdamsAda60, Reference Bott and MilnorBM58]. In particular, this means that for
$H(\pi _{8m-1}(S^{4m})) \subseteq \mathbb {Z}$
are index 2 subgroups and stabilisation is a split surjection, [Reference AdamsAda60, Reference Bott and MilnorBM58]. In particular, this means that for
![]() $m> 2$
, the Euler class e is always even for rank
$m> 2$
, the Euler class e is always even for rank
![]() $4m$
oriented vector bundles over
$4m$
oriented vector bundles over
![]() $S^{4m}$
. When
$S^{4m}$
. When
![]() $m = 1, 2$
, the maps
$m = 1, 2$
, the maps
![]() $\mathrm {e}$
and H are both onto and
$\mathrm {e}$
and H are both onto and
![]() $\mathrm {e} = H \circ J_{4m-1,4m} \equiv S$
mod
$\mathrm {e} = H \circ J_{4m-1,4m} \equiv S$
mod
![]() $2$
[Reference WallWal62, page 171] and
$2$
[Reference WallWal62, page 171] and
![]() $H \equiv S$
mod
$H \equiv S$
mod
![]() $2$
by Toda’s computations mentioned above. These computations show that for
$2$
by Toda’s computations mentioned above. These computations show that for
![]() ${m=1}$
,
${m=1}$
,
![]() $H \oplus S : \pi _7(S^4) \cong \mathbb {Z} \oplus \mathbb {Z}/12 \to \mathbb {Z} \oplus \mathbb {Z}/24$
sends
$H \oplus S : \pi _7(S^4) \cong \mathbb {Z} \oplus \mathbb {Z}/12 \to \mathbb {Z} \oplus \mathbb {Z}/24$
sends
![]() $(x,y) \mapsto (x,x+2y)$
. For
$(x,y) \mapsto (x,x+2y)$
. For
![]() $m=2$
, the map
$m=2$
, the map
![]() $H \oplus S : \pi _{15}(S^8) \cong \mathbb {Z} \oplus \mathbb {Z}/120 \to \mathbb {Z} \oplus \mathbb {Z}/240$
is also given by
$H \oplus S : \pi _{15}(S^8) \cong \mathbb {Z} \oplus \mathbb {Z}/120 \to \mathbb {Z} \oplus \mathbb {Z}/240$
is also given by
![]() $(x,y) \mapsto (x,x+2y)$
. It follows that
$(x,y) \mapsto (x,x+2y)$
. It follows that
![]() $H \equiv S$
mod
$H \equiv S$
mod
![]() $2$
as asserted.
$2$
as asserted.
3.2 Estimating
 $\mathcal {S}^{\mathrm {\boldsymbol {st}}}_{\mathrm {\boldsymbol {h}}}\textbf{(}M\textbf{)}$
$\mathcal {S}^{\mathrm {\boldsymbol {st}}}_{\mathrm {\boldsymbol {h}}}\textbf{(}M\textbf{)}$
In this section, we give upper and lower bounds for the homotopy stable class of certain
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds. To state these bounds, we require a certain amount of notation.
$8m$
-manifolds. To state these bounds, we require a certain amount of notation.
Let m be a positive integer and let
![]() $\{a, b\}$
be a pair of positive integers. Since the dimensions
$\{a, b\}$
be a pair of positive integers. Since the dimensions
![]() $8$
and
$8$
and
![]() $16$
are exceptional, we introduce the factor
$16$
are exceptional, we introduce the factor
 $$ \begin{align*} c_m := \begin{cases} 2 & m = 1 \text{ or } 2, \\ 1 & m> 2, \end{cases} \end{align*} $$
$$ \begin{align*} c_m := \begin{cases} 2 & m = 1 \text{ or } 2, \\ 1 & m> 2, \end{cases} \end{align*} $$
to handle the exceptional dimensions. We define
and write
for some coprime
![]() $a',b'$
. Set
$a',b'$
. Set
For a positive integer n, we let
![]() $\mathcal {P}_n$
be the set of prime factors of n:
$\mathcal {P}_n$
be the set of prime factors of n:
We set
![]() $\overline j_m = j_m/\gcd (\,j_m, d)$
and consider the sets
$\overline j_m = j_m/\gcd (\,j_m, d)$
and consider the sets
![]() $\mathcal {P}_{\! A}$
,
$\mathcal {P}_{\! A}$
,
![]() $\mathcal {P}_{\overline j_m}$
and their intersection
$\mathcal {P}_{\overline j_m}$
and their intersection
the set of primes dividing both
![]() $\overline {j}_m$
and A. We define the nonnegative integers
$\overline {j}_m$
and A. We define the nonnegative integers
Now we can state the main theorem of this section. Its proof occupies the remainder of the section.
Theorem 3.3. Let m be a positive integer and let
![]() $\{a, b\}$
be a pair of positive integers such that
$\{a, b\}$
be a pair of positive integers such that
![]() $\mathfrak {bp}_{m} \mid ab$
. If
$\mathfrak {bp}_{m} \mid ab$
. If
![]() $d = \gcd (a, b)$
and
$d = \gcd (a, b)$
and
![]() $\overline j_m = j_m/\gcd (\,j_m, d)$
, then the closed,
$\overline j_m = j_m/\gcd (\,j_m, d)$
, then the closed,
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds
$8m$
-manifolds
![]() $M_{a, b}$
constructed in Section 3.5 satisfy the following:
$M_{a, b}$
constructed in Section 3.5 satisfy the following:
-
(1)
 $M_{a,b}$
has hyperbolic intersection form;
$M_{a,b}$
has hyperbolic intersection form; -
(2)
 $|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| = 2^{q_{A}}$
and
$|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| = 2^{q_{A}}$
and -
(3)
 $2^{q_{A, m}} \leq |\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})| \leq \lfloor ((\overline{j}_m)^2 +2\overline {j}_m + 4)/{4} \rfloor $
.
$2^{q_{A, m}} \leq |\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})| \leq \lfloor ((\overline{j}_m)^2 +2\overline {j}_m + 4)/{4} \rfloor $
.
Adams’ work on
![]() $j_m$
[Reference AdamsAda66], a theorem of von Staudt and Clausen (see [Reference Ireland and RosenIR90, Theorem 3, page 233]) on the denominator of
$j_m$
[Reference AdamsAda66], a theorem of von Staudt and Clausen (see [Reference Ireland and RosenIR90, Theorem 3, page 233]) on the denominator of
![]() $B_m$
, and a result of von Staudt on the numerator of
$B_m$
, and a result of von Staudt on the numerator of
![]() $B_m$
(see [Reference MilnorMil58b, Lemma 2]) combine to show that
$B_m$
(see [Reference MilnorMil58b, Lemma 2]) combine to show that
Since
![]() $2$
and
$2$
and
![]() $3$
certainly lie in the latter set,
$3$
certainly lie in the latter set,
![]() $|\mathcal {P}_{j_m}| \geq 2$
. Now define
$|\mathcal {P}_{j_m}| \geq 2$
. Now define
By choosing a and b with some care, we obtain the following corollary, which implies Theorem 1.2.
Corollary 3.4. Let m be a positive integer and let
![]() $\{a, b\}$
be a pair of positive, coprime integers such that
$\{a, b\}$
be a pair of positive, coprime integers such that
![]() $\mathfrak {bp}_{m} \mid ab$
and
$\mathfrak {bp}_{m} \mid ab$
and
![]() $j_m/c_m \mid A = abc_m^2$
. Then the closed,
$j_m/c_m \mid A = abc_m^2$
. Then the closed,
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds
$8m$
-manifolds
![]() $M_{a, b}$
constructed in Section 3.5 have hyperbolic intersection form and satisfy that
$M_{a, b}$
constructed in Section 3.5 have hyperbolic intersection form and satisfy that
![]() $2 \leq 2^{q_m} \leq |\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})|$
.
$2 \leq 2^{q_m} \leq |\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})|$
.
In particular, any coprime, positive
![]() $a,b$
such that
$a,b$
such that
![]() $\mathfrak {bp}_m \cdot j_m/c_m$
divides
$\mathfrak {bp}_m \cdot j_m/c_m$
divides
![]() $A=abc_m^2$
satisfy the hypotheses of the corollary. Note that changing A does not alter the lower bound, which is purely a function of m.
$A=abc_m^2$
satisfy the hypotheses of the corollary. Note that changing A does not alter the lower bound, which is purely a function of m.
Proof. Since a and b are coprime,
![]() $d = c_m$
,
$d = c_m$
,
![]() $\overline j_m = j_m/c_m$
and
$\overline j_m = j_m/c_m$
and
![]() $\mathcal {P}_{\overline j_m} = \mathcal {P}_{j_m}$
(using
$\mathcal {P}_{\overline j_m} = \mathcal {P}_{j_m}$
(using
![]() $4\mid j_m$
for
$4\mid j_m$
for
![]() $m=1,2$
). Since
$m=1,2$
). Since
![]() $j_m /c_m = \overline j_m \mid A$
, we see that
$j_m /c_m = \overline j_m \mid A$
, we see that
![]() $\mathcal {P}_{\overline j_m} \subseteq \mathcal {P}_{\! A}$
and therefore
$\mathcal {P}_{\overline j_m} \subseteq \mathcal {P}_{\! A}$
and therefore
![]() $\mathcal {P}_{\! A, m} = \mathcal {P}_{\overline j_m} = \mathcal {P}_{j_m}$
, so that
$\mathcal {P}_{\! A, m} = \mathcal {P}_{\overline j_m} = \mathcal {P}_{j_m}$
, so that
![]() $q_{A,m} = q_m$
. Since
$q_{A,m} = q_m$
. Since
![]() $q_m \geq 1$
, the corollary follows from the lower bound in Theorem 3.3(3).
$q_m \geq 1$
, the corollary follows from the lower bound in Theorem 3.3(3).
3.3 The almost-diffeomorphism classification of
 $\textbf{(}4m{-}1\textbf{)}$
-connected
$\textbf{(}4m{-}1\textbf{)}$
-connected
 $8m$
-manifolds
$8m$
-manifolds
In this section, we recall the relevant part of Wall’s classification results for closed,
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds. Recall that two closed manifolds
$8m$
-manifolds. Recall that two closed manifolds
![]() $M_0$
and
$M_0$
and
![]() $M_1$
are almost diffeomorphic if there is a homotopy sphere
$M_1$
are almost diffeomorphic if there is a homotopy sphere
![]() $\Sigma $
and a diffeomorphism
$\Sigma $
and a diffeomorphism
![]() $f : M_0 \# \Sigma \to M_1$
.
$f : M_0 \# \Sigma \to M_1$
.
Let M be a closed,
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifold, and equip M with an orientation. The intersection form of M is a symmetric bilinear form
$8m$
-manifold, and equip M with an orientation. The intersection form of M is a symmetric bilinear form
The obstruction class of M is the homomorphism
defined by representing a homology class x by a smoothly embedded sphere
![]() $S^{4m}_x \hookrightarrow M$
, whose existence is ensured by Hurewicz theorem and [Reference HaefligerHae61, Theorem 1(a)], and then taking the homotopy class of the clutching map of the stable normal bundle of
$S^{4m}_x \hookrightarrow M$
, whose existence is ensured by Hurewicz theorem and [Reference HaefligerHae61, Theorem 1(a)], and then taking the homotopy class of the clutching map of the stable normal bundle of
![]() $S^{4m}_x$
. The map
$S^{4m}_x$
. The map
![]() $S\alpha _M$
is the stabilisation of a map
$S\alpha _M$
is the stabilisation of a map
![]() $\alpha _M$
defined by taking the normal bundle of
$\alpha _M$
defined by taking the normal bundle of
![]() $S^{4m}_x$
. This is important in the proof of Theorem 3.7 below. As shown by Wall [Reference WallWal62, page 171 and Lemma 2], if
$S^{4m}_x$
. This is important in the proof of Theorem 3.7 below. As shown by Wall [Reference WallWal62, page 171 and Lemma 2], if
![]() $m = 1, 2$
, then the existence of rank
$m = 1, 2$
, then the existence of rank
![]() $4m$
vector bundles over
$4m$
vector bundles over
![]() $S^{4m}$
with odd Euler class implies that the obstruction class is characteristic for the intersection form; that is, if
$S^{4m}$
with odd Euler class implies that the obstruction class is characteristic for the intersection form; that is, if
![]() $m=1$
or
$m=1$
or
![]() $2$
, then for all
$2$
, then for all
![]() $x \in H_{4m}(M)$
,
$x \in H_{4m}(M)$
,
For
![]() $m>2$
, by Wall [Reference WallWal62, page 171], there is no relation between
$m>2$
, by Wall [Reference WallWal62, page 171], there is no relation between
![]() $S\alpha _M$
and
$S\alpha _M$
and
![]() $\lambda _M$
. As also shown in [Reference WallWal62, page 171 and Lemma 2], since
$\lambda _M$
. As also shown in [Reference WallWal62, page 171 and Lemma 2], since
![]() $\mathrm {e} = H \circ J_{4m-1,4m}$
and since for
$\mathrm {e} = H \circ J_{4m-1,4m}$
and since for
![]() $m>2$
we have that
$m>2$
we have that
![]() $H \circ J_{4m-1,4m}$
is even, the Euler number is always even and therefore
$H \circ J_{4m-1,4m}$
is even, the Euler number is always even and therefore
![]() $\lambda _M(x,x) \equiv 0~\mod {2}$
for all
$\lambda _M(x,x) \equiv 0~\mod {2}$
for all
![]() $x \in H_{4m}(M)$
.
$x \in H_{4m}(M)$
.
For the homotopy classification, we consider the stable J-homomorphism
The homotopy obstruction class of M,
![]() $S\alpha ^{\mathrm {h}}_M$
, is the composition of
$S\alpha ^{\mathrm {h}}_M$
, is the composition of
![]() $S\alpha _M$
with
$S\alpha _M$
with
![]() $J_{4m-1}$
,
$J_{4m-1}$
,
Since
![]() $j_1$
and
$j_1$
and
![]() $j_2$
are divisible by
$j_2$
are divisible by
![]() $2$
, the congruence of (†) implies that if
$2$
, the congruence of (†) implies that if
![]() $m = 1, 2$
, then
$m = 1, 2$
, then
We now define the invariants we use to classify
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds up to almost diffeomorphism and homotopy equivalence.
$8m$
-manifolds up to almost diffeomorphism and homotopy equivalence.
Definition 3.5 (Extended symmetric form)
Fix a homomorphism
![]() $v : G \to \mathbb {Z}/2$
from an abelian group G to
$v : G \to \mathbb {Z}/2$
from an abelian group G to
![]() $\mathbb {Z}/2$
. An extended symmetric form over v consists of a triple
$\mathbb {Z}/2$
. An extended symmetric form over v consists of a triple
![]() $(H,\lambda ,p)$
where:
$(H,\lambda ,p)$
where:
-
(1) H is a finitely generated free
 $\mathbb {Z}$
-module;
$\mathbb {Z}$
-module; -
(2)
 $\lambda : H \times H \to \mathbb {Z}$
is a symmetric, bilinear form and
$\lambda : H \times H \to \mathbb {Z}$
is a symmetric, bilinear form and -
(3)
 $f : H \to G$
is a homomorphism such that
$f : H \to G$
is a homomorphism such that
 $\lambda (x, x) \equiv v \circ f(x)$
mod
$\lambda (x, x) \equiv v \circ f(x)$
mod
 $2$
.
$2$
.
Two extended symmetric forms
![]() $(H,\lambda , f)$
and
$(H,\lambda , f)$
and
![]() $(H',\lambda ',f')$
are equivalent if there is an isometry
$(H',\lambda ',f')$
are equivalent if there is an isometry
![]() $h : (H,\lambda ) \to (H',\lambda ')$
such that
$h : (H,\lambda ) \to (H',\lambda ')$
such that
![]() $f' \circ h = f : H \to G$
.
$f' \circ h = f : H \to G$
.
In our applications to
![]() $8m$
-manifolds, the group G is either the infinite cyclic group
$8m$
-manifolds, the group G is either the infinite cyclic group
![]() $\pi _{4m-1}(SO) \cong \mathbb {Z}$
or the finite cyclic group
$\pi _{4m-1}(SO) \cong \mathbb {Z}$
or the finite cyclic group
![]() $\mathrm {Im}(J_{4m-1}) \cong \mathbb {Z}/j_m$
. Due to the existence of rank
$\mathrm {Im}(J_{4m-1}) \cong \mathbb {Z}/j_m$
. Due to the existence of rank
![]() $4m$
bundles over
$4m$
bundles over
![]() $S^{4m}$
with odd Euler number when
$S^{4m}$
with odd Euler number when
![]() $m=1,2$
, and the nonexistence of such bundles for
$m=1,2$
, and the nonexistence of such bundles for
![]() $ m\geq 3$
, we set v to be nonzero for
$ m\geq 3$
, we set v to be nonzero for
![]() $m = 1, 2$
(recall
$m = 1, 2$
(recall
![]() $2 \mid j_1$
and
$2 \mid j_1$
and
![]() $2\mid j_2$
) and zero for
$2\mid j_2$
) and zero for
![]() $m> 2$
. Hence for
$m> 2$
. Hence for
![]() $m>2$
, (3) is just the requirement that
$m>2$
, (3) is just the requirement that
![]() $\lambda _M$
be even. With these conventions on v, the following assignments define extended symmetric forms.
$\lambda _M$
be even. With these conventions on v, the following assignments define extended symmetric forms.
Definition 3.6 (The extended symmetric forms of M)
Let M be an oriented
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifold.
$8m$
-manifold.
-
(1) The smooth extended symmetric form of M is the triple
with $$ \begin{align*} ( H_{4m}(M),\lambda_M, S\alpha_M ) \end{align*} $$
$$ \begin{align*} ( H_{4m}(M),\lambda_M, S\alpha_M ) \end{align*} $$
 $G \cong \mathbb {Z}$
.
$G \cong \mathbb {Z}$
.
-
(2) The homotopy extended symmetric form of M is the triple
with $$ \begin{align*} (H_{4m}(M),\lambda_M, S\alpha^{\mathrm{h}}_M ) \end{align*} $$
$$ \begin{align*} (H_{4m}(M),\lambda_M, S\alpha^{\mathrm{h}}_M ) \end{align*} $$
 $G \cong \mathbb {Z}/j_m$
.
$G \cong \mathbb {Z}/j_m$
.
The following result is a direct consequence of classification results of Wall [Reference WallWal62, page 170 and Lemma 8].
Theorem 3.7 (Wall)
Let
![]() $M_1$
and
$M_1$
and
![]() $M_2$
be closed, oriented,
$M_2$
be closed, oriented,
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds. The manifolds
$8m$
-manifolds. The manifolds
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are:
$M_2$
are:
-
(1) almost diffeomorphic, via an orientation-preserving diffeomorphism, if and only if their smooth extended symmetric forms are equivalent;
-
(2) homotopy equivalent, via a degree one homotopy equivalence, if and only if their homotopy extended symmetric forms are equivalent.
When applying these classifications, we have to factor out the effect of the orientation choice on the extended symmetric forms.
Proof. We start with the almost-diffeomorphism classification (1). As mentioned above, the homomorphism
![]() $S\alpha _M$
is the stabilisation of a certain quadratic form, the extended quadratic form of M, which is the map
$S\alpha _M$
is the stabilisation of a certain quadratic form, the extended quadratic form of M, which is the map
defined by representing a homology class by a smoothly embedded sphere
![]() $S^{4m} \hookrightarrow ~M$
, and then taking the classifying map in
$S^{4m} \hookrightarrow ~M$
, and then taking the classifying map in
![]() $\pi _{4m-1}(SO_{4m})$
of the normal bundle of the embedded sphere. For all
$\pi _{4m-1}(SO_{4m})$
of the normal bundle of the embedded sphere. For all
![]() $x, y \in H_{4m}(M)$
, [Reference WallWal62, Lemma 2] and the fact that
$x, y \in H_{4m}(M)$
, [Reference WallWal62, Lemma 2] and the fact that
![]() $\mathrm {e} = H \circ J_{4m-1,4m}$
prove that
$\mathrm {e} = H \circ J_{4m-1,4m}$
prove that
![]() $\alpha _M$
relates to the intersection form of M by the equations
$\alpha _M$
relates to the intersection form of M by the equations
Here the map
![]() $\mathrm {e} : \pi _{4m-1}(SO_{4m}) \to \mathbb {Z}$
is the Euler number of the corresponding bundle and
$\mathrm {e} : \pi _{4m-1}(SO_{4m}) \to \mathbb {Z}$
is the Euler number of the corresponding bundle and
![]() $\tau \in \pi _{4m-1}(SO_{4m})$
is the clutching function of the tangent bundle of
$\tau \in \pi _{4m-1}(SO_{4m})$
is the clutching function of the tangent bundle of
![]() $S^{4m}$
. Wall also proved [Reference WallWal62, page 170] that the triple
$S^{4m}$
. Wall also proved [Reference WallWal62, page 170] that the triple
![]() $(H_{4m}(M),\lambda _M,\alpha _M)$
is a complete almost-diffeomorphism invariant of M. In fact, Wall stated his classification in terms of almost-closed manifolds: compact manifolds with boundary a homotopy sphere. However, this also yields the almost-diffeomorphism classification, as follows. If the extended symmetric forms of two closed
$(H_{4m}(M),\lambda _M,\alpha _M)$
is a complete almost-diffeomorphism invariant of M. In fact, Wall stated his classification in terms of almost-closed manifolds: compact manifolds with boundary a homotopy sphere. However, this also yields the almost-diffeomorphism classification, as follows. If the extended symmetric forms of two closed
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds are equivalent, then by the almost-closed classification, the manifolds are diffeomorphic after removing a ball
$8m$
-manifolds are equivalent, then by the almost-closed classification, the manifolds are diffeomorphic after removing a ball
![]() $D^{8m}$
from each. Gluing the balls back in compatibly with the diffeomorphism might change one of the manifolds by connected sum with a homotopy sphere, but nonetheless, the two closed manifolds are almost diffeomorphic. However, almost-diffeomorphic manifolds are diffeomorphic after removing a ball from each and then by the classification the extended symmetric forms are equivalent.
$D^{8m}$
from each. Gluing the balls back in compatibly with the diffeomorphism might change one of the manifolds by connected sum with a homotopy sphere, but nonetheless, the two closed manifolds are almost diffeomorphic. However, almost-diffeomorphic manifolds are diffeomorphic after removing a ball from each and then by the classification the extended symmetric forms are equivalent.
As mentioned above,
![]() $S\alpha _M := S \circ \alpha _M$
, where
$S\alpha _M := S \circ \alpha _M$
, where
![]() $S : \pi _{4m-1}(SO_{4m}) \to \pi _{4m-1}(SO)$
is the stabilisation homomorphism. The homotopy exact sequence of the fibration
$S : \pi _{4m-1}(SO_{4m}) \to \pi _{4m-1}(SO)$
is the stabilisation homomorphism. The homotopy exact sequence of the fibration
![]() $SO_{4m} \to SO_{4m+1} \to S^{4m}$
shows that the kernel of S is generated by
$SO_{4m} \to SO_{4m+1} \to S^{4m}$
shows that the kernel of S is generated by
![]() $\tau $
[Reference Levine, Ranicki, Levitt and QuinnLev85, Lemma 1.3 and Theorem 1.4] and since
$\tau $
[Reference Levine, Ranicki, Levitt and QuinnLev85, Lemma 1.3 and Theorem 1.4] and since
is injective by (*), it follows that the pair
![]() $(\lambda _M(x, x), S\alpha _M(x)) = ( \mathrm {e}(\alpha _M(x)), S(\alpha _M(x)) ) \in \mathbb {Z} \oplus \pi _{4m-1}(SO) \cong \mathbb {Z} \oplus \mathbb {Z}$
determines
$(\lambda _M(x, x), S\alpha _M(x)) = ( \mathrm {e}(\alpha _M(x)), S(\alpha _M(x)) ) \in \mathbb {Z} \oplus \pi _{4m-1}(SO) \cong \mathbb {Z} \oplus \mathbb {Z}$
determines
![]() $\alpha _M(x)$
for all
$\alpha _M(x)$
for all
![]() $x \in H_{4m}(M)$
. The theorem now follows from Wall’s almost-diffeomorphism classification.
$x \in H_{4m}(M)$
. The theorem now follows from Wall’s almost-diffeomorphism classification.
The proof of the homotopy classification is similar. By Wall [Reference WallWal62, Lemma 8], the triple
![]() $(H_{4m}(M), \lambda _M, \alpha _M^h:= J_{4m-1, 4m} \circ \alpha _M)$
is a complete homotopy invariant of the manifolds under consideration. Since
$(H_{4m}(M), \lambda _M, \alpha _M^h:= J_{4m-1, 4m} \circ \alpha _M)$
is a complete homotopy invariant of the manifolds under consideration. Since
![]() $\mathrm {e} = HJ$
and
$\mathrm {e} = HJ$
and
is injective by (*), it follows that the pair
![]() $(\lambda _M(x, x), S\alpha ^{\mathrm {h}}_M(x)) = ( H(\alpha ^{\mathrm {h}}_M(x)), S(\alpha ^{\mathrm {h}}_M(x)) ) \in \mathbb {Z} \oplus \pi ^s_{4m-1}$
determines
$(\lambda _M(x, x), S\alpha ^{\mathrm {h}}_M(x)) = ( H(\alpha ^{\mathrm {h}}_M(x)), S(\alpha ^{\mathrm {h}}_M(x)) ) \in \mathbb {Z} \oplus \pi ^s_{4m-1}$
determines
![]() $\alpha ^{\mathrm {h}}_M(x)$
for all
$\alpha ^{\mathrm {h}}_M(x)$
for all
![]() $x \in H_{4m}(M)$
. The theorem now follows from Wall’s homotopy classification.
$x \in H_{4m}(M)$
. The theorem now follows from Wall’s homotopy classification.
3.4 Stable almost-diffeomorphism classification of
 $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
 $8m$
-manifolds
$8m$
-manifolds
In this section, we give the stable classification of closed
![]() $(4m{-}1)$
- connected
$(4m{-}1)$
- connected
![]() $8m$
-manifolds up to connected sum with homotopy
$8m$
-manifolds up to connected sum with homotopy
![]() $8m$
-spheres. Define the nonnegative integer
$8m$
-spheres. Define the nonnegative integer
![]() $d_M$
by the equation
$d_M$
by the equation
Equivalently,
![]() $d_M$
is the divisibility of
$d_M$
is the divisibility of
![]() $S\alpha _M \in H^{4m}(M)$
, where, since M is
$S\alpha _M \in H^{4m}(M)$
, where, since M is
![]() $(4m{-}1)$
- connected, we may regard
$(4m{-}1)$
- connected, we may regard
![]() $S\alpha _M$
as an element of the group
$S\alpha _M$
as an element of the group
![]() $H^{4m}(M)$
via the inverse of the evaluation map
$H^{4m}(M)$
via the inverse of the evaluation map
![]() $\operatorname{ev} : H^{4m}(M) \to \operatorname{Hom}(H_{4m}(M),\mathbb {Z})$
, which is an isomorphism. In particular, it makes sense to consider the class
$\operatorname{ev} : H^{4m}(M) \to \operatorname{Hom}(H_{4m}(M),\mathbb {Z})$
, which is an isomorphism. In particular, it makes sense to consider the class
![]() $(S\alpha _M)^2 \in H^{8m}(M) \cong \mathbb {Z}$
.
$(S\alpha _M)^2 \in H^{8m}(M) \cong \mathbb {Z}$
.
Theorem 3.8. Two closed, oriented,
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds M and N with the same Euler characteristic are almost-stably diffeomorphic, via an orientation-preserving diffeomorphism, if and only if the following hold:
$8m$
-manifolds M and N with the same Euler characteristic are almost-stably diffeomorphic, via an orientation-preserving diffeomorphism, if and only if the following hold:
-
(1)
 $d_M = d_N$
;
$d_M = d_N$
; -
(2)
 $\sigma (M) = \sigma (N)$
;
$\sigma (M) = \sigma (N)$
; -
(3)
 $\langle (S\alpha _M)^2, [M] \rangle = \langle (S\alpha _N)^2,[N]\rangle $
.
$\langle (S\alpha _M)^2, [M] \rangle = \langle (S\alpha _N)^2,[N]\rangle $
.
Proof. First, we note that
![]() $d_M$
, the signature and
$d_M$
, the signature and
![]() $(S\alpha _M)^2$
are invariants of orientation-preserving almost-stable diffeomorphisms, so one implication holds.
$(S\alpha _M)^2$
are invariants of orientation-preserving almost-stable diffeomorphisms, so one implication holds.
For the other implication, we assume that M and N are such that
![]() $d_M = d_{N}$
,
$d_M = d_{N}$
,
![]() $\sigma (M) = \sigma (N)$
, and
$\sigma (M) = \sigma (N)$
, and
![]() $(S\alpha _M)^2 = (S\alpha _N)^2$
and we show that M and N are stably diffeomorphic. The normal
$(S\alpha _M)^2 = (S\alpha _N)^2$
and we show that M and N are stably diffeomorphic. The normal
![]() $(4m{-}1)$
-type of M and N is determined by
$(4m{-}1)$
-type of M and N is determined by
![]() $d = d_M = d_N$
and is described as follows. Let d be a nonnegative integer. Let
$d = d_M = d_N$
and is described as follows. Let d be a nonnegative integer. Let
![]() $BO\langle {4m{-}1}\rangle \to BO$
be the
$BO\langle {4m{-}1}\rangle \to BO$
be the
![]() $(4m{-}1)$
-connected cover of
$(4m{-}1)$
-connected cover of
![]() $BO$
and let
$BO$
and let
![]() $p \in H^{4m}(BO\langle {4m{-}1}\rangle ) \cong \mathbb {Z}$
be a generator. We regard
$p \in H^{4m}(BO\langle {4m{-}1}\rangle ) \cong \mathbb {Z}$
be a generator. We regard
![]() $\rho _d(p)$
, the mod d reduction of p, as a map
$\rho _d(p)$
, the mod d reduction of p, as a map
![]() $\rho _d(p) : BO\langle {4m{-}1}\rangle \to K(\mathbb {Z}/d, 4m)$
and define
$\rho _d(p) : BO\langle {4m{-}1}\rangle \to K(\mathbb {Z}/d, 4m)$
and define
![]() $BO\langle {4m{-}1, d_M}\rangle $
to be the homotopy fibre of
$BO\langle {4m{-}1, d_M}\rangle $
to be the homotopy fibre of
![]() $\rho _d(p)$
. The normal
$\rho _d(p)$
. The normal
![]() $(4m{-}1)$
-type of M and N is represented by the fibration given by the composition
$(4m{-}1)$
-type of M and N is represented by the fibration given by the composition
For brevity, use
![]() $(B_d, \eta _d)$
to denote the fibration
$(B_d, \eta _d)$
to denote the fibration
![]() $\eta _d : BO\langle {4m{-}1, d}\rangle \to BO$
. We assert that M and N admit unique normal
$\eta _d : BO\langle {4m{-}1, d}\rangle \to BO$
. We assert that M and N admit unique normal
![]() $(4m{-}1)$
-smoothings
$(4m{-}1)$
-smoothings
![]() $\overline \nu _M : M \to B_d$
and
$\overline \nu _M : M \to B_d$
and
![]() $\overline \nu _N : N \to B_d$
. We prove the assertion for M, as the proof for N is identical. Since M is
$\overline \nu _N : N \to B_d$
. We prove the assertion for M, as the proof for N is identical. Since M is
![]() $(4m{-}1)$
-connected, its stable normal bundle
$(4m{-}1)$
-connected, its stable normal bundle
![]() $\nu _M : M \to BO$
lifts (up to homotopy) uniquely to
$\nu _M : M \to BO$
lifts (up to homotopy) uniquely to
![]() $\nu _{4m-1} : M \to BO\langle 4m{-}1 \rangle $
. To lift
$\nu _{4m-1} : M \to BO\langle 4m{-}1 \rangle $
. To lift
![]() $\nu _{4m{-}1}$
to
$\nu _{4m{-}1}$
to
![]() $B_d$
, we consider the long exact sequence (of pointed sets) of the fibration
$B_d$
, we consider the long exact sequence (of pointed sets) of the fibration
where on the left, we use
![]() $[M,\Omega K(\mathbb {Z}/d,4m)]=[M, K(\mathbb {Z}/d,4m-1)]= H^{4m-1} (M;\mathbb {Z}/d)=0$
, because M is
$[M,\Omega K(\mathbb {Z}/d,4m)]=[M, K(\mathbb {Z}/d,4m-1)]= H^{4m-1} (M;\mathbb {Z}/d)=0$
, because M is
![]() $(4m{-}1)$
-connected. The assertion is now proved by noting that
$(4m{-}1)$
-connected. The assertion is now proved by noting that
![]() $\nu _{4m{-}1} \in [M,BO\langle 4m{-}1 \rangle ]$
maps to
$\nu _{4m{-}1} \in [M,BO\langle 4m{-}1 \rangle ]$
maps to
![]() $S\alpha _M \in H^{4m}(M;\mathbb {Z}/d)$
, which is zero by definition of the divisibility
$S\alpha _M \in H^{4m}(M;\mathbb {Z}/d)$
, which is zero by definition of the divisibility
![]() $d_M$
.
$d_M$
.
By [Reference KreckKre99, Theorem 2], M and N are orientation preserving stably diffeomorphic if
Since homotopy
![]() $8m$
-spheres have a unique
$8m$
-spheres have a unique
![]() $(B_d, \eta _d)$
-structure, there is a well-defined homomorphism
$(B_d, \eta _d)$
-structure, there is a well-defined homomorphism
![]() $\Theta _{8m} \to \Omega _{8m}(B_d, \eta _d)$
. Now the arguments in Wall’s computation of the Grothendieck groups of almost-closed
$\Theta _{8m} \to \Omega _{8m}(B_d, \eta _d)$
. Now the arguments in Wall’s computation of the Grothendieck groups of almost-closed
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds [Reference WallWal62, Theorem 2] show that there is an exact sequence
$8m$
-manifolds [Reference WallWal62, Theorem 2] show that there is an exact sequence
where
![]() $\sigma ([M, \overline \nu _M]) = \sigma _M$
and
$\sigma ([M, \overline \nu _M]) = \sigma _M$
and
![]() $S\alpha ^2([M, \overline \nu _M]) = (S\alpha _M)^2([M])$
. It follows that there is a homotopy
$S\alpha ^2([M, \overline \nu _M]) = (S\alpha _M)^2([M])$
. It follows that there is a homotopy
![]() $8m$
-sphere
$8m$
-sphere
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $[M \# \Sigma , \overline \nu _{M \# \Sigma }] = [N, \overline \nu _N] \in \Omega _{8m}(B_d, \eta )$
. Hence,
$[M \# \Sigma , \overline \nu _{M \# \Sigma }] = [N, \overline \nu _N] \in \Omega _{8m}(B_d, \eta )$
. Hence,
![]() $M \# \Sigma $
and N are stably diffeomorphic and so M and N are almost-stably diffeomorphic.
$M \# \Sigma $
and N are stably diffeomorphic and so M and N are almost-stably diffeomorphic.
3.5 Construction of the manifolds
 $M_{a, b}$
$M_{a, b}$
In this section, we construct the manifolds
![]() $M_{a,b}$
appearing in Theorem 3.3. Let a and b be positive integers such that
$M_{a,b}$
appearing in Theorem 3.3. Let a and b be positive integers such that
![]() $\mathfrak {bp}_m \mid ab$
. We build simply connected, closed
$\mathfrak {bp}_m \mid ab$
. We build simply connected, closed
![]() $8m$
-manifolds
$8m$
-manifolds
![]() $M_{a,b}$
with the cohomology ring of
$M_{a,b}$
with the cohomology ring of
![]() $S^{4m} \times S^{4m}$
by attaching handles to an
$S^{4m} \times S^{4m}$
by attaching handles to an
![]() $8m$
-ball. We attach to
$8m$
-ball. We attach to
![]() $D^{8m}$
two
$D^{8m}$
two
![]() $4m$
-handles
$4m$
-handles
![]() $h_x$
and
$h_x$
and
![]() $h_y$
, diffeomorphic to
$h_y$
, diffeomorphic to
![]() $D^{4m}\times D^{4m}$
, using attaching maps
$D^{4m}\times D^{4m}$
, using attaching maps
![]() $\phi _x,\phi _y : S^{4m-1} \times \{0\} \to S^{8m-1}$
with linking number
$\phi _x,\phi _y : S^{4m-1} \times \{0\} \to S^{8m-1}$
with linking number
![]() $1$
. Note that for
$1$
. Note that for
![]() $m \geq 1$
, 2-component links
$m \geq 1$
, 2-component links
![]() $S^{4m-1} \sqcup S^{4m-1} \hookrightarrow S^{8m-1}$
are classified up to smooth isotopy by the linking number, an integer [Reference HaefligerHae62, Theorem in Section 5]. There is more data needed for the attaching maps, which for each
$S^{4m-1} \sqcup S^{4m-1} \hookrightarrow S^{8m-1}$
are classified up to smooth isotopy by the linking number, an integer [Reference HaefligerHae62, Theorem in Section 5]. There is more data needed for the attaching maps, which for each
![]() $4m$
-handle corresponds to a choice of framing for the attaching sphere
$4m$
-handle corresponds to a choice of framing for the attaching sphere
![]() $S^{4m{-}1} \subseteq S^{8m-1}$
. The framings that induce a given orientation are in one to one correspondence with homotopy classes of maps
$S^{4m{-}1} \subseteq S^{8m-1}$
. The framings that induce a given orientation are in one to one correspondence with homotopy classes of maps
![]() $[S^{4m{-}1},SO_{4m}]$
, where the class of the constant map corresponds to the framing that extends over an embedded
$[S^{4m{-}1},SO_{4m}]$
, where the class of the constant map corresponds to the framing that extends over an embedded
![]() $4m$
-disc
$4m$
-disc
![]() $D^{4m} \subseteq S^{8m-1}$
. Recall from (*) that
$D^{4m} \subseteq S^{8m-1}$
. Recall from (*) that
![]() $\pi _{4m{-}1}(SO_{4m}) \cong \mathbb {Z} \oplus \mathbb {Z}$
, detected by
$\pi _{4m{-}1}(SO_{4m}) \cong \mathbb {Z} \oplus \mathbb {Z}$
, detected by
![]() $\mathrm {e} \oplus S$
(although this map is not an isomorphism). We are attaching
$\mathrm {e} \oplus S$
(although this map is not an isomorphism). We are attaching
![]() $4m$
-handles
$4m$
-handles
![]() $h_x \ h_y$
; let x and y denote the corresponding classes in
$h_x \ h_y$
; let x and y denote the corresponding classes in
![]() $(4m)$
th homology and let
$(4m)$
th homology and let
![]() $\xi _x,\xi _y \in \pi _{4m-1}(SO_{4m})$
be the framings for the attaching maps.
$\xi _x,\xi _y \in \pi _{4m-1}(SO_{4m})$
be the framings for the attaching maps.
Since we want
![]() $\lambda (x,x)=0$
, we require that
$\lambda (x,x)=0$
, we require that
![]() $\mathrm {e}(\xi _x) = 0$
but we are otherwise free to choose
$\mathrm {e}(\xi _x) = 0$
but we are otherwise free to choose
![]() $\xi _x$
. Recall that
$\xi _x$
. Recall that
![]() $c_m = 2$
if
$c_m = 2$
if
![]() $m = 1, 2$
and
$m = 1, 2$
and
![]() $c_m = 1$
if
$c_m = 1$
if
![]() $m \!> \! 2$
, fix an isomorphism
$m \!> \! 2$
, fix an isomorphism
![]() $\pi _{4m-1}(SO) = \mathbb {Z}$
and choose
$\pi _{4m-1}(SO) = \mathbb {Z}$
and choose
![]() $\xi _x$
such that
$\xi _x$
such that
![]() $S(\xi _x) = a c_m$
. By the discussion following (*), we can find such a
$S(\xi _x) = a c_m$
. By the discussion following (*), we can find such a
![]() $\xi _x$
for any choice of a. Similarly, we attach the handle
$\xi _x$
for any choice of a. Similarly, we attach the handle
![]() $h_y$
with
$h_y$
with
![]() $\mathrm {e}(\xi _y) = 0$
and
$\mathrm {e}(\xi _y) = 0$
and
![]() $S(\xi _y) = b c_m$
. Again, we can find such a
$S(\xi _y) = b c_m$
. Again, we can find such a
![]() $\xi _y$
for any b. After attaching the pair of
$\xi _y$
for any b. After attaching the pair of
![]() $4m$
-handles, we write
$4m$
-handles, we write
![]() $W := W_{a, b}$
for the resulting compact
$W := W_{a, b}$
for the resulting compact
![]() $8m$
-manifold with boundary. Note that there is a homotopy equivalence
$8m$
-manifold with boundary. Note that there is a homotopy equivalence
![]() $W \simeq S^{4m} \vee S^{4m}$
. As above, let x and y be generators of
$W \simeq S^{4m} \vee S^{4m}$
. As above, let x and y be generators of
![]() $\mathbb {Z}^2 \cong H_{4m}(W)$
and let
$\mathbb {Z}^2 \cong H_{4m}(W)$
and let
![]() $\{x^*, y^*\}$
be the dual basis for
$\{x^*, y^*\}$
be the dual basis for
![]() $\mathbb {Z}^2 \cong H^{4m}(W) = H_{4m}(W)^*$
. The manifold
$\mathbb {Z}^2 \cong H^{4m}(W) = H_{4m}(W)^*$
. The manifold
![]() $W=W_{a, b}$
has smooth extended symmetric form given by
$W=W_{a, b}$
has smooth extended symmetric form given by
 $$ \begin{align*} ( H_{4m}(W), \lambda_W, S\alpha_W ) = \left( \mathbb{Z}^2, \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), \left( \begin{array}{c} a c_m \\ b c_m \end{array} \right) : \mathbb{Z}^2 \to \mathbb{Z} \right), \end{align*} $$
$$ \begin{align*} ( H_{4m}(W), \lambda_W, S\alpha_W ) = \left( \mathbb{Z}^2, \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), \left( \begin{array}{c} a c_m \\ b c_m \end{array} \right) : \mathbb{Z}^2 \to \mathbb{Z} \right), \end{align*} $$
where the notation for
![]() $S\alpha _W$
means that
$S\alpha _W$
means that
![]() $S\alpha _W(x) = ac_m$
and
$S\alpha _W(x) = ac_m$
and
![]() $S\alpha _W(y) = bc_m$
.
$S\alpha _W(y) = bc_m$
.
Alternatively, the construction thus far can be achieved by taking the two
![]() $D^{4m}$
-bundles over
$D^{4m}$
-bundles over
![]() $S^{4m}$
determined by
$S^{4m}$
determined by
![]() $\xi _{x}$
and
$\xi _{x}$
and
![]() $\xi _{y}$
, and plumbing them together once.
$\xi _{y}$
, and plumbing them together once.
The boundary of
![]() $W_{a, b}$
is a homotopy
$W_{a, b}$
is a homotopy
![]() $(8m{-1})$
-sphere, which we denote by
$(8m{-1})$
-sphere, which we denote by
![]() $\Sigma _{a, b}$
. In particular,
$\Sigma _{a, b}$
. In particular,
![]() $\partial W_{1, 1}$
is by definition the homotopy sphere
$\partial W_{1, 1}$
is by definition the homotopy sphere
![]() $\Sigma _Q$
from [Reference Krannich and ReinholdKR20, Section 2]. More generally,
$\Sigma _Q$
from [Reference Krannich and ReinholdKR20, Section 2]. More generally,
![]() $\partial W_{a,b}$
is given as follows.
$\partial W_{a,b}$
is given as follows.
Lemma 3.9.
![]() $[\partial W_{a, b}] = [ab \Sigma _Q] \in \Theta _{8m-1}$
.
$[\partial W_{a, b}] = [ab \Sigma _Q] \in \Theta _{8m-1}$
.
Proof. Recall from [Reference WallWal67, Section 17] the group
![]() $A^{\langle {4m}\rangle }_{8m}$
of bordism classes of
$A^{\langle {4m}\rangle }_{8m}$
of bordism classes of
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds with boundary a homotopy sphere, where the bordisms are required to be h-cobordisms on the boundary. Addition is via boundary connected sum. Taking the boundary defines a homomorphism
$8m$
-manifolds with boundary a homotopy sphere, where the bordisms are required to be h-cobordisms on the boundary. Addition is via boundary connected sum. Taking the boundary defines a homomorphism
![]() $A^{\langle {4m}\rangle }_{8m} \to \Theta _{8m-1}$
, and the characteristic numbers
$A^{\langle {4m}\rangle }_{8m} \to \Theta _{8m-1}$
, and the characteristic numbers
![]() $\sigma $
and
$\sigma $
and
![]() $(S\alpha )^2$
of (Ω) are also well defined on
$(S\alpha )^2$
of (Ω) are also well defined on
![]() $A^{\langle {4m}\rangle }_{8m}$
. Indeed, Wall [Reference WallWal62, Theorems 2 and 3] proved that
$A^{\langle {4m}\rangle }_{8m}$
. Indeed, Wall [Reference WallWal62, Theorems 2 and 3] proved that
![]() $\sigma \oplus (S\alpha )^2 : A^{\langle {4m}\rangle }_{8m} \to \mathbb {Z}^2$
is an injective homomorphism. Since
$\sigma \oplus (S\alpha )^2 : A^{\langle {4m}\rangle }_{8m} \to \mathbb {Z}^2$
is an injective homomorphism. Since
![]() $W_{a, b}$
satisfies
$W_{a, b}$
satisfies
![]() $\sigma (W_{a, b}) = 0$
and
$\sigma (W_{a, b}) = 0$
and
![]() $(S\alpha _{W_{a, b}})^2 = 2abc_m^2$
, we have that
$(S\alpha _{W_{a, b}})^2 = 2abc_m^2$
, we have that
![]() $(S\alpha _{W_{1, 1}})^2 = 2c_m^2$
and so
$(S\alpha _{W_{1, 1}})^2 = 2c_m^2$
and so
where the last equality used that
![]() $(S\alpha )^2$
is a homomorphism. Since
$(S\alpha )^2$
is a homomorphism. Since
![]() $\sigma \oplus (S\alpha )^2$
is injective,
$\sigma \oplus (S\alpha )^2$
is injective,
![]() $W_{a,b} = \natural ^{ab} W_{1,1} \in A^{\langle {4m}\rangle }_{8m}$
. So
$W_{a,b} = \natural ^{ab} W_{1,1} \in A^{\langle {4m}\rangle }_{8m}$
. So
![]() $\partial W_{a,b}$
and
$\partial W_{a,b}$
and
![]() $\partial (\natural ^{ab} W_{1,1}) = ab \Sigma _Q$
are h-cobordant and therefore diffeomorphic.
$\partial (\natural ^{ab} W_{1,1}) = ab \Sigma _Q$
are h-cobordant and therefore diffeomorphic.
From Lemma 3.9 and our assumption that
![]() $\mathfrak {bp}_m \mid ab$
, it follows that
$\mathfrak {bp}_m \mid ab$
, it follows that
![]() $[\Sigma _{a, b}] = 0 \in \Theta _{8m-1}$
, so that there is a choice of diffeomorphism
$[\Sigma _{a, b}] = 0 \in \Theta _{8m-1}$
, so that there is a choice of diffeomorphism
![]() $f : \Sigma _{a, b} \to S^{8m-1}$
. We write
$f : \Sigma _{a, b} \to S^{8m-1}$
. We write
![]() $M_{a, b, f} = W_{a, b} \bigcup _f D^{8m}$
for the closure of
$M_{a, b, f} = W_{a, b} \bigcup _f D^{8m}$
for the closure of
![]() $W_{a, b}$
built using a diffeomorphism
$W_{a, b}$
built using a diffeomorphism
![]() $f : \Sigma _{a, b} \to S^{8m-1}$
. We also use
$f : \Sigma _{a, b} \to S^{8m-1}$
. We also use
![]() $M_{a, b}$
to ambiguously denote any
$M_{a, b}$
to ambiguously denote any
![]() $M_{a, b, f}$
. For any other choice of diffeomorphism
$M_{a, b, f}$
. For any other choice of diffeomorphism
![]() $f'$
,
$f'$
,
![]() $M_{a,b,f}$
and
$M_{a,b,f}$
and
![]() $M_{a,b,f'}$
are almost diffeomorphic.
$M_{a,b,f'}$
are almost diffeomorphic.
Let us record the values of the key invariants on
![]() $M_{a,b}$
. The stable almost-diffeomorphism invariants of
$M_{a,b}$
. The stable almost-diffeomorphism invariants of
![]() $M_{a,b}$
are
$M_{a,b}$
are
![]() $d_{M_{a,b}}= \mathrm {gcd}(a, b)c_m$
,
$d_{M_{a,b}}= \mathrm {gcd}(a, b)c_m$
,
![]() $\sigma (M_{a,b}) = 0$
and
$\sigma (M_{a,b}) = 0$
and
![]() $(S\alpha _{M_{a,b}})^2 = 2abc_m^2$
. The extended symmetric form of
$(S\alpha _{M_{a,b}})^2 = 2abc_m^2$
. The extended symmetric form of
![]() $M: =M_{a,b}$
is the same as that of W:
$M: =M_{a,b}$
is the same as that of W:
 $$ \begin{align*} ( H_{4m}(M), \lambda_M, S\alpha_M ) = \left( \mathbb{Z}^2, \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), \left( \begin{array}{c} a c_m \\ b c_m \end{array} \right) : \mathbb{Z}^2 \to \mathbb{Z} \right). \end{align*} $$
$$ \begin{align*} ( H_{4m}(M), \lambda_M, S\alpha_M ) = \left( \mathbb{Z}^2, \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), \left( \begin{array}{c} a c_m \\ b c_m \end{array} \right) : \mathbb{Z}^2 \to \mathbb{Z} \right). \end{align*} $$
This completes the construction of the manifolds
![]() $M_{a,b}$
.
$M_{a,b}$
.
3.6 The proof of Theorem 3.3
Now that we have constructed the
![]() $(4m{-}1)$
- connected
$(4m{-}1)$
- connected
![]() $8m$
-manifolds
$8m$
-manifolds
![]() $M_{a,b}$
, we are ready to prove Theorem 3.3.
$M_{a,b}$
, we are ready to prove Theorem 3.3.
Proof of Theorem 3.3
Let a and b be positive integers such that
![]() $\mathfrak {bp}_m \mid ab$
. By construction, the oriented manifolds
$\mathfrak {bp}_m \mid ab$
. By construction, the oriented manifolds
![]() $M_{a,b}$
have hyperbolic intersection form, so Theorem 3.3(1) is immediate.
$M_{a,b}$
have hyperbolic intersection form, so Theorem 3.3(1) is immediate.
As before, write
![]() $d:= \gcd (a,b)c_m$
and define
$d:= \gcd (a,b)c_m$
and define
![]() $A:= abc_m^2/d^2$
. Let
$A:= abc_m^2/d^2$
. Let
![]() $p_{1},\ldots ,p_{q_A+1}$
be the prime-power factors of A, which are powers of pairwise distinct primes. Then there are
$p_{1},\ldots ,p_{q_A+1}$
be the prime-power factors of A, which are powers of pairwise distinct primes. Then there are
![]() $2^{q_A}$
ways to express A as a product
$2^{q_A}$
ways to express A as a product
![]() $y_iz_i$
of coprime positive integers, counting unordered pairs
$y_iz_i$
of coprime positive integers, counting unordered pairs
![]() $\{y_i,z_i\}$
. We consider the
$\{y_i,z_i\}$
. We consider the
![]() $8m$
-manifolds
$8m$
-manifolds
For each i,
![]() $d_{M_i} = d$
,
$d_{M_i} = d$
,
![]() $\sigma (M_i) =0$
and
$\sigma (M_i) =0$
and
![]() $\langle (S\alpha _{M_i})^2,[M_i]\rangle = 2dy_idz_i= 2d^2 A = 2abc_m^2$
. Therefore, the manifolds
$\langle (S\alpha _{M_i})^2,[M_i]\rangle = 2dy_idz_i= 2d^2 A = 2abc_m^2$
. Therefore, the manifolds
![]() $M_i$
are pairwise almost-stably diffeomorphic by Theorem 3.8. A priori they cannot all lie in
$M_i$
are pairwise almost-stably diffeomorphic by Theorem 3.8. A priori they cannot all lie in
![]() $\mathcal {S}^{\mathrm {st}}(M_{a, b})$
, but the ambiguity of whether they are actually stably diffeomorphic is removed by more carefully choosing the diffeomorphisms
$\mathcal {S}^{\mathrm {st}}(M_{a, b})$
, but the ambiguity of whether they are actually stably diffeomorphic is removed by more carefully choosing the diffeomorphisms
![]() $f_i : \Sigma _i \to S^{8m-1}$
used to glue on
$f_i : \Sigma _i \to S^{8m-1}$
used to glue on
![]() $D^{8m}$
in the construction of the
$D^{8m}$
in the construction of the
![]() $M_i$
. By changing the choice of the identification
$M_i$
. By changing the choice of the identification
![]() $f_i$
, we change
$f_i$
, we change
![]() $M_i$
by connected sum with an exotic sphere of our choice. The
$M_i$
by connected sum with an exotic sphere of our choice. The
![]() $M_i$
are only determined up to this choice in our construction, so let us assume we made this consistently so that
$M_i$
are only determined up to this choice in our construction, so let us assume we made this consistently so that
![]() $M_i \in \mathcal {S}^{\mathrm { st}}(M_{a, b})$
for every
$M_i \in \mathcal {S}^{\mathrm { st}}(M_{a, b})$
for every
![]() $i=1,\ldots ,2^{q_{A}}$
. In
$i=1,\ldots ,2^{q_{A}}$
. In
![]() $\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}$
, this choice of the
$\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}$
, this choice of the
![]() $f_i$
is in any case irrelevant.
$f_i$
is in any case irrelevant.
When we discuss extended symmetric forms on
![]() $\mathbb {Z}^2$
, we always mean with respect to a particular choice of basis. For
$\mathbb {Z}^2$
, we always mean with respect to a particular choice of basis. For
![]() $M_i$
, with its fixed choice of fundamental class
$M_i$
, with its fixed choice of fundamental class
![]() $[M_i]$
, we use a basis with respect to which the intersection form is represented by
$[M_i]$
, we use a basis with respect to which the intersection form is represented by
![]() $H^+(\mathbb {Z}) = (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix})$
. We have constructed the
$H^+(\mathbb {Z}) = (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix})$
. We have constructed the
![]() $M_i$
so that, with respect to such a basis,
$M_i$
so that, with respect to such a basis,
![]() $S\alpha _{M_i} : \mathbb {Z}^2 \to \mathbb {Z}$
is represented by
$S\alpha _{M_i} : \mathbb {Z}^2 \to \mathbb {Z}$
is represented by
![]() $(\begin {smallmatrix} ac_m \\bc_m \end {smallmatrix})$
with
$(\begin {smallmatrix} ac_m \\bc_m \end {smallmatrix})$
with
![]() $ab>0$
and
$ab>0$
and
![]() $c_m \in \{1,2\}$
.
$c_m \in \{1,2\}$
.
The smooth extended symmetric forms of the
![]() $M_i$
are pairwise distinct, since isometries of the rank two hyperbolic intersection form can only change the sign and permute the basis elements. The map
$M_i$
are pairwise distinct, since isometries of the rank two hyperbolic intersection form can only change the sign and permute the basis elements. The map
![]() $S\alpha _{M_i} : \mathbb {Z}^2 \to \mathbb {Z}$
is given by
$S\alpha _{M_i} : \mathbb {Z}^2 \to \mathbb {Z}$
is given by
![]() $(dy_i,dz_i)$
. Since the unordered pairs
$(dy_i,dz_i)$
. Since the unordered pairs
![]() $\{dy_i,dz_i\}$
are pairwise distinct, by the almost-diffeomorphism classification of Theorem 3.7(1), the
$\{dy_i,dz_i\}$
are pairwise distinct, by the almost-diffeomorphism classification of Theorem 3.7(1), the
![]() $M_i$
are pairwise distinct up to orientation-preserving almost diffeomorphism. We are able to deduce that
$M_i$
are pairwise distinct up to orientation-preserving almost diffeomorphism. We are able to deduce that
![]() $|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| \geq 2^{q_{A}}$
once we have factored out the effect of the choice of orientation of the
$|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| \geq 2^{q_{A}}$
once we have factored out the effect of the choice of orientation of the
![]() $M_i$
. In other words, we must show that there are also no orientation-reversing almost diffeomorphisms from
$M_i$
. In other words, we must show that there are also no orientation-reversing almost diffeomorphisms from
![]() $M_i$
to
$M_i$
to
![]() $M_j$
, for
$M_j$
, for
![]() $i \neq j$
, or equivalently that there is no orientation-preserving diffeomorphism
$i \neq j$
, or equivalently that there is no orientation-preserving diffeomorphism
![]() $M_i \cong -M_j$
.
$M_i \cong -M_j$
.
Changing the orientation of
![]() $M_j$
changes the smooth extended symmetric form, with respect to the same basis for
$M_j$
changes the smooth extended symmetric form, with respect to the same basis for
![]() $H_{4m}(M)$
, by altering the sign of the intersection form, but does not affect
$H_{4m}(M)$
, by altering the sign of the intersection form, but does not affect
![]() $S\alpha _{M_j}$
. To see this, note that while changing the orientation of
$S\alpha _{M_j}$
. To see this, note that while changing the orientation of
![]() $M_j$
changes the induced orientation of the fibres of the normal bundle of an embedded sphere x,
$M_j$
changes the induced orientation of the fibres of the normal bundle of an embedded sphere x,
![]() $S\alpha _{M_j}(x) \in \pi _{4m-1}(SO)$
is the clutching map of this normal bundle, and this is unaffected by the orientation of the fibres.
$S\alpha _{M_j}(x) \in \pi _{4m-1}(SO)$
is the clutching map of this normal bundle, and this is unaffected by the orientation of the fibres.
The isometries from the rank two hyperbolic form
![]() $H^+(\mathbb {Z}) = (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix})$
to its negative
$H^+(\mathbb {Z}) = (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix})$
to its negative
![]() $-H^+(\mathbb {Z})$
consist of the self-isometries of the hyperbolic form, namely
$-H^+(\mathbb {Z})$
consist of the self-isometries of the hyperbolic form, namely
![]() $\pm \operatorname{\mathrm {Id}}$
and
$\pm \operatorname{\mathrm {Id}}$
and
![]() $(\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix})$
, composed with either
$(\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix})$
, composed with either
![]() $(\begin {smallmatrix} 1 & 0 \\ 0 & -1 \end {smallmatrix})$
or
$(\begin {smallmatrix} 1 & 0 \\ 0 & -1 \end {smallmatrix})$
or
![]() $(\begin {smallmatrix} -1 & 0 \\ 0 & 1 \end {smallmatrix})$
. Thus an orientation-reversing almost diffeomorphism could identify the smooth extended symmetric form characterised by
$(\begin {smallmatrix} -1 & 0 \\ 0 & 1 \end {smallmatrix})$
. Thus an orientation-reversing almost diffeomorphism could identify the smooth extended symmetric form characterised by
![]() $(H^+(\mathbb {Z}),\pm \{v,w\})$
with one of the extended symmetric forms
$(H^+(\mathbb {Z}),\pm \{v,w\})$
with one of the extended symmetric forms
![]() $(-H^+(\mathbb {Z}),\pm \{-v,w\})$
or
$(-H^+(\mathbb {Z}),\pm \{-v,w\})$
or
![]() $(-H^+(\mathbb {Z}),\pm \{v,-w\})$
. However, for both
$(-H^+(\mathbb {Z}),\pm \{v,-w\})$
. However, for both
![]() $M_i$
and
$M_i$
and
![]() $-M_i$
, the corresponding pair of integers is
$-M_i$
, the corresponding pair of integers is
![]() $\pm \{v,w\} = \pm \{dy_i,dz_i\}$
, where both elements have the same sign. So our manifolds
$\pm \{v,w\} = \pm \{dy_i,dz_i\}$
, where both elements have the same sign. So our manifolds
![]() $\{M_i\}$
are indeed distinct up to almost diffeomorphism. This proves that
$\{M_i\}$
are indeed distinct up to almost diffeomorphism. This proves that
![]() $|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| \geq ~2^{q_{A}}$
.
$|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| \geq ~2^{q_{A}}$
.
Next we prove that
![]() $|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| \leq 2^{q_{A}}$
. Any closed
$|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| \leq 2^{q_{A}}$
. Any closed
![]() $8m$
-manifold M that is almost-stably diffeomorphic to
$8m$
-manifold M that is almost-stably diffeomorphic to
![]() $M_{a,b}$
is also necessarily
$M_{a,b}$
is also necessarily
![]() $(4m{-}1)$
-connected, the divisibility of
$(4m{-}1)$
-connected, the divisibility of
![]() $S\alpha _M$
is d and the intersection form is rank two, indefinite and even, and therefore either hyperbolic or
$S\alpha _M$
is d and the intersection form is rank two, indefinite and even, and therefore either hyperbolic or
![]() $-H^+(\mathbb {Z})$
. If M and
$-H^+(\mathbb {Z})$
. If M and
![]() $M_{a,b}$
are almost-stably diffeomorphic, then there is an orientation on M such that M and
$M_{a,b}$
are almost-stably diffeomorphic, then there is an orientation on M such that M and
![]() $M_{a,b}$
are almost-stably diffeomorphic via an orientation-preserving stable diffeomorphism. Use this orientation and choose a basis for
$M_{a,b}$
are almost-stably diffeomorphic via an orientation-preserving stable diffeomorphism. Use this orientation and choose a basis for
![]() $H_{4m}(M)$
with respect to which the intersection form of M is
$H_{4m}(M)$
with respect to which the intersection form of M is
![]() $H^+(\mathbb {Z})$
. Observe that the manifolds
$H^+(\mathbb {Z})$
. Observe that the manifolds
![]() $M_i$
cover all possibilities for
$M_i$
cover all possibilities for
![]() $S\alpha _M$
while keeping
$S\alpha _M$
while keeping
![]() $(S\alpha _M)^2$
a fixed multiple of the dual fundamental class. (If
$(S\alpha _M)^2$
a fixed multiple of the dual fundamental class. (If
![]() $S\alpha _M = (\begin {smallmatrix} -ac_m \\ bc_m \end {smallmatrix})$
, for example, then
$S\alpha _M = (\begin {smallmatrix} -ac_m \\ bc_m \end {smallmatrix})$
, for example, then
![]() $(S\alpha _M)^2 = -2abc_m^2 <0$
, whereas
$(S\alpha _M)^2 = -2abc_m^2 <0$
, whereas
![]() $(S\alpha _{M_{a,b}})^2 = 2abc_m^2>0$
. This would contradict that
$(S\alpha _{M_{a,b}})^2 = 2abc_m^2>0$
. This would contradict that
![]() $M_{a,b}$
and M are orientation-preserving almost-stably diffeomorphic.) It follows by Theorem 3.7(1) that every such M is almost-stably diffeomorphic to one of the
$M_{a,b}$
and M are orientation-preserving almost-stably diffeomorphic.) It follows by Theorem 3.7(1) that every such M is almost-stably diffeomorphic to one of the
![]() $M_i$
, and therefore
$M_i$
, and therefore
![]() $|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| \leq 2^{q_{A}}$
as desired. This completes the proof of Theorem 3.3(2).
$|\mathcal {S}^{\mathrm {st}}(M_{a, b})/\Theta _{8m}| \leq 2^{q_{A}}$
as desired. This completes the proof of Theorem 3.3(2).
To prove (3), we need to estimate the size of the homotopy stable class of
![]() $M_{a,b}$
from above and below. We begin with the upper bound. As above, every closed
$M_{a,b}$
from above and below. We begin with the upper bound. As above, every closed
![]() $8m$
-manifold M stably diffeomorphic to
$8m$
-manifold M stably diffeomorphic to
![]() $M_{a,b}$
has an orientation such that M has hyperbolic intersection form and
$M_{a,b}$
has an orientation such that M has hyperbolic intersection form and
![]() $d_M=d$
. The possibilities for
$d_M=d$
. The possibilities for
![]() $S\alpha _M^h$
, up to equivalence of extended symmetric forms, are therefore given by an unordered pair of elements of
$S\alpha _M^h$
, up to equivalence of extended symmetric forms, are therefore given by an unordered pair of elements of
![]() $\mathbb {Z}/j_m$
, both of which are divisible by d. Such an element of
$\mathbb {Z}/j_m$
, both of which are divisible by d. Such an element of
![]() $\mathbb {Z}/j_m$
lies in the subgroup generated by
$\mathbb {Z}/j_m$
lies in the subgroup generated by
![]() $\gcd (\,j_m, d)$
, and so there are
$\gcd (\,j_m, d)$
, and so there are
![]() $\overline j_m = j_m/\gcd (\,j_m, d)$
possibilities. We assert that there are
$\overline j_m = j_m/\gcd (\,j_m, d)$
possibilities. We assert that there are
 $$ \begin{align*} \displaystyle\frac{\overline j_m (\,\overline j_m + 1)}{2} \end{align*} $$
$$ \begin{align*} \displaystyle\frac{\overline j_m (\,\overline j_m + 1)}{2} \end{align*} $$
such pairs. To see this, there are
![]() ${\overline {j}_m \choose 2} = {\overline j_m (\,\overline j_m - 1)}/{2}$
choices with distinct elements
${\overline {j}_m \choose 2} = {\overline j_m (\,\overline j_m - 1)}/{2}$
choices with distinct elements
![]() $(x,y)$
, and
$(x,y)$
, and
![]() $\overline {j}_m$
choices of the form
$\overline {j}_m$
choices of the form
![]() $(x,x)$
. Then
$(x,x)$
. Then
![]() ${\overline j_m (\,\overline j_m - 1)}/{2} + \overline {j}_m = {\overline j_m (\,\overline j_m + 1)}/{2}$
, which is the count asserted. Next, we also factor out the action of
${\overline j_m (\,\overline j_m - 1)}/{2} + \overline {j}_m = {\overline j_m (\,\overline j_m + 1)}/{2}$
, which is the count asserted. Next, we also factor out the action of
![]() $\mathbb {Z}/2$
on our set of unordered pairs which multiplies both numbers by
$\mathbb {Z}/2$
on our set of unordered pairs which multiplies both numbers by
![]() $-1$
. In the case that
$-1$
. In the case that
![]() $\overline {j}_m$
is even, there are
$\overline {j}_m$
is even, there are
![]() ${\overline {j}_m}/{2} {+} 1$
fixed points of this action of the form
${\overline {j}_m}/{2} {+} 1$
fixed points of this action of the form
![]() $(x,-x)$
, and also
$(x,-x)$
, and also
![]() $(0,{\overline {j}_m}/{2})$
is a fixed point. Thus, there are precisely
$(0,{\overline {j}_m}/{2})$
is a fixed point. Thus, there are precisely
![]() ${\overline {j}_m}/{2}+2$
fixed points of the
${\overline {j}_m}/{2}+2$
fixed points of the
![]() $\mathbb {Z}/2$
action on the set with
$\mathbb {Z}/2$
action on the set with
![]() ${\overline j_m (\,\overline j_m + 1)}/{2}$
elements. A short calculation then shows that there are
${\overline j_m (\,\overline j_m + 1)}/{2}$
elements. A short calculation then shows that there are
 $$ \begin{align*} \displaystyle\frac{\overline{j}_m^2 +2\overline{j}_m + 4}{4} \end{align*} $$
$$ \begin{align*} \displaystyle\frac{\overline{j}_m^2 +2\overline{j}_m + 4}{4} \end{align*} $$
orbits. A similar calculation for
![]() $\overline {j}_m$
odd gives
$\overline {j}_m$
odd gives
 $$ \begin{align*} \displaystyle\frac{(\,\overline{j}_m + 1)^2}{4} = \bigg\lfloor \displaystyle\frac{\overline{j}_m^2 +2\overline{j}_m + 4}{4} \bigg\rfloor \end{align*} $$
$$ \begin{align*} \displaystyle\frac{(\,\overline{j}_m + 1)^2}{4} = \bigg\lfloor \displaystyle\frac{\overline{j}_m^2 +2\overline{j}_m + 4}{4} \bigg\rfloor \end{align*} $$
orbits. The right-hand side is equal for both parities of
![]() $\overline {j}_m$
and gives our desired upper bound. Note that this upper bound does not take into account the requirement for the product
$\overline {j}_m$
and gives our desired upper bound. Note that this upper bound does not take into account the requirement for the product
![]() $ab$
to be constant within a stable diffeomorphism class.
$ab$
to be constant within a stable diffeomorphism class.
It remains to prove that
![]() $2^{q_{A, m}} \leq |\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})|$
. As above, let
$2^{q_{A, m}} \leq |\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})|$
. As above, let
![]() $p_{1},\ldots ,p_{q_A+1}$
be the prime-power factors of A, which are powers of pairwise distinct primes. By reordering if necessary, assume that
$p_{1},\ldots ,p_{q_A+1}$
be the prime-power factors of A, which are powers of pairwise distinct primes. By reordering if necessary, assume that
![]() $p_1,\ldots ,p_{q_{A,m}+1}$
are the prime-powers of the form
$p_1,\ldots ,p_{q_{A,m}+1}$
are the prime-powers of the form
![]() $p^{\ell }$
, where
$p^{\ell }$
, where
![]() $p \mid \overline j_m$
. (It could be that the highest exponent of p that divides
$p \mid \overline j_m$
. (It could be that the highest exponent of p that divides
![]() $\overline j_m$
is less than the highest exponent of p that divides A.) Recall that
$\overline j_m$
is less than the highest exponent of p that divides A.) Recall that
![]() $d = \gcd (a,b) c_m$
and write
$d = \gcd (a,b) c_m$
and write
 $$ \begin{align*}d' := d \cdot \prod_{\iota=q_{A,m}+2}^{q_{A} +1} p_{\iota} \text{ and } A' := \prod_{\iota=1}^{q_{A,m} +1} p_{\iota}.\end{align*} $$
$$ \begin{align*}d' := d \cdot \prod_{\iota=q_{A,m}+2}^{q_{A} +1} p_{\iota} \text{ and } A' := \prod_{\iota=1}^{q_{A,m} +1} p_{\iota}.\end{align*} $$
Note that
![]() $d'A' =dA$
. There are
$d'A' =dA$
. There are
![]() $2^{q_{A,m}}$
essentially distinct ways to express
$2^{q_{A,m}}$
essentially distinct ways to express
![]() $A'$
as a product
$A'$
as a product
![]() $v_iw_i$
of coprime positive integers, counting unordered pairs
$v_iw_i$
of coprime positive integers, counting unordered pairs
![]() $\{v_i,w_i\}$
. We consider the
$\{v_i,w_i\}$
. We consider the
![]() $8m$
-manifolds
$8m$
-manifolds
For each i,
![]() $d_{M_i} = d$
,
$d_{M_i} = d$
,
![]() $\sigma (M_i) =0$
and
$\sigma (M_i) =0$
and
![]() $\langle (S\alpha _{M_i})^2,[M_i]\rangle = 2dv_id'w_i = 2dd' A' = 2d^2 A = 2abc_m^2$
. Therefore, the
$\langle (S\alpha _{M_i})^2,[M_i]\rangle = 2dv_id'w_i = 2dd' A' = 2d^2 A = 2abc_m^2$
. Therefore, the
![]() $M_i$
are pairwise almost-stably diffeomorphic by Theorem 3.8; so, up to homotopy equivalence, they are all stably diffeomorphic. As above, the ambiguity of whether they are actually stably diffeomorphic is removed by more carefully choosing the diffeomorphisms
$M_i$
are pairwise almost-stably diffeomorphic by Theorem 3.8; so, up to homotopy equivalence, they are all stably diffeomorphic. As above, the ambiguity of whether they are actually stably diffeomorphic is removed by more carefully choosing the diffeomorphisms
![]() $f_i : \Sigma \to S^{8m-1}$
used to glue on
$f_i : \Sigma \to S^{8m-1}$
used to glue on
![]() $D^{8m}$
in the construction of the
$D^{8m}$
in the construction of the
![]() $M_i$
. Let us assume once again that we made this choice consistently so that
$M_i$
. Let us assume once again that we made this choice consistently so that
![]() $M_i \in \mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})$
for every
$M_i \in \mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})$
for every
![]() $i=1,\ldots ,2^{q_{A,m}}$
.
$i=1,\ldots ,2^{q_{A,m}}$
.
Next we show that the
![]() $M_i$
are distinct up to homotopy equivalence. For this, by Theorem 3.7, we need to distinguish their homotopy extended symmetric forms, by showing that the maps
$M_i$
are distinct up to homotopy equivalence. For this, by Theorem 3.7, we need to distinguish their homotopy extended symmetric forms, by showing that the maps
![]() $S\alpha _{M_i}^h : \mathbb {Z}^2 \to \mathbb {Z}/j_m$
are pairwise distinct, up to precomposing with an isometry of the hyperbolic form, or to allow for the possibility of an orientation-reversing homotopy equivalence, up to an isometry between the hyperbolic form and its negative. This means we have to show that the unordered pair of elements of
$S\alpha _{M_i}^h : \mathbb {Z}^2 \to \mathbb {Z}/j_m$
are pairwise distinct, up to precomposing with an isometry of the hyperbolic form, or to allow for the possibility of an orientation-reversing homotopy equivalence, up to an isometry between the hyperbolic form and its negative. This means we have to show that the unordered pair of elements of
![]() $\mathbb {Z}/j_m$
determining
$\mathbb {Z}/j_m$
determining
![]() $S\alpha _{M_i}^h$
and
$S\alpha _{M_i}^h$
and
![]() $S\alpha _{M_j}^h$
are distinct up to changing signs.
$S\alpha _{M_j}^h$
are distinct up to changing signs.
Let
![]() $M_i$
and
$M_i$
and
![]() $M_j$
be two of our manifolds, for
$M_j$
be two of our manifolds, for
![]() $i \neq j$
. We show that they are not homotopy equivalent. First,
$i \neq j$
. We show that they are not homotopy equivalent. First,
![]() $\gcd (d,j_m)$
divides d, so divides
$\gcd (d,j_m)$
divides d, so divides
![]() $dv_i$
and
$dv_i$
and
![]() $d'w_i$
. As above, write
$d'w_i$
. As above, write
![]() $\overline {j}_m := j_m/\gcd (d,j_m)$
. The map
$\overline {j}_m := j_m/\gcd (d,j_m)$
. The map
![]() $S\alpha _{M_i}^h : \mathbb {Z}^2 \to \mathbb {Z}/j_m$
factors as
$S\alpha _{M_i}^h : \mathbb {Z}^2 \to \mathbb {Z}/j_m$
factors as
for all i, where
![]() $\mathbb {Z}/\overline {j}_m \to \mathbb {Z}/j_m$
is the standard inclusion sending
$\mathbb {Z}/\overline {j}_m \to \mathbb {Z}/j_m$
is the standard inclusion sending
![]() $1$
to
$1$
to
![]() $\gcd (d,j_m)$
. Define
$\gcd (d,j_m)$
. Define
 $$ \begin{align*} \overline{d} := \displaystyle\frac{d}{\gcd(d,j_m)} \quad \text{and}\quad \overline{d}' := \displaystyle\frac{d'}{\gcd(d,j_m)} = \overline{d} \cdot \prod_{\iota=q_{A,m}+2}^{q_{A} +1} p_{\iota}. \end{align*} $$
$$ \begin{align*} \overline{d} := \displaystyle\frac{d}{\gcd(d,j_m)} \quad \text{and}\quad \overline{d}' := \displaystyle\frac{d'}{\gcd(d,j_m)} = \overline{d} \cdot \prod_{\iota=q_{A,m}+2}^{q_{A} +1} p_{\iota}. \end{align*} $$
We obtain
 $$ \begin{align*} S\kern1.2pt\overline{\alpha}^h_{M_i} = \begin{pmatrix} \overline{d} v_i \\ \overline{d}'w_i \end{pmatrix} : \mathbb{Z}^2 \to \mathbb{Z}/\overline{j}_m. \end{align*} $$
$$ \begin{align*} S\kern1.2pt\overline{\alpha}^h_{M_i} = \begin{pmatrix} \overline{d} v_i \\ \overline{d}'w_i \end{pmatrix} : \mathbb{Z}^2 \to \mathbb{Z}/\overline{j}_m. \end{align*} $$
It suffices to prove that for
![]() $i \neq j$
, the resulting pairs
$i \neq j$
, the resulting pairs
![]() $\{\overline {d}v_i,\overline {d}'w_i\}$
and
$\{\overline {d}v_i,\overline {d}'w_i\}$
and
![]() $\{\overline {d}v_j,\overline {d}'w_j\}$
are distinct, up to signs and switching the orders. Note that
$\{\overline {d}v_j,\overline {d}'w_j\}$
are distinct, up to signs and switching the orders. Note that
![]() $\gcd (\overline {d},\overline {j}_m) =1 = \gcd (\overline {d}',\overline {j}_m)$
.
$\gcd (\overline {d},\overline {j}_m) =1 = \gcd (\overline {d}',\overline {j}_m)$
.
Let p be a prime dividing
![]() $A'$
. Up to possibly changing the orders of
$A'$
. Up to possibly changing the orders of
![]() $v_i$
and
$v_i$
and
![]() $w_i$
, and of
$w_i$
, and of
![]() $v_j$
and
$v_j$
and
![]() $w_j$
, assume that p divides
$w_j$
, assume that p divides
![]() $v_i$
and
$v_i$
and
![]() $v_j$
. If so, p does not divide
$v_j$
. If so, p does not divide
![]() $w_i$
and
$w_i$
and
![]() $w_j$
, since
$w_j$
, since
![]() $\gcd (v_i,w_i) = 1 = \gcd (v_j,w_j)$
.
$\gcd (v_i,w_i) = 1 = \gcd (v_j,w_j)$
.
Now let
![]() $q \neq p$
be a prime dividing
$q \neq p$
be a prime dividing
![]() $A'$
such that either:
$A'$
such that either:
-
(i) q divides
 $w_j$
but q does not divide
$w_j$
but q does not divide
 $w_i$
or
$w_i$
or -
(ii) q divides
 $w_i$
but q does not divide
$w_i$
but q does not divide
 $w_j$
.
$w_j$
.
Without loss of generality suppose that (i) holds. Then also q divides
![]() $v_i$
but q does not divide
$v_i$
but q does not divide
![]() $v_j$
, since both pairs
$v_j$
, since both pairs
![]() $(v_i,w_i)$
and
$(v_i,w_i)$
and
![]() $(v_j,w_j)$
are coprime. There exists such a q, unless
$(v_j,w_j)$
are coprime. There exists such a q, unless
![]() $q_{A,m} =0$
, in which case
$q_{A,m} =0$
, in which case
![]() $2^{q_{A,m}} =1$
and we have nothing to prove anyway. So we can assume that
$2^{q_{A,m}} =1$
and we have nothing to prove anyway. So we can assume that
![]() $q_{A,m}$
is positive and that such a q exists. The idea is that the primes p and q are chosen so that they divide the same element of the unordered pair associated with the homotopy extended symmetric form for
$q_{A,m}$
is positive and that such a q exists. The idea is that the primes p and q are chosen so that they divide the same element of the unordered pair associated with the homotopy extended symmetric form for
![]() $M_i$
, but divide different elements of the unordered pair for
$M_i$
, but divide different elements of the unordered pair for
![]() $M_j$
. It is this distinction we want to detect.
$M_j$
. It is this distinction we want to detect.
We consider the images of the four elements
![]() $\overline {d}v_i$
,
$\overline {d}v_i$
,
![]() $\overline {d\,}'w_i$
,
$\overline {d\,}'w_i$
,
![]() $\overline {d}v_j$
and
$\overline {d}v_j$
and
![]() $\overline {d\,}'w_j$
of
$\overline {d\,}'w_j$
of
![]() $\mathbb {Z}/\overline {j}_m$
under the canonical surjections
$\mathbb {Z}/\overline {j}_m$
under the canonical surjections
Since p and q divide
![]() $\overline {j}_m$
and
$\overline {j}_m$
and
![]() $\gcd (\overline {d},\overline {j}_m)=1 = \gcd (\overline {d\,}',\overline {j}_m)$
, we know that p and q do not divide
$\gcd (\overline {d},\overline {j}_m)=1 = \gcd (\overline {d\,}',\overline {j}_m)$
, we know that p and q do not divide
![]() $\overline {d}$
and do not divide
$\overline {d}$
and do not divide
![]() $\overline {d}'$
. Therefore, for the
$\overline {d}'$
. Therefore, for the
![]() $\mathbb {Z}/p$
reductions, we have
$\mathbb {Z}/p$
reductions, we have
while for the
![]() $\mathbb {Z}/q$
reductions, we have
$\mathbb {Z}/q$
reductions, we have
We indicate one of these calculations briefly, that
![]() $\rho _p(\overline {d\,}'w_i) \neq 0$
, to give the idea. If
$\rho _p(\overline {d\,}'w_i) \neq 0$
, to give the idea. If
![]() $\overline {d\,}'w_i$
are
$\overline {d\,}'w_i$
are
![]() $0$
modulo p, then for some
$0$
modulo p, then for some
![]() $a,b \in \mathbb {Z}$
, we would have
$a,b \in \mathbb {Z}$
, we would have
![]() $ap = \overline {d}'w_i + b\overline {j}_m \in \mathbb {Z}$
. However,
$ap = \overline {d}'w_i + b\overline {j}_m \in \mathbb {Z}$
. However,
![]() $p \mid \overline {j}_m$
and so p divides
$p \mid \overline {j}_m$
and so p divides
![]() $\overline {d\,}'w_i$
, which is a contradiction.
$\overline {d\,}'w_i$
, which is a contradiction.
Note that switching the sign of an element in
![]() $\mathbb {Z}/\overline {j}_m$
preserves whether or not its image under
$\mathbb {Z}/\overline {j}_m$
preserves whether or not its image under
![]() $\rho _p$
or
$\rho _p$
or
![]() $\rho _q$
is zero. Let us summarise the calculations above. For
$\rho _q$
is zero. Let us summarise the calculations above. For
![]() $\{\overline {d}v_i,\overline {d\,}'w_i\}$
, one element is zero under the reductions modulo p and q, while the other element is nonzero under both reductions. However, for the pair
$\{\overline {d}v_i,\overline {d\,}'w_i\}$
, one element is zero under the reductions modulo p and q, while the other element is nonzero under both reductions. However, for the pair
![]() $\{\overline {d}v_j,\overline {d\,}'w_j\}$
, we have shown that precisely one element is zero under each of the modulo p and modulo q reductions. Switching the orders of the elements and switching signs preserves these descriptions, and therefore
$\{\overline {d}v_j,\overline {d\,}'w_j\}$
, we have shown that precisely one element is zero under each of the modulo p and modulo q reductions. Switching the orders of the elements and switching signs preserves these descriptions, and therefore
![]() $M_i$
and
$M_i$
and
![]() $M_j$
are not homotopy equivalent. It follows that
$M_j$
are not homotopy equivalent. It follows that
![]() $|\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})|$
is at least
$|\mathcal {S}^{\mathrm {st}}_{\mathrm {h}}(M_{a, b})|$
is at least
![]() $2^{q_{A, m}}$
, as desired.
$2^{q_{A, m}}$
, as desired.
4 Stably equivalent spin
 $^{c}$
structures on 4-manifolds
$^{c}$
structures on 4-manifolds
As explained in the introduction, the homotopy stable class is trivial for every closed, simply connected 4-manifold. However, a parallel phenomenon occurs when one considers equivalence classes of spin
![]() $^{c}$
structures on the tangent bundle. In this section, we illustrate this on
$^{c}$
structures on the tangent bundle. In this section, we illustrate this on
![]() $S^2 \times S^2$
.
$S^2 \times S^2$
.
For all
![]() $n \geq 2$
, the group
$n \geq 2$
, the group
![]() $\operatorname{\mathrm {Spin}}_n$
is the connected double cover of
$\operatorname{\mathrm {Spin}}_n$
is the connected double cover of
![]() $SO_n$
and the group
$SO_n$
and the group
![]() $\mathbb {Z}/2$
acts by deck transformations. The group
$\mathbb {Z}/2$
acts by deck transformations. The group
![]() $\mathbb {Z}/2$
acts on
$\mathbb {Z}/2$
acts on
![]() $U_1 \cong S^1$
by
$U_1 \cong S^1$
by
![]() $\{\pm 1\}$
. We quotient out the diagonal action on the product to obtain:
$\{\pm 1\}$
. We quotient out the diagonal action on the product to obtain:
There are well-defined maps
which are defined by
![]() $\operatorname{\mathrm {pr}}_1([\lambda , A]) = \lambda $
and
$\operatorname{\mathrm {pr}}_1([\lambda , A]) = \lambda $
and
![]() $\operatorname{\mathrm {pr}}_2([\lambda , A]) = A$
, where
$\operatorname{\mathrm {pr}}_2([\lambda , A]) = A$
, where
![]() $(\lambda , A) \in U_1 \times \operatorname{\mathrm {Spin}}_n$
.
$(\lambda , A) \in U_1 \times \operatorname{\mathrm {Spin}}_n$
.
There are natural inclusions
![]() $\operatorname{\mathrm {Spin}}^{c}_n \hookrightarrow \operatorname{\mathrm {Spin}}^{c}_{n+1}$
and the stable spin
$\operatorname{\mathrm {Spin}}^{c}_n \hookrightarrow \operatorname{\mathrm {Spin}}^{c}_{n+1}$
and the stable spin
![]() $^c$
group is defined by
$^c$
group is defined by
![]() $\operatorname{\mathrm {Spin}}^{c} := \operatorname{\mathrm {colim}}_{n \to \infty } \operatorname{\mathrm {Spin}}^{c}_n$
. There are also stable projections
$\operatorname{\mathrm {Spin}}^{c} := \operatorname{\mathrm {colim}}_{n \to \infty } \operatorname{\mathrm {Spin}}^{c}_n$
. There are also stable projections
where
![]() $SO$
is the stable special orthogonal group. We use the same notation
$SO$
is the stable special orthogonal group. We use the same notation
![]() $\operatorname{\mathrm {pr}}_1$
,
$\operatorname{\mathrm {pr}}_1$
,
![]() $\operatorname{\mathrm {pr}}_2$
for the induced maps on classifying spaces.
$\operatorname{\mathrm {pr}}_2$
for the induced maps on classifying spaces.
Definition 4.1. Let M be a closed, oriented n-manifold. A spin
![]() $^{c}$
structure on M is a lift
$^{c}$
structure on M is a lift

of the stable tangent bundle’s classifying map to
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}$
.
$B\!\:\operatorname{\mathrm {Spin}}^{c}$
.
For more background on spin
![]() $^{c}$
structures on 4-manifolds, we refer to, for example, [Reference Gompf and StipsiczGS99, Section 2.4.1] and [Reference ScorpanSco05, Sections 10.2 and 10.7].
$^{c}$
structures on 4-manifolds, we refer to, for example, [Reference Gompf and StipsiczGS99, Section 2.4.1] and [Reference ScorpanSco05, Sections 10.2 and 10.7].
Lemma 4.2 [Reference Gompf and StipsiczGS99, Proposition 2.4.16]
Every oriented
![]() $4$
-manifold admits a spin
$4$
-manifold admits a spin
![]() $^{c}$
structure.
$^{c}$
structure.
Proof. In [Reference Gompf and StipsiczGS99], spin
![]() $^{c}$
structures on
$^{c}$
structures on
![]() $4$
-manifolds are defined by using
$4$
-manifolds are defined by using
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}_4$
in place of
$B\!\:\operatorname{\mathrm {Spin}}^{c}_4$
in place of
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}$
, and [Reference Gompf and StipsiczGS99, Proposition 2.4.16] proves the existence of a lift of the classifying map of the (unstable) tangent bundle to
$B\!\:\operatorname{\mathrm {Spin}}^{c}$
, and [Reference Gompf and StipsiczGS99, Proposition 2.4.16] proves the existence of a lift of the classifying map of the (unstable) tangent bundle to
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}_4$
. Composing with the maps to the colimit, this implies the existence of a spin
$B\!\:\operatorname{\mathrm {Spin}}^{c}_4$
. Composing with the maps to the colimit, this implies the existence of a spin
![]() $^{c}$
-structure in the sense of Definition 4.1.
$^{c}$
-structure in the sense of Definition 4.1.
Definition 4.3 (Equivalence of spin
 $^c$
structures)
$^c$
structures)
Let M be a closed, oriented
![]() $4$
-manifold.
$4$
-manifold.
-
(1) Two spin
 $^{c}$
structures
$^{c}$
structures
 $\mathfrak {s}_1$
and
$\mathfrak {s}_1$
and
 $\mathfrak {s}_2$
on M are equivalent if there is an orientation- preserving diffeomorphism
$\mathfrak {s}_2$
on M are equivalent if there is an orientation- preserving diffeomorphism
 $f : M \to M$
such that
$f : M \to M$
such that
 $\mathfrak {s}_1, \mathfrak {s}_2 \circ f : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
are homotopic over
$\mathfrak {s}_1, \mathfrak {s}_2 \circ f : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
are homotopic over
 $BSO$
; that is, there is homotopy K and a commutative diagram where K restricts to
$BSO$
; that is, there is homotopy K and a commutative diagram where K restricts to
 $\mathfrak {s}_1$
on
$\mathfrak {s}_1$
on
 $M \times \{0\}$
and
$M \times \{0\}$
and
 $\mathfrak {s}_2 \circ f$
on
$\mathfrak {s}_2 \circ f$
on
 $M \times \{1\}$
.
$M \times \{1\}$
.
-
(2) Two spin
 $^{c}$
structures
$^{c}$
structures
 $\mathfrak {s}_1$
and
$\mathfrak {s}_1$
and
 $\mathfrak {s}_2$
are homotopic if they are equivalent as in the previous item, with
$\mathfrak {s}_2$
are homotopic if they are equivalent as in the previous item, with
 $f=\operatorname{\mathrm {Id}}_M$
.
$f=\operatorname{\mathrm {Id}}_M$
.
Recall that the projection onto the first component gives a compatible collection of maps
![]() $\operatorname{\mathrm {pr}}_1 : B\!\:\operatorname{\mathrm {Spin}}^{c}_n \to BU_1$
,
$\operatorname{\mathrm {pr}}_1 : B\!\:\operatorname{\mathrm {Spin}}^{c}_n \to BU_1$
,
![]() $n \in \mathbb {N}$
. Therefore, passing to the colimit and keeping the same notation, we obtain a map
$n \in \mathbb {N}$
. Therefore, passing to the colimit and keeping the same notation, we obtain a map
![]() $\operatorname{\mathrm {pr}}_1 : B\!\:\operatorname{\mathrm {Spin}}^{c} \to BU_1$
.
$\operatorname{\mathrm {pr}}_1 : B\!\:\operatorname{\mathrm {Spin}}^{c} \to BU_1$
.
Definition 4.4. Via the map
![]() $\operatorname{\mathrm {pr}}_1 : B\!\:\operatorname{\mathrm {Spin}}^{c} \to BU_1$
, a spin
$\operatorname{\mathrm {pr}}_1 : B\!\:\operatorname{\mathrm {Spin}}^{c} \to BU_1$
, a spin
![]() $^{c}$
structure
$^{c}$
structure
![]() $\mathfrak {s} : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
on a 4-manifold M determines a line bundle
$\mathfrak {s} : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
on a 4-manifold M determines a line bundle
![]() $\mathcal {L}_{\mathfrak {s}}$
. The first Chern class of
$\mathcal {L}_{\mathfrak {s}}$
. The first Chern class of
![]() $\mathfrak {s}$
is defined by
$\mathfrak {s}$
is defined by
Noting that
![]() $BU_1$
is a
$BU_1$
is a
![]() $K(\mathbb {Z},2)$
,
$K(\mathbb {Z},2)$
,
![]() $c_1(\mathfrak {s})$
corresponds to
$c_1(\mathfrak {s})$
corresponds to
![]() $\operatorname{\mathrm {pr}}_1 \circ \mathfrak {s} : M \to BU_1$
under the isomorphism
$\operatorname{\mathrm {pr}}_1 \circ \mathfrak {s} : M \to BU_1$
under the isomorphism
![]() $H^2(M) \cong [M,BU_1]$
. The map
$H^2(M) \cong [M,BU_1]$
. The map
![]() $\operatorname{\mathrm {pr}}_1$
can be interpreted as a determinant and
$\operatorname{\mathrm {pr}}_1$
can be interpreted as a determinant and
![]() $\mathcal {L}_{\mathfrak {s}}$
is called the determinant line bundle of
$\mathcal {L}_{\mathfrak {s}}$
is called the determinant line bundle of
![]() $\mathfrak {s}$
. The next lemma follows from [Reference Gompf and StipsiczGS99, Proposition 2.4.16].
$\mathfrak {s}$
. The next lemma follows from [Reference Gompf and StipsiczGS99, Proposition 2.4.16].
Lemma 4.5. Let M be a closed, oriented 4-manifold.
-
(i) For every spin
 $^{c}$
structure
$^{c}$
structure
 $\mathfrak {s}$
on M, reduction modulo 2 is such that: where
$\mathfrak {s}$
on M, reduction modulo 2 is such that: where $$ \begin{align*} H^2(M) &\to H^2(M;\mathbb{Z}/2) \\ c_1(\mathfrak{s}) & \mapsto w_2(M), \end{align*} $$
$$ \begin{align*} H^2(M) &\to H^2(M;\mathbb{Z}/2) \\ c_1(\mathfrak{s}) & \mapsto w_2(M), \end{align*} $$
 $w_2(M)$
is the second Stiefel–Whitney class.
$w_2(M)$
is the second Stiefel–Whitney class.
-
(ii) There is a transitive action of
 $H^2(M)$
on the set of homotopy classes of spin
$H^2(M)$
on the set of homotopy classes of spin
 $^{c}$
structures on M, such that for
$^{c}$
structures on M, such that for
 $x \in H^2(M)$
,
$x \in H^2(M)$
,  $$ \begin{align*}c_1(x \cdot \mathfrak{s}) = c_1(\mathfrak{s}) + 2x \in H^2(M).\end{align*} $$
$$ \begin{align*}c_1(x \cdot \mathfrak{s}) = c_1(\mathfrak{s}) + 2x \in H^2(M).\end{align*} $$
-
(iii) If
 $H_1(M)$
is 2-torsion free, then this action is free.
$H_1(M)$
is 2-torsion free, then this action is free.
Proof. As mentioned during the proof of Lemma 4.2, in [Reference Gompf and StipsiczGS99], spin
![]() $^{c}$
structures are defined by using
$^{c}$
structures are defined by using
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}_4$
in place of
$B\!\:\operatorname{\mathrm {Spin}}^{c}_4$
in place of
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}$
and therefore the Chern class of a spin
$B\!\:\operatorname{\mathrm {Spin}}^{c}$
and therefore the Chern class of a spin
![]() $^{c}$
-structure is defined using
$^{c}$
-structure is defined using
![]() $\operatorname{\mathrm {pr}}_1 : B\!\:\operatorname{\mathrm {Spin}}^{c}_4 \to BU_1$
. However, since the map
$\operatorname{\mathrm {pr}}_1 : B\!\:\operatorname{\mathrm {Spin}}^{c}_4 \to BU_1$
. However, since the map
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}_4 \to BU_1$
factors through
$B\!\:\operatorname{\mathrm {Spin}}^{c}_4 \to BU_1$
factors through
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}$
, both definitions of the Chern class coincide and so the lemma follows from [Reference Gompf and StipsiczGS99, Proposition 2.4.16].
$B\!\:\operatorname{\mathrm {Spin}}^{c}$
, both definitions of the Chern class coincide and so the lemma follows from [Reference Gompf and StipsiczGS99, Proposition 2.4.16].
As a consequence, every characteristic cohomology class
![]() $y \in H^2(M)$
can be realised as the first Chern class of some spin
$y \in H^2(M)$
can be realised as the first Chern class of some spin
![]() $^{c}$
structure on M, and if
$^{c}$
structure on M, and if
![]() $H_1(M)$
is 2-torsion free, then this spin
$H_1(M)$
is 2-torsion free, then this spin
![]() $^{c}$
structure is uniquely determined by y. Here recall that y being characteristic means that
$^{c}$
structure is uniquely determined by y. Here recall that y being characteristic means that
![]() $\langle x \cup x,[M] \rangle \equiv \langle x\cup y ,[M] \rangle\, \mod {2}$
for every
$\langle x \cup x,[M] \rangle \equiv \langle x\cup y ,[M] \rangle\, \mod {2}$
for every
![]() $x \in H^2(M)$
.
$x \in H^2(M)$
.
The next lemma is immediate from the fact that the Chern class is an invariant of a spin
![]() $^{c}$
structure, and is natural.
$^{c}$
structure, and is natural.
Lemma 4.6. If two spin
![]() $^{c}$
structures
$^{c}$
structures
![]() $\mathfrak {s}_1$
and
$\mathfrak {s}_1$
and
![]() $\mathfrak {s}_2$
on a closed, oriented 4-manifold M are equivalent, then there is an isometry of the intersection form on
$\mathfrak {s}_2$
on a closed, oriented 4-manifold M are equivalent, then there is an isometry of the intersection form on
![]() $H^2(M)$
sending
$H^2(M)$
sending
![]() $c_1(\mathfrak {s}_1)$
to
$c_1(\mathfrak {s}_1)$
to
![]() $c_1(\mathfrak {s}_2)$
.
$c_1(\mathfrak {s}_2)$
.
![]() $\Box $
$\Box $
To define stable equivalence of spin
![]() $^{c}$
structures, fix once and for all the preferred spin
$^{c}$
structures, fix once and for all the preferred spin
![]() $^{c}$
structure
$^{c}$
structure
![]() $\mathfrak {s}_g$
on
$\mathfrak {s}_g$
on
![]() $W_g := \#^g S^2 \times S^2$
, to be the spin
$W_g := \#^g S^2 \times S^2$
, to be the spin
![]() $^{c}$
structure with
$^{c}$
structure with
![]() $c_1(\mathfrak {s}_g) = 0 \in H^2(W_g)$
. Such a spin
$c_1(\mathfrak {s}_g) = 0 \in H^2(W_g)$
. Such a spin
![]() $^{c}$
structure exists by Lemma 4.5.
$^{c}$
structure exists by Lemma 4.5.
Definition 4.7 (Stable equivalence of spin
 $^c$
structures)
$^c$
structures)
Two spin
![]() $^{c}$
structures
$^{c}$
structures
![]() $\mathfrak {s}_1$
and
$\mathfrak {s}_1$
and
![]() $\mathfrak {s}_2$
on a closed, oriented 4-manifold M are stably equivalent if there exists
$\mathfrak {s}_2$
on a closed, oriented 4-manifold M are stably equivalent if there exists
![]() $g \in \mathbb {N}_0$
such that the induced spin
$g \in \mathbb {N}_0$
such that the induced spin
![]() $^{c}$
structures on
$^{c}$
structures on
![]() $M \# W_g$
, extending
$M \# W_g$
, extending
![]() $\mathfrak {s}_1$
and
$\mathfrak {s}_1$
and
![]() $\mathfrak {s}_2$
using the fixed spin
$\mathfrak {s}_2$
using the fixed spin
![]() $^{c}$
structure
$^{c}$
structure
![]() $\mathfrak {s}_g$
on
$\mathfrak {s}_g$
on
![]() $W_g$
, are equivalent.
$W_g$
, are equivalent.
The stable classification of spin
![]() $^{c}$
structures
$^{c}$
structures
![]() $\mathfrak {s}$
on simply connected
$\mathfrak {s}$
on simply connected
![]() $4$
-manifolds M is analogous to the almost-stable classification of
$4$
-manifolds M is analogous to the almost-stable classification of
![]() $(4m{-}1)$
-connected
$(4m{-}1)$
-connected
![]() $8m$
-manifolds from Theorem 3.8 and we want to apply Kreck’s stable diffeomorphism theorem [Reference KreckKre99, Corollary 3]. Since Kreck works with the stable normal bundle, while it is convenient for us to work with the stable tangent bundle, we make some brief general remarks about moving between tangential and normal bundle data in the modified surgery setting; for the analogous discussion in classical surgery, see, for example, [Reference Crowley, Lück and MackoCLM, Lemma 6.39].
$8m$
-manifolds from Theorem 3.8 and we want to apply Kreck’s stable diffeomorphism theorem [Reference KreckKre99, Corollary 3]. Since Kreck works with the stable normal bundle, while it is convenient for us to work with the stable tangent bundle, we make some brief general remarks about moving between tangential and normal bundle data in the modified surgery setting; for the analogous discussion in classical surgery, see, for example, [Reference Crowley, Lück and MackoCLM, Lemma 6.39].
Remark 4.8. Recall that given a fibration
![]() $\xi : B \to BSO$
and an oriented manifold M, a normal
$\xi : B \to BSO$
and an oriented manifold M, a normal
![]() $\xi $
-structure on M is a lift
$\xi $
-structure on M is a lift
![]() $\overline {\nu } : M \to B$
of the stable normal bundle
$\overline {\nu } : M \to B$
of the stable normal bundle
![]() $\nu _M : M \to BSO$
and
$\nu _M : M \to BSO$
and
![]() $\overline \nu $
is called a normal k-smoothing if it is
$\overline \nu $
is called a normal k-smoothing if it is
![]() $(k{+}1)$
-connected [Reference KreckKre99, Section 2]. Note that the fibration
$(k{+}1)$
-connected [Reference KreckKre99, Section 2]. Note that the fibration
![]() $\xi $
is not required to be
$\xi $
is not required to be
![]() $(k{+}1)$
-coconnected so that, in Kreck’s terminology, the fibration
$(k{+}1)$
-coconnected so that, in Kreck’s terminology, the fibration
![]() $\xi $
need not be the normal k-type of M. Now let
$\xi $
need not be the normal k-type of M. Now let
![]() $i : BSO \to BSO$
be the map classifying the passage from a stable bundle to its stable inverse. Since the Whitney sum
$i : BSO \to BSO$
be the map classifying the passage from a stable bundle to its stable inverse. Since the Whitney sum
![]() $\tau _M \oplus \nu _M$
of the stable tangent and normal bundles of M is canonically trivialised, we have
$\tau _M \oplus \nu _M$
of the stable tangent and normal bundles of M is canonically trivialised, we have
![]() $\nu _M = i \circ \tau _M$
. Setting
$\nu _M = i \circ \tau _M$
. Setting
![]() $-\xi := i \circ \xi $
, it follows that if
$-\xi := i \circ \xi $
, it follows that if
![]() $\overline \nu : M \to B$
is a normal
$\overline \nu : M \to B$
is a normal
![]() $(-\xi )$
-structure on M, then
$(-\xi )$
-structure on M, then
![]() $\overline \tau = \overline \nu $
defines a stable tangential
$\overline \tau = \overline \nu $
defines a stable tangential
![]() $\xi $
-structure on M, and vice versa. We call a stable tangential
$\xi $
-structure on M, and vice versa. We call a stable tangential
![]() $\xi $
-structure
$\xi $
-structure
![]() $\overline \tau : M \to B$
a tangential k-smoothing if it is
$\overline \tau : M \to B$
a tangential k-smoothing if it is
![]() $(k{+}1)$
-connected. With these observations and definitions, we can pass freely between (stable) tangential
$(k{+}1)$
-connected. With these observations and definitions, we can pass freely between (stable) tangential
![]() $\xi $
-manifolds and normal
$\xi $
-manifolds and normal
![]() $(-\xi )$
-manifolds, applying Kreck’s results to the latter. In particular, if
$(-\xi )$
-manifolds, applying Kreck’s results to the latter. In particular, if
![]() $(M_0, \overline \tau _0)$
and
$(M_0, \overline \tau _0)$
and
![]() $(M_1, \overline \tau _1)$
are n-dimensional tangential k-smoothings in
$(M_1, \overline \tau _1)$
are n-dimensional tangential k-smoothings in
![]() $(B, \xi )$
that are tangentially
$(B, \xi )$
that are tangentially
![]() $(B, \xi )$
-bordant, then the corresponding normal k-smoothings in
$(B, \xi )$
-bordant, then the corresponding normal k-smoothings in
![]() $(B, -\xi )$
are normally
$(B, -\xi )$
are normally
![]() $(B, -\xi )$
-bordant; and so when
$(B, -\xi )$
-bordant; and so when
![]() $n = 2q$
and
$n = 2q$
and
![]() $k = q{-1}$
, we may conclude that
$k = q{-1}$
, we may conclude that
![]() $(M_0, \overline \tau _0)$
and
$(M_0, \overline \tau _0)$
and
![]() $(M_1, \overline \tau _1)$
are stably
$(M_1, \overline \tau _1)$
are stably
![]() $(B, \xi )$
-diffeomorphic.
$(B, \xi )$
-diffeomorphic.
Remark 4.9. We also note that the stable
![]() $\operatorname{\mathrm {spin}}^{c}$
structure
$\operatorname{\mathrm {spin}}^{c}$
structure
![]() $\mathfrak {s}_g$
defined above on
$\mathfrak {s}_g$
defined above on
![]() $W_g$
corresponds to the normal structure
$W_g$
corresponds to the normal structure
![]() $\overline \nu _c$
on
$\overline \nu _c$
on
![]() $W_g$
defined in [Reference KreckKre99, page 721], which is used in Kreck’s stable diffeomorphism results [Reference KreckKre99, Theorem 2 and Corollary 3]. Moreover, the discussion just prior to [Reference KreckKre99, Theorem 2] and its proof show that [Reference KreckKre99, Theorem 2 and Corollary 3] can be strengthened to include the normal
$W_g$
defined in [Reference KreckKre99, page 721], which is used in Kreck’s stable diffeomorphism results [Reference KreckKre99, Theorem 2 and Corollary 3]. Moreover, the discussion just prior to [Reference KreckKre99, Theorem 2] and its proof show that [Reference KreckKre99, Theorem 2 and Corollary 3] can be strengthened to include the normal
![]() $(B, -\xi )$
-structure; specifically, they yield respectively s-cobordisms and stable diffeomorphisms of normal
$(B, -\xi )$
-structure; specifically, they yield respectively s-cobordisms and stable diffeomorphisms of normal
![]() $(B, -\xi )$
-manifolds, where stabilisation is with the normal
$(B, -\xi )$
-manifolds, where stabilisation is with the normal
![]() $(-\xi )$
-manifold
$(-\xi )$
-manifold
![]() $(W_g, \overline \nu _c)$
. As a consequence, below we obtain stable diffeomorphisms of tangential
$(W_g, \overline \nu _c)$
. As a consequence, below we obtain stable diffeomorphisms of tangential
![]() $B\!\:\operatorname{\mathrm {Spin}}^c$
manifolds, where the stabilisation is with
$B\!\:\operatorname{\mathrm {Spin}}^c$
manifolds, where the stabilisation is with
![]() $(W_g, \mathfrak {s}_g)$
.
$(W_g, \mathfrak {s}_g)$
.
Returning to
![]() $4$
-manifolds, note in particular that a 1-smoothing has to be 2-connected. While we work with simply connected 4-manifolds, so
$4$
-manifolds, note in particular that a 1-smoothing has to be 2-connected. While we work with simply connected 4-manifolds, so
![]() $\pi _1(M) =1 = \pi _1(B\!\:\operatorname{\mathrm {Spin}}^{c})$
, the map
$\pi _1(M) =1 = \pi _1(B\!\:\operatorname{\mathrm {Spin}}^{c})$
, the map
![]() $M \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
classifying a spin
$M \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
classifying a spin
![]() $^c$
structure need not be surjective on
$^c$
structure need not be surjective on
![]() $\pi _2$
. To mitigate this, we make the following definition.
$\pi _2$
. To mitigate this, we make the following definition.
Given
![]() $(M, \mathfrak {s})$
, we define the divisibility
$(M, \mathfrak {s})$
, we define the divisibility
![]() $d(\mathfrak {s}) \in \mathbb {N}_0$
of
$d(\mathfrak {s}) \in \mathbb {N}_0$
of
![]() $c_1(\mathfrak {s})$
by the equation
$c_1(\mathfrak {s})$
by the equation
Let
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
be the homotopy fibre of the mod d spin
$B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
be the homotopy fibre of the mod d spin
![]() $^c$
first Chern class, so that there is a fibre sequence
$^c$
first Chern class, so that there is a fibre sequence
By construction,
![]() $\pi : B\!\:\operatorname{\mathrm {Spin}}^{c}(d) \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
is a fibration, and the universal stable bundle over
$\pi : B\!\:\operatorname{\mathrm {Spin}}^{c}(d) \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
is a fibration, and the universal stable bundle over
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}$
pulls back to a stable bundle over
$B\!\:\operatorname{\mathrm {Spin}}^{c}$
pulls back to a stable bundle over
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
.
$B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
.
Definition 4.10. Let M be a closed, oriented n-manifold. A spin
![]() $^{c}(d)$
structure on M is a lift
$^{c}(d)$
structure on M is a lift

of the stable tangent bundle’s classifying map to
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
. We denote a manifold with a
$B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
. We denote a manifold with a
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
-structure by
$\operatorname{\mathrm {spin}}^{c}(d)$
-structure by
![]() $(M, \mathfrak {s}(d))$
and the corresponding bordism groups by
$(M, \mathfrak {s}(d))$
and the corresponding bordism groups by
![]() $\Omega _*^{\operatorname{\mathrm {Spin}}^{c}(d)}$
.
$\Omega _*^{\operatorname{\mathrm {Spin}}^{c}(d)}$
.
For example, the trivial
![]() $\operatorname{\mathrm {spin}}^{c}$
structure
$\operatorname{\mathrm {spin}}^{c}$
structure
![]() $\mathfrak {s}_g$
on
$\mathfrak {s}_g$
on
![]() $W_g$
used in Definition 4.7 lifts to the trivial
$W_g$
used in Definition 4.7 lifts to the trivial
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
structure
$\operatorname{\mathrm {spin}}^{c}(d)$
structure
![]() $\mathfrak {s}_g(d)$
on
$\mathfrak {s}_g(d)$
on
![]() $W_g$
.
$W_g$
.
Lemma 4.11. The following assertions hold:
-
(1)
 $\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))=\mathbb {Z}$
for
$\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))=\mathbb {Z}$
for
 $d \neq 0$
and
$d \neq 0$
and
 $\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))=0$
for
$\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))=0$
for
 $d=0$
;
$d=0$
; -
(2) if
 $(M,\mathfrak {s})$
is a simply connected
$(M,\mathfrak {s})$
is a simply connected
 $\operatorname{\mathrm {spin}}^{c}$
manifold, then M admits a
$\operatorname{\mathrm {spin}}^{c}$
manifold, then M admits a
 $\operatorname{\mathrm {spin}}^c(d)$
structure
$\operatorname{\mathrm {spin}}^c(d)$
structure
 $\mathfrak {s}(d)$
for
$\mathfrak {s}(d)$
for
 $d:=d(\mathfrak {s})$
such that the map
$d:=d(\mathfrak {s})$
such that the map
 $\mathfrak {s}(d) : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
is
$\mathfrak {s}(d) : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
is
 $2$
-connected. In particular,
$2$
-connected. In particular,
 $\mathfrak {s}(d)$
defines a tangential
$\mathfrak {s}(d)$
defines a tangential
 $1$
-smoothing into
$1$
-smoothing into
 $B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
.
$B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
.
Proof. We have
![]() $\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}) \cong \mathbb {Z}$
, and so the long exact sequence of a fibration in homotopy groups yields
$\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}) \cong \mathbb {Z}$
, and so the long exact sequence of a fibration in homotopy groups yields
Since also
![]() $\pi _1(B\!\:\operatorname{\mathrm {Spin}}^{c})\kern1.2pt{=}\kern1.2pt1$
, we have that
$\pi _1(B\!\:\operatorname{\mathrm {Spin}}^{c})\kern1.2pt{=}\kern1.2pt1$
, we have that
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
is
$B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
is
![]() $1$
-connected and
$1$
-connected and
![]() $\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d)) \kern1pt{\cong} \mathbb {Z}$
for
$\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d)) \kern1pt{\cong} \mathbb {Z}$
for
![]() $d\neq 0$
. A similar calculation shows that
$d\neq 0$
. A similar calculation shows that
![]() $\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(0))=\pi _2(B\!\:\operatorname{\mathrm {Spin}}) =0.$
In fact, it then follows from Whitehead’s theorem that the map
$\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(0))=\pi _2(B\!\:\operatorname{\mathrm {Spin}}) =0.$
In fact, it then follows from Whitehead’s theorem that the map
![]() $B\!\:\operatorname{\mathrm {Spin}} \to B\!\:\operatorname{\mathrm {Spin}}^{c}(0)$
, obtained from factoring the canonical map
$B\!\:\operatorname{\mathrm {Spin}} \to B\!\:\operatorname{\mathrm {Spin}}^{c}(0)$
, obtained from factoring the canonical map
![]() $B\!\:\operatorname{\mathrm {Spin}} \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
through
$B\!\:\operatorname{\mathrm {Spin}} \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
through
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}(0)$
, is a homotopy equivalence. This concludes the proof of the first assertion.
$B\!\:\operatorname{\mathrm {Spin}}^{c}(0)$
, is a homotopy equivalence. This concludes the proof of the first assertion.
We now assume that
![]() $(M,\mathfrak {s})$
is a simply connected
$(M,\mathfrak {s})$
is a simply connected
![]() $\operatorname{\mathrm {spin}}^{c}$
manifold and prove the second assertion. The first point follows by observing that in the exact sequence
$\operatorname{\mathrm {spin}}^{c}$
manifold and prove the second assertion. The first point follows by observing that in the exact sequence
the spin
![]() $^{c}$
structure
$^{c}$
structure
![]() $\mathfrak {s} \in [M,B\!\:\operatorname{\mathrm {Spin}}^{c}]$
is mapped to zero, by definition of
$\mathfrak {s} \in [M,B\!\:\operatorname{\mathrm {Spin}}^{c}]$
is mapped to zero, by definition of
![]() $d(\mathfrak {s})$
. It only remains to show that
$d(\mathfrak {s})$
. It only remains to show that
![]() $\mathfrak {s}(d)$
is
$\mathfrak {s}(d)$
is
![]() $2$
-connected. Since this is clear for
$2$
-connected. Since this is clear for
![]() $d=0$
, we assume that
$d=0$
, we assume that
![]() $d \neq 0$
. As we know that
$d \neq 0$
. As we know that
![]() $\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c})=\mathbb {Z}$
and
$\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c})=\mathbb {Z}$
and
![]() $\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))=\mathbb {Z}$
, the long exact sequence of the fibration and the definition of
$\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))=\mathbb {Z}$
, the long exact sequence of the fibration and the definition of
![]() $d=d(\mathfrak {s})$
imply that
$d=d(\mathfrak {s})$
imply that
![]() $\operatorname{\mathrm {Im}}(\mathfrak {s}_*)=d\mathbb {Z} \subseteq \mathbb {Z}=\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c})$
and therefore
$\operatorname{\mathrm {Im}}(\mathfrak {s}_*)=d\mathbb {Z} \subseteq \mathbb {Z}=\pi _2(B\!\:\operatorname{\mathrm {Spin}}^{c})$
and therefore
![]() $\mathfrak {s}(d)$
is surjective on
$\mathfrak {s}(d)$
is surjective on
![]() $\pi _2$
, as required.
$\pi _2$
, as required.
Our aim is now to construct an injective map
![]() $\Omega _*^{\operatorname{\mathrm {Spin}}^{c}(d)} \to \mathbb {Z} \oplus \mathbb {Z}$
. The first component of this map is the signature, while the second arises as a characteristic number obtained from
$\Omega _*^{\operatorname{\mathrm {Spin}}^{c}(d)} \to \mathbb {Z} \oplus \mathbb {Z}$
. The first component of this map is the signature, while the second arises as a characteristic number obtained from
![]() $\mathfrak {s}(d) : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
by pulling back a universal class
$\mathfrak {s}(d) : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
by pulling back a universal class
![]() $c_1/d \in H^2( B\!\:\operatorname{\mathrm {Spin}}^{c}(d))$
that we now define. For
$c_1/d \in H^2( B\!\:\operatorname{\mathrm {Spin}}^{c}(d))$
that we now define. For
![]() $d \neq 0$
, Lemma 4.11 implies that
$d \neq 0$
, Lemma 4.11 implies that
![]() $H^2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))$
is an infinite cyclic group. It is generated by a class
$H^2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))$
is an infinite cyclic group. It is generated by a class
![]() $c_1/d \in H^2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))$
such that the pullback
$c_1/d \in H^2(B\!\:\operatorname{\mathrm {Spin}}^{c}(d))$
such that the pullback
![]() $\pi ^*(c_1)$
of the spin
$\pi ^*(c_1)$
of the spin
![]() $^c$
first Chern class, satisfies
$^c$
first Chern class, satisfies
For
![]() $d=0$
,
$d=0$
,
![]() $H^2(B\!\:\operatorname{\mathrm {Spin}}^{c}(0)) = H^2(B\!\:\operatorname{\mathrm {Spin}}) =0$
and we set
$H^2(B\!\:\operatorname{\mathrm {Spin}}^{c}(0)) = H^2(B\!\:\operatorname{\mathrm {Spin}}) =0$
and we set
![]() $c_1/d =0$
. As is conventional for characteristic classes, given a
$c_1/d =0$
. As is conventional for characteristic classes, given a
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
structure
$\operatorname{\mathrm {spin}}^{c}(d)$
structure
![]() $\mathfrak {s}(d) : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
, we write
$\mathfrak {s}(d) : M \to B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
, we write
![]() $c_1/d(\mathfrak {s}(d)) := \mathfrak {s}(d)^*(c_1/d) \in H^2(M)$
. For example, the trivial
$c_1/d(\mathfrak {s}(d)) := \mathfrak {s}(d)^*(c_1/d) \in H^2(M)$
. For example, the trivial
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
-structure
$\operatorname{\mathrm {spin}}^{c}(d)$
-structure
![]() $\mathfrak {s}_g(d)$
on
$\mathfrak {s}_g(d)$
on
![]() $W_g$
is characterised by
$W_g$
is characterised by
![]() $c_1/d(\mathfrak {s}_g(d)) = 0$
.
$c_1/d(\mathfrak {s}_g(d)) = 0$
.
Lemma 4.12. There is an injective homomorphism
 $$ \begin{align*} \Theta : \Omega_4^{\operatorname{\mathrm{Spin}}^{c}(d)} &\to \mathbb{Z} \oplus \mathbb{Z}, \\ [N,\mathfrak{s}(d)] & \mapsto ( \sigma(N), \langle(c_1/d(\mathfrak{s}(d)))^2,[N]\rangle ). \end{align*} $$
$$ \begin{align*} \Theta : \Omega_4^{\operatorname{\mathrm{Spin}}^{c}(d)} &\to \mathbb{Z} \oplus \mathbb{Z}, \\ [N,\mathfrak{s}(d)] & \mapsto ( \sigma(N), \langle(c_1/d(\mathfrak{s}(d)))^2,[N]\rangle ). \end{align*} $$
Proof. The given map is a homomorphism, and is a bordism invariant because the signature is bordism invariant and because
![]() $c_1^2$
is a characteristic number and therefore so is
$c_1^2$
is a characteristic number and therefore so is
![]() $(c_1/d)^2$
.
$(c_1/d)^2$
.
It remains to prove injectivity of
![]() $\Theta $
. Let
$\Theta $
. Let
![]() $(M, \mathfrak {s}(d))$
be a spin
$(M, \mathfrak {s}(d))$
be a spin
![]() $^c(d)$
-manifold with vanishing signature and
$^c(d)$
-manifold with vanishing signature and
![]() $(c_1/d(\mathfrak {s}(d)))^2 = 0$
. Since
$(c_1/d(\mathfrak {s}(d)))^2 = 0$
. Since
![]() $\pi _1(B\!\:\operatorname{\mathrm {Spin}}^{c}(d)) = 1$
, after preliminary surgeries over
$\pi _1(B\!\:\operatorname{\mathrm {Spin}}^{c}(d)) = 1$
, after preliminary surgeries over
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
we may assume that M is simply connected. Since
$B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
we may assume that M is simply connected. Since
![]() $\sigma (M) = 0$
, the homeomorphism classification of smooth simply connected
$\sigma (M) = 0$
, the homeomorphism classification of smooth simply connected
![]() $4$
-manifolds [Reference FreedmanFre82] means that we can assume that M is homeomorphic to one of the following model manifolds:
$4$
-manifolds [Reference FreedmanFre82] means that we can assume that M is homeomorphic to one of the following model manifolds:
 $$ \begin{align*} M \cong_{\mathrm{TOP}} \begin{cases} W_g & d \text{ even,} \\ X_g & d \text{ odd,} \end{cases} \end{align*} $$
$$ \begin{align*} M \cong_{\mathrm{TOP}} \begin{cases} W_g & d \text{ even,} \\ X_g & d \text{ odd,} \end{cases} \end{align*} $$
where
![]() $X_g := \#^g S^2 \widetilde {\times } S^2$
. In other words, M is a possibly exotic
$X_g := \#^g S^2 \widetilde {\times } S^2$
. In other words, M is a possibly exotic
![]() $W_g$
or
$W_g$
or
![]() $X_g$
. Now, exotic pairs of simply connected 4-manifolds are h-cobordant [Reference WallWal64, Theorem 2], and the spin
$X_g$
. Now, exotic pairs of simply connected 4-manifolds are h-cobordant [Reference WallWal64, Theorem 2], and the spin
![]() $^c(d)$
-structure on M propagates along an h-cobordism to a spin
$^c(d)$
-structure on M propagates along an h-cobordism to a spin
![]() $^c(d)$
structure on either
$^c(d)$
structure on either
![]() $W_g$
or
$W_g$
or
![]() $X_g$
, as appropriate. Hence, we may assume that
$X_g$
, as appropriate. Hence, we may assume that
![]() $(M, \mathfrak {s}(d))$
is diffeomorphic to either
$(M, \mathfrak {s}(d))$
is diffeomorphic to either
![]() $(W_g, \mathfrak {s}^{\prime }_g(d))$
or
$(W_g, \mathfrak {s}^{\prime }_g(d))$
or
![]() $(X_g, \mathfrak {s}^{\prime \prime }_g(d))$
for some spin
$(X_g, \mathfrak {s}^{\prime \prime }_g(d))$
for some spin
![]() $^c(d)$
structure
$^c(d)$
structure
![]() $\mathfrak {s}^{\prime }_g(d)$
or
$\mathfrak {s}^{\prime }_g(d)$
or
![]() $\mathfrak {s}^{\prime \prime }_g(d)$
. Now, M has a standard coboundary N,
$\mathfrak {s}^{\prime \prime }_g(d)$
. Now, M has a standard coboundary N,
![]() $\partial N = M$
, where
$\partial N = M$
, where
 $$ \begin{align*} N \cong \begin{cases} Y_g & d \text{ even,} \\ Z_g & d \text{ odd.} \end{cases} \end{align*} $$
$$ \begin{align*} N \cong \begin{cases} Y_g & d \text{ even,} \\ Z_g & d \text{ odd.} \end{cases} \end{align*} $$
Here
![]() $Y_g := \natural ^g D^3 \times S^2$
and
$Y_g := \natural ^g D^3 \times S^2$
and
![]() $Z_g := \natural ^g D^3 \widetilde {\times } S^2$
, where
$Z_g := \natural ^g D^3 \widetilde {\times } S^2$
, where
![]() $D^3 \widetilde {\times } S^2 \to S^2$
is the nontrivial bundle. By assumption,
$D^3 \widetilde {\times } S^2 \to S^2$
is the nontrivial bundle. By assumption,
![]() $(c_1/d(\mathfrak {s}(d)))^2 = 0$
and it follows that
$(c_1/d(\mathfrak {s}(d)))^2 = 0$
and it follows that
![]() $c_1/d(\mathfrak {s}(d)) \in L$
, for some lagrangian
$c_1/d(\mathfrak {s}(d)) \in L$
, for some lagrangian
![]() $L \subseteq H^2(M)$
. Now, the automorphisms of the intersection form act transitively on the set of lagrangians (see, for example, [Reference WallWal64, pages 144–145]); and Wall [Reference WallWal64, page 144] also showed that every isometry of the intersection form of
$L \subseteq H^2(M)$
. Now, the automorphisms of the intersection form act transitively on the set of lagrangians (see, for example, [Reference WallWal64, pages 144–145]); and Wall [Reference WallWal64, page 144] also showed that every isometry of the intersection form of
![]() $H^2(M)$
is realised by a diffeomorphism. Hence, we may assume that
$H^2(M)$
is realised by a diffeomorphism. Hence, we may assume that
![]() $c_1/d(\mathfrak {s}(d)) \in H^2(M)$
lies in the standard lagrangian of
$c_1/d(\mathfrak {s}(d)) \in H^2(M)$
lies in the standard lagrangian of
![]() $H^2(M)$
, and so is the restriction to the boundary of c for some
$H^2(M)$
, and so is the restriction to the boundary of c for some
![]() $c \in H^2(N)$
. Since
$c \in H^2(N)$
. Since
![]() $H^2(N) \to H^2(M)$
is onto a summand, it follows that N admits a spin
$H^2(N) \to H^2(M)$
is onto a summand, it follows that N admits a spin
![]() $^c(d)$
-structure
$^c(d)$
-structure
![]() $\mathfrak {s}_{N}(d)$
that restricts to
$\mathfrak {s}_{N}(d)$
that restricts to
![]() $\mathfrak {s}(d)$
. Hence,
$\mathfrak {s}(d)$
. Hence,
![]() $(N, \mathfrak {s}_{N}(d))$
is a spin
$(N, \mathfrak {s}_{N}(d))$
is a spin
![]() $^c(d)$
null-bordism of
$^c(d)$
null-bordism of
![]() $(M, \mathfrak {s}(d))$
, and so
$(M, \mathfrak {s}(d))$
, and so
![]() $\Theta $
is indeed injective.
$\Theta $
is indeed injective.
Next, using Lemma 4.12, we deduce the stable classification of spin
![]() $^{c}$
structures on simply connected 4-manifolds.
$^{c}$
structures on simply connected 4-manifolds.
The fibration sequence defining
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
gives rise to an exact sequence
$B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
gives rise to an exact sequence
If M is simply connected, then
![]() $[M,\Omega K(\mathbb {Z}/d,2)] \cong [M,K(\mathbb {Z}/d,1)] \cong H^1(M;\mathbb {Z}/d) =0$
, so if a lift of
$[M,\Omega K(\mathbb {Z}/d,2)] \cong [M,K(\mathbb {Z}/d,1)] \cong H^1(M;\mathbb {Z}/d) =0$
, so if a lift of
![]() $\operatorname{\mathrm {spin}}^{c}$
structure
$\operatorname{\mathrm {spin}}^{c}$
structure
![]() $\mathfrak {s}$
to a spin
$\mathfrak {s}$
to a spin
![]() $^{c}(d)$
structure
$^{c}(d)$
structure
![]() $\mathfrak {s}(d)$
exists, then it is essentially unique.
$\mathfrak {s}(d)$
exists, then it is essentially unique.
A spin
![]() $^{c}(d)$
structure
$^{c}(d)$
structure
![]() $\mathfrak {s}(d)$
on M induces a spin
$\mathfrak {s}(d)$
on M induces a spin
![]() $^{c}(d)$
structure on
$^{c}(d)$
structure on
![]() $M \# W_g$
, for any g: as in Definition 4.7, we extend the associated
$M \# W_g$
, for any g: as in Definition 4.7, we extend the associated
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
structure on M by the spin
$\operatorname{\mathrm {spin}}^{c}(d)$
structure on M by the spin
![]() $^c(d)$
structure on
$^c(d)$
structure on
![]() $W_g$
with
$W_g$
with
![]() $c_1=0$
. By the previous paragraph, since
$c_1=0$
. By the previous paragraph, since
![]() $W_g$
is simply connected, there is an essentially unique such
$W_g$
is simply connected, there is an essentially unique such
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
structure on
$\operatorname{\mathrm {spin}}^{c}(d)$
structure on
![]() $W_g$
. Then a lift to a spin
$W_g$
. Then a lift to a spin
![]() $^{c}(d)$
structure on M determines such a lift on
$^{c}(d)$
structure on M determines such a lift on
![]() $M \# W_g$
. We can therefore define stable equivalence of spin
$M \# W_g$
. We can therefore define stable equivalence of spin
![]() $^{c}(d)$
structures. The definition is identical to the definition for spin
$^{c}(d)$
structures. The definition is identical to the definition for spin
![]() $^{c}(d)$
structure, just replacing
$^{c}(d)$
structure, just replacing
![]() $\operatorname{\mathrm {Spin}}^{c}$
with
$\operatorname{\mathrm {Spin}}^{c}$
with
![]() $\operatorname{\mathrm {Spin}}^{c}(d)$
throughout Definition 4.3(1) and Definition 4.7.
$\operatorname{\mathrm {Spin}}^{c}(d)$
throughout Definition 4.3(1) and Definition 4.7.
Theorem 4.13. Let M be a closed, oriented, simply connected 4-manifold. Two spin
![]() $^{c}$
structures
$^{c}$
structures
![]() $\mathfrak {s}_1$
and
$\mathfrak {s}_1$
and
![]() $\mathfrak {s}_2$
on M are stably equivalent if and only if
$\mathfrak {s}_2$
on M are stably equivalent if and only if
![]() $d(\mathfrak {s}_1) = d(\mathfrak {s}_2) \in \mathbb {N}_0$
and
$d(\mathfrak {s}_1) = d(\mathfrak {s}_2) \in \mathbb {N}_0$
and
![]() $c_1(\mathfrak {s}_1)^2 = c_1(\mathfrak {s}_2)^2 \in H^4(M)$
.
$c_1(\mathfrak {s}_1)^2 = c_1(\mathfrak {s}_2)^2 \in H^4(M)$
.
Proof. For the forward direction, the square of the Chern class and its divisibility are preserved by stable equivalence because we fixed the spin
![]() $^{c}$
structure on
$^{c}$
structure on
![]() $W_g$
to be the structure with trivial first Chern class, and because equivalence of spin
$W_g$
to be the structure with trivial first Chern class, and because equivalence of spin
![]() $^{c}$
structures preserves Chern numbers and the divisibility.
$^{c}$
structures preserves Chern numbers and the divisibility.
For the reverse direction, by Lemma 4.12, for a fixed 4-manifold M, two spin
![]() $^{c}$
structures
$^{c}$
structures
![]() $\mathfrak {s}_1$
and
$\mathfrak {s}_1$
and
![]() $\mathfrak {s}_2$
on M with
$\mathfrak {s}_2$
on M with
![]() $d(\mathfrak {s}_1) = d(\mathfrak {s}_2) =d$
determine
$d(\mathfrak {s}_1) = d(\mathfrak {s}_2) =d$
determine
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
-structures
$\operatorname{\mathrm {spin}}^{c}(d)$
-structures
![]() $\mathfrak {s}_1(d)$
and
$\mathfrak {s}_1(d)$
and
![]() $\mathfrak {s}_2(d)$
, and therefore elements of
$\mathfrak {s}_2(d)$
, and therefore elements of
![]() $\Omega _4^{\operatorname{\mathrm {Spin}}^{c}(d)}$
. Since
$\Omega _4^{\operatorname{\mathrm {Spin}}^{c}(d)}$
. Since
![]() $c_1(\mathfrak {s}_1)^2 = c_1(\mathfrak {s}_2)^2$
, it follows that
$c_1(\mathfrak {s}_1)^2 = c_1(\mathfrak {s}_2)^2$
, it follows that
![]() $(c_1/d(\mathfrak {s}_1(d)))^2 = (c_1/d(\mathfrak {s}_2(d)))^2$
: for
$(c_1/d(\mathfrak {s}_1(d)))^2 = (c_1/d(\mathfrak {s}_2(d)))^2$
: for
![]() $d=0$
, this is automatic; for
$d=0$
, this is automatic; for
![]() $d \neq 0$
, apply
$d \neq 0$
, apply
![]() $\pi ^*$
to
$\pi ^*$
to
![]() $c_1(\mathfrak {s}_1)^2 = c_1(\mathfrak {s}_2)^2$
and use (ϖ). Therefore, since
$c_1(\mathfrak {s}_1)^2 = c_1(\mathfrak {s}_2)^2$
and use (ϖ). Therefore, since
![]() $\sigma (M)$
is independent of tangential structures, by Lemma 4.12,
$\sigma (M)$
is independent of tangential structures, by Lemma 4.12,
![]() $(M,\mathfrak {s}_1(d))$
and
$(M,\mathfrak {s}_1(d))$
and
![]() $(M,\mathfrak {s}_1(d))$
are bordant over
$(M,\mathfrak {s}_1(d))$
are bordant over
![]() $B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
. Using Remark 4.8, we transfer to stable normal structures and apply Kreck’s stable diffeomorphism theorem [Reference KreckKre99, proof of Theorem 2 and Corollary 3], which in the current situation implies that
$B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
. Using Remark 4.8, we transfer to stable normal structures and apply Kreck’s stable diffeomorphism theorem [Reference KreckKre99, proof of Theorem 2 and Corollary 3], which in the current situation implies that
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
structures on M are stably equivalent if they are bordant. Here we use that the maps
$\operatorname{\mathrm {spin}}^{c}(d)$
structures on M are stably equivalent if they are bordant. Here we use that the maps
![]() $M \to B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
are 1-smoothings by Lemma 4.11 and that stabilisation is with
$M \to B\!\:\operatorname{\mathrm {Spin}}^{c}(d)$
are 1-smoothings by Lemma 4.11 and that stabilisation is with
![]() $(W_g, \mathfrak {s}_g(d))$
. Via the map
$(W_g, \mathfrak {s}_g(d))$
. Via the map
![]() $\pi : B\!\:\operatorname{\mathrm {Spin}}^{c}(d) \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
, a stable equivalence of
$\pi : B\!\:\operatorname{\mathrm {Spin}}^{c}(d) \to B\!\:\operatorname{\mathrm {Spin}}^{c}$
, a stable equivalence of
![]() $\operatorname{\mathrm {spin}}^{c}(d)$
structures determines a stable equivalence of
$\operatorname{\mathrm {spin}}^{c}(d)$
structures determines a stable equivalence of
![]() $\operatorname{\mathrm {spin}}^{c}$
structures.
$\operatorname{\mathrm {spin}}^{c}$
structures.
Now we are ready to prove the main result of this section. Let
![]() $C \in \mathbb {Z}$
be such that
$C \in \mathbb {Z}$
be such that
![]() $|C| \geq 16$
and
$|C| \geq 16$
and
![]() $8 \mid C$
. Define
$8 \mid C$
. Define
![]() $P(C) := |\mathcal {P}_{C/8}|$
, namely the number of distinct primes dividing
$P(C) := |\mathcal {P}_{C/8}|$
, namely the number of distinct primes dividing
![]() $C/8$
. We consider
$C/8$
. We consider
![]() $S^2 \times S^2$
with a fixed orientation. This determines an identification
$S^2 \times S^2$
with a fixed orientation. This determines an identification
![]() $H^4(S^2 \times S^2)=\mathbb {Z}$
.
$H^4(S^2 \times S^2)=\mathbb {Z}$
.
Theorem 4.14. For every
![]() $C \in \mathbb {Z}$
with
$C \in \mathbb {Z}$
with
![]() $|C| \geq 16$
and
$|C| \geq 16$
and
![]() $8 \mid C$
, there are
$8 \mid C$
, there are
![]() $n:= 2^{P(C)-1}$
stably equivalent spin
$n:= 2^{P(C)-1}$
stably equivalent spin
![]() $^{c}$
structures
$^{c}$
structures
![]() $\mathfrak {s}_1,\ldots ,\mathfrak {s}_n$
on
$\mathfrak {s}_1,\ldots ,\mathfrak {s}_n$
on
![]() $S^2 \times S^2$
with
$S^2 \times S^2$
with
![]() $c_1(\mathfrak {s}_i)^2 = C \in H^4(S^2 \times S^2) = \mathbb {Z}$
that are all pairwise inequivalent.
$c_1(\mathfrak {s}_i)^2 = C \in H^4(S^2 \times S^2) = \mathbb {Z}$
that are all pairwise inequivalent.
Proof. Let
![]() $M := S^2 \times S^2$
. Let
$M := S^2 \times S^2$
. Let
![]() $x,y \in H^2(M) \cong \mathbb {Z}^2$
be generators dual to
$x,y \in H^2(M) \cong \mathbb {Z}^2$
be generators dual to
![]() $[\operatorname{\mathrm {pt}} \times S^2]$
and
$[\operatorname{\mathrm {pt}} \times S^2]$
and
![]() $[S^2 \times \operatorname{\mathrm {pt}}]$
respectively. So
$[S^2 \times \operatorname{\mathrm {pt}}]$
respectively. So
![]() $xy =1 \in H^4(M)$
while
$xy =1 \in H^4(M)$
while
![]() $x^2=y^2=0$
. Henceforth, we identify
$x^2=y^2=0$
. Henceforth, we identify
![]() $H^4(M) \cong \mathbb {Z}$
. Let
$H^4(M) \cong \mathbb {Z}$
. Let
![]() $Q:= C/8$
. There are
$Q:= C/8$
. There are
![]() $P(C)$
prime powers dividing Q. Up to switching the order and multiplying both by
$P(C)$
prime powers dividing Q. Up to switching the order and multiplying both by
![]() $-1$
, there are
$-1$
, there are
![]() $2^{P(C)-1}$
ways to write Q as a product of coprime integers
$2^{P(C)-1}$
ways to write Q as a product of coprime integers
![]() $Q =q_1q_2$
. For each such factorisation, let
$Q =q_1q_2$
. For each such factorisation, let
![]() $\mathfrak {s}_i$
be a spin
$\mathfrak {s}_i$
be a spin
![]() $^{c}$
structure with
$^{c}$
structure with
Such spin
![]() $^{c}$
structures exist by Lemma 4.5: every characteristic element of
$^{c}$
structures exist by Lemma 4.5: every characteristic element of
![]() $H^2(M)$
can be realised as the first Chern class of some spin
$H^2(M)$
can be realised as the first Chern class of some spin
![]() $^{c}$
structure. Note that
$^{c}$
structure. Note that
and
![]() $d(\mathfrak {s}_i)=2$
for every i. Thus by Theorem 4.13, all the
$d(\mathfrak {s}_i)=2$
for every i. Thus by Theorem 4.13, all the
![]() $\mathfrak {s}_i$
are stably equivalent to one another. However, as we saw in the proof of Proposition 2.2, there is no isometry of the intersection pairing of M that sends
$\mathfrak {s}_i$
are stably equivalent to one another. However, as we saw in the proof of Proposition 2.2, there is no isometry of the intersection pairing of M that sends
![]() $(2q_1,2q_2)$
to
$(2q_1,2q_2)$
to
![]() $(2q_1',2q_2')$
in
$(2q_1',2q_2')$
in
![]() $H^2(M) \cong \mathbb {Z}^2$
for distinct unordered pairs
$H^2(M) \cong \mathbb {Z}^2$
for distinct unordered pairs
![]() $\{q_1,q_2\}$
and
$\{q_1,q_2\}$
and
![]() $\{q_1',q_2'\}$
. By Lemma 4.6, it follows that the
$\{q_1',q_2'\}$
. By Lemma 4.6, it follows that the
![]() $\{\mathfrak {s}_i\}$
are pairwise inequivalent spin
$\{\mathfrak {s}_i\}$
are pairwise inequivalent spin
![]() $^{c}$
structures.
$^{c}$
structures.
Acknowledgements
We would like to thank the anonymous referee for several helpful comments and corrections, especially in Section 4. We would also like to thank Manuel Krannich for advice about the homotopy sphere
![]() $\Sigma _Q$
, Jens Reinhold for comments on an earlier draft of this paper, and Csaba Nagy for pointing out a mistake in a previous version of the proof of Theorem 4.13.
$\Sigma _Q$
, Jens Reinhold for comments on an earlier draft of this paper, and Csaba Nagy for pointing out a mistake in a previous version of the proof of Theorem 4.13.