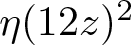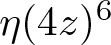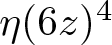1. Introduction
In Serre’s work [Reference Serre11] on applications of his groundbreaking theory [Reference Serre10] on connections between CM (Complex Multiplication) newforms and lacunarity, he characterizes the vanishingness of the coefficients of the infinite products:
\begin{align*}
q\prod_{n=1}^{\infty}\left(1-q^{12n}\right)^{2}=\sum_{n=1}^{\infty}A\left(n\right)q^{n},\quad
q\prod_{n=1}^{\infty}\left(1-q^{6n}\right)^{4}=\sum_{n=1}^{\infty}B\left(n\right)q^{n},\quad
& q\prod_{n=1}^{\infty}\left(1-q^{4n}\right)^{6}\\ & \qquad =\sum_{n=1}^{\infty}C\left(n\right)q^{n}
\end{align*}and shows the following:
(1)
$A\left(n\right)=0$ if and only if $n\not\equiv1\pmod{12}$, or $n\equiv1\pmod{12}$ has a prime factor $p\not\equiv 1\pmod{12}$ with odd exponent.(2)
$B\left(n\right)=0$ if and only if $n\not\equiv1\pmod{6}$, or $n\equiv1\pmod{6}$ has a prime factor $p\equiv2\pmod{3}$ with odd exponent.(3)
$C\left(n\right)=0$ if and only if $n\not\equiv1\pmod{4}$, or $n\equiv1\pmod{4}$ has a prime factor $p\equiv3\pmod{4}$ with odd exponent.
This characterization of the vanishingness also justifies that the series expansions for the products are lacunary. Setting 
$q={\rm e}^{2\pi iz}$ for 
${\rm Im}\left(z\right) \gt 0$ and writing 
$\eta\left(z\right)=q^{\frac{1}{24}}\prod_{n=1}^{\infty}\left(1-q^{n}\right)$ for the Dedekind eta function, it follows that these infinite products are all actually eta quotients, namely, 
$\eta(12z)^{2}$, 
$\eta\left(6z\right)^{4}$ and 
$\eta\left(4z\right)^{6}$, which as functions in z are CM newforms by 
$\mathbb{Q}[i]$ or 
$\mathbb{Q}[\sqrt{-3}]$. We call an eta quotient that is a CM newform a CM eta quotient.
Martin [Reference Martin8] proved that there are only finitely many eta quotients that are newforms, and thus, there are only a finite number of CM eta quotients. Martin’s work allows us to deduce that there are exactly 28 CM eta quotients. This motivates the present work describing necessary and sufficient conditions under which the Fourier coefficients of the CM eta quotients vanish. The number of CM eta quotients under consideration may be reduced by taking into account twists. For a series 
$f\left(q\right)=\sum_{n=1}^{\infty}a\left(n\right)q^{n}$, the coefficients of the series can be twisted by an arithmetic function χ via 
$\left(f\otimes\chi\right)\left(q\right):=\sum_{n=1}^{\infty}\chi\left(n\right)a\left(n\right)q^{n}$. The twist 
$f\otimes \chi$ has the same support as f assuming that 
$\chi\left(n\right)=0$ only if 
$a\left(n\right)=0$. In light of this, one can reduce the number of CM eta quotients in Martin’s list inequivalent up to twists. These CM eta quotients are tabulated in Table 1. An index is assigned to each eta quotient in Table 1 for further reference.
Table 1. A full list of CM eta quotients up to twisting.
For the reader’s reference, the remaining 10 CM eta quotients and their relations with those in Table 1 are listed as follows:
\begin{align*}
\frac{\eta \left(4 z\right)^9 \eta \left(12 z\right)^9}{\eta \left(2 z\right)^3 \eta \left(6
z\right)^3 \eta \left(8 z\right)^3 \eta \left(24 z\right)^3}&=\eta \left(2 z\right)^3 \eta \left(6 z\right)^3\otimes \left(\frac{-4}{n}\right), \\
\frac{\eta \left(8 z\right)^{18}}{\eta \left(4 z\right)^6 \eta \left(16 z\right)^6}&=\eta\left(4z\right)^{6}\otimes\left(\frac{-8}{n}\right),\\
\frac{\eta \left(8 z\right)^8}{\eta \left(4 z\right)^2 \eta \left(16 z\right)^2}&=\eta\left(4z\right)^{2}\eta\left(8z\right)^{2}\otimes\left(\frac{-8}{n}\right),\\
\frac{\eta \left(12 z\right)^{12}}{\eta \left(6 z\right)^4 \eta \left(24 z\right)^4}&=\eta\left(6z\right)^{4}\otimes\left(\frac{-4}{n}\right), \\ \frac{\eta \left(4 z\right)^3 \eta \left(44 z\right)^3}{\eta \left(2 z\right) \eta \left(8 z\right) \eta
\left(22 z\right) \eta \left(88 z\right)}&=\eta\left(2z\right)\eta\left(22z\right)\otimes\left(\frac{-4}{n}\right),\\
\frac{\eta \left(8 z\right)^3 \eta \left(40 z\right)^3}{\eta \left(4 z\right) \eta \left(16 z\right)
\eta \left(20 z\right) \eta \left(80 z\right)}&=\eta\left(4z\right)\eta\left(20z\right)\otimes\left(\frac{-8}{n}\right),\\ \frac{\eta \left(16 z\right)^4}{\eta \left(8 z\right) \eta \left(32 z\right)}&=\eta\left(8z\right)\eta\left(16z\right)\otimes\left(-1\right)^{\frac{n-1}{8}},\\
\frac{\eta \left(12 z\right)^3 \eta \left(36 z\right)^3}{\eta \left(6 z\right) \eta \left(18
z\right) \eta \left(24 z\right) \eta \left(72 z\right)}&=\eta\left(6z\right)\eta\left(18z\right)\otimes\left(\frac{-4}{n}\right), \\
\frac{\eta \left(24 z\right)^6}{\eta \left(12 z\right)^2 \eta \left(48 z\right)^2}&=\eta\left(12z\right)^{2}\otimes\left(\frac{-8}{n}\right).
\end{align*} For each eta quotient in Table 1, we use the index i from the first column to define a corresponding indexed function 
$f_{i}\left(z\right)=\prod_{d|N}\eta\left({\rm d}z\right)^{r_{d}}$ and write 
$f_{i}\left(z\right)=\sum_{n=1}^{\infty}a_{i}\left(n\right)q^{n}$. Theorem 1.1 is the main result of this work and characterizes the vanishing of the coefficients of each indexed eta quotient.
Theorem 1.1. If 
$a_{i}(n)$ denotes the coefficient of q n in the eta quotient of index i in Table 1, then:
(1)
$a_{1}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{3}$, or $n\equiv1\pmod{3}$ has a prime factor $p\equiv2\pmod{3}$ with odd exponent,(2)
$a_{2}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{4}$, or $n\equiv1\pmod{4}$ has a prime factor $p\equiv3\pmod{4}$ with odd exponent,(3)
$a_{3}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{6}$, or $n\equiv1\pmod{6}$ has a prime factor $p\equiv2\pmod{3}$ with odd exponent,(4)
$a_{4}\left(n\right)=0$ if and only if n has a prime factor $p\equiv5,7\pmod{8}$ with odd exponent,(5)
$a_{5}\left(n\right)=0$ if and only if n has a prime factor $p\equiv 3,5,6\pmod{7}$ with odd exponent,(6)
$a_{6}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{2}$, or $n\equiv1\pmod{2}$ has a prime factor $p\equiv 2\mod{3}$ with odd exponent,(7)
$a_{7}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{4}$, or $n\equiv1\pmod{4}$ has a prime factor $p\equiv3\pmod{4}$ with odd exponent,(8)
$a_{8}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{2}$, or $n\equiv1\pmod{2}$ has a prime factor $p\equiv5,7\pmod{8}$ with odd exponent,(9)
$a_{9}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{3}$, or $n\equiv1\pmod{3}$ has a prime factor $p\equiv2\pmod{3}$ with odd exponent,(10)
$a_{10}\left(n\right)=0$ if and only if n has a prime factor $p\equiv3\pmod{4}$ with odd exponent,(11)
$a_{11}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{4}$, or $n\equiv1\pmod{4}$ has a prime factor $p\equiv3\pmod{4}$ with odd exponent,(12)
$a_{12}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{3}$, or $n\equiv1\pmod{3}$ has a prime factor $p\not\equiv 1,4,7,16\pmod{21}$ with odd exponent,(13)
$a_{13}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{8}$, or $n\equiv1\pmod{8}$ has a prime factor $p\not\equiv 1\pmod{8}$ with odd exponent,(14)
$a_{14}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{12}$, or $n\equiv1\pmod{12}$ has a prime factor $p\not\equiv 1\pmod{12}$ with odd exponent,(15)
$a_{15}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{4}$, or $n\equiv1\pmod{4}$ has a prime factor $p\not\equiv1,9\pmod{20}$ with odd exponent,(16)
$a_{16}\left(n\right)=0$ if and only if n has a prime factor p not a square modulo 23 with odd exponent or a prime factor p not equal to 23 that is representable by $2x^{2}+xy+3y^{2}$ with exponent $e_{p}\equiv2\pmod{3}$,(17)
$a_{17}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{2}$, or $n\equiv1\pmod{2}$ has a prime factor p not a square modulo 11 or a prime factor p not equal to 11 that is representable by $3x^{2}+2xy+4y^{2}$ with exponent $e_{p}\equiv2\pmod{3}$,(18)
$a_{18}\left(n\right)=0$ if and only if $n\not\equiv1\pmod{6}$, or $n\equiv1\pmod{6}$ has a prime factor $p\equiv2\pmod{3}$ with odd exponent or a prime factor $p\equiv 1\pmod{3}$ that is representable by $4x^{2}+2xy+7y^{2}$ with exponent $e_{p}\equiv2\pmod{3}$.
The remainder of this work is organized as follows. In § 2, we review the notion of CM newforms and their fundamentals, as well as express all the CM eta quotients in Table 1 in terms of generalized theta functions. Proofs of Theorem 1.1 are distributed into the subsequent three sections in accordance with their commonness. In the final section, we conclude with generalizations of the results on the cases of weight 1 in terms of binary quadratic forms.
2. Review of CM newforms and their basic properties
Let 
$f\left(z\right)=\sum_{n=1}^{\infty}a\left(n\right)q^{n}$ be a newform of weight k, and level 
$\Gamma_{0}\left(N\right)$ with some character χ. Then one can first recall that its Fourier coefficients 
$a\left(n\right)$ satisfy the recursive relation:
\begin{equation}
a\left(\ell\right)a\left(n\right)=a\left(\ell n\right)+\chi\left(\ell\right)\ell^{k-1}a\left(n/\ell\right)
\end{equation}for any positive integer n and any prime 
$\ell$, where 
$a\left(x\right)$ is set to be 0 if x is not an integer, and possess the multiplicative property that 
$a\left(mn\right)=a\left(m\right)a\left(n\right)$ for any positive integers 
$m,n$ such that 
$\gcd\left(m,n\right)=1$. Therefore, investigations on 
$a\left(n\right)$ can be boiled down to analysis on 
$a\left(p\right)$ for p prime.
For any Dirichlent character ϕ of conductor m, a newform 
$f\left(z\right)$ is said to be with CM by ϕ if 
$a\left(p\right)\phi\left(p\right)=a\left(p\right)$ for all 
$p\nmid Nm$, also called a CM newform by ϕ. Characterizations of CM newforms for certain different cases have been established by Ribet [Reference Ribet9] and Kani [Reference Kani7], which are briefly summarized as follows.
2.1. CM newforms of weight k > 1
It is known [Reference Deligne and Serre4, (6.3)] that a CM newform of weight k > 1 exists only if ϕ is a quadratic character associated to some quadratic field K. In such case, 
$f\left(z\right)$ is also called a CM newform by K. In his groundbreaking work [Reference Ribet9], Ribet gives a full characterization of such newforms and justifies that any CM newform of weight k > 1 by a quadratic field K must come from a Hecke character ψK associated to K and be of the form:
\begin{equation*}
f\left(z\right)=\sum_{\substack{\mathfrak{a}\subset \mathcal{O}_{K}\\ integral}}\psi_{K}\left(\mathfrak{a}\right)\mathcal{N}\left(\mathfrak{a}\right)^{\frac{k-1}{2}}q^{\mathcal{N}\left(\mathfrak{a}\right)},
\end{equation*}where 
$\mathcal{N}\left(\cdot\right)$ denotes the norm of an ideal. In particular, when K is imaginary of discriminant 
$-d \lt 0$ and class number 1, one can show (see, e.g., [Reference Huber, Mc Laughlin and Ye5, Corollary 2.2]) that 
$f\left(z\right)$ must be a linear combination of the generalized theta functions:
\begin{equation*}
\sum_{\alpha\in \beta+\mathfrak{m}}\alpha^{k-1}q^{\mathcal{N}\left(\alpha\right)}\quad\text{over} \beta\in \left(\mathcal{O}_{K}/\mathfrak{m}\right)^{\times},
\end{equation*}for some integral ideal 
$\mathfrak{m}$ with 
$\mathcal{N}\left(\mathfrak{m}\right)=N/d$. Building upon this, one can explicitly express the CM eta quotients of weight k > 1 in Table 1 in terms of generalized theta functions and obtain the following lemma.
Lemma 2.1. Write ζ 3 for the primitive third root of unity 
$e^{\frac{2\pi i}{3}}$. Then the following identities hold:
\begin{align}
\eta \left(3 z\right)^2 \eta \left(9 z\right)^2 = \sum_{m,n=-\infty}^{\infty}\left(\left(3m+1\right)+\left(3n\right)\zeta_{3}\right)q^{\mathcal{N}\left(\left(3m+1\right)+\left(3n\right)\zeta_{3}\right)},
\end{align}
\begin{align}
\eta \left(4 z\right)^2 \eta \left(8 z\right)^2 = \sum_{m,n=-\infty}^{\infty}\left(2m-2n+1+\left(2m+2n\right)i\right)q^{\mathcal{N}\left(2m-2n+1+\left(2m+2n\right)i\right)},
\end{align}
\begin{align}
\eta \left(6 z\right)^4
&=\sum_{m,n=-\infty}^{\infty}\left(2m-4n+1+\left(4m-2n\right)\zeta_{3}\right)q^{\mathcal{N}\left(2m-4n+1+\left(4m-2n\right)\zeta_{3}\right)},
\end{align}
\begin{align}
\eta \left(z\right)^2 \eta \left(2 z\right) \eta \left(4 z\right) \eta \left(8 z\right)^2 = \frac{1}{2}\sum_{m,n=-\infty}^{\infty}\left(m+n\sqrt{-2}\right)^{2}q^{\mathcal{N}\left(m+n\sqrt{-2}\right)},
\end{align}
\begin{align}
\eta \left(z\right)^3 \eta \left(7 z\right)^3 &= \frac{1}{2}\sum_{m,n=-\infty}^{\infty}\left(m+n\frac{1+\sqrt{-7}}{2}\right)^2q^{\mathcal{N}\left(m+n\frac{1+\sqrt{-7}}{2}\right)},
\end{align}
\begin{align}
\eta \left(2 z\right)^3 \eta \left(6 z\right)^3 &= \frac{1}{2}\sum_{m,n=-\infty}^{\infty}\left(m+n+(2n)\zeta_{3}\right)^2q^{\mathcal{N}\left(m+n+(2n)\zeta_{3}\right)},
\end{align}
\begin{align}
\eta \left(4 z\right)^6 &=\frac{1}{2}\sum_{m,n=-\infty}^{\infty}\left(2m+1+2ni\right)^2q^{\mathcal{N}\left(2m+1+2ni\right)},
\end{align}
\begin{align}
\frac{\eta \left(4 z\right)^5 \eta \left(8 z\right)^5}{\eta \left(2 z\right)^2 \eta \left(16 z\right)^2} &= \frac{1}{2}\sum_{m,n=-\infty}^{\infty}\left(2m+1+2n\sqrt{-2}\right)^{2}q^{\mathcal{N}\left(2m+1+2n\sqrt{-2}\right)}\\
&\quad -\frac{1}{2}\sum_{m,n=-\infty}^{\infty}\left(2m+1+\left(2n+1\right)\sqrt{-2}\right)^{2}q^{\mathcal{N}\left(2m+1+\left(2n+1\right)\sqrt{-2}\right)},
\end{align}
\begin{align}
\eta \left(3 z\right)^8 = \frac{1}{3}\sum_{m,n=-\infty}^{\infty}\left(\left(m-2n+1\right)+\left(2m-n\right)\zeta_{3}\right)^3q^{\mathcal{N}\left(\left(m-2n+1\right)+\left(2m-n\right)\zeta_{3}\right)},
\end{align}
\begin{align}
\eta \left(z\right)^4 \eta \left(2 z\right)^2 \eta \left(4 z\right)^4 &= \frac{1}{4}\sum_{m,n=-\infty}^{\infty}\left(m+ni\right)^4q^{\mathcal{N}\left(m+ni\right)},
\end{align}
\begin{align}
\frac{\eta \left(8 z\right)^{38}}{\eta \left(4 z\right)^{14} \eta \left(16 z\right)^{14}} &= \sum_{m,n=-\infty}^{\infty}\left(4m+1+4ni\right)^4q^{\mathcal{N}\left(4m+1+4ni\right)}\\
&\quad -\sum_{m,n=-\infty}^{\infty}\left(4m+1+\left(4n+2\right)i\right)^4q^{\mathcal{N}\left(4m+1+\left(4n+2\right)i\right)}.
\end{align}Remark 2.1. Identities (2.6)–(2.8) were first discovered and proved by Chan et al. [Reference Chan, Cooper and Liaw1] using properties of spherical theta functions.
Remark 2.2. In recent work [Reference Chang2], using a different approach, Chang characterizes 
$a_{3}\left(p\right)$ for prime 
$p\equiv1\pmod{6}$ and 
$a_{7}\left(p\right)$ for prime 
$p\equiv1\pmod{4}$ and shows that 
$a_{3}\left(p\right)=X+Y$ for integers X, Y such that 
$2X\equiv Y+1\pmod{6}$ and 
$X\equiv1\pmod{2}$, and 
$a_{7}\left(p\right)=2\left(X^{2}-Y^{2}\right)$ for integers X, Y such that 
$X^{2}+Y^{2}=p$ and 
$X\equiv1\pmod{2}$ and 
$Y\equiv0\pmod{2}$. A careful inspection of Equations (2.4) and (2.8) leads one to recover Chang’s results.
2.2. CM newforms of weight 1
In recent work [Reference Kani7], Kani extends Ribet’s results to the case of CM newforms of weight 1 and level 
$\Gamma_{0}\left(D\right)$ with character 
$({-D}/{n})$ by an imaginary quadratic field 
$K=\mathbb{Q}[\sqrt{-D}]$, where −D is a form discriminant. He showed that any such CM newform must be a linear combination of
\begin{equation*}
\sum_{x,y=-\infty}^{\infty}q^{Q\left(x,y\right)}=\sum_{n=0}^{\infty}\left(\sum_{Q(x,y)=n}1\right)q^{n}\quad\text{over}\ \left[Q(x,y)=ax^{2}+bxy+cy^{2}\right]\in {\rm Cl}\left(D\right),
\end{equation*}where 
${\rm Cl}\left(D\right)$ denotes the class group of primitive positive definite binary quadratic forms of discriminant −D. As a consequence, one can relate the CM eta quotients of weight 1 in Table 1 to classical theta series associated with binary quadratic forms.
Lemma 2.2. The following identities hold.
\begin{align}
\eta \left(3 z\right) \eta \left(21 z\right)&= \frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{x^2+xy+16y^2=n}1-\sum_{4x^2+xy+4y^2=n}1\right)q^{n},
\end{align}
\begin{align}
\eta \left(8 z\right) \eta \left(16 z\right)&= \frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{x^2+32y^2=n}1-\sum_{4x^2+4xy+9y^2=n}1\right)q^{n},
\end{align}
\begin{align}
\eta \left(12 z\right)^2 &= \frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{x^2+36y^2=n}1-\sum_{4x^2+9y^2=n}1\right)q^{n},
\end{align}
\begin{align}
\eta\left(4z\right)\eta\left(20z\right) &= \frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{x^2+20y^2=n}1-\sum_{4x^2+5y^2=n}1\right)q^{n},
\end{align}
\begin{align}
\eta \left(z\right) \eta \left(23 z\right) &= \frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{x^2+xy+6y^2=n}1-\sum_{2x^2+xy+3y^2=n}1\right)q^{n},
\end{align}
\begin{align}
\eta \left(2 z\right) \eta \left(22 z\right) &=\frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{x^2+11y^2=n}1-\sum_{3x^2+2xy+4y^2=n}1\right)q^{n},
\end{align}
\begin{align}
\eta \left(6 z\right) \eta \left(18 z\right) &=\frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{x^2+27y^2=n}1-\sum_{4x^2+2xy+7y^2=n}1\right)q^{n}.
\end{align}3. Proofs of Theorem 1.1 (1)–(11)
The proofs of items (1)–(11) of Theorem 1.1 are very similar to one another, which can be generally elaborated as follows. Note that the coefficients 
$a_{i}\left(n\right)$ satisfy the multiplicative property, 
$a_{i}\left(n\right)=\prod_{p|n}a_{i}\left(p^{e_{p}}\right)$, given the prime factorization 
$n=\prod_{p|n}p^{e_{p}}$ of n. Therefore, the analysis of the vanishing of 
$a_{i}\left(n\right)$ may be decomposed into local parts 
$a_{i}\left(p^{e_{p}}\right)$. As observed in the remarks given at the beginning of § 2.1, when a newform has CM by an imaginary quadratic field K of class number 1, its Fourier development is enumerated by the norms of elements of 
$\mathcal{O}_{K}$. So for p inert in 
$\mathcal{O}_{K}$ with ep odd, it is clear that 
$p^{e_{p}}$ cannot be represented by the norm of any element of 
$\mathcal{O}_{K}$, and this justifies all the if-parts of items (1)–(11).
For their only-if-parts, it suffices to show that 
$a_{i}\left(p^{e_{p}}\right)\ne0$ for p not inert, or p inert with ep even. This can be achieved by the explicit descriptions for 
$a_{i}\left(n\right)$ given in Lemma 2.1. In what follows, we give the proof for item (11) as an illustration and leave the cases of items (1)–(10) to the reader.
Proof of the only-if-part of item (11)
Suppose that p is an odd prime not inert in 
$\mathbb{Z}[i]$. Then there is a unique 
$\pi\in\mathbb{Z}[i]$ up to complex conjugation such that either 
$\pi\equiv 1\pmod{4\mathbb{Z}[i]}$ or 
$\pi\equiv1+2i\pmod{4\mathbb{Z}[i]}$, and 
$\mathcal{N}\left(\pi\right)=p$, and therefore, by Equation (2.12), 
$a_{11}\left(p\right)=\pm\left(\pi^{4}+\overline{\pi}^{4}\right)\ne0$. Moreover, it follows that 
$a_{11}\left(p\right)\not\equiv0\pmod{p}$, since π and 
$\overline{\pi}$ are coprime. Note by Equation (2.1) that:
\begin{equation*}
a_{11}\left(p^{m}\right)\equiv a_{11}\left(p\right)^{m}\pmod{p}.
\end{equation*} Therefore, 
$a_{11}\left(p^{m}\right)\not\equiv0\pmod{p}$, and thus, 
$a_{11}\left(p^{m}\right)\ne0$.
Now suppose that p is inert with ep even. Since 
$\mathbb{Z}[i]$ is a PID, it is clear that any 
$\alpha\in\mathbb{Z}[i]$ such that 
$\mathcal{N}\left(\alpha\right)=p^{e_{p}}$ must be of the form 
$\alpha =\pm p^{e_{p}/2},\,\pm ip^{e_{p}/2}$. Thus, by Equation (2.12), 
$a_{11}\left(p^{e_{p}}\right)=p^{2e_{p}}\ne0$.
4. Proofs of Theorem 1.1 (12)–(15)
Instead of directly proving items (12)–(15) of Theorem 1.1, we do a bit more and establish explicit formulas for their associated 
$a_{i}\left(p^{m}\right)$, after which the assertions follow immediately. These formulas are summarized in the following proposition.
Proposition 4.1. For 
$i=12,\ldots,15$, let 
$a_{i}\left(n\right)$ be defined as in § 1. Given a non-negative integer m and a prime p. The following assertions hold.
- (1)
(a) For n = 7,
$a_{12}\left(7^{m}\right)=\left(-1\right)^{m}$,(b) for
$p\equiv1,4,16\pmod{21}$,
\begin{equation*}
a_{12}\left(p^{m}\right)=\begin{cases}
m+1 & \text{if}\ p=X^{2}+XY+2Y^{2}\ \text{with}\ 3|Y,\\
\left(-1\right)^{m}\left(m+1\right) & \text{otherwise,}
\end{cases}
\end{equation*}(c) for
$p\equiv2,8,11\pmod{21}$,
\begin{equation*}
a_{12}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
\left(-1\right)^{m/2}&\text{otherwise,}
\end{cases}
\end{equation*}(d) for
$p\equiv 5,10,13,17,19,20\pmod{21}$,
\begin{equation*}
a_{12}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
1&\text{otherwise.}
\end{cases}
\end{equation*}
- (2)
(a) For
$p\equiv 1\pmod{8}$,
\begin{equation*}
a_{13}\left(p^{m}\right)=\begin{cases}
m+1 &\text{if}\ p=X^{2}+2Y^{2}\ \text{with}\ 4|Y,\\
\left(-1\right)^{m}\left(m+1\right) &\text{otherwise,}
\end{cases}
\end{equation*}(b) for
$p\equiv3\pmod{8}$,
\begin{equation*}
a_{13}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
\left(-1\right)^{m/2}&\text{otherwise,}
\end{cases}
\end{equation*}(c) for
$p\equiv 5,7\pmod{8}$,
\begin{equation*}
a_{13}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
1&\text{otherwise.}
\end{cases}
\end{equation*}
- (3)
(a) For
$p\equiv 1\pmod{12}$,
\begin{equation*}
a_{14}\left(p^{m}\right)=\begin{cases}
m+1 &\text{if}\ p=X^{2}+Y^{2}\ \text{with}\ 6|Y,\\
\left(-1\right)^{m}\left(m+1\right) &\text{otherwise,}
\end{cases}
\end{equation*}(b) for
$p\equiv5\pmod{12}$,
\begin{equation*}
a_{14}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
\left(-1\right)^{m/2}&\text{otherwise,}
\end{cases}
\end{equation*}(c) for
$p\equiv 7,11\pmod{12}$,
\begin{equation*}
a_{14}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
1&\text{otherwise.}
\end{cases}
\end{equation*}
- (4)
(a) For n = 5,
$a_{15}(5^{m})=(-1)^{m}$,(b) for
$p\equiv 1,9\pmod{20}$,
\begin{equation*}
a_{15}\left(p^{m}\right)=\begin{cases}
m+1 &\text{if}\ p=X^{2}+5Y^{2}\ \text{with}\ 2|Y,\\
\left(-1\right)^{m}\left(m+1\right) &\text{otherwise,}
\end{cases}
\end{equation*}(c) for
$p\equiv3,7\pmod{20}$,
\begin{equation*}
a_{15}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
\left(-1\right)^{m/2}&\text{otherwise,}
\end{cases}
\end{equation*}(d) for
$p\equiv 11,13,17,19\pmod{20}$,
\begin{equation*}
a_{15}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
1&\text{otherwise.}
\end{cases}
\end{equation*}
Proofs of items of Proposition 4.1 are very similar, especially the first three cases, whose corresponding maximal quadratic orders are all of class number 1. The last case has to make use of the classical fact [Reference Cox3, p. 31] that a prime p is not equal to 5 can be represented by 
$X^{2}+5Y^{2}$ if and only if 
$p\equiv1,9\pmod{20}$. As such, we give the proof of item (1) only and leave the others to the reader.
Proof of Proposition 4.1 (1)
Item (a) follows from 
$a_{12}\left(7\right)=-1$ and the recursive formula (2.1). Note that
\begin{align}
x^{2}+xy+16y^{2}&=\left(x-y\right)^{2}+\left(x-y\right)\left(3y\right)+2\left(3y\right)^{2},
\end{align}
\begin{align}
4x^{2}+xy+4y^{2}&=\left(x+2y\right)^{2}+\left(x+2y\right)\left(x-y\right)+2\left(x-y\right)^{2}.
\end{align} Then for 
$p\equiv1,4,16\pmod{21}$, since 
$p\equiv1,2,4\pmod{7}$, p must be uniquely representable by 
$X^{2}+XY+2Y^{2}$ up to complex conjugation and multiplication by a unit. The induced fact that 
$p\equiv1\pmod{3}$ implies that such a representation verifies either 
$Y\equiv0\pmod{3}$ or 
$X-Y\equiv0\pmod{3}$. Up to a multiplier of a unit, there are exactly two representations for the former case and one for the latter case. Therefore, by Equations (4.1) and (4.2), p is representable by either 
$x^{2}+xy+16y^{2}$ or 
$4x^{2}+xy+4y^{2}$, each of which has exactly four solutions. Whence by Equation (2.13), 
$a_{12}\left(p\right)=2$ if p can be represented by 
$X^{2}+XY+2Y^{2}$ with 
$3|Y$, since otherwise 
$a_{12}\left(p\right)=-2$. These facts, together with Equation (2.1), yield the desired formula for 
$p\equiv1,4,16\pmod{21}$.
For 
$p\equiv2,8,11\pmod{21}$, since 
$p\equiv2\pmod{3}$ and 
$x^{2}+xy+16y^{2}\equiv 4x^{2}+xy+4y^{2}\equiv x^{2}+xy+y^{2}\equiv 0,1\pmod{3}$, neither of 
$x^{2}+xy+16y^{2}$ and 
$4x^{2}+xy+4y^{2}$ represent p, and thus 
$a_{12}\left(p\right)=0$, and with 
$({-7}/{p})=1$ and Equation (2.1), the corresponding formula follows.
For 
$p\equiv5,10,13,17,19,20\pmod{21}$, clearly, p is not a square modulo 7, while both 
$x^{2}+xy+16y^{2}$ and 
$4x^{2}+xy+4y^{2}$ are of discriminant 
$-63=-7\times 3^{2}$, neither of them can represent p. Therefore, 
$a_{12}\left(p\right)=0$, and with 
$({-7}/{p})=-1$ and Equation (2.1), the corresponding formula follows.
Remark 4.1. The common vanishing in these four cases is related to the fact that their attached form class groups are all 
$\mathbb{Z}/4\mathbb{Z}$, and the principal genus classes of the form class groups associated with their corresponding maximal orders consist of exactly one form class. This also explains why the representability of p by the binary quadratic forms of these four cases can be interpreted in terms of congruences, which, however, is not the case for items (16)–(18) of Theorem 1.1. Moreover, following this observation and using the genus theory of binary quadratic forms, one can find a uniform interpretation and extension of Proposition 4.1. We shall return to this in § 6.
Remark 4.2. In fact, one can check that both quadratic forms involved in Equation (2.13) lie in the same genus of 
${\rm Cl}(63)$, so by the classical Siegel–Weil theorem (see, e.g., [Reference Wang and Pei12, Chapter 7]), one can replace one of them by Eisenstein series and obtain the alternative expression:
\begin{align*}
\eta(3z)\eta(21z)&=-1+\sum_{n=1}^{\infty}\left(\sum_{x^{2}+xy+16y^{2}=n}1-\frac{1}{2}\left(\sum_{d|n}\left(\frac{-7}{d}\right)+\sum_{d|n}\left(\frac{-3}{d}\right)\left(\frac{21}{n/d}\right)\right)\right)q^{n}\\
&\quad -\frac{3}{2}\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-7}{d}\right)\right)q^{9n}.
\end{align*}Combining this with Equation (4.2), one can also recover Proposition 4.1 (1). For the reader’s reference, we also record the analogous expressions for the other companions as follows:
\begin{align*}
\eta(8z)\eta(16z)&=-1+\sum_{n=1}^{\infty}\left(\sum_{x^{2}+32y^{2}=n}1-\frac{1}{2}\left(\sum_{d|n}\left(\frac{-8}{d}\right)+\sum_{d|n}\left(\frac{-4}{d}\right)\left(\frac{8}{n/d}\right)\right)\right)q^{n}\\
&\quad +\frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-8}{d}\right)\right)q^{2n}-\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-8}{d}\right)+\sum_{d|n}\left(\frac{-4}{d}\right)\left(\frac{8}{n/d}\right)\right)q^{4n}\\
&\quad +\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-8}{d}\right)\right)q^{8n}-2\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-8}{d}\right)\right)q^{16n},\\
\eta(12z)^{2}&=-1+\sum_{n=1}^{\infty}\left(\sum_{x^{2}+36y^{2}=n}1-\frac{1}{2}\left(\sum_{d|n}\left(\frac{-4}{d}\right)+\sum_{d|n}\left(\frac{-3}{d}\right)\left(\frac{12}{n/d}\right)\right)\right)q^{n}\\
&\quad+\frac{1}{2}\sum_{n=1}^{\infty}\left(\left(\sum_{d|n}\left(\frac{-4}{d}\right)-\sum_{d|n}\left(\frac{-3}{d}\right)\left(\frac{12}{n/d}\right)\right)\right)q^{2n}\\
&\quad-\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-4}{d}\right)+\sum_{d|n}\left(\frac{-3}{d}\right)\left(\frac{12}{n/d}\right)\right)q^{4n}\\
&\quad-\frac{3}{2}\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-4}{d}\right)\right)q^{9n}+\frac{3}{2}\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-4}{d}\right)\right)q^{18n},\\
\eta(4z)\eta(20z)&=-1+\sum_{n=1}^{\infty}\left(\sum_{x^{2}+20y^{2}=n}1-\frac{1}{2}\left(\sum_{d|n}\left(\frac{-20}{d}\right)+\sum_{d|n}\left(\frac{-4}{d}\right)\left(\frac{5}{n/d}\right)\right)\right)q^{n}\\
&\quad+\frac{1}{2}\sum_{n=1}^{\infty}\left(\left(\sum_{d|n}\left(\frac{-20}{d}\right)-\sum_{d|n}\left(\frac{-4}{d}\right)\left(\frac{5}{n/d}\right)\right)\right)q^{2n}\\
&\quad-\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-20}{d}\right)+\sum_{d|n}\left(\frac{-4}{d}\right)\left(\frac{5}{n/d}\right)\right)q^{4n}.
\end{align*}Remark 4.3. In [Reference Serre11], Serre justifies Theorem 1.1(14) by finding the Hecke theta series for 
$\eta(12z)^{2}$ using Galois representations. We literally use an alternative expression for 
$\eta(12z)^{2}$ to recover Serre’s result.
5. Proofs of Theorem 1.1 (16)–(18)
Similar to the cases of (12)–(15), we establish the following formulas for 
$a_{i}\left(n\right)$ for 
$i=16,\ldots,18$ as an intermediate step towards items (16)–(18) of Theorem 1.1.
Proposition 5.1. For 
$i=16,\ldots,18$, let 
$a_{i}\left(n\right)$ be defined as in Section 1, and let Di denote 23, 44 and 108, respectively. Also write 
$Q_{i}\left(x,y\right)$ for the principal binary quadratic form of discriminant 
$-D_{i}$, i.e., 
$x^{2}+xy+6y^{2}$, 
$x^{2}+11y^{2}$ and 
$x^{2}+27y^{2}$, respectively. For a non-negative integer m and a prime p, the following assertions hold.
(1) One has that
$a_{16}\left(23^{m}\right)=a_{17}\left(11^{m}\right)=1$,(2) for p such that
$\left(\frac{-D_{i}}{p}\right)=1$,
\begin{equation*}
a_{i}\left(p^{m}\right)=\begin{cases}
m+1&\text{if}\ p\ \text{is representable by}\ Q_{i}\left(x,y\right),\\
1&\text{if}\ p\ \text{is irrepresentable by}\ Q_{i}\left(x,y\right)\ \text{and}\ m\equiv0\pmod{3},\\
-1&\text{if}\ p\ \text{is irrepresentable by}\ Q_{i}\left(x,y\right)\ \text{and}\ m\equiv1\pmod{3},\\
0&\text{otherwise,}
\end{cases}
\end{equation*}(3) for p such that
$\left(\frac{-D_{i}}{p}\right)=-1$,
\begin{equation*}
a_{i}\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
1&\text{otherwise.}
\end{cases}
\end{equation*}
Proof. Items (1) and (3) are straightforward by Equations (2.17)–(2.19) and Equation (2.1). For item (2), first note that the form class groups 
${\rm Cl}\left(D_{i}\right)$ are all of class number 3, and thus, all three form classes of 
${\rm Cl}\left(D_{i}\right)$ lie in the same genus. Here, two of them are equivalent by 
${\rm GL}_{2}\left(\mathbb{Z}\right)$. By the theory of quadratic orders (see, e.g., [Reference Cox3]), it is well known that for a split prime p, it is representable by either the principal form 
$Q_{i}\left(x,y\right)$ with exactly four solutions or a non-principal form with exactly two solutions. Therefore, by Equation (2.17)–(2.19), one can find that 
$a_{i}\left(p\right)=2$ if p is representable by 
$Q_{i}\left(x,y\right)$; otherwise 
$a_{i}\left(p\right)=-1$. From these, together with Equation (2.1), the desired formulas follow.
Remark 5.1. Similar to what is noted in Remark 4.4, Proposition 5.1 can also be derived by the following alternative expressions for the CM eta quotients associated with 
$a_{i}\left(n\right)$,
\begin{align*}
\eta\left(z\right)\eta\left(23z\right)
&=-\frac{3}{4}+\sum_{n=1}^{\infty}\left(\frac{3}{4}\sum_{x^{2}+xy+6y^{2}=n}1-\frac{1}{2}\sum_{d|n}\left(\frac{-23}{d}\right)\right)q^{n},\\
\eta\left(2z\right)\eta\left(22z\right)
&=-\frac{3}{4}+\sum_{n=1}^{\infty}\left(\frac{3}{4}\sum_{x^{2}+11y^{2}=n}1-\frac{1}{2}\sum_{d|n}\left(\frac{-11}{d}\right)\right)q^{n}\\
&\quad -\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-11}{d}\right)\right)q^{4n},\nonumber\\
\eta\left(6z\right)\eta\left(18z\right)
&=-\frac{3}{4}+\sum_{n=1}^{\infty}\left(\frac{3}{4}\sum_{x^{2}+27y^{2}=n}1-\frac{1}{2}\sum_{d|n}\left(\frac{-3}{d}\right)\right)q^{n}\\
&\quad +\frac{1}{2}\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-3}{d}\right)\right)q^{3n}-1\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-3}{d}\right)\right)q^{4n}\nonumber\\
&\quad-\frac{3}{2}\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-3}{d}\right)\right)q^{9n}+1\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-3}{d}\right)\right)q^{12n}\nonumber\\
&\quad-3\sum_{n=1}^{\infty}\left(\sum_{d|n}\left(\frac{-3}{d}\right)\right)q^{36n}.\nonumber
\end{align*}6. Further remarks on Proposition 4.1
As noted in Remark 4.3, those analogous formulas deduced in Proposition 4.1 via Lemma 2.12 are by some means related to the fact that their attached form class groups are all 
$\mathbb{Z}/4\mathbb{Z}$, and the principal genus classes of the form class groups associated to their corresponding maximal orders all consist of one form class. We now detail how these work.
Let 
$-D=f^{2}(-d) \lt 0$ with −d a fundamental discriminant be a form discriminant such that the attached form class group 
${\rm Cl}(D)=\langle [Q]\rangle\cong \mathbb{Z}/4\mathbb{Z}$, and 
${\rm Cl}(d)^{2}=\{[\tilde{Q}_{0}]\}$, where 
$\tilde{Q}_{0}$ denotes the principal form of discriminant −d. Take the character χ of 
${\rm Cl}(D)$ such that 
$\chi([Q])=i$. Then writing 
$[Q_{0}]=[Q]^{4}$ for the identity of 
${\rm Cl}(D)$, where Q 0 is the principal form, and 
$[Q_2]=[Q]^{2}$, the difference:
\begin{equation*}
\sum_{n=1}^{\infty}a(n)q^{n}=\frac{1}{2}\sum_{n=0}^{\infty}\left(\sum_{Q_{0}(x,y)=n}1-\sum_{Q_{2}(x,y)=n}1\right)q^{n}=\frac{1}{2}\sum_{j=1}^{4}\chi([Q]^{j})\sum_{x,y=-\infty}^{\infty}q^{Q^{j}(x,y)}
\end{equation*}is actually a normalized 
$\mathbb{T}(f)$-eigenform [Reference Kani6, Theorem 12] with quadratic character 
$\left(\frac{-D}{\cdot}\right)$, where 
$\mathbb{T}(f)$ denotes the algebra generated by Hecke operators Tn with 
$\gcd(n,f)=1$. Therefore, for n coprime to f, the coefficients a(n) satisfy the recursive relation (2.1) and multiplicativity, so to compute a(n), it is sufficient to find a(p) for 
$p|n$.
By the genus theory of binary quadratic forms, for p split in 
$\mathbb{Q}[\sqrt{-d}]$ and such that 
$p=\tilde{Q}_{0}(X,Y)\pmod{d}$ is solvable, p is uniquely representable by 
$\tilde{Q}_{0}(X,Y)$ up to complex conjugation and multiplication by a unit, since 
${\rm Cl}(d)^{2}=\{[\tilde{Q}_{0}]\}$ by assumption. Furthermore, if 
$p=Q_{0}(x,y)\pmod{D}$ is also solvable, then p is representable by either of Q 0 and Q 2, which accordingly implies that 
$a(p)=2$ or 
$a(p)=-2$, and the former case is equivalent to that 
$p=\tilde{Q}_{0}(X,Y)$ with 
$f|Y$. Otherwise, neither of Q 0 and Q 2 represent p, which yields that 
$a(p)=0$. In summary, one obtains the following generalization of Proposition 4.1: for any positive integer m,
(1) for p such that
$\left(\frac{-d}{p}\right)=1$, and both $p=\tilde{Q}_{0}(X,Y)\pmod{d}$ and $p=Q_{0}(x,y)\pmod{D}$ are solvable,
\begin{equation*}
a(p^{m})=\begin{cases}
m+1&\text{if}\ p=\tilde{Q}_{0}(X,Y)\ \text{with}\ f|Y,\\
(-1)^{m}(m+1)&\text{otherwise,}
\end{cases}
\end{equation*}(2) for p such that
$\left(\frac{-d}{p}\right)=1$, and $p=Q_{0}(x,y)\pmod{D}$ is unsolvable,
\begin{equation*}
a\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
\left(-1\right)^{m/2}&\text{otherwise,}
\end{cases}
\end{equation*}(3) for p such that
$\left(\frac{-d}{p}\right)=-1$,
\begin{equation*}
a\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
1&\text{otherwise.}
\end{cases}
\end{equation*}
Finally, it is noteworthy to mention that one can generalize Proposition 5.1 in a similar manner by noticing that the form class groups are all 
$\mathbb{Z}/3\mathbb{Z}$. Specifically, if we suppose that 
$-D \lt 0$ is a form discriminant such that 
${\rm Cl}(D)=\langle [Q_{0}], [Q_{1}], [Q_{1}]^{-1}\rangle\cong\mathbb{Z}/3\mathbb{Z}$, where Q 0 denotes the principal form of discriminant −D, and define
\begin{equation*}
\sum_{n=1}^{\infty}b(n)q^{n}=\frac{1}{2}\sum_{n=0}^{\infty}\left(\sum_{Q_{0}(x,y)=n}1-\sum_{Q_{1}(x,y)=n}1\right)q^{n}=\frac{1}{2}\sum_{j=1}^{3}\chi([Q_{1}]^{j})\sum_{x,y=-\infty}^{\infty}q^{Q_{1}^{j}(x,y)},
\end{equation*}where the character χ of 
${\rm Cl}(D)$ is chosen by 
$\chi([Q_{1}])=e^{\frac{2\pi i}{3}}$, then for any positive integer m,
(1) for p such that
$\left(\frac{-D}{p}\right)=1$,
\begin{equation*}
b\left(p^{m}\right)=\begin{cases}
m+1&\text{if}\ p\ \text{is representable by}\ Q_{0}\left(x,y\right),\\
1&\text{if}\ p\ \text{is irrepresentable by}\ Q_{0}\left(x,y\right)\ \text{and}\ m\equiv0\pmod{3},\\
-1&\text{if}\ p\ \text{is irrepresentable by}\ Q_{0}\left(x,y\right)\ \text{and}\ m\equiv1\pmod{3},\\
0&\text{otherwise,}
\end{cases}
\end{equation*}(2) for p such that
$\left(\frac{-D}{p}\right)=-1$,
\begin{equation*}
b\left(p^{m}\right)=\begin{cases}
0&\text{if}\ m\ \text{is odd,}\\
1&\text{otherwise.}
\end{cases}
\end{equation*}
Acknowledgement
The authors thank the referee for his/her comments, corrections and suggestions.
Funding Statement
Dongxi Ye was supported by the Guangdong Basic and Applied Basic Research Foundation (grant no. 2023A1515010298).
