1 Introduction
The creation of a magnetically confined laboratory electron–positron plasma (Pedersen et al.
Reference Pedersen, Danielson, Hugenschmidt, Marx, Sarasola, Schauer, Schweikhard, Surko and Winkler2012; Saitoh et al.
Reference Saitoh, Pedersen, Hergenhahn, Stenson, Paschkowski and Hugenschmidt2014) is becoming a new element of inspiration for some researchers in the field of plasma physics. These systems, while apparently exotic (especially for non-relativistic regimes), can contribute to the understanding of some important properties of physical phenomena in electron–ion plasmas. The role of dispersive waves in fast magnetic reconnection in ordinary plasmas, for instance, has been put into perspective by particle-in-cell simulations (Bessho & Bhattacharjee Reference Bessho and Bhattacharjee2005; Daughton & Karimabadi Reference Daughton and Karimabadi2007) and fluid theory and simulation results of electron–positron plasmas (Chacón, Simakov & Zocco Reference Chacón, Simakov and Zocco2007; Zocco, Chacón & Simakov Reference Zocco, Chacón and Simakov2008, Reference Zocco, Chacón and Simakov2009). Similarly, the study of pair plasmas can be relevant in other contexts, such as the energy dynamics of decaying turbulence (Makwana et al.
Reference Makwana, Zhdankin, Li, Daughton and Cattaneo2015; Guo et al.
Reference Guo, Li, Daughton, Li and Liu2016). There is an increasing number of analytical results discussed in the recent literature, but most of these are valid only linearly. Nonlinear results are rare (Helander Reference Helander2017), and models that combine computational realisability and physical verisimilitude are desirable. In this article we revisit some aspects of recent linear results, and propose a possible route towards a reduced kinetic nonlinear model for electron–positron plasmas. We present some fluid equations similar to those of Chacón et al. (Reference Chacón, Simakov, Lukin and Zocco2008), but in the framework of gyrokinetics for magnetic reconnection (Zocco & Schekochihin Reference Zocco and Schekochihin2011; Loureiro, Schekochihin & Zocco Reference Loureiro, Schekochihin and Zocco2013; Zocco Reference Zocco2015; Zocco et al.
Reference Zocco, Loureiro, Dickinson, Numata and Roach2015; Loureiro et al.
Reference Loureiro, Dorland, Fazendeiro, Kanekar, Mallet, Vilelas and Zocco2016). The new aspect here introduced is in the quasi-neutrality equation. The smallest kinetic scale that enters the quasi-neutrality equation is taken to be the Larmor scale,
![]() $\unicode[STIX]{x1D70C}_{e}=v_{\text{the}}/\unicode[STIX]{x1D6FA}_{c}$
, which is assumed to be much smaller than the inertial scale
$\unicode[STIX]{x1D70C}_{e}=v_{\text{the}}/\unicode[STIX]{x1D6FA}_{c}$
, which is assumed to be much smaller than the inertial scale
![]() $d_{e}=\unicode[STIX]{x1D70C}_{e}/\sqrt{\unicode[STIX]{x1D6FD}}$
, where
$d_{e}=\unicode[STIX]{x1D70C}_{e}/\sqrt{\unicode[STIX]{x1D6FD}}$
, where
![]() $\unicode[STIX]{x1D6FD}$
is the ratio of kinetic to plasma pressure,
$\unicode[STIX]{x1D6FD}$
is the ratio of kinetic to plasma pressure,
![]() $\unicode[STIX]{x1D6FA}_{c}=eB/(mc)$
is the cyclotron frequency,
$\unicode[STIX]{x1D6FA}_{c}=eB/(mc)$
is the cyclotron frequency,
![]() $v_{\text{the}}$
the thermal speed and
$v_{\text{the}}$
the thermal speed and
![]() $B$
the strength of the equilibrium magnetic field. The inclusion of the Debye length is avoided (Helander Reference Helander2014; Helander & Connor Reference Helander and Connor2016), as this would require a covariant treatment. However, the possible effects of the displacement current are discussed. Some considerations on linear waves and reconnecting instabilities are given in § 2. In § 6, we propose an adaptation of the kinetic reduced electron heating model (KREHM) equations (Zocco & Schekochihin Reference Zocco and Schekochihin2011) to low-beta pair plasmas. Particular attention is devoted to the isothermal limit. Conclusions are in § 7.
$B$
the strength of the equilibrium magnetic field. The inclusion of the Debye length is avoided (Helander Reference Helander2014; Helander & Connor Reference Helander and Connor2016), as this would require a covariant treatment. However, the possible effects of the displacement current are discussed. Some considerations on linear waves and reconnecting instabilities are given in § 2. In § 6, we propose an adaptation of the kinetic reduced electron heating model (KREHM) equations (Zocco & Schekochihin Reference Zocco and Schekochihin2011) to low-beta pair plasmas. Particular attention is devoted to the isothermal limit. Conclusions are in § 7.
2 Linear analysis
In our system, density fluctuations for electrons (
![]() $e^{-}=-|e|$
) and positrons (
$e^{-}=-|e|$
) and positrons (
![]() $e^{+}=|e|$
) are calculated by taking the zeroth moment of the perturbed distribution function
$e^{+}=|e|$
) are calculated by taking the zeroth moment of the perturbed distribution function
![]() $\unicode[STIX]{x1D6FF}f_{e^{\mp }}=-e^{\mp }\unicode[STIX]{x1D711}F_{0}/T_{0}+h_{e^{\mp }}$
. The non-adiabatic part of
$\unicode[STIX]{x1D6FF}f_{e^{\mp }}=-e^{\mp }\unicode[STIX]{x1D711}F_{0}/T_{0}+h_{e^{\mp }}$
. The non-adiabatic part of
![]() $\unicode[STIX]{x1D6FF}f$
satisfies the electromagnetic gyrokinetic equation of Frieman & Chen (Reference Frieman and Chen1982),
$\unicode[STIX]{x1D6FF}f$
satisfies the electromagnetic gyrokinetic equation of Frieman & Chen (Reference Frieman and Chen1982),
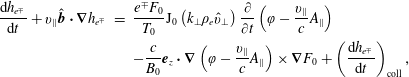 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\text{d}h_{e^{\mp }}}{\text{d}t}+v_{\Vert }\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}h_{e^{\mp }} & = & \displaystyle \displaystyle \frac{e^{\mp }F_{0}}{T_{0}}\text{J}_{0}\left(k_{\bot }\unicode[STIX]{x1D70C}_{e}\hat{v}_{\bot }\right)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D711}-\frac{v_{\Vert }}{c}A_{\text{}\Vert \text{}}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\frac{c}{B_{0}}\boldsymbol{e}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\unicode[STIX]{x1D711}-\frac{v_{\Vert }}{c}A_{\Vert }\right)\times \unicode[STIX]{x1D735}F_{0}+\left(\frac{\text{d}h_{e^{\mp }}}{\text{d}t}\right)_{\text{coll}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\text{d}h_{e^{\mp }}}{\text{d}t}+v_{\Vert }\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}h_{e^{\mp }} & = & \displaystyle \displaystyle \frac{e^{\mp }F_{0}}{T_{0}}\text{J}_{0}\left(k_{\bot }\unicode[STIX]{x1D70C}_{e}\hat{v}_{\bot }\right)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D711}-\frac{v_{\Vert }}{c}A_{\text{}\Vert \text{}}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\frac{c}{B_{0}}\boldsymbol{e}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\unicode[STIX]{x1D711}-\frac{v_{\Vert }}{c}A_{\Vert }\right)\times \unicode[STIX]{x1D735}F_{0}+\left(\frac{\text{d}h_{e^{\mp }}}{\text{d}t}\right)_{\text{coll}},\end{eqnarray}$$
where
![]() $\text{d}/\text{d}t=\unicode[STIX]{x2202}_{t}+B_{0}^{-1}\{\text{J}_{0}\unicode[STIX]{x1D711},\!\}$
,
$\text{d}/\text{d}t=\unicode[STIX]{x2202}_{t}+B_{0}^{-1}\{\text{J}_{0}\unicode[STIX]{x1D711},\!\}$
,
![]() $\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}=\unicode[STIX]{x2202}_{z}-B_{0}^{-1}\{\text{J}_{0}A_{\Vert },\!\},$
$\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}=\unicode[STIX]{x2202}_{z}-B_{0}^{-1}\{\text{J}_{0}A_{\Vert },\!\},$
![]() $\{A,B\}=\unicode[STIX]{x2202}_{x}A\unicode[STIX]{x2202}_{y}B-\unicode[STIX]{x2202}_{y}A\unicode[STIX]{x2202}_{x}B,$
$\{A,B\}=\unicode[STIX]{x2202}_{x}A\unicode[STIX]{x2202}_{y}B-\unicode[STIX]{x2202}_{y}A\unicode[STIX]{x2202}_{x}B,$
![]() $v_{\Vert }$
is the particle velocity in the
$v_{\Vert }$
is the particle velocity in the
![]() $z$
-direction, parallel to the guide field of modulus
$z$
-direction, parallel to the guide field of modulus
![]() $B_{0}$
,
$B_{0}$
,
![]() $\hat{v}_{\bot }$
is the particle velocity, perpendicular to it, normalised to the thermal speed
$\hat{v}_{\bot }$
is the particle velocity, perpendicular to it, normalised to the thermal speed
![]() $v_{\text{the}}=\sqrt{2T_{0}/m}$
, where
$v_{\text{the}}=\sqrt{2T_{0}/m}$
, where
![]() $T_{0}$
is the reference temperature of the Maxwellian equilibrium
$T_{0}$
is the reference temperature of the Maxwellian equilibrium
![]() $F_{0}$
,
$F_{0}$
,
![]() $x$
and
$x$
and
![]() $y$
are Cartesian space coordinates orthogonal to
$y$
are Cartesian space coordinates orthogonal to
![]() $z$
, and
$z$
, and
![]() $\text{J}_{0}=\text{J}_{0}(k_{\bot }\unicode[STIX]{x1D70C}_{e}\hat{v}_{\bot })$
is the Bessel function. Here
$\text{J}_{0}=\text{J}_{0}(k_{\bot }\unicode[STIX]{x1D70C}_{e}\hat{v}_{\bot })$
is the Bessel function. Here
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $A_{\Vert }$
are the electrostatic potential, and the parallel component of the magnetic vector potential, respectively. In gyrokinetics, perturbations can vary across the equilibrium magnetic field on a small scale (of the order of the Larmor radius), but equilibrium quantities vary slowly on a macroscopic length,
$A_{\Vert }$
are the electrostatic potential, and the parallel component of the magnetic vector potential, respectively. In gyrokinetics, perturbations can vary across the equilibrium magnetic field on a small scale (of the order of the Larmor radius), but equilibrium quantities vary slowly on a macroscopic length,
![]() $L.$
Furthermore, perturbed quantities vary slowly along the equilibrium magnetic field
$L.$
Furthermore, perturbed quantities vary slowly along the equilibrium magnetic field
![]() $k_{\Vert }/k_{\bot }\equiv \unicode[STIX]{x1D716}_{GK}\sim \unicode[STIX]{x1D70C}_{e}/L\ll 1$
, and evolve on a time scale which is much longer than the inverse cyclotron frequency,
$k_{\Vert }/k_{\bot }\equiv \unicode[STIX]{x1D716}_{GK}\sim \unicode[STIX]{x1D70C}_{e}/L\ll 1$
, and evolve on a time scale which is much longer than the inverse cyclotron frequency,
![]() $\unicode[STIX]{x1D6FA}^{-1}.$
Thus, densities evolve following the familiar continuity equation
$\unicode[STIX]{x1D6FA}^{-1}.$
Thus, densities evolve following the familiar continuity equation
with
![]() $u_{\Vert ,e^{\mp }}=n_{0}^{-1}\int \text{d}^{3}\boldsymbol{v}\unicode[STIX]{x1D6FF}f_{e^{+}}v_{\Vert }$
. We are using the local approximation
$u_{\Vert ,e^{\mp }}=n_{0}^{-1}\int \text{d}^{3}\boldsymbol{v}\unicode[STIX]{x1D6FF}f_{e^{+}}v_{\Vert }$
. We are using the local approximation
for the background density gradient, which introduces effects associated with the diamagnetic frequency
![]() $\unicode[STIX]{x1D714}_{\ast e^{\mp }}=\mp \text{i}v_{\text{the}}/(2L_{n})\unicode[STIX]{x1D70C}_{e}\unicode[STIX]{x2202}_{y},$
where
$\unicode[STIX]{x1D714}_{\ast e^{\mp }}=\mp \text{i}v_{\text{the}}/(2L_{n})\unicode[STIX]{x1D70C}_{e}\unicode[STIX]{x2202}_{y},$
where
![]() $\unicode[STIX]{x1D735}n_{0}/n_{0}\approx -L_{n}^{-1}$
,
$\unicode[STIX]{x1D735}n_{0}/n_{0}\approx -L_{n}^{-1}$
,
![]() $\left(\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}t\right)_{\text{coll}}$
is the collisional operator and
$\left(\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}t\right)_{\text{coll}}$
is the collisional operator and
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{e}\ll 1$
.
$k_{\bot }\unicode[STIX]{x1D70C}_{e}\ll 1$
.
Poisson’s equation for the electrostatic potential,
![]() $\unicode[STIX]{x1D711}$
, is derived from the quasi-neutrality condition
$\unicode[STIX]{x1D711}$
, is derived from the quasi-neutrality condition
We consider the ansatz
![]() $h_{e^{\mp }}=\left(e^{\mp }\unicode[STIX]{x1D711}/T_{0}+\unicode[STIX]{x1D6FF}n_{e^{\mp }}/n_{0}+2v_{\Vert }u_{\Vert e^{\mp }}/v_{\text{the}}^{2}\right)F_{0}+g_{e^{\mp }},$
where
$h_{e^{\mp }}=\left(e^{\mp }\unicode[STIX]{x1D711}/T_{0}+\unicode[STIX]{x1D6FF}n_{e^{\mp }}/n_{0}+2v_{\Vert }u_{\Vert e^{\mp }}/v_{\text{the}}^{2}\right)F_{0}+g_{e^{\mp }},$
where
![]() $\int \text{d}^{3}\boldsymbol{v}g_{e^{\mp }}=\int \text{d}^{3}\boldsymbol{v}v_{\Vert }g_{e^{\mp }}\equiv 0.$
Then
$\int \text{d}^{3}\boldsymbol{v}g_{e^{\mp }}=\int \text{d}^{3}\boldsymbol{v}v_{\Vert }g_{e^{\mp }}\equiv 0.$
Then
where we see that
if
![]() $k_{\bot }d_{e}\sim 1$
, with
$k_{\bot }d_{e}\sim 1$
, with
![]() $d_{e}=c/\unicode[STIX]{x1D714}_{pl}$
,
$d_{e}=c/\unicode[STIX]{x1D714}_{pl}$
,
![]() $\unicode[STIX]{x1D714}_{pl}^{2}=4\unicode[STIX]{x03C0}n_{0}e^{2}/(cm_{e}),$
$\unicode[STIX]{x1D714}_{pl}^{2}=4\unicode[STIX]{x03C0}n_{0}e^{2}/(cm_{e}),$
![]() $\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x03C0}n_{0}T_{0}/B^{2}\ll 1$
, and
$\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x03C0}n_{0}T_{0}/B^{2}\ll 1$
, and
guarantees balance in (2.5). Equation (2.5) is valid, strictly speaking, only if perpendicular temperature fluctuations, associated with finite Larmor radius effects, are neglected. We consider this regime for the moment, and leave a more rigorous treatment of temperature, density and parallel magnetic fluctuations for the section which is concerned with nonlinear physics. Before proceeding, however, we notice that (2.5) is similar to the quasi-neutrality condition used by Helander (Reference Helander2014) where the Debye length is replaced by the Larmor scale. This is a fundamental requirement to avoid the otherwise awkward condition
![]() $d_{e}\sim \unicode[STIX]{x1D706}_{D}$
, which would imply
$d_{e}\sim \unicode[STIX]{x1D706}_{D}$
, which would imply
![]() $v_{\text{the}}\sim c.$
Following Helander & Connor (Reference Helander and Connor2016), we retain perpendicular magnetic perturbations, but neglect magnetic compressibility,
$v_{\text{the}}\sim c.$
Following Helander & Connor (Reference Helander and Connor2016), we retain perpendicular magnetic perturbations, but neglect magnetic compressibility,
![]() $\unicode[STIX]{x1D6FF}B_{\Vert }$
.
$\unicode[STIX]{x1D6FF}B_{\Vert }$
.
We then calculate the
![]() $v_{\Vert }$
-moment of (2.1), to obtain
$v_{\Vert }$
-moment of (2.1), to obtain
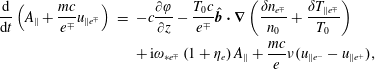 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\left(A_{\Vert }+\frac{mc}{e^{\mp }}u_{\Vert e^{\mp }}\right) & = & \displaystyle \displaystyle -c\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}z}-\frac{T_{0}c}{e^{\mp }}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{\unicode[STIX]{x1D6FF}n_{e^{\mp }}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}}{T_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\text{i}\unicode[STIX]{x1D714}_{\ast e^{\mp }}\left(1+\unicode[STIX]{x1D702}_{e}\right)A_{\Vert }+\frac{mc}{e}\unicode[STIX]{x1D708}(u_{\Vert e^{-}}-u_{\Vert e^{+}}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\left(A_{\Vert }+\frac{mc}{e^{\mp }}u_{\Vert e^{\mp }}\right) & = & \displaystyle \displaystyle -c\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}z}-\frac{T_{0}c}{e^{\mp }}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{\unicode[STIX]{x1D6FF}n_{e^{\mp }}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}}{T_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\text{i}\unicode[STIX]{x1D714}_{\ast e^{\mp }}\left(1+\unicode[STIX]{x1D702}_{e}\right)A_{\Vert }+\frac{mc}{e}\unicode[STIX]{x1D708}(u_{\Vert e^{-}}-u_{\Vert e^{+}}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D702}_{e}=n_{0}\unicode[STIX]{x1D735}T_{0}/(T_{0}\unicode[STIX]{x1D735}n_{0})$
,
$\unicode[STIX]{x1D702}_{e}=n_{0}\unicode[STIX]{x1D735}T_{0}/(T_{0}\unicode[STIX]{x1D735}n_{0})$
,
![]() $\unicode[STIX]{x1D708}$
a constant collision frequency,
$\unicode[STIX]{x1D708}$
a constant collision frequency,
![]() $\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}=n_{0}^{-1}\int \text{d}v_{\Vert }2\hat{v}_{\Vert }^{2}h_{e^{\mp }}$
and a simple Lenard–Bernstein collisional model operator has been used (Lenard & Bernstein Reference Lenard and Bernstein1958; Zocco & Schekochihin Reference Zocco and Schekochihin2011). Parallel Ampère’s law gives
$\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}=n_{0}^{-1}\int \text{d}v_{\Vert }2\hat{v}_{\Vert }^{2}h_{e^{\mp }}$
and a simple Lenard–Bernstein collisional model operator has been used (Lenard & Bernstein Reference Lenard and Bernstein1958; Zocco & Schekochihin Reference Zocco and Schekochihin2011). Parallel Ampère’s law gives
where the displacement current has been neglected. Equation (2.2), if we take into account of (2.5), implies that
where
![]() $v_{A,e}=B/\sqrt{4\unicode[STIX]{x03C0}m_{e}n_{0}}$
is the Alfvén speed based on the electron mass. Notice that
$v_{A,e}=B/\sqrt{4\unicode[STIX]{x03C0}m_{e}n_{0}}$
is the Alfvén speed based on the electron mass. Notice that
![]() $v_{A,e}$
is defined using the electron density only. The system is closed with an equation for the parallel temperature fluctuations, derived using a highly collisional fluid closure,
$v_{A,e}$
is defined using the electron density only. The system is closed with an equation for the parallel temperature fluctuations, derived using a highly collisional fluid closure,
![]() $\unicode[STIX]{x1D708}\gg \unicode[STIX]{x1D714}$
, for the flux of energy (Zocco & Schekochihin Reference Zocco and Schekochihin2011; Zocco et al.
Reference Zocco, Loureiro, Dickinson, Numata and Roach2015)
$\unicode[STIX]{x1D708}\gg \unicode[STIX]{x1D714}$
, for the flux of energy (Zocco & Schekochihin Reference Zocco and Schekochihin2011; Zocco et al.
Reference Zocco, Loureiro, Dickinson, Numata and Roach2015)
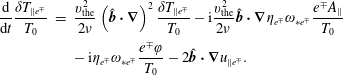 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}}{T_{0}} & = & \displaystyle \displaystyle \frac{v_{\text{the}}^{2}}{2\unicode[STIX]{x1D708}}\left(\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)^{2}\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}}{T_{0}}-\text{i}\frac{v_{\text{the}}^{2}}{2\unicode[STIX]{x1D708}}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}_{e^{\mp }}\unicode[STIX]{x1D714}_{\ast e^{\mp }}\frac{e^{\mp }A_{\Vert }}{T_{0}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,\text{i}\unicode[STIX]{x1D702}_{e^{\mp }}\unicode[STIX]{x1D714}_{\ast e^{\mp }}\frac{e^{\mp }\unicode[STIX]{x1D711}}{T_{0}}-2\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}u_{\Vert e^{\mp }}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}}{T_{0}} & = & \displaystyle \displaystyle \frac{v_{\text{the}}^{2}}{2\unicode[STIX]{x1D708}}\left(\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)^{2}\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}}{T_{0}}-\text{i}\frac{v_{\text{the}}^{2}}{2\unicode[STIX]{x1D708}}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}_{e^{\mp }}\unicode[STIX]{x1D714}_{\ast e^{\mp }}\frac{e^{\mp }A_{\Vert }}{T_{0}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,\text{i}\unicode[STIX]{x1D702}_{e^{\mp }}\unicode[STIX]{x1D714}_{\ast e^{\mp }}\frac{e^{\mp }\unicode[STIX]{x1D711}}{T_{0}}-2\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}u_{\Vert e^{\mp }}.\end{eqnarray}$$
This is just a choice that facilitates the forthcoming discussion. More precisely, we are considering the semi-collisional limit (Drake & Lee Reference Drake and Lee1977)
withFootnote
1
![]() $\unicode[STIX]{x1D714}\sim \unicode[STIX]{x1D714}_{\ast e}$
. Electron thermal conduction effects are negligible for
$\unicode[STIX]{x1D714}\sim \unicode[STIX]{x1D714}_{\ast e}$
. Electron thermal conduction effects are negligible for
then (2.11) becomes
The system could easily be left completely kinetic, then (2.11) would couple to higher-order moments. However, each of these moments would follow a universal equation when projected on the basis of Hermite polynomials which allows for an efficient treatment of the non-isothermal case
![]() $\unicode[STIX]{x1D6FF}T_{\Vert }\neq 0$
(Zocco & Schekochihin Reference Zocco and Schekochihin2011; Loureiro et al.
Reference Loureiro, Schekochihin and Zocco2013; Zocco Reference Zocco2015; Zocco et al.
Reference Zocco, Loureiro, Dickinson, Numata and Roach2015; Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016). In the truly collisionless case the hierarchy of Hermite moments generates a plasma response which was proven to be equivalent to the collisionless response evaluated via Landau contour integration (Zocco Reference Zocco2015). The isothermal approximation instead,
$\unicode[STIX]{x1D6FF}T_{\Vert }\neq 0$
(Zocco & Schekochihin Reference Zocco and Schekochihin2011; Loureiro et al.
Reference Loureiro, Schekochihin and Zocco2013; Zocco Reference Zocco2015; Zocco et al.
Reference Zocco, Loureiro, Dickinson, Numata and Roach2015; Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016). In the truly collisionless case the hierarchy of Hermite moments generates a plasma response which was proven to be equivalent to the collisionless response evaluated via Landau contour integration (Zocco Reference Zocco2015). The isothermal approximation instead,
![]() $\unicode[STIX]{x1D6FF}T_{\Vert }\equiv 0,$
would be described by the electron response of the nonlinear model of Schep, Pegoraro & Kuvshinov (Reference Schep, Pegoraro and Kuvshinov1994). In the context of linear magnetic reconnection, the presence of temperature fluctuations is a technicality that has an impact on the transition from collisional to collisionless regimes, but it is irrelevant when one wants to estimate reconnection rates for very small but finite collisionality. The inclusion of the resonant electron response (i.e. Landau resonance) is not necessary to obtain the correct reconnection rates in the collisionless limit, since the relevant condition to transition into a collisionless reconnection regime is that the inertial scale exceeds the resistive one, and this can occur even when collisions are finite.Footnote
2
For this reason, we are justified in using (2.11) and yet consider a collisionless limit for linear magnetic reconnection. This is a well-known fact for electron–ion plasmas (Ottaviani & Porcelli Reference Ottaviani and Porcelli1995), and electron–positron plasmas do not seem to be an exception. Of all the three regimes discussed (highly collisional, truly collisionless, kinetic non-isothermal with finite collisions), the last is certainly the most realistic one. Nonlinearly, the role of high-order moments that couple to the equation for temperature fluctuations is very important, as was shown by Loureiro et al. (Reference Loureiro, Schekochihin and Zocco2013) for electron–ion plasmas. The evolution of high-order moments of the distribution function is a consequence of the formation of small-scale structures in velocity space, which gives rise to heating even in the limit of vanishing collisionality (in steady state or sufficiently slow dynamics) (Zocco & Schekochihin Reference Zocco and Schekochihin2011). There is no reason to believe that the same phenomenon cannot occur in pair plasmas.
$\unicode[STIX]{x1D6FF}T_{\Vert }\equiv 0,$
would be described by the electron response of the nonlinear model of Schep, Pegoraro & Kuvshinov (Reference Schep, Pegoraro and Kuvshinov1994). In the context of linear magnetic reconnection, the presence of temperature fluctuations is a technicality that has an impact on the transition from collisional to collisionless regimes, but it is irrelevant when one wants to estimate reconnection rates for very small but finite collisionality. The inclusion of the resonant electron response (i.e. Landau resonance) is not necessary to obtain the correct reconnection rates in the collisionless limit, since the relevant condition to transition into a collisionless reconnection regime is that the inertial scale exceeds the resistive one, and this can occur even when collisions are finite.Footnote
2
For this reason, we are justified in using (2.11) and yet consider a collisionless limit for linear magnetic reconnection. This is a well-known fact for electron–ion plasmas (Ottaviani & Porcelli Reference Ottaviani and Porcelli1995), and electron–positron plasmas do not seem to be an exception. Of all the three regimes discussed (highly collisional, truly collisionless, kinetic non-isothermal with finite collisions), the last is certainly the most realistic one. Nonlinearly, the role of high-order moments that couple to the equation for temperature fluctuations is very important, as was shown by Loureiro et al. (Reference Loureiro, Schekochihin and Zocco2013) for electron–ion plasmas. The evolution of high-order moments of the distribution function is a consequence of the formation of small-scale structures in velocity space, which gives rise to heating even in the limit of vanishing collisionality (in steady state or sufficiently slow dynamics) (Zocco & Schekochihin Reference Zocco and Schekochihin2011). There is no reason to believe that the same phenomenon cannot occur in pair plasmas.
3 Small thermal conductivity: waves
We consider the approximation of small thermal conductivity, therefore
We use (3.1) in (2.8), we then add the parallel moment equations (2.8) of the two species, to notice that diamagnetic effects cancel exactly. Thus, we obtain
On the other hand, Poisson’s equation (2.5), after using the continuity equations and Ampère’s law (2.9), becomes
By combining (3.2) and (3.3), we obtain
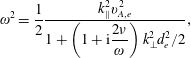 $$\begin{eqnarray}\unicode[STIX]{x1D714}^{2}=\frac{1}{2}\frac{k_{\Vert }^{2}v_{A,e}^{2}}{\displaystyle 1+\left(1+\text{i}\frac{2\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D714}}\right)k_{\bot }^{2}d_{e}^{2}/2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}^{2}=\frac{1}{2}\frac{k_{\Vert }^{2}v_{A,e}^{2}}{\displaystyle 1+\left(1+\text{i}\frac{2\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D714}}\right)k_{\bot }^{2}d_{e}^{2}/2},\end{eqnarray}$$
where we are taking the limit
Thus, we find no drift wave, a result also obtained by Helander (Reference Helander2014). In the ‘collisionless’ regime (
![]() $\unicode[STIX]{x1D714}\gg \unicode[STIX]{x1D708}$
) we find the dispersive waves
$\unicode[STIX]{x1D714}\gg \unicode[STIX]{x1D708}$
) we find the dispersive waves
which, at long wavelengths, becomes a shear Alfvén wave,
where the factor of
![]() $2$
in the denominator stems from the unconventional definition of
$2$
in the denominator stems from the unconventional definition of
![]() $v_{A}$
after (2.10), which only involved half the density.
$v_{A}$
after (2.10), which only involved half the density.
In the presence of collisions, electron thermal conduction induces a damping at short wavelengths
Perhaps not surprisingly, (3.8) defines the semi-collisional scale introduced by Drake & Lee (Reference Drake and Lee1977).
Had we retained the Debye length instead of the Larmor radius in (2.5) (
![]() $\unicode[STIX]{x1D70C}_{e}^{2}\rightarrow \unicode[STIX]{x1D706}_{D}^{2}$
), we would have found two waves travelling at the speed of light, which we prefer not to allow for, because the displacement current has been neglected in Ampère’s law (2.9). This would have been true also in the isothermal limit (
$\unicode[STIX]{x1D70C}_{e}^{2}\rightarrow \unicode[STIX]{x1D706}_{D}^{2}$
), we would have found two waves travelling at the speed of light, which we prefer not to allow for, because the displacement current has been neglected in Ampère’s law (2.9). This would have been true also in the isothermal limit (
![]() $\unicode[STIX]{x1D6FF}T_{\Vert }=0$
). Then, (3.4) would have been
$\unicode[STIX]{x1D6FF}T_{\Vert }=0$
). Then, (3.4) would have been
which, again, cannot be accepted. Had one retained the whole hierarchy of moments coupled to (2.11), valid for arbitrary collisionality, they would still have entered the dispersion relation via the
![]() $k_{\bot }^{2}\unicode[STIX]{x1D706}_{D}^{2}$
term and yielded a wave travelling at the speed of light. We conclude that the collisionless electromagnetic limit must be at least Lorentz–Poincaré invariant. As already anticipated, the reason is more apparent if one ponders the consequences of allowing the electrostatic potential to vary on the Debye scale, while letting the current vary on the inertial scale,
$k_{\bot }^{2}\unicode[STIX]{x1D706}_{D}^{2}$
term and yielded a wave travelling at the speed of light. We conclude that the collisionless electromagnetic limit must be at least Lorentz–Poincaré invariant. As already anticipated, the reason is more apparent if one ponders the consequences of allowing the electrostatic potential to vary on the Debye scale, while letting the current vary on the inertial scale,
![]() $d_{e}$
. This implies
$d_{e}$
. This implies
which demands a relativistic description. An electromagnetic gyrokinetic theory that retains Larmor radius effects seems to suffer from a similar problem, since in this case
where
![]() $\unicode[STIX]{x1D70C}_{e}$
is the Larmor radius and
$\unicode[STIX]{x1D70C}_{e}$
is the Larmor radius and
![]() $v_{A,e}$
the Alfvén speed. However, while (3.10) is a condition on the kinetic energy of particles, which can be met in extreme conditions, (3.11) is simply stating that Alfvén waves must be allowed to travel at the speed of light. This is a perfectly acceptable physical requirement provided Maxwell’s equations are kept consistent with a covariant description, therefore including the displacement current in Ampère’s law. We must stress that all frequencies must then be taken to be much smaller than the cyclotron frequency, as required by a gyrokinetic theory. Some of these aspects have also been pointed out by a recent work of Stenson et al. (Reference Stenson, Horn-Stanja, Stoneking and Pedersen2017).
$v_{A,e}$
the Alfvén speed. However, while (3.10) is a condition on the kinetic energy of particles, which can be met in extreme conditions, (3.11) is simply stating that Alfvén waves must be allowed to travel at the speed of light. This is a perfectly acceptable physical requirement provided Maxwell’s equations are kept consistent with a covariant description, therefore including the displacement current in Ampère’s law. We must stress that all frequencies must then be taken to be much smaller than the cyclotron frequency, as required by a gyrokinetic theory. Some of these aspects have also been pointed out by a recent work of Stenson et al. (Reference Stenson, Horn-Stanja, Stoneking and Pedersen2017).
4 Alfvén waves
We could insist on keeping a finite Debye length in our electromagnetic equations. In this case, the displacement current in Ampère’s law should be retained, since it plays a crucial role in establishing charge neutrality and generating Langmuir waves. In this case our model equations will indeed be suitable for a covariant formulation. Thus, we consider a modified version of (2.3b) of Helander & Connor (Reference Helander and Connor2016) where the displacement current has been added
This replaces (2.9). Poisson’s law, since we are using the radiation (Coulomb) gauge,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{A}=0$
, does not change. Let us first show that the collisionless isothermal response derived using our (2.2) and (2.8) gives the same result as (3.7) of Helander & Connor (Reference Helander and Connor2016) for
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{A}=0$
, does not change. Let us first show that the collisionless isothermal response derived using our (2.2) and (2.8) gives the same result as (3.7) of Helander & Connor (Reference Helander and Connor2016) for
![]() $d_{e}^{-1}\ll k_{\bot }\ll \unicode[STIX]{x1D706}_{D}^{-1}$
, which is the regime of interest of the future APEX experiment (Pedersen et al.
Reference Pedersen, Danielson, Hugenschmidt, Marx, Sarasola, Schauer, Schweikhard, Surko and Winkler2012; Saitoh et al.
Reference Saitoh, Pedersen, Hergenhahn, Stenson, Paschkowski and Hugenschmidt2014). Now quasi-neutrality (2.5) (with
$d_{e}^{-1}\ll k_{\bot }\ll \unicode[STIX]{x1D706}_{D}^{-1}$
, which is the regime of interest of the future APEX experiment (Pedersen et al.
Reference Pedersen, Danielson, Hugenschmidt, Marx, Sarasola, Schauer, Schweikhard, Surko and Winkler2012; Saitoh et al.
Reference Saitoh, Pedersen, Hergenhahn, Stenson, Paschkowski and Hugenschmidt2014). Now quasi-neutrality (2.5) (with
![]() $\unicode[STIX]{x1D70C}_{e}\rightarrow \sqrt{2}\unicode[STIX]{x1D706}_{D}$
) and Ohm’s law (2.8) (with
$\unicode[STIX]{x1D70C}_{e}\rightarrow \sqrt{2}\unicode[STIX]{x1D706}_{D}$
) and Ohm’s law (2.8) (with
![]() $\unicode[STIX]{x1D708}\rightarrow 0$
) become
$\unicode[STIX]{x1D708}\rightarrow 0$
) become
and
For
![]() $\unicode[STIX]{x1D706}_{D}^{-1}\gg k_{\bot }\gg d_{e}^{-1}$
, when
$\unicode[STIX]{x1D706}_{D}^{-1}\gg k_{\bot }\gg d_{e}^{-1}$
, when
![]() $\unicode[STIX]{x1D706}_{D}\ll d_{e},$
we obtain a dispersive Langmuir wave
$\unicode[STIX]{x1D706}_{D}\ll d_{e},$
we obtain a dispersive Langmuir wave
where
![]() $\unicode[STIX]{x1D714}_{pl}$
is the plasma frequency. Equation (4.4) indeed coincides with the high-frequency limit of the electrostatic wave that solves (3.7) of Helander & Connor (Reference Helander and Connor2016). For the range of wavelengths of interest, the displacement current does not seem to have an effect. A full kinetic treatment would damp this wave (See Mishchenko et al.
Reference Mishchenko, Zocco, Helander and Könies2017).
$\unicode[STIX]{x1D714}_{pl}$
is the plasma frequency. Equation (4.4) indeed coincides with the high-frequency limit of the electrostatic wave that solves (3.7) of Helander & Connor (Reference Helander and Connor2016). For the range of wavelengths of interest, the displacement current does not seem to have an effect. A full kinetic treatment would damp this wave (See Mishchenko et al.
Reference Mishchenko, Zocco, Helander and Könies2017).
We now turn our attention to Alfvénic perturbations, which should connect to the wave just found in the electrostatic limit,
![]() $\unicode[STIX]{x1D706}_{D}\gg \unicode[STIX]{x1D70C}_{e}$
. We rewrite Poisson’s law and Ampère’s law for the collisionless drift-kinetic case ((3.3) and (3.4) of Helander & Connor Reference Helander and Connor2016)
$\unicode[STIX]{x1D706}_{D}\gg \unicode[STIX]{x1D70C}_{e}$
. We rewrite Poisson’s law and Ampère’s law for the collisionless drift-kinetic case ((3.3) and (3.4) of Helander & Connor Reference Helander and Connor2016)
where the coefficients were evaluated by Helander & Connor (Reference Helander and Connor2016):
![]() $a_{11}=1+\unicode[STIX]{x1D706}_{D}^{2}k_{\bot }^{2}+\unicode[STIX]{x1D701}Z(\unicode[STIX]{x1D701})$
,
$a_{11}=1+\unicode[STIX]{x1D706}_{D}^{2}k_{\bot }^{2}+\unicode[STIX]{x1D701}Z(\unicode[STIX]{x1D701})$
,
![]() $a_{22}=-\unicode[STIX]{x1D701}^{2}\left[1+\unicode[STIX]{x1D701}Z(\unicode[STIX]{x1D701})\right]+k_{\bot }^{2}d_{e}^{2},$
$a_{22}=-\unicode[STIX]{x1D701}^{2}\left[1+\unicode[STIX]{x1D701}Z(\unicode[STIX]{x1D701})\right]+k_{\bot }^{2}d_{e}^{2},$
![]() $a_{21}=-a_{12}=\unicode[STIX]{x1D701}\left[1+\unicode[STIX]{x1D701}Z(\unicode[STIX]{x1D701})\right]$
, with
$a_{21}=-a_{12}=\unicode[STIX]{x1D701}\left[1+\unicode[STIX]{x1D701}Z(\unicode[STIX]{x1D701})\right]$
, with
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D714}/(k_{\Vert }v_{\text{the}})$
and
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D714}/(k_{\Vert }v_{\text{the}})$
and
![]() $Z$
is the plasma dispersion function (Fried, Hendrick & McCune Reference Fried, Hendrick and McCune1968). When (4.1) is used instead of (2.9), we have that
$Z$
is the plasma dispersion function (Fried, Hendrick & McCune Reference Fried, Hendrick and McCune1968). When (4.1) is used instead of (2.9), we have that
and
For Alfvénic perturbations we must expand the plasma dispersion function for large arguments,Footnote 3 since
Setting to zero the determinant of the matrix of (4.5), for
![]() $k_{\bot }\unicode[STIX]{x1D706}_{D}\sim k_{\bot }\unicode[STIX]{x1D70C}_{e}\sim \sqrt{\unicode[STIX]{x1D6FD}}\ll 1,$
then gives
$k_{\bot }\unicode[STIX]{x1D706}_{D}\sim k_{\bot }\unicode[STIX]{x1D70C}_{e}\sim \sqrt{\unicode[STIX]{x1D6FD}}\ll 1,$
then gives
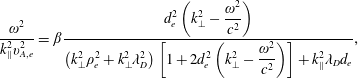 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D714}^{2}}{k_{\Vert }^{2}v_{A,e}^{2}}=\unicode[STIX]{x1D6FD}\frac{\displaystyle d_{e}^{2}\left(k_{\bot }^{2}-\frac{\unicode[STIX]{x1D714}^{2}}{c^{2}}\right)}{\displaystyle \left(k_{\bot }^{2}\unicode[STIX]{x1D70C}_{e}^{2}+k_{\bot }^{2}\unicode[STIX]{x1D706}_{D}^{2}\right)\left[1+2d_{e}^{2}\left(k_{\bot }^{2}-\frac{\unicode[STIX]{x1D714}^{2}}{c^{2}}\right)\right]+k_{\Vert }^{2}\unicode[STIX]{x1D706}_{D}d_{e}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D714}^{2}}{k_{\Vert }^{2}v_{A,e}^{2}}=\unicode[STIX]{x1D6FD}\frac{\displaystyle d_{e}^{2}\left(k_{\bot }^{2}-\frac{\unicode[STIX]{x1D714}^{2}}{c^{2}}\right)}{\displaystyle \left(k_{\bot }^{2}\unicode[STIX]{x1D70C}_{e}^{2}+k_{\bot }^{2}\unicode[STIX]{x1D706}_{D}^{2}\right)\left[1+2d_{e}^{2}\left(k_{\bot }^{2}-\frac{\unicode[STIX]{x1D714}^{2}}{c^{2}}\right)\right]+k_{\Vert }^{2}\unicode[STIX]{x1D706}_{D}d_{e}},\end{eqnarray}$$
which is a kinetically modified Alfvén wave. Since
we have
When
![]() $(k_{\Vert }^{2}/k_{\bot }^{2})v_{A,e}/c\equiv \unicode[STIX]{x1D716}_{GK}^{2}v_{A,e}/c\gg \sqrt{\unicode[STIX]{x1D6FD}},$
for
$(k_{\Vert }^{2}/k_{\bot }^{2})v_{A,e}/c\equiv \unicode[STIX]{x1D716}_{GK}^{2}v_{A,e}/c\gg \sqrt{\unicode[STIX]{x1D6FD}},$
for
![]() $\unicode[STIX]{x1D70C}_{e}\sim \unicode[STIX]{x1D706}_{D}$
, the
$\unicode[STIX]{x1D70C}_{e}\sim \unicode[STIX]{x1D706}_{D}$
, the
![]() $k_{\Vert }^{2}\unicode[STIX]{x1D706}_{D}d_{e}$
in the denominator is dominant, and we have
$k_{\Vert }^{2}\unicode[STIX]{x1D706}_{D}d_{e}$
in the denominator is dominant, and we have
However, (4.12) was derived for
![]() $\unicode[STIX]{x1D6FD}^{1/4}\ll \unicode[STIX]{x1D716}_{GK}.$
Since, in gyrokinetics,
$\unicode[STIX]{x1D6FD}^{1/4}\ll \unicode[STIX]{x1D716}_{GK}.$
Since, in gyrokinetics,
![]() $\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{c}\sim \unicode[STIX]{x1D716}_{GK}$
is necessary for wave propagation, we are effectively considering a subsidiary electrostatic limit in which the wave in (4.12) does not propagate. When
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{c}\sim \unicode[STIX]{x1D716}_{GK}$
is necessary for wave propagation, we are effectively considering a subsidiary electrostatic limit in which the wave in (4.12) does not propagate. When
![]() $\unicode[STIX]{x1D716}_{GK}^{2}v_{A,e}/c\ll \sqrt{\unicode[STIX]{x1D6FD}}$
, the same term is negligible, and we have
$\unicode[STIX]{x1D716}_{GK}^{2}v_{A,e}/c\ll \sqrt{\unicode[STIX]{x1D6FD}}$
, the same term is negligible, and we have
which, in the subsidiary
![]() $d_{e}^{2}k_{\bot }^{2}\rightarrow \infty$
limit, for
$d_{e}^{2}k_{\bot }^{2}\rightarrow \infty$
limit, for
![]() $\unicode[STIX]{x1D706}_{D}\gg \unicode[STIX]{x1D70C}_{e}$
gives
$\unicode[STIX]{x1D706}_{D}\gg \unicode[STIX]{x1D70C}_{e}$
gives
This result agrees with (4.4) and with the high-frequency solution of (3.7) of Helander & Connor (Reference Helander and Connor2016). Our results suggest that, in a low-beta gyrokinetic theory, the displacement current can be neglected only if
5 Tearing instability
We now consider an equilibrium magnetic field whose lines can reconnect. This is achieved if we add to the constant guide field a small component,
![]() $\boldsymbol{B}_{0}\rightarrow B_{0}\boldsymbol{e}_{z}+B_{y}(x)\boldsymbol{e}_{y},$
and
$\boldsymbol{B}_{0}\rightarrow B_{0}\boldsymbol{e}_{z}+B_{y}(x)\boldsymbol{e}_{y},$
and
![]() $B_{y}$
changes sign for some
$B_{y}$
changes sign for some
![]() $x=x_{r}.$
The characteristic scale for the variation of the reconnecting field,
$x=x_{r}.$
The characteristic scale for the variation of the reconnecting field,
![]() $B_{y},$
is the shear length,
$B_{y},$
is the shear length,
![]() $L_{s}.$
At the location where reconnection occurs,
$L_{s}.$
At the location where reconnection occurs,
![]() $x\approx x_{r}$
, for
$x\approx x_{r}$
, for
![]() $x_{r}=0$
, we have
$x_{r}=0$
, we have
Poisson’s law and Ohm’s law become, respectively
and
which can easily be cast in the form presented in Zocco & Schekochihin (Reference Zocco and Schekochihin2011). Now, we have
and
where
![]() $\unicode[STIX]{x1D6FF}=L_{s}\unicode[STIX]{x1D714}/(k_{y}v_{\text{the}})$
,
$\unicode[STIX]{x1D6FF}=L_{s}\unicode[STIX]{x1D714}/(k_{y}v_{\text{the}})$
,
![]() $\tilde{\unicode[STIX]{x1D711}}=(c/v_{\text{the}})\unicode[STIX]{x1D711},$
and
$\tilde{\unicode[STIX]{x1D711}}=(c/v_{\text{the}})\unicode[STIX]{x1D711},$
and
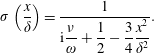 $$\begin{eqnarray}\unicode[STIX]{x1D70E}\left(\frac{x}{\unicode[STIX]{x1D6FF}}\right)=\frac{1}{\displaystyle \text{i}\frac{\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D714}}+{\displaystyle \frac{1}{2}}-{\displaystyle \frac{3}{4}}{\displaystyle \frac{x^{2}}{\unicode[STIX]{x1D6FF}^{2}}}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}\left(\frac{x}{\unicode[STIX]{x1D6FF}}\right)=\frac{1}{\displaystyle \text{i}\frac{\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D714}}+{\displaystyle \frac{1}{2}}-{\displaystyle \frac{3}{4}}{\displaystyle \frac{x^{2}}{\unicode[STIX]{x1D6FF}^{2}}}}.\end{eqnarray}$$
Since we are always assuming
![]() $\unicode[STIX]{x1D70C}_{e}\ll d_{e}\sim \unicode[STIX]{x1D6FF}$
, we are effectively in a one-fluid limit, the ultralow beta discussed in Zocco & Schekochihin (Reference Zocco and Schekochihin2011). We report on the collisionless case, the results apply to the collisional case in a straightforward manner. The analysis is known but we reproduce some key steps for the sake of clarity. One can introduce the function
$\unicode[STIX]{x1D70C}_{e}\ll d_{e}\sim \unicode[STIX]{x1D6FF}$
, we are effectively in a one-fluid limit, the ultralow beta discussed in Zocco & Schekochihin (Reference Zocco and Schekochihin2011). We report on the collisionless case, the results apply to the collisional case in a straightforward manner. The analysis is known but we reproduce some key steps for the sake of clarity. One can introduce the function
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D709}A_{\Vert }^{\prime }(\unicode[STIX]{x1D709})-A_{\Vert }(\unicode[STIX]{x1D709}),$
where
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D709}A_{\Vert }^{\prime }(\unicode[STIX]{x1D709})-A_{\Vert }(\unicode[STIX]{x1D709}),$
where
![]() $\unicode[STIX]{x1D709}=x/\unicode[STIX]{x1D6FF}_{\text{in}}$
, and
$\unicode[STIX]{x1D709}=x/\unicode[STIX]{x1D6FF}_{\text{in}}$
, and
![]() $\unicode[STIX]{x1D6FF}_{\text{in}}=\sqrt{4\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}_{e}^{2}},$
to obtain one equation for
$\unicode[STIX]{x1D6FF}_{\text{in}}=\sqrt{4\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}_{e}^{2}},$
to obtain one equation for
![]() $\tilde{\unicode[STIX]{x1D712}}=-1+\unicode[STIX]{x1D712}/\unicode[STIX]{x1D712}_{0},$
$\tilde{\unicode[STIX]{x1D712}}=-1+\unicode[STIX]{x1D712}/\unicode[STIX]{x1D712}_{0},$
where
![]() $\unicode[STIX]{x1D706}^{2}=4\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}_{e}/d_{e}^{2}$
,
$\unicode[STIX]{x1D706}^{2}=4\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}_{e}/d_{e}^{2}$
,
![]() $\unicode[STIX]{x1D6FC}=\sqrt{2\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D6FF}},$
$\unicode[STIX]{x1D6FC}=\sqrt{2\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D6FF}},$
![]() $G=(\unicode[STIX]{x1D6FF}^{2}/x^{2})(\unicode[STIX]{x1D70E}^{-1}-2)$
, the ‘prime’ is the derivative with respect to
$G=(\unicode[STIX]{x1D6FF}^{2}/x^{2})(\unicode[STIX]{x1D70E}^{-1}-2)$
, the ‘prime’ is the derivative with respect to
![]() $\unicode[STIX]{x1D709}$
, and
$\unicode[STIX]{x1D709}$
, and
![]() $\unicode[STIX]{x1D712}_{0}$
is a constant of integration. The dispersion relation for the rescaled eigenvalue
$\unicode[STIX]{x1D712}_{0}$
is a constant of integration. The dispersion relation for the rescaled eigenvalue
![]() $\unicode[STIX]{x1D706}^{2}$
is then
$\unicode[STIX]{x1D706}^{2}$
is then
where
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
is the parameter that measures the discontinuity of the derivative of
$\unicode[STIX]{x1D6E5}^{\prime }$
is the parameter that measures the discontinuity of the derivative of
![]() $A_{\Vert }^{\text{MHD}}$
across the reconnection layer, and
$A_{\Vert }^{\text{MHD}}$
across the reconnection layer, and
![]() $A_{\Vert }^{\text{MHD}}$
is the stable solution found in the ideal magnetohydrodynamics (MHD) region,
$A_{\Vert }^{\text{MHD}}$
is the stable solution found in the ideal magnetohydrodynamics (MHD) region,
![]() $x\rightarrow \infty$
so that
$x\rightarrow \infty$
so that
![]() $E_{\Vert }\rightarrow 0$
(Furth, Killeen & Rosenbluth Reference Furth, Killeen and Rosenbluth1963). As already pointed out in Zocco & Schekochihin (Reference Zocco and Schekochihin2011), there is no need to solve (5.7) exactly to predict how the eigenvalue
$E_{\Vert }\rightarrow 0$
(Furth, Killeen & Rosenbluth Reference Furth, Killeen and Rosenbluth1963). As already pointed out in Zocco & Schekochihin (Reference Zocco and Schekochihin2011), there is no need to solve (5.7) exactly to predict how the eigenvalue
![]() $\unicode[STIX]{x1D706}^{2}$
, hence the reconnection rate
$\unicode[STIX]{x1D706}^{2}$
, hence the reconnection rate
![]() $\unicode[STIX]{x1D6FE}$
, scales with physical quantities. For
$\unicode[STIX]{x1D6FE}$
, scales with physical quantities. For
![]() $\unicode[STIX]{x1D70C}_{e}\ll \unicode[STIX]{x1D6FF}$
, from (5.7), we have
$\unicode[STIX]{x1D70C}_{e}\ll \unicode[STIX]{x1D6FF}$
, from (5.7), we have
![]() $\tilde{\unicode[STIX]{x1D712}}^{\prime }/\unicode[STIX]{x1D709}\sim \unicode[STIX]{x1D706}^{2}.$
Since
$\tilde{\unicode[STIX]{x1D712}}^{\prime }/\unicode[STIX]{x1D709}\sim \unicode[STIX]{x1D706}^{2}.$
Since
![]() $\unicode[STIX]{x1D709}\sim 1$
, then
$\unicode[STIX]{x1D709}\sim 1$
, then
![]() $\int _{0}^{\infty }(\tilde{\unicode[STIX]{x1D712}}^{\prime }/\unicode[STIX]{x1D709})\sim \unicode[STIX]{x1D706}^{2}$
, which implies
$\int _{0}^{\infty }(\tilde{\unicode[STIX]{x1D712}}^{\prime }/\unicode[STIX]{x1D709})\sim \unicode[STIX]{x1D706}^{2}$
, which implies
where
![]() $\unicode[STIX]{x1D6FE}=\text{Im}[\unicode[STIX]{x1D714}]$
. This is the equivalent of the collisionless result found for electron–ion plasmas by Drake & Lee (Reference Drake and Lee1977), where the Alfvén speed is based on the electron mass. The collisional counterpart is recovered by replacing
$\unicode[STIX]{x1D6FE}=\text{Im}[\unicode[STIX]{x1D714}]$
. This is the equivalent of the collisionless result found for electron–ion plasmas by Drake & Lee (Reference Drake and Lee1977), where the Alfvén speed is based on the electron mass. The collisional counterpart is recovered by replacing
![]() $d_{e}\rightarrow \sqrt{\unicode[STIX]{x1D708}d_{e}^{2}/\unicode[STIX]{x1D6FE},}$
to obtain the traditional result of Furth et al. (Reference Furth, Killeen and Rosenbluth1963) (but based on the electron Alfvén speed). When
$d_{e}\rightarrow \sqrt{\unicode[STIX]{x1D708}d_{e}^{2}/\unicode[STIX]{x1D6FE},}$
to obtain the traditional result of Furth et al. (Reference Furth, Killeen and Rosenbluth1963) (but based on the electron Alfvén speed). When
![]() $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\gg 1,$
the current is limited by the scale
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\gg 1,$
the current is limited by the scale
![]() $\unicode[STIX]{x1D6FF}_{\text{in}}$
, so that
$\unicode[STIX]{x1D6FF}_{\text{in}}$
, so that
![]() $\unicode[STIX]{x2202}_{x}^{2}A_{\text{}\Vert \text{}}\sim A_{\Vert }/\unicode[STIX]{x1D6FF}_{\text{in}}^{2}$
. Then, one replaces
$\unicode[STIX]{x2202}_{x}^{2}A_{\text{}\Vert \text{}}\sim A_{\Vert }/\unicode[STIX]{x1D6FF}_{\text{in}}^{2}$
. Then, one replaces
![]() $\unicode[STIX]{x1D6E5}^{\prime }\rightarrow \unicode[STIX]{x1D6FF}_{\text{in}}^{-1}$
in (5.8) to obtain
$\unicode[STIX]{x1D6E5}^{\prime }\rightarrow \unicode[STIX]{x1D6FF}_{\text{in}}^{-1}$
in (5.8) to obtain
![]() $\unicode[STIX]{x1D706}^{2}\sim 1$
, which yields (Basu & Coppi Reference Basu and Coppi1981)
$\unicode[STIX]{x1D706}^{2}\sim 1$
, which yields (Basu & Coppi Reference Basu and Coppi1981)
which gives the scaling
![]() $\unicode[STIX]{x1D6FE}\sim (k_{y}v_{A,e})^{2/3}(\unicode[STIX]{x1D708}d_{e}^{2}/L_{s}^{2})^{1/3}$
of Coppi et al. (Reference Coppi, Galvão, Pellat, Rosenbluth and Rutherford1976) in the collisional limit.
$\unicode[STIX]{x1D6FE}\sim (k_{y}v_{A,e})^{2/3}(\unicode[STIX]{x1D708}d_{e}^{2}/L_{s}^{2})^{1/3}$
of Coppi et al. (Reference Coppi, Galvão, Pellat, Rosenbluth and Rutherford1976) in the collisional limit.
6 Improved nonlinear model
The inclusion of the Larmor scale in (2.5), instead of the Debye length, allowed us to avoid a covariant treatment. The use of the drift-kinetic model of Zocco & Schekochihin (Reference Zocco and Schekochihin2011) helped us, but we did not exploit its full nonlinear potential yet. For this, fields amplitudes must be ordered more carefully. Equation (2.1), in fact, is nothing more than a drift-kinetic equation that one could have considered regardless of the results of Zocco & Schekochihin (Reference Zocco and Schekochihin2011). If one wants to consider the nonlinear
![]() $\boldsymbol{E}\times \boldsymbol{B}$
frequency
$\boldsymbol{E}\times \boldsymbol{B}$
frequency
![]() $\unicode[STIX]{x1D714}\sim (c/B_{0})k^{2}\unicode[STIX]{x1D711}$
and the streaming term, after using (2.5), we find that
$\unicode[STIX]{x1D714}\sim (c/B_{0})k^{2}\unicode[STIX]{x1D711}$
and the streaming term, after using (2.5), we find that
So, a nonlinear electromagnetic gyrokinetic theory that retains inertial effects must be developed to first order in a small Larmor radius expansion. This also implies that magnetic compressibility now must be retained to first order, since
Perpendicular magnetic fluctuations are ordered by balancing the electrostatic and the vector potential amplitudes of the gyrokinetic potential
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D711}-(v_{\Vert }/c)A_{\Vert },$
then
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D711}-(v_{\Vert }/c)A_{\Vert },$
then
where
![]() $u_{\bot }\sim ck_{\bot }\unicode[STIX]{x1D711}/B_{0}.$
In many relevant situations, the spatial variation of all quantities along the exact magnetic field is required, then
$u_{\bot }\sim ck_{\bot }\unicode[STIX]{x1D711}/B_{0}.$
In many relevant situations, the spatial variation of all quantities along the exact magnetic field is required, then
![]() $k_{\bot }\unicode[STIX]{x1D6FF}B_{\bot }\sim k_{\Vert }B_{0},$
which implies
$k_{\bot }\unicode[STIX]{x1D6FF}B_{\bot }\sim k_{\Vert }B_{0},$
which implies
and is naturally consistent with our fundamental ordering
![]() $k_{\bot }d_{e}\sim 1$
. We therefore use
$k_{\bot }d_{e}\sim 1$
. We therefore use
which is different from what the continuity equation (2.2) would have implied
Having completed the amplitude orderings, in order to obtain fluid-like equations, one can separate the first two moments of the perturbed distribution function, but considering first-order terms
 $$\begin{eqnarray}\displaystyle h_{e^{\mp }} & = & \displaystyle \displaystyle \left[\frac{e^{\mp }\left(\unicode[STIX]{x1D711}^{(0)}+\unicode[STIX]{x1D711}^{(1)}\right)}{T_{0}}+\left(\frac{\unicode[STIX]{x1D6FF}n_{e^{\mp }}^{(0)}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}n_{e^{\mp }}^{(1)}}{n_{0}}\right)+2\frac{v_{\Vert }\left(u_{\Vert e^{\mp }}^{(0)}+u_{\Vert e^{\mp }}^{(1)}\right)}{v_{\text{the}}^{2}}\right]F_{0}\nonumber\\ \displaystyle & & \displaystyle +\displaystyle \,g^{(0)}+g^{(1)}+O(k_{\bot }^{4}\unicode[STIX]{x1D70C}_{e}^{4}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h_{e^{\mp }} & = & \displaystyle \displaystyle \left[\frac{e^{\mp }\left(\unicode[STIX]{x1D711}^{(0)}+\unicode[STIX]{x1D711}^{(1)}\right)}{T_{0}}+\left(\frac{\unicode[STIX]{x1D6FF}n_{e^{\mp }}^{(0)}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}n_{e^{\mp }}^{(1)}}{n_{0}}\right)+2\frac{v_{\Vert }\left(u_{\Vert e^{\mp }}^{(0)}+u_{\Vert e^{\mp }}^{(1)}\right)}{v_{\text{the}}^{2}}\right]F_{0}\nonumber\\ \displaystyle & & \displaystyle +\displaystyle \,g^{(0)}+g^{(1)}+O(k_{\bot }^{4}\unicode[STIX]{x1D70C}_{e}^{4}),\end{eqnarray}$$
where
![]() $\int \,\text{d}^{3}\boldsymbol{v}g=\int \,\text{d}^{3}\boldsymbol{v}v_{\Vert }g\equiv 0$
to all orders in
$\int \,\text{d}^{3}\boldsymbol{v}g=\int \,\text{d}^{3}\boldsymbol{v}v_{\Vert }g\equiv 0$
to all orders in
![]() $k_{\bot }^{2}\unicode[STIX]{x1D70C}_{e}^{2}\sim \unicode[STIX]{x1D6FD}\ll 1.$
When magnetic compressibility is retained, the gyrokinetic potential on the right-hand side of (2.1) becomes
$k_{\bot }^{2}\unicode[STIX]{x1D70C}_{e}^{2}\sim \unicode[STIX]{x1D6FD}\ll 1.$
When magnetic compressibility is retained, the gyrokinetic potential on the right-hand side of (2.1) becomes
where
We notice that, due to its parity in velocity space, the new
![]() $\unicode[STIX]{x1D6FF}B_{\Vert }$
term enters in the equation for density fluctuations. Let us evaluate the density moment of (2.1) after using (6.8), and subtract the two results obtained, one for each species. To leading order we have
$\unicode[STIX]{x1D6FF}B_{\Vert }$
term enters in the equation for density fluctuations. Let us evaluate the density moment of (2.1) after using (6.8), and subtract the two results obtained, one for each species. To leading order we have
To next order, (2.4) gives
which now proves our previous statement on the validity of (2.5), since here
are the perpendicular temperature fluctuations. As usual, they drive parallel magnetic compressional perturbations
which have to be taken into account in the first-order continuity equation. The electrostatic potential is determined by the difference of the first-order density fluctuations of the two species. We then subtract the two first-order continuity equations, and obtain the generalised vorticity equation
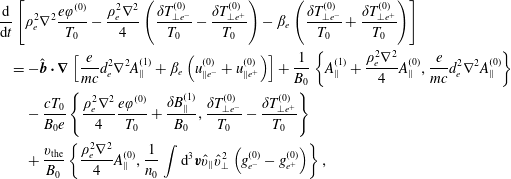 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\left[\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}\frac{e\unicode[STIX]{x1D711}^{(0)}}{T_{0}}-\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\left(\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{-}}^{(0)}}{T_{0}}-\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{+}}^{(0)}}{T_{0}}\right)-\unicode[STIX]{x1D6FD}_{e}\left(\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{-}}^{(0)}}{T_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{+}}^{(0)}}{T_{0}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =-\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{e}{mc}d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}A_{\Vert }^{(1)}+\unicode[STIX]{x1D6FD}_{e}\left(u_{\Vert e^{-}}^{(0)}+u_{\Vert e^{+}}^{(0)}\right)\right]+\frac{1}{B_{0}}\left\{A_{\Vert }^{(1)}+\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}A_{\Vert }^{(0)},\frac{e}{mc}d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}A_{\Vert }^{(0)}\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad -\,\frac{cT_{0}}{B_{0}e}\left\{\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\frac{e\unicode[STIX]{x1D711}^{(0)}}{T_{0}}+\frac{\unicode[STIX]{x1D6FF}B_{\Vert }^{(1)}}{B_{0}},\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{-}}^{(0)}}{T_{0}}-\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{+}}^{(0)}}{T_{0}}\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,\frac{v_{\text{the}}}{B_{0}}\left\{\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}A_{\Vert }^{(0)},\frac{1}{n_{0}}\int \text{d}^{3}\boldsymbol{v}\hat{v}_{\Vert }\hat{v}_{\bot }^{2}\left(g_{e^{-}}^{(0)}-g_{e^{+}}^{(0)}\right)\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\left[\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}\frac{e\unicode[STIX]{x1D711}^{(0)}}{T_{0}}-\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\left(\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{-}}^{(0)}}{T_{0}}-\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{+}}^{(0)}}{T_{0}}\right)-\unicode[STIX]{x1D6FD}_{e}\left(\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{-}}^{(0)}}{T_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{+}}^{(0)}}{T_{0}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =-\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{e}{mc}d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}A_{\Vert }^{(1)}+\unicode[STIX]{x1D6FD}_{e}\left(u_{\Vert e^{-}}^{(0)}+u_{\Vert e^{+}}^{(0)}\right)\right]+\frac{1}{B_{0}}\left\{A_{\Vert }^{(1)}+\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}A_{\Vert }^{(0)},\frac{e}{mc}d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}A_{\Vert }^{(0)}\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad -\,\frac{cT_{0}}{B_{0}e}\left\{\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\frac{e\unicode[STIX]{x1D711}^{(0)}}{T_{0}}+\frac{\unicode[STIX]{x1D6FF}B_{\Vert }^{(1)}}{B_{0}},\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{-}}^{(0)}}{T_{0}}-\frac{\unicode[STIX]{x1D6FF}T_{\bot e^{+}}^{(0)}}{T_{0}}\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,\frac{v_{\text{the}}}{B_{0}}\left\{\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}A_{\Vert }^{(0)},\frac{1}{n_{0}}\int \text{d}^{3}\boldsymbol{v}\hat{v}_{\Vert }\hat{v}_{\bot }^{2}\left(g_{e^{-}}^{(0)}-g_{e^{+}}^{(0)}\right)\right\},\end{eqnarray}$$
where the terms multiplying an explicit
![]() $\unicode[STIX]{x1D6FD}_{e}$
come from (6.13). We now evaluate all the terms of the right-hand side. To zeroth order, (2.8) is valid, and we have
$\unicode[STIX]{x1D6FD}_{e}$
come from (6.13). We now evaluate all the terms of the right-hand side. To zeroth order, (2.8) is valid, and we have
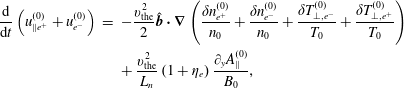 $$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\left(u_{\Vert e^{+}}^{(0)}+u_{e^{-}}^{(0)}\right) & = & \displaystyle \displaystyle -\frac{v_{\text{the}}^{2}}{2}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{\unicode[STIX]{x1D6FF}n_{e^{+}}^{(0)}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}n_{e^{-}}^{(0)}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\bot ,e^{-}}^{(0)}}{T_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\bot ,e^{+}}^{(0)}}{T_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\displaystyle \frac{v_{\text{the}}^{2}}{L_{n}}\left(1+\unicode[STIX]{x1D702}_{e}\right)\frac{\unicode[STIX]{x2202}_{y}A_{\Vert }^{(0)}}{B_{0}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\left(u_{\Vert e^{+}}^{(0)}+u_{e^{-}}^{(0)}\right) & = & \displaystyle \displaystyle -\frac{v_{\text{the}}^{2}}{2}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{\unicode[STIX]{x1D6FF}n_{e^{+}}^{(0)}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}n_{e^{-}}^{(0)}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\bot ,e^{-}}^{(0)}}{T_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\bot ,e^{+}}^{(0)}}{T_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\displaystyle \frac{v_{\text{the}}^{2}}{L_{n}}\left(1+\unicode[STIX]{x1D702}_{e}\right)\frac{\unicode[STIX]{x2202}_{y}A_{\Vert }^{(0)}}{B_{0}},\end{eqnarray}$$
where we see that diamagnetic effects do not cancel. The sum
![]() $\unicode[STIX]{x1D6FF}n_{e^{+}}^{(0)}+\unicode[STIX]{x1D6FF}n_{e^{-}}^{(0)}$
can be evaluated by using the zeroth-order continuity equations
$\unicode[STIX]{x1D6FF}n_{e^{+}}^{(0)}+\unicode[STIX]{x1D6FF}n_{e^{-}}^{(0)}$
can be evaluated by using the zeroth-order continuity equations
To first order, only the difference
![]() $u_{\Vert e^{-}}^{(1)}-u_{\Vert e^{+}}^{(1)}=(e/mc)d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}A_{\Vert }^{(1)}$
enters the vorticity equation, thus we obtain
$u_{\Vert e^{-}}^{(1)}-u_{\Vert e^{+}}^{(1)}=(e/mc)d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}A_{\Vert }^{(1)}$
enters the vorticity equation, thus we obtain
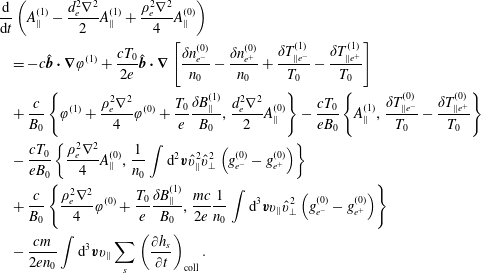 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\left(A_{\Vert }^{(1)}-\frac{d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{2}A_{\Vert }^{(1)}+\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}A_{\Vert }^{(0)}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =-c\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}^{(1)}+\frac{cT_{0}}{2e}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{\unicode[STIX]{x1D6FF}n_{e^{-}}^{(0)}}{n_{0}}-\frac{\unicode[STIX]{x1D6FF}n_{e^{+}}^{(0)}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{-}}^{(1)}}{T_{0}}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{+}}^{(1)}}{T_{0}}\right]\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\frac{c}{B_{0}}\left\{\unicode[STIX]{x1D711}^{(1)}+\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D711}^{(0)}+\frac{T_{0}}{e}\frac{\unicode[STIX]{x1D6FF}B_{\Vert }^{(1)}}{B_{0}},\frac{d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{2}A_{\Vert }^{(0)}\right\}-\frac{cT_{0}}{eB_{0}}\left\{A_{\Vert }^{(1)},\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{-}}^{(0)}}{T_{0}}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{+}}^{(0)}}{T_{0}}\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\frac{cT_{0}}{eB_{0}}\left\{\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}A_{\Vert }^{(0)},\frac{1}{n_{0}}\int \text{d}^{2}\boldsymbol{v}\hat{v}_{\Vert }^{2}\hat{v}_{\bot }^{2}\left(g_{e^{-}}^{(0)}-g_{e^{+}}^{(0)}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\frac{c}{B_{0}}\left\{\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D711}^{(0)}+\frac{T_{0}}{e}\frac{\unicode[STIX]{x1D6FF}B_{\Vert }^{(1)}}{B_{0}},\frac{mc}{2e}\frac{1}{n_{0}}\int \text{d}^{3}\boldsymbol{v}v_{\Vert }\hat{v}_{\bot }^{2}\left(g_{e^{-}}^{(0)}-g_{e^{+}}^{(0)}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\frac{cm}{2en_{0}}\int \text{d}^{3}\boldsymbol{v}v_{\Vert }\mathop{\sum }_{s}\left(\frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}t}\right)_{\text{coll}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\left(A_{\Vert }^{(1)}-\frac{d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{2}A_{\Vert }^{(1)}+\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}A_{\Vert }^{(0)}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =-c\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}^{(1)}+\frac{cT_{0}}{2e}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{\unicode[STIX]{x1D6FF}n_{e^{-}}^{(0)}}{n_{0}}-\frac{\unicode[STIX]{x1D6FF}n_{e^{+}}^{(0)}}{n_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{-}}^{(1)}}{T_{0}}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{+}}^{(1)}}{T_{0}}\right]\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\frac{c}{B_{0}}\left\{\unicode[STIX]{x1D711}^{(1)}+\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D711}^{(0)}+\frac{T_{0}}{e}\frac{\unicode[STIX]{x1D6FF}B_{\Vert }^{(1)}}{B_{0}},\frac{d_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{2}A_{\Vert }^{(0)}\right\}-\frac{cT_{0}}{eB_{0}}\left\{A_{\Vert }^{(1)},\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{-}}^{(0)}}{T_{0}}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{+}}^{(0)}}{T_{0}}\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\frac{cT_{0}}{eB_{0}}\left\{\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}A_{\Vert }^{(0)},\frac{1}{n_{0}}\int \text{d}^{2}\boldsymbol{v}\hat{v}_{\Vert }^{2}\hat{v}_{\bot }^{2}\left(g_{e^{-}}^{(0)}-g_{e^{+}}^{(0)}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\frac{c}{B_{0}}\left\{\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D711}^{(0)}+\frac{T_{0}}{e}\frac{\unicode[STIX]{x1D6FF}B_{\Vert }^{(1)}}{B_{0}},\frac{mc}{2e}\frac{1}{n_{0}}\int \text{d}^{3}\boldsymbol{v}v_{\Vert }\hat{v}_{\bot }^{2}\left(g_{e^{-}}^{(0)}-g_{e^{+}}^{(0)}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\frac{cm}{2en_{0}}\int \text{d}^{3}\boldsymbol{v}v_{\Vert }\mathop{\sum }_{s}\left(\frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}t}\right)_{\text{coll}}.\end{eqnarray}$$
An equation for
![]() $g^{(0)}$
is derived by subtracting (2.2) and (2.8) from the gyrokinetic equation, and using (6.7). The result is
$g^{(0)}$
is derived by subtracting (2.2) and (2.8) from the gyrokinetic equation, and using (6.7). The result is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-9.60004pt}\displaystyle \frac{\text{d}}{\text{d}t}g_{e^{\mp }}^{(0)}+v_{\Vert }\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(g_{e^{\mp }}^{(0)}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}^{(0)}}{T_{0}}F_{0}\right)-C[g_{e^{\mp }}^{(0)}]\nonumber\\ \displaystyle & & \displaystyle \hspace{-9.60004pt}~\displaystyle =\left(1-2\frac{v_{\Vert }^{2}}{v_{\text{the}}^{2}}\right)\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}u_{\Vert e^{\mp }}^{(0)}F_{0}-\frac{cT_{0}}{eB_{0}}\frac{\unicode[STIX]{x2202}_{y}}{L_{T}}\left[\left(\hat{v}^{2}-\frac{3}{2}\right)\frac{e\unicode[STIX]{x1D711}^{(0)}}{T_{0}}-\left(\hat{v}^{2}-\frac{5}{2}\right)\frac{v_{\Vert }}{c}\frac{eA_{\Vert }^{(0)}}{T_{0}}\right]F_{0},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-9.60004pt}\displaystyle \frac{\text{d}}{\text{d}t}g_{e^{\mp }}^{(0)}+v_{\Vert }\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(g_{e^{\mp }}^{(0)}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{\mp }}^{(0)}}{T_{0}}F_{0}\right)-C[g_{e^{\mp }}^{(0)}]\nonumber\\ \displaystyle & & \displaystyle \hspace{-9.60004pt}~\displaystyle =\left(1-2\frac{v_{\Vert }^{2}}{v_{\text{the}}^{2}}\right)\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}u_{\Vert e^{\mp }}^{(0)}F_{0}-\frac{cT_{0}}{eB_{0}}\frac{\unicode[STIX]{x2202}_{y}}{L_{T}}\left[\left(\hat{v}^{2}-\frac{3}{2}\right)\frac{e\unicode[STIX]{x1D711}^{(0)}}{T_{0}}-\left(\hat{v}^{2}-\frac{5}{2}\right)\frac{v_{\Vert }}{c}\frac{eA_{\Vert }^{(0)}}{T_{0}}\right]F_{0},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
and
![]() $\hat{v}^{2}={\hat{v}_{\Vert }}^{2}+{\hat{v}_{\bot }}^{2}.$
Equation (6.18) is the extension of the kinetic reduced electron heating model equation (Zocco & Schekochihin Reference Zocco and Schekochihin2011) to the case of finite density and temperature gradients (Zocco et al.
Reference Zocco, Loureiro, Dickinson, Numata and Roach2015; Loureiro et al.
Reference Loureiro, Dorland, Fazendeiro, Kanekar, Mallet, Vilelas and Zocco2016). For the evolution of the fields, again, the important quantities are the difference and the sum the electron and positron equations. From the difference we obtain
$\hat{v}^{2}={\hat{v}_{\Vert }}^{2}+{\hat{v}_{\bot }}^{2}.$
Equation (6.18) is the extension of the kinetic reduced electron heating model equation (Zocco & Schekochihin Reference Zocco and Schekochihin2011) to the case of finite density and temperature gradients (Zocco et al.
Reference Zocco, Loureiro, Dickinson, Numata and Roach2015; Loureiro et al.
Reference Loureiro, Dorland, Fazendeiro, Kanekar, Mallet, Vilelas and Zocco2016). For the evolution of the fields, again, the important quantities are the difference and the sum the electron and positron equations. From the difference we obtain
where we used the fact that
![]() $\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FB}^{2}A_{\Vert }^{(0)}=0,$
and the diamagnetic cancellation. On the other hand, the sum gives
$\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FB}^{2}A_{\Vert }^{(0)}=0,$
and the diamagnetic cancellation. On the other hand, the sum gives
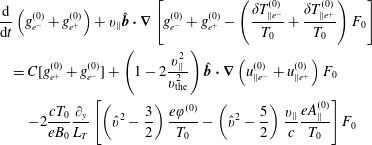 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\left(g_{e^{-}}^{(0)}+g_{e^{+}}^{(0)}\right)+v_{\Vert }\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[g_{e^{-}}^{(0)}+g_{e^{+}}^{(0)}-\left(\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{-}}^{(0)}}{T_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{+}}^{(0)}}{T_{0}}\right)F_{0}\right]\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =C[g_{e^{+}}^{(0)}+g_{e^{-}}^{(0)}]+\left(1-2\frac{v_{\Vert }^{2}}{v_{\text{the}}^{2}}\right)\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(u_{\Vert e^{-}}^{(0)}+u_{\Vert e^{+}}^{(0)}\right)F_{0}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad -2\frac{cT_{0}}{eB_{0}}\frac{\unicode[STIX]{x2202}_{y}}{L_{T}}\left[\left(\hat{v}^{2}-\frac{3}{2}\right)\frac{e\unicode[STIX]{x1D711}^{(0)}}{T_{0}}-\left(\hat{v}^{2}-\frac{5}{2}\right)\frac{v_{\Vert }}{c}\frac{eA_{\Vert }^{(0)}}{T_{0}}\right]F_{0}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\text{d}}{\text{d}t}\left(g_{e^{-}}^{(0)}+g_{e^{+}}^{(0)}\right)+v_{\Vert }\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[g_{e^{-}}^{(0)}+g_{e^{+}}^{(0)}-\left(\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{-}}^{(0)}}{T_{0}}+\frac{\unicode[STIX]{x1D6FF}T_{\Vert e^{+}}^{(0)}}{T_{0}}\right)F_{0}\right]\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =C[g_{e^{+}}^{(0)}+g_{e^{-}}^{(0)}]+\left(1-2\frac{v_{\Vert }^{2}}{v_{\text{the}}^{2}}\right)\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(u_{\Vert e^{-}}^{(0)}+u_{\Vert e^{+}}^{(0)}\right)F_{0}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad -2\frac{cT_{0}}{eB_{0}}\frac{\unicode[STIX]{x2202}_{y}}{L_{T}}\left[\left(\hat{v}^{2}-\frac{3}{2}\right)\frac{e\unicode[STIX]{x1D711}^{(0)}}{T_{0}}-\left(\hat{v}^{2}-\frac{5}{2}\right)\frac{v_{\Vert }}{c}\frac{eA_{\Vert }^{(0)}}{T_{0}}\right]F_{0}\end{eqnarray}$$
and the diamagnetic contribution does not cancel. It remains to specify the collisional operator. We notice that, for sufficiently large collisionality, temperature fluctuations must become isotropic, that is
![]() $\unicode[STIX]{x1D6FF}T_{\bot }=\unicode[STIX]{x1D6FF}T_{\Vert }.$
This is achieved with the simple collision operator model
$\unicode[STIX]{x1D6FF}T_{\bot }=\unicode[STIX]{x1D6FF}T_{\Vert }.$
This is achieved with the simple collision operator model
Finally, with the equation for
![]() $g_{e^{\mp }}^{(1)}$
, we can close our system. This is obtained from
$g_{e^{\mp }}^{(1)}$
, we can close our system. This is obtained from
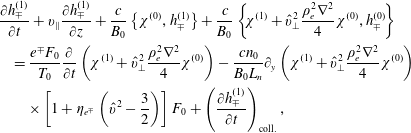 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}h_{\mp }^{(1)}}{\unicode[STIX]{x2202}t}+v_{\Vert }\frac{\unicode[STIX]{x2202}h_{\mp }^{(1)}}{\unicode[STIX]{x2202}z}+\frac{c}{B_{0}}\left\{\unicode[STIX]{x1D712}^{(0)},h_{\mp }^{(1)}\right\}+\frac{c}{B_{0}}\left\{\!\unicode[STIX]{x1D712}^{(1)}+\hat{v}_{\bot }^{2}\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D712}^{(0)},h_{\mp }^{(0)}\!\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{e^{\mp }F_{0}}{T_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D712}^{(1)}+\hat{v}_{\bot }^{2}\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D712}^{(0)}\right)-\frac{cn_{0}}{B_{0}L_{n}}\unicode[STIX]{x2202}_{y}\left(\unicode[STIX]{x1D712}^{(1)}+\hat{v}_{\bot }^{2}\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D712}^{(0)}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad \times \left[1+\unicode[STIX]{x1D702}_{e^{\mp }}\left(\hat{v}^{2}-\frac{3}{2}\right)\right]F_{0}+\left(\frac{\unicode[STIX]{x2202}h_{\mp }^{(1)}}{\unicode[STIX]{x2202}t}\right)_{\text{coll.}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}h_{\mp }^{(1)}}{\unicode[STIX]{x2202}t}+v_{\Vert }\frac{\unicode[STIX]{x2202}h_{\mp }^{(1)}}{\unicode[STIX]{x2202}z}+\frac{c}{B_{0}}\left\{\unicode[STIX]{x1D712}^{(0)},h_{\mp }^{(1)}\right\}+\frac{c}{B_{0}}\left\{\!\unicode[STIX]{x1D712}^{(1)}+\hat{v}_{\bot }^{2}\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D712}^{(0)},h_{\mp }^{(0)}\!\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{e^{\mp }F_{0}}{T_{0}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D712}^{(1)}+\hat{v}_{\bot }^{2}\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D712}^{(0)}\right)-\frac{cn_{0}}{B_{0}L_{n}}\unicode[STIX]{x2202}_{y}\left(\unicode[STIX]{x1D712}^{(1)}+\hat{v}_{\bot }^{2}\frac{\unicode[STIX]{x1D70C}_{e}^{2}\unicode[STIX]{x1D6FB}^{2}}{4}\unicode[STIX]{x1D712}^{(0)}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad \times \left[1+\unicode[STIX]{x1D702}_{e^{\mp }}\left(\hat{v}^{2}-\frac{3}{2}\right)\right]F_{0}+\left(\frac{\unicode[STIX]{x2202}h_{\mp }^{(1)}}{\unicode[STIX]{x2202}t}\right)_{\text{coll.}},\end{eqnarray}$$
where the equations for all the fields have already been derived. We leave this expression implicit, and proceed considering the limiting case of collisionless isothermal species. This is the limit in which the KREHM equations (Zocco & Schekochihin Reference Zocco and Schekochihin2011) reduce to the Schep Pegoraro and Kuvshinov two-fluid model (Schep et al. Reference Schep, Pegoraro and Kuvshinov1994). However, now we expect a new result. Indeed, even if our quasi-neutrality equation, (6.11), looks similar to a long-wavelength electrostatic ion response
its physical content is rather different. Indeed, the equation for the electrostatic potential (which, for pair plasmas, must come from the first-order quasi-neutrality condition, while for electron–ion plasmas comes from the zeroth-order quasi-neutrality condition), in both cases, has the form of a vorticity equation (6.14). However, finite Larmor radius effects introduce a magnetic compressional dynamics that will manifest and generate a qualitatively different set of equations from the equivalent electron–ion ones. Let us derive this new set of nonlinear equations for collisionless magnetic reconnection and turbulence in magnetised isothermal pair plasmas. We want to stress that the isothermal collisionless limit is a crude approximation and its validity should always be tested against the solution of the reduced kinetic problem, (6.23), as it has been done for electron–ion plasmas by Loureiro et al. (Reference Loureiro, Schekochihin and Zocco2013).
We introduce the field-line-following coordinate,
![]() $l$
, and integrate (6.10) along the perturbed field lines. Since, for
$l$
, and integrate (6.10) along the perturbed field lines. Since, for
![]() $l\rightarrow \mp \infty ,$
the solution must decay to zero, we set to zero the resulting constant of integration. The electric field, therefore, to zeroth order satisfies the ideal MHD equation
$l\rightarrow \mp \infty ,$
the solution must decay to zero, we set to zero the resulting constant of integration. The electric field, therefore, to zeroth order satisfies the ideal MHD equation
with
We are considering the isothermal response, thus,
![]() $g_{e^{\mp }}\equiv 0.$
By inspecting (6.18) and (6.23), we observe that they are homogeneous, and therefore consistent with these solutions, only if
$g_{e^{\mp }}\equiv 0.$
By inspecting (6.18) and (6.23), we observe that they are homogeneous, and therefore consistent with these solutions, only if
![]() $L_{n}\rightarrow \infty .$
We consider this limit.
$L_{n}\rightarrow \infty .$
We consider this limit.
Then, the generalised Ohm’s law reduces to
while the vorticity equation gives
Due to finite magnetic compressibility, this is coupled to the equations for the total density
![]() $2\unicode[STIX]{x1D6FF}n^{(0)}=\unicode[STIX]{x1D6FF}n_{e^{-}}^{(0)}+\unicode[STIX]{x1D6FF}n_{e^{+}}^{(0)}$
and the velocity
$2\unicode[STIX]{x1D6FF}n^{(0)}=\unicode[STIX]{x1D6FF}n_{e^{-}}^{(0)}+\unicode[STIX]{x1D6FF}n_{e^{+}}^{(0)}$
and the velocity
![]() $V_{\Vert }^{(0)}=u_{\Vert e^{-}}^{(0)}+u_{\Vert e^{+}}^{(0)}$
$V_{\Vert }^{(0)}=u_{\Vert e^{-}}^{(0)}+u_{\Vert e^{+}}^{(0)}$
We found a set of six equations for the six unknowns
![]() $A_{\Vert }^{(0)},$
$A_{\Vert }^{(0)},$
![]() $\unicode[STIX]{x1D711}^{(0)}$
,
$\unicode[STIX]{x1D711}^{(0)}$
,
![]() $A_{\Vert }^{(1)}$
,
$A_{\Vert }^{(1)}$
,
![]() $\unicode[STIX]{x1D711}^{(1)}$
,
$\unicode[STIX]{x1D711}^{(1)}$
,
![]() $V_{\Vert }^{(0)}$
and
$V_{\Vert }^{(0)}$
and
![]() $\unicode[STIX]{x1D6FF}n^{(0)}$
. We see that compressible effects enter the vorticity equation (6.28) through
$\unicode[STIX]{x1D6FF}n^{(0)}$
. We see that compressible effects enter the vorticity equation (6.28) through
![]() $\unicode[STIX]{x1D6FD}_{e}$
because quasi-neutrality is valid to first order in the small Larmor radius expansion. The new term, proportional to
$\unicode[STIX]{x1D6FD}_{e}$
because quasi-neutrality is valid to first order in the small Larmor radius expansion. The new term, proportional to
![]() $V_{\Vert }=u_{\Vert e^{-}}^{(0)}+u_{\Vert e^{+}}^{(0)},$
couples the electromagnetic system of equations for
$V_{\Vert }=u_{\Vert e^{-}}^{(0)}+u_{\Vert e^{+}}^{(0)},$
couples the electromagnetic system of equations for
![]() $\unicode[STIX]{x1D711}^{(1)}$
and
$\unicode[STIX]{x1D711}^{(1)}$
and
![]() $A_{\Vert }^{(1)}$
to the fluid equations (6.29) and (6.30). It is easy to show that these equations support the compressional sound wave
$A_{\Vert }^{(1)}$
to the fluid equations (6.29) and (6.30). It is easy to show that these equations support the compressional sound wave
![]() $\unicode[STIX]{x1D714}=v_{\text{the}}k_{\Vert }/\sqrt{2},$
which is linearly strongly damped in the electrostatic limit (Helander & Connor Reference Helander and Connor2016; Mishchenko et al.
Reference Mishchenko, Zocco, Helander and Könies2017). In the low-frequency limit
$\unicode[STIX]{x1D714}=v_{\text{the}}k_{\Vert }/\sqrt{2},$
which is linearly strongly damped in the electrostatic limit (Helander & Connor Reference Helander and Connor2016; Mishchenko et al.
Reference Mishchenko, Zocco, Helander and Könies2017). In the low-frequency limit
![]() $\unicode[STIX]{x1D714}\ll k_{y}v_{\text{the}}(\unicode[STIX]{x2202}_{x}A_{\Vert }^{(0)}/B_{0})\sim k_{z}v_{\text{the}},$
such damping is negligible. Thus, (6.25)–(6.30) are valid for sub-Alfvénic instabilities,
$\unicode[STIX]{x1D714}\ll k_{y}v_{\text{the}}(\unicode[STIX]{x2202}_{x}A_{\Vert }^{(0)}/B_{0})\sim k_{z}v_{\text{the}},$
such damping is negligible. Thus, (6.25)–(6.30) are valid for sub-Alfvénic instabilities,
![]() $\unicode[STIX]{x1D714}\sim k_{y}v_{A,e}\unicode[STIX]{x1D706},$
with
$\unicode[STIX]{x1D714}\sim k_{y}v_{A,e}\unicode[STIX]{x1D706},$
with
![]() $\unicode[STIX]{x1D706}\ll \sqrt{\unicode[STIX]{x1D6FD}_{e}}\ll 1$
, provided nonlinear collisionless heating is negligible (
$\unicode[STIX]{x1D706}\ll \sqrt{\unicode[STIX]{x1D6FD}_{e}}\ll 1$
, provided nonlinear collisionless heating is negligible (
![]() $g_{e^{\mp }}\equiv 0$
). This is definitely true for the reconnecting instabilities presented in § 5.
$g_{e^{\mp }}\equiv 0$
). This is definitely true for the reconnecting instabilities presented in § 5.
7 Conclusion
We presented a simple study of non-relativistic electron–positron plasmas in a magnetised sheared slab. The two species were described by using the drift-kinetic model. Linear results are presented for nearly electrostatic perturbations,
![]() $\unicode[STIX]{x1D6FF}B_{\bot }/B_{0}\sim \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}_{GK}\ll e\unicode[STIX]{x1D711}/T_{0}\sim \unicode[STIX]{x1D716}_{GK},$
where
$\unicode[STIX]{x1D6FF}B_{\bot }/B_{0}\sim \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}_{GK}\ll e\unicode[STIX]{x1D711}/T_{0}\sim \unicode[STIX]{x1D716}_{GK},$
where
![]() $\unicode[STIX]{x1D716}_{GK}=k_{\Vert }/k_{\bot }$
is the small expansion parameter of gyrokinetic theory,
$\unicode[STIX]{x1D716}_{GK}=k_{\Vert }/k_{\bot }$
is the small expansion parameter of gyrokinetic theory,
![]() $k_{\Vert }$
and
$k_{\Vert }$
and
![]() $k_{\bot }$
are the wave vectors for perturbations parallel and perpendicular to the equilibrium magnetic field,
$k_{\bot }$
are the wave vectors for perturbations parallel and perpendicular to the equilibrium magnetic field,
![]() $B_{0}$
, and
$B_{0}$
, and
![]() $\unicode[STIX]{x1D6FD}$
is the ratio of kinetic to magnetic plasma pressure. We emphasised the role of the electron Alfvén wave. This is supported by the system and connects, in the electrostatic limit, to high-frequency K-modes. Current driven instabilities are described by a formalism equivalent to that of an electron–ion plasma, but with the Alfvén speed based on the electron mass. A nonlinear electromagnetic model is also presented. Here, nonlinear frequencies associated with electrostatic fluctuations are allowed to compete with the characteristic frequencies of wave–particle resonant interaction. The resulting hybrid fluid-kinetic model is an extension of the KREHM of Zocco & Schekochihin (Reference Zocco and Schekochihin2011), where finite Larmor radius effects are retained. The specific case of isothermal species is derived in detail, and its limitations are discussed. This constitutes a new set of equations for nonlinear electromagnetic phenomena in magnetised pair plasmas. The results are, at present, highly speculative. The first magnetically confined pair plasmas will definitely be dominated by electrostatic effects, because of their extremely low density. Our nonlinear electromagnetic model could perhaps be a useful tool to design high density magnetically confined electron–positron plasmas.
$\unicode[STIX]{x1D6FD}$
is the ratio of kinetic to magnetic plasma pressure. We emphasised the role of the electron Alfvén wave. This is supported by the system and connects, in the electrostatic limit, to high-frequency K-modes. Current driven instabilities are described by a formalism equivalent to that of an electron–ion plasma, but with the Alfvén speed based on the electron mass. A nonlinear electromagnetic model is also presented. Here, nonlinear frequencies associated with electrostatic fluctuations are allowed to compete with the characteristic frequencies of wave–particle resonant interaction. The resulting hybrid fluid-kinetic model is an extension of the KREHM of Zocco & Schekochihin (Reference Zocco and Schekochihin2011), where finite Larmor radius effects are retained. The specific case of isothermal species is derived in detail, and its limitations are discussed. This constitutes a new set of equations for nonlinear electromagnetic phenomena in magnetised pair plasmas. The results are, at present, highly speculative. The first magnetically confined pair plasmas will definitely be dominated by electrostatic effects, because of their extremely low density. Our nonlinear electromagnetic model could perhaps be a useful tool to design high density magnetically confined electron–positron plasmas.
Acknowledgements
I am grateful to M. Barnes, J. Connor, P. Helander, N. Loureiro, A. Mishchenko, A. Schekochihin and T. Sunn Pedersen for valuable discussions that helped me understand many aspects of this work. Part of this work was presented at the first conference ‘Frontiers in Plasma Physics’, held at the Abbey of the Most Holy Trinity of Spineto (Sarteano, Italy) under the auspices of the Journal of Plasma Physics (Cambridge University Press).


