1. Introduction
Hardy–Weinberg equilibrium (HWE) is an important phenomenon in population genetics and it has been a subject of intense consideration and a powerful research tool in population genetics (Crow, Reference Crow1988). Deviation from HWE is called Hardy–Weinberg disequilibrium (HWD), which may be generated by many different evolutionary forces, including non-random mating, selection, genetic drift and so on. Testing HWD can help detection of such evolutionary forces (Weir, Reference Weir1996; Deng et al., Reference Deng, Chen and Recker2001). In addition, HWD may also be introduced by genotyping errors (Lee, Reference Lee2003), which is a factor responsible for low power of association studies. A very important application of HWD is in case–control disease association studies (Chen & Chatterjee, Reference Chen and Chatterjee2007) or case-only association studies (Nielsen et al., Reference Nielsen, Ehm and Weir1999; Lee, Reference Lee2003; Weinberg & Morris, Reference Weinberg and Morris2003). In case–control studies, genotype frequencies of the case population are compared with HWE predicted genotype frequencies from the control population. A significant deviation of a marker from HWD implies the association of the locus with the disease. In case-only studies, a significant HWD of a marker within the case population implies marker-disease association if the entire population is assumed to be in HWE. A more detailed review of application of HWD to genetic association studies can be found in Salanti et al. (Reference Salanti, Amountza, Ntzani and Ioannidis2005).
Many statistical methods have been developed to test HWE, including the χ2 test (Li, Reference Li1955; Hernandez & Weir, Reference Hernandez and Weir1989) and the exact test (Fisher, Reference Fisher1935; Haldane, Reference Haldane1954; Chapco, Reference Chapco1976; Guo & Thompson, Reference Guo and Thompson1992; Rohlfs & Weir, Reference Rohlfs and Weir2008). Bayesian statistics have also been applied to HWD analysis by drawing posterior credibility of the estimated HWD parameter (Ayres & Balding, Reference Ayres and Balding1998; Shoemaker et al., Reference Shoemaker, Painter and Weir1998). These methods have been substantially validated and applied to population genetics. They can be summarized in two general categories: (1) a parametric hypothesis test and (2) an exact test. In the parametric hypothesis test, there is a HWD parameter to estimate and a test is performed on this parameter. The most common parameters are the inbreeding coefficient (f) for two alleles, the fixation index (fij) for multiple alleles, the additive HWD parameter (D) for two alleles and the corresponding multiple allelic HWD parameter (Dij). Please see Weir (Reference Weir1996) for details of these parameters. There are two versions of the exact test. The first version remains in its original form of the exact test (Fisher, Reference Fisher1935; Guo & Thompson, Reference Guo and Thompson1992), in which the proportion of the extreme samples was counted as the P-values. The second version of the exact test requires a parametric estimation of the HWD parameter and a test statistic. All possible samples from the hypergeometric distribution of genotype counts under the null model are evaluated. The test statistics are then ranked to form a null distribution (Rousset & Raymond, Reference Rousset and Raymond1995). Different test statistics may generate different ranks and thus have different P-values for the same data.
It appears that existing methods are already mature and do not have much room to improve. However, one aspect has been ignored in all HWD studies, which is a conditional test for one locus given the genotypes of other loci. If the multiple loci are in low linkage disequilibrium (LD), conditional tests would not offer any advantage over the individual locus tests (one locus at a time). However, if these loci are in high LD, conditional tests will lead to different results. A locus in HWD detected separately may not be truly in HWD, but caused by the HWD of another locus in high LD with the one of interest. This Type I error has not been recognized in the literature. None of the existing methods have addressed this problem. Some of the pooling methods deal with multiple loci (Hill et al., Reference Hill, Babiker, Ranford-Cartwright and Walliker1995; Ayres & Balding, Reference Ayres and Balding1998). However, these methods were based on the assumption of same inbreeding coefficient for all loci and thus gained power when different loci are combined. There has been no report in the literature to jointly estimate HWD for multiple loci.
One approach to tackling this problem is to extend the contingency table to cover multiple loci. The dimension of the table would rise rapidly as the number of loci increases. This may explain why people choose to avoid HWD testing for multiple loci. It is feasible to test HWD for a pair of loci simultaneously, but the method may not be easily extended to multiple loci. Here, we proposed an entirely different approach to handle multiple locus HWD test, a generalized linear model (GLM) approach. The GLM is a well-known model for analysing discrete data (McCullagh & Nelder, Reference McCullagh and Nelder1989). Connection of the HWD problem to GLM is not obvious. If we treat the genotype or allele count as the response variable, there are no predictors. If we treat the genotype counts as predictors, there is no response variable. We previously developed a GLM for testing multiple locus segregation distortion (Zhan & Xu, Reference Zhan and Xu2011). In that model, we proposed a hidden linear predictor, called liability. The response variables are the genotype counts. In this study, we adopted that model to perform HWD test. The key difference between the GLM and the existing methods is that we can use a linear predictor to measure the strength of HWD. With the proposed linear predictor, we can handle multiple loci easily by combining all locus-specific HWD parameters into a single linear predictor. Parameter estimation and hypothesis test can be performed under the GLM framework.
We first introduced the GLM for a single locus. We then extended the model to conditional analysis for two loci. Finally, we addressed conditional tests for multiple loci. Simulation experiments were performed to validate the GLM for the single locus and two loci analyses. A real single nucleotide polymorphism (SNP) dataset was used to demonstrate the multiple locus conditional tests.
2. Theory and method
(i) Model for single locus
Let A 1 and A 2 be two alleles in a biallelic population and A 1A 1, A 1A 2 and A 2A 2 be the three possible genotypes. Denote the observed counts of the three genotypes by n 11, n 12 and n 22. The estimated frequencies of the two alleles are p 1 = (2n 11+n 12)/(2n) and p 2 = (2n 22+n 12)/(2n), respectively, where n=n 11+n 12+n 22 is the sample size. Under HWE, the predicted genotypic frequencies are ϕ11=p 12, ϕ12 = 2p 1p 2 and ϕ22=p 22, respectively. Rather than using the classical heterozygosity reduction index f or the disequilibrium D as the parameter to measure the amount of departure from HWE, we proposed a new parameter for HWD. This parameter takes any real number without the awkward constraint as that in the D parameter. The new parameter can be derived based on the selection theory, in which the heterozygosity deficiency (or excess) is formulated as selection against (or in favour of) heterozygote. Let ψ11 = ψ22 be the fitness of the two homozygotes and ψ12 be the fitness of the heterozygote. The relative fitness of the heterozygote over the homozygotes is ψ12/ψ11. This relative fitness of a non-unity value represents the departure from HWE. This is the dominance model of fitness selection.
We now reparameterize the fitness using ψ11 = ψ22 = Φ(0) = 1/2 and ψ12 = Φ(θ), where Φ() is the standardized cumulative normal distribution and θ is the new HWD parameter. If θ = 0, then ψ12 = Φ(0) = 1/2 and the relative fitness of the heterozygote is 1 (compared with that of the homozygotes) and the population is in HWE. If θ < 0, selection is against the heterozygote while θ > 0 means selection against homozygotes. Note that HWD may be caused by many other factors, including inbreeding, genetic drift and population subdivision. The selection parameter θ also indicates heterozygote deficiency if θ < 0 and heterozygote excess if θ > 0. We can estimate and test θ as the parameter of departure from HWE. The null hypothesis is H 0:θ = 0. We can see that −∞ < θ < +∞ and thus there is no constraint on this parameter. We could have set ψ11 = ψ22 = 1, but parameter θ under this set up would not be zero under HWE. It is equally valid to define ψ12 = Φ(−θ) so that θ > 0 represents heterozygosity deficiency. More discussion on the relative fitness is given in the last section of the manuscript.
Using the Bayes theorem, we can find the probabilities of the three genotypes, as shown below:
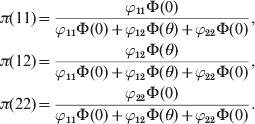 $$\eqalign{ \pi \lpar 11\rpar \equals \tab {{\varphi _{\setnum{11}} \rmPhi \lpar 0\rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar 0\rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar 0\rpar }}\comma \cr \pi \lpar 12\rpar \equals \tab {{\varphi _{\setnum{12}} \rmPhi \lpar \theta \rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar 0\rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar 0\rpar }}\comma \cr \pi \lpar 22\rpar \equals \tab {{\varphi _{\setnum{22}} \rmPhi \lpar 0\rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar 0\rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar 0\rpar }}. \cr} $$
$$\eqalign{ \pi \lpar 11\rpar \equals \tab {{\varphi _{\setnum{11}} \rmPhi \lpar 0\rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar 0\rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar 0\rpar }}\comma \cr \pi \lpar 12\rpar \equals \tab {{\varphi _{\setnum{12}} \rmPhi \lpar \theta \rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar 0\rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar 0\rpar }}\comma \cr \pi \lpar 22\rpar \equals \tab {{\varphi _{\setnum{22}} \rmPhi \lpar 0\rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar 0\rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar 0\rpar }}. \cr} $$These probabilities are considered the posterior probabilities of the three genotypes under the Bayesian framework. The HWE predicted probabilities serve as the prior probabilities. The fitness of each genotype then serves as the likelihood. One can easily see that, when θ = 0, the posterior probabilities converge to the HWE probabilities.
The log-likelihood function is constructed using the multinomial distribution of the data, as shown by
The derivative of L(θ) with respect to θ is
where φ() is the standardized normal density. Setting the derivative to zero and solving for θ leads to the maximum likelihood estimate (MLE) of the parameter,
The variance of the estimate is approximated by the inverse of the information,
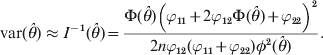 $${\rm var} \lpar \hats{\theta }\rpar \approx I^{ \minus \setnum{1}} \lpar \hats{\theta }\rpar \equals {{\rmPhi \lpar \hats{\theta }\rpar \left( {\varphi _{\setnum{11}} \plus 2\varphi _{\setnum{12}} \rmPhi \lpar \hats{\theta }\rpar \plus \varphi _{\setnum{22}} } \right)^{\setnum{2}} } \over {2n\varphi _{\setnum{12}} \lpar \varphi _{\setnum{11}} \plus \varphi _{\setnum{22}} \rpar \phi ^{\setnum{2}} \lpar \hats{\theta }\rpar }}.$$
$${\rm var} \lpar \hats{\theta }\rpar \approx I^{ \minus \setnum{1}} \lpar \hats{\theta }\rpar \equals {{\rmPhi \lpar \hats{\theta }\rpar \left( {\varphi _{\setnum{11}} \plus 2\varphi _{\setnum{12}} \rmPhi \lpar \hats{\theta }\rpar \plus \varphi _{\setnum{22}} } \right)^{\setnum{2}} } \over {2n\varphi _{\setnum{12}} \lpar \varphi _{\setnum{11}} \plus \varphi _{\setnum{22}} \rpar \phi ^{\setnum{2}} \lpar \hats{\theta }\rpar }}.$$Significance test for H 0:θ = 0 may be performed in two ways, the likelihood ratio test (LRT) and the Wald test. The former is defined as
The Wald test is
Under the null hypothesis, both statistics asymptotically follow the χ12 distribution and thus the critical value χ1,0·952 = 3·84 can be used to declare significance at the α = 0·05 Type I error rate. One caveat of the Wald test is that if the genotype counts extremely deviate from HWE, the second derivative of L(θ) with respect to θ may not be defined, leading to no estimate of the variance. This problem does not apply to the LRT because it does not require the second derivative. We call this model the GLM because the HWD parameter θ is a linear predictor and the link function is probit. The novelty of the model is that we used a linear predictor θ to measure the strength of HWD.
This paragraph shows an example using the proposed GLM and compared it with the Fisher's exact test. Let the counts of the three genotypes be n 11 = 24, n 12 = 39 and n 11 = 37 with a sample size n = 100. The genotypic frequencies predicted under HWE are ϕ11 = 0·1892, ϕ12 = 0·4916 and ϕ22 = 0·3192. The GLM estimated HWD parameter is ![]() $\hats{\theta } \equals \minus 0 \cdot 4380$ with an estimation error
$\hats{\theta } \equals \minus 0 \cdot 4380$ with an estimation error ![]() $\sqrt {{\rm var} \lpar \hats{\theta }\rpar } \equals \sqrt {0{\cdot}03499} \equals 0 {\cdot} 1870$. The Wald and LRT statistics are Wald = 5·4844 and LRT = 4·1467, respectively. The corresponding P-values for the two tests are 0·0192 and 0·0413, respectively. Using Fisher's exact test, the P-value is 0·0423, close to the P-value of the LRT.
$\sqrt {{\rm var} \lpar \hats{\theta }\rpar } \equals \sqrt {0{\cdot}03499} \equals 0 {\cdot} 1870$. The Wald and LRT statistics are Wald = 5·4844 and LRT = 4·1467, respectively. The corresponding P-values for the two tests are 0·0192 and 0·0413, respectively. Using Fisher's exact test, the P-value is 0·0423, close to the P-value of the LRT.
(ii) Model for two loci
The single locus model is just an alternative way to test HWD. The main goal of proposing this new test statistic is to facilitate a conditional test for each of two loci that are in LD. If two loci are in linkage equilibrium, there is no advantage for the conditional test. However, if the two loci are in high LD, the HWD of one locus may be caused by the HWD of the other locus. The conditional test may correct the confounding. It is easy to use an indicator variable for the genotype of each locus for each individual. Let A 1A 1, A 1A 2 and A 2A 2 be the three ordered genotypes for the first locus. The genotype indicator variable for individual j is defined by a 1 × 3 vector Xj. For example, if individual j is of type A 1A 1, then Xj = [1 0 0]. Let B 1B 1, B 1B 2 and B 2B 2 be the three ordered genotypes for the second locus. The genotype indicator variable of individual j for the second locus is defined by a 1 × 3 vector Yj. For example, if individual j is of type B 1B 2 for the second locus, then Yj = [0 1 0]. We now use θX and θY, respectively, to denote the HWD parameters for the two loci. Let us define δ = [0 1 0]T as a 3 × 1 vector of constants. We can see that Yjδ = 1 if j is heterozygote for the second locus and Yjδ = 0 otherwise. Conditional on θY for the second locus, the posterior probabilities of the three genotypes of individual j for the first locus are
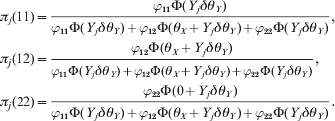 $$\eqalign{ {\pi _{j} \lpar 11\rpar \equals} \tab { {\varphi _{\setnum{11}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta _{X} \plus Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar }}\comma \cr { \pi _{j} \lpar 1 2 \rpar \equals} \tab { {\varphi _{\setnum{12}} \rmPhi \lpar \theta _{X} \plus Y_{j} \delta \theta _{Y} \rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta _{X} \plus Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar }}\comma \cr \pi _{j} \lpar {2 2 \rpar} \equals \tab { {\varphi _{\setnum{22}} \rmPhi \lpar 0 \plus Y_{j} \delta \theta _{Y} \rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta _{X} \plus Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar }}. \cr} $$
$$\eqalign{ {\pi _{j} \lpar 11\rpar \equals} \tab { {\varphi _{\setnum{11}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta _{X} \plus Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar }}\comma \cr { \pi _{j} \lpar 1 2 \rpar \equals} \tab { {\varphi _{\setnum{12}} \rmPhi \lpar \theta _{X} \plus Y_{j} \delta \theta _{Y} \rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta _{X} \plus Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar }}\comma \cr \pi _{j} \lpar {2 2 \rpar} \equals \tab { {\varphi _{\setnum{22}} \rmPhi \lpar 0 \plus Y_{j} \delta \theta _{Y} \rpar } \over {\varphi _{\setnum{11}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{12}} \rmPhi \lpar \theta _{X} \plus Y_{j} \delta \theta _{Y} \rpar \plus \varphi _{\setnum{22}} \rmPhi \lpar Y_{j} \delta \theta _{Y} \rpar }}. \cr} $$Let ![]() $\pi _{j} \equals \left[ {\matrix{ {\pi _{j} \lpar 11\rpar } \tab {\pi _{j} \lpar 12\rpar } \tab {\pi _{j} \lpar 22\rpar } \cr} } \right]^{\rm T} $ and thus ln(πj) is a 3 × 1 column vector as shown below:
$\pi _{j} \equals \left[ {\matrix{ {\pi _{j} \lpar 11\rpar } \tab {\pi _{j} \lpar 12\rpar } \tab {\pi _{j} \lpar 22\rpar } \cr} } \right]^{\rm T} $ and thus ln(πj) is a 3 × 1 column vector as shown below:
We define the conditional log likelihood function for θX given θY by
Maximizing this likelihood function and finding the solution of θX gives the conditional MLE of θX. Unfortunately, an explicit solution for the MLE of θX is hard to find. A numerical solution may have to be resorted to e.g. the Newton method, which has the following iteration form:
where L′(θX(t)) and L″(θX(t)) are the first- and second-order derivatives of the log-likelihood function with respect to θX evaluated at θX = θX(t). When the iteration process converges, we get the MLE of θX conditional on θY, denoted by ![]() $\hats{\theta }_{X} $, whose variance can be approximated by
$\hats{\theta }_{X} $, whose variance can be approximated by
Once θX is estimated, we construct the likelihood function for θY conditional on θX using the same approach. Define the posterior probabilities of the three genotypes for the second locus by
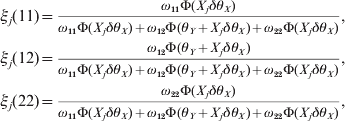 $$\eqalign{ \xi _{j} \lpar 11\rpar \equals \tab {{\omega _{\setnum{11}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar } \over {\omega _{\setnum{11}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{12}} \rmPhi \lpar \theta _{Y} \plus X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{22}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar }}\comma \cr \xi _{j} \lpar 12\rpar \equals \tab {{\omega _{\setnum{12}} \rmPhi \lpar \theta _{Y} \plus X_{j} \delta \theta _{X} \rpar } \over {\omega _{\setnum{11}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{12}} \rmPhi \lpar \theta _{Y} \plus X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{22}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar }}\comma \cr \xi _{j} \lpar 22\rpar \equals \tab {{\omega _{\setnum{22}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar } \over {\omega _{\setnum{11}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{12}} \rmPhi \lpar \theta _{Y} \plus X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{22}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar }}\comma \cr} $$
$$\eqalign{ \xi _{j} \lpar 11\rpar \equals \tab {{\omega _{\setnum{11}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar } \over {\omega _{\setnum{11}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{12}} \rmPhi \lpar \theta _{Y} \plus X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{22}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar }}\comma \cr \xi _{j} \lpar 12\rpar \equals \tab {{\omega _{\setnum{12}} \rmPhi \lpar \theta _{Y} \plus X_{j} \delta \theta _{X} \rpar } \over {\omega _{\setnum{11}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{12}} \rmPhi \lpar \theta _{Y} \plus X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{22}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar }}\comma \cr \xi _{j} \lpar 22\rpar \equals \tab {{\omega _{\setnum{22}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar } \over {\omega _{\setnum{11}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{12}} \rmPhi \lpar \theta _{Y} \plus X_{j} \delta \theta _{X} \rpar \plus \omega _{\setnum{22}} \rmPhi \lpar X_{j} \delta \theta _{X} \rpar }}\comma \cr} $$where ω11=q 12, ω12 = 2q 1q 2 and ω22=q 22 are the HWE predicted genotype frequencies for the second locus. The conditional log likelihood function for θY is
where
Conditional on θY to estimate θX and then conditional on θX to estimate θY will complete just one cycle of iterations. The Newton iteration process continues until the sequence converges. After convergence, we obtain the MLE of both parameters, denoted by ![]() $\hats{\theta }_{X} $ and
$\hats{\theta }_{X} $ and ![]() $\hats{\theta }_{Y} $ for the two loci.
$\hats{\theta }_{Y} $ for the two loci.
Again, both the likelihood ratio and the Wald test statistics are used to perform the HWD tests. The LRT statistics are
and
for the two loci. The corresponding Wald tests are
and
We now show the result of an example using the GLM method. The joint genotype counts of the two loci (X and Y) of the example are given below,

We performed a contingency table association test for the data. The χ2 test statistic for the association is 78·52 with a P-value of less than 0·0001, showing strong LD between the two loci. The marginal tests of HWD for individual loci showed that ![]() $\hats{\theta }_{X} \equals \minus 0 {\cdot}7215 \pm 0 {\cdot}1640$ and
$\hats{\theta }_{X} \equals \minus 0 {\cdot}7215 \pm 0 {\cdot}1640$ and ![]() $\hats{\theta }_{Y} \equals \minus 0 {\cdot} 4684 \pm 0 {\cdot}1833$ for the two loci. The corresponding P-values are 0·00001 for locus X and 0·01064 for locus Y, meaning that both loci deviate from HWE. The conditional tests, however, showed that
$\hats{\theta }_{Y} \equals \minus 0 {\cdot} 4684 \pm 0 {\cdot}1833$ for the two loci. The corresponding P-values are 0·00001 for locus X and 0·01064 for locus Y, meaning that both loci deviate from HWE. The conditional tests, however, showed that ![]() $\hats{\theta }_{X} \equals \minus 0 {\cdot}6294 \pm 0 {\cdot}1630$ and
$\hats{\theta }_{X} \equals \minus 0 {\cdot}6294 \pm 0 {\cdot}1630$ and ![]() $\hats{\theta}_{Y} \equals \minus 0 {\cdot}2489 \pm 0 {\cdot}1850$ for the two loci. The corresponding P-values are 0·00011 for locus X and 0·1785 for locus Y. The conclusion is that the marginal HWD for locus Y is actually caused by the HWD of locus X due to LD.
$\hats{\theta}_{Y} \equals \minus 0 {\cdot}2489 \pm 0 {\cdot}1850$ for the two loci. The corresponding P-values are 0·00011 for locus X and 0·1785 for locus Y. The conclusion is that the marginal HWD for locus Y is actually caused by the HWD of locus X due to LD.
We now show another example where the two loci are in linkage equilibrium. The frequency table is

The χ2 test statistic for LD between X and Y is 0·6629 with a very large P-value of 0·9558, i.e. the LD is not significant. The marginal HWD analysis for individual loci produced ![]() $\hats{\theta }_{X} \equals \minus 0 {\cdot}7215 \pm 0 {\cdot}1640$ and
$\hats{\theta }_{X} \equals \minus 0 {\cdot}7215 \pm 0 {\cdot}1640$ and ![]() $\hats{\theta }_{Y} \equals \minus 0 {\cdot} 5426 \pm 0 {\cdot} 1766$ for the two loci. The corresponding P-values are 0·0000109 for locus X and 0·00213 for locus Y, meaning that both loci deviate from HWE. The conditional analysis showed that
$\hats{\theta }_{Y} \equals \minus 0 {\cdot} 5426 \pm 0 {\cdot} 1766$ for the two loci. The corresponding P-values are 0·0000109 for locus X and 0·00213 for locus Y, meaning that both loci deviate from HWE. The conditional analysis showed that ![]() $\hats{\theta }_{X} \equals \minus 0 {\cdot} 6471 \pm 0 {\cdot}1544$ and
$\hats{\theta }_{X} \equals \minus 0 {\cdot} 6471 \pm 0 {\cdot}1544$ and ![]() $\hats{\theta }_{Y} \equals \minus 0 {\cdot} 4632 \pm 0 {\cdot}1610$ for the two loci. The corresponding P-values are 0·0000278 for locus X and 0·00403 for locus Y. The marginal tests and conditional tests gave the same conclusion that both loci deviate from HWE.
$\hats{\theta }_{Y} \equals \minus 0 {\cdot} 4632 \pm 0 {\cdot}1610$ for the two loci. The corresponding P-values are 0·0000278 for locus X and 0·00403 for locus Y. The marginal tests and conditional tests gave the same conclusion that both loci deviate from HWE.
(iii) Model for multiple loci
Extension to multiple loci is straightforward except that the notation becomes a little bit more complicated. We will not provide the detail of the multiple locus model, but only point out the key step of the extension. Recall that the conditional posterior probabilities for the three genotypes of the first locus given the HWD parameter of the second locus requires an additional term in the linear predictor, Y jδθY, as shown in eqn (8). For multiple loci, this additional term is replaced by a term called offset, which includes effects of all other loci except the current one of interest. Suppose that we have m loci for the joint analysis. When the kth locus is considered given the effects of all other loci, the relative fitness for this locus are individual specific, ψ11 = ψ22 = Φ(oj) and ψ12 = Φ(θk+oj), where
is the offset and Xjk′ is the genotype indicator vector (1 × 3) for individual j at locus k′.
Theoretically, one can perform such a conditional test for as many loci as desired. There is a computational issue when the number of loci is too large. Another issue is the model identifiability problem. Since the θ parameter is a linear predictor (a first moment parameter), we can easily assign each θ a normal prior distribution, which makes the model a generalized linear mixed model (GLMM). The GLMM may be considered as a penalized GLM. If the variance of the normal prior is further assigned a hyper prior, the model will then become the Bayesian hierarchical GLM. If the number of loci is extremely large, we must take the penalized model using the GLMM approach, which deserves further investigation.
3. Simulation studies
All analyses were conducted using an R package ‘hwdglm’ developed in this study. The package can be downloaded from our personal website: www.statgene.ucr.edu. There are three functions within the package: (1) hwd1.glm() for single locus HWD detection; (2) hwd2.glm() for joint detection of HWD for two loci; and (3) hwdm.glm() for joint detection of HWD for m loci (m > 1).
(i) Model for single locus
This simulation experiment aimed to validate the new model and compare the new model with the exact test. The following factors were considered in the simulation: (i) minor allele frequency (p 1), (ii) sample size (n) and (iii) strength of HWD. We used the traditional inbreeding coefficient f as the degree of HWD to generate the data, although we never tried to estimate f. For the Fisher's exact test, we presented the estimated D and the P-value. The HWE.test () function of the R package ‘genetics’ was used for the exact test. This method is labelled ‘EXACT’. For the new method, we used the hwd1.glm() function of the ‘hwdglm’ package to perform the analysis. We reported the estimated θ and its estimation error. In addition, we also reported the P-values drawn from the LRT and the Wald test. The new method is labelled ‘GLM’.
The data were generated under the following multinomial distribution:
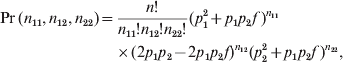 $$\eqalign{ \Pr \lpar n_{\setnum{11}} \comma n_{\setnum{12}} \comma n_{\setnum{22}} \rpar \equals \tab {{n\exclam } \over {n_{\setnum{11}} \exclam n_{\setnum{12}} \exclam n_{\setnum{22}} \exclam }}\lpar p_{\setnum{1}}^{\setnum{2}} \plus p_{\setnum{1}} p_{\setnum{2}} f \hskip2pt \rpar ^{n_{{\setnum{11}}} } \cr \tab \times \lpar 2p_{\setnum{1}} p_{\setnum{2}} \minus 2p_{\setnum{1}} p_{\setnum{2}} f\rpar ^{n_{{\setnum{12}}} } \lpar p_{\setnum{2}}^{\setnum{2}} \plus p_{\setnum{1}} p_{\setnum{2}} f \rpar ^{n_{{\setnum{22}}} } \comma \cr} $$
$$\eqalign{ \Pr \lpar n_{\setnum{11}} \comma n_{\setnum{12}} \comma n_{\setnum{22}} \rpar \equals \tab {{n\exclam } \over {n_{\setnum{11}} \exclam n_{\setnum{12}} \exclam n_{\setnum{22}} \exclam }}\lpar p_{\setnum{1}}^{\setnum{2}} \plus p_{\setnum{1}} p_{\setnum{2}} f \hskip2pt \rpar ^{n_{{\setnum{11}}} } \cr \tab \times \lpar 2p_{\setnum{1}} p_{\setnum{2}} \minus 2p_{\setnum{1}} p_{\setnum{2}} f\rpar ^{n_{{\setnum{12}}} } \lpar p_{\setnum{2}}^{\setnum{2}} \plus p_{\setnum{1}} p_{\setnum{2}} f \rpar ^{n_{{\setnum{22}}} } \comma \cr} $$where p 1 is the minor allele frequency and p 2 = 1−p 1 is the major allele frequency. This model was used to generate the data and is not the model for estimating the HWD parameter.
The minor allele frequency was examined at five levels: 0·1, 0·2, 0·3, 0·4 and 0·5. The sample size was set at the following levels: 50, 100, 200, 300 and 500. The f value (representing the degree of HWD) was examined at the following levels: 0·0, 0·1, 0·2, 0·3, 0·4 and 0·5. The situation of f = 0 represents the null model, which was simulated to examine the Type I errors of various methods compared. The simulation experiments with f > 0 were used to examine the statistical powers. The total number of combinations of the three factors is 5 × 5×6 = 150. Combining with the two methods, the simulation would generate too many data points for presentation. Therefore, we used a subset of the 150 cases to perform the simulations and drew general conclusions about the new method. We did not expect any better performance of the new method than the exact method. We would be satisfied as long as the performance of the new method is not too much worse than the existing method. That would make the new method a reasonable substitution for the exact method so that extension to two or more loci would be well justified.
Under each scenario, the simulation was replicated 1000 times. For each replicate, a P-value less than a nominal 0·05 indicated a detection of HWD. Under the null model, the proportion of replicates in which HWD was detected represents the empirical Type I error. If this Type I error is around 0·05, we say that the Type I error is under our control. Otherwise, the test is either too conservative or too liberal. Under the alternative models (f > 0), the proportion of replicates with significant HWD detection becomes the statistical power.
Table 1 shows the empirical Type I error when χ0·95,12 = 3·84 was used as the critical value for the test. Both the Wald test and the LRT under the GLM are over conservative when the minor allele frequency is small. However, when the minor allele frequency reaches 0·4, the empirical Type I error is close to the theoretical nominal value of 0·05. The Fisher's exact test is slightly conservative when the minor allele frequency is small. In conclusion, the GLM is more conservative than the exact test. In practice, if one uses χ0·95,12 = 3·84 as the critical value for the test, the result will be over-conservative, which implies a low power. Wigginton et al. (Reference Wigginton, Cutler and Abecasis2005) stated that even in a sample size of 1000, the actual type I error rates for both goodness-of-fit tests and exact tests may be much different from the nominal values. Our conclusion is consistent with Wigginton et al. (Reference Wigginton, Cutler and Abecasis2005). Hernandez & Weir (Reference Hernandez and Weir1989) also observed the same conservativeness.
Table 1. Empirical Type I errors for the new method compared with the exact test obtained from a simulation experiment with 1000 replicates

To control the Type I error at the claimed 0·05 level, one would need an empirical critical value less χ0·95,12 = 3·84. Hernandez & Weir (Reference Hernandez and Weir1989) suggested to use χ0·95,0·52 = 2 × 4 as the critical value. We decided to use the χ12 distribution to draw the critical value. We performed additional simulations to draw the empirical critical values for the test statistics (Wald and LRT). The results are listed in Table 2. The critical values are clearly less than χ0·95,12 = 3·84 when the minor allele frequency is small. For the Fisher's exact test, we should also correct the Type I error at low minor allele frequencies.
Table 2. Empirical critical values from χ12 distribution to achieve 0·05 Type I error rate for the new method compared with the exact method obtained from a simulation study with 1000 replicates

We now use these empirical critical values (Table 2) to examine the powers under various scenarios. We examined the power using f = 0·2 as an example to show the powers of the new method. The empirical powers are given in Table 3. First, the LRT test of the GLM is similar to the exact test in all situations. When the minor allele frequency is low, the power of the Wald test is also close to that of the exact test. However, as the minor allele frequency reaches 0·4 or above, the Wald test is more powerful than both the LRT test and the exact test, especially when the sample size is small. This observation is unexpected. We proposed this new GLM method as a suitable substitute for the exact test and never expected it to outperform the exact test. Similar trends were also observed for other f values (see supplemental Tables S1–S4 for the power comparisons under other f values).
Table 3. Empirical statistical power of HWD detection for the new method compared with the exact method (f = 0·2)

(ii) Model for two loci
Although the two loci model does not depend on whether LD is gametic or zygotic, for simplicity of simulation, we only considered gametic LD between two loci. Let the first locus (X) be the primary locus with HWD and the second locus (Y) be the secondary locus in HWE. The two loci have LD measured by r, the correlation between the indicator variables of allele A 1 of the first locus and allele B 1 of the second locus. The genotype transition matrix from the first locus to the second locus is
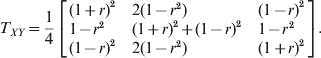 $$T_{XY} \equals {1 \over 4}\left[ {\matrix{ {\lpar 1 \plus r\rpar ^{\setnum{2}} } \hfill \tab {2\lpar 1 \minus r^{\setnum{2}} \rpar } \hfill \tab {\lpar 1 \minus r\rpar ^{\setnum{2}} } \hfill \cr {1 \minus r^{\setnum{2}} } \hfill \tab {\lpar 1 \plus r\rpar ^{\setnum{2}} \plus \lpar 1 \minus r\rpar ^{\setnum{2}} } \hfill \tab {1 \minus r^{\setnum{2}} } \hfill \cr {\lpar 1 \minus r\rpar ^{\setnum{2}} } \hfill \tab {2\lpar 1 \minus r^{\setnum{2}} \rpar } \hfill \tab {\lpar 1 \plus r\rpar ^{\setnum{2}} } \hfill \cr} } \right].$$
$$T_{XY} \equals {1 \over 4}\left[ {\matrix{ {\lpar 1 \plus r\rpar ^{\setnum{2}} } \hfill \tab {2\lpar 1 \minus r^{\setnum{2}} \rpar } \hfill \tab {\lpar 1 \minus r\rpar ^{\setnum{2}} } \hfill \cr {1 \minus r^{\setnum{2}} } \hfill \tab {\lpar 1 \plus r\rpar ^{\setnum{2}} \plus \lpar 1 \minus r\rpar ^{\setnum{2}} } \hfill \tab {1 \minus r^{\setnum{2}} } \hfill \cr {\lpar 1 \minus r\rpar ^{\setnum{2}} } \hfill \tab {2\lpar 1 \minus r^{\setnum{2}} \rpar } \hfill \tab {\lpar 1 \plus r\rpar ^{\setnum{2}} } \hfill \cr} } \right].$$For example, the conditional probability of B 1B 1 given A 1A 2 takes the element of the second row and the first column of the above transition matrix,
Given f for the primary locus and r for the LD, we simulated genotypes of the two loci one individual at a time. First, we calculated ![]() $\pi \equals \lsqb \matrix{ {\pi \lpar 11\rpar } \tab {\pi \lpar 12\rpar } \tab {\pi \lpar 22\rpar \rsqb } \cr} $ using equation (1) and simulated Xj from the multivariate Bernoulli distribution with a probability vector π. We then simulated Yj from the multivariate Bernoulli distribution with a probability vector taking one of the three rows of matrix TXY, depending on the simulated genotype for the first locus. When f > 0, both loci would show HWD, but only the first locus is of true HWD and the appeared HWD of the second locus is purely caused by LD. We used f = 0·2 as an example to demonstrate the empirical powers of the conditional and marginal analyses. The marginal analysis was conducted using the single locus model, ignoring the LD. The simulation was replicated 1000 times under each scenario. For the first locus, the detection of HWD is called the power. For the second locus, the detection of HWD is called the Type I error. The results are given in Table 4. The powers for the first locus of the conditional and marginal analyses are very similar. The Type I error for the second locus, however, is different when the LD level is high. Compared with the marginal analysis, the conditional analysis has lowered the Type I error for the second locus, but cannot fully control the Type I error when LD is too high. The power and Type I error analysis under other f values showed a similar trend (see supplemental Tables S5–S8). The conclusion from the two loci analysis was that the conditional method can control the Type I error for the second locus at some degree.
$\pi \equals \lsqb \matrix{ {\pi \lpar 11\rpar } \tab {\pi \lpar 12\rpar } \tab {\pi \lpar 22\rpar \rsqb } \cr} $ using equation (1) and simulated Xj from the multivariate Bernoulli distribution with a probability vector π. We then simulated Yj from the multivariate Bernoulli distribution with a probability vector taking one of the three rows of matrix TXY, depending on the simulated genotype for the first locus. When f > 0, both loci would show HWD, but only the first locus is of true HWD and the appeared HWD of the second locus is purely caused by LD. We used f = 0·2 as an example to demonstrate the empirical powers of the conditional and marginal analyses. The marginal analysis was conducted using the single locus model, ignoring the LD. The simulation was replicated 1000 times under each scenario. For the first locus, the detection of HWD is called the power. For the second locus, the detection of HWD is called the Type I error. The results are given in Table 4. The powers for the first locus of the conditional and marginal analyses are very similar. The Type I error for the second locus, however, is different when the LD level is high. Compared with the marginal analysis, the conditional analysis has lowered the Type I error for the second locus, but cannot fully control the Type I error when LD is too high. The power and Type I error analysis under other f values showed a similar trend (see supplemental Tables S5–S8). The conclusion from the two loci analysis was that the conditional method can control the Type I error for the second locus at some degree.
4. Real data analysis
The purpose of the real data analysis is to demonstrate the difference between the marginal and conditional analyses. The data were downloaded from the website of a book entitled Applied Statistical Genetics with R (Foulkes, Reference Foulkes2009: http://people.umass.edu/foulkes/asg/data/FMS_data.txt).
Table 4. Empirical statistical power (locus X) and Type I error (locus Y) of HWD detection for the new method (f = 0·2)

The dataset (FAMuSS) contains 1397 college students genotyped for 225 SNPs across multiple genes. We analysed a gene named ‘akt1’, which included 24 SNPs. We used both the marginal and the conditional methods to analyse the HWD for the 24 SNPs.
First, we expected the 24 SNPs to have high pairwise LD because they all came from the same gene. We used the LD(snp1,snp2) function of the R package ‘genetics’ to test all pairwise LD. Among the 24(24 − 1)/2 = 276 pairs of SNPs, a total of 243 pairs have P-values less than 0·05. The average P-value for all the 276 pairs is 0·04. The LD is very strong among the 24 SNPs. This means that the HWD tests for the conditional and marginal analyses should be very different.
The estimated HWD parameters (θ) for the 24 SNPs are plotted in Fig. 1 for both the marginal analysis (left panel) and the conditional analysis (right panel). For the marginal analysis, seven SNPs are significant (P < 0·05). For the conditional analysis, six SNPs are significant (P < 0·05). Among the significant SNPs detected here, only four were detected by both methods. Except for two SNPs, the estimated θ are all negative for the marginal analysis. This means that almost all loci show heterozygote deficiency for the marginal analysis. The situation is quite different for the conditional analysis. Among the 24 SNPs, about half have positive estimates of θ. An interesting observation comes from akt1_t10726c_t12868c (the 5th SNP from the top). The marginal test shows that this SNP significantly deviates from HWE, but the conditional analysis shows that it does not. The appeared HWD in the marginal analysis may be caused by LD between this SNP and the next one (akt1_t10598a_t12740a, the 6th SNP from the top). The LD analysis (see Table S9) showed that the D′ estimate between the two SNPs is 0·9785 with a correlation coefficient of 0·6169. The χ2 test statistic is 589. This analysis clearly demonstrates the advantage of the conditional analysis over the marginal analysis. The two different estimates of θ also share some level of similarity, with a Pearson correlation of 0·66. The Wald test statistics for the 24 SNPs obtained from both analyses are plotted in Fig. 2, again showing differences and similarities between the two analyses.

Fig. 1. Comparison of the estimated HWD parameters (θ) for the marginal (left panel) and conditional (right panel) analyses. The SNP names are shown in the left margin of each panel and the P-values are shown in the right margin of each panel. The x-axis represents the estimated θ (dot) and the θ ± 2 se (bar).

Fig. 2. Comparison of the Wald-test statistics for the 24 SNPs in gene akt1 obtained from the marginal (blue) and conditional (pink) analyses.
5. Discussion
We developed a GLM approach to testing HWD jointly for multiple loci. However, the method also works well for a single locus. Simulation studies showed that the method is over-conservative for low minor allele frequencies if the nominal 0·05 Type I error obtained from the χ2 distribution is used as the criterion of test. The Fisher's exact test is also conservative when the minor allele frequency is low. This is consistent with other reports (Hernandez & Weir, Reference Hernandez and Weir1989; Wigginton et al., Reference Wigginton, Cutler and Abecasis2005). When both methods were compared under the same experimentally controlled Type I error rate of 0·05, the GLM method is more powerful than the exact test, which is a surprise. We never expected the new method to outperform the exact method for single locus analysis. Therefore, the new method can be a good (or even a better) substitute for the exact method for single locus analysis. For multiple locus joint analysis, the new method is the only one available in the literature.
The new parameter θ is an alternative measurement of the heterozygote deficiency or excess. There is no explicit relationship between the new parameter and the D parameter of Weir (Reference Weir1996) or the Wright's fixation index f. However, the sign of θ should be opposite to the sign of D or f. A negative θ means heterozygote deficiency, which is represented by a positive D or f.
LD between two loci is contributed by digenic LD and higher-order trigenic and quadrigenic LD. Our GLM does not depend on the type of LD. In the simulation study, we considered only the digenic LD for the reason of simplicity. Higher-order LD may exist in real populations, but they are not expected to be strong in general (Jiang et al., Reference Jiang, Wang, Moore and Yang2012). Therefore, the conclusion obtained from the simulation of gametic LD should be sufficiently general.
Understanding the fact that the new method is conservative with a true Type I error lower than the nominal Type I error, we should correct this and use an empirical P-value criterion to test HWD in real data analysis. Two approaches may be taken to draw the empirical P-values for the Wald-test statistic, the exact test and the permutation test. The hypergeometric distribution of the genotype count under the biallelic system facilitates both tests. For the exact test, all possible outcomes from the hypergeometric distribution are evaluated and the empirical distribution of the Wald test statistic is drawn, from which the empirical P-value is calculated as the proportion of the more extreme samples than the actual observed Wald test statistic (Hernandez & Weir, Reference Hernandez and Weir1989; Rousset & Raymond, Reference Rousset and Raymond1995; Weir, Reference Weir1996). The exact test applies to small samples, say <200. For the permutation test, one simply draws 1000 or more random samples from the hypergeometric distribution. Empirical P-value is then drawn from the proportion of extreme samples (Guo & Thompson, Reference Guo and Thompson1992). The permutation test applies to large samples.
Further investigation is required regarding the criterion of significance declaration for the multiple locus joint analysis. One can arbitrarily lower the P-value criterion to increase the stringency of the test. The change of stringency depends on the number of SNPs included in the model (Lessios, Reference Lessios1992). The multiple test issue is a common problem in all genetic analyses, including the HWD test. Any approaches taken by the genome-wide association study (GWAS) for Type I error control can be adopted here for the HWD analysis. A typical approach, for example, is to control the false discovery rate (FDR).
HWD may be caused by any evolutionary forces. The one investigated in this study represents only one evolutionary force, non-random mating (including inbreeding and assortative mating), which only changes the heterozygosity to homozygote ratio (compared with the HWE predicted ratio) and does not distinguish between the two homozygotes. This can be reflected by our assignment of ψ11 = ψ22 = Φ(0) = 1/2. We did not replace Φ(0) by 1/2 in the formulation because that would make extension difficult. With Φ(0) appearing in the model, we can extend the model easily to take into account other evolutionary forces, e.g. selection. In fact, none of the existing methods for HWD have taken into account selection. The extension is straightforward by adding another effect, ϑ, that represents the fitness difference between the two homozygotes. The relative fitness of the three genotypes are then expressed by ψ11 = Φ(ϑ), ψ12 = Φ(θ) and ψ22 = Φ (−ϑ), where ϑ acts like the ‘additive’ effect and θ the ‘dominance’ effect. The GLM then involves two HWD parameters. The algorithm developed in this study applies to two and multiple parameters with only slight modification. The two-parameter model for HWD test requires a χ2 test with two degrees of freedom (asymptotically). Such a test is sufficiently general for HWD caused by any evolutionary forces. This topic deserves a further investigation.
Our initial study showed that choosing the relative fitness of ψ11 = exp(0), ψ12 = exp(θ) and ψ12 = exp(0) worked equally well (data not shown). Under this reparameterization, the link function is log. In the single locus situation, the explicit MLE under the log link is
The variance of ![]() $\hats{\theta }$ is
$\hats{\theta }$ is
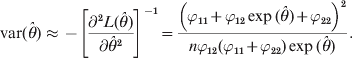 $${\rm var} \lpar \hats{\theta }\rpar \approx \minus \left[ {{{\partial ^{\setnum{2}} L\lpar \hats{\theta }\rpar } \over {\partial \hats{\theta }^{\setnum{2}} }}} \right]^{ \minus \setnum{1}} \equals {{\left( {\varphi _{\setnum{11}} \plus \varphi _{\setnum{12}} \exp \lpar \hats{\theta }\rpar \plus \varphi _{\setnum{22}} } \right)^{\setnum{2}} } \over {n\varphi _{\setnum{12}} \lpar \varphi _{\setnum{11}} \plus \varphi _{\setnum{22}} \rpar \exp \lpar \hats{\theta }\rpar }}.$$
$${\rm var} \lpar \hats{\theta }\rpar \approx \minus \left[ {{{\partial ^{\setnum{2}} L\lpar \hats{\theta }\rpar } \over {\partial \hats{\theta }^{\setnum{2}} }}} \right]^{ \minus \setnum{1}} \equals {{\left( {\varphi _{\setnum{11}} \plus \varphi _{\setnum{12}} \exp \lpar \hats{\theta }\rpar \plus \varphi _{\setnum{22}} } \right)^{\setnum{2}} } \over {n\varphi _{\setnum{12}} \lpar \varphi _{\setnum{11}} \plus \varphi _{\setnum{22}} \rpar \exp \lpar \hats{\theta }\rpar }}.$$We now show an example of the log link analysis. Let the data be n 11 = 24, n 12 = 39 and n 22 = 37. The estimated θ and the estimation error are
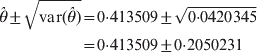 $$\eqalign{ \hats{\theta } \pm \sqrt {{\rm var} \lpar \hats{\theta }\rpar } \tab \equals 0 {\cdot}413509 \pm \sqrt {0 {\cdot} 0420345} \cr \tab \equals 0 {\cdot}413509 \pm 0 {\cdot}2050231\cr} $$
$$\eqalign{ \hats{\theta } \pm \sqrt {{\rm var} \lpar \hats{\theta }\rpar } \tab \equals 0 {\cdot}413509 \pm \sqrt {0 {\cdot} 0420345} \cr \tab \equals 0 {\cdot}413509 \pm 0 {\cdot}2050231\cr} $$and the Wald test statistic is Wald = 4·0678. The results are similar to the probit link analysis. There are two advantages using the log link function. First, the computational behaviour of the log link function is better because the occurrence of floating errors is extremely low compared with the probit link function where θ in Φ(θ) has to be constrained between −5 and 5 to avoid numerical overfloating. Secondly, ψ12 = exp(θ) can be interpreted as the fitness odds ratio of the heterozygote to the homozygotes. An odds ratio of less than unity indicates heterozygosity deficit and an odds ratio of greater than unity indicates heterozygosity excess. We examined both the log and probit link functions, but decided to pursue the probit link because the log link did not work well for two and more loci. The reason is unclear and deserves further in-depth investigation.
Literature search did not show any evidence of using GLM for HWD analysis. The only closed method is the log linear approach of Lindley (Reference Lindley1988), who defined two linear parameters,
where P 11, P 12 and P 22 represent the observed frequencies of the three genotypes, and α and β are analogous to the ‘dominance’ and ‘additive’ effects discussed earlier.
A typical GLM problem has closed forms of the first and second derivatives of the likelihood function with respect to the parameters for multiple independent variables. Our problem is atypical because it does not enjoy that property when two or more loci are considered. Fortunately, numerical differentiation is routinely conducted nowadays. With the high computer power, analytic and numerical differentiations do not seem to matter too much. In particular, finding the MLE of parameters is iterative anyway. Therefore, our atypical GLM problem is not much inferior to a typical GLM problem.
The number of SNPs handled by the joint analysis can be limited, say 100 at most. The method in its current form cannot be applied to genome-wide HWD in a simultaneous manner, although the single locus model is very practical. To perform a joint analysis for several thousand SNPs simultaneously, a penalty is required. Since the HWD parameter, θk for the kth locus, has been formulated as a first moment parameter, the L 1 penalty (Lasso) or the L 2 penalty (Ridge) or both (Elastic net) can be used. This opens a new avenue for the application of the penalized GLM.
Finally, if a large population is stratified and consists of many local populations of different demographic regions (population subdivision), the HWD of the whole population is also expected to be high. The θ parameter estimated from the whole population would be denoted by θIT, corresponding to F IT (Holsinger & Weir, Reference Holsinger and Weir2009). If the HWE predicted genotypic frequencies are calculated from each local populations and these population-specific genotype frequencies are used as the prior probabilities for the corresponding local populations, the estimated θ parameter (assuming all local populations have the same θ) would be denoted by θIS, analogous to F IS. The corresponding θ parameter representing population differentiation may be derived from θST = θIT − θIS, corresponding to the population differentiation index F ST (Holsinger & Weir, Reference Holsinger and Weir2009). We may then use
to measure population differentiation. This new parameter takes a domain between 0 and 1 with zero meaning no differentiation and one being maximum differentiation. This extension will shed new light on future population differentiation studies.
6. Supplemental Material
There are eight supplemental tables (Tables S1–S8). The first four tables (Tables S1–S4) show results of additional simulations for power analysis under the single locus model. The last four tables (Tables S5–S8) give the results of additional simulations for power (primary locus) and Type I error (secondary locus) under the two loci model. These supplemental documents are available under the Paper Information link at the Genetics Research website (http://www.journals.cambridge.org/GrH). The R package ‘hwdglm’ is available from the author's personal website: http://www.statgen.ucr.edu.
We thank two anonymous reviewers for their informative comments on the first version of the manuscript. The project was supported by the USDA National Institute of Food and Agriculture Grant 2007-02784.










