1. Introduction

Polar ice cores drilled at different sites in Antarctica and Greenland (Reference Gow and WilliamsonGOW and Williamson, 1976: Reference Russell-Head and BuddRussell-Head and Budd, 1979; Reference Herron and LangwayHerron and Langway, 1982; Lpenkov and others, 1989; reveal strong fabrics, with significant alignment off axes of individual crystals along some preferential directions, induced by strains to which the ice is subject as it descends from the free surface to depth in an ice sheet. The fabric created during the ice deformation gives rise to macroscopic anisotropy of the medium which considerably affects polar ice-sheet dynamic behaviour over long time-scales. This has been confirmed by numerical simulations carried out by Reference MangeneyMangeney and others (1996), who have applied a transversely isotropic flow law. with a rotational .symmetry axis assumed to be vertical everywhere, to the ice-sheet flow problem with a non-evolving ice fabric derived from the measurements made along the GRIP ice core (Thorstcinsson and others, 1997). It has been found that for a given, fixed in time, free-surface elevation the assumption of the ice anisotropy results in much faster ice (low compared to the isotropic case, and an estimated accumulation rate required to maintain a steady-state flow exceeds by more than 1.5 times the rate for isotropic ice. Similar conclusions have been drawn by Reference Mangeney, Califano and HutterMangeney and others 1997), who considered a more realistic problem in which the free-surface elevation was calculated lor a fixed accumulation rate. Their numerical results showed that the ice anisotropy, as well as leading to a globally faster flow, significantly increases shear stresses near the bedrock, makes the free surface flatter in the ice-divide region, and smooths out the effects of the bed topography. This clearly indicates that the strain-induced anisotropy must be included in any large-scale numerical model of polar ice sheets if realistic results are to be obtained. However, there is still no generally accepted constitutive law describing the anisotropic behaviour of polar ice. This is partly because of the complexity of physical phenomena taking place on the microscale of single crystals during the fabric formation, but also because of difficulties associated with t he mathematical modelling of the strain-induced, evolving in time, anisotropy.

Following Reference Lliboutry and DuvalLliboutry and Duval (1985) and Aliev 1992 . we distinguish three main regions along the depth of a typical polar ice sheet in accordance with the microscopic processes which dominate the ice-fabric evolution.

• (1) In the upper part of a large ice sheet, extending from approximately 100m under the free surface to about one-third of its thickness, shear stresses are negligibly small compared to normal stresses. Deformation is mainly due to dislocation glide on basal planes, and caxes of grains rotate towards compressional axes. The grain-sizc increases linearly with the age of ice, which is here nearly proportional lo its depth, and no new grains are created.

• (2) Between approximately one-third and two-thirds of the ice cap thickness, the shear stresses gradually increase, though they are still smaller than the normal stresses. With increasing deformation and strain energy stored in grains, the fabric continues to strengthen and the process of polygomsation(also called rotation mrvstallisationj occurs. In this process new grains, with orientations similar to old grains which are not consumed by new nuclei, are produced. The average grain-size changes little with depth throughout this region,

• (3) In the region directly over the bedrock, the shear stresses dominate the normal stresses, which combined with high temperatures initiates the process of migration(or dynamic) recrystallisation.New, strain-free, grains with their caxes at high angles (~45°) to compressional axes are created at the expense of old grains which are consumed by new nuclei. Abrupt changes in the average grain-size are usually observed in this region, but generally the grains are much larger than in region 2.

In order to construct a macroscopic constitutive law for anisotropic polycrystalline ice, a basic and physically motivated approach is to derive an average response of ice aggregate from the properties of individual grains and assumptions on crystal interactions, To date, most of the existing anisotropic models include only the mechanism of the grain c-axis rotation, which dominates the fabric formation and evolution in the upper part of an ice sheet, although some attempts to incorporate the ecrystallisation process, prevailing in deeper regions of ice sheets, have already been made. Reference AzuraaAzurma (1994) and Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) assume that individual crystals deform only by basal glide, the glide direction is determined by that of the maximum macroscopic shear stress in the polycrystal, and the crystal (microscopic) and polycrystal (macroscopic) stresses, which may be different in this model, arc related by a geometric tensor associated with the c-axis and glide directions. Reference LliboutryLliboutry (1993) assumes that the microscopic stress acting on each individual grain is equal to the bulk macroscopic stress applied to the polycrystal, and formulates a flow law for a transversely isotropic aggregate. Reference Castelnau and DuvalCastelnau and Duval (1994) and Van derVeen and Whillans (1994) extended Lliboutry’s homogeneous stress model (also called the static model) to any type of evolving anisotropy by considering a polycrystal consisting of a finite number of grains. Reference Van der Veen and WhillansVan der Veen and Whillans (1994) are the first to include the recrystallisation mechanism in their model, and consider two alternative criteria to determine the onset of recrystallisation in terms of threshold accumulated strains of crystals. Another, more general, approach is the visco-plastic self-consistcnt (VPSC) model developed by Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others (1996). In this formulation, the single crystal is treated as an embedded idealised geometric inclusion in an infinite medium with properties of an assumed form supposed to represent the macroscopic behaviour. In contrast to the models discussed above, in which individual crystals can glide only on basal planes, in the VPSG model crystal slips on basal, prismatic and pyramidal planes arc considered, and stresses and strain rates are assumed to depend on the crystal lographic orientation.

In all the above theories, which can be called discrete grain models, usually about 200—400 grains are needed to properly describe the ice fabric at a given point. Since in typical large-scale numerical models for ice-sheet flows the number of mesh nodes can exceed 10⁵, it is obvious that discrete rain models are not suitable for simulations run on currently available computers. Therefore, in order to significantly reduce the number of variables involved in the description of ice fabric, another approach, in which the polycrystalline aggregate is treated as a continuum, has been adopted. In this approach a so-called orientation distribution function (ODF), defining continuous weightings to the grain C-axis orientation, has been applied. Although the eonccpt of the ODF is already well established in material science (Reference BungeBunge, 1982), it was first introduced to the field of theoretical glaciology only recently by Reference LliboutryLliboutry (1993), Reference Meyssonnier and PhilipMeyssonnier and Philip (1996) and Reference Svendsen and HutterSvendsen and Hotter (1996). Reference Meyssonnier and PhilipMeyssonnier and Philip 1996 formulated a transversely isotropic flow law for a polycrystalline ice using the ODF concept and the VPSC model by adopting some simplifying assumptions on the single grain behaviour, namely, that the crystal is transversely isotropic and offers small resistance to shearing parallel to its basal planes, and the response is governed by a linearly viscous law. Reference Svendsen and HutterSvendsen and Hutter (1996) employed the ODF approach to derive analytically a frame-indifferent viscous law which incorporates the fabric through a single structure tensor defined by an axis of assumed transverse isotropy. This theory has been considerably extended by Gödert and Hutter(1998, in press). However, the complicated calculations required to follow the evolving properties of individual ice elements will add considerably to numerical treatments ol large ice-sheet flows. A transversely isotropic flow law that avoids the use of an orientation distribution function has been proposed by Reference Van der Veen and WhillansVan der Veen and Whillans (1990). They modify Reference JohnsonJohnson’s (1977) law for a transversely’ isotropic viscoelastic solid by replacing material measures of stress and strain rate by spatial measures. However, they include the vertical (gravity) direction in the material structure, so this model cannot be treated as a valid constitutive relation for the response to general loading.

Dependence of the fabric on ice deformation implies that transverse isotropy of the medium can occur only if the flow in the ice sheet induces uniform stretches in some plane, say a horizontal plane in a gravity-dominated flow under a central dome, in which case a transversely isotropic fabric with the vertical as its rotational symmetry axis develops. Elsewhere in the ice sheet, however, such particular symmetry of the iceflow does not take place in general, and consquently the icedeformation, and hence the ice fabric, does not have rotational symmetry about any axis. Therefore, in order to more realistically describe the strain-induced ice fabric, a more general form of anisotropy is needed. Such increased generality is offered by orthotropic models. Although, strictly, the orthotropy does not occur for any arbitrary loading because of the fabric evolution which destroys any (already developed) orthotropic symmetries in the material, the assumption of orthotropy is strongly supported by observational data showing that the fabric in ice sheets does, in fact, usually reveal this type of material symmetry (this is in part due to the dynamic recrystallisation, not considered here, which helps to sustain the earlier created orthotropv despite the changes in the strain configuration).

In the paper, two orthotropic viscous models arc presented. The first model, formulated by Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier (in press), stems from analysis of the behaviour of a single ice grain in a polycrystal under the assumption of stress homogeneity, following Reference LliboutryLliboutry (1993) and Reference Van der Veen and WhillansVan der Veen and Whillans (1994). Assuming transverse isotropy for each individual crystal and a linear response to deviatoric stresses, the macroscopic strain rate of the aggregate is derived by applying the ODF concept. Compared to Reference Meyssonnier and PhilipMeyssonnier and Philip (1996), Reference Svendsen and HutterSvendsen and Hutter (1996) and Reference Godert and HotterGodert and Hutter (1998), additional parameters arc introduced into the ODF. Owing to the extra parameters, the derivation of a macroscopically orthotropic (instead of transversely isotropic) viscous law relating the strain rate to the deviatoric stress and three structure tensors is possible.

The second orthotropic model considered here has been formulated by Reference Morland, Staroszczyk and StaroszczykMorland and Staroszczyk (1998) and further extended by Staroszczyk and Morland (in press). In this approach it is assumed that the macroscopic mechanical respouse of ice can be described in terms of the fabric induced purely by macroscopic deformation, and all microscopic processes occurring at the grain level are ignored. The assumption that the induced anisotropy depends only on the current strains and not on the deformation history is a considerable simplification since, in general, the fabric evolution is a path-dependent process. It is believed, however,that this approximation is the simplest approach to an evolving anisotropic viscous law that could be tractable in large-scale sheet dynamics, since it requires that only current deformation gradients are calculated in addition to the velocity and pressure fields. The constitutive relation is derived from the general frame-indifferent orthotropic representation (Reference Boehler and BoehlerBoehler, 1987), and expresses the dcviatoric stress in terms of the current strain rate, deformation and three structure tensors. The relation is separable in the isotropic dependence on strain rate and fabric dependence on deformation, and in its simplified form has only one independent fabric function that fully describes the orlhotropic viscous response of ice. Although in this approach local interactions between individual crystals are excluded from the analysis, this method allows good qualitative agreement with observations, and flexibility to correlate with detailed experimental results.

The two orthotropic models are used to determine the viscous response of icc to simple stress and strain configurations, corresponding to those occurring in the uniaxial compression and simple shear tests carried out in a laboratory. The predictions of both theories are compared, and the influence of some model parameters on calculated responses is investigated. Additionally, the results for simple shear given by the micro macroscopic model are compared with the results obtained from a discrete grain model in which no assumptions are made about material symmetries) in order to verify the validity of the assumed orthotropic behaviour of polycrystalline ice.

2. Micro-Macroscopic Model

This model, formulated by Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier (in press), incorporates the basic micromechanism taking place on the grain level during the ice deformation, namely, the rotation of crystal caxes towards the axes of compression and away from the axes of extension. The macroscopic viscous outflow law which expresses the strain rates in terms of the deviatoric stresses is derived from the behaviour of individual grains by applying the homogenisation method based on the ODF approach,

In the following, three Cartesian reference frames are used to describe the behaviour of ice on the microscale of a single grain and the macroscale of a polycrystal:

{R} with axes x_iis a fixed global reference frame;

{R^o}is a privileged frame of an orthotropic polycrystal, whose axes (x_i)^o coincide with the orthogonal privileged directions in the material;

{R^g} with axes (x_i)^g is a local frame associated with an individual grain, whose (x₃)^g axis coincides with the c axis of this grain.

Microscopic quantities associated with an individual grain are indicated by a tilde, and superscripts “g”and “o” are used to denote non-scalar quantities expressed, respectively, in the focal {R^g} and the privileged orthotropic {R^o} frames. Where no superscript is applied, respective symbols refer to macroscopic quantities expressed in the global coordinate system {R}. Since the individual ice grain is assumed here to be transversely isotropic, with its c axis being the rotational symmetry axis, the grain position relative to the global reference frame {R} can be uniquely described by means of two angles: the co-latitude for zenith angle) θ and the longitude Φ (see Fig. 1) These two angles determine the rotation matrix R. (cf. Reference Meyssonnier and PhilipMeyssonnier and Philip. 1996) which connects components of vectors and tensors in {R} and {R^g}.

Fig. 1. Global and local reference frames, with angles θ and Φ difining the c-axis orientation if a grain.

Following Reference LliboutryLliboutry (1993) and Reference Van der Veen and WhillansVan der Veen and Whillans (1994), the hypothesis of tfic stress homogeneity in ice aggregate has been adopted

stating that the microscopic stress in each grain, irrespective of the grain orientation, is equal to the macroscopic (bulk) stress σ applied to the polycrystal. The deviatoric stress σ^´ is defined by

where pis the mean pressure, I is the unit tensor, and tr σdenotes the trace of σ. Since the ice is assumed incompressi ble, pis a workless constraint not given by a constitutive law, but determined by the momentum balance and boundary conditions.

Further, it is assumed that the transversely isotropic crystal deforms mainly by simple shear parallel Lo its basal plane,and its response to stress is linearly viscous. Adopting the simple relation (Reference Meyssonnier and PhilipMeyssonnier and Philip, 1996) between the microscopic strain rate D^~ and the microscopic deviatoric stress which is equal to the macroscopic stress σ^´ in view of Equation (1), the transversely isotropic How law can be expressed in the form

where M^~=c ® c is the structure tensor defined in the global reference frame {R} by the unit vector c = (sinθcosΦ, sinθsinΦ, cosθ) associated with the grain caxis, and ψis the fluidity (reciprocal viscosity) for shearing parallel to the crystal basal plane. The parameter β is the ratio of the shear viscosity in a plane parallel to the caxis to the shear viscosity in a plane of isotropy (normal to the c axis) and can be regarded as a measure of the grain anisotropy. When β=0, the grain can deform only by basal glide, as assumed in the Reference LliboutryLliboutry (1993) and Reference Van der Veen and WhillansVan der Veen and Whillans (1994) models, while β=1 means that the grain is isotropic. In what follows it is also assumed that each grain in a polycrystal occupies the same volume and the number of grains does not change during the deformation, i.e. the grain growth, polygonisation and dynamic recrystallisation phenomena are not accounted for in this model.

The macroscopic (bulk) strain rateD of the polycrystal, in response to the macroscopic deviatoric stress σ^´ is defined as the average of the strain rates of its constituent grains. Various homogenisation techniques can be employed to calculate the average strain rates in the ice aggregate. In the discrete grain models (Reference Azuma and Goto-AzumaAzuma, 1994; Reference Van der Veen and WhillansVan der Veen and Whillans, 1994; Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996) with a finite number of grains, the components of D are simply arithmetic means of the corresponding components of D. In our continuum model with an infinite number of grains, we make use of the ODFconcept, which describes the ice fabric in terms of the relative density of grains whose caxes have the orientation (θ,Φ)in the global reference frame {R}. In the ODF approach, the weighted average of a quantity A(θ,Φ) is defined by

where f(θ,Φ) is the proportion of grains with orientation (θ,Φ) in the element “area” θdθdΦ, and by definition

Note that in the case of isotropy we have f(θ,Φ) = 1, and for transverse isotropy, with x₃ being the rotational symmetry axis, the ODFdoes not depend on Φ i.e. f(θ,Φ)== f(θ).

Hence, by the weighted average definition (Equation (4)), the components of the macroscopic strain rates in the global reference frame {R} are given by

Once the ODF has been determined, Equations (3) and (6) yield the relation between the macroscopic strain rate D and the deviatoric stress σ^´In order to describe the evolution of the ODF, consider the motion of the single grain, i.e. the rotation of its caxis in the global coordinate system {R}. Following Reference Meyssonnier and PhilipMeyssonnier and Philip (1996), the rotation matrix R that defines t he orientation of the grain in {R} is governed by the relation

where R^T is the transpose of R, the superposed dot denotes the time derivative, W^g and W^~ are spins (rates of rotation) of the grain in the local and global reference frames, respectively, and c^g = (0, 0,1). Since during the grain deformation the original parallel glide planes remain parallel to each other, the velocity component along the crystal caxis, when expressed in the rotating frame {R^g} attached to the grain, is a function ofXj only. This leads to the kinematic relations

which are a direct consequence of the adopted system of reference frames. In order to close the system of governing equations, three additional conditions arc required, and these arc adopted by assuming that the microscopic and macroscopic spins are equal, i.e.

The above equation is closely related to the Reference TaylorTaylor (1938) assumption which postulates the equality of micro- and macroscopic velocity gradients. The combination of constraints (Equations (1) and (9)) adopted here is exactly the same as that used by Reference Godert and HotterGodert and Hutter (1998). With Equations (8) and (9), Equation (7) provides two relations which describe the change in (lie grain orientation by

Since recrystallisation is not taken into consideration, and hence the total number of grains in the polycrystal is conserved, it follows from the continuity equation (5) that the ODF satisfies the relation

Equations (10-12) completely describe the evolution of ice fabric for any type of macroscopic anisotropy that is based on the assumed behaviour of ice on the microscale of individual crystals. In the case of orthotropic anisotropy, the medium possesses three planes of reflexional symmetry, which in the reference frame {R°} are the planes ((x₁)^o,(x₂)^o),((x₁)^o),(x₃)^o)and ((x₂)^o,(x₃)^o) these material symmetries must be accounted for in the ODF. Following Reference Meyssonnier and PhilipMeyssonnier and Philip (1996), and using analytical results obtained by Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier (in press), we adopt the following form of the ODF;

where k₁, k₂,k₃ and Φ° are parameters, the latter being the angle of rotation of the orthotropic frame { R^o} with respect to the global reference frame -{r}. Since the grain-conservation relation (Equation (5)) implies that k₁, k₂, k₃ = 1,only three parameters in Equation (13) are independent. Now, by substituting Equation (3) into Equation (6), and using Equation (13) in Equation (4), we obtain the orthotropic, linearly viscous law relating the macroscopic strain-rates to the macroscopic deviatoric stresses by

where M^r _o = e^r _o ® e^r _o arc three structure tensors defined by the orthotropic axes unit vectors e^r _o, and J_r = tr(M^r _oσ^´)are three invariants. The six response coefficients α_i(i=1,...,6) are functions of the grain rheological parameters ψ and β

and N₃₀,N₃₂,N₅₀,N₅₂,N₅₄ are five moments defined by

In the case of ice isotropy, i.e. when f(θ,Φ) = 1 and kl = k2 = k3 = 1, the above moments are

and the six material coefficients defined by Equation (15) become

With the above parameters, and in view of the identity M₁ ^o+M₂ ^o+M₃ ^o= I , the orthotropie constitutive law (Equation (14)) reduces to the linear Glen’s flow law for isotropic ice

where ψ₀ is the fluidit y of the mac rosco pica lly isotropic p olycrysta l, which is related to the individual crys tal fluidity ψby

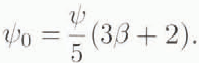
It follows from the la tter formula th at in the case of isotropic crystals (β = 1) the macroscopic fluidity ψ₀ equals the grain fluidity Φ while in the case of the most ani so tropic crystals (β= 0), when the grain deform ation occ urs only by basal glide, ψ₀= 0.4ψ.

3. Continuum model

In this continuum approach, proposed by Morl and Staroszczyk (1998) and further developed by Staroszczyk and Morland and (in press), the phenomena taking place on the microsca le of individual grains, as opposed to the model considered in section 2, are ignored , and it is assumed that the macroscopic response of ice depends only on the fabric induced solely by the mac roscopic deformations. Although this is a considerable simplification, it is beli eved th at such an approach to an eyoh-ing an iso tropic constitutive law is wel l suited to the large-scale ice-sheet modelling,since it req uires only that the deformation g radi ent field has to be determined during the ice flow in orde r to describe the fa bric development. The chosen (arm of the orth otropic viscous law is the relation between the frame-indifferent deviatoric Cauchy stress σ_´, c urrent strain rate D , Cauchy-Green stra in tensor B, and three structure tensors M_r(r = 1,2,3) defined by the outer products of the current principal stretch axes unit vectors e_r(r= 1,2,3).

Let OX_i(i = 1, 2,3) be spati al recta ng ular Cartesian coordinates with OX_i(i = 1, 2,3) particle reference coordinates,and V_i the velocity components, then the deformation gradient F and strain rate D have the components

The strain B , unit vectors e_r(i=1,2,3)and squares of the principa l stretches b_r(r= 1, 2, 3) are defined by

where λ_r(r = 1, 2,3) are principal stretches a long the principal axes e_r, and the three structure tensors M_r are given by

Ice is assumed incompressible, so

In order to derive the macroscopic flow law for anisotropic ice, we follow Boehlcr’s (1987) theory for frame-indifferent relations between tensors and vectors, which ensures that material properties are independent of the observer.In the case or a symme tric tensor (here σ^´) being a function of two oth er symmetric tensors (here D and B ), the general orthotropic representation is

where the 12 response coeffcients Φ(i = 1, ...., 12) are functions of the 19 invariants

subject to the constraints that the deviatoric Cauchy tress has zero trace, and the material is incompressible, so that only II coefficients Φ_i are independent, and only 18 invariants I_j are non-trivial, since I₁₉ = 1. An alternative constitutive law for the strain rate D in terms or the deviatoric stress σ^´ and the strain B , corresponding to the usual glaciological approach for the isotropic fluid model, can be formulated simila rly by interchanging σ^´ and D in Equation (25) and (26).

We require that Equation (25) reduces to an isotropic visco us-fluid law

where Φ₁, Φ₂ depend on two invariants tr D² and det D,when there is no fabric; that is, in the initial undeformed state F = I when the principal stretches are equal, necessarily λ_l = λ₂ = λ₃= 1 by the incompressibility co ndition (Equation (24)), or subsequently when F = I or when F corresponds to a rigid rotation of the ice clement. The conventional glaciological model is Φ₂= 0 and Φ₁ depends only on tr . The above prescription asserts that there is fabric - some alignment of initi ally randomly distributed c axes - only when there are differential principal stretches,i.e. when B≠I.

Following Staroszczyk and Morland (in press), we simplify the general law (Equation (25)) by ignoring tensor dependence on D², B² and DB, and the terms involving M_r without D or B, i.e. we restrict attention to a reduced model with a linear tensor dependence of σ^´ on D and B. Hence, we adopt the relation

where the Φ_r+3 and Φ₁₂ terms have been modi fi ed to recover zero trace, noting that the included scalar tr (M_rD ) = I_r,and the scalar tr (DB) = I₁₃+ I₁₄ +I₁₅. Equation (28) still represents a non-linearly viscous law since, in general, the response functions Φ_r+3 and Φ₁₂ depend on D. Wc further express these fun ctions in sep a rable forms which factor out im'a riants depending only on the deformation B and retain a common dependence on inva riants involving the strain rate D:

Where

The response functions (Eq ua tions (29) and (30)) have to satisfy the isotropic fluid law (Equation (27)) when B=I and hence I₂₁= I₂₂= 3; thus

where the functions h and g are normalised by

We restrict attention to a simple model with the fabric response function h depending only on the principal stretches λ_r(through I_r+3= b_r=λ_r ²), and the function g depending only on the invariant measure of total deformation I₂₁ = tr B; thus

where μ₀= 1/Φ₀ is the (consta nt) isotropic fluid viscosity (when bl = b2 = b3 = 1), and

Now, with Equations (34) and (32), the constitutive law (Equation (28)) expressed in terms of the two resp onse functions h and 9 and the viscosity μ₀ takes the linear form

Staroszczyk and Morland (in press) derived equalities and inequ a lities which have to be sati sfi ed by instal1laneous viscositiesties u_i)^j (i, j = 1, 2,3; i =1= j ), depending on the relative magnitudes of the principal stretches. With the ordering b1≥b2≥b3 there are six distinct sets of relative values of (b_r)(r= 1, 2, 3), and for each of them corresponding relations order μ₁₂,μ₁₃ and μ₂₃ in the coordinate frame of the principal stretch axes. By using the viscosity relation corresponding to the pla ne flow, i. e. when λ₂ = λ₂ = 1, hence b₃ = l/b₁ and K = b₁ + 1 + b₁ ^-1, it is possible to express g(K ) in terms of h(b_r), namely,

where

The limit of Equation (37) as b₁→1, K → 3, combined with the normalisation (34)₄ gives

which is a restriction on h(b_r) at b=1. Rewriting the function g(K) as

where G(K) is bounded, it can be shown that the limit of Equation (37) as b₁→α, K~b₁, yields the relation

That is, in view of Equation (37), only one fabric response function, h(b_r), remains free for prescription, subject to Equation (39). In order to further restrict this function, the model defined by Equation (36) is used to predictthe viscous response of ice at large deformations in the axial compression and simple shear conditions. For such configurations, Reference Budd and JackaBudd and Jacka (1989) present experimental data obtained for a steady-state flow (when the microprocesses of grain rotation, polygonisation and dynamic recrystallisation balance one another) and determine the limit ratios off abric-induced viscosity to (maximum) isotropic viscosity. These empirical ratios, expressed in terms of so-called enhancement fctors for compression and shear, provide two further relations connecting h(α), h(0) and G(α)(Staroszczyk and MOrland, in press ). For the uniaxial compression the viscous law (Equation (36)) yields

where A is the reciprocal of the axial enhancement factor, and for the simple shear in the plane flow we obtain

where S is the reciprocal of the shear enhancement factor. Equations (41–43) provide the following values of h(0), h(α) and G(α):

Despite several simplifying assumptions adopted to derive the model (36) with the single fabric function h(b_r) from the general orthotropic law (Equation (25)), this approach still retains considerable flexibility to correlate with observed data. In fact, only three specific restrictions are imposed on the function h: Equation (39) to yield a valid response in the isotropic state, and Equations (44) ₁ and (44)₂ to match the enhancement factors for compression and simple shearing at large strains. However, it is also required that the function h(b_r) yield a response which satisfies the viscosity relations derived in Straroszcyk and Morland (in press), otherwise physically invalid responses can be obtained.

4. Model Comparisons

The two orthotropic models described in sections 2 and 3 arc now applied to explore the viscous response of ice to simple deformation histories, corresponding to those taking place in typical laboratory tests. For the sake of brevity, throughout this section we will refer to the micro-macroscopic model as model A, and to the continuum model as model B.

First we consider an axial compression in the x₂ direction, defined by the axial stretch λ<1, with equal lateral stretches λ₁ and λ₃ along the x₁ and x₃ coordinate axes, for which the deformation field is described by

and the associated velocities, in view of Equations (45) ₄ and (45)₅ are

With Equations (45) and (46), the Cauchy-Green strain tensor B and the strain-rate tensor D are given by

and the three structure tensors, due to the coincidence of the principal stretch axes e_r with the coordinate axes x_r, are defined by

The deviatoric stresses (Equations (2)) are given by the diagonal tensor

The response of ice predicted by model A, defined by Equation(14), is illustrated in Figure 2, which shows the evolution of the normalised axial viscosity with increasing principal stretch λ₁ for different values of the grain-anisotropy parameter β. The curves corresponding to β = 0.10, 0.15, 0.20, 0.25 are labelled Al, A2, A3, A4, respectively, and the same labelling applies in subsequent plots illustrating the results given by this model. It is seen from the figure that the micro-macroscopic model predicts very slight softening of ice (decrease in viscosity) during the first stage of uniaxial loading, for the stretches 1≤λ₁1.2 (0.7λ1). The softening stage is followed by a phase of considerable hardening of ice, particularly pronounced for the stretches in the range 1.3 ^A|^ 1.7 (0.35 ^ Aa ^ 0.6) and small values of the parameter β (i.e.for very anisotropic ice grains). As the deformation continues, all the grain c axes rotate towards the compression axis (here the x₂ axis), and at large strains the macroscopic viscosity of a polycrystal approaches the axial viscosity of a single crystal. Since the latter viscosity is (1/β) larger than the viscosity for shearing on crystal basal planes, it follows from Equation (20) that the limit macroscopic viscosity for compression is given in terms of β by the relation

Fig. 2. Evolution qftlze ratio σ^´ ₂₂/(2μ₀D₂₂) with illmasing stretch λ_l increasing compression for different values of β in model A.

The viscous response of ice yielded by model B is determined by the function h(b_r). There is a variety of possible functions, as long as they satisfy some very general conditions (Staroszczyk and Morland, in press), and this gives the model ample flexibility to correlate with observations. For illustrations, we apply simple monotornic increasing functions

where h₀ and h_α=h(α) Equation (51) is a free parameter, and α in Equations (51) and (52) is determined by Equation (39). The limit values h(0) and h(α) are related through Equations (44) to A and S,, the reciprocalsof the enhancement factors. In Staroszczyk and Morland (in press) both A and S were chosen less than unity (both enhancement factors greater than unity), which corresponds to the values measured by Reference Budd and JackaBudd and Jacka (1989) for warm ice near melting. Here, in order to compare the predictions of the two orthotropic models, we adopt A > 1 (an enhancement factor for compression less than unity), meaning the increase in viscosity with increasing deformation, which according to Reference Pimienta, Duval and LipenkovPimienta and others (1987) is the case for the response of cold ice subjected to stress levels typically occurring in polar ice sheets. The value of A can be as high as 10 for a single-maximum fabric, as has been found experimentally by Reference Pimienta, Duval and LipenkovPimienta and others (1987), although recently Reference MangeneyMangeney and others (1996) calculated the value of about 3 for the ice near the bottom of the GRIP ice core, deduced from the data provided by Reference Thorsteinsson, Kipfstuhl and MillerThorsteinsson and others (1997). We carry out the simulations for two values of this factor, namely, A = 2.2, which is smaller, and A = 4.6, which is larger than the value obtained for the GRIP ice, though both orthotropic models are flexible in this respect and allow much larger values of A to be implemented. Since Expression (50), defining the asymptotic value of viscosity, is simply the reciprocal of the enhancement factor, A, it relates the parameter A in model B to the parameter β in model A. Hence, we find that the selected values A = 2.2 and A = 4.6 correspond to β=0.25 and β=0.10, respectively. Associated with the chosen values of A are the factors S=0.55 and S0.46= being the limit values of the normalised viscosity in simple shear, which correspond, respectively, to β=0.25 and β=0.10 in model A, as will be shown shortly in Figure 6. In view of Equations (44), we have the following connections:

The response functions hdetermined by the limit values in Equations (54) are illustrated in Figure 3, and very similar plots can be obtained for Equations (53). Henceforth, she curves labelled Bl, B2, B3 correspond to Equation (51) with m = 1,1.5,2, respectively, and the curves labelled B4 correspond to Equation (52).

Fig. 3. Fig. 3. Adopted forms of the fabric response function h(b_r) in model B.

With Equations (477#x2013;49), the constitutive law (Equation (36)) leads to the following relation describing the behaviour of ice in uniaxial compression:

where K = 2b₁ + b ⁻² ₁ . The evolution of the axial viscosity d22/(2Φ0D22) with increasing stretch At for the adopted forms of the fabric response function h(b_r)is illustrated in Figure 4 for the parameters in Equation (53), and in Figure 5 for the parameters in Equations (54). We note that the inlluence of the function h(b _r) on the predicted response of ice is most significant during the first phase of deformation. We see that the functions in Equation (51) with m = 1.5 and m = 2, curves B2 and B3, respectively, yield responses which agree quite well with the responses given by model A, curves A1 and A4, particularly for the set of parameters in Equations (54).

Fig. 4. Evolution of the ratio σ^´ ₂₂/(2μ₀D₂₂) with increasing stretch Al in uniaxial compressionJor dif.ferentJabric response functions h( b_r) in model B. The results Jor A = 4.6 and S = 0.46 are compared with the prediction of model AJor μ= 0.10.

Fig. 5. >Evolution of the ratio σ^´ ₂₂/(2μ₀D₂₂) with increasing stretch Al in uniaxial compressionJor differentfabric response Junctions h( b_r) in model B. The results Jor A = 2.2 and S = 0.55 are compared with the prediction of model A for β = 0.25.

Next we consider a simple shear at constant strain rate D₁₂ = 1/2 γ which follows an initial plane compression and stretch that has been frozen at constant λ₂ = λ₁ ^-1 蠄 1 by the removal of the stress and strain rate. The deformation field is now described by

the corresponding velocities are

and the strain and strain-rate tensors arc defined by

The principal stretch squares b_i (i=1,2,3), the eigenvalues of B, are given by

and the associated principal vectors e_r are determined by Equation (22) ₂. In terms of these vectors, the three structure tensors are expressed by

The response of ice to simple shearing given by model A, defined by Equation (14), is illustrated in Figure 6, which shows the evolution of the normalised viscosity σ^´ ₁₂/(μ₀ γ) With increasing shear k started from the isotropic state (λ₁=λ₂= 1) for different values of the grain-anisotropy parameter β We note that the model predicts initial hardening of ice (for strains K≲1), with a more significant increase in viscosity taking place for smaller values of β(i.e. for more anisotropic ice grains). As shearing continues, the initial hardening is followed by the softening phase, with a monotonic decrease in viscosity until an asymptotic value is reached at large strains, This limit value is given by

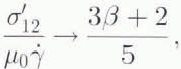
and follows from Equation (20), since at very large shear deformations all crystals are aligned for easy glide on basal planes I their caxes are approximately parallel to one another; and hence in the limit the macroscopic viscosity of a polycrystal approaches the viscosity of an individual grain.

In Figure 6 we also show the results predicted by a discrete grain model, with 800 grains, for β=0.10(curve Dl), and β=0.255 (curve D4). The discrete model is based on the same assumptions as model A, except that no restrictions on material symmetries are imposed, so il has a more general character than the orthotropic model. Therefore, comparisons between the predictions of both models should give some indication whether the assumption of orthotropy of ice is justified. The results obtained seem to support the validity of this assumption, since the maximum relative discrepancies between curves A1 and Di, and A4 and D4, do not exceed 15% for k ~ 1, and for larger shear strains (k≲5) die agreement between the results given by both models is very good.

The behaviour of ice predicted by model B, defined by

Fig. 6. Evolution of the ratioσ^´ ₁₂/(μ₀ γ) with increasing strain k in simple shear started from an isotropic state (λ₂= 1) for different values of βin model A. Also shown are the results given by the discrete grain model for β= 0.10 (curve Dl) and β=0.25(curve D4).

Equation (36) with Equations (58—60), is described

where now k = b₁+ b₁ ⁻¹ + 1. Figures 7 and 8 show, for different fabric response functions (Equations (51) and (52)), the evolution of the viscosity ratio σ^´ ₁₂/(μ₀γ) with shear _ started from the isotropic stare (λ₁ = λ₂2 = 1). The same sets of parameters as in the uniaxial compression simulations are used, i.e. those in Equation (53) for Figure 7 and those in Equation (54) for Figure 8, and again the results yielded by model B are compared with the predictions of the micro-macroscopic model A (curves A1 and A4). It cats be observed that now, for simple shear, the discrepancies between the responses given by the two models are more considerable than in the case of uniaxial compression, especially for the parameters in Equation (53) (Fig. 7), corresponding to more anisotropic grains (smaller value of β) in model A, or “stiffer” ice (larger value of the viscosity factor A) in model B. For the parameters in Equation (54) (Fig. 8), a good qualitative agreement between the two models is still readied, although model A predicts more significant increase in ice viscosity during the initial phase of shearing. However, the discrepancies between the two models are still limited to relatively small (compared to those occurring in ice-sheet flows) shear strains, so it is anticipated that in realistic ice-sheet flow simu lations the two constitutive theories should yield similar predictions for most of an ice sheet, apart from a region near the ice divide, where (relatively) small shear deformations occur.

Fig. 7. Fig. 6. Evolution of the ratio σ^´ ₁₂/(μ₀ γ) with increasing strain k in simple shear started from an isotropic state (λ₂ = 1) for different response functions h(b_r) in model B. The resultsfor A = 4.6 and S = 0.46 are compared with the prediction qf model A jor β= 0.10.

Fig. 8. Evoluation of the ratio σ^´ ₁₂/(μ₀ γ) with increasing strain r;, in simple shear started from an isotra/lic state (λ₂ = 1) jor different fabric response functions h(b_r) in model B. The resultsfor A = 2.2 and S = 0.55 are compared with the prediction qf model A jor β= 0.25.

5. Conclusions

We have presented two orthotropic models for viscous response of ice based on two fundamentally different approaches. The first, a micro-macroscopic model, has been derived from the behaviour of individual ice grains and incorporates the mechanism of crystal rotation in response to shear stresses. The second, a macroscopic model, was constructed by applying the general theory of frame-indifferent(objective) relations for materials with orthotropic anisotropy. The results of numerical simulations for continued uniaxial compression and simple shearing have shown that for appropriately chosen model parameters a good correlation between the responses given by the two theories can be achieved. Both models predict significant hardening of ice in compression, and initial hardening followed by softening in simple shear, which seems to agree with the observed behaviour of cold ice at low stress levels. The theoretical results, however, should be verified against detailed experimental data; unfortunately, very few relevant data on cold ice are available, since practically all laboratory tests performed to date have been carried out on warm ice near melting and at relatively high deviatoric stresses. It is also anticipated that the numerical simulations of realistic ice-sheet flow’s and the comparison of results obtained in this way with in situ data should throw some light on the validity of the assumptions made in the paper: first of all, whether the assumption of orthotropic behaviour of ice is justified, or a more general form of anisotropic constitutive law is required.

Further work should concentrate on including in the models other micromechanisms, such as rotation and migration (dynamic) recrystallisation. This will, however, add considerably to the complexity of theoretical formulations. This is particularly true of the micro-macroscopic model, and, to the authors’ knowledge, very few attempts to incorporate recrystallisation have yet been made. In terms of extending its generality, the continuum model is more flexible, since only the modification of response functions is required, although in order to account for a more complex mechanical behaviour more tensor generators may be needed in the constitutive law. Finally, we would like to emphasise that in order lo construct a model that properly describes the behaviour of ice in polar ice sheets, more experimental work on cold ice needs to be done to provide reliable input data for the theory.

Acknowledgements

The authors would like to thank two anonymous referees for thorough reviews that have helped to improve the paper. Part, of this work was done while the first author was visiting the Laboratoire de Glaciologie, Saint-Martin-d’Heres, France, supported by EISMINT Exchange Grant No. 9709 funded by the European Science Foundation.