1. Introduction
It is commonly claimed or assumed in historical linguistics that the expected direction of morphological change is for low token frequency members of inflectional paradigms to be replaced with innovative forms based on higher token frequency paradigm members.Footnote 2 For example, Mańczak (Reference Mańczak and Fisiak1980) claims that high token frequency forms (e.g. singular number, 3rd person) are likely to serve as analogical bases for the remaking of other forms, and Bybee (e.g. Reference Bybee1985, Reference Bybee1995) that high token frequency forms have a high degree of lexical autonomy and are thus less susceptible to replacement by new forms.
This study provides empirical confirmation of this hypothesis, using a dataset of morphological changes involving ancient Greek verbs. On the basis of this evidence, I will argue for a theory of morphology in which at least some fully inflected forms are stored in memory, and others are predicted on the basis of stored forms, by extending formal patterns of implication from stored exemplars.
This supplies new diachronic evidence for the question of how speakers predict unknown inflected forms of a lexeme. This problem, termed the Paradigm Cell Filling Problem (PCFP) by Ackerman, Blevins & Malouf (Reference Ackerman, Blevins and Malouf2009), is hardly trivial in a language like ancient Greek, with inflectional paradigms containing hundreds of forms, and extensive allomorphy that is not predictable on the basis of extramorphological information such as phonology or semantics. Greek is neither unusual in this regard, nor an especially extreme case. The diachronic evidence presented here supports the view of Ackerman et al. (Reference Ackerman, Blevins and Malouf2009) that the solution to the PCFP lies in the implicational structure of inflectional paradigms. This position also fits with psycholinguistic research (e.g. Taft Reference Taft1979, Losiewicz Reference Losiewicz1992, Baayen, Dijkstra & Schreuder Reference Baayen, Dijkstra and Schreuder1997, Baayen et al. Reference Baayen, McQueen, Dijkstra, Schreuder, Baayen and Schreuder2003, Hay Reference Hay2001, Milin et al. Reference Milin, Kuperman, Kostic and Baayen2009, Lõo et al. Reference Lõo, Järvikivi, Tomaschek, Tucker and Baayen2018) showing that the speed with which inflected words are processed is a function of their token frequency, and suggesting that there is competition in processing between on-the-fly morphological analysis and retrieving forms from memory as unanalysed wholes.
A similar theoretical position underlies the proportional model of analogical change. In this model, an instance of morphological change is represented as the solution of a proportion a: b = c: x, where x represents some novel form standing in the same formal and functional relationship to c as b does to a. For example, the plural brethren was replaced (in most of its senses) by brothers in the history of English, on the model of exemplars like sister ~ sisters. This form of representation dates back at least as far as Hermann Paul, who introduced analogical proportions in the 1880 edition of his Principien der Sprachgeschichte (Paul Reference Paul1880), and was intended as a representation of a psychological process underpinning the creation of new forms. While this model of morphological change continues to be used in mainstream historical linguistics, it has been subjected to a number of critiques over the years, most forcefully from generativists in the late 1960s and early 1970s, who charged that it was insufficiently predictive. In this paper I will outline a computational implementation of the proportional model which, when supplemented with token frequency information, makes verifiable predictions for diachrony. This confirms the essential insight of the proportional model, that speakers draw on implicational patterns in stored exemplars to solve the PCFP.
Note that token frequency (frequency in language use, estimated on the basis of corpora) is distinct from type frequency (the frequency of a particular type of lexeme, such as an inflection class, in the lexicon). Type frequency also influences morphological change, in that productive patterns of inflection (or derivation), which apply to a large number of lexemes, tend to be extended diachronically to new lexemes, at the expense of irregular or unproductive patterns (e.g. Bybee Reference Bybee1995, Sims-Williams Reference Sims‐Williams2016). In the example given above, the lexeme sister makes a plausible analogical model for brother because it belongs to the highest type frequency class of nouns which form plurals with the suffix -s. This study focusses not on the type frequency of analogical models, but the token frequency of analogical targets and bases: respectively, the forms affected by analogical replacement (e.g. brethren → brothers), and the forms on which these innovative forms are based (e.g. brother).
The paper is structured as follows. In Section 1 I will explore the theoretical assumptions underlying the proportional model and compare their diachronic implications with those of other morphological theories. I argue that the proportional model better accommodates evidence from morphological change, but that in its traditional form it is too vague and unconstrained to be predictive. In the rest of the paper I suggest an approach to overcoming these limitations by giving the proportional model a precise computational formalisation, and supplementing it with external constraints based on token frequency, to make specific and testable predictions about morphological change. Section 2 outlines a method for delimiting a possibility space of analogical proportions and estimating their viability using token frequency statistics. This section also introduces the synchronic and diachronic data on which the model is tested, and the results are given in Section 3. In Section 4 I propose an extension to the model which estimates the relative probability of a potential innovative form from the viability of all the proportions underlying it, and assess this model against the diachronic data. Finally, in Section 5, I will discuss the interpretation of the results and draw theoretical conclusions.
1.1 Morphological theory and morphological change
Language change is not irrelevant to synchronic theory. It is desirable on the grounds of economy to be able to state synchronic and diachronic generalisations concisely within a single model, and for this to be possible, we need synchronic theories to contain the same entities and properties we need to refer to when we are describing language change. Moreover, if we believe that language change occurs as a by-product of the cognitive processes that underlie language acquisition and performance, then diachrony is a valuable source of evidence for a synchronic theory which aims to model how speakers actually produce inflected forms. A comparison may be drawn with recent work on morphomes, a term coined by Aronoff (Reference Aronoff1994) to describe semantically and morphosyntactically unmotivated patterns of distribution of morphological formants within paradigms, which nonetheless recur systematically across the lexicon. The diachronic persistence of morphomes (as documented extensively by e.g. Maiden Reference Maiden2005, Reference Maiden2013, Reference Maiden2018) is generally taken as a form of evidence for their psychological reality to speakers, which in turn is part of the justification for granting them a place in synchronic theories (e.g. Stump’s Reference Stump2001 ‘morphomic rules of inflection’), with the added benefit of reducing redundancy in linguistic descriptions (Blevins Reference Blevins2006). In this section I will discuss a few influential theoretical approaches of the last century and contrast their implications for diachrony, arguing that the evidence of analogical change supports a theory in which inflected words may be stored whole in the lexicon.
1.1.1 Analogy in generative linguistics
Paul Kiparsky’s Ph.D. thesis (Kiparsky Reference Kiparsky1965) set in motion a research programme recharacterising the neogrammarian toolkit of sound change and analogy within the framework of generative linguistics, in which analogical change was recast as change either to phonological or morphological rules (see King Reference King Robert1969). A number of criticisms of analogy were made – not all of which can be discussed here – but one major motivation for getting rid of the proportional model was that it allows the representation of vastly more changes than actually occur, many of which are intuitively extremely unlikely. For example, Kiparksy (Reference Kiparsky, Anderson and Jones1974) points out that we do not expect a new verb *heye meaning ‘to see’ on the basis of a proportion ear: hear = eye: x, though this proportion is structurally indistinguishable from those which have supposedly generated actual forms such as sister: sisters = brother: x. Footnote 3
Instead, he argued, analogy can only be successfully constrained by the requirement that it should be a simplification of grammar. This was an attempt to reconcile synchrony and diachrony: grammar simplification was claimed to follow from the way that the learner’s evaluation measure chooses the simplest grammar (in terms of minimum description length) compatible with the linguistic data they are exposed to. Ultimately, this claim was not borne out by empirical evidence. Putting aside the difficulty of measuring grammatical complexity (e.g. Miestamo, Karlsson & Sinnemäki Reference Miestamo, Sinnemäki and Karlsson2008, Sampson, Gil & Trudgill Reference Sampson, Gil and Trudgill2009), analogy often seems to be neutral in its effect on the complexity of grammar, and sometimes appears to complicate it (e.g. Thomason Reference Thomason and Christie1976, Sims-Williams & Enger Reference Sims-Williams and Enger2021).
Moreover, because it constrains change at the level of underlying grammar rather than surface language, this approach sits awkwardly with the observation that formal similarities between inflected surface forms appear to motivate many examples of analogy. For example in Latin, the 4th declension noun senātus ‘senate’ had its genitive singular form senātūs replaced by a 2nd declension form, senātī, apparently because the 2nd and 4th declensions shared word-final -us in the nominative singular (see (1) below; 4th declension noun portus ‘port’, which was unaffected by the change, is included for comparison; compare examples discussed by Vincent Reference Vincent, Anderson and Jones1974). By comparison, lexemes lacking -us in the nominative singular (such as 3rd declension princeps ‘ruler’) were not affected.

These problems led the theory to be gradually amended, with an increasing role gradually assigned to the mechanism of language acquisition: ‘the assumption that analogy must represent simplification with respect to the adult grammar is entirely unwarranted. The most that we can legitimately claim is that analogical innovations represent analyses which are optimal at the particular stage of language acquisition at which these analyses arise and for the particular set of primary linguistic data which is under consideration by the language learner at that stage’ (Kiparsky Reference Kiparsky and Kachru1978, reprinted in Kiparsky Reference Kiparsky2012: 230). Regardless of whether this position is correct, it brings us no closer to constraining analogy than the proportional model did.
1.1.2 Realisational theories
Inflection classes involve conditional exponence, whereby the expression of certain morphosyntactic or morphosemantic properties depends on how other such properties are expressed in other forms belonging to the same paradigm. A change like (1) above involves the extension of conditional exponence: identifying the same element -us in the nominative singular of senātus and a 2nd declension form like animus justifies extending the element -ī from the genitive singular of animus to the genitive singular of senātus.
In realisational theories of morphology (e.g. Anderson Reference Anderson1992, Stump Reference Stump2001), rules of exponence ‘spell out’ or ‘realise’ sets of morphosyntactic properties which are already present in the input to rules, deriving surface forms ready for syntactic insertion. Inflectional affixes are encoded as part of the rules of exponence, which operate on roots or stems in the lexicon,Footnote 4 but need not be meaningful in themselves. These theories differ from morphemic approaches in that they regard the word as the minimum unit of language that is necessarily meaningful, without presuming that the relationship between individual elements of meaning and form at the sub-word level will be one-to-one. Conditional exponence is captured by introducing arbitrary inflection class indices to roots or stems, which partly determine which of a number of competing rules of exponence applies.
This kind of account not only generates the correct forms, but does so in a way that captures generalisations economically, by stating them only once at the relevant level instead of repeating redundant information. But because the derivations of the members of a paradigm are isolated from each other,Footnote 5 so that rules of exponence cannot refer to inflected words, it accommodates diachronic generalisations less well.
Diachronically, lexemes are more likely to transfer between inflection classes which are similar in the sense that they share exponents. Such cases of inflection class transfer can be modelled as changes to the inflection class of a root, but because the inflection classes themselves are represented as arbitrary indices without internal structure, the points of similarity between them which motivate the change are not represented in the synchronic model (see Parker, Reynolds & Sims Reference Parker, Reynolds, Sims, Sims and Ussishkin2022, who demonstrate using computational simulations how shared exponents condition the restructuring of inflection classes). Changes involving partial mergers of inflection classes present even more of a problem. Consider again the example of (1) above, where the genitive singular senātūs of the 4th declension noun senātus ‘senate’ was replaced by senātī, a form based on the 2nd declension. Because other forms of senātus remain consistent with the 4th declension, this change cannot simply be analysed as a change to the inflection class of senātus. We can only get around this problem by adding a lexically specific realisation rule for the genitive singular of senātus, obscuring its similarities to both the 4th and 2nd declensions. Recall that noun types with nominative singular forms not ending in -us, such as princeps ‘ruler’ (see (1) above), were excluded from this change. But from the point of view of the architecture of a realisational model, there is no reason the same change should not happen in the paradigm of a 3rd declension noun like princeps, generating a new genitive singular principī (replacing principis).
1.1.3 Word-based morphology
In realisational theories words are seen as the fundamental meaning-bearing unit of language, but they are nonetheless constructed morphotactically out of more basic forms (i.e. stems, and affixes encoded as part of realisation rules). In contrast, analogical proportions are associated with a notion of word structure rooted in the ancient grammarians, which sees the word as the basic unit of language, and regards the morphological component of grammar as a set of abstract formal and functional relationships between inflected words stored in memory. In a Classical word-and-paradigm approach redundancy in morphological descriptions is limited by stipulating only a single exemplary paradigm for each pattern of inflection, and a minimal set of diagnostic principal parts for remaining lexemes. Under this approach sub-word units like stems and affixes can be seen as abstractions arising from the organisation of words into paradigms; for this reason it is termed ‘abstractive’ by Blevins (Reference Blevins2006, Reference Blevins2016). Recurring elements of form may or may not correspond to consistent elements of meaning or morphosyntax, and there is no requirement that each inflected word can be uniquely cut up into a single correct segmentation. Instead, comparison across different paradigmatic dimensions may suggest different segmentations that are equally valid.
Under this approach, an explanation for why senātī is more probable than principī is built into the synchronic architecture. A form like senātī can be seen as an extension of the relationship between the nominative and genitive singular forms in the paradigms of second declension nouns such as animus ‘spirit’. This can be represented unproblematically in an analogical proportion (2), or schematically as in Table 1.
The schematic notation spells out what the proportional notation leaves implicit: a change principis ⟶ principī is less likely than senātūs ⟶ senātī, because the nominative singular princeps lacks the final sequence -us, and thus fails to meet the description of the input (Xus) in the schematic rule which derives animī from animus.
Table 1 Schematic rule deriving genitive singular from nominative singular forms.

For the neogrammarians this was not just a descriptive model, but also a psycholinguistic one. The stipulation of exemplary paradigms and diagnostic forms in a word-based approach correspond to storage in memory, and the remaining forms are predicted by a process of pattern-matching.Footnote 6 Analogy was not just a mechanism of change, but also the basic mechanism of morphological production by which conventional forms are also produced (e.g. Paul Reference Paul1877: 324–325; Paul Reference Paul1886: 88–89; Morpurgo Davies Reference Morpurgo Davies1978). Analogical proportions are an idealised visual representation of this process. In a proportion of the form a : b = c : x, x represents an unknown form, while a and b represent the exemplar on whose basis it is to be predicted. A procedure for deriving the form of b from a is computed – for (2), this can be informally stated as ‘exchange -us for -ī’ – and applied to c, which stands in the same functional relationship to x as a does to b.
Morphological productivity can be modelled using analogical proportions because of the way that inflectional paradigms are structured. Instead of distributing allomorphy randomly, they tend to contain recurring patterns of interpredictability between their forms. In recent years, these have been the subject of renewed interest, particularly since Ackerman et al.’s (Reference Ackerman, Blevins and Malouf2009) articulation of the Paradigm Cell Filling problem. One strand of research has shown that cross-linguistically, the predictability of inflectional paradigms tends to be much higher than is logically necessary, as the result of implicative structure: see in particular Stump & Finkel’s (Reference Stump and Finkel2007, Reference Stump and Finkel2013) work on the typology of principal part systems (specifically the ‘Depth-of-Inference Contrast’, Stump & Finkel Reference Stump and Finkel2013: 215), and Ackerman & Malouf’s (Reference Ackerman and Malouf2013) ‘low conditional entropy conjecture’. Carstairs-McCarthy’s structural constraints on inflection classes (Carstairs Reference Carstairs1983, Reference Carstairs1984, Reference Carstairs and Fisiak1985, Reference Carstairs1987; Carstairs-McCarthy Reference Carstairs-Mccarthy1994, Reference Carstairs-Mccarthy1998), while not expressed in implicational terms, can also be reduced to a set of constraints on implicational structure (Blevins Reference Blevins, Müller, Gunkel and Zifonun2004). A growing body of research explicitly or implicitly addressing the PCFP suggests that speakers are sensitive to implicational structure: e.g. Ackerman & Malouf Reference Ackerman, Malouf, Hippisley and Stump2016, Bonami & Beniamine Reference Bonami and Beniamine2016, Sims & Parker Reference Sims and Parker2016, Blevins et al. Reference Blevins, Milin, Ramscar, Kiefer, Blevins and Bartos2017, Malouf Reference Malouf2017; see also Albright Reference Albright2002, Reference Albright and Good2008, Reference Albright2009, who shows that the direction of levelling of morphophonological alternations can be predicted by a model which selects the most informative member of a morphological paradigm as the base.
1.1.4 Limitations of the proportional model
For the Neogrammarians, proportions were not just a useful shorthand, but an attempt to capture the psychological process underpinning linguistic productivity. Their essential insight that speakers use implicative relations between inflected words stored in memory as a source of evidence for predicting unknown forms is supported both by the evidence of morphological change and by typological findings on implicative structure in inflectional paradigms. But as a notational device, there is much that analogical proportions leave implicit. As a result, the diachronic implications of the synchronic theory are imprecise.
When presented with an analogical proportion, the reader is left to guess to what extent the lexemes given as the model (items a and b in the proportion) and the environment of the change (c and x) are standing in for sets of lexemes.

The example in (2) above could also have been based on any noun of the second declension, such as the word for ‘slave’, which inflects in the same way as animus, see (4), and it affected other words which, like senātus, belong to the 4th declension, such as arcus ‘bow’ in (5). Likewise the extent of the base (a and c) and the target (b and x) are not made explicit: (2) could equally be based on the accusative singular, as in (3), and it also affected forms other than the genitive singular in some nouns, see (6).
The only constraints which come implicitly with the proportional notation are that there must be both a formal and functional operation mapping a to b which can also be applied to c, giving a solution for x. These operations may refer to particular formal or functional features which must be present in their inputs. In this case, the set of permissible inputs is the set of words which meet the functional description [nominative, singular] and the formal description ‘Xus’. (7) is rendered invalid by its failure to satisfy the formal description: since princeps lacks the final segment -us, we cannot ‘exchange us for ī’.

If the proportional model is to make concrete and testable predictions, we need to supplement it with a method for generating a possibility space of proportions from synchronic data, and ranking the viability of each proportion in that space. In the following section, I will outline a method for generating a set of proportions based on synchronic data from ancient Greek verbal paradigms, and show how these can be supplemented with information about the relative token frequency of morphosyntactic categories to derive a successful ranking of each proportion’s viability, i.e. its probability of generating a form x which is attested in subsequent language change.
1.1.5 Comparison with existing computational models of analogy
The model of analogical change that will be developed in this paper is a computationally implemented version of the proportional model traditionally used in historical linguistics, extended and supplemented with statistical information about the relative token frequency of paradigm cells. Since computational models of analogy already exist, readers might wonder why another one is needed. Therefore, before getting into the details of my model, I will briefly explain its fundamental differences from some influential existing approaches to modelling analogy computationally.
The most well known computational models of analogy are Skousen’s Analogical Modelling of Language (AML; Skousen Reference Skousen1989) and the Tilburg Memory-Based Learner (TiMBL, a specific implementation of memory-based learning; Daelemans & Van den Bosch Reference Daelemans and van den Bosch2005, Daelemans et al. Reference Daelemans, Zavrel, Van der Sloot and van den Bosch2010). While they use different algorithms (see Eddington Reference Eddington, Skousen, Lonsdale and Parkinson2002 for a comparison), both are feature-based classification models which attempt to predict the linguistic behaviour of items by comparing them to exemplars stored in memory, and selecting analogical models from among these exemplars. Both have been successful in modelling a wide range of linguistic phenomena. They are designed to model synchronic learning and productivity, but can be adapted to accommodate examples of language change involving the redistribution of linguistic items between preexisting categories, such as which negative prefix an adjective uses (Chapman & Skousen Reference Chapman and Skousen2005), or which inflection class a verb belongs to (Strik Reference Strik2015). However, the categories to be predicted and their possible values have to be pre-selected and built into exemplars, as do the variables and values likely to be useful for prediction, in order for the system to predict the behaviour of a new item. Therefore they cannot straightforwardly accommodate changes that alter the system of categories itself, such as cases of morphological resegmentation or restructuring of inflection classes. This makes them unsuitable for modelling the diachronic dataset used here, which involves inflection classes merging partially or fully before ultimately collapsing into a single class (2.1.2). By contrast, the model developed here takes unsegmented surface forms as input, and performs on-the-fly morphological analyses of subsets of these surface forms, without attempting any global analysis. No analysis is built into exemplars beyond a set of associations between inflected words, represented as phonological strings, and the lexemes and paradigm cells that they instantiate. This gives it the flexibility to accommodate a broader variety of changes, such as the resegmentation of the 3pl suffix -on as -n (with the preceding -o being attributed to the stem), which resulted in the creation of a new suffix -osan (see 2.1.2.1). In other words, it is an abstractive model in which words have no universally valid segmentation; some proportions will support decomposition into the same stems and suffixes that a human linguist would be likely to find, others will yield alternative idiosyncratic segmentations, and some will be unsolvable, supporting no segmentation at all.
Another point of contrast is that the central concern of both AML and TiMBL is the selection of analogical models, while this paper is concerned with typical properties of analogical bases and targets (Table 2). The notion of an analogical base has no equivalent in AML or TiMBL. Their focus has been primarily on type rather than token frequency, because type frequency has a much clearer effect on analogical model selection (e.g. see discussion and references in Eddington Reference Eddington2004). To the extent that token frequency has been considered within this work, it is the token frequency of lexemes serving as competing analogical models or destinations (in the terminology of Table 2), rather than paradigm cells. For example, Strik (Reference Strik2015: Chapter 9) explains patterns of (resistance to) inflection class shift in Frisian as the result of analogical pressure as predicted by an AML model, combined with lexical token frequency. While type frequency effects undoubtedly play a large role in analogical change, the goal of this study is to isolate the effects of token frequency on analogical base and target selection: in other words, which paradigm cells are affected by analogical change, and which paradigm cells are used as the basis for creating novel forms.Footnote 7
Table 2 The anatomy of an analogical proportion a : b = c : x.

2. Method
The synchronic data used in this study consists of aorist (past perfective) active subparadigms of ancient Greek verbs, where several sets of person-number suffixes were in competition. The diachronic data consists of novel aorist active forms attested after the period represented by the synchronic data (the 5th century BC) and before 400 AD, involving the reorganisation and extension of these suffixes to new lexical enviroments. This synchronic data will be described in 2.1.1, and the diachronic data in 2.1.2.
From the synchronic data, I calculated a set of analogical proportions of the form a : b = c : x, where a/b (the model) and c/x (the destination) are representatives of different inflection classes, and a/c (the base) and b/x (the target) represent paradigm cells with distinct person/number features (Table 2). I adapted an algorithm by Lepage (Reference Yves1998) to compute a solution for x for each of these proportions. The procedure for generating and solving these proportions will be described in 2.2.
I then obtained statistics on the relative frequency of each person-number combination in Greek (2.3), to see how the token frequency of the base and target of a proportion affects the viability of a proportion – that is, the probability that it it is successful, in that it generates a form which is attested in the diachronic data.
In the sample of hypothetical proportions generated in 2.2, I measured the probability that a proportion with each person-number value appearing in either its base or target was successful. These measures were then compared to the relative token frequency of each person-number value in Section 3.
Finally, I used a logistic regression model to derive an estimate of the viability of a proportion, taking into account the relative frequency of the person-number value of both its base and target (4.1). I then built on this to estimate the relative probability of a potential innovative form as a function of the viability of all the proportions underlying it (4.2). In 4.3 I test the predictions of this extended model against the diachronic dataset, and assess the significance of the results.
2.1 Test case
2.1.1 Synchronic data
The Attic dialect of Classical Greek (spoken in the region of Attica, which included the city of Athens, in the 5th century BC) had four distinctions of inflection class in the past perfective (aorist) active, each of which selected distinct but overlapping sets of suffixes to express the person and number of the verb’s subject.Footnote 8 Suffix allomorphy neither determines or is determined by stem allomorphy (Sims-Williams Reference Sims‐Williams2016: 316–318): for instance, verbs which use the weak aorist person-number suffixes typically form their aorist stem by adding a suffix -s to the imperfective stem, but there are many exceptions. These four patterns of suffix allomorphy are exemplified in Table 3 in order of type frequency.
Table 3 Classical aorist and perfect active suffixes. Those in the shaded cells survived into Byzantine and Modern Greek (see Table 4).

In post-Classical Greek the present perfect started to merge semantically with the aorist, and eventually became synonymous with it, creating a new form of morphological overabundance, whereby multiple forms occupy the same paradigm cells (Thornton Reference Thornton, Maiden, Smith, Goldbach and Hinzelin2011). This added another set of competing aorist forms to the four already mentioned.
Already in Classical Greek, there was extensive formal overlap between these competing sets of suffixes. Table 3 contains only 17 distinct suffixes, although five sets of six person–number values allows a theoretical maximum of 30 exponents. In particular, the suffixes of the perfect differed from those of the weak aorist only in the 3pl, the root and kappatic aorist have identical plural formations, and the 3sg suffix -e(n) is shared by all but the root aorist class. In Medieval Greek, these five sets of suffixes merged into a single aorist active paradigm (Table 4): while variation remained in the second and third plural cells, it was no longer conditioned by lexeme.Footnote 9 The suffixes which survived this merger correspond to the grey cells in Table 3.
Table 4 Byzantine and Modern Greek past active suffixes.

Before merging completely, these suffixes influenced each other in a variety of ways. For example, a new suffix -osan frequently replaces 3pl -on in the strong aorist (and also the imperfect, which had the same suffixes as the strong aorist) from the third century BC onwards, showing influence from the root aorist 3pl -san. This was eventually ousted by -an. This innovation seems to be an extension of the formal relationship between first person singular and third person plural forms in verbs with root aorists to strong aorists (Table 5)
Table 5 Proportional representation of 3pl forms in -osan.

2.1.2 Diachronic data
The diachronic data consists of examples of morphological changes in the aorist active involving cross-contamination between these sets of suffixes, between 400 BC and 400 AD, collected from online databases of texts.Footnote 10 This period runs roughly from the conquests of Alexander the Great in the mid-4th century BC (and with them the standardisation of Greek in the form of the Hellenistic Koine, based on the Attic dialect), through the period of Roman administration of the Greek world, to the establishment of Christianity as state religion in the Eastern Roman empire under the emperor Theodosius I, marking the beginning of the Byzantine empire.
2.1.2.1 Changes affecting strong aorist verbs
In Hellenistic Greek, the distinction between the strong and weak aorist paradigms was gradually lost. Strong aorist verbs with weak aorist endings, illustrated in (8) below, are extremely common in this period. Strong aorist verbs are also occasionally found with the 3pl suffix -āsi, originating in the present perfect, see (9); this is unsurprising, since the present perfect was becoming increasingly synonymous with the aorist, and its suffixes differed from those of the weak aorist only in the third person plural.

In the early stages of the merger of strong and weak aorist, third person plural forms in -osan are very common:

These reveal the influence of the root aorist (see Table 5 above) and perhaps also the kappatic aorist (a parallel change occurred in the imperfect, which had the same set of suffixes as the strong aorist). These forms were briefly very common, but soon afterwards lost ground to forms with the suffix -an of the weak aorist (see (14) below). In the Septuagint (a 3rd-century Greek translation of the Old Testament), ḗlthosan outnumbers ḗlthan by 122 counts to nine, while in later papyri ḗlthan is found 74 times, compared to only six counts of ḗlthosan.
2.1.2.2 Changes affecting weak aorist verbs
Although weak aorist forms tended more often to replace strong aorist forms (see (14) below), the endings of the strong aorist also spread to weak aorist verbs, particularly in the second person (11). While they are much less common than forms in -osan (see (16) below), we also find occasional 3pl forms in -asan (12), which may be based on either the root or kappatic aorist pattern.

2.1.2.3 Changes affecting kappatic aorist verbs
The kappatic aorist had always shared the endings of the weak aorist in its singular forms. Verbs with kappatic aorists started to assimilate fully to the weak aorist paradigm in the late Attic of the 4th century, starting with third plural forms in -an (13), which had been attested even earlier in the Ionic dialect. These were followed by 1pl -amen and 2pl -ate, which become standard in the Koine, and may equally have originated from the present perfect (which shared not only the singular person/number suffixes of the kappatic aorist, like the weak aorist, but also the stem-final suffix -k). The 3pl perfect suffix -āsi is also found (14), showing the definite influence of the present perfect. After the loss of distinctive vowel length, the kappatic 3pl édosan (from dídōmi ‘give’) creates an alternative paradigm with stem-final -s (15). This is also supported by the future dṓsō. Kappatic aorists were also occasionally influenced by the strong aorist (see (17) below), particularly in second person forms (16).


2.1.2.4 Changes affecting present perfect forms
Finally, the endings of the perfect were distinct from those of the weak aorist only in the third plural forms (-an/āsi), and this distinction is frequently erased by the spread of -an from the weak aorist to forms with perfect stems (17).

The combined effect of these changes, along with the later elimination of the root aorist pattern (which took place beyond our cut-off point of AD 400; see Horrocks Reference Horrocks2010: 302–303) was to reduce the five sets of aorist person-number suffixes in Table 3 to the single set of suffixes found in Byzantine and Modern Greek.
2.2 A computational implementation of the proportional model
This section describes how I implemented the proportional model to create a sample of analogical proportions from the synchronic Greek data, solve these proportions for x, and identify which of the solutions matched innovative forms found in the diachronic data. In 2.2.1 I describe a set of steps for solving analogical proportions which were automated as a computer program, giving a precise definition of the intuitive solution to an analogical proportion, and of the circumstances under which a proportion is ill-formed (2.2.1.2). 2.2.2 will outline a method for generating a sample of analogical proportions from the synchronic Greek data.
2.2.1 An algorithm for solving analogical proportions
The proportional notation relies on our ability to make an intuitive leap from a specific exemplar like animus : animī to a general operation deriving one form from the other. It is worth examining precisely how this leap is made, since the abstract relationship between two related words can always be understood in a number of ways. In the previous section, we characterised the procedure for deriving animī from animus as ‘exchange -us for -ī’, but any of (18)–(24) would work equally well.
In this section I will outline an algorithmic method for solving a proportion of the form a : b = c : x which identifies the intuitively correct analysis of the relationship between a and b, and excludes unintuitive analyses like (18)–(24). This models how speakers make productive generalisations from stored exemplars, although the algorithm described here is not intended as an implementational model (i.e. a step-by-step account of how speakers actually produce analogical forms). It is useful for two reasons: firstly, it gives a coherent and precise functional definition of what many linguists would regard as the intuitive answer to a proportion. Secondly, it makes it possible to generate and analyse a large number of proportional analogies automatically, which would be impractical to do manually.
The input to the algorithm is a set of three inflected words, whose role in the proportion is indicated by the labels a, b and c. Each of a, b, and c consists of a functional description that describes how the inflected words are used, and a formal description that describes their phonological form. The functional description is a set of lexical, morphosemantic and morphosyntactic properties, and the formal description is a sequence of symbols representing phonological segments.
In theory, we need to generate both a functional and formal description for x. Informally, the functional description of x consists of all lexical, morphosemantic and morphosyntactic elements of b and c which are not shared with a, plus any lexical, morphosemantic and morphosyntactic elements which a, b, and c all have in common. For example, the proportion given in (25) has the solution [horse feminine singular genitive]. If we model functional descriptions as sets of lexical and morphosyntactic/morphosemantic properties, the functional description of x can be obtained using a few simple set-theoretic operations. The formula for obtaining this solution is given in (26), and illustrated with a Venn diagram in Figure 1.
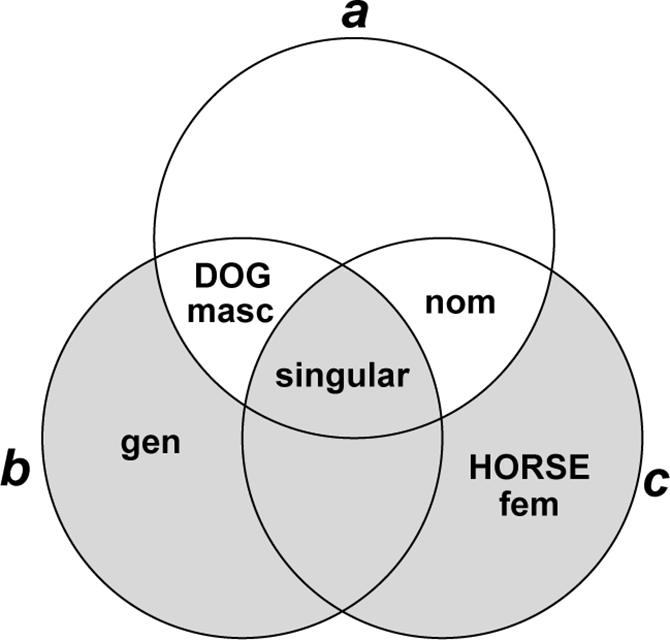
Figure 1 Venn diagram representing the solution of a proportion a : b = c : x (the shaded area represents the solution x).
This paper will focus exclusively on the neutralisation of meaningless alternations of form, which entails that the functional description of x will always be identical to that of b in all but the lexical element. But in theory, modelling the functional side of proportion-solving as a set-theoretic operation allows changes which eliminate meaningless allomorphy and those which neutralise the expression of morphosyntactic contrasts to be understood as variations on the same theme. As described in section 2.1.2, the weak and strong aorist (which differed in all but the 3sg suffix -e) began to merge from the 3rd century BC onwards, resulting in forms like ébala ‘I threw’ for earlier ébalon (27). Much later, in around the 9th century AD, a parallel merger took place between the suffixes of the aorist and the imperfect, resulting in forms like éballa ‘I was throwing’ for earlier éballon (28). Proportions (27) and (28) parallel each other exactly on the formal side, but on the functional side (27) neutralises a distinction of inflection class (because items a and c have identical morphosyntactic properties), while (28) neutralises a formal distinction which was partly responsible for conveying imperfective vs. perfective aspect (although this distinction is still expressed in the verb stem, as it continues to be in Modern Greek).


The formal description of the solution to a proportion is equivalent to its functional description in that it consists of all the formal elements of b and c which are not also found in a, along with any formal elements shared by a, b and c. However, because the elements of the formal description must also be put together in a particular order, finding the formal description of x cannot be achieved only by set-theoretic operations.
My implementation generates a formal description for x using an adaptation of an algorithm by Lepage (Reference Yves1998) (analyses like (18) above are excluded by the fact that the formal descriptions contain no information about morphological structure). The algorithm works by iteratively running a matching algorithm between a and b, each time (i) moving anything in b which precedes the match to the right edge of x, (ii) deleting matched material in a and b, and (iii) swapping b and c. The matching algorithm runs again with new values for a, b, and c, until every element of a has been matched and removed. At this point what remains of b is added to x, and x is yielded as the output of the algorithm. Table 6 shows how this generates a solution for animus : animī = senātus : x. Footnote 11
Table 6 Step-by-step solution for animus : animī = senātus : x.

This algorithm puts the intuitive value of x on a systematic footing, which in turn enables the solving of analogical proportions to be automated. In Section 2.2.2 I will develop a framework for computationally generating and solving a large number of proportions, and explore their statistical properties.Footnote 12
2.2.1.1 Limitations of the algorithm
This algorithm has certain limitations. It only works for flat sequences, and cannot accomodate hierarchical structure (e.g. it cannot alter part of a feature bundle, or insert something into a syllable). Therefore it cannot cope with proportions where the procedure for deriving b from a must make reference to suprasegmental features like being syllable-final, or having the same place of articulation as the following segment. For example, it cannot solve an equation like dog : god = pan : nap , because it does not recognise that d in dog shares the property of being word-initial with p in pan, but has the property of being word-final in god. Similarly, it cannot deal with phenomena like reduplication or vowel harmony, which require recognising that segments are wholly or partially identitical to other segments in the same word, unless these features are encoded as segments (for example, to incorporate possible changes involving the extension of vowel lengthening/shortening and reduplication in my Greek data, I encoded vowel length using the symbol <:> following the vowel, and I encoded the reduplicating consonant of the perfect prefix as <R>). To accommodate these cases, a more sophisticated procedure for identifying similarities and differences between phonological sequences would be required, but the version described here is sufficient to capture the phenomena relevant to this data.
My implementation of this algorithm adds initial and final word boundary symbols to a, b, and c. This helps it to find the intuitively correct solution of certain proportions which in theory allow more than one solution, such gradūs : gradibus = ūsūs : ūsibus (instead of ibusūs).
In some cases there are multiple orders in which subsequences between a and b/c can be identified, not all of which lead to a solution. My implementation deals with this by iterating through the possibilities, ultimately yielding an error only if none of these attempts lead to a solution for x. By default, the matching algorithm identifies the match closest to the left edge of a, and extends it as far as possible in b. If the first attempt leads to an error, it tries looking for a match in c instead of b. If this fails, it attempts to identify matches starting from the right edge of a, instead of the left edge (matching initially with b, and then with c in case of an error).
2.2.1.2 Well-formedness constraints
In order to be well-formed, a proportion must meet the structural requirement that a is entirely composed of elements shared with b and c. If this is not the case, the algorithm above will not be able to generate a prediction for x, because at some point before the end criterion has been met (before a is empty), it will fail to find a match between a and b. In this case my implementation produces an error. A step-by-step example is given in Table 7.
Table 7 Step-by-step procedure for an ill-formed proportion.

The same restriction in principle applies to the functional side of the proportion (although this is not implemented in this paper, as explained in 2.2.1). This captures what is wrong with a proportion like cat : catalogue = bat : x (Morpurgo Davies Reference Morpurgo Davies1978: 51). While a phonological solution batalogue can be found without any problem, no elements of meaning are shared between cat and bat on the one axis, or cat and catalogue on the other, making batalogue uninterpretable (unless catalogue is reanalysed as containing the element cat, e.g. ‘a catalogue of cats’).
2.2.2 Defining the possibility space
The next step is to define a possibility space of proportions representing hypothetical morphological changes; in other words, to create a sample of proportions which can be solved using the algorithm described above, whose solutions we will then look for in the diachronic data. This is essential, because we can only determine what factors encouraged attested changes to happen when we consider them against the background of possible changes that did not take place.
I am assuming that sets of person/number suffixes are more likely to merge when they are already competitors in the same set of paradigm cells (see 2.2.1). In other words, the greater the number of features shared between a and c, the more likely a proportion is to generate an attested form for x. A formal relationship is more likely to spread to the aorist active, therefore, if it is attested in the aorist active for other verbs. This assumption is built into my test, because I am only considering changes which involve analogical influence between synonymous sets of forms. Occasionally formal patterns do spread to parts of paradigms where they are not previously attested, e.g. the merger of past perfective and imperfective illustrated in (27)–(28) above. A superficial look at the development of Greek suggests that this is less common than influence between competitors in the same paradigm cells. By considering only aorist active allomorphs, I am controlling for this potential factor, in order to isolate the effects of token frequency as much as possible.
Given five patterns of aorist inflection (weak, strong, root and kappatic aorist and perfect), and six combinations of person and number, the maximum number of proportions of the form a : b = c : x is 600.Footnote 13 I wrote a program to generate these 600 proportions, and attempted to predict a value x for each of them, using a computer implementation of the algorithm described in 2.2.1.
Because the items in these proportions are acting as representatives of patterns of inflection, rather than individual verbs, the values for x represent idealised types of innovative form, rather than individual forms. For example, both élipas ‘you (sg) left’ (replacing élipes), and ébalas ‘you (sg) threw’ (replacing ébales) represent tokens of the same type of form, in which the 2sg suffix of the weak aorist has been extended to verbs with original strong aorist paradigms. Because the historical record rarely attests full paradigms for each verb at a given point in time, I have only been able to make a binary distinction in this paper between attested and unattested values for each x, irrespective of how many tokens of each type are attested. For most types, a large number of forms are attested, of which a few representative examples are given in 2.1.2. The paradigm of édōsa (seen in example (15) above) is the only example I have used where a single verb is affected. My implementation also represents phonological sequences which are constant throughout individual aorist active paradigms with an arbitrary symbol, to improve the efficiency of the matching algorithm described in 2.2.1, while still replicating its results. I also represented vowel length and reduplication of consonants using arbitrary symbols, as described in 2.2.1.
From this theoretical maximum of 600 proportions, we must subtract the number of proportions which fail to make a unique prediction for x (e.g. (29); for these proportions, the algorithm in 2.2.1 generates an error as described in 2.2.1.2).

I will also assume that there is a strong constraint against new forms which would violate surface phonotactics. For example, I am excluding (30)–(31) because the forms they generate have nasals in syllable codas, which are not allowed in Greek, unless they are the final segment in the word. My program excluded these proportions by consulting a dataset of illegal phonological sequences each time it predicted a value for x, and discarding the proportions for which x contained an illegal sequence.


Finally, we want to exclude proportions which generate a form that is already present in the synchronic data (e.g. (32)). The purpose of computing the set of possible proportions is to see what sets those which predict attested forms apart from those which predict unattested forms. Clearly, the distinction between attested and unattested is meaningless for these proportions. My program excluded them by searching for each x in the synchronic dataset of Classical Attic forms, and discarding proportions for which x is attested amongst these forms.

Subtracting these three groups of ineligible proportions from our upper bound of 600 leaves 249 possible proportions (Table 8). Since multiple proportions can predict a single form (e.g. (33)–(34)), the number of forms generated by these proportions is much fewer (106).


Table 8 Calculating the number of possible proportions.

2.3 Measuring token frequency
Next, the sample of proportions generated in the previous section were supplemented with token frequency statistics, such that each proportion in the sample is associated with a figure for the relative token frequency of the morphosyntactic property sets in its base and target cells. These figures will be used to estimate the probability of potential innovative forms in Section 4.
I obtained statistics on the token frequency of each person/number using a program which automatically parses each word in the Perseus Project’s (www.perseus.tufts.edu) corpus of xml texts.Footnote 14 The results vary depending on which authors are included in the corpus (see the sample in Figures 2–5), although the singular is always more frequent than the plural, and the third person is always more frequent than the first and second person. Naturally, written texts do not always reflect spoken language accurately, and a text’s genre influences which real or imaginary speech act participants are involved. For example, narrative texts (e.g. Xenophon, Figure 4) will inevitably overrepresent the third person. By comparison, Plato’s writings use the 1sg, 2sg and 1pl comparatively more often (Figure 3), since they are largely in the form of dialogues between two characters, while works of rhetoric (e.g. Demosthenes, Figure 5) contain a greater number of 2pl forms, since they are written as speeches addressed to an assembly. Of the genres represented in the Perseus collection, drama is likely to be the best approximation to a spoken corpus, because it contains a high proportion of dialogue between a relatively wide variety of speakers. The comedies of Aristophanes (Figure 2) are particularly appropriate because they are written in more colloquial language than that of the Greek tragedians. For these reasons I chose Aristophanes’ works as a corpus for the token frequency statistics to be compared with the result of the previous section.
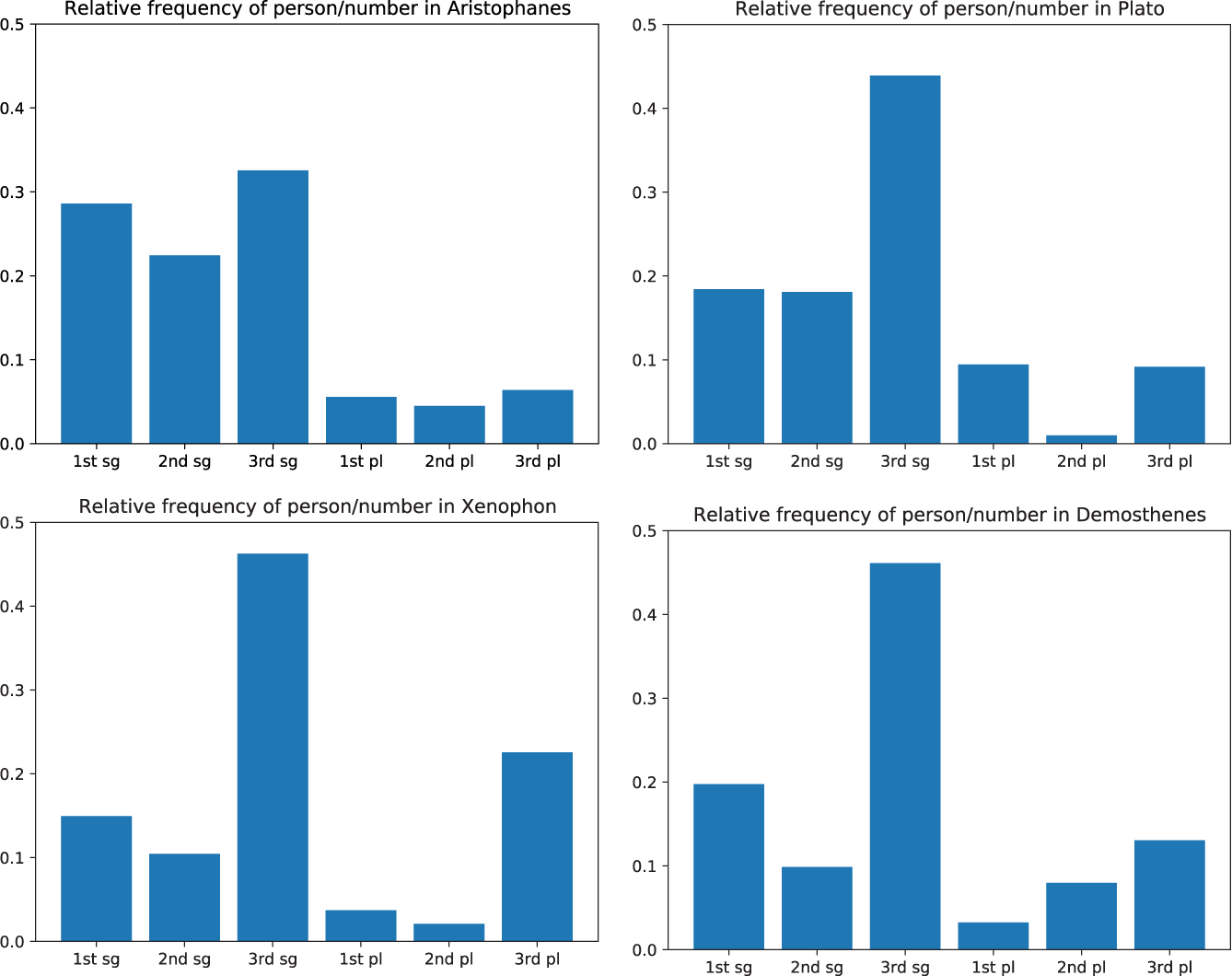
Figures 2–5 (Colour online) Relative frequency of person/number values in the works of four Greek authors writing in the Attic dialect.
These figures measure the token frequency of whole inflected words occupying paradigm cells with particular person/number values, regardless of which suffixes realise person and number within those words. Because of the large amount of allomorphy in ancient Greek (the allomorphy described in 2.1.1 only scratches the surface), cell frequency is a poor measure of the frequency of sub-word forms. This distinction is important, because these figures are to be used as estimates for the token frequencies of inflected words in proportions, averaging over inevitable differences in lexical frequency.
3. Results Footnote 15
3.1 Comparing the set of potential proportions with the diachronic data
The next step is to look for the forms generated by our sample of proportions in the diachronic data described in 2.2.1. Of the 106 potential innovative forms generated by the 249 eligible proportions computed in 2.2.2, 22 are actually attested diachronically. These 22 forms correspond to 64 proportions (Table 9).
Table 9 Possible vs attested proportions/forms.

Given a proportion with a particular person/number value appearing in its base or target, we can express the probability that it is successful – i.e. that it generates an attested form for x – as the number of times that person/number value appears in the base/target of a successful proportion, divided by the number of times it does so in a possible proportion (Table 10). These statistics (rows e–f of Table 10) can now be compared with the token frequency of each person/number combination.
Table 10 Likelihood of each person/number value appearing in the base (row e) and target (row f) of a successful proportion.

3.2 Correlation with token frequency
The diagrams below show the correlation between the relative frequency of each person/number combination and its likelihood of serving as a base (Figure 6) and target (Figure 7) in a proportion that predicts an attested form. There is a strong positive correlation (r = 0.96, p = .002) for base frequency, and a strong negative correlation for target frequency (r = −0.97, p = .002). This correlation strongly supports the hypothesis that the viability of a proportion – i.e. the probability that the form it generates is historically attested – depends partly on the token frequency of the forms in its base and target.

Figure 6 (Colour online) Correlation between relative frequency and base likelihood.
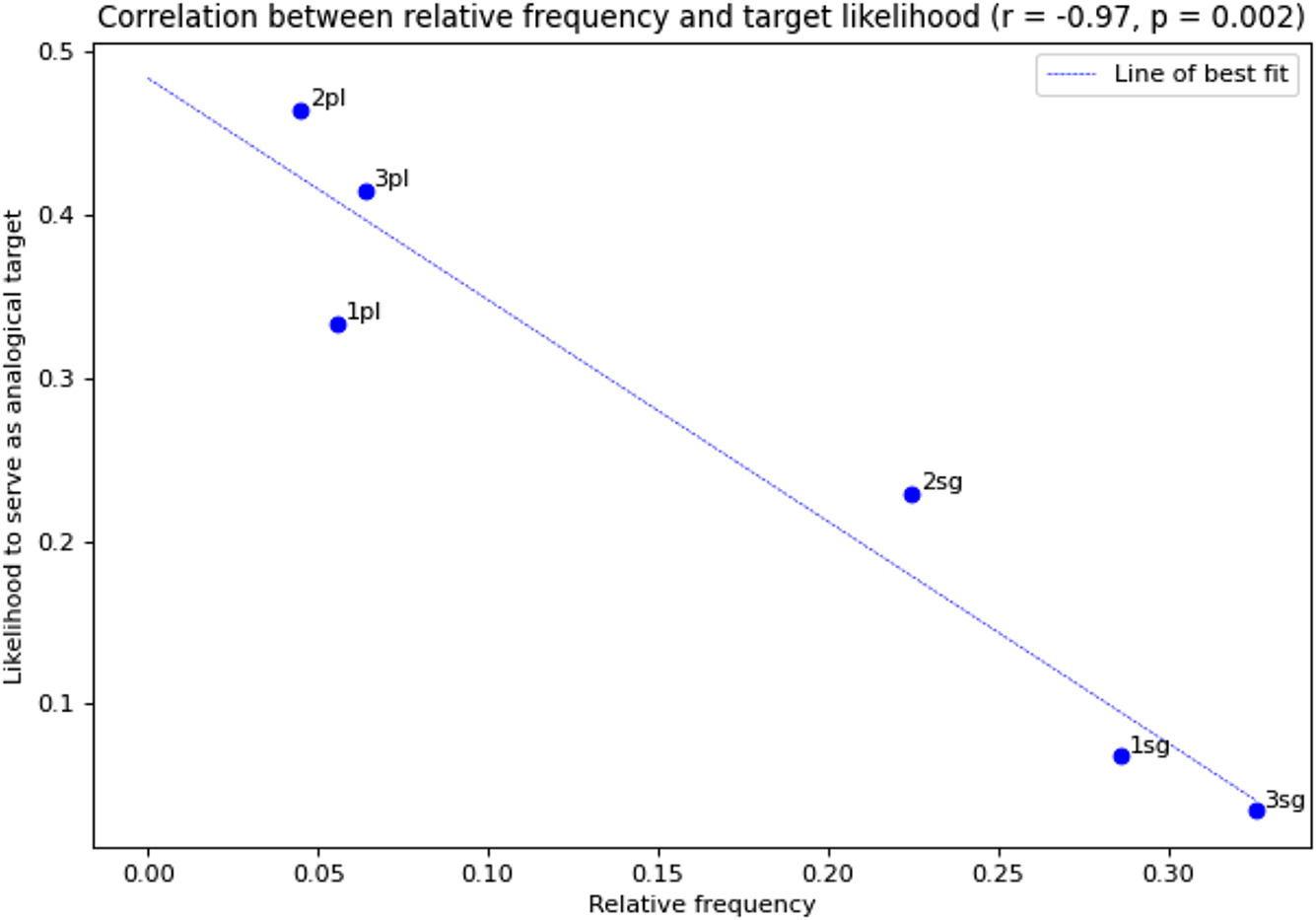
Figure 7 (Colour online) Correlation between relative frequency and target likelihood.
4. Extending the model
4.1 Logistic regression
Section 3 established that the viability of an analogical proportion correlates positively with the relative frequency of its base, and negatively with the relative frequency of its target. The next step is to develop a model that combines measures of base and target frequency to derive an estimate of a proportion’s viability. A logistic regression model was fitted to the sample of hypothetical proportions, in which the dependent variable is equal to 1 if the proportion’s prediction for x is attested diachronically, 0 otherwise (Table 11). This showed a highly significant positive effect of the relative token frequency of the base, and a highly significant negative effect of the relative token frequency of the target, confirming that proportions with high frequency bases and low frequency targets are more likely to generate diachronically attested forms. The model was then used to produce a viability score for proportions V(p): an estimate of the probability that a proportion generates a form attested in the diachronic data, given the relative token frequency of the cells appearing in its base and target.
Table 11 Logistic regression results.

4.2 Estimating the probability of forms
So far we have come up with a way to rank the viability of proportions, but ideally we would like to rank the probability of forms, many of which are generated by multiple proportions (Table 12). It makes intuitive sense that forms supported by a greater number of proportions should have a higher probability of being attested, all other things being equal.
Table 12 Proportions underlying three hypothetical forms.
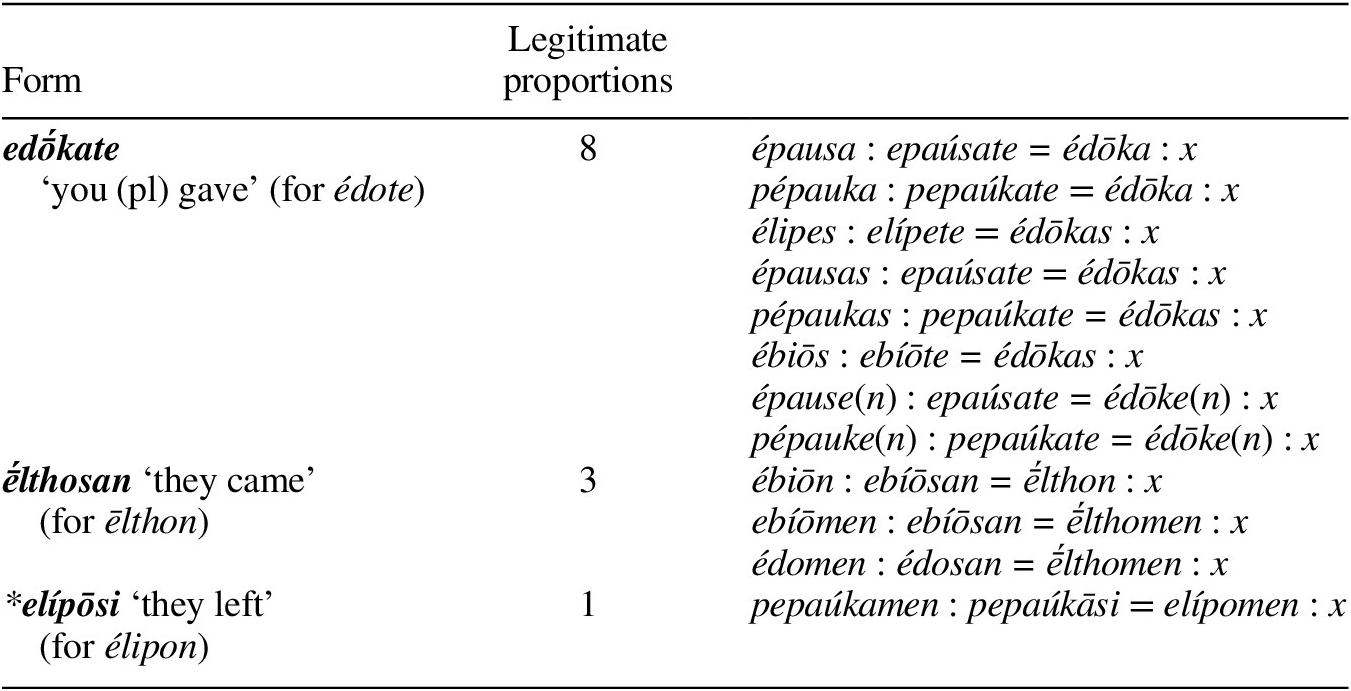
Table 13 gives the viability score for each of the three proportions underlying a form like ḗlthosan. If analogical forms come about through speakers extending formal patterns of implication, and each proportion represents a formal pattern of implication, each of the proportions i–iii represent alternative ways for ḗlthosan to come into existence. The probability of ḗlthosan should, therefore, be a function of the viability of the proportions underlying it: if one or more of them is extended, ḗlthosan will be attested. The form ḗlthosan will not be attested only in the case that none of these proportions are extended.
Table 13 Possible proportions underlying ḗlthosan in Table 12.

Following this line of reasoning, a probability score M(x) for a form x can be derived as follows. First we identify the set of all legitimate proportions X that generate the form x. For each of these proportions, the viability score V(p) represents an indirect measure of the form x coming into existence via a particular proportional model; therefore, the complement of the viability score (1−V(p)) represents an indirect measure of the probability that x will not come into existence via this model. By calculating the product of 1−V(p) for all proportions which are members of X, we can obtain an indirect measure of the probability that x will not come into existence via any proportional model, i.e. that it will not be attested in the diachronic data. Finally, the complement of this product gives us a measure of the probability that the form x will be produced on the basis of at least one proportion. This is given as a formula in (35), and the calculation for x = ḗlthosan (using the viability scores listed in Table 13) is shown in (36).

In Section 1.1. 5 I highlighted how the proportional notation does not make explicit the extent to which a, b, c and x are merely representative examples of the base, target, model and destination in a change. This method of calculating the probability of an analogical form deals with this vagueness by treating the probability of an attested form as a function of the viability of all possible proportions which could underlie it.
This reasoning is based on the assumption that these events are independent and do not exclude each other. In a monolithic variety of a language without any internal variation, this assumption would not hold, because any change would alter the synchronic state of the language and thereby alter the sample space of possible changes. This phenomenon, whereby past events limit the range of possible future outcomes, is known as path dependence. However, during the time period in question, Greek was used over a huge area and for a wide variety of purposes, leading to rich dialectal and sociolectal variation. Moreover, higher register forms of Greek were heavily influenced by the prestigious standard of classical Attic, which is the source of our synchronic data (2.1.2). This sociolinguistic situation makes Greek particularly suited to a study of this type: the high degree of variation creates multiple paths along which the language can evolve, and the continued influence of the synchronic starting point from which the sample space was calculated (2.2.2) minimises the effect of path dependence. As a result, the assumption of the probability model is borne out: forms which might be expected to be mutually exclusive in a monolithic Greek are simultaneously attested in the diachronic data. For example, alongside classical Attic eîpon and eîpan ‘they said’, we also find eípāsi, eípasan and eíposan, reflecting all of the 3pl allomorphs in 2.1.2. Often multiple forms are attested in a single text: e.g. the Septuagint contains the variants ḗlthan, ḗlthon and ḗlthosan for the aorist active 3pl of the verb ‘to go’ (for an overview of geographical and sociolinguistic variation in the Hellenistic and Roman Greek empires, and the persistent influence of classical Attic, see Horrocks Reference Horrocks2010).
Note that the probability score as calculated in (36) is not a direct estimate of form probability, but merely a measure which is expected to correlate with form probability. The viability score developed in 4.1 directly estimates the probability that the form predicted by a proportion is attested in the diachronic data, but says nothing about whether that proportion actually contributed to the creation of the form in question. However, we are now treating each proportion as a potential event leading to the creation of a form x, and the viability score as a measure of the probability of that event. As such, we expect the viability score to be consistently overgenerous (because the logistic regression model underlying it treats all proportions underlying a form as successes, even if they were irrelevant to the creation of the form), and therefore we expect the probability score based on it (35) to consistently overestimate form probability. This is not a problem for present purposes, since we are seeking to rank the probabilities of forms, rather than to measure these probabilities directly (and in fact any direct measure of probability would be arbitrary, because the length of the time period chosen for the diachronic data is arbitrary).
If this is a valid method for ranking the probability of forms, we should expect the 22 attested forms in the sample to have a higher average probability score than the 84 hypothetical forms which are not attested. Furthermore, the distribution of forms between the attested and unattested group should be consistent with their probability scores: as the probability score of a form increases, its likelihood of being in the attested rather than the unattested group should also increase.
4.3 Results
The predictions of this extended model are well supported by the diachronic Greek data. The average probability score of the attested forms is much higher than that of the unattested forms (Table 14). Fitting a logistic regression model revealed a reliable effect of probability score as estimated by the combined model on the actual probability of a form x appearing in the diachronic data (logit coefficient: 3.4760, SE = 0.987, z = 3.521, p = .00043). Figure 8 provides a visual representation of the distribution of probability scores in the unattested and attested groups. The two violin plots are scaled so that each has the same area. The area of each plot between two given values of y represents an estimate of the relative probability of an observation falling within that range of values. This illustrates how as the probability score increases, the number of forms in the unattested group decreases, while the number of forms in the attested group increases.
Table 14 Average probability scores for attested and unattested analogical forms.


Figure 8 (Colour online) Violin and box plots illustrating the distribution of probability scores in the unattested and attested portions of the sample of hypothetical analogical forms.
5. Conclusions
5.1 The influence of token frequency on morphological change
The results of this study show how token frequency influences the probability of morphological change: infrequent forms are more likely to be replaced by innovative forms, and these innovative forms are more likely to be based on frequent forms. An analogical proportion’s probability of generating an innovative form that will actually be used increases with the token frequency of its base, and decreases with the token frequency of its target, while the probability of an analogical form is greater when it is supported by a larger number of analogical proportions.
This is to be expected if analogical forms come about through speakers predicting forms which they have not encountered, or which cannot be retrieved quickly enough from memory in performance, when faced with the Paradigm Cell Filling Problem. High token frequency forms are more accessible in memory and more likely to be used as the basis for predicting new forms, while low token frequency forms are less accessible and more likely to be replaced. This supports the psycholinguistic claim that even regularly formed inflected forms can be stored and accessed in memory as unanalysed wholes. This does not preclude productivity, since meaningful parts can emerge and be extended when required using analogy. Of course, this does not necessarily mean that sub-word units cannot also be stored in memory, only that they do not have to be – even when it is possible to cut up words into individually meaningful parts, we cannot assume speakers actually do so.
5.2 Possible extensions of the model
More research is needed to identify statistical tendencies of morphological change and how these tendencies weigh against each other. It is likely that closer semantic and morphosyntactic similarity between the items in a proportion increases its viability. For example, the suffixes of the weak aorist replaced those of the strong aorist earlier than they extended to the imperfect in Greek, even though the strong aorist and imperfect had identical suffixes. Plausibly, this is because the strong and weak aorist were competitors in the same paradigm cells, with identical values for all morphosyntactic features, so were in closer competition than the aorist and imperfect suffixes, which competed as exponents of tense, mood, voice, person, and number, but differed in aspect (see 2.2.1). I have kept this variable constant in this study by restricting the sample space to proportions where a and c occupy morphosyntactically identical paradigm cells, as do b and x (as explained in 2.2.2). Similarly, it is likely that the phonological closeness of the items in a proportion increases its viability: this might explain why the pattern of drive ~ drove has spread to dive (~ dived → dove) in some varieties of English, but not to e.g. mime (~ mimed → *mome). Measures of similarity have been successfully used in other models of analogy and morphological change such as those discussed in 1.1.5, and could also be incorporated into the model proposed here.
Sims-Williams (Reference Sims‐Williams2016) shows that type frequency also influences the diachronic productivity of morphological patterns. This could be incorporated into the model presented here in two ways. Firstly, the type frequency of each pattern of inflection described in 2.1.1 could be added as an explicit predictor variable for the model (parts a/b) and destination (c/x) of each proportion in the same way as token frequency was for the base and target. Alternatively, if the sample space of proportions were generated using individual lexemes instead of abstract lexeme types, the effect of type frequency might emerge naturally from the model, since higher type frequency patterns will be reflected by a greater number of proportions pointing to the same forms. All other things being equal, this will increase the probability of these forms in the model.
5.3 Implications for morphological theory
This paper has presented a computationally implemented extension of the proportional model of analogy that has long been used in historical linguistics. Its success in predicting patterns of morphological change supports the essential insight behind the proportional model, that morphological change involves the extension of implicational relationships between inflected words.Footnote 16 The predictive value of the token frequency of the analogical base is particularly significant. Under decompositional theories of morphology, there is no reason why properties of the analogical base should have any influence on change, because these have no independent existence in the synchronic framework; they are merely the short-lived outputs of grammar. These results are better accommodated within abstractive theories as discussed in 1.1.3.
So far, complete synchronic formal descriptions of the morphology of natural languages have been implemented in decompositional terms, but not yet in abstractive ones. Indeed, it is not obvious what an abstractive description would look like. For example, Malouf (Reference Malouf2017) presents a computationally implemented abstractive model using a recurrent neural network that predicts unknown forms on the basis of partial paradigms (see also Elsner et al. Reference Elsner, Sims, Erdmann, Hernandez, Jaffe, Jin, Johnson, Karim, King, Nunes, Oh, Rasmussen, Shain, Antetomaso, Dickinson, Diewald, McKenzie and Stevens-Guille2019 on computational models of morphological reinflection – i.e. predicting inflected forms from other inflected forms – more generally). This shows that it is possible to learn to solve the paradigm cell filling problem using mappings between inflected surface forms, but the grammar that results from this learning cannot be accessed directly. While techniques exist to uncover the internal structure of trained neural networks to a certain extent (e.g. Malouf Reference Malouf2017: 447–453), this lack of interpretability makes such a model inappropriate for descriptive purposes. On the other hand, we would like something more explicit than the sets of principal parts and exemplary paradigms familiar from school grammars, which in any case must represent an unrealistic idealisation. The model presented here uses the solving of analogical proportions – a mechanism that is both intuitively easy to interpret and can be given a precise algorithmic definition – to generate a set of possible realisations for paradigm cells, and then assigns them a probability ranking. Its success in predicting the direction of change suggests that a synchronic model using analogical proportions, which could be tested against diachronic evidence, may be worth pursuing.























