Motivations and Goals
Ice-core paleoclimate studies rely heavily on the stable isotope ratios δ18O and δD to provide detailed records of past temperatures. The ice-core isotope records are themselves continually modified by diffusion, at first rapidly in firn, and then more slowly in solid ice (Johnson, 1977; Reference Whillans and GrootesWhillans and Grootes, 1985). The effect of firn diffusion is to homogenize the isotope record of a length scale that is generally small compared to the record of individual climate changes, as measured along an ice core. However, the seasonal isotopic record will the modified considerably by diffusion in the firn. Therefore, researchers have largely avoided interpreting the seasonal isotope record (exceptions are referred to below) even though aspects of the seasonal climate are quite important
Two of these aspects deserve special attention. First, it is desirable to know the seasonal cycle amplitude (defined as the deviation of maximum summer or minimum winter δ values from the annual mean) for inferring changes in mean summer and mean winter temperatures (e.g. Reference Jouzel, Merlivat, Petit and LoriusJouzel and others, 1983; Reference Morgan and van OmmenMorgan and Van Ommen, 1997), for inferring changes in annual temperature variability, for studying aspects of climate dynamics from the historical perspective (e.g. Reference BarlowBarlow and others, 1997), for identifying how climate trends vary from one location to another (Reference Kuivinen, Lawson, Rowe and ClausenKuivinen and others. 1996; Reference Rowe, Kuivinen, Bathke and ClausenRowe and others, 1996), for understanding the relationship between stable-isotope ratios and temperature (Reference Peel, Mulvaney and DavisonPeel and others, 1988; Reference Aristarain, Jouzel and PourchetAristarain and others. 1986: Reference Van Ommen and MorganVan Ommen and Morgan, 1997), for understanding the relationship between temperature and climate forcing from shortlived events such as volcanic eruptions (White and others, in press), and possibly for inferring the history of sea-ice extent (Reference Fisher and KoernerFisher and Koerner, 1988). One particularly intriguing use of seasonal isotopic data is the recent suggestion by L. Barlow that Greenland experienced unusually cold summers at the time of the demise of the Norse settlements in southern Greenland (Reference PringlePringle, 1997; Reference BarlowBarlow and others, 1997). The seasonal isotope records used in all of these studies, except Fisher and Koerner’s, have been modified to some extent by diffusion, and this may affect results (less so for the high-accumulation sites on the Antarctic Peninsula than for the dry inland sites).
A second aspect of the seasonal climate deserving special attention is the seasonal distribution of precipitation. If the accumulation rate is not constant through a year, either due to seasonal wind scour (Reference Fisher, Koerner, Paterson, Dansgaard, Gundestrup and ReehFisher and others, 1983) or due to seasonal variation of precipitation (Reference Bromwich, Robasky, Keen and BolzanBromwich and others, 1993), the mean annual δ value will not accurately reflect the true mean annual temperature (Reference DansgaardDansgaard, 1964; Reference Fisher and KoernerFisher and Koerner, 1988; Reference Peel, Mulvaney and DavisonPeel and others. 1988; Reference Steig, Grootes and StuiverSteig and others, 1994; Reference Shuman, Alley, Anandakrishnan, White, Grootes and StearnsShuman and others, 1995). Changes in the magnitude of this bias will appear in isotope records as climatic temperature changes that in fact never happened, or will change the apparent magnitude of real temperature changes. For instance, attention has recently focused on changing season-alily of precipitation as one of the possible reasons (Reference Fawcett, Agústsdóttir, Alley and ShumanFawcett and others. 1997) for the low sensitivity of δ values to temperature changes at major climate transitions (Reference Cuffey, Clow, Alley, Stuiver and WaddingtonCuffey and others, 1995; Reference Johnsen, Dahl-Jensen, Dansgaard and GundestrupJohnsen and others, 1995). It may be possible to infer a long-term history of precipitation seasonality from properties of isotope records alone using a measure of the deviation of the annual 5-depth curve from sinusoidal, such as the difference between mean and median (measured from the frequency distribution of δ values for a given year). This is because the annual temperature cycle is roughly sinusoidal, with mean and median nearly identical (this can be seen, for example, from the symmetry of the curves in Figure 8 of Reference Shuman, Fahnestock, Bindschadler, Alley and StearnsShuman and others (1996)). A significant seasonal bias to precipitation will deform this curve in a manner that may be statistically measurable.
A goal of the present paper is to determine how accurately one can reconstruct these two seasonal parameters (amplitude and deviation from sinusoidal shape) from detailed isotope records that have undergone diffusion in polar firn. We focus on firn diffusion because information that survives the firn diffusion will survive for a long time in the ice beneath, due to the much slower rate of diffusion there (Reference JohnsenJohnsen, 1977; Reference Whillans and GrootesWhillans and Grootes, 1985, Fig. 7).This survival time will depend on the strain rate and tempera-lure at the ice-core site. Johnson’s calculations suggest survival times of as much as 10 000 years at Greenland sites (his figures 4, 5 and 6).
To accomplish this goal, we must have an accurate quantitative physical understanding of the fun-diffusion process. We will first use data from the GISP2 ice-core record in central Greenland (Reference Stuiver, Grootes and BraziunasStuiver and others, 1995) to show that the firn-dilfusion theory of Reference Whillans and GrootesWhillans and Grootes (1985) is essentially correct; this theory predicts rather well the measured decay of the seasonal δl8O cycle in the GISP2 record. We will introduce two minor modifications. One of these modifications is based on physics and concerns the enhancement of vapor diffusivity at high altitude due to the low atmospheric pressure there. The other is simply a parameter adjustment that is physically plausible and which improves the prediction. Next, we broaden our geographic perspective by predicting the seasonal cycle decay al other ice-core sites, using the modified theory, and show that these predictions are in good agreement with published data from four core sites. These results give us confidence that we can model the diffusion process reasonably well. We then use synthetic “data" records, with known seasonal parameters, to evaluate the accuracy of reconstructions. These synthetic data are diffused and sampled to mimic a real ice-core record. The diffusion process is mathematically reversed and we compare the undiffused records with the originals. These synthetic analyses are specifically designed for central Greenland ice cores, but we indicate how results can be modified for different locations, as long as the Reference Whillans and GrootesWhillans and Grootes (1985) theory applies (dry firn).
I. Diffusion in Firn
1.1. Calculating diffusion
According to the Reference Whillans and GrootesWhillans and Grootes (1985) theory, the isotopic composition of firn will change through time t as


in a reference frame fixed to the firn, which is not deforming, and which has no strong density and temperature gradients the effect of such gradients has been shown by Reference Whillans and GrootesWhillans and Grootes (1985) to be negligible in firn). Here, z is depth (variation in horizontal directions is ignored), δ refers to either δl8O or δD, α, is isotopic diffusivity, m is molar weight of water, R is the gas constant, P is saturation vapor pressure for water vapor over ice, P is firn density and T is absolute temperature. The function ω is the effective diffusivity of water vapor through firn, accounting for the blocking effect of ice grains that interfere with vapor paths. Whillans and Grootes related this to density and diffusivity of water vapor in air Ωa, using a simple linear relation

where ρc is the pore close-off density, approximately 820kgm−3. Reference ColbeckColbeck (1993) reviewed theory and experimental data on vapor diffusion in snow and concluded that in air vapor diffuses more effectively in low-density snow titan in air, so that ω ≈ 5Ωa. For our purposes, we will write a more general relation

and use our data to constrain 7 and p*. We use the relations for P and Ωa reported in Reference Whillans and GrootesWhillans and Grootes (1985), with one modification. The water-vapor diffusivity is inversely proportional to the total air pressure, due to the reduction in mean free path of diffusing gas molecules as pressure increases (Reference ReifReif, 1967). Because the air pressure decreases with increasing altitude, we include this dependence explicitly and write

where Pa is the air pressure in atmospheres, and Ωa1 is the diffusivity of water vapor in air at 1 atmosphere pressure, and is Equation (9) from Reference Whillans and GrootesWhillans and Grootes (1985) (compare 10 Reference Geiger and PoirerGeiger and Poirer, 1973, equation 13.63). For central Greenland, the nominal effect of the lower atmospheric pressure is 10 enhance the diffusivity by a factor of approximately 1.5, because atmospheric pressure there is approximately 0.68 atmospheres (Steams and Weidner, 1991; Steams, 1997).
The possibility that water-vapor diffusivity is enhanced in snow by as much as y = 5 is at first sight disturbing. However, the evidence for a high y specifically only applies for vapor diffusion that is driven by a temperature gradient. In our case, the diffusion is driven by gradients in isotopic composition. The isotopic diffusivity in solid ice is several orders of magnitude less than the corresponding diffusivity in vapor. Thus, in contrast to its role in thermally driven diffusion, the solid ice here acts essentially as a passive obstruction to the diffusive flux. Therefore, we expect that y = 1, We are not certain of this, however, and will at first allow y to vary. Below, we show that y = 1 actually allows the best fit to data.
The most appropriate value for p* is harder to predict, because the blocking effect of the solid ice matrix depends not only on the void fraction but also on the tortuosity and connectivity of the vapor paths. The latter enhance the blockage effect so that p* 917kgm−3. Simplicity is the primary justification for the functional form (1 - p/p*) but the data of Reference Schwander, Stauffer and SiggSchwander and others (1988, p. 143) show that a linear relation is approximately correct.
Consider a section of an isotope record, of length L, such that there is no net flux of vapor into or out of the ends of the section. This could represent, for instance, a perfectly sinusoidal record, with a section taken from peak-lo-peak. Then Equation (1) has the well-known Solution

where the coefficients An are the Fourier coefficients for the initial isotope curve S(z,0). In an ice sheet, we need to include the effects of vertical strain and a variable isotopic diffusivity. We do this following Reference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and RechHammer and others (1978), as follows. Introduce a new depth coordinate, Lz = z, and let α and L be functions of time. Assume the section of firn strains uniformly such that L(t) = L0[l + e(t)]. Then vvc can write the solution to Equation (1) as

where ρ * is a time-averaged effective diffusivity

On an infinite domain, the corresponding solution to Equation (1) is the convolution of the initial δ profile and a Gaussian filter with a standard deviation with respect to z of 2v/v,ri(l+c) (Haberman, 1987). As Reference JohnsenJohnsen (1977) and Reference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and RechHammer and others (1978) have pointed out, the effect of diffusion is thus to average over a length scale proportional to \/o*t(l + e) (see below, Equation (10)). We find it most intuitive to refer to the length scale containing approximate!) two-thirds of the averaging filter (plus and minus one standard deviation), normalized to the annual layer thickness. This is 4\/n*t. divided by the thickness of annual layers at the surface. This quantity is used later in figure 12.
To calculate α* for application to the GISP2 data, it is necessary to specify a relation for the strain as a function of time of burial in the firn. The strain rate consists of a densification term and an ice-flux divergence term (see e.g. Culfey and others, 1994) that is constant with depth and time, and has an approximate value of —jj, where b is the ice-equivalent accumulation rate (0.24 m a-1), and H is the ice-equivalent ice-sheet thickness (3000 m). In this study, we only consider the upper 200 m of the ice sheet (less than 7% of the total ice thickness), so our assumption of a constant strain rate is reasonable and relatively unimportant. We use the density profile measured at GISP2 (Reference Alley and KociAlley and Koci, 1990). In practice, to calculate the integral in Equation (8) from ice-core data, we convert it to a depth integral that is weighted according to the local age-depth gradient in the ice sheet. Define a new vertical coordinate, C which is depth below the ice-sheet surface. Then, using Equations (2) and (4).

where ρ0 is the density of snow at the surface. The calculations are independent of this parameter because α* is divided by the square of L0 in Equation (7). The age of lira at a given depth, t(c), and hence the depth-age gradient, are known from counting annual δ cycles, and is confirmed independently by both visual stratigraphy and electrical conductivity measurements (Reference MeeseMeese and others, 1994). The group is PΩaT−l temperature-dependent. To incorporate this most accurately, we use the Guffey and others (1994) temperature model to track PΩaT−l as a function of time along the paths of layers being buried. This is potentially important in the upper 30 or so meters of the firn, because the diffusivity will vary by almost a factor of 2 between -29;: and -34°C. The temperature model is forced by a mean annual surface temperature that is the calibrated nlt!0 history δ = 0.53T-18.2 (Reference Cuffey, Alley, Grootcs, Bolzan and AnandakrishnanCuffey and others, 1994: Reference Stuiver, Grootes and BraziunasStuiver and others, 1995). Above 12 m, where the seasonal variation in temperature is important, we assume the temperature varies sinusoidally in response to a sinusoidal surface-temperature forcing of amplitude 20 G. We use the corresponding annual time-average of PΩaT−l in Equation (9) (Reference BowBow, 1982). All subsequent diffusion calculations in this paper use Equations (7) and (9). We address the undetermined constants 7 and p* in the following section.
1.2. A test of this diffusion model
To test our understanding of firn diffusion, we measure the decay of the annual δl8O cycle with depth in the - GISP2 core and compare with model calculations. This test is imperfect, because we do not have independent information about how the seasonal δl8O amplitude at deposition changed during the past several centuries.
For an annual b cycle, delimited from summer peak to summer peak, we define the seasonal amplitude as half the average of the magnitudes of the summer to winter and winter to summer h changes. For the GISP2 core, the b record was measured and analyzed by Reference Stuiver, Grootes and BraziunasStuiver and others (1995). We use data from 1.5 to 200 m below the surface. The upper meter is excluded because rapid diffusion not described by the Whillans and Grootes model is possible there due to ventilation (Reference Clarke, Fisher and WaddingtonClarke and others, 1987). We normalize the amplitudes to their value at the top of the firn column, which is chosen as the intersection on a log-log plot of the z= 0.1 line and a best-fit line through the upper 10 m of amplitude vs depth data.
If we consider one annual laver at a time, the thickness of each annual layer at time of deposition corresponds to the L0 in Equation (7); thin layers diffuse more rapidly than (Stick layers (Reference JohnsenJohnsen, 1977). To compare model predictions with the amplitude data, we take a 2 m average layer thickness around each year and calculate the corresponding unstrained surface thickness, which we use for L0 in Equation (7). Using this average for L0 simply makes the result easier to compare with the data (comparing a smooth curve to noisy data is easier than comparing a noisy curve to noisy-data). Using Equation (7), we calculate the amplitude decay of a single sinusoid for each year (A = 2π). We perform the same calculation for various values of ρ* and y.
1.3. Results of the test, further tests and implications for firn processes
First we calculate the seasonal amplitude decay using r = 1 and the suggested ρ* value from Reference Whillans and GrootesWhillans and Grootes (1985) (p* = 820), and find that the match to the GISP2 δ18O data is very good in the upper firn (Fig. 1), but that the calculation underpredicts amplitudes by a factor of 5 at the base of the firn column. Though not perfect, we think this match is impressive given that Whillans and Grootes did no adjusting of parameters, and that their theory is independent of ice-core data. A factor of 5 underprediction of amplitudes at the base of the firn corresponds to an overprediction of the isotopic diffusivity by a multiple ofonly 1.7- For comparison, a factor of 5 overprediction of the diffusivity would lead to underprediction of amplitudes by 4 orders of magnitude.

Fig. 1. The decay of seasonal amplitude o/GISP2 δ18 0 cycles, as a function of time of burial. The measured amplitudes of Reference Stuiver, Grootes and BraziunasStuiver and others (1995) are shown, along with the a priori prediction of the Reference Whillans and GrootesWhillans and Grooles (1985) model, and the prediction if the diffusivity of water vapor is enhanced by a factor of 5 throughout the firn column.
The fit can be improved by adjusting ρ* and r. To optimize these constants, we define a mismatch index J, which measures the root-mean-square difference of predicted and measured amplitudes for the most recent 350 years, weighted so that the most recent 100 years have equal weight to the previous 250 years (adding weight to the upper part of the borehole simply ensures that the optimized prediction matches the data there). J is minimized for the values ρ* = 730 and r = 1.0, for which there is an excellent match between predicted and measured amplitudes (Fig. 2). The minimum in the J surface is unambiguous (Fig. 3).
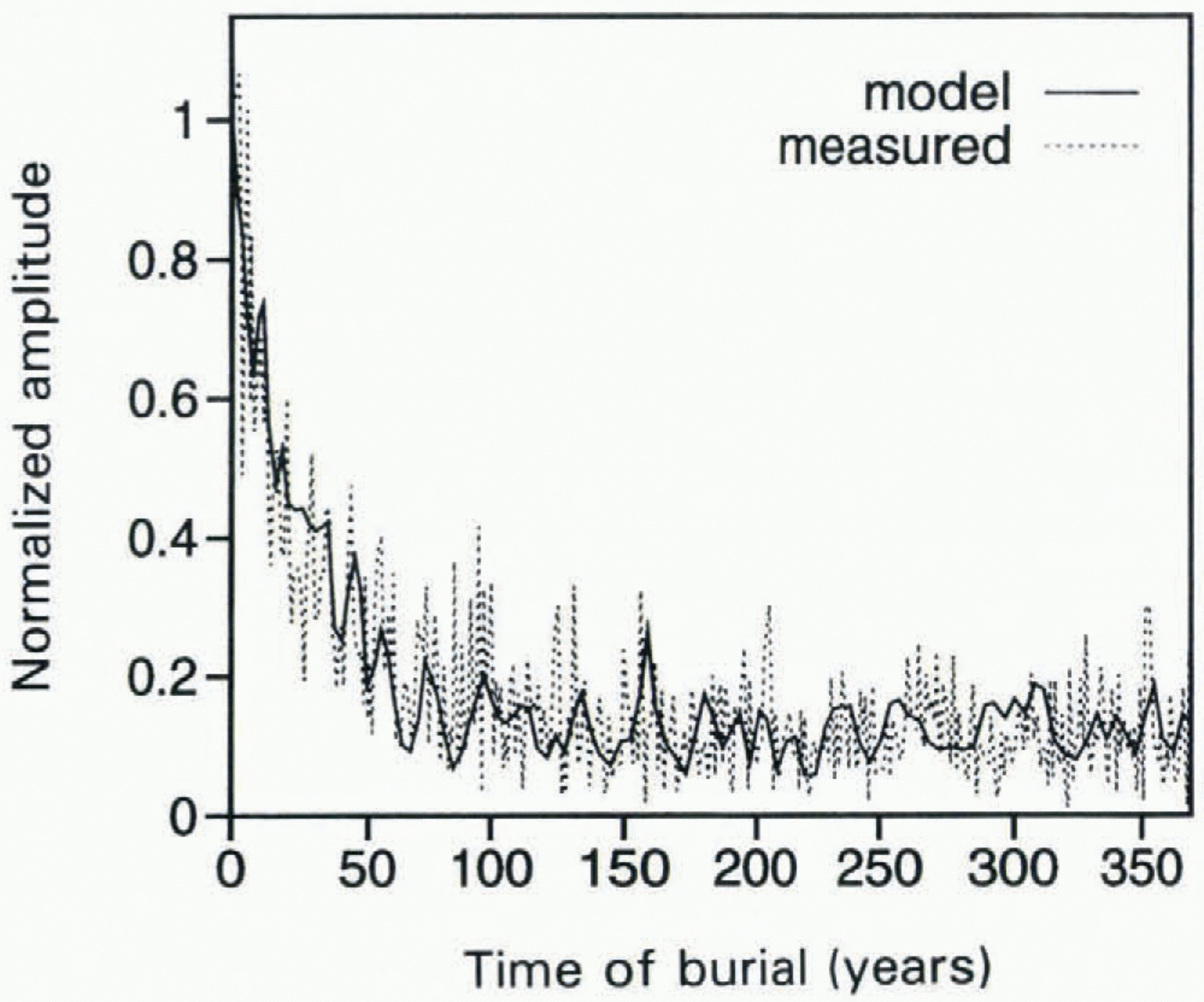
Fig. 2. The modeled and measured seasonal amplitude decay for the model values p* = 730 and y = 1.

Fig. 3. The mismatch of seasonal amplitude measurements and model prediction as a function of the parameters (a) p* and (b) y.
We can further test this firn-diffusion model, and in particular the generality of the values y= I and p* = 730, using- published data from other ice-cure sites. This is particularly important because our estimate of these values would be affected by changes in the seasonal amplitude at time of deposition at GISP2, especially if amplitudes for the most recent several decades are anomalous. Predictions for decay of the seasonal isotopic amplitude at various well-known locations on the ice sheets are shown in figures 4 and 5, using constant values for accumulation rate and temperature (table 1), and using Equations (7) and (9). For four sites that are climatologically very different, we can compare- these predictions to published data (Fig. 5). The comparison is very good. There are no adjustable parameters in the predictions and the data are entirely independent of GISP2 data. The data are our best guess at most-appropriate values for the amplitudes and were selected prior to the prediction. However, as before, this is an imperfect test, because changes in the seasonal amplitudes at time of deposition are essentially unknown; by using multiple sites, whose seasonal amplitudes are not necessarily correlated, we have only reduced the chance that this is a problem.

Fig. 4. The predicted decay of the amplitude of the seasonal isotopic cycle (normalized to the amplitude at the surface) at several well-known ice-core sites.

Fig. 5. The predicted decay of the amplitude of the seasonal isotopic cycle (normalized to the amplitude ai the surface) at several well-known ice-core sites for which, published measurements are available. Also shown are spot estimates of the measured amplitudes at depth normalized to the modern near-surface amplitude. The isotopic amplitude data are the present authors’approximations taken from: Dalinger Dome; Reference Aristarain, Jouzel and PourchetAristarain and others. 1986. fig. 3. p. 74 (surface amplitude = 45 = amplitude after 80 years = 20); South Pole; Reference Jouzel, Merlivat, Petit and LoriusJouzel and others. 1983, fig. 2, p. 2695 (surface amplitude = 85, amplitude after 80 rears = 15); Milcent; Reference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and RechHammer and others. 1978, their magnificent Figure 4 (surface amplitude = 13. amplitude after 80 years = 7); Crête; Reference Johnsen, Robin and RobinJohnsen and Robin, 1983, fig. 3.15 (surface amplitude = 16, amplitude after 145year s = 2). Amplitudes are per mille.
The reduction of diffusion rate in the deep firn implied by ρ* being less than pore close-off density (820 kg m −3) is not surprising given that diffusion through porous materials is generally slowed by tortuous vapor paths and boundary effects in addition to reduction of void fraction and void connectivity (Reference Geiger and PoirerGeiger and Poirer, 1973, p. 467-72; Reference Schwander, Stauffer and SiggSchwander and others, 1988), and Reference Whillans and GrootesWhillans and Grootes [1985, p.3915) clearly recognized this. Unfortunately, because we have no independent measure of seasonal amplitude at time of deposition, we cannot better constrain the blockage effect.
The fact that y = 1 has two implications. First, it supports our including the enhancement of diffusivity at high altitude. Second, it shows that a significant enhancement of water-vapor diffusivity in snow relative to air is not appropriate in this ease. Using the recommended enhancement of Reference ColbeckColbeck (1993), y = 5, in fact leads to unquestionably excessive diffusion (Fig. 1). This supports our contention that vapor dux driven by gradients in isotopic composition should be calculated in a manner different from vapor flux driven by temperature gradients.
Table 1.1 Environmental data and relative preservation of annual isotopic cycles after diffusion in firn, for various ice-core sites in Greenland (GTSP2, Dye3, Milcent, Crête) and Antarctica (Dalinger Dome, Siple Dome. Smith Pole, Vostok). Values for accumulation rate (b), mean temperature (T) and approximate depth to ρ* (ζ,) are from Reference Herron, Dual and LangwayHerron and Langway, 1980 (Dye 3, Vostok, Crête), Reference Alley and KociAlley and Koci. 1990 and Reference Bolzan and StrobelBolzan and Strobel, 1994 (GISP2), Reference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and RechHammer and others, 1978 (Milcent), Reference Aristarain, Jouzel and PourchetAristarain and others. 1986 (Dalinger Dome), Reference Jouzel, Merlivat, Petit and LoriusJouzel and others. 1983 (South Pole), and Mayewski and others, in press (Siple Dome). Approximate atmospheric pressures (Pa) are estimated from the elevations of the sites using an atmospheric scale height of8 km, except fir South Pole and CISP2, where the pressures are measured (Reference Jouzel, Merlivat, Petit and LoriusJouzel and others, 1983; Steams. 1997)

The satisfactory predictions of Equations (7) and (9), the physically very plausible values for the optimized parameters and the independence of the theoretical framework from ice-core data together provide strong evidence that the Whillans and Grootes theory is “substantially correct" as they assert. In particular, the theory seems to incorporate properly the important environmental variables, temperature and accumulation rate.
One further implication of our value for ρ* concerns the mobility of gases in the firn column, Reference Sowers, Bender, Raynaud and KorotkevichSowers and others (1992) divided the firn air column (which is the interconnected air column from the surface of the ice sheet down to the depth at which pores become completely surrounded by ice; into three sections with respect to mobility of gases: an upper, convective zone, a diffusive column and a non-diffusive zone deep in the firn.lb first approximation, our ρ* corresponds to the boundary between Sowers and others’ diffusive and non-diffusive zones. Our analysis supports the validity of the non-diffusive zone concept, and the correspondingly smaller age difference between the gas record and the ice record in an ice core (Reference Sowers, Bender, Raynaud and KorotkevichSowers and others. 1992). ρ* = 730 implies a non-diffusive zone of approximately 25 m thickness. However, our analysis is not well-suited to finding this boundary due to the variability of seasonal amplitudes.
1.4. Johnsen’s theory and constant diffusion-length hypothesis
The Reference Whillans and GrootesWhillans and Grootes (1985) theory was motivated in part by the earlier-published theory of Reference JohnsenJohnsen (1977). The two theories share their most important components: an isotopic diffusivity proportional to both water-vapor pressure and diffusivity in air, storage of water molecules in the solid matrix and slowed diffusion at increased densities. Consequently, predictions from both theories as to how firn diffusion depends on the temperature and accumulation rate are fundamentally in agreement, though the later theory adds elements that are essential for quantitative accuracy. Reference JohnsenJohnsen (1977, Equation (5)) noted that the total extent of diffusion of the isotopic record between the surface and the base of the firn can be conveniently expressed as the diffusion length Lf defined by

where Ab and A0 are seasonal amplitudes at the base and top of the firn, respectively. In our notation, ρiLf = p0✓2α*t. Johnsen suggested that Lf is approximately a constant, not because the rate of diffusion is independent of temperature and accumulation rate but because the density depth profile depends on these variables; warmer sites density faster, countering the increase of P and Ωa at higher temperatures.
To investigate the dependence of if on temperature and accumulation rate in our modified Whillans and Grootes theory, we link diffusion calculations (Equations (7) and (9)) to a densification model, as did Johnsen. We represent the depth density profile at core site by the empirical formulation of Reference Herron, Dual and LangwayHerron and Langway (1980) and calculate Lf as a function of accumulation rate and temperature (Fig. 6). Here, we also plot the locations in accumulation rate-temperature spare of ice-core sites in Greenland, Antarctica and the Antarctic ice shelves. The sites have all been those reported in Table 1 of Reference Herron, Dual and LangwayHerron and Langway (1980) In Green-land accumulation rate and temperature are in general correlated such that the trend of these sites is parallel to isolines of Lf so Johnsen was approximately correct in saying that Lf is a constant. However, this is not true for Antarctica, not through time in Greenland or Antarctica.

Fig. 6. Estimated diffusion length in ice (ρ = 917) as a function of accumulation rate and temperature. We have not accounted for differences in atmospheric pressure in this figure. Asterisks are Greenland sites, squares are Antarctic ice-sheet sites, and diamonds are Antarctic ice-shelf sites (Reference Herron, Dual and LangwayHerron and Langway, 1980. table 1).
II. Determining What Seasonal Paleo-Climate Information Can Be Recovered
The results of Part I show that we can model the diffusion process with sufficient accuracy to explore the potential for recovering seasonal paleoclimate data. For all diffusion calculations in Part II, we assume a constant temperature of -31.5°C below 12 m, and use ρ* and 7 values which accurately reproduce amplitude decay through the firn column at GISP2 in this isothermal case (the change in parameter values is small and is merely a convenience with no consequence for the results), At GISP2, the base of the firn (where ρ = 820) is at approximately 75 m depth.
We create synthetic ice-core records that store information about a known δ180 history and undiffuse the records to see how much of this information we can recover. Each half-year of the isotope history has a known amplitude (magnitude of summer-peak to winter-trough δ change) and a known shape that deviates from a true sinusoid. In reality, the shape of the annual δ(z) can be quite variable; there may be subsidiary extremes (e.g. Reference Shuman, Alley, Anandakrishnan, White, Grootes and StearnsShuman and others, 1995), or the thickness of the summer and winter parts of the curve may be different. We will explicitly consider only the latter case but the results are essentially valid for any sub-annual features of comparable frequency content (Equation (7)). For our purposes, the specific shape of the annual curve is not important, so we conveniently define it for the qth year as (with z = 0) defined as the center of the curve)

where (Zq1 + Zq2) is the thickness of tire layer, the rising and falling amplitudes (Δ) and thicknesses are allowed to differ, and the exponent μ determines the summer to winter bias (Fig. 7). Define the summer bias ratio fs for the annual layer as the thickness of snow with δ value greater than (δmin+ δmax)/2, divided by the annual layer thickness. For a perfect sinusoid, fs = 0.5. For fs > 0.5, the annual layer is biased towards summer snow, the most likely type of bias in the dry ice-sheet interiors. The relation between μ and fs is

Using curves of the forms (11), we construct synthetic isotope records for an arbitrary number of years, making sure δ is chosen so the synthetic record has no discontinuities. We vary the parameters Δqk, Zqk and fsq as normal random variables, with known mean and standard deviation. We can therefore customize records to perform specific numerical tests.
For each test, we diffuse the synthetic record according to Equations (7) and (9), and then sample the record at uniform spacing (the records are assumed to be uniformly strained, so a uniform depth spacing implies uniform sampling through paleo-time). Each sample is the mean δ value for its interval. To imitate the uncertainty introduced in the measurement process, we can perturb each sample by adding a normal random variable of mean zero and standard deviation 0.1 per mille, a typical conservative value for this uncertainly. Hereafter, we refer to the result as a synthetic ice-core record.
Finally, we reverse the diffusion process by letting each spectral component of the diffused and sampled record grow exponentially instead of decay as in Equation (7). This undiffusion process is notoriously unstable because amplitude growth is a strong function of frequency, so it is necessary to filter the synthetic record (e.g. Reference JohnsenJohnsen, 1977). We plot the log of A02 vs frequency and estimate a linear curve for the peaks in the noise spectrum, Nn2 (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992). Following Johnsen (who, however, used the measurement error as an estimate for the noise spectrum), we apply the optimal filter

and use the Án for the reverse diffusion. We compare the resulting undiffused record with the original.
II. 1 Four numerical experiments
We perform four numerical experiments. For each, the characteristics of the synthetic records are shown in Table 2.
Test 1 determines how accurately we can reconstruct seasonal amplitudes after firn diffusion if here is no seasonally bias in the data (fs = 0.5 throughout), as a function of sample size. The error resulting from the undiffusion process is the excess of the total error over the error resulting purely from the finite sampling interval. We can calculate the latter easily. Suppose we sample a sinusoidal record with an annual wavelength A and amplitude Δtrue, and maximum at z = 0. Sample N times per annual cycle, on average, and let the center zc. sample containing the maximum he a uniform random variable on the interval (-λ/2N, λ/2N). Then the average sampling error for this sinusoidal record is:

Equation (14) is strictly true only for even N. In the following tests, where fs ≠ 0.5 (the sampling error curve in Figure 9), we substitute Equation (11) for the cosine in Equation (14) and calculate the integrals numerically. Reference JohnsenJohnsen 1977) eliminated the effects of sampling bias as part of bis filtering scheme. We choose to show it explicitly for clarity.
Test 2 determines how accurately we can reconstruct seasonal amplitudes after firn diffusion, as a function of the summer bias ratio /s. We perform the test on seven records of uniform fs
For Test3 we set fs = 0.7 and examine how accurately we can reconstruct fs as a function of time of burial in the firn, for two eases. For one case, we perturb the sampled “data" to mimic the measurement error for a real ice-core record. In the other, we do not, in order to mimic an ideal record that has lost information via the diffusion process alone.
For Test 4 we use a synthetic record that is as close as possible to a real ice core. Both Δ and fs vary along the record, and the sampled diffused record is perturbed to mimic measurement error. We plot the error in reconstructions of both amplitude and fs as functions of time of burial.
Table 2. Characteristics of synthetic records. Mean (m) and standard deviation (σ) for half-year layer thickness (Z), half-year amplitude (Δ), seasonally bias (fs) sample measurement error (M) number of half years in the synthetic record (Q), and average number of samples: per synthetic year (N). We chose minimum possible values for Z of 0.05 m and 0.15 for fs. In addition, fs has a maximum possible value of0.85. In terms of Z and Δ, all synthetic records are identical. The mean amplitude changes every 20 annual cycles and has the five possible values listed below. After manipulation, the ends of the synthetic record are truncated to eliminate end effects, leaving 88 years of record


Fig. 7. Examples of how the parameter μ affects the seasonally biased isotope-depth curves given by Equation (11). If the annual temperature and isotopic composition of precipitation follows a sinusoidal pattern through the year, then the curves correspond to: uniform snowfall throughout the year (top curve), and increasingly depleted snowfall in the winter (lower curves). This figure specifically shows the role of μ only. The synthetic records we actually use are not uniform and symmetric like these curves because we allow Z and Δ, and sometimes μ, to vary randomly (table 1).
For all these tests, we report the average magnitude of error for reconstructed amplitudes (Δr) and reconstructed seasonality bias factors (fs r)as

where the q refers to a given half-year, which are Q in number. If diffusion removes all information about the original seasonal history, there will be no annual cycles and εΔ= 1. If diffusion removes all information about the sub-annual seasonal history, then all recovered fs values are 0.5 (i.e. perfect sinusoids are recovered from originally non-sinusoidal shapes) and if will be a number (call it εf0) that depends on the parent history’s fsi values. It is most intuitive to define the “information content" remaining after a given time of burial as the error relative to the error after diffusion has eliminated all information about the original history:

When I=1, all information about the original isotope history is recoverable. When I= 0, nothing is known of the original Δ or fs<i history.
II.2. Results of numerical tests
If an isotope record is sampled more than 15 times per year, and the parent isotope history has no seasonality bias, one can reconstruct synthetic seasonal amplitudes with an average error of 5% after diffusion through the whole firn (Fig. 8) at GISP2 Ten samples per year, a typical number for the GISP2 core, gives an error that is still less than 10%. For less than about ten samples per year, most of the εΔ is due to the sampling bias error (Fig. 8).

Fig. 8. Error in reconstructed amplitudes as a function of average sample frequency (N) after 200years of diffusion, and compared to sampling error. The sampling-error curve is Equation (14).
If we allow a uniform seasonality bias, the error in reconstructed amplitudes after firn diffusion is still less than 10% for fs<i ≤ 0.65 (Fig. 9). For more pronounced seasonality bias, however, the error grows considerably, almost attaining 30% at /s = 0.8.The problem is not one of sampling resolution (Fig. 9); it results from loss of information in the diffusion process. Clearly, sizeable errors in amplitude reconstruction are possible if/s is not known.

Fig. 9. Error in reconstructed amplitudes as a function of precipitation seasonality bias fs< with N = 20, after 200years of diffusion. Sampling-error curve from Equations (11) and (14).
Can we recover fs<i by undiffusing? In the most favorable case, when fs is uniform and there is no random error in the measurement process we have no hope of recovering fs<i after diffusion through the firn (Fig. 10) at GISP2. In fact, we cannot recover this parameter within 10% after only a few decades. When we include a random measurement error, the picture is slightly worse, because the sub-annual signal is more quickly buried in noise; there is no evidence of seasonal bias remaining after 75 years (Fig. 10).

Fig. 10. Reconstructed fs raines for a record with uniform fs = 0.7, as a function of time of burial. For the “no-measurement error" curve, the sampled synthetic diffused record was not perturbed by a random error. For the “measurement error" curve, it was N = 20.
Undiffusion of a more realistic ice-core-like isotope record, in which all parameters vary, shows the same pattern (Fig. 11). No information about the sub-animal signal fs<i remains after little more than half a century. The error in seasonal amplitude reconstructions is around 10% after 200 years, approximately twice that for uniform fs<i equal to 0.6, the mean value of fs for this more realistic record. Similar relations would be obtained for other values of mean fs<i.

Fig. 11. Loss of information about amplitude (IΔ) and seasonally bios (If), as a Junction of time of burial. This is for an ice-core-like record with variable fs of mean value 0.6, which has a measurement error N = 20.
II.3. Implications for paleoclimate studies
Errors in reconstructions of synthetic data are not necessarily identical to errors in reconstructions of real data. In particular, the undiffusing process is sensitive to the filtered frequency spectrum of the record and the filtering depends on the nature of the noise in the record. This is the reason for the lack of smoothness of the curves in Figures 8-11, and the slightly negative information values in Figure 11. However, we have made our synthetic records as similar as possible to real ice-core records and assert that the following implications of our results are solid.
It is clear that information about sub-annual characteristics of the δ(ζ) curve is rapidly lost by firn diffusion in central Greenland. We suggest there is little point in measuring annual properties of the δ-depth record such as annual mean minus median, in an attempt to learn about past changes in the seasonal timing of precipitation. Similarly, examining shapes of annual δ(z) curves will teach us nothing about the nature of individual years. Instead, they will reflect the variability of neighboring annual cycles in the record, because diffusion homogenizes the record on a length scale comparable to the hall-annual thickness after only several decades. To see this, we plot the ratio of diffusive-length scale (see section on “Calculating diffusion”) to annual layer thickness for various burial times (Fig. 12; also see Reference Johnsenjohnsen, 1977, p. 213).

Fig. 12. The diffusive averaging length (4y✓δ*t) normalized to the thickness of an annual layer, as a function of time of burial.
Contrary to this dismal situation for sub-annual reconstructions, there is some hope for recovering useful information about seasonal amplitudes. However, one important implication of the averaging length in Figure 12 is that changes in amplitudes from year-to-year are meaningless without a back-diffusion calculation, even in the absence of seasonal precipitation bias. In addition, there is unfortunately still some uncertainty in the absolute values for reconstructed seasonal amplitudes resulting from uncertainty in the parameters ρ* and r. This is because changes in seasonal amplitude at the time of deposition, especially in recent decades, could be affecting our optimization of these values at GISP2. While we are encouraged by the success of these values in predicting cumulative amplitude decay at several other sites, better constraint would be valuable. However, if one considers only the record from below the depth corresponding to ρ* then relative amplitudes are retrievable to within a modest error. If one can find independent evidence showing that snowfall has been reasonably uniform throughout each year, so /s<0.65 or so, then this error is around 10% or less (Fig. 9). If fs<i has been variable, but the average fs<i < 0.6 or so, the average error in reconstructed amplitudes is also around 10% but the error for individual years may be large (see figs 11 and 9). For the larger mean fs<i values, errors will be much greater (Fig. 9), Thus, without independent information or theoretical considerations that constrain or limit fs<i, amplitude reconstructions will be tenuous. Note that isotopic data on seasonably of precipitation suggest there is currently significant snowfall throughout the year at GISP2 (Reference Shuman, Alley, Anandakrishnan, White, Grootes and StearnsShuman and others, 1995). However, comparison with temperature records suggests that this has not always been the ease (Reference Steig, Grootes and StuiverSteig and others, 1994; Faweett and others, 1997). Also, other geochemical data suggest that GISP2 snowfall has a significant winter deficit (Reference Jaffrezo, Davidson, Legrand and DibbJaffrezo and others, 1994; Reference Dibb and andDibb, 1996) as do model-based estimates (Reference Bromwich, Robasky, Keen and BolzanBromwich and others, 1993).
A reconstructed isotope history may still be of interest, though. A sizeable (greater than 10%) change in mean reconstructed amplitude indicates some change in the annual climate; either the shape of the annual δ curve has changed considerably or the seasonal amplitude has changed, or both. Also note that, because diffusion rate is sensitive to temperature, spurious changes in reconstructed amplitude can result from changes in the temperature structure of the fini. A proper undiffusion calculation should involve accurate heat-flow modeling, and possibly even changes in the density structure. Depending on the length of record of interest, diffusion in the solid ice should also be included (Reference JohnsenJohnsen, 1977).
II.4. Recovery at other locations
It is possible that sub-annual characteristics of δ records in locations other than central Greenland will survive firn diffusion. To good approximation, one can transform our synthetic results to other locations with less diffusion as follows. The extent of diffusion, and hence the results in Figure 11, are a function only of α*t/L02. The loss of information at some new location l after a time of burial tl will be equal to the loss of informât ion at GISP2 after tG years of burial if

where T is the mean annual temperature. It is most convenient to separate the isotopic diffusivity into a temperature-and pressure-dependent coefficient and a density-dependent part <iα = α0(T, Pa)(ρρ* - ρ2) To calculate α* using Equation (9), we approximate the depth-density profile for ρ ≤ ρ* as

where the depth scale is given by ρ(ζ*) = ρ*. Selling the constant c = 0.25 reproduces the GISP2 density profile quite well. The corresponding depth-age scale is found by integrating ρ(ζ)(ρib)−1. These approximations for density and depth age can be used to evaluate α* using Equation (9). In doing so, we also neglect the εi, and use c = 0.25, which gives the scaling relation

For locations with i/ > ÎG, diffusion of the seasonal cycle is slower than at GISP2; it takes t; years to achieve the same total smoothing that is achieved at GISP2 in tc, years. Equation (19) has no algebraic solution but it is easily solved numerically. The solution depends strongly on the mean annual temperature and the accumulation rate, and only very weakly on the depth of the fini column. For example, at Dye 3, which has a higher accumulation rate (0.55 m a−1) and higher mean tempérât tire (-20°C) than GTSP2, diffusion of the annual signal occurs more slowly than at GISP2, because the high accumulation rate dominates. Solving Equation (19) for f at Dye 3 and using the result to stretch the axis in Figure 11 shows that, in contrast to GISP2, some sub-annual information survives firn diffusion at Dye 3 (Fig. 13). Reconstructions are possibly useful. Note, however, that melt occurs on the warmest days of summer at Dye 3 (Reference Herron, Herron and LangwayHerron and others, 1981). This melt does not penetrate deeply, so the dry-Era diffusion theory is also applicable here below the topmost meter. The denser layers produced by refreeze of the melt will hinder diffusion to some extent, probably reducing the effective value for ρ*, and strengthening our conclusion that reconstructions can be made accurately there. The melt should be explicitly considered in the interpretation of the reconstructed record, though. An excellent site for seasonal reconstructions in Antarctica is Law Dome (Reference Morgan and van OmmenMorgan and van Ommen, 1997). Here, the diffusion length at the firn base is approximately 0.08 m {Fig. 6; temperature and accumulation rate at Law Dome are approximately 21ÛC and 0.7 m a, respectively), a mere 11% of the annual layer thickness.
Examples of the coefficients in Equation (19) have been given in Table 1, together with equivalent times ti corrcsponding to 15 and 50 years of burial at GISP2. Very dry and cold sites like Vostok lose information rapidly due to the small accumulation rate. Siple Dome is an example of the worst possible location, one with a high temperature but relatively low accumulation rate. Of course, the high-accumulation sites in southern Greenland and on the Antarctic Peninsula have the best preservation. However, the presence of surface melt at such sites changes the interpretation of the reconstructed records. We suggest that to attain seasonal records that have been neither significantly influenced by melt nor corrupted irrecoverably by diffusion, a set of ice cores should be drilled at locations where the accumulation is as high as possible but the melt negligible. In Greenland, such a location would exist somewhere on the ice divide between GISP2 and Dye 3. In Antarctica, such locations may exist on local domes close to the coast.

Fig. 13. Estimated comparison of diffusional information loss at Dye 3, southern Greenland, arid GISP2, central Greenland.
Conclusion
The Reference Whillans and GrootesWhillans and Grootes (1985) theory for isotope diffusion in firn makes generally accurate predictions in central Greenland, demonstrating that diffusional vapor flux through firn pore spaces and the consequent smoothing of isotopic profiles is reasonably well understood. Central Greenland data suggest, but do not prove, that the diffusivity of water vapor in firn air is accurately predicted by the relations used by Whillans and Grootes, if one accounts for the increase of diffusivity at high altitude, and that the blocking effect of the solid matrix can be described by using an effective pore-isolation density of ρ* = 730 kg m−3.Comparison of model predictions with limited data from southern Greenland, the Antarctic Peninsula and the South Pole lend further credence to the vapor-flux diffusion model and our minor modifications to it.
Meaningful reconstructions of the shapes of annual isotope cycles at G1SP2 are not possible but may be possible at locations with substantially higher accumulation rates: e.g. Dye 3 in Greenland and Law Dome in Antarctica). Consequently, we will not be able to infer a history of precipitation seasonally at GISP2 using δ18O records alone. Reconstructions of seasonal amplitude are accurate to within about 10%, if there is little seasonal bias in the isotope record. However, without independent information about seasonal bias, one should not interpret changes in reconstructed amplitudes as changes in seasonal amplitude at the time of deposition but rather as a change in seasonal climate of uncertain nature. To recover seasonal isotopic records, ice cores should be drilled for this purpose at locations with as high an accumulation rate as possible without there being significant melt.
Acknowledgements
We thank M. Stuiver and P. Grootes for making available isotopic data from GISP2. and S. Johnsen and an anonymous reviewer for helpful comments. We also thank P. Lombard for valuable input, and R. Alley, B. Hallet, D. Morse, C. Raymond and E. Waddington for constructive criticisms, and P. Grootes for reading an earlier version of this paper. This paper is based, in part, on work done under a U.S. National Science Foundation Graduate Research Fellowship to K.C. (1992-94).

















